Какая точка лежит на прямой заданной уравнением

Глава 1. Уравнение прямой (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4

Глава 1. Уравнение прямой

Геометрия развивается по многим направлениям. Возникновение компьютеров привело к появлению такой области математики как вычислительная геометрия. При создании современных приложений часто требуется разработка эффективных алгоритмов для определения взаиморасположения различных объектов на плоскости, вычисления расстояний между ними, вычисления площадей фигур и др.

В данной главе излагается материал, частично известный вам из курса математики. Мы рассмотрим методы решения геометрических задач, которые эффективно реализуются с помощью компьютера, что позволит вам по другому взглянуть на вопросы, изучаемые в рамках школьного курса геометрии. Для этого придется воспользоваться аналитическим представлением геометрических объектов.

1. 1. Формы записи уравнения прямой

В задачах часто приходится задавать на плоскости различные геометрические объекты. Простейшими геометрическими фигурами на плоскости являются точка и прямая. Точка задается указанием своих координат, например A(15; –5), B(x1; y1). Прямую можно задавать с помощью уравнения прямой. Существуют различные формы записи уравнения прямой. Выбор какой-то конкретной зависит от исходных данных, задающих прямую на плоскости. (Могут быть заданы координаты двух точек, через которые проводится прямая, или коэффициенты при неизвестных в линейном уравнении).

В декартовых координатах каждая прямая определяется уравнением первой степени. Уравнение вида

называется общим уравнением прямой.

Если в общем уравнении прямой коэффициент при y не равен нулю, то уравнение можно разрешить относительно y:

Обозначая k = и b = ,

получаем уравнение вида y = kx + b. Если же B = 0, то уравнение имеет вид

Уравнение y = kx + b называется уравнением прямой с угловым коэффициентом; k – угловой коэффициент, b – величина отрезка, который отсекает прямая на оси Oy, считая от начала координат (рис. 1).

Уравнение y – y0 = k(x–x0) – это уравнение прямой с угловым коэффициентом k, которая проходит через точку с координатами (x0; y0).

Рассмотрим две точки с координатами (x1; y1) и (x2; y2), лежащие на прямой y = kx + b. Их координаты удовлетворяют уравнению прямой:

Вычитая из второго равенства первое, имеем y2 – y1 = k(x2 – x1), или

k =

Пусть точка с координатами (x; y) – произвольная точка на прямой, проходящей через точки с координатами (x1; y1) и (x2; y2) ( рис. 2 ). Тогда, с учетом того факта, что она имеет тот же коэффициент наклона, получаем

k =

= или =

=

является уравнением прямой, которая проходит через точки с координатами (x1; y1) и (x2; y2). Недостатком этой формулы является ее неопределенность при x1 = x2 и (или) y1 = y2. Поэтому ее лучше использовать в виде

Алгоритм для определения значений коэффициентов A, B, C общего уравнения прямой, проходящей через точки (x1; y1) и (x2; y2), будет следующим [1] :

C:= – x1*(y2 – y1)+y1*(x2 – x1)

Рассмотрим пример: x1 = 0, y1 = 0, x2 = 1, y2 = 2. Уравнение прямой, проходящей через точки (x1; y1) и (x2; y2) будет следующим:

C = –x1 * (y2 – y1) + y1 * (x2 – x1) = 0 * 2 + 0 * 1 = 0. ЌСледовательно, уравнение прямой будет иметь вид 2х – у = 0.

1. 2. Положение точек относительно прямой

Множество точек прямой, проходящей через две точки с координатами (x1; y1) и (x2; y2), удовлетворяет уравнению

Это значит, что если имеется точка с координатами (x0; y0) и (x0 – x1) * (y2 – y1) – (y0 – y1) * (x2 – x1) = 0, то эта точка лежит на прямой. B дальнейшем, вместо выражения (x – x1) * (y2 – y1) – (y – y1) * (x2 – x1) мы иногда будем использовать для краткости обозначение Ax + By + C или f(x1, y1, x2, y2, x, y).

Прямая Ax + By + C = 0, проходящая через две заданные точки с координатами (x1; y1) и (x2; y2), разбивает плоскость на две полуплоскости. Рассмотрим возможные значения выражения Ax + By + C.

1) Ax + By + C = 0 – определяет геометрическое место точек, лежащих на прямой.

Запишем алгоритм для определения, лежит ли точка с координатами (x3; y3) на прямой, проходящей через точки (x1; y1) и (x2; y2). Переменная P – переменная логического типа, которая имеет значение «истина», если точка лежит на прямой и «ложь» в противном случае.

если (x3 – x1)*(y2 – y1) – (y3 – y1)*(x2 – x1)=0

2) Ax + By + C > 0 – определяет геометрическое место точек, лежащих по одну сторону от прямой.

3) Ax + By + C рис. 3 точки (x3; y3) и (x4; y4) лежат по одну сторону от прямой, точки (x3; y3) и (x5; y5) по разные стороны от прямой, а точка (x6; y6) лежит на прямой.

Рассмотрим пример: x1 = 1, y1 = 2, x2 = 5, y2 = 6. Уравнение прямой, проходящей через точки (x1; y1) и (x2; y2), будет следующим:

Следовательно, уравнение прямой будет иметь вид 4х – 4у + 4 = 0 или x – y + 1 = 0. Подставим координаты точек (3; 4), (1; 1), (2; 0), (0; 2) в уравнение прямой. Получим:

1 * 3 – 1 * 4 + 1 = 0, 1 * 2 – 1 * 0 + 1 > 0,

1 * 1 – 1 * 1 + 1 > 0, 1 * 0 – 1 * 2 + 1 L:=»по одну»

Z1:=(x3 – x1)*(y2 – y1) – (y3 – y1)*(x2 – x1)

Z2:=(x4 – x1)*(y2 – y1) – (y4 – y1)*(x2 – x1)

½ то L:=»по разные» (1. 3)

1.3. Взаимное расположение двух отрезков

Пусть нам необходимо определить взаимное расположение двух отрезков. Отрезки на плоскости заданы координатами своих концевых точек. Предположим, что концевые точки одного из отрезков имеют координаты (x1; y1) и (x2; y2), а концевые точки другого – (x3; y3) и (x4; y4). Пусть общее уравнение первой прямой, проходящей через точки (x1;y1) и (x2;y2), имеет вид A1x + B1y + C1 = 0, а второй прямой, проходящей через точки (x3;y3) и (x4;y4), A2x + B2y + C2 = 0.

Определим расположение точек (x3; y3) и (x4; y4) относительно первой прямой. Если они расположены по одну сторону от прямой, то отрезки не могут пересекаться. Аналогично можно определить положение точек (x1; y1) и (x2; y2) относительно другой прямой.

Таким образом, если значения пары выражений Z1 = A1x3 + B1y3 + C1 и Z2 = A1x4 + B1y4 + C1 имеют разные знаки или Z1*Z2 = 0, а также пары Z3 = A2x1 + B2y1 + C2 и Z4 = A2x2 + B2y2 + C2 имеют разные знаки или Z3*Z4 = 0, то отрезки пересекаются. Если же значения пар выражений Z1 и Z2, или Z3 и Z4, имеют одинаковые знаки, то отрезки не пересекаются.

Различные случаи расположения отрезков показаны на рис. 4 .

На этом рисунке отрезки с концами в точках (x1; y1), (x2; y2) и (x4; y4), (x5; y5) пересекаются, отрезки с концами в точках (x1; y1), (x2; y2) и (x3; y3), (x4; y4) не пересекаются, а отрезки с концами в точках (x3; y3), (x4; y4) и (x4; y4) и (x5; y5) имеют общую вершину, что можно считать частным случаем пересечения.

Алгоритм для определения, пересекаются ли два отрезка с концами в точках (x1; y1), (x2; y2) и (x3; y3), (x4; y4) будет следующим:

Z1:=(x3 – x1)*(y2 – y1) – (y3 – y1)*(x2 – x1)

Z2:=(x4 – x1)*(y2 – y1) – (y4 – y1)*(x2 – x1)

Z3:=(x1 – x3)*(y4 – y3) – (y1 – y3)*(x4 – x3)

Z4:=(x2 – x3)*(y4 – y3) – (y2 – y3)*(x4 – x3)

Приведенный фрагмент алгоритма не учитывает крайней ситуации, когда два отрезка лежат на одной прямой. В этом случае (x3 – x1) * (y2 – y1) – (y3 – y1) * (x2 – x1) = 0 и (x4 – x1) * (y2 – y1) – (y4 – y1) * (x2 – x1) = 0.

На рис. 5 отрезки, лежащие на одной прямой не пересекаются, а на рис. 6 – отрезки пересекаются.

Для того, чтобы определить взаимное расположение таких отрезков, поступим следующим образом. Обозначим

Здесь k1 является левой, а k2 – правой точкой проекции первого отрезка (отрезка, заданного координатами (x1; y1), (x2; y2)) на ось Ox. Аналогично k3 является левой, а k4 – правой точкой проекции второго отрезка (отрезка, заданного координатами (x3; y3), (x4; y4)) на ось Ox. Аналогично ищем преокции на ось OY.

Отрезки, лежащие на одной прямой будут пересекаться тогда, когда их проекции на каждую ось пересекаются. (Следует заметить, что если проекции двух произвольных отрезков пересекаются, то это не значит, что и сами отрезки пересекаются, что видно на рис. 7 ).

Для определения взаимного расположения проекций на ось OX воспользуемся следующим фактом (см. рис. 5 и рис. 6 ): координата левой точки пересечения проекций Lx равна max(k1; k3), т. е. максимальной из координат левых точек проекций. Рассуждая аналогично для правых точек проекций, получим, что координата правой точки Rx пересечения равна min(k2; k4). Для того, чтобы отрезки пересекались, необходимо, чтобы левая координата пересечения проекций была не больше правой координаты пересечения отрезков (такой случай имеет место на рис. 5 , когда Lx = х3, а Rx = х2). Поэтому условием пересечения проекций является выполнение неравенства Lx £ Rx. Аналогично можно вычислить величины Lу и Rу, беря соответствующие проекции на ось Оу.

Следует отметить, что длина пересечения проекций в этом случае равна величине Lx– Rx (если Lx– Rx = 0, то проекции имеют только общую точку).

1.4. Точка пересечения отрезков

Для определения места пересечения отрезков (если известно, что они пересекаются), достаточно определить точку пересечения прямых, на которых эти отрезки лежат.

Пусть A1x + B1y + C1 = 0 является уравнением прямой, проходящей через концевые точки первого отрезка, а A2x + B2y + C2 = 0 является уравнением прямой, проходящей через концевые точки второго отрезка.

Тогда для определения точки пересечения отрезков достаточно решить систему уравнений

Домножив первое уравнение на A2, а второе уравнение на A1, получим

Вычитая из первого уравнения второе, можно найти значение y:

y =

Аналогично можно вычислить значение x:

x =

Это справедливо в случае, если выражение A2 * B1 – A1 * B2 ¹ 0. Но мы уже знаем, что отрезки пересекаются и не лежат на одной прямой. А это невозможно, если A2 * B1 – A1 * B2 = 0.

2.1 Расстояния между точками. Расстояние от точки до прямой

Расстояние между точками M1(x1; y1) и M2(x2; y2) на плоскости ( рис. 8 ) определяется по формуле

D = .

Расстояние от точки до прямой на плоскости определяется как длина отрезка перпендикуляра, опущенного из точки на прямую. Уравнение вида

,

где T = , причем С £ 0 (чего можно достигнуть изменением знака выражения), называется нормальным уравнением прямой. Это уравнение обладает тем свойством, что при подстановке координат произвольной точки в выражение (Ax + By + C)/T получается значение, по абсолютной величине равное расстоянию от точки до прямой ( рис. 9 ).

Запишем алгоритм для определения расстояния от точки (x3; y3) до прямой, проходящей через точки (x1; y1) и (x2; y2).

C:= – x1*(y2 – y1)+y1*(x2 – x1) (1. 5)

Рассмотрим пример: x1 = 0, y1 = 0, x2 = 3, y2 = 4 x3 = –1, y3 = 7. Уравнение прямой, проходящей через точки (x1; y1) и (x2; y2), будет следующим:

Т = = = = 5,

D = = = 5.

2.2. Расстояние между точкой и отрезком

Для определения расстояния между точкой и отрезком необходимо выяснить, пересекает ли перпендикуляр, опущенный из данной точки на прямую, проходящую через концы отрезка, сам отрезок. Если перпендикуляр пересекает отрезок, то расстояние между точкой и отрезком равно расстоянию между точкой и прямой, проходящей через отрезок. (Эту задачу вы уже умеете решать.)

Если перпендикуляр не пересекает отрезок, то расстояние между точкой и отрезком равно минимальному из расстояний между точкой и одним из концов отрезка.

Для определения взаимного расположения отрезка и перпендикуляра поступим следующим образом.

Рассмотрим треугольник, образованный тремя точками, две из которых (x1; y1) и (x2; y2) являются концами данного отрезка, а третья – данная точка с координатами (x3; y3) (см. рис. 10 , б, в). Конечно, может оказаться, что все точки лежат на одной прямой и такого треугольника не существует. В этом случае, однако, мы будем полагать, что треугольник существует, правда он вырожденный (особый). В вырожденном треугольнике длины сторон могут быть равными 0 (см. рис. 10 , а).

Более того, мы будем полагать, что данный отрезок является основанием рассматриваемого треугольника (см. рис. 10 , б, в).

При таких предположениях для решения исходной задачи нам достаточно определить, является ли один из углов при основании тупым или нет. Действительно, если один из углов при основании является тупым, то перпендикуляр, опущенный из вершины, соответствующей исходной точке, не попадает на основание (отрезок). Иначе перпендикуляр, опущенный из вершины, соответствующей исходной точке, попадает на основание (отрезок).

Для решения последней задачи воспользуемся следующим свойством. Пусть a, b, c – длины сторон треугольника, причем с – длина основания. Тогда треугольник является тупоугольным при основании, если

Поэтому, вычислив значения квадратов длин сторон, нетрудно определить, пересекает ли перпендикуляр, опущенный из точки (x3; y3) на прямую, отрезок с концами в точках (x1; y1) и (x2; y2). И если не пересекает, то расстояние от точки до отрезка равно минимуму из величин a, b. Если же пересекает, то необходимо воспользоваться свойством нормального уравнения прямой .

§ 3. Многоугольники

3.1. Виды многоугольников

Ломаной называется фигура, которая состоит из точек A1, A2, . An и соединяющих их отрезков A1A2, A2A3, . An – 1An ( рис. 11 , а). Точки называются вершинами ломаной, а отрезки – звеньями. Наиболее распространенным способом задания ломаной является использование таблицы, элементы которой соответствуют координатам вершин ломаной в порядке ее обхода из одного конца в другой. Длиной ломаной называется сумма длин ее звеньев.

Многоугольником называется замкнутая ломаная линия без самопересечений (рис. 11, б).

Плоским многоугольником называется конечная часть плоскости, ограниченная многоугольником (рис. 11, в).

Обход плоского многоугольника называется положительным, если при обходе область расположена по левую руку, и отрицательным, если область остается по правую руку.

Расстояние между фигурами на плоскости определяется как длина минимального отрезка, один конец которого принадлежит одной фигуре, а второй конец – другой фигуре.

3.2. Выпуклость многоугольников

Многоугольник является выпуклым, если для каждой прямой, проходящей через любую его сторону, все остальные вершины лежат в одной полуплоскости относительно прямой. Проверим для каждой прямой, проходящей через вершины (x1; y1) и (x2; y2), (x2; y2) и (x3; y3), . (xn – 1; yn – 1) и (xn; yn), (xn; yn) и (x1; y1) взаимное расположение вершин многоугольника. Если они каждый раз расположены в одной полуплоскости относительно проведенной прямой, то многоугольник выпуклый. Если же найдется прямая, проходящая через одну из сторон, и пара вершин многоугольника, лежащих по разные стороны относительно проведенной прямой, то многоугольник не является выпуклым. Случаи выпуклого и невыпуклого многоугольников изображены на рис. 12.

Можно заметить, что для каждой прямой, проходящей через вершины (x1; y1) и (x2; y2), (x2; y2) и (x3; y3), . (xn – 1; yn – 1) и (xn; yn), (xn; yn) и (x1; y1) достаточно ограничится определением взаимного расположения вершин многоугольника (xn; yn) и (x3; y3), (x1; y1) и (x4; y4), . (xn – 2; yn – 2) и (x1; y1), (xn – 1; yn – 1) и (x2; y2), соответственно. Если они каждый раз расположены в одной полуплоскости относительно проведенной прямой, то многоугольник выпуклый. Если же найдется прямая и пара вершин многоугольника, лежащих по разные стороны относительно проведенной прямой, то многоугольник не является выпуклым. Поэтому для определения, является ли многоугольник выпуклым, достаточно воспользоваться алгоритмом

нц для i от 1 до n

½ j:= mod( i, n +1 ) : номер вершины после вершины i

½ k:= mod (j, n +1) : номер вершины после вершины j

½½ то m:=n : номер вершины перед вершиной i

Уравнения прямой в пространстве — это уравнения двух пересекающихся плоскостей

В данном разделе продолжим изучение темы уравнения прямой в пространстве с позиции стереометрии. Это значит, что мы будем рассматривать прямую линию в трехмерном пространстве как линию пересечения двух плоскостей.

Согласно аксиомам стереометрии, если две плоскости не совпадают и имеют одну общую точку, то они также имею одну общую прямую, на которой лежат все точки, которые являются общими для двух плоскостей. Используя уравнения двух пересекающихся плоскостей, мы можем определить прямую линию в прямоугольной системе координат.

По ходу рассмотрения темы приведем многочисленные примеры, ряд графических иллюстраций и развернутых решений, необходимых для лучшего усвоения материала.

Уравнения двух плоскостей, задающих прямую линию в пространстве

Пусть даны две плоскости, которые не совпадают между собой и пересекаются. Обозначим их как плоскость α и плоскость β . Разместим их в прямоугольной системе координат O х у z трехмерного пространства.

Как мы помним, любую плоскость в прямоугольной системе координат задает общее уравнение плоскости вида A x + B y + C z + D = 0 . Будем считать, что плоскости α соотвествует уравнение A 1 x + B 1 y + C 1 z + D 1 = 0 , а плоскости β уравнение A 2 x + B 2 y + C 2 z + D 2 = 0 . В этом случае нормальные вектора плоскостей α и β n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) не коллинеарны, так как плоскости не совпадают между собой и е размещаются параллельно друг другу. Запишем это условие следующим образом:

n 1 → ≠ λ · n 2 → ⇔ A 1 , B 1 , C 1 ≠ λ · A 2 , λ · B 2 , λ · C 2 , λ ∈ R

Чтобы освежить в памяти материал по теме «Параллельность плоскостей», смотрите соответствующий раздел нашего сайта.

Линию пересечения плоскостей обозначим буквой a . Т.е. a = α ∩ β . Эта прямая представляет собой множество точек, которые являются общими для обеих плоскостей α и β . Это значит, что все точки прямой линии a удовлетворяют обоим уравнениям плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . Фактически, они являются частным решением системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .

Общее решение системы линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 определяет координаты всех точек линии, по которой происходит пересечение двух плоскостей α и β . Это значит, что с его помощью мы можем определить положение прямой в прямоугольной системе координат O x y z .

Рассмотрим описанную теорию еще раз, теперь уже на конкретном примере.

Прямая O x – это прямая, по которой пересекаются координатные плоскости O x y и O x z . Зададим плоскость O x y уравнением z = 0 , а плоскость O x z уравнением у = 0 . Такой подход мы подробно разобрали в разделе «Неполное общее уравнение плоскости», так что, в случае затруднений, можно обратиться к этому материалу повторно. В этом случае координатная прямая O x определяется в трехмерной системе координат системой из двух уравнений вида y = 0 z = 0 .

Нахождение координат точки, лежащей на прямой, по которой пересекаются плоскости

Рассмотрим задачу. Пусть в трехмерном пространстве задана прямоугольная система координат O х у z . Линия, по которой пересекаются две плоскости a , задана системой уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 . Дана точка трехмерного пространства M 0 x 0 , y 0 , z 0 .

Давайте определим, принадлежит ли точка M 0 x 0 , y 0 , z 0 заданной прямой линии a .

Для того, чтобы получить ответ на вопрос задачи, подставим координаты точки М 0 в каждое из двух уравнений плоскости. Если в результате подстановки оба уравнения превратятся в верные равенства A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 , то точка М 0 принадлежит каждой из плоскостей и принадлежит заданной линии. Если хотя бы одно из равенств A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 окажется неверным, то точка М 0 не принадлежит прямой линии.

Рассмотрим решение примера

Прямая линия задана в пространстве уравнениями двух пересекающихся плоскостей вида 2 x + 3 y + 1 = 0 x — 2 y + z — 3 = 0 . Определите, принадлежат ли точки M 0 ( 1 , — 1 , 0 ) и N 0 ( 0 , — 1 3 , 1 ) прямой линии пересечения плоскостей.

Решение

Начнем с точки М 0 _. Подставим ее координаты в оба уравнения системы 2 · 1 + 3 · ( — 1 ) + 1 = 0 1 — 2 · ( — 1 ) + 0 — 3 = 0 ⇔ 0 = 0 0 = 0 .

В результате подстановки мы получили верные равенства. Это значит, что точка М 0 принадлежит обеим плоскостям и расположена на линии их пересечения.

Подставим в оба уравнения плоскости координаты точки N 0 ( 0 , — 1 3 , 1 ) . Получаем 2 · 0 + 3 · — 1 3 + 1 = 0 0 — 2 · — 1 3 + 1 — 3 = 0 ⇔ 0 = 0 — 1 1 3 = 0 .

Как вы видите, второе уравнение системы превратилось в неверное равенство. Это значит, что точка N 0 не принадлежит заданной прямой.

Ответ: точка М 0 принадлежит прямой линии, а точка N 0 не принадлежит.

Теперь предлагаем вам алгоритм нахождения координат некоторой точки, принадлежащей прямой линии, если прямая в пространстве в прямоугольной системе координат O x y z определяется уравнениями пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .

Количество решений системы из двух линейных уравнений с темя неизвестными A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 бесконечно. Любое из этих решений может стать решением задачи.

Пусть в трехмерном пространстве задана прямая линия уравнениями двух пересекающихся плоскостей вида x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 . Найдите координаты любой из точек этой прямой.

Решение

Перепишем систему уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 ⇔ x + 0 y + 3 z = — 7 2 x + 3 y + 3 z = — 2 .

Возьмем отличный от нуля минор второго порядка в качестве базисного минора основной матрицы системы 1 0 2 3 = 3 ≠ 0 . Это значит, что z – это свободная неизвестная переменная.

Перенесем слагаемые, содержащие свободную неизвестную переменную z в правые части уравнений:

x + 0 y + 3 z = — 7 2 x + 3 y + 3 z = — 2 ⇔ x + 0 y = — 7 — 3 z 2 x + 3 y = — 2 — 3 z

Введем произвольное действительное число λ и примем, что z = λ .

Тогда x + 0 y = — 7 — 3 z 2 x + 3 y = — 2 — 3 z ⇔ x + 0 y = — 7 — 3 λ 2 x + 3 y = — 2 — 3 λ .

Для решения полученной системы уравнений применим метод Крамера:

∆ = 1 0 2 3 = 1 · 3 — 0 · 1 = 2 ∆ x = — 7 — 3 λ 0 — — 3 λ 3 = — 7 — 3 λ · 3 — 0 · ( — 2 — 3 λ ) = 21 — 9 λ ⇒ x = ∆ x ∆ = — 7 — 3 λ ∆ y = 1 — 7 — 3 λ 2 — 2 — 3 λ = 1 · — 2 — 3 λ — — 7 — 3 λ · = 12 + 3 λ ⇒ y = ∆ y ∆ = 4 + λ

Общее решение системы уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 будет иметь вид x = — 7 — 3 λ y = 4 + λ z = λ , где λ ∈ R .

Для получения частного решения системы уравнений, которое даст нам искомые координаты точки, принадлежащей заданной прямой, нам необходимо взять конкретное значение параметра λ . Если λ = 0 , то x = — 7 — 3 · 0 y = 4 + 0 z = 0 ⇔ x = — 7 y = 4 z = 0 .

Это позволяет нам получить координаты искомой точки — 7 , 4 , 0 .

Проверим верность найденных координат точки методом подстановки их в исходные уравнения двух пересекающихся плоскостей — 7 + 3 · 0 + 7 = 0 2 · ( — 7 ) + 3 · 4 + 3 · 0 + 2 = 0 ⇔ 0 = 0 0 = 0 .

Ответ: — 7 , 4 , 0

Направляющий вектор прямой, по которой пересекаются две плоскости

Давайте рассмотрим, как определить координаты направляющего вектора прямой, которая задана уравнениями двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . В прямоугольной системе координат 0хуz направляющий вектор прямой неотделим от прямой линии.

Как мы знаем, прямая перпендикулярна по отношению к плоскости в том случае, когда она перпендикулярна по отношению к любой прямой, лежащей в данной плоскости. Исходя из вышесказанного, нормальный вектор плоскости перпендикулярен любому ненулевому вектору, лежащему в данной плоскости. Эти два факта помогут нам в нахождении направляющего вектора прямой.

Плоскости α и β пересекаются по линии a . Направляющий вектор a → прямой линии a расположен перпендикулярно по отношению к нормальному вектору n 1 → = ( A 1 , B 1 , C 1 ) плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и нормальному вектору n 2 → = ( A 2 , B 2 , C 2 ) плоскости A 2 x + B 2 y + C 2 z + D 2 = 0 .

Направляющий вектор прямой a представляет собой векторное произведение векторов n → 1 = ( A 1 , B 1 , C 1 ) и n 2 → = A 2 , B 2 , C 2 .

a → = n → 1 × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2

Зададим множество всех направляющих векторов прямой как λ · a → = λ · n 1 → × n 2 → , где λ — это параметр, который может принимать любые действительные значения, отличные от нуля.

Пусть прямая в пространстве в прямоугольной системе координат O х у z задана уравнениями двух пересекающихся плоскостей x + 2 y — 3 z — 2 = 0 x — z + 4 = 0 . Найдем координаты любого направляющего вектора этой прямой.

Решение

Плоскости x + 2 y — 3 z — 2 = 0 и x — z + 4 = 0 имеют нормальные векторы n 1 → = 1 , 2 , — 3 и n 2 → = 1 , 0 , — 1 . Примем за направляющий вектор прямой линии, являющейся пересечением двух заданных плоскостей, векторное произведение нормальных векторов:

a → = n → 1 × n 2 → = i → j → k → 1 2 — 3 1 0 — 1 = i → · 2 · ( — 1 ) + j → · ( — 3 ) · 1 + k → · 1 · 0 — — k → · 2 · 1 — j → · 1 · ( — 1 ) — i → · ( — 3 ) · 0 = — 2 · i → — 2 j → — 2 k →

Запишем ответ в координатной форме a → = — 2 , — 2 , — 2 . Тем, кто не помнит, как это делается, рекомендуем обратиться к теме «Координаты вектора в прямоугольной системе координат».

Ответ: a → = — 2 , — 2 , — 2

Переход к параметрическим и каноническим уравнениям прямой в пространстве

Для решения ряда задач проще использовать параметрические уравнения прямой в пространстве вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ или канонические уравнения прямой в пространстве вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ . В этих уравнениях a x , a y , a z — координаты направляющего вектора прямой, x 1 , y 1 , z 1 — координаты некоторой точки прямой, а λ — параметр, принимающий произвольные действительные значения.

От уравнения прямой вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 можно перейти к каноническим и параметрическим уравнениям прямой линии в пространстве. Для записи канонических и параметрических уравнений прямой нам понадобятся навыки нахождения координат некоторой точки прямой, а также координат некоторого направляющего вектора прямой, заданной уравнениями двух пересекающихся плоскостей.

Рассмотрим написанное выше на примере.

Зададим прямую линию в трехмерной системе координат уравнениями двух пересекающихся плоскостей 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 . Напишем канонические и параметрические уравнения этой прямой.

Решение

Найдем координаты направляющего вектора прямой, который является векторным произведением нормальных векторов n 1 → = 2 , 1 , — 1 плоскости 2 x + y — z — 1 = 0 и n 2 → = ( 1 , 3 , — 2 ) плоскости x + 3 y — 2 z = 0 :

a → = n 1 → × n 2 → = i → j → k → 2 1 — 1 1 3 — 2 = i → · 1 · ( — 2 ) + j → · ( — 1 ) · 1 + k → · 2 · 3 — — k → · 1 · 1 — j → · 2 · ( — 2 ) — i → · ( — 1 ) · 3 = i → + 3 · j → + 5 · k →

Координаты направляющего вектора прямой a → = ( 1 , 2 , 5 ) .

Следующим шагом является определение координат некоторой точки заданной прямой линии, которыми является одно из решений системы уравнений: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ 2 x + y — z = 1 x + 3 y — 2 z = 0 .

Возьмем в качестве минорной матрицы системы определитель 2 1 1 3 = 2 · 3 — 1 · 1 = 5 , который отличен от нуля. В этом случае переменная z является свободной. Перенесем слагаемые с ней в правые части каждого уравнения и придаем переменной произвольное значение λ :

2 x + y — z = 1 x + 3 y — 2 z = 0 ⇔ 2 x + y = 1 + z x + 3 y = 2 z ⇔ 2 x + y = 1 + λ x + 3 y = 2 λ , λ ∈ R

Применяем для решения полученной системы уравнений метод Крамера:

∆ = 2 1 1 3 = 2 · 3 — 1 · 1 = 5 ∆ x = 1 + λ 1 2 λ 3 = ( 1 + λ ) · 3 — 1 · 2 λ = 3 + λ ⇒ x = ∆ x ∆ = 3 + λ 5 = 3 5 + 1 5 · λ ∆ y = 2 1 + λ 1 2 λ = 2 · 2 λ — ( 1 + λ ) · 1 = — 1 + 3 λ ⇒ y = ∆ y ∆ = — 1 + 3 λ 5 = — 1 5 + 3 5 · λ

Получаем: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ x = 3 5 + 1 5 y = — 1 5 + 3 5 z = λ

Примем λ = 2 для того, чтобы получить координаты точки прямой линии: x 1 = 3 5 + 1 5 · 2 y 1 = — 1 5 + 3 5 · 2 z 1 = 2 ⇔ x 1 = 1 y 1 = 1 z 1 = 2 . Теперь мы имеем достаточно данных для того, чтобы записать канонические и параметрические уравнения данной прямой в пространстве: x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ x — 1 1 = y — 1 3 = z — 2 5 x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ x = 1 + 1 · λ y = 1 + 3 · λ z = 2 + 5 · λ ⇔ x = 1 + λ y = 1 + 3 · λ z = 2 + 5 · λ

Ответ: x — 1 1 = y — 1 3 = z — 2 5 и x = 1 + λ y = 1 + 3 · λ z = 2 + 5 · λ

Данная задача имеет еще один способ решения.

Нахождение координат некоторой точки прямой проводится при решении системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .

В общем случае ее решения можно записать в виде искомых параметрических уравнений прямой в пространстве x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ .

Получение канонических уравнений проводится следующим образом: решаем каждое из полученных уравнений относительно параметра λ , приравниваем правые части равенства.

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y λ = z — z 1 a z ⇔ x — x 1 a x = y — y 1 a y = z — z 1 a z

Применим данный способ к решению задачи.

Зададим положение прямой линии уравнениями двух пересекающихся плоскостей 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 . Напишем параметрическое и каноническое уравнения для этой прямой линии.

Решение

Решение системы из двух уравнений с тремя неизвестными проводится аналогично тому, как мы делали это в предыдущем примере. Получаем: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ x = 3 5 + 1 5 · λ y = — 1 5 + 3 5 · λ z = λ .

Это параметрические уравнения прямой в пространстве.

Канонические уравнения получаем следующим образом: x = 3 5 + 1 5 · λ y = — 1 5 + 3 5 · λ z = λ ⇔ λ = x — 3 5 1 5 λ = y + 1 5 3 5 λ = z 1 ⇔ x — 3 5 1 5 = y + 1 5 3 5 = z 1

Полученные в обоих примерах уравнения отличаются внешне, однако они эквивалентны, так как определяют одно и то же множество точек трехмерного пространства, а следовательно и одну и ту же прямую линию.

Ответ: x — 3 5 1 5 = y + 1 5 3 5 = z 1 и x = 3 5 + 1 5 · λ y = — 1 5 + 3 5 · λ z = λ

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2

Вступление

Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.

Начнем с взаимного расположения точки относительно прямой, луча и отрезка.

Задача №1

Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.

Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P₁(x₁, y₁), P₂(x₂, y₂). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P₁P₂ и P₁M и по его знаку сделать вывод.

Задача №2

Определить принадлежит ли точка лучу.

Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P₁(x₁, y₁) — начало луча, а P₂(x₂, y₂) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.

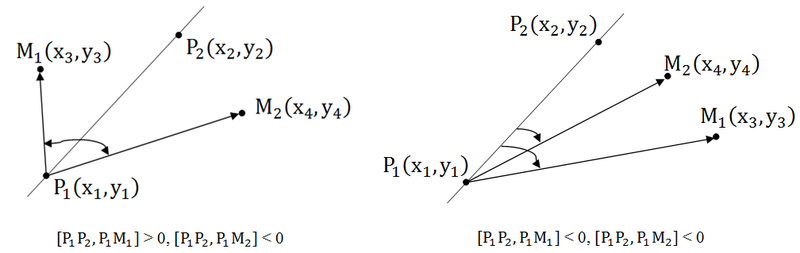
Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P₁(x₁, y₁), где P₂(x₂, y₂) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (P₁P₂, P₁M) ≥ 0 – скалярное произведение (точка лежит на луче)

Задача №3

Определить принадлежит ли точка отрезку.

Решение
Пусть точки P₁(x₁, y₁), P₂(x₂, y₂) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P₁, P₂. Далее нам нужно определить лежит ли точка между точками P₁ и P₂, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP₁, MP₂). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P₁(x₁, y₁), P₂(x₂, y₂) необходимо и достаточно выполнения условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (MP₁,MP₂) ≤ 0 – скалярное произведение (точка лежит между P₁ и P₂)

Задача №4

Взаимное расположение двух точек относительно прямой.

Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.

Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] 0 – точки лежат по одну сторону.
3. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] = 0 – одна (или две) из точек лежит на прямой.

Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] ≤ 0.

Задача №5

Определить пересекаются ли две прямые.

Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0. Тогда условие параллельности прямых заключается в том, что a₁b₂ — a₂b₁ = 0.
Если же прямые заданы точками P₁(x₁, y₁), P₂(x₂, y₂), M₁(x₃, y₃), M₂(x₄, y₄), то условие их параллельности заключается в проверки косого произведения векторов P₁P₂ и M₁M₂: если оно равно нулю, то прямые параллельны.

В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b₁, a₁), (-b₂, a₂) которые называются направляющими векторами.

Задача №6

Определить пересекаются ли два отрезка.

Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:

Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P₁P₂, P₁M₂] > 0, [P₁P₂, P₁M₁] [P₁P₂, P₁M₂] * [P₁P₂, P₁M₁] 2 + b 2 ).

Задача №8

Расстояние от точки до луча.

Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.

В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.

Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP₁P₂ – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
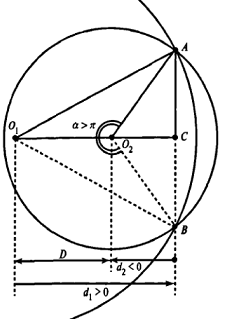
1. (P₁M, P₁P₂) 2 .

Теперь рассмотрим случай, когда центр второго круга O₂ находится между точками O₁ и C. В этом случае получим отрицательное значение величины d₂. Использование отрицательного значения d₂ приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.

Заключение

Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.