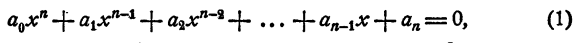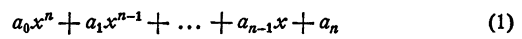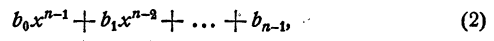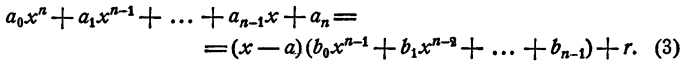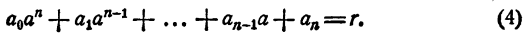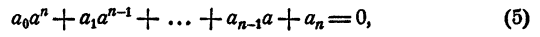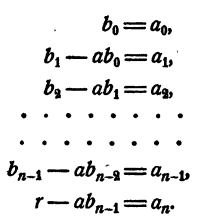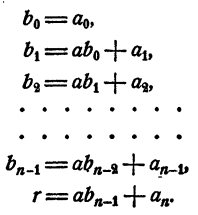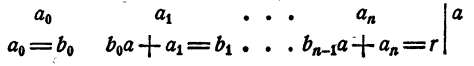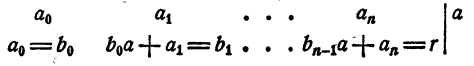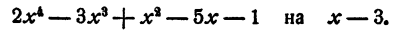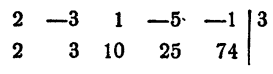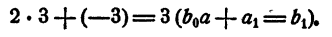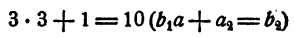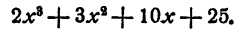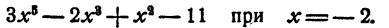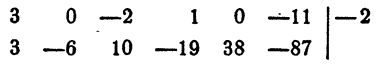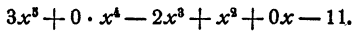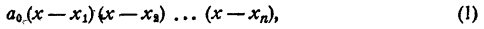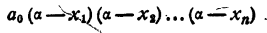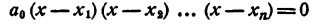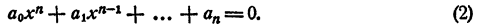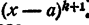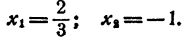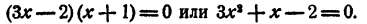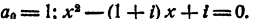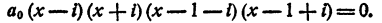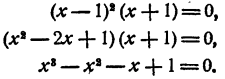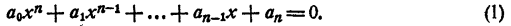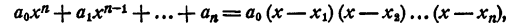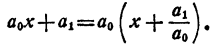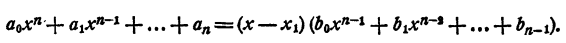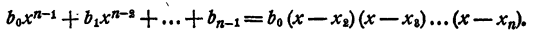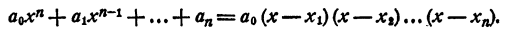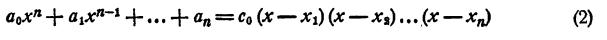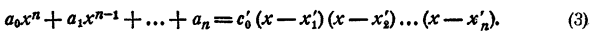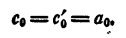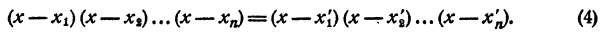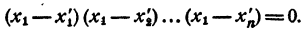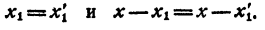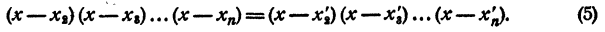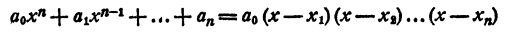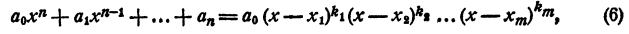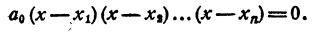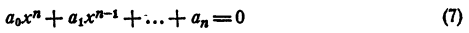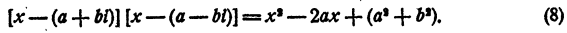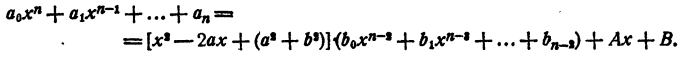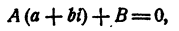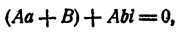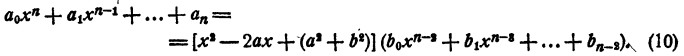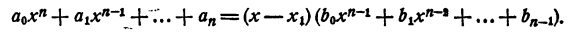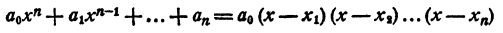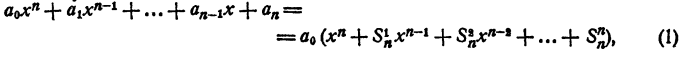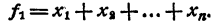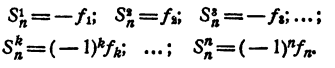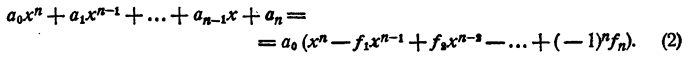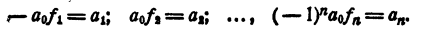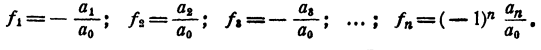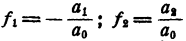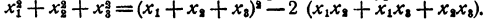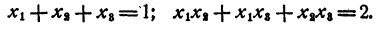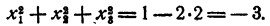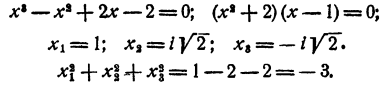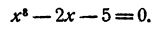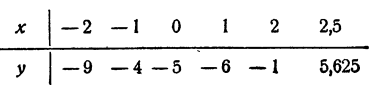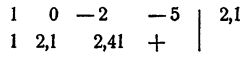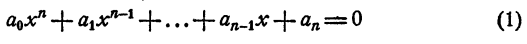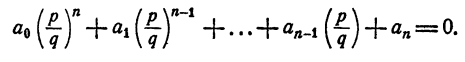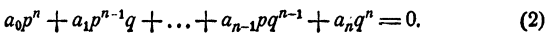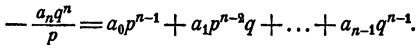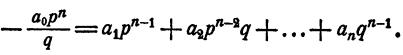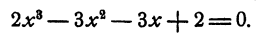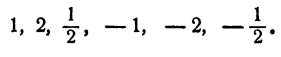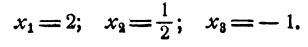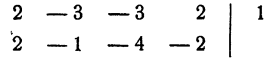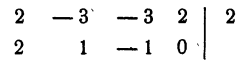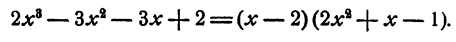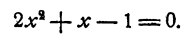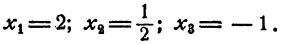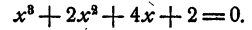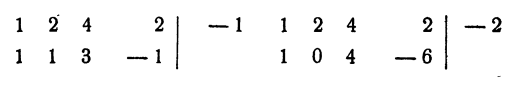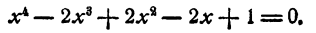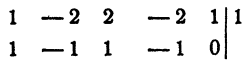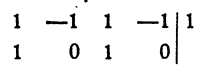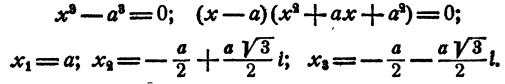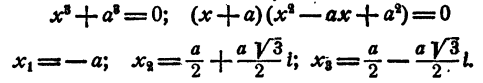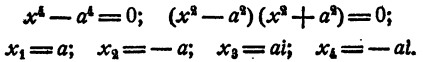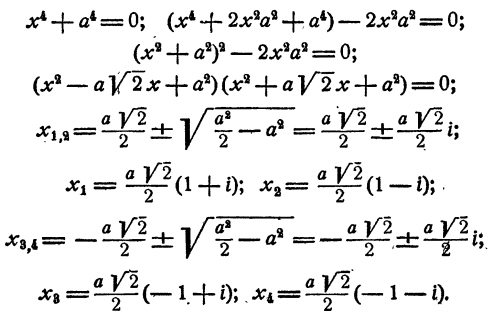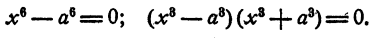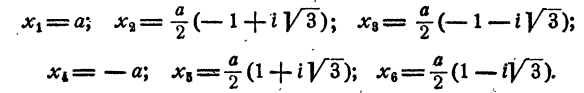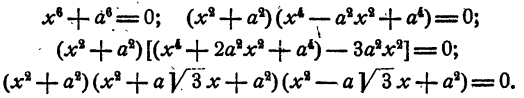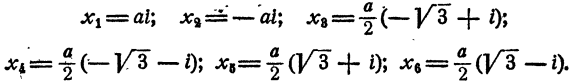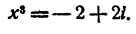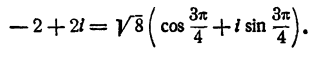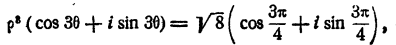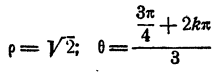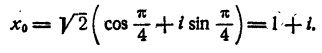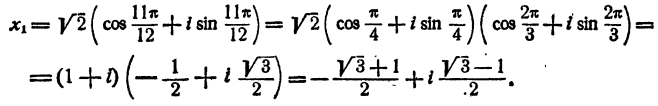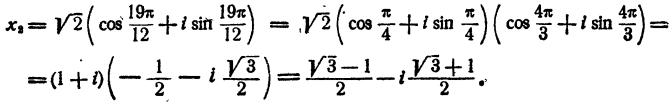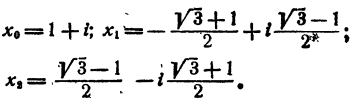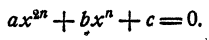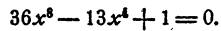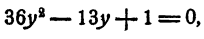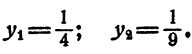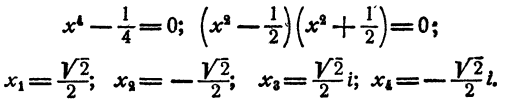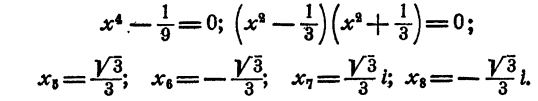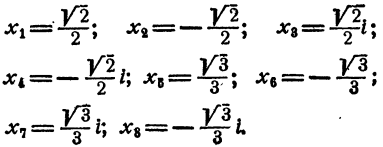Какие корни имеет уравнение xn a

Определение. Арифметическим корнем n-й степени из числа a называют неотрицательное число, n-я степень которого равна а.

Арифметический корень обозначают n √a. Число n называют показателем корня, а само число a — подкоренным выражением. Знак корня √ называют радикалом.

При четных n функция f(x)=x n четна, следовательно, если a>0, то уравнение x n =a кроме корня x₁= n √a, имеет так же корень x₂=- n √a. Если a=0, то корень всего один: x=0. Если a n возрастает на всей числовой прямой, ее область значений — множество всех действительных чисел. Применяя теорему о корне, находим, что уравнение x n =a имеет один корень для любого значения a, и, в частности, при a n √a.

Резюмируя вышесказанное, можно сделать вывод: принечетном n существует корень n-й степени из любого числа a и притом только один.

Для корней нечетной степени справедливо равенство:

n √-a=— n √a

Доказывается это равенство просто.
(- n √a) n =(-1) n ( n √a) n =-1*a=-a, то есть число — n √a есть корень n-й степени из -а, но такой корень при нечетном n единственный, следовательно n √-a=- n √a.

Вышеприведенное равенство поволяет выражать и вычислять корни с нечетной степенью из отрицательных чисел.

Для любого действительного x: n √a n = |x|, если n четно; n √a n = x, если n нечетно.

Считают, что корень первой степени из числа равен этому же числу. Квадратным корнем называют корень второй степени (при этом показатель степени опускают и пишут просто знак радикала). Корень третьей степени называют кубическим корнем.

РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Простейшими тригонометрическими уравнениями называют уравнения

Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.

19.1. Уравнение cos x = a

Объяснение и обоснование

Корни уравненияcosx=a.

2.Частые случаи решения уравнения sin x = a.

Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).

Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда

Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,

Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,

Примеры решения задач

Замечание. Ответ к задаче 1 часто записывают в виде:

19.3. Уравнения tg x = a и ctg x = a

Объяснение и обоснование

1.Корни уравнений tg x = a и ctg x = a

Рассмотрим уравнение tg x = a. На промежутке функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x₁ = arctg a и для этого корня tg x = a.

Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения tg x = a:

При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈ Z).

Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞). Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x₁=arсctg a.

Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения ctg x = a:

таким образом, уравнение ctg x = 0 имеет корни

Примеры решения задач

Вопросы для контроля

Какие уравнения называют простейшими тригонометрическими?
Запишите формулы решения простейших тригонометрических уравнений. В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
Выведите формулы решения простейших тригонометрических уравнений.
Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.

Упражнения

Решите уравнение (1-11)

Найдите корни уравнения на заданном промежутке (12-13)

Уравнения высших степеней в математике с примерами решения и образцами выполнения

Уравнение n-й степени с одним неизвестным:

Определение:

Уравнением n-й степени с одним неизвестным х называется уравнение

где 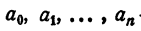— любые комплексные числа, а₀ ≠ 0, n— натуральное.

Изучение уравнения (1) в общем виде выходит за рамки школьного курса алгебры. В этой главе рассматриваются лишь некоторые свойства уравнения (1) и, кроме того, изучаются некоторые его частные виды.

Деление многочлена относительно х на х—а

Теорема:

Остаток от деления многочлена относительно х на двучлен х — а равен значению этого многочлена при х, равном а.

Доказательство:

Разделим многочлен n-й степени

на двучлен х — а. Как известно, частным (неполным) в этом случае будет многочлен n— 1 степени

а остатком — некоторое число r. Так как делимое равно делителю, умноженному на частное, плюс остаток, то

Равенство (3) есть тождество, оно справедливо при любых значениях х. В частности, оно справедливо и при х = а. При х = а. первое слагаемое правой части равенства (3) обращается в нуль, а потому

Следствие:

Для того чтобы многочлен относительно х делился на двучлен х — а, необходимо и достаточно, чтобы число а было корнем этого многочлена, т. е. чтобы при х = а многочлен обращался в нуль.

Доказательство:

Необходимость:

Пусть многочлен (1) делится на х — а, т. е. остаток r равен нулю. Тогда на основании равенства (4)

т. е. а — корень многочлена (1).

Достаточность:

Пусть а — корень многочлена (1), т. е. имеет место равенство (5). Тогда на основании равенства (4) r = 0, т. е. многочлен (1) делится на двучлен х — а.

Рассмотрим вновь тождество (3). Если в правой части его раскрыть скобки и сделать приведение подобных членов, в результате должен получиться тот же многочлен, что и в левой части. На этом основании, приравнивая коэффициенты при одинаковых степенях х, получаем

Перепишем эти равенства так:

Полученные равенства показывают, что коэффициенты частного и остаток, т. е. , удобно вычислять последовательно одно за другим. Эти вычисления обычно располагают следующим образом:

Пример:

Решение:

Первый коэффициент 2 второй строки просто сносится (b₀ = а₀). Второй коэффициент 3 получен так:

Третий коэффициент 10 получен так:

и т. д. Неполное частное равно

Пример:

Найти значение многочлена

Решение:

Искомое значение многочлена равно остатку от деления многочлена на x + 2

В двух местах первой строки потребовалось вписать 0. Объясняется это тем, что делимое имеет следующий вид:

Обычно члены, коэффициенты которых равны нулю, пропускаются. Здесь их пропускать нельзя.

Составление уравнения n-й степени по его корням

Теорема:

Каковы бы ни были числа можно составить уравнение n-й степени, корнями которого будут эти числа и только они. Доказательство. Составим произведение

где a₀ — любое число, отличное от нуля. При x = x₁ двучлен x — x₁ обращается в нуль, значит, при этом значении х обращается в нуль и произведение (1). При х = х₂ обращается в нуль двучлен х — x₂, и опять произведение (1) обращается в нуль. То же самое происходит при х =x₃; х = хₙ.

Пусть теперь х = а, где a — число, отличное от x₁ x₂ , …., хₙ . Ни одна из разностей а— x₁ а— x₂ ,…..о— хₙ „ не равна нулю. Число а₀ тоже отлично от нуля. Значит, и произведение

отлично от нуля.

Таким образом, уравнение

имеет корнями x₁ x₂ , …., хₙ и только эти числа.

Раскрыв скобки и выполнив приведение подобных членов, получим в левой части уравнения многочлен n-й степени относительно х, т. е.

Корнями уравнения (2) являются числа x₁ x₂ , …., хₙ и только эти числа.

Возможно, что корни x₁ x₂ , …., хₙ уравнения (2) не все различны между собой. В этих случаях говорят, что уравнение (2) имеет кратные корни. Так, например, если x₁ = x₂ и отлично от других корней уравнения (2), число является корнем второй кратности уравнения (2). Левая часть уравнения (2) делится в этом случае на (x — x₁ )³ и не делится на (х — x₁)³. Если x₁ = x₂ = x₃ и отлично от других корней уравнения (2), число x₁ является корнем третьей кратности уравнения (2). Левая часть уравнения (2) делится в этом случае на (х — x₁ )³ и не делится на (х— x₁ )⁴.

Вообще корнем кратности k уравнения (2) называется такое число а, что левая часть уравнения (2) делится на (х — а)ᵏ и не делится на

Пример:

Составить уравнение второй степени, корни которого

Решение:

. Положим а₀ = 3. Имеем

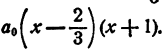
Пример:

Составить уравнение второй степени, корни которого x₁ = 1; х₂ =i.

Решение:

Положим

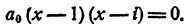
Пример:

Составить уравнение четвертой степени, корни которого i; —i; 1+i; 1-i

Решение:

Пример:

Составить уравнение третьей степени, корни которого x₁ = 1; х₂ = 1; х₃ = — 1.

Решение:

. Положим а₀ = 1.

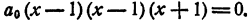
Число единица является здесь корнем второй кратности,

Основная теорема алгебры и некоторые следствия из нее

Мы видели, что, выбрав произвольные п комплексных чисел, можно составить уравнение п-й степени, корнями которого будут выбранные числа. Коэффициенты этого уравнения могут при -этом оказаться как вещественными, так и мнимыми. Возникает следующий весьма важный вопрос.

Дано уравнение n-й степени с комплексными коэффициентами

Можно ли утверждать, что среди комплексных чисел найдется хоть одно число, являющееся корнем этого уравнения?

В свое время мы видели, что среди целых чисел нет числа, являющегося корнем уравнения 2х— 3 = 0 с целыми коэффициентами. Среди положительных чисел нет числа, являющегося корнем уравнения x+ 1 = 0 с положительными коэффициентами.

Среди рациональных чисел нет числа, являющегося корнем уравнения x² — 2 = 0 с рациональными коэффициентами. Среди действительных чисел нет числа, являющегося корнем уравнения x²+ 1 = 0 с действительными коэффициентами.

Понятно поэтому, сколь важное значение имеет поставленный вопрос. Ответ на него дает основная теорема алгебры.

Всякое уравнение n-й степени с любыми комплексными коэффициентами имеет комплексный корень.

Доказательство этой теоремы выходит за рамки школьной программы.

Теорема:

Всякий многочлен n-й степени с любыми комплексными коэффициентами может быть представлен и притом единственным образом в виде произведения п двучленов первой степени, т. е.

где a ≠ 0, n ≥ 1. (Два таких разложения, отличающиеся только порядком расположения множителей, не считаются различными.)

Доказательство:

Доказательство разбивается на две части. В первой части доказывается возможность представления многочлена n-й степени в виде произведения п двучленов первой степени, во второй—единственность такого представления.

Для n = 1 теорема верна, так как

Предположим, что теорема справедлива для многочленов степени n—1.

Согласно основной теореме алгебры многочлен 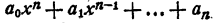имеет по крайней мере один корень x₁ и, следовательно, делится на х — х₁ т. е.

Для многочлена 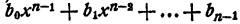теорема справедлива. Значит,

Допустим, что имеется два таких разложения:

Так как коэффициенты при хⁿ в правой и левой частях равенств (2) и (3) должны быть равны, то

Приравниваем правые части равенств (2) и (3). После сокращения на а₀ имеем

Методом математической индукции докажем, что правая и левая части равенства (4) состоят из соответственно равных множителей, но, быть может, записанных в другом порядке.

Для n= 1 утверждение, очевидно, справедливо.

Пусть утверждение справедливо для произведений, состоящих из n—1 множителей. Докажем, что утверждение справедливо и для произведений, состоящих из n множителей.

Левая часть равенства (4) при x = x₁ обращается в нуль. Значит, при x = x₁ обращается в нуль и правая часть этого равенства, т. е.

Произведение равно нулю. Значит, хоть один из сомножителей равен нулю. Допустим, что 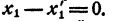В случае необходимости мы можем изменить нумерацию сомножителей так, чтобы первым был множитель, равный нулю. Тогда

Сократим равенство (4) на х— x₁ получим

По допущению правая и левая части равенства (5) состоят из соответственно равных множителей, но, быть может, записанных в другом порядке. Приписав в каждую часть равенства (5) по одинаковому множителю х— x₁ получим, что правая и левая части равенства (4) состоят из соответственно равных сомножителей.

Теорема доказана полностью.

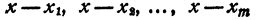
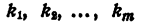
некоторые из сомножителей правой части могут быть одинаковы. Обозначив различные из них, а буквами кратность их вхождения, получим

где 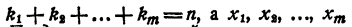все различны между собой

Представление левой части уравнения в виде (6) называется представлением левой части уравнения в канонической форме.

Теорема:

Всякое уравнение п-й степени с любыми комплексными коэффициентами имеет ровно п корней, среди которых могут быть и равные друг другу.

Доказательство:

где a₀ ≠ 0, n ≥ 0 Как доказано, левая часть может быть представлена в виде произведения n множителей первой степени. Таким образом, имеем

При x=x₁; х = х₂; х=хₙ левая часть уравнения превращается в нуль и, следовательно, х₁, х₂, …,xₙ— корни уравнения. Покажем, что никакое число а, отличное от х₁ х₂,…..хₙ, не может быть корнем этого уравнения.

Действительно, произведение а₀ (а — x₁) (а — х ₂ ,)… (а — x ₙ )не равно нулю, так как ни один из множителей его не равен нулю. Таким образом, корнями рассматриваемого уравнения являются числа x₁; х ₂ ;…; x ₙ и других корней нет.

Следствие:

Уравнение n-й степени имеет n корней, если каждый корень считать столько раз, какова его кратность.

Теорема:

Если уравнение n-й степени имеет действительные коэффициенты и мнимое число а + bi является корнем этого уравнения, то и сопряженное число а — bi является также корнем этого уравнения.

Доказательство:

Пусть мнимое число а + bi является корнем уравнения

с действительными коэффициентами. Требуется доказать, что сопряженное число а — bi также является корнем уравнения (7). Составим многочлен

Этот многочлен имеет действительные коэффициенты. Разделим левую часть уравнения (7) на многочлен (8). В частном получим многочлен n— 2 степени с действительными коэффициентами, в остатке многочлен степени не выше первой и тоже с действительными коэффициентами.

Так как делимое равно делителю, умноженному на частное плюс остаток, то

Положим в этом равенстве х = а + bi . Получим

так как и левая часть равенства и трехчлен 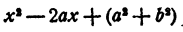при х = а + bi обращаются в нуль. Имеем

Так как b ≠ 0, то A = 0. Из первого уравнения системы (9) имеем В = 0. Выходит, что остаток Ах + В равен нулю, т. е.

При х = а — bi первый сомножитель правой части равенства (10) превращается в нуль, значит, и левая часть равенства тоже обращается в нуль. Значит, число а — bi является корнем уравнения (7).

Теорема:

Всякий многочлен n-й степени с действительными коэффициентами может быть представлен в виде произведения многочленов первой или второй степени с действительными коэффициентами.

Доказательство этой теоремы проводится методом математической индукции. Теорема, очевидно, справедлива для многочленов первой и второй степени. При этом многочлен второй степени либо имеет действительные корни и тогда разлагается на множители первой степени с действительными коэффициентами, либо он имеет два мнимых сопряженных корня, и тогда он на множители с действительными коэффициентами не разлагается.

Допустим, что теорема справедлива для многочленов n— 2 степени и многочленов n—1 степени. Докажем, что тогда она справедлива и для многочленов n-й степени.

Пусть 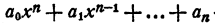— многочлен n-й степени с действительными коэффициентами.

Если этот многочлен имеет действительный корень x₁ то он представляется в виде произведения многочлена первой степени на многочлен n—1 степени с действительными коэффициентами, т. е.

Если же многочлен действительных корней не имеет, то он имеет мнимый корень а + bi и сопряженный с ним корень а — bi. В этом случае многочлен представляется в виде произведения трехчлена второй степени на многочлен n— 2 степени с действительными коэффициентами, т. е.

Так как теорема для многочленов п—1 степени и многочленов n— 2 степени справедлива, то она справедлива и для многочленов степени n.

Теорема Виета

легко получить теорему Виета для уравнений любой степени. Перепишем это равенство так:

К правой части этого равенства применим правило умножения двучленов, первые члены которых одинаковы (см. гл. VIII, § 5). Получаем

где 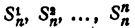имеют тот же смысл, что и в гл. VIII. Обозначим знаком f₁ сумму корней уравнения (1), т. е.

Знаком f₂ обозначим сумму всевозможных произведений корней, взятых по два. Подобный же смысл имеют знаки f₃, f₄, …, f ₙ . Тогда

Равенство (1) теперь можно переписать так:

Приравнивая коэффициенты при одинаковых степенях х в правой и левой частях равенства (2), получим

Последние равенства и выражают теорему Виета для уравнения любой степени. При n= 2, т. е. для уравнения 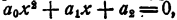получаем известный результат:

Пример:

Не решая уравнения 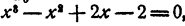, определить сумму квадратов его корней.

Решение:

Пусть х₁ x₂, х₃, — корни данного уравнения. Рассмотрим равенство

По теореме Виета

Полученный результат означает, что среди чисел х₁ x₂, х₃, имеются мнимые, иначе сумма квадратов их не могла бы быть отрицательной.

Предложенное уравнение нетрудно решить и подсчитать сумму квадратов корней непосредственно:

О решении уравнений высших степеней

Прежде всего возникает такой вопрос: можно ли для уравнений любой степени составить формулы для выражения корней уравнения через его коэффициенты, подобно известной формуле для квадратного уравнения? Оказывается, что это можно сделать для уравнений 3-й и 4-й степени, при этом формулы эти содержат столь сложные радикалы, что на практике ими предпочитают не пользоваться.

Что же касается уравнений выше 4-й степени, то доказано, что для них при помощи радикалов такие формулы составить нельзя.

В математике разработан ряд способов, дающих возможность вычислить любой корень любого уравнения с любой точностью. Один из таких способов разработан великим русским математиком, творцом неевклидовой геометрии Н. И. Лобачевским.

Ограничимся рассмотрением графического способа. Этот способ может применяться для вычисления действительных корней уравнений с действительными коэффициентами.

Пример:

Вычислить вещественные корни уравнения

Решение:

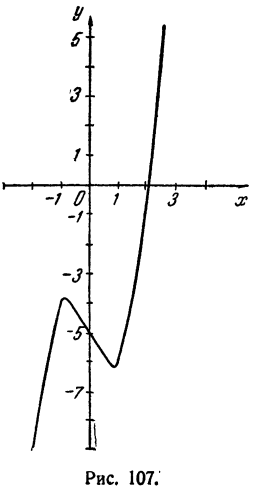
Построим график функции у = х³ — 2х— 5 (рис. 107). Имеем

Нетрудно видеть, что при x > 2,5 первое слагаемое х³ будет столь большим сравнительно с остальными, что у будет положительным числом.

По мере продвижения направо от х = 2,5 график будет подниматься кверху и, следовательно, больше пересекать ось Ох не будет.

Точно так же при х

Это означает, что точка 2,1 лежит правее корня, так как соответствующая ордината положительна (см. график).

Таким образом, 2 Вычисление рациональных корней уравнений с целыми коэффициентами

Теорема:

Для того чтобы несократимая дробь 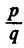была корнем уравнения

с целыми коэффициентами, необходимо, чтобы р было делителем свободного члена аₙ, a q было делителем старшего коэффициента а₀.

Доказательство:

Пусть 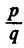—корень уравнения (1), т. е. имеет место тождество

Умножим обе части тождества на qⁿ, получим

Из тождества (2) имеем

Правая часть равенства — целое число. Значит, 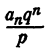целое.

По условию, дробь 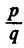несократима, значит, ни одно простое число, входящее в р, в число q не входит. По этой причине ни одно простое число, входящее в р, не может входить и в qⁿ. Выходит, что аₙ делится на р.

Из тождества (2) имеем

Так как ни одно простое число, входящее в q, не входит в р, число 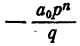может быть целым только тогда, когда а₀ делится на q.

Следствие:

Если уравнение имеет целые коэффициенты и старший из них равен единице, то рациональными корнями такого уравнения могут быть только целые числа.

Действительно, а₀ = 1, a q — делитель а₀ . Значит, q = ± 1, а тогда 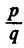целое.

Следствие:

Целые корни уравнения с целыми коэффициент тами являются делителями свободного члена.

Пример:

Вычислить рациональные корни уравнения

Решение:

Свободный член равен 2. Поэтому для р возможны только следующие значения: 1, —1, 2 и —2.

Старший коэффициент равен 2. Поэтому для q возможны только следующие значения: 1, —1, 2, —2.

Составляя всевозможными способами несократимые дроби 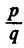найдем, что рациональные корни данного уравнения, если они имеются, содержатся среди следующих чисел:

Подстановкой в уравнение легко выяснить, что из этих шести

чисел удовлетворяют уравнению 2, 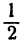,— 1.

Таким образом, уравнение имеет три рациональных корня:

Для испытания, является ли данное число корнем уравнения, удобно пользоваться правилом сокращенного деления многочлена на двучлен х — а. Для данного примера эти испытания проводятся так:

1 не является корнем уравнения, так как при делении левой части уравнения на х — 1 в остатке получилось — 2.

Испытываем число 2

2 — корень уравнения. В результате деления оказалось, что

Поэтому для отыскания остальных корней данного уравнения достаточно решить уравнение

Ответ.

Пример:

Найти рациональные корни уравнения

Решение:

Старший коэффициент уравнения равен единице, поэтому рациональными корнями уравнения могут быть только целые числа.

Делители свободного члена суть: 1,2, — 1, — 2. Сразу видно,-что никакое положительное число не может быть корнем данного уравнения, так как при любом положительном значении х левая часть уравнения положительна. Остается испытать — 1 и — 2:

Ответ. Уравнение рациональных корней не имеет.

Полученный в последнем примере результат означает, что корни рассматриваемого уравнения иррациональные или мнимые.

Пример:

Решение:

Выясним прежде всего, не имеет ли уравнение рациональных корней. Испытанию подлежат два числа 1 и — 1:

x₁² = 1. Остальные корни данного уравнения являются корнями уравнения третьей степени х³ — х² + х —1=0:

x₂ = 1. Остальные корни данного уравнения являются корнями квадратного уравнения х² + 1 = 0.

Ответ. x₁ = x₂ = 1; х₃ = i; x₄= — 1.

Решение двучленных уравнений 3-й, 4-й и 6-й степени

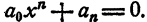
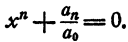
Определение. Двучленным уравнением n-й степени называется уравнение вида Очевидно, что делением на a₀ такое уравнение сводится к уравнению Если коэффициенты уравнения действительны, то двучленное уравнение можно представить в виде хⁿ — аⁿ = 0 или хⁿ + aⁿ= 0 где а — положительное число.

В этом параграфе излагается решение двучленных уравнений с действительными коэффициентами при n= 3, 4 и 6.

Уравнение имеет один действительный и два мнимых сопряженных корня.

Уравнение имеет два действительных и два мнимых сопряженных корня.

Уравнение имеет две пары мнимых сопряженных корней.

Уравнение распадается на два кубических двучленных уравнения. На основании рассмотренного в п. а)

Уравнение имеет два действительных и две пары мнимых сопряженных корней

Уравнение распадается на три квадратных уравнения. Решая их, получаем

Уравнение имеет три пары мнимых сопряженных корней.

Замечание. Пользуясь извлечением корня n-й степени из комплексного числа, можно решить двучленное уравнение хⁿ = а любой степени n при любой правой части а.

Корнями уравнения хⁿ = а являются все значения корня n-й степени из а.

Пример: