Как решать квадратные уравнения
О чем эта статья:
Понятие квадратного уравнения
Уравнение — это равенство, содержащее переменную, значение которой нужно найти.
Например, х + 8 = 12 — это уравнение, которое содержит переменную х.
Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.
Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.
А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.
Решить уравнение — значит найти все его корни или доказать, что их не существует.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.
Квадратные уравнения могут иметь два корня, один корень или не иметь корней.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b 2 − 4ac. А вот свойства дискриминанта:
- если D 0, есть два различных корня.
С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.
Разобраться в теме еще быстрее с помощью опытного преподавателя можно на курсах по математике в онлайн-школе Skysmart.
Приведенные и неприведенные квадратные уравнения
Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.
Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.
Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.
Давайте-ка на примерах — вот у нас есть два уравнения:
- x 2 — 2x + 6 = 0
- x 2 — x — 1/4 = 0
В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x 2 ), а значит уравнение называется приведенным.
- 2x 2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.
Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.
Пример 1. Превратим неприведенное уравнение: 8x 2 + 20x — 9 = 0 — в приведенное.
Для этого разделим обе части исходного уравнения на старший коэффициент 8:
Ответ: равносильное данному приведенное уравнение x 2 + 2,5x — 1,125 = 0.
Полные и неполные квадратные уравнения
В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax 2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.
Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.
Неполное квадратное уравнение —— это квадратное уравнение вида ax 2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
| Для самых любопытных объясняем откуда появились такие названия: | |
|---|---|
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. Решение неполных квадратных уравненийКак мы уже знаем, есть три вида неполных квадратных уравнений:
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам. Как решить уравнение ax 2 = 0Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0. Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней. Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0. Пример 1. Решить −6x 2 = 0.
Как решить уравнение ax 2 + с = 0Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный. Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами. Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи. Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней.
Пример 1. Найти решение уравнения 8x 2 + 5 = 0.
Разделим обе части на 8: Ответ: уравнение 8x 2 + 5 = 0 не имеет корней. Как решить уравнение ax 2 + bx = 0Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0. Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение: Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a. Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня: Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0 0,5x = 0,125, Ответ: х = 0 и х = 0,25. Как разложить квадратное уравнениеС помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так: Формула разложения квадратного трехчлена Если x1 и x2 — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x1) (x − x2). Дискриминант: формула корней квадратного уравненияЧтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так: где D = b 2 − 4ac — дискриминант квадратного уравнения. Эта запись означает: Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться. Алгоритм решения квадратных уравнений по формулам корнейТеперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни. В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней. Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться! Примеры решения квадратных уравненийКак решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике. Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.
Ответ: единственный корень 3,5. Пример 2. Решить уравнение 54 — 6x 2 = 0.
Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую Ответ: два корня 3 и — 3. Пример 3. Решить уравнение x 2 — х = 0.
Ответ: два корня 0 и 1. Пример 4. Решить уравнение x 2 — 10 = 39.
Ответ: два корня 7 и −7. Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.
D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112 Ответ: корней нет. В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся. Формула корней для четных вторых коэффициентовРассмотрим частный случай. Формула решения корней квадратного уравнения Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставим в формулу корней: 2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″> Для удобства вычислений обозначим выражение n 2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид: где D1 = n 2 — ac. Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения. Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
Формула ВиетаЕсли в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену. Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства: Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам. Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0. Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре: Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит: Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента: Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное. Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется: Результат проделанных вычислений в том, что мы убедились в справедливости выражения: Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она: Обратная теорема Виета Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0. Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение. Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″> Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы. Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже. Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам: Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p> Упрощаем вид квадратных уравненийЕсли мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту. Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0. Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100. Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов. Покажем, как это работает на примере 12x 2 — 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто. А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0. Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 — 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0. Связь между корнями и коэффициентамиМы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты: Из этой формулы, можно получить другие зависимости между корнями и коэффициентами. Например, можно применить формулы из теоремы Виета: Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 — 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3. Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты: Квадратные уравнения. Основные понятияЭтот видеоурок доступен по абонементуУ вас уже есть абонемент? Войти На занятии будет введено понятие квадратного уравнения, рассмотрены его два вида: полное и неполное. Отдельное внимание на уроке будет уделено разновидностям неполных квадратных уравнений, во второй половине занятия будет рассмотрено множество примеров. Обыкновенные дифференциальные уравненияСодержание: Обыкновенные дифференциальные уравненияПри решении многих задач математики, техники, экономики и других отраслей науки бывает трудно установить закон, связывающий искомые и известные переменные величины. Но удается установить связь между производными или дифференциалами этих переменных, которая выражается уравнениями или системами уравнений. Такие уравнения называют дифференциальными уравнениями. Термин «дифференциальное уравнение» введен в 1676 году В. Лейбницом. Мы рассмотрим только уравнения с функциями одной переменной и обычными производными, которые называют обычными дифференциальными уравнениями. Основные понятия о дифференциальных уравненияхОпределение. Дифференциальным уравнением называется уравнение, которое связывает независимую переменную x, искомую функцию y = f (x) и еепроизводные или дифференциалы разных порядков, то есть уравнение Важно понять, что искомая функция в дифференциальном уравнении входит под знак дифференциала или под знак производной. Определение. Порядком дифференциального уравнения называется наивысший порядок производной от неизвестной функции, входящей в дифференциальное уравнение. Так, уравнение y’ – 2 xy 2 + 5 = 0 является дифференциальным уравнением первого порядка, а уравнения y» + 2 y’ – y – sin x = 0 — дифференциальным уравнением второго порядка. Определение. Решением дифференциального уравнения (7.1) называется такая функция y = φ (x), которая при подстановке в уравнение (7.1) превращает его в тождество. Например, для дифференциального уравнения Следует заметить, что y = x 2 не единственное решение уравнения. Это уравнение имеет бесконечное множество решений, которые можно записать так: y = x 2 + C. Дифференциальные уравнения первого порядкаОпределение. Дифференциальным уравнением первого порядка называется уравнение, которое связывает независимую переменную x, искомую функцию y = f (x) и ее первую производную: Поскольку производную можно записать в виде отношения дифференциалов, то в уравнение производная может не входить, а будут входить дифференциалы неизвестной функции и независимой переменной. Если уравнение (7.2) решить относительно у’, то оно будет иметь вид: Простые примеры показывают, что дифференциальное уравнение может иметь бесконечное множество решений. Это мы видим на примере уравнения (7.2). Легко убедиться также, что дифференциальное уравнение Как видим, в решение указанных дифференциальных уравнений входит произвольное число C. Предоставляя постоянной C различные значения, будем получать различные решения дифференциального уравнения. Определение. Общим решением дифференциального уравнения (7.3) называется функция Если функция (7.5) выражается неявно, то есть в виде Определение. Частным решением дифференциального уравнения (7.3) называется такое решение, которое получается из общего решения (7.5) при некотором конкретном значении постоянной C. Ф (х, у, С0) называется частным интегралом дифференциального уравнения. На практике при решении конкретных задач часто приходится находить не все решения, а решение, которое удовлетворяет определенным начальным условиям. Одной из таких задач является задача Коши, которая для дифференциального уравнения первого порядка формулируется так: среди всех решений дифференциального уравнения (7.3) найти такое решение y, которое при заданном значении независимой переменной x = x0 равна заданному значению y0 , то есть y (x0) = y0 или Условие (7.7) называется начальным условием решения. Покажем на примере, как найти частное решение дифференциального уравнения, когда известно общее решение и задано начальное условие. Мы видим, что дифференциальное уравнение Ответ на вопрос о том, при каких условиях уравнение (7.4) имеет ТЕОРЕМА (о существовании и единственности решения). Если функция f (x, y) и ее частная производная Теорема Коши дает достаточные условия существования единого решения дифференциального уравнения (7.4). Заметим, что в условии теоремы не требуется существования частной производной График произвольного частного решения дифференциального уравнения называется интегральной кривой. Общему решению отвечает семья кривых. Так мы проверили, что уравнение Уравнение Если задано начальное условие Надо заметить, что нахождение решения дифференциального уравнения часто называют интегрированием уравнения. При этом операцию интегрирования функций называют квадратурой. Общего метода решения дифференциальных уравнений первого порядка не существует. Рассмотрим некоторые методы решения отдельных типов дифференциальных уравнений. Дифференциальные уравнения с разделенными переменнымиОпределение. Уравнение вида В этом уравнении каждая из переменных находится только в той части уравнения, где находится ее дифференциал. Уравнение dy = f (x) dx является частным случаем уравнения (7.8). Чтобы решить уравнение (7.8), надо проинтегрировать обе его части: Понятно, что произвольную постоянную С можно записывать в любой части равенства. Пример 1. Решить дифференциальное уравнение: Решение. Проинтегрируем левую и правую части уравнения, причем для удобства потенцирования, произвольную постоянную запишем в виде ln |C| получим: Дифференциальные уравнения с разделяющимися переменнымиОпределение. Уравнение вида В этом уравнении переменные еще не разделены, но, поделив обе части уравнения на произведение f2 (y) g1 (x), получим уравнение с разделенными переменными: Интегрируя это уравнение, запишем Получили общий интеграл данного уравнения. Пример 2. Решить дифференциальное уравнение Решение. Поделим обе части этого уравнения на (y + 1) (x 2 + 1), после чего получим Интегрируя, получим Пример 3. Найти частное решение дифференциального уравнения (1 + x 2 ) dy + ydx = 0, удовлетворяющее начальному условию y (0) = 1. Решение. Отделим переменные, поделив уравнение на y ⋅ (1 + x 2 ), и проинтегрируем данное уравнение: Получили общий интеграл дифференциального уравнения. Используя начальное условие, найдем произвольную постоянную С: Найденную постоянную подставим в общий интеграл и отыщем частное решение: Однородные дифференциальные уравненияОпределение. Функция двух переменных f (x, y) называется однородной n- го измерения, если выполняется условие Например, f (x, y) = x 2 + y 2 , f (tx, ty) = t 2 f (x 2 + y 2 ) — однородная функция второго измерения. Определение. Дифференциальное уравнение Покажем, что это уравнение можно свести к уравнению с разделенными переменными. Из формулы (7.12) найдем y’ = u + xu’ и уравнение После интегрирования получим Чаще всего не удается найти функцию u явно выраженной, тогда, после интегрирования, в левую часть следует подставить Пример 1. Найти решение однородного уравнения Решение. Заменой y = xu сведем заданное уравнение к уравнению Отделяя переменные, найдем Линейные дифференциальные уравненияОпределение. Линейным дифференциальным уравнением первого порядка называется уравнение, которое содержит искомую функцию и ее производную в первой степени без их произведения: Здесь P (x), Q (x) — известные функции независимой переменной x. Например, y’ + 2 xy = x 2 . Если Q (x) = 0, то уравнение (7.13) называется линейным однородным и является уравнением с разделяющимися переменными. Если Q (x) ≠ 0, то уравнение (7.13) называется линейным неоднородным, которое можно решить несколькими способами. Рассмотрим метод Бернулли, с помощью которого уравнение (7.13) можно свести к интегрированию двух дифференциальных уравнений первого порядка с разделяющимися переменными. Решение дифференциального уравнения (7.13) ищем в виде y = u (x) v (x) или y = uv, (7.14) Из равенства y = uv найдем производную y’: Подставим y и y’ в уравнение (7.13): Выберем функцию v такой, чтобы v’ + P (x) v = 0. (7.15) Сначала найдем v из уравнения (7.15). Под неопределенным интегралом здесь будем понимать какую-то одну первообразную от функции P (x), то есть v будет определенной функцией от x. Зная v, находим u из уравнения (7.16): Здесь мы уже берем для u все первообразные. Найденные функции u и v подставляем в (7.14) и получаем общее решение линейного дифференциального уравнения: При решении конкретных примеров проще выполнять эти выкладки, чем применять громоздкую формулу (7.17). Пример 1. Решить дифференциальное уравнение Выражение, стоящее в скобках, приравниваем к нулю, имеем Отделим переменные, домножив обе части уравнения на Общее решение запишется: Пример 2. Найти частное решение дифференциального уравнения Решение. Заданное уравнение — это линейное неоднородное уравнение первого порядка, решение которого ищем в виде y = u⋅v. Подставим v в уравнение и найдем u: Общее решение дифференциального уравнения будет: Подставляем начальные условия в найденное решение и находим С: Из общего решения получаем частное решение Дифференциальное уравнение БернуллиОпределение. Уравнения вида Данное уравнение отличается от уравнения (7.13) только множителем y» (или x») в правой части. Для того, чтобы права часть данного уравнения была такой, как в (7.13), разделим его левую и праву часть на y»: Сделаем замену: Мы получили линейное дифференциальное уравнение относительно новой переменной Пример 1. Найти общее решение дифференциального уравнения xy’ + y = y 2 ln x. Решение. Данное уравнение решим, сделав замену z = u (x) ⋅ v (x). Выбираем функцию v (x) так, чтобы выражение в скобках равнялось нулю, и эта функция была бы частным решением уравнения Тогда Проинтегрировав правую часть этого уравнения по частям, получим Обыновенное дефференциальное уравнениеОбыкновенным дифференциальным уравнением называется любое соотношение, связывающее независимую переменную Обыкновенное дифференциальное уравнение может быть приведено к виду Здесь Число Обыкновенные дифференциальные уравнения первого порядка, разрешенные относительно производной. уравнения, интегрируемые в квадратурах По этой ссылке вы найдёте полный курс лекций по высшей математике: Основные понятия и определенияПонятие об уравнении первого порядка, разрешенном относительно производной. В соответствии со сказанным во введении, уравнение первого порядка имеет вид В этой главе мы будем рассматривать уравнение, разрешенное относительно производной: Наряду с этим уравнением мы всегда будем рассматривать перевернутое уравнение используя последнее в окрестности тех точек, в которых Во многих случаях оказывается целесообразным «место уравнении (2) и (2′) рассматривать одно равносильное им дифференциальное уравнение Обе переменные Умножая обе части уравнения (3) на некоторую функцию где Иногда уравнение записывают *з так называемой симметрической форме: Возможно вам будут полезны данные страницы: Решение уравнения. Предположим, что правая часть уравнения (2),
справедливое для всех значений Так как наряду с уравнением (2) рассматривается перевернутое уравнение (2′), то и решения
Примеры с решениемПример 1. является решением уравнения в интервале справедливое при всех значениях Пример 2.Функция Пример 3. является решением уравнения в интервале Иногда функцию Системы обыкновенных дифференциальных уравненийПри решении многих задач нужно найти функции y1 = y1 (x), y2 = y2 (x), . yn = yn (x), которые удовлетворяют системе дифференциальных уравнений, содержащих независимую переменную x , искомые y1 , y2 , . yn и их производные. Пример. Пусть материальная точка массы m имеет криволинейную траекторию движения в пространстве. Определить положение точки в любой момент времени t, когда на нее действует сила Положение точки в любой момент времени t определяется ее координатами x, y, z; следовательно, x, y, z являются функциями от t. Проекциями вектора скорости точки на оси координат будут производные x’ , y’ , z’. Мы получили систему трех дифференциальных уравнений второго порядка. В случае движения, когда траектория является плоской кривой, лежит, например, в плоскости Оxy, получим систему двух уравнений для определения неизвестных функций x (t) и y (t): Рассмотрим простейшие системы дифференциальных уравнений. Системы дифференциальных уравнений первого порядкаСистема n уравнений первого порядка с n неизвестными функциями имеет вид: где x — независимая переменная, y1, y2, . yn — неизвестные функции. Если в левой части уравнений системы стоят производные первого порядка, а правые части уравнений вовсе не содержат производных, то такая система уравнений называется нормальной. Решением системы называется совокупность функций y1, y2, . yn, которые превращают каждое уравнение системы в тождество относительно x. Задача Коши для системы (7.38) состоит в нахождении функций y1, y2, . yn , удовлетворяющих систему (7.38) и заданные начальные условия: Интегрирование системы (7.38) делают следующим образом. Дифференцируем по x первое уравнение системы (7.38): Из первых (n-1) уравнений определим y2, y3, . yn: и подставим их значения в последнее уравнение системы (7.40) для определения y1: Продифференцируем это выражение (n-1) раз, определим Для того, чтобы полученное решение удовлетворяло заданным начальным условиям, остается только найти значение произвольных постоянных из уравнений (7.42) и (7.43) так, как мы это делали для одного дифференциального уравнения. Пример 1. Проинтегрировать систему Из первого уравнения системы найдем Общим решением этого уравнения является Подберем постоянные С1 и С2 так, чтобы выполнялись начальные условия. На основании (*) и (**) имеем: Системы линейных дифференциальных уравнений с постоянными коэффициентамиСистема дифференциальных уравнений: Эту систему можно решать путем сведения к одному уравнению n-го порядка, как это было показано выше. Но эту систему можно решить и другим способом. Покажем, как это делается. Будем искать решение системы (7.44) в виде: Надо определить постоянные α1, α2, . αn и k так, чтобы функции (7.45) удовлетворяли систему (7.44). Подставим функции (7.45) в систему (7.44): Сократим на e kt и преобразуем систему, сведя ее к такой системе: Это система линейных алгебраических уравнений относительно α1, α2, . αn. Составим определитель системы: Мы получим нетривиальные (ненулевые) решения (7.45) только при таких k, при которых определитель превратится в ноль. Получаем уравнение n-го порядка для определения k: Это уравнение называется характеристическим уравнением для системы (7.44). Рассмотрим отдельные случаи на примерах: 1) Корни характеристического уравнения действительны и различны. Решение системы записывается в виде: Пример 2. Найти общее решение системы уравнений: Решение. Составим характеристическое уравнение: Решение системы ищем в виде Составим систему (7.46) для корня k1 и найдем Откуда Далее составляем систему (7.46) для k = 4: Откуда 2) Корни характеристического уравнения различны, но среди них есть комплексные: k1 = α + iβ, k2 = α – iβ. Этим корням будут отвечать решения: Можно доказать также, что истинные и мнимые части комплексного решения также будут решениями. Таким образом, получим два частных решения: Соответствующие комбинации функций (7.49) войдут в общий решение системы. Пример 3. Найти общее решение системы Решение. Составляем характеристическое уравнение: Подставляем поочередно k1, k2 в систему (7.46), найдем Запишем уравнение (7.47) и (7.48) для наших данных Перепишем эти решения в таком виде: За частные решения можно взять отдельно действительные и отдельно мнимые части: Общим решением системы будет Присылайте задания в любое время дня и ночи в ➔ Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института. Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды. Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги. источники: http://interneturok.ru/lesson/algebra/8-klass/kvadratnye-uravneniya-prodolzhenie/kvadratnye-uravneniya-osnovnye-ponyatiya http://natalibrilenova.ru/obyiknovennyie-differentsialnyie-uravneniya/ |

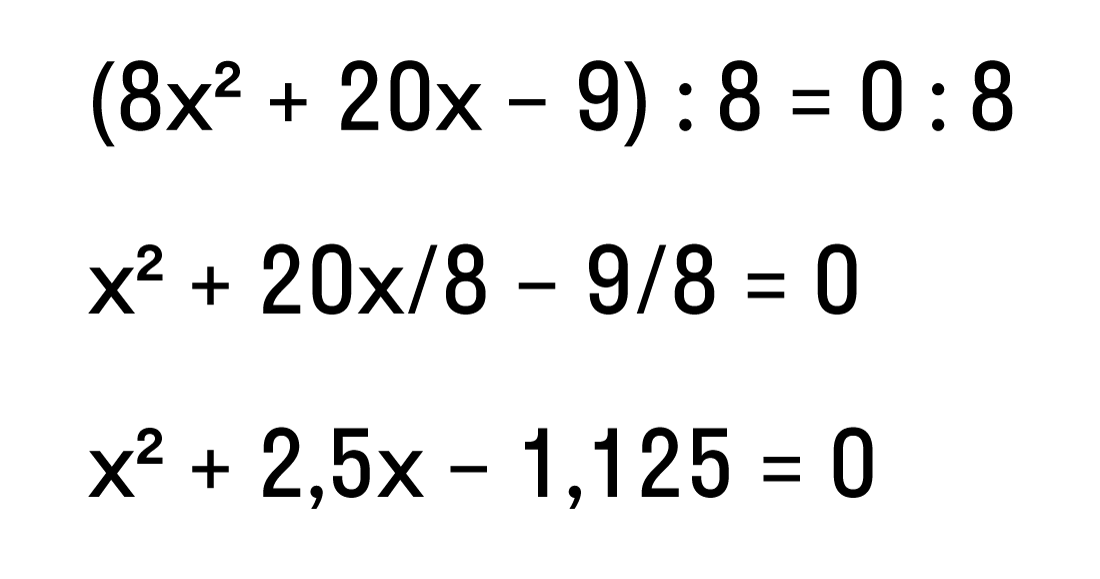
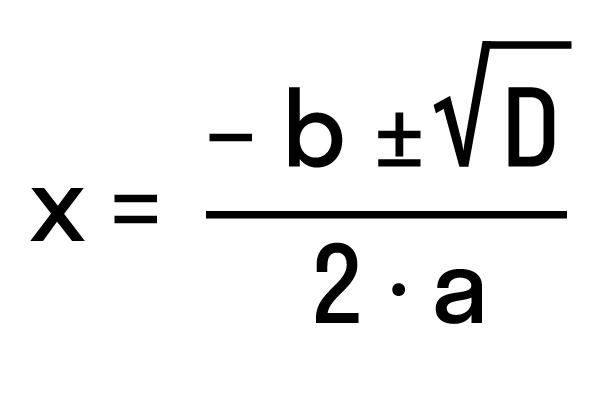
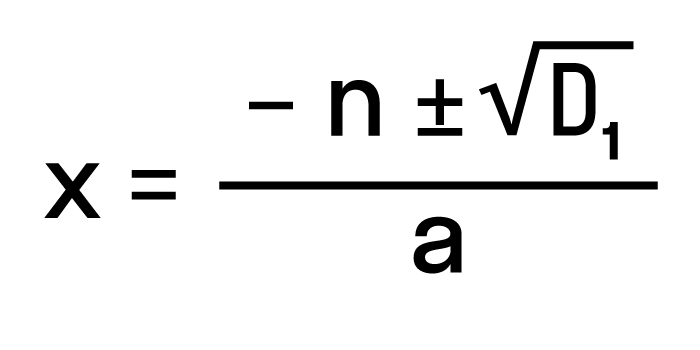
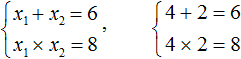
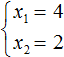
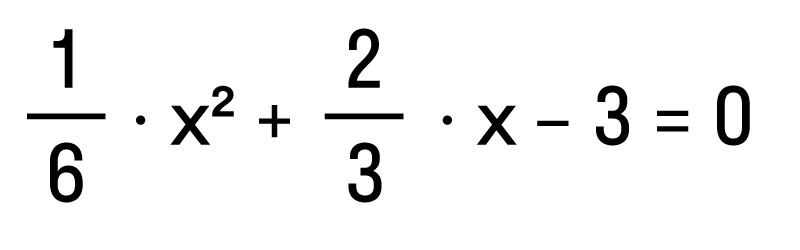
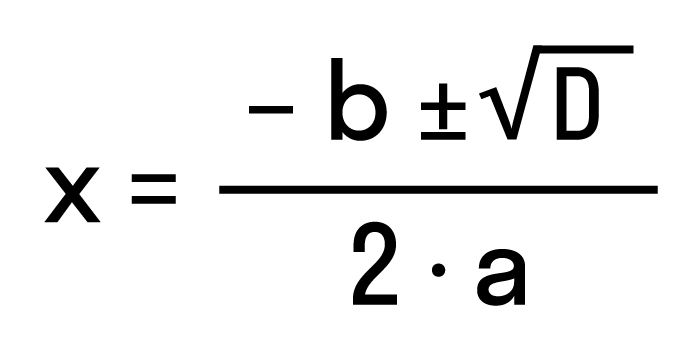

 (7.1)
(7.1) . (7.4)
. (7.4) имеет решениями функции y = Cx, а дифференциальное уравнение
имеет решениями функции y = Cx, а дифференциальное уравнение  — функции
— функции  где C — произвольное число.
где C — произвольное число. (7.7)
(7.7) имеет общее решение y = Cx. Зададим начальное условие
имеет общее решение y = Cx. Зададим начальное условие  . Подставим эти значения в общее решение, получим 6 = 2С, откуда С = 3. Следовательно, функция y = 3x удовлетворяет и дифференциальное уравнение, и начальное условие.
. Подставим эти значения в общее решение, получим 6 = 2С, откуда С = 3. Следовательно, функция y = 3x удовлетворяет и дифференциальное уравнение, и начальное условие. определены и непрерывные в области G, которая содержит точку M0 (x0; y0) , то существует единственное решение y = φ (x) уравнения (7.4), которое удовлетворяет начальному условию: y (x0) = y0.
определены и непрерывные в области G, которая содержит точку M0 (x0; y0) , то существует единственное решение y = φ (x) уравнения (7.4), которое удовлетворяет начальному условию: y (x0) = y0. .
. имеет общее решение y = Cx, то ему соответствует семья прямых,
имеет общее решение y = Cx, то ему соответствует семья прямых,  имеет общее решение, ему соответствует семья равносторонних гипербол (рис. 2).
имеет общее решение, ему соответствует семья равносторонних гипербол (рис. 2). 
 то это означает, что задана точка M0 (x0;y0), через которую должна проходить интегральная кривая, отвечающая искомому частному решению. Таким образом, отыскание частного решения дифференциального уравнения по заданному начальному условию геометрически означает, что из семьи
то это означает, что задана точка M0 (x0;y0), через которую должна проходить интегральная кривая, отвечающая искомому частному решению. Таким образом, отыскание частного решения дифференциального уравнения по заданному начальному условию геометрически означает, что из семьи  .
. , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 


 — это общее решение дифференциального уравнения.
— это общее решение дифференциального уравнения.  является частным решением данного уравнения.
является частным решением данного уравнения.
 .
. .
.


 — общий интеграл дифференциального уравнения.
— общий интеграл дифференциального уравнения.
 откуда
откуда 

 будем иметь:
будем иметь: 
 (7.11)
(7.11)  или y = xu, (7.12)
или y = xu, (7.12)  примет вид: u + xu’ = φ (u),
примет вид: u + xu’ = φ (u),  , откуда
, откуда  .
.
 вместо u.
вместо u. 
 или
или  .
. откуда
откуда  или
или  , то есть
, то есть  .
.  .
. , откуда
, откуда 


 (7.17)
(7.17) .
.  или
или  . (7.18)
. (7.18) или
или 
 , тогда
, тогда  .
. 
 который удовлетворяет начальному условию y (0) = 0.
который удовлетворяет начальному условию y (0) = 0.




 .
. (или
(или  )
) 





 .
.  Тогда
Тогда 



 .
. , а при y -1 = z = uv, имеем
, а при y -1 = z = uv, имеем 
 искомую функцию
искомую функцию  и производные искомой функции
и производные искомой функции  до некоторого порядка включительно.
до некоторого порядка включительно.
 — известная функция, заданная в некоторой области
— известная функция, заданная в некоторой области 
 т. е. наивысший из порядков производных, входящих в (1), называется порядком уравнения.
т. е. наивысший из порядков производных, входящих в (1), называется порядком уравнения.


 обращается в бесконечность.
обращается в бесконечность.
 и
и  входят в это уравнение уже равноправно, и любую из них мы можем принять за независимую переменную.
входят в это уравнение уже равноправно, и любую из них мы можем принять за независимую переменную. получаем более симметричное уравнение:
получаем более симметричное уравнение:
 Обратно, всякое уравнение вида (4) можно переписать в виде уравнений (2) или (2′), разрешая его относительно
Обратно, всякое уравнение вида (4) можно переписать в виде уравнений (2) или (2′), разрешая его относительно  или
или  так что уравнение (4) равносильно следующим двум уравнениям:
так что уравнение (4) равносильно следующим двум уравнениям:

 определена на некотором подмножестве
определена на некотором подмножестве  вещественной плоскости
вещественной плоскости  Функцию
Функцию  определенную в интервале
определенную в интервале  мы будем называть решением уравнения (2) в этом интервале*, если:
мы будем называть решением уравнения (2) в этом интервале*, если: для всех значений
для всех значений  из интервала
из интервала  (Отсюда следует, что решение
(Отсюда следует, что решение  представляет собою функцию, непрерывную ею всей области определения).
представляет собою функцию, непрерывную ею всей области определения). обращает уравнение (2) в тождество:
обращает уравнение (2) в тождество: 
 из интервала
из интервала  Это означает, что при любом
Это означает, что при любом  из интервала
из интервала  точка
точка  принадлежит множеству
принадлежит множеству  и
и 
 этого перевернутого уравнения естественно присоединять к решениям уравнения (2).
этого перевернутого уравнения естественно присоединять к решениям уравнения (2).

 ибо она определена и дифференцируема в эгои интервале, и, подставляя се в уравнение (9), получаем тождество:
ибо она определена и дифференцируема в эгои интервале, и, подставляя се в уравнение (9), получаем тождество:

 есть решение равнения
есть решение равнения  в интервале
в интервале 



 обращающую уравнение (2) в тождество (7), т. е. решение уравнения (2), называют интегралом этого уравнения. Мы будем употреблять термин интеграл только в смысле п. 16.
обращающую уравнение (2) в тождество (7), т. е. решение уравнения (2), называют интегралом этого уравнения. Мы будем употреблять термин интеграл только в смысле п. 16. .
. . Искомыми неизвестными функциями в этой задаче будут три функции x = x (t), y = y (t), z = z (t). Эти
. Искомыми неизвестными функциями в этой задаче будут три функции x = x (t), y = y (t), z = z (t). Эти 

 (7.38)
(7.38) (7.39)
(7.39)
 их выражениями f1, f2, . fn из уравнений системы (7.38), получим уравнение
их выражениями f1, f2, . fn из уравнений системы (7.38), получим уравнение 


 (7.40)
(7.40) (7.41)
(7.41)
 как функции от x, C1, C2, . Cn. Подставим эти функции в (7.41), найдем
как функции от x, C1, C2, . Cn. Подставим эти функции в (7.41), найдем  (7.43)
(7.43)

 . Подставляем сюда значение
. Подставляем сюда значение  и
и  из системы, получим
из системы, получим 

 и подставим в полученное нами уравнение:
и подставим в полученное нами уравнение:  или
или 
 (*)
(*)  (**)
(**)
 (7.44)
(7.44)  (7.45)
(7.45)
 (7.46)
(7.46)



 или k 2 – 5k + 4 = 0, корни которого k1 = 1, k2 = 4.
или k 2 – 5k + 4 = 0, корни которого k1 = 1, k2 = 4.
 и
и  :
:  или
или 
 Положив
Положив  получим
получим 





 (7.47)
(7.47) (7.48)
(7.48) (7.49)
(7.49)  — действительные числа, которые определяются через
— действительные числа, которые определяются через  .
.
 или k 2 + 12k + 37 = 0, корни которого k1 = –6 + i, k2 = –6 – i .
или k 2 + 12k + 37 = 0, корни которого k1 = –6 + i, k2 = –6 – i .







