Каким образом можно получить аналитически дифференциальное уравнение объекта

Обработка результатов эксперимента и анализ

По результатам опытов 2-4 на одном графике (для лучшего их сопоставления и анализа) построить переходные характеристики.

Статическую характеристику объекта (опыт 1) и переходную характеристику двухемкостного объекта (опыт 5) поместить на отдельных графиках.

Обработку переходных характеристик осуществлять графически: к кривой разгона в точке с наибольшей крутизной характеристики провести касательную до пересечения с осью абсцисс и линией нового установившегося значения. По точкам пересечений найти значение параметра Т_об и t. Коэффициент усиления К определить по выражению:

Относительные входные Dm и выходные Ds∞величины объекта рассчитать по формулам:

где — Qп.м., Н₀ — номинальные значения расхода и уровня (в работе принято Qп.м.=17,5*10 -6 м 3 /с, Н₀=0,1м).

С учетом полученных численных значений Т_об и t записать дифференциальные уравнения объектов, найти их решения. Рассчитать теоретическую кривую разгона для опыта 5 и сравнить ее с экспериментальной. Провести анализ полученных результатов. Например, динамическая характеристика одноемкостного статического объекта описывается линейным дифференциальным уравнением первого порядка:

А уравнение кривой разгона такого объекта имеет вид:

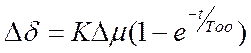
Содержание отчета

Отчет должен содержать следующее:

1. Номер, наименование и цель работы, дату ее выполнения;

таблицы результатов измерений;

2. Графики статистической и переходных характеристик;

3. Дифференциальные уравнения объектов;

4. График теоретической кривой разгона, совмещенный с переходной характеристикой опыта 5;

1. Что такое статическая характеристика?

2. Как различают объекты по виду статической характеристики?

3. Как определить коэффициент усиления объекта по графику и аналитическому выражению статической характеристики?

4. Что такое динамическая характеристика объекта?

5. Как подразделяются объекты по виду динамической характеристики?

6. Как определяются статические и динамические характеристики?

7. В какой форме можно представить статические и динамические характеристики объекта?

8. Каким образом можно получить аналитически дифференциальное уравнение объекта?

9. Как влияет нагрузка объекта на постоянную времени Т_об и коэффициент усиления К?

10. Как влияет емкость на Т_об и К?

11. По какой причине происходит самовыравнивание объекта?

12. Как влияет самовыравнивание на Т_об и К?

\|	следующая лекция ==>
\|	Описание лабораторной установки. Цель работы: освоить методы измерений и оценки основных параметров микроклимата производственных помещений и режима работы кондиционера.

Не нашли, что искали? Воспользуйтесь поиском:

Каким образом можно получить аналитически дифференциальное уравнение объекта

Для нахождения аналитических решений дифференциальных уравнений в Maple применяется команда dsolve(eq,var,options), где eq – дифференциальное уравнение, var – неизвестные функции, options – параметры. Параметры могут указывать метод решения задачи, например, по умолчанию ищется аналитическое решение: type=exact. При составлении дифференциальных уравнений для обозначения производной применяется команда diff, например, дифференциальное уравнение y»+y=x записывается в виде: diff(y(x),x$2)+y(x)=x.

Общее решение дифференциального уравнения зависит от произвольных постоянных, число которых равно порядку дифференциального уравнения. В Maple такие постоянные, как правило, обозначаются как _С1, _С2, и т.д.

Общее решение неоднородного линейного дифференциального уравнения всегда выводится так, чтобы была четко видна, структура этого решения. Как известно, общее решение неоднородного линейного дифференциального уравнения равно сумме общего решения соответствующего однородного дифференциального уравнения и частного решения этого же неоднородного дифференциального уравнения. Поэтому в строке вывода решение неоднородного линейного дифференциального уравнения всегда состоит из слагаемых, которые содержат произвольные постоянные (это общее решения соответствующего однородного дифференциального уравнения), и слагаемых без произвольных постоянных (это частное решения этого же неоднородного дифференциального уравнения).

Команда dsolve выдает решение дифференциального уравнения в невычисляемом формате. Для того, чтобы с решением можно было бы работать далее (например, построить график решения) следует отделить правую часть полученного решения командой rhs(%).

1. Найти общее решение дифференциального уравнения y’+ycosx=sinxcosx.

Итак, решение искомого уравнения есть функция

Замечание: при записи решения диффреренциального уравнения в Maple в строке вывода произвольная постоянная обозначена как _С1.

Найти общее решение дифференциального уравнения второго порядка y» — 2y’+y=sinx+e — x.

Замечание: так как исходное уравнение было второго порядка, то полученное решение содержит две произвольные константы, которые в Maple обычно обознаются как _С1 и _С2. Первые два слагаемых представляют собой общее решение соответствующего однородного дифференциального уравнения, а вторые два – частное решение неоднородного дифференциального уравнения.

3. Найти общее решение дифференциального уравнения порядка y»+k2y=sin(qx) в двух случаях: q ¹ k и q=k (резонанс).

Теперь найдем решение в случае резонанса. Для этого перед вызовом команды dsolve следует приравнять q=k.

Фундаментальная (базисная) система решений.

Команда dsolveпредставляет возможность найти фундаментальную систему решений (базисные функции) дифференциального уравнения. Для этого в параметрах команды dsolve следует указать output=basis.

Найти фундаментальную систему решений дифференциального уравнения: y(4)+2y»+y=0.

>dsolve(de, y(x), output=basis);

Решение задачи Коши или краевой задачи.

Команда dsolve может найти решение задачи Коши или краевой задачи, если помимо дифференциального уравнения задать начальные или краевые условия для неизвестной функции. Для обозначения производных в начальных или краевых условиях используется дифференциальный оператор , например, условие y»(0)=2 следует записать в виде

1. Найти решение задачи Коши: y(4)+y»=2cosx, y(0)= — 2, y'(0)=1, y»(0)=0, y»'(0)=0.

y(x)= — 2cos(x) — xsin(x)+ х

2. Найти решение краевой задачи:кккк

y(x)=2x — p + p cos(x)

Замечание: для построения графика решения предварительно следует отделить правую часть полученного выражения.

Системы дифференциальных уравнений.

Команда dsolve может найти решение системы дифференциальных уравнений (или задачи Коши), если в ней указать: dsolve(,), где sys — система дифференциальных уравнений, x(t),y(t),… — набор неизвестных функций.

Найти решение системы дифференциальных уравнений:

Найдены две функции x(t) и y(t), которые зависят от двух произвольных постоянных _С1 и _С2.

Приближенное решение дифференциальных уравнений с помощью степенных рядов.

Для многих типов дифференциальных уравнений не может быть найдено точное аналитическое решение. В этом случае дифференциальное уравнение можно решить с помощью приближенных методов, и, в частности, с помощью разложения в степенной ряд неизвестной функции.

Чтобы найти приближенное решение дифференциального уравнения в виде степенного ряда, в команде dsolve следует после переменных указать параметр type=series (или просто series). Для того, чтобы указать порядок разложения n, т.е. порядок степени, до которой производить разложение, следует перед командой dsolve вставить определение порядка с помощью команды Order:=n.

Если ищется общее решение дифференциального уравнения в виде разложения в степенной ряд, то коэффициенты при степенях х найденного разложения будут содержать неизвестные значения функции в нуле y(0) и ее производных D(y)(0), (D@@2)(y)(0) и т.д. Полученное в строке вывода выражение будет иметь вид, похожий на разложение искомого решения в ряд Маклорена, но с другими коэффициентами при степенях х. Для выделения частного решения следует задать начальные условия y(0)=у1, D(y)(0)=у2, (D@@2)(y)(0)=у3 и т.д., причем количество этих начальных условий должно совпадать с порядком соответствующего дифференциального уравнения.

Разложение в степенной ряд имеет тип series, поэтому для дальнейшей работы с этим рядом его следует преобразовать в полином с помощью команды convert(%,polynom), а затем выделить правую часть полученного выражения командой rhs(%).

1. Найти решение задачи Коши:

y(0)=0>, y(x), type=series);

В полученном решении слагаемое O(x^5) означает, что точность разложения была до 5-го порядка.

2. Найти общее решение дифференциального уравнения y»(х) — y3(х)=е — хcosx, в виде разложения в степенной ряд до 4-го порядка. Найти разложение при начальных условиях: y(0)=1, y'(0)=0.

>restart; Order:=4: de:=diff(y(x),x$2)-

Замечание: в полученном разложении запись D(y)(0) обозначает производную в нуле: y'(0). Для нахождения частого решения осталось задать начальные условия:

3. Найти приближенное решение в виде степенного ряда до 6-го порядка и точное решение задачи Коши:

Замечание: тип решения дифференциального уравнения в виде ряда есть series, поэтому для дальнейшего использования такого решения (вычислений или построения графика) его обязательно следует конвертировать в полином с помощью команды convert

На этом рисунке видно, что наилучшее приближение точного решения степенным рядом достигается примерно на интервале — 1

Численное решение дифференциальных уравнений

Численное решение дифференциальных уравнений с помощью команды dsolve. Построение графиков решений дифференциальных уравнений с помощью команды odeplot.

Для того, чтобы найти численное решение дифференциального уравнения (задачи Коши или краевой задачи) в команде dsolve следует указать параметр type=numeric (или просто numeric). Тогда команда решения дифференциального уравнения будет иметь вид dsolve(eq, vars, type=numeric, options), где eq – уравнения, vars – список неизвестных функций, options – параметры, позволяющие указать метод численного интегрирования дифференциального уравнения. В Maple реализованы такие методы: method=rkf45 — метод Рунге-Кутта-Фельберга 4-5-ого порядка (установлен по умолчанию); method=dverk78 – метод Рунге-Кутта 7-8 порядка; mtthod=classical – классический метод Рунге-Кутта 3-его порядка; method=gear и method=mgear – одношаговый и многошаговый методы Гира.

График численного решения дифференциального уравнения можно построить с помощью команды odeplot(dd, [x,y(x)], x=x1..x2), где в качестве функции используется команда dd:=dsolve(, y(x), numeric) численного решения, после нее в квадратных скобках указывают переменную и неизвестную функцию [x,y(x)], и интервал x=x1..x2 для построения графика.

1. Найти численное и приближенное решение в виде степенного ряда до 6-ого порядка задачи Коши: ,

Сначала найдем численное решение задачи Коши

Замечание: в строке вывода появляется сообщение о том, что при решении использован метод rkf45. Во избежание вывода строк, не несущих полезной информации, рекомендуется отделять промежуточные команды двоеточием. Если необходимо получить значение решения при каком-то фиксированном значении переменной х (заодно будет выведено значение производной решения в этой точке), например, при х=0.5, то следует набрать:

Теперь найдем приближенное решение задачи Коши в виде степенного ряда и построим графики численного решения и полученного степенного ряда в интервале их наилучшего совпадения.

Наилучшее приближение решения степенным рядом достигается примерно на интервале — 1

2. Построить графики решений задачи Коши системы дифференциальных уравнений:

х ‘(t)=2y(t)sin(t) — х (t) — t,

Пакет графического представления решений дифференциальных уравнений Detools.

Для численного решения задачи Коши, построения графиков решения и фазовых портретов в Maple имеется специальный пакет DEtools.

Команда DEplot из пакета DEtools строит численными методами графики решения или фазовые портреты. Эта команда аналогична команде odeplot, но более функциональна. Она, в отличие от odeplot, сама производит численное решение дифференциального уравнения. Основные параметры DEplot похожи на параметры odeplot: DEplot(de, vars, range, x=х1..х2, y=у1..у2, cond, ptions), где de — дифференциальное уравнение или система дифференциальных уравнений; vars – список неизвестных функций; range – диапазон измерения независимой переменной; cond – начальные условия; x=х1..х2 и y=у1..у2 – диапазоны изменения функций; options – дополнительные параметры.

Наиболее часто используемые параметры: linecolor=цвет линии; scene=[x,y] — определяет, какие зависимости выводить на график; iterations=число итераций, необходимое для повышения точности вычислений (по умолчанию это число равно 1); stepsize=число, равное расстоянию между точками на графике, по умолчанию оно равно (x2 — x1)/20, этот параметр необходим для вывода более гладкой кривой решения;obsrange=true/false — прерывать или нет вычисления, если график решения выходит за установленный для рисования интервал.

Для решения дифференциального уравнения n-ого порядка начальные условия можно задавать в более компактной форме: [x0, y0, y’0, y»0,…], где x0 — точка, в которой задаются начальные условия, y0 — значение искомой функции в точке x0, y’0, y»0,… — значения производных первой, второй и т.д. до (n — 1)-ого порядка.

Нарисовать график решения дифференциального уравнения:

, у(0)=0,у'(0)=1 ,у»(0)=1 , в интервале .

> restart; with(D Е tools):

(D@@2)(y)(0)=1]], stepsize=.1, linecolor=black,

Построение фазовых портретов систем дифференциальных уравнений.

Для дифференциального уравнения порядка выше первого команда DEplot рисует только кривые решений дифференциальных уравнений, а для систем дифференциальных уравнений первого порядка могут быть нарисованы и фазовые портреты.

С помощью команды DEplot можно построить фазовый портрет в плоскости (x, y), для системы двух дифференциальных уравнений:

Если система дифференциальных уравнений является автономной, то на фазовом портрете будет построено поле направлений в виде стрелок. Размер стрелок регулируется параметром arrows=SMALL, MEDIUM, LARGE, LINE или NONE.

Для того, чтобы нарисовать весь фазовый портрет, необходимо для каждой фазовой траектории указывать начальные условия: например, для системы двух дифференциальных уравнений первого порядка несколько начальных условий в команде DEplots указываются после задания диапазона изменения независимой переменной t: [[x(0)=x1, y(0)=y1], [x(0)=x2, y(0)=y2],…, [x(0)=xn, y(0)=yn]].

Начальные условия можно задавать в более компактной форме: [t0, x0, y0], где t0 — точка, в которой задаются начальные условия, x0 и y0 — значения искомых функций в точке t0.

Фазовый протрет системы двух дифференциальных уравнений первого порядка можно также построить с помощью команды phaseportrait(sys, [x,y],x1..x2,[[cond]]), где sys — система двух дифференциальных уравнений первого порядка, [x,y] — имена искомых функций, x1..x2 — интервал, на котором следует построить фазовый портрет, а в фигурных скобках указываются начальные условия. Эта команда находится в пакете DEtools, поэтому данный пакет должен быть предварительно загружен.

1. Построить фазовый портрет системы дифференциальных уравнений:

для нескольких наборов начальных условий: х(0)=1, у(0)=0.2; х(0)=0, у(0)=1; х(0)=1, у(0)=0.4; х(0)=1, у(0)=0.75; х(0)=0, у(0)=1.5; х(0)= — 0.1, у(0)=0.7.

> restart; with(D Е tools):

stepsize=0.1, arrows=none, linecolor=black);

2. Построить фазовый портрет с полем направлений автономной системы

для различных начальных условий х(0)=1, у(0)=0; х(0)= — 1, у(0)=0; х(0)= p , у(0)=1; х(0)= — p , у(0)=1; х(0)=3 p , у(0)=0.2; х(0)=3 p , у(0)=1; х(0)=3 p , у(0)=1.8; х(0)= — 2 p , у(0)=1;.

> restart; with(D Е tools):

3. Построить фазовый портрет системы дифференциальных уравнений:

Начальные условия, диапазон изменения переменной и размеры координатных осей подбираются самостоятельно из соображений наглядности фазового портрета.

Переходная функция (переходная характеристика)

Эта динамическая характеристика применяется для описания одноканальных систем

с нулевыми начальными условиями

Переходная характеристика h(t) — это реакция системы на входное единичное ступенчатое воздействие при нулевых начальных условиях.

— момент возникновения входного воздействия

Рис.2.4. Переходная характеристика системы

Переходные характеристики для различных значений активного сопротивления в электрической цепи:

Чтобы определить переходную характеристику аналитически, следует решить дифференциальное уравнение при нулевых начальных условиях и u(t)=1(t).

Для реальной системы переходную характеристику можно получить экспериментальным путем; при этом на вход системы следует подавать ступенчатое воздействие и фиксировать реакцию на выходе. Если ступенчатое воздействие отлично от единицы, то характеристику на выходе следует разделить на величину входного воздействия.

Зная переходную характеристику, можно определить реакцию системы на произвольное входное воздействие с помощью интеграла свертки

(2.8)

где — переменная интегрирования.2.5. Импульсная характеристика
(импульсная функция)

Данная характеристика используется для описания одноканальных систем вида (2.3) с нулевыми начальными условиями.

Импульсная характеристика (функция) — это реакция системы на входное единичное импульсное воздействие при нулевых начальных условиях.

Дельта-функция обладает следующими свойствами:

(2.9)

С помощью дельта-функции моделируется реальное входное воздействие типа удара.

Рис.2.5. Импульсная характеристика системы

Импульсные характеристики для различных значений активного сопротивления в электрической цепи:

Импульсная функция позволяет вычислить реакцию системы на произвольное входное воздействие при нулевых начальных условиях по выражению

(2.10)

Переходная функция и импульсная функция однозначно связаны между собой соотношениями

(2.11)

что позволяет по одной известной характеристике определить вторую.

Переходная матрица

Эта характеристика применяется для описания многоканальных систем вида (2.1) — (2.2) при нулевых входных воздействиях, то есть для автономных систем типа:

(2.12)

Переходная матрица — это решение матричного дифференциального уравнения

(2.13)

при нулевых входных воздействиях и единичных начальных условиях

где

Она обладает следующими свойствами:

для любого

(2.14)

Зная переходную матрицу, можно определить реакцию системы

на произвольное входное воздействие при любых начальных условиях x(0) по выражению

(2.15)

Здесь первое слагаемое — свободная составляющая движения, второе — вынужденная. Для выходных переменных имеем

(2.16)

Если система имеет нулевые начальные условия x(0)=0, то

(2.17)

(2.18)

Матрица называется матричной импульсной функцией потому что каждая компонента ее представляет собой импульсную функцию , которая является реакцией i-го выхода на j-ое импульсное входное воздействие при нулевых остальных входных воздействиях и начальных условиях.

Для многоканальных систем может быть определена также матричная переходная характеристика в виде

(2.19)

Для линейных систем с постоянными параметрами переходная матрица Ф(t) представляет собой матричную экспоненту

(2.20)

где

С учетом (2.20) выражения (2.15) и (2.16) принимают вид

(2.21)

(2.22)

Матричная импульсная функция линейной системы с постоянными коэффициентами следующая:

(2.23)

При небольших размерах или простой структуре матрицы A выражение (2.20) может быть использовано для точного представления переходной матрицы с помощью элементарных функций. В случае большой размерности матрицы A следует использовать существующие программы для вычисления матричного экспоненциала.

Передаточная функция

Наряду с обыкновенными дифференциальными уравнениями в теории автоматического управления используются различные их преобразования. Для линейных систем эти уравнения удобнее записывать в символической форме с использованием так называемого оператора дифференцирования

что позволяет преобразовывать дифференциальные уравнения как алгебраические и ввести новую динамическую характеристику — передаточную функцию.

Рассмотрим этот переход для многоканальных систем вида (2.6)

Запишем уравнение состояния в символической форме:

что позволяет определить вектор состояния

(2.24)

и выходные переменные системы

(2.25)

Матрица взаимосвязи между выходными переменными и управляющими воздействиями в выражении (2.25) при нулевых начальных условиях называется матричной передаточной функцией и обозначается

(2.26)

Она представляет собой матрицу со следующими компонентами:

(2.27)

где — скалярные передаточные функции, которые представляют собой отношение выходной величины к входной в символической форме при нулевых начальных условиях

Собственными передаточными функциями i-го канала называются компоненты передаточной матрицы , которые находятся на главной диагонали. Составляющие, расположенные выше или ниже главной диагонали, называются передаточными функциями перекрестных связей между каналами.

Обратная матрица находится по выражению

(2.28)

где — присоединенная матрица. Как следует из (2.28), все скалярные передаточные функции, которые являются элементами передаточной матрицы (2.27), содержат одинаковый знаменатель — det(pI-A). Он называется характеристическим полиномом и имеет n-ый порядок.

Если теперь характеристический полином приравнять нулю, то получим характеристическое уравнение системы,

A(p) = det(pI-A) = 0.

(2.29)

Определить передаточную матрицу для объекта

где

Воспользуемся выражением для передаточной матрицы (2.27) и найдем предварительно обратную матрицу (2.29). Здесь

Транспонированная матрица имеет вид

a det(pI-A) = p -2p+1, .

где — транспонированная матрица. В результате получим следующую обратную матрицу:

и передаточную матрицу объекта

Чаще всего передаточные функции применяются для описания одноканальных систем вида

(2.30)

Используя оператор дифференцирования, запишем уравнение (2.30) в символической форме и найдем передаточную функцию как отношение выходной величины к входной:

(2.31)

где — характеристический полином.

Передаточные функции принято записывать в стандартной форме:

(2.32)

где — коэффициент передачи;

Передаточную матрицу (передаточную функцию) можно также определить с помощью изображений Лапласа или Карсона-Хевисайда. Если подвергнуть одному из этих преобразований обе части дифференциального уравнения и найти соотношения между входными и выходными величинами при нулевых начальных условиях, то получим ту же самую передаточную матрицу (2.26) или функцию (2.31).

Для того, чтобы в дальнейшем различать преобразования дифференциальных уравнений, будем использовать следующие обозначения:

— оператор дифференцирования;

— оператор преобразования Лапласа.

Получив одну из динамических характеристик объекта, можно определить все остальные. Переход от дифференциальных уравнений к передаточным функциям и обратно осуществляется с помощью оператора дифференцирования p.

Рассмотрим взаимосвязь между переходными характеристиками и передаточной функцией. Выходная переменная находится через импульсную функцию в соответствии с выражением (2.10),

Подвергнем его преобразованию Лапласа,

и получим y(s) = g(s)u(s). Отсюда определим импульсную функцию:

(2.33)

Таким образом, передаточная функция — есть преобразование по Лапласу от импульсной функции.

Определить передаточную функцию объекта, дифференциальное уравнение которого имеет вид

Используя оператор дифференцирования d/dt = p, запишем уравнение объекта в символической форме

на основании которого определим искомую передаточную функцию объекта

Модальные характеристики

Модальные характеристики соответствуют свободной составляющей движения системы (2.6) или, другими словами, отражают свойства автономной системы типа (2.12)

(2.34)

Будем искать ее решение в виде экспоненты

(2.35)

где — скалярная экспонента, — вектор начальных условий.

Подставляя решение (2.35) в исходное уравнение (2.34), после преобразований получим

(2.36)

Система уравнений (2.36) будет иметь ненулевое решение относительно , если

(2.37)

Уравнение (2.37) называется характеристическим и имеет n-корней , которые называются собственными значениями матрицы A. При подстановке собственных значений в (2.37) получим

где — собственные векторы,

Совокупность собственных значений и собственных векторов представляет собой модальные характеристики системы.

Для (2.34) могут существовать лишь следующие экспоненциальные решения

(2.38)

которые называют модами. В случае, когда собственные значения вещественные и различные по значениям, полное решение системы (2.34) представляет собой линейную комбинацию мод:

(2.39)

Для получения характеристического уравнения системы достаточно общий знаменатель передаточной матрицы (передаточной функции) приравнять нулю (2.29).

Частотные характеристики

Если на вход объекта подавать периодический сигнал заданной амплитуды и частоты, то на выходе будет также периодический сигнал той же частоты, но в общем случае другой амплитуды со сдвигом по фазе. Взаимосвязь между параметрами периодических сигналов на входе и выходе объекта определяют частотные характеристики. Чаще всего их используют для описания одноканальных систем:

, n >= m.

(2.40)

Формально обобщенная частотная характеристика может быть получена из передаточной функции заменой p на

(2.41)

и представлена в виде

(2.42)

Составляющие обобщенной частотной характеристики имеют самостоятельное значение и следующие названия:

вещественная частотная характеристика (ВЧХ),
мнимая частотная характеристика (МЧХ),
амплитудная частотная характеристика (АЧХ),
фазовая частотная характеристика (ФЧХ).

Частотная характеристика по выражению (2.42) может быть построена на комплексной плоскости. В этом случае конец вектора, соответствующий комплексному числу , при изменении от 0 до прочерчивает на комплексной плоскости кривую, которая называется амплитудно-фазовой характеристикой (АФХ).

Рис.2.6. Пример амплитудно-фазовой характеристики системы

Фазо-частотная характеристика (ФЧХ) — графическое отображение зависимости сдвига по фазе между входным и выходным сигналами в зависимости от частоты,

Для определения числитель и знаменатель W(j ) разлагаются на множители не выше второго порядка

тогда , где знак «+» относится к i=1,2. l (числителю передаточной фунции), знак «-» -к i=l+1. L (знаменателя передаточной функции).

Каждое из слагаемых определяется выражением

где .

Наряду с АФХ отдельно строят и все остальные частотные характеристики. Так АЧХ показывает, как пропускает звено сигнал различной частоты; причем оценкой пропускания является отношение амплитуд выходного и входного сигнала. ФЧХ показывает фазовые сдвиги, вносимые системой на различных частотах.

Помимо рассмотренных частотных характеристик в теории автоматического управления используются логарифмические частотные характеристики. Удобство работы с ними объясняется тем, что операции умножения и деления заменяются на операции сложения и вычитания. Построенная в логарифмическом масштабе АЧХ, называется логарифмической амплитудной частотной характеристикой (ЛАЧХ)

(2.43)

Эта величина выражается в децибелах (дб). При изображении ЛАЧХ удобнее по оси абсцисс откладывать частоту в логарифмическом масштабе, то есть , выраженную в декадах (дек).

Рис.2.7. Пример логарифмической амплитудной частотной характеристики

В логарифмическом масштабе может быть изображена также и ФЧХ:

Рис.2.8. Пример логарифмической фазовой частотной характеристики

ЛФХ, реальная и асимптотическая ЛАЧХ системы, передаточная функция которой имеет вид:

(2.44)

Рис. 2.9. Реальная и асимптотическая ЛАЧХ системы

Рис. 2.10. ЛФХ системы

СТРУКТУРНЫЙ МЕТОД

3.2. Пропорциональное звено (усилительное, безынерционное)

3.3. Дифференцирующее звено

3.4. Интегрирующее звено

3.5. Апериодическое звено

3.6. Форсирующее звено (пропорционально — дифференцирующее)

3.7. Звено 2-го порядка

3.8. Структурные преобразования

3.8.1. Последовательное соединение звеньев

3.8.2. Параллельное соединение звеньев

3.8.3. Обратная связь

3.8.4. Правило переноса

3.9. Переход от передаточных функций к уравнениям состояния с пользованием структурных схем

3.10. Область применимости структурного метода

Введение

Для расчета различных систем автоматического управления их обычно разбивают на отдельные элементы, динамическими характеристиками которых являются дифференциальные уравнения не выше второго порядка. Причем различные по своей физической природе элементы могут описываться одинаковыми дифференциальными уравнениями, поэтому их относят к определенным классам, называемым типовыми звеньями.

Изображение системы в виде совокупности типовых звеньев с указанием связей между ними называется структурной схемой. Она может быть получена как на основе дифференциальных уравнений (раздел 2), так и передаточных функций. Данный способ и составляет суть структурного метода.

Предварительно рассмотрим подробнее типовые звенья, из которых состоят системы автоматического управления.

Пропорциональное звено

(усилительное, безынерционное)

Пропорциональным называется звено, которое описывается уравнением

y = k u.

(3.1)

Передаточная функция звена следующая:

(3.2)

а соответствующая ей структурная схема приведена на рис. 3.1.

Рис.3.1. Структурная схема пропорционального звена

Переходная характеристика (реакция звена на скачкообразное входное воздействие) имеет вид: h(t) = k

1(t) .

Импульсная функция имеет вид:

g(t) = k .

Модальные характеристики (собственные значения и собственные векторы) для пропорционального звена отсутствуют.

Заменив в передаточной функции p на j получим следующие частотные характеристики:

Рис.3.2 ВЧХ пропорционального звена

— амплитудно-фазовую: W (j ) k , — вещественную частотную характеристику: R( )=k , — мнимую частотную характеристику, I( )=0 .

Амплитудная частотная характеристика (АЧХ) определяется соотношением:

(3.3)

и имеет тот же вид, что и ВЧХ. Выражение для ФЧХ:

(3.4)

Это означает, что амплитуда периодического входного сигнала усиливается в k — раз, а фазовый сдвиг отсутствует.

Рис.3.3 АФХ пропорционального звена

АФХ звена имеет вид точки на комплексной плоскости (рис. 3.3). ЛАЧХ звена представляет собой прямую, параллельную оси абсцисс:

L( )=20lg[A( )]=20lg(k)

(3.5)

Рис.3.4 ЛАЧХ пропорционального звена

Как видим (3.3.), (3.4.), пропорциональное звено пропускает входные сигналы без искажений.

Дифференцирующее звено

Дифференцирующим называется звено, которое описывается дифференциальным уравнением:

y = k .

(3.6)

Его передаточная функция имеет вид:

W(p) = y(p)/u(p) = kp.

(3.7)

Рис.3.5. Переходная характеристика звена

Переходная характеристика дифференцирующего звена: h(t) = k (t- ).

Рис.3.6. Импульсная характеристика

Импульсная функция имеет вид

g(t) = k

(t-

(3.8)

Получим теперь частотные характеристики звена.

АФХ : W(j ) = j k , совпадает с положительной мнимой полуосью на комплексной плоскости;

ВЧХ : R( ) = 0 ,

МЧХ : I( ) = k ,

АЧХ : ,

ФЧХ : ,то есть для всех частот звено вносит постоянный фазовый сдвиг;

Рис.3.7. ЛАЧХ дифференцирующего звена

ЛАЧХ :

L( )=20lg(k )= 20lg(k)+20lg( ).

(3.9)

Как видно из графика рис.3.7, дифференцирующее звено усиливает высокочастотные сигналы.

Интегрирующее звено

Это звено, уравнение которого имеет вид:

(3.10)

От интегрального перейдем к дифференциальному уравнению звена

(3.11)

а затем к его передаточной функции

(3.12)

Переходная характеристика звена имеет вид:

(3.13)

а импульсная функция —

(3.14)

Определим частотные характеристики интегрирующего звена.

АФХ:

; ВЧХ:

; МЧХ:

;

АЧХ:

;

(3.15)

ФЧХ : .

Звено имеет постоянный фазовый сдвиг, который не зависит от частоты.

АФХ интегрирующего звена изображается на комплексной плоскости и имеет вид, представленный на рис.3.8.

Рис.3.9. ЛАЧХ интегрирующего звена

Получим логарифмическую амплитудно-частотную характеристику:

(3.16)

она имеет вид прямой на плоскости (рис.3.9).

имеет единственный корень, , который представляет собой модальную характеристику интегрирующего звена.

Апериодическое звено

Апериодическим называется звено, дифференциальное уравнение которого имеет вид

(3.17)

Перейдем к его стандартному описанию, для чего разделим обе части (3.17) на коэффициент a₀ ,

(3.18)

где , — коэффициент передачи звена.

Заменив в (3.18) d/dt на p, перейдем к символической записи дифференциального уравнения,

(Tp+1)y = ku,

(3.19)

и определим передаточную функцию апериодического звена:

(3.20)

Рис.3.10. Переходная характеристика

Его переходную характеристику можно найти как решение уравнения (3.18) при u=1(t) и y(0)=0,

h(t) = k(1- )·1(t).

(3.21)

Рис.3.11. Импульсная функция

Импульсную функцию вычислим по соотношению:

g(t)= (t)= ·1(t).

(3.22)

Для определения модальных характеристик запишем характеристическое уравнение звена

A(p) = Тр + 1 = 0

(3.23)

и вычислим его корень р = -1/Т .

Выражение, соответствующее АФХ апериодического звена имеет вид:

(3.24)

Рис.3.12. ВЧХ звена

Построим отдельно вещественную частотную характеристику по выражению

(3.25)

Рис.3.13. МЧХ звена

Мнимую частотную характеристику апериодического звена строим по соотношению

(3.26)

Рис.3.14. АЧХ апериодического звена

Построим амплитудную частотную характеристику по выражению:

(3.27)

Рис.3.15. ФЧХ апериодического звена

ФЧХ звена определяется соотношением

(3.28)

Рис.3.16 АФХ апериодического звена.

На комплексной плоскости строим АФХ апериодического звена по выражению (3.24), которая имеет вид полуокружности и приведена на рис.3.16. Определим теперь логарифмическую амплитудную частотную характеристику в виде:

(3.29)

Наиболее просто можно построить асимптотическую ЛАЧХ. В этом случае рассматривают отдельно области высоких (ОВЧ) и низких частот (ОНЧ) и для каждой определяют свою асимптоту:

1) ОНЧ: >1/T, L( )=20lg(k)-20lg(T ).

(3.31)

Частота 1/T называется собственной частотой апериодического звена.

Рис.3.17. ЛАЧХ апериодического звена

На рис.3.17 действительная ЛАЧХ показана пунктирной линией и несколько отличается от асимптотической, причем наибольшая погрешность будет на собственной частоте звена.

3.6. Форсирующее звено
(пропорционально — дифференцирующее)

Форсирующимназывается звено, дифференциальное уравнение которого имеет вид

y = k₁ u + k₂ .

(3.32)

Как видим, его можно представить как сумму пропорционального и дифференцирующего звеньев.

Передаточная функция форсирующего звена,

записывается в стандартной форме

W(p) = k (1+Tp),

(3.33)

где k=k₁ — коэффициент передачи, T=k₂/k₁ — постоянная времени звена.

Определим теперь его переходную характеристику

h(t- )= 1(t- )+ (t- )

(3.34)

и импульсную функцию

g(t)= (t) = (t) + (t).

(3.35)

Рис.3.18. Переходная характеристика форсирующего звена

Запишем выражения для частотных характеристик.

АФХ: W(j

)=k(1+jT

);

(3.36)

ВЧХ: R( )=k

МЧХ: I( )=k ;

АЧХ: A( )= k ;

ФЧХ:

;

(3.37)

ЛАЧХ: L(

)= 20 lg k + 10 lg(1+T)

(3.38)

Рис.3.19. ЛАЧХ форсирующего звена

Асимптотическую ЛАЧХ форсирующего звена можно получить, рассматривая отдельно области низких и высоких частот, как в случае апериодического звена, или суммируя ЛАЧХ пропорционального и дифференцирующего звеньев.

Рис.3.20 АФХ форсирующего звена