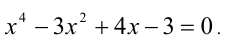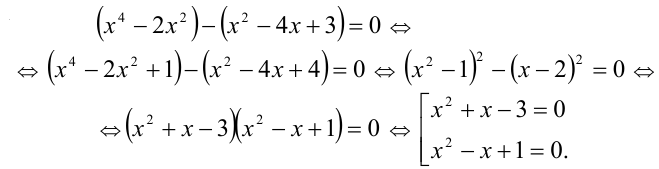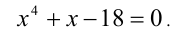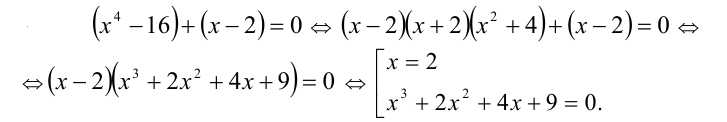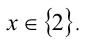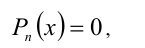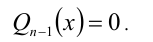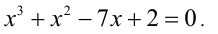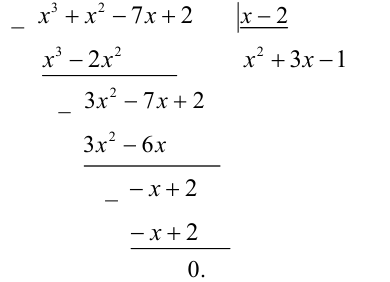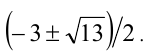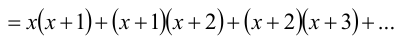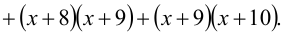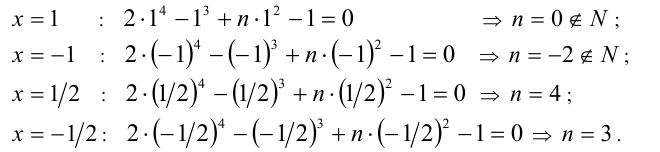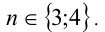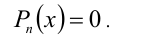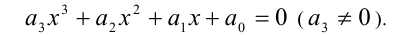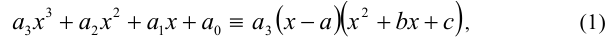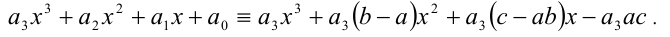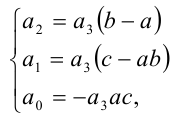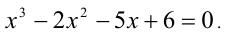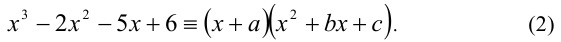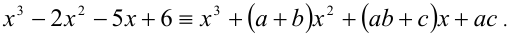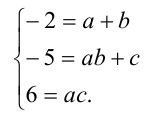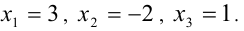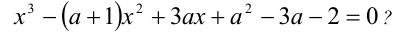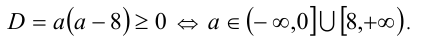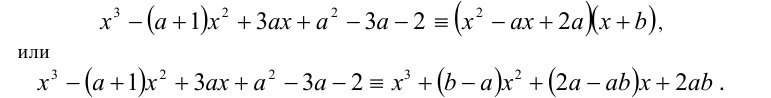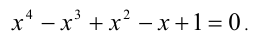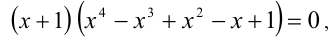Какими способами можно решать целые уравнения

Методы решения целых алгебраических уравнений

Методы решения целых алгебраических уравнений

Разложение на множители

Часть целых алгебраических уравнений (или аналогичных неравенств) степени n выше 2-й могут быть решены путём разложения многочлена в левой части уравнения (неравенства) на множители с помощью таких известных приёмов, как группировка и вынесение общего множителя за скобки. Иногда для достижения цели приходится прибавлять и одновременно вычитать одно и то же выражение. Отметим, что порой разложение на множители этим способом требует определённого искусства.

Если разложение на множители удалось выполнить, то решение алгебраического уравнения сводится к решению совокупности нескольких уравнений, но более низкой степени. Неравенство после разложения на множители можно решать методом интервалов.

Пример №176.

Решить уравнение

Решение:

Из 1-го уравнения находим корни 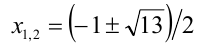, а второе не имеет решений.

Пример №177.

Найти все положительные корни уравнения

Решение:

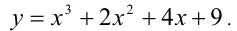
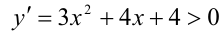
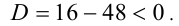
Покажем, что второе уравнение в совокупности не имеет положительных решений. Действительно, рассмотрим функцию Её производная при всех действительных x, так как Следовательно, функция всюду монотонно возрастает, при этом y(0) = 5 . Отсюда следует, что при x > 0 её график не пересекает оси абсцисс.

Ответ:

Подбор корня с последующим понижением степени уравнения

При решении алгебраических уравнений и неравенств степени выше второй можно использовать общий принцип последовательного понижения степени уравнения (неравенства).

Пусть требуется решить уравнение n -й степени

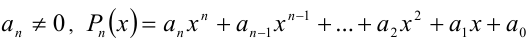
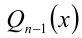
где целый рациональный алгебраический многочлен n -й степени. Если удалось подобрать (любым способом) какой-либо корень данного уравнения, то для нахождения остальных корней уравнения следует поделить многочлен на разность X — Х0 (или целенаправленной группировкой слагаемых, выделяя разность , разложить этот многочлен на множители). В результате деления образуется некоторый многочлен , степень которого на единицу меньше первоначальной. Таким образом, задача свелась к решению алгебраического уравнения степени n — 1 :

Пример №178.

Решить уравнение

Решение:

Заметим, что x = 2 является корнем данного уравнения. Найдём другие корни этого уравнения:

Решая уравнение 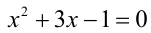, находим ещё два корня

Эта ссылка возможно вам будет полезна:

Пример №179.

Решить уравнение

Решение:

Легко заметить, проанализировав структуру уравнения, что числа x = 0 и x = -10 являются решениями данного уравнения. С другой стороны, ясно, что это квадратное уравнение, а поэтому может иметь не более двух корней. Так как два корня уравнения уже подобраны, то других корней нет.

В некоторых случаях, для того чтобы не подбирать корень «вслепую», можно воспользоваться следующим методом.

Метод поиска рациональных корней у многочленов с целыми коэффициентами

Для решения такого рода уравнений и неравенств используется метод, в основе которого лежит Теорема 9 из предыдущего пункта. Рассмотрим подробнее суть этого метода. Пусть требуется найти рациональные корни уравнения n -й степени

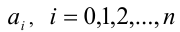
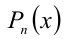
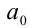
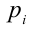
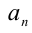
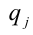
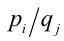
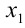
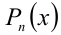
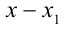
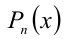
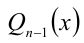
причём все коэффициенты алгебраического многочлена являются целыми числами. Поиск рациона-льных корней можно свести к перебору ограниченного количества вариантов. Для этого необходимо, во-первых, найти все целочислен-ные делители свободного члена (их конечное число, однако если этот коэффициент содержит слишком много делителей, то это затрудняет поиск корней в уравнении). Обозначим, например, эти делители через . Во-вторых, следует найти все натуральные делители старшего коэффициента уравнения . Обозначим эти делители через . В-третьих, надо составить всевозможные дроби вида . Наконец, перебирая по очереди все такие дроби, проверить, является ли в действительности каждая из них корнем данного уравнения. Найдя таким образом первый корень , вы или сразу понижаете степень уравнения делением многочлена на разность , (причём в силу следствия из теоремы Безу обязательно разделится нацело на этот линейный двучлен) и получаете некоторый многочлен степени на единицу меньшей, чем первоначальная. Или, перебирая все дроби, находите все рациональные корни и уже затем понижаете степень уравнения сразу на столько порядков, сколько рациональных корней удалось найти, и ищете оставшиеся иррациональные корни. В любом случае задача сводится к решению уравнения более низкой степени.

Пример №180.

При каких натуральных n уравнение 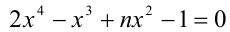имеет рациональные корни?

Решение:

Воспользуемся приведённым выше методом. Свободный член имеет два целочисленных делителя: ± 1, а старший коэффициент — два натуральных делителя: 1,2. Поэтому рациональные корни следует искать среди чисел 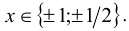Подставим их поочерёдно в уравнение.

Ответ:

Метод неопределённых коэффициентов

Иногда для решения целых алгебраических уравнений (неравенств) с одной или несколькими неизвестными используют метод неопределённых коэффициентов. Пусть, например, решается уравнение

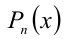
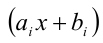
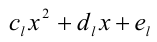
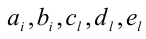
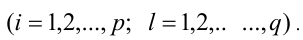
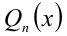
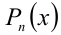
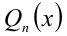
Суть метода состоит в том, что многочлен в левой части уравнения представляется в виде произведения линейных и(или) квадратичных сомножителей с неизвестными (неопределёнными) коэффициентами Чтобы найти эти коэффициенты, раскрывают скобки в указанном произведении и приводят образовавшийся при этом многочлен к стандарт-ному виду. Так как два многочлена и одной степени тождественно равны тогда и только тогда,

когда равны коэффициенты при одинаковых степенях переменной x, то, приравнивая эти коэффициенты, получают систему уравнений относительно неизвестных коэффициентов. Эту систему решают (или подбирают любое решение). Найденные таким способом коэффи-циенты 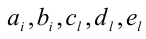становятся определёнными и их значения подставляются в исходное разложение. К недостаткам метода можно отнести то, что получаемая система уравнений для нахождения коэффициентов может оказаться громоздкой и трудной даже в подборе решения.

Рассмотрим применение этого метода на примере решения кубического уравнения. Допустим, требуется решить уравнение

Известно, что многочлен третьей степени всегда можно представить в виде произведения многочленов первой и второй степеней. Таким образом, сразу для всех действительных значений переменной x должно выполняться равенство

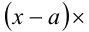
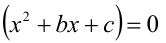
где числа а,b,c являются в данном случае искомыми неопределён-ными коэффициентами. Найдём их значения. После этого останется подставить их в правую часть (1) и, приравняв её к нулю, решить уравнение для нахождения всех корней уравнения.

Чтобы найти коэффициенты а,b,c, раскроем скобки в правой части тождества (1) и приведём образовавшийся при этом многочлен к стандартному виду

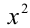
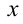
Многочлены третьей степени тождественно равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях x . Приравнивая коэффициенты при , и свободные члены, получаем систему трёх алгебраических уравнений относительно трёх неизвестных а,b,c :

решая которую (можно даже просто подобрать любое решение этой системы) находим коэффициенты.

Пример №181.

Решить уравнение

Решение:

Воспользуемся для решения методом неопределённых коэффициентов. Будем искать разложение многочлена, стоящего в левой части уравнения, в виде

Раскрыв скобки, приведём многочлен в правой части к стандартному виду

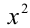
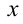
Приравнивая коэффициенты слева и справа при ,и свободные члены, получаем в итоге систему трёх уравнений с тремя неизвестными коэффициентами а,b,c:

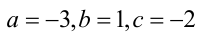
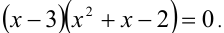
Найдя подбором решение подставим найденные коэффициенты в разложение (2). Таким образом, исходное уравнение приобретает вид Оно имеет три корня

Пример №182.

При каких значениях а все корни уравнения 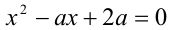являются корнями уравнения

Решение:

Чтобы первое из уравнений имело корни, необходимо, чтобы его дискриминант был неотрицателен, т.е.

Далее, второй многочлен в силу теоремы Безу должен делиться нацело на первый многочлен. Иными словами, должно найтись такое b , что при всех действительных x справедливо тождество

Для нахождения неопределённых коэффициентов (в данном случае в их роли выступают а и b ) воспользуемся известным фактом, что два кубических многочлена, стоящие по разные стороны от знака равенства, тождественно равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях переменной x . Приравнивая эти коэффициенты, получаем систему уравнений

Метод умножения на функцию

Иногда, применяя приём умножения обеих частей уравнения (неравенства) на некоторую функцию, удаётся упростить уравнение (неравенство).

Пример №183.

Решить уравнение

Решение:

Заметим, что x = — 1 (и вообще никакое отрицательное число) не является корнем данного уравнения. Домножим обе части данного уравнения на выражение (х +1). Получаем уравнение-следствие

множество решений которого состоит из всех решений исходного уравнения и числа x = -1. Это число является посторонним корнем, возникшем как раз в результате умножения уравнения на функцию, имеющую действительный нуль. Применяя известную формулу сокращенного умножения, получаем существенно более простое уравнение 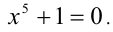Поскольку уравнение не имеет других решений, кроме x = -1, то приходим к ответу.

Ответ: уравнение не имеет решений.

Рассмотрим некоторые виды целых алгебраических уравнений, решаемые в основном при помощи специально подобранных подстановок.

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Эти страницы возможно вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Способы решения целых уравнений

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Министерство образования Российской Федерации

Методическая разработка по математике в 9 классе по теме:

«Способы решения целых уравнений»

МБОУ СОШ№13 города Костромы

Коржева Наталия Александровна

Кострома 2014 г.

Анализируя результаты проверки знаний выпускников средней школы по математике, можно сказать что, уровень математической подготовки не удовлетворяет тем целям, которые были поставлены перед учителем с пятого класса. Если некоторые шаблоны и алгоритмы школьниками и усвоены, то любое отступление от стандарта в формулировке задач и упражнений приводят ученика в замешательство. Это происходит потому, что в средней школе не уделяется достаточно внимания развивающей стороне математики. На экзамене ученик ищет шаблоны выполнения определенных заданий и поэтому видоизменение заданий в ту или иную сторону, приводит ученика в замешательство. В школьном курсе, как алгебры, а особенно геометрии на изучение некоторых вопросов отведено недостаточное количество часов, в учебнике недостаточно представлены способы решения задач, которые встречаются на экзамене. Так, например, в школьном курсе не рассматриваются формулы решения кубических уравнений, деление многочленов. Между тем круг задач, которые целесообразно решать в школе, значительно шире стандартной задачи «Решить уравнение» — можно говорить и о числе корней уравнения, и о нахождении целых и рациональных корней и т.д. Поэтому один из таких крупных разделов как «Тождественные преобразования многочленов и решение целых уравнений» необходимо обогатить заданиями, связанными с теоремой о корне, теоремой о целых корнях уравнения. Подобное расширение внутри этой важнейшей темы послужило бы глубокому и прочному усвоению базовых знаний, умений и навыков, которые позволят решать более широкий спектр задач, развить мышление учащихся, расширить их математический аппарат. Кроме того, существует большой разрыв между математикой, которая преподается в средней школе, и наиболее живыми и важными для естествознания и техники разделами современной математической науки. Материал по данной теме вполне доступен для изучения учащимися 9 классов. Его изучение подготовит ребят к успешному усвоению курса алгебры в старшей школе. В отличие от большинства тем школьного курса алгебры, ориентированных в целом на изучение функций, приемы решения уравнений представляет собой математический аппарат для решения задач более широкого содержания — прежде всего решения уравнений. Они позволяют учащимся решать уравнения третьих и более высоких степеней с целыми коэффициентами, которые в школьном курсе не рассматриваются.

Методическая разработка может быть использована учителями математики как на уроках так и на занятиях в рамках элективного курса.

Данная методическая разработка позволяет реализовать достижение следующих целей:

Расширить и углубить знания учащихся по решению целых уравнений с одной переменной высших степеней

Подготовить учащихся к применению знаний в нестандартной ситуации, обеспечить устойчивую мотивацию при решении целых уравнений

Приобретение учащимися уверенности в решении задач по данной теме

1. Беседа с учащимися

2. Система упражнений и задач, формирующих интерес к изучению темы «Способы решения целых уравнений»

3. Повторение, систематизация и обобщение знаний

4. Расширение и углубление знаний

5. Система заданий для самостоятельной работы, домашнее задание

Беседа с учащимися

Ребята! Вам предстоит итоговая аттестация по математике. Чтобы успешно сдать экзамен, вы должны знать математику не только на минимальном уровне, но и уметь применить ваши знания в нестандартных ситуациях. Наша задача: систематизация и обобщение, расширение и углубление знаний по решению целых уравнений с одной переменной со степенями, выше второй степени. Уравнение — это самая простая и распространенная математическая задача. Вы накопили некоторый опыт решения разнообразных уравнений и нам нужно привести свои знания в порядок, разобраться в приемах решения нестандартных уравнений. Уравнения сами по себе представляют интерес для изучения. Самые ранние рукописи свидетельствуют о том, что в Древнем Вавилоне и Древнем Египте были известны приемы решения линейных уравнений. Квадратные уравнения умели решать около 2000 лет назад до н.э. вавилоняне. Стандартные приемы и методы решения элементарных алгебраических уравнений являются составной частью решения всех типов уравнений. В простейших случаях решение уравнения с одним неизвестным распадается на два шага: 1) преобразование уравнения к стандартному виду; 2) решение стандартного уравнения. Полностью алгоритмизировать процесс решения уравнений нельзя, однако полезно запомнить наиболее употребительные приемы, общие для всех типов целых уравнений, позволяющих привести уравнение к стандартному виду «Произведение равно нулю» и понижающих степень множителей. Для уравнений высшей степени известны формулы корней, но они очень сложные Многие уравнения при применении нестандартных приемов решаются гораздо короче и проще.

Система упражнений и задач, формирующих интерес к изучению темы «Способы решения целых уравнений»

Предлагаются задания повышенной трудности

1) х 2 — 6│х│+8 = 0 2) х 5 +2х+1 = 0

3) х 5 +х 3 +2х – 4 = 0 4) (х+1)(х+2)(х+4)(х+5) = 40

5) 2х 4 +х 3 -6х 2 +х+2=0 6) (х+2)(х+3)(х+8)(х+12) = 4х 2

7) х 3 – 8х 2 + 13х -2=0 8) 2х 4 – 2х 3 – х +1 = 0

Задание для учащихся: проанализируйте данные уравнения, ответив на следующие вопросы:

1.Какое уравнение называется целым и есть ли среди данных уравнений — целые?

2. Как найти степень целого уравнения, сколько корней может иметь уравнение с одной переменной первой, второй, третьей степени?

3. Могли бы вы для какого-нибудь уравнения предложить способ решения?

4.Какие способы решения целых уравнений вы можете назвать?

5. Можно ли здесь применить один из названных вами способов?

3. Повторение, систематизация и обобщение знаний

Повторение известных методов решения уравнений.

Метод разложения на множители

Если уравнение равносильными преобразованиями можно привести к виду f(x)·q(x)=0, то f(x)=0 или q(x)=0, если х удовлетворяет области допустимых значений переменной.

Введение новой переменной (замена переменной)

Заменим некоторое выражение в уравнении новой переменной и получим более простое уравнение относительно новой переменной. Решая полученное уравнение, находим значение введенной переменной. Возвращаясь к старой переменной, решаем уравнения и вычислим корни исходного уравнения.

Рассмотрим уравнение f(x)=q(x). Строим в одной системе координат графики функций у = f(x) и у = q(x). Абсциссы точек пересечения этих графиков являются корнями уравнения (Этот способ не всегда обеспечивает высокую точность значений корней уравнения).

Цель проведения: повторить известные виды целых уравнений и известные способы их решения

x 3 — 8х 2 –х +8 =0

x 3 -2х 2 -4х +8 =0

x 3 – 3х 2 -4х = 0

(х 2 – 3х +1)(х 2 -3х +3)=3

(2х + 1) 2 + 4(2х +1) = 221

После выполнения самостоятельной работы учащиеся проверяют ответы, еще раз обсуждают выбор способа решения целых уравнений и после сдают самостоятельную работу.

Рассмотрим решение более сложных заданий:

1). Найти сумму корней уравнения (х+1)(х+2)(х+4)(х+5) = 40

Произведение 1 и 4, 2 и 3 множителей заменим квадратными трехчленами

(х 2 +6х+5)(х 2 +6х+8) = 40. Вводим новую переменю у = х 2 +6х+5 и получим квадратное уравнение относительно у: у 2 +3у – 40 =0. Находим корни этого уравнения и корни исходного уравнения, х ₁ = 0, х ₂ =-6. Сумма корней равна -6.

2) . Решите уравнение (х+2)(х+3)(х+8)(х+12) = 4х 2

Произведение 1 и 4, 2 и 3 множителей заменим квадратными трехчленами

(х 2 + 14х + 24)(х 2 + 11х +24)= 4х 2 . Обе части уравнения разделим на х 2 ≠ 0 и получим уравнение (х+24/х +14)(х+24/х +11)=4. Пусть х+24/х=у, тогда (у+14)(у+11)=4,

Получим квадратное уравнение у 2 +25у+150=0, корнями которого будут числа -10; -15. Возвращаясь к замене получим корни исходного уравнения:

4. Расширение и углубление знаний

Рассмотрим некоторые приемы решения целых уравнений и теоремы из курса алгебры о решении уравнений.

Теорема1: О корне многочлена .

Если число а является корнем многочлена Р(х) = а ₀ х п + а ₁ х п-1 +….+а _п-1 х + а _п , где а ₀ ≠0, то этот многочлен можно представить в виде произведения (х-а)Р ₁ (х), где Р ₁ (х) – многочлен п-1-й степени

Теорема 2: О целых корнях уравнения

Если уравнение а ₀ х п + а ₁ х п-1 +….+а _п-1 х + а _{п =0,} в котором все коэффициенты целые числа, причем свободный член отличен от нуля, имеет целый корень, то этот корень является делителем свободного члена.

Возвратимся к ранее предложенным заданиям . Есть много интересных методов решения уравнений. Не следует думать, что любое нестандартное уравнение труднее для решения, чем стандартное.

При решении уравнений высших степеней иногда применяется процедура угадывания хотя бы одного корня. Угаданный корень позволяет понизить степень многочлена на единицу, дальше достаточно выполнить деление уголком. Для нахождения корней многочлена полезно знать теорему о целых корнях уравнения. Рассмотрим, как она применяется при решении уравнений. Приведем примеры решения целых уравнений с использованием указанных теорем. Сначала проверяем, являются ли числа 1 и -1 корнями многочлена.

Здесь нам помогут такие факты:

Если сумма всех коэффициентов многочлена равна нулю, то число 1 является корнем многочлена.

Например, в многочлене 3х 2 -2х 3 — 7х +6 сумма коэффициентов равна нулю:

3 -2-7+6=0 . Легко проверить, что х=1 является корнем многочлена.

Свободный член считается коэффициентом при нулевой степени переменной, поскольку а _{n =} а _n х 0 . а – свободный член многочлена.

Например, в многочлене 5х 4 +3х 3 + 2х 2 +5х +1 сумма коэффициентов при четных степенях х: 5 +2 +1 =8 , и сумма коэффициентов при нечетных степенях х : 3 +5 =равна 8. Легко проверить, что х= -1 является корнем многочлена.

Если ни 1, ни -1 не являются корнями многочлена, то двигаемся дальше.

Рассмотрим, например, многочлен 2х 3 – 3х 2 + 5х -14

Делители свободного члена: +1;-1;+2;-2;+7;-7

Сумма всех коэффициентов многочлена равна : 2-3+5-14 ≠ 0 следовательно, число 1 не является корнем многочлена.

Сумма коэффициентов при четных степенях х : -3-14=-17

Сумма коэффициентов при нечетных степенях х: 2+5=7; -17 ≠7,

следовательно, число -1 также не является корнем многочлена.

Проверим, является ли число 2 корнем многочлена, получаем верное равенство, следовательно, число 2 является корнем многочлена. Значит, по теореме о корне, многочлен 2х 3 — 3х 2 + 5х -14 делится без остатка на двучлен х-2 .

Как разделить многочлен на двучлен?

Многочлен можно разделить на двучлен столбиком.

Разделим многочлен на двучлен x -2 столбиком:

_2 x 3 -3 x 2 +5 x -14 x -2

2 x 3 -4 x 2 2 x 2 + x +7

Пример 2 (Задание можно решить также с помощью замены переменной)

Разложить на множители многочлен

P(x) = x 4 + 4х 2 -5

Среди делителей свободного члена число 1 является корнем данного

многочлена P(x) , а это значит , что из теоремы о целых корнях

P(x) делится на (x – 1) без остатка.

_x 4 + 4x 2 – 5 x – 1

x 4 – x 3 x 3 + x 2 + 5x + 5

P(x)/(x – 1) = x 3 + x 2 + 5x + 5 , значит P(x) = (x – 1)(x 3 + x 2 + 5x + 5).

Среди делителей свободного члена многочлена x 3 + x 2 + 5x + 5

x = -1 является его корнем, а это значит, что x 3 + x 2 + 5x + 5 делится на (x + 1) без остатка

_x 3 + x 2 +5x + 5 x + 1

(x 3 + x 2 +5x + 5)/(x + 1) = x 2 +5 , значит x 2 +5x + 5 = (x +1)(x 2 +5).

P(x) = (x – 1)(x +1)(x 2 +5) .

Двучлен (x 2 + 5) на множители не раскладывается, т.к. действительных корней не имеет, поэтому P(x) далее на множители не раскладывается.

Ответ: x 4 + 4x 2 – 5 = (x – 1)(x +1)(x 2 +5) .

Пример 3 . Решить уравнение х 3 -8х 2 + 13х -2 =0.

Если уравнение имеет целый корень, то в силу теоремы 2 он является делителем числа -2, т.е. равен одному из чисел 1,-1,2,-2. Проверка убеждает нас, что корнем уравнения является число 2. Значит в силу теоремы многочлен х 3 -8х 2 + 13х -2 можно представить в виде в виде (х-2) F (х), где F (х) – многочлен второй степени. Для того, чтобы найти многочлен F (х), разделим, многочлен х 3 -8х 2 + 13х -2 на двучлен х-2. Деление многочленов выполним «уголком».

_х 3 -8х 2 +13х -2 х-2

x 3 -2 x 3 x 2 -6 x +1

Значит исходное уравнение можно представить в виде (х- 2 ) (х 2 -6х +1) =0.

Отсюда х-2=0 или х 2 — 6х +1 =0, Первое уравнение имеет корень – число 2, второе уравнение имеет два корня: 3 -, 3 +

Пример 4 . Доказать, что уравнение 2х 4 – 2х3 — х +1 = 0 не имеет целых корней. Целыми корнями могут быть делители свободного члена -1,1. Непосредственной проверкой убеждаемся, что ни одно из них не является корнем уравнения.

Использование монотонности функции.

Вспомним определение возрастающей и убывающей функций:

Функция называется возрастающей на некотором промежутке, если произвольному большему значению аргумента соответствует т большее значение функции.

Функция называется убывающей на некотором промежутке, если произвольному большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Теорема 3 . Если y = g(x) – монотонно возрастает на промежутке I и y = f(x) – монотонно возрастает на промежутке I, то y = g(x)+f(x) – монотонно возрастает на промежутке I.

Теорема 4 . Если y = f(x) возрастает (убывает) на промежутке I, то уравнение f(x) = a имеет на промежутке I не более одного корня.

Теорема 5 . Если y = f(x) возрастает на I, а y = g(x) убывает на I, то уравнение f(x) = g(x) на промежутке I имеет не более одного корня.

Пример 5. Решите уравнение: x 5 +x 3 +2x-4=0.

Решение: Функция f(x) = x 5 +x 3 +2x-4 возрастает как сумма трех возрастающих функций y = x 5 , y = x 3 и y = 2x-4 на R. Тогда уравнение f(x) = 0 имеет не более одного корня. Вспомним правило: все целые корни многочлена Р(х) с целыми коэффициентами содержатся среди делителей свободного члена.

Испытывая делители свободного члена, находим, что x=1.

Других целых корней у уравнения нет.

Пример 6 . Решить уравнение х 5 + 2х — 3= 0

Представим в виде х 5 = — 2х +3.

Функция у = х 5 –возрастающая, а функция у = -2х +3 – убывающая на R , значит уравнение имеет не более одного корня. Угадываем корень х = 1.

Использование четности функции

Вспомним определение четной функции:

Функция называется четной, если ее область определения симметрична относительно нуля и выполняется равенство f(-x)= f(x). График четной функции симметричен относительно оси ординат. При решении уравнения достаточно найти его неотрицательные корни, остальные восстановить по соображению симметрии.

Пример 7. Решить уравнение х 2 — 6│х│+8 = 0 и найти произведение корней.

у= х 2 — 6│х│+8 — четная функция. Решим уравнение для неотрицательных х.

х 2 — 6х+8 = 0, х ₁ =2 и х ₂ =4 (оба корня годятся). По соображениям симметрии

х ₃ = — 2 и х ₄ = — 4. Произведение корней -2·2·(-4)·4=64 Ответ. 64.

Решение возвратных уравнений

Возвратным уравнением называется уравнение вида

а ₀ х п + а ₁ х п-1 +….+а _п-1 х + а _п =0 _, в котором коэффициенты членов уравнения, одинаково отстоящих от начала и конца, равны, т.е. а к = а п-к , где к =0,1,2,….п.

Рассмотрим пример возвратного уравнения четвертой степени.

Пример 8. Решить уравнение: х 4 – 5х 3 + 6 – 5х +1 = 0.

Воспользуемся тем, что коэффициенты членов многочлена, записанного в левой части уравнения, одинаково удаленных от начала и конца, равны между собой. Разделив обе части уравнения на х 2 , получим равносильное ему уравнение.

х 2 -5х+6 – 5/х + 1/х 2 = 0

Сгруппируем первый член с последним и второй с четвертым, получим:

(х 2 + 1/х 2 ) -5(х + 1/х) + 6 =0

Введем новую переменную: у = х +1/х и возведем левую и правую часть в квадрат, тогда

x 2 + 2 +1/х 2 = у 2

Выполнив подстановку, получим

решая это квадратное уравнение получим: у ₁ =1 и у ₂ =4, значит

х + 1/х=1 или х + 1/х=4.

Решая эти уравнения, найдем, что первое из них не имеет корней, а второе имеет два корня:

Пример 9 . Решить уравнение 2х 4 +х 3 -6х 2 +х+2=0

Это возвратное уравнение

Разделим обе части уравнения на х 2 ≠ 0. 2х 2 +х – 6 +1/х+2/(х 2 )=0.

Сгруппируем 2(х 2 +1/(х 2 ))+(х+1/х) -6=0, вводим новую переменную у=х+1/х и получим уравнение 2(у 2 -2)+у -6=0, 2у 2 + у -10=0.

Выделим названия рассмотренных способов и приемов решения целых уравнений:

— Разложение на множители

— Использование четности функции

— Использование монотонности функции

— Умножение меньшего множителя на больший и умножение двух средних множителей с последующей заменой переменной

— Подбор корня и деление многочленов столбиком

— Деление на x 4 с последующей заменой переменной

Контрольное задание: Проверьте как вы усвоили новый материал, постарайтесь для каждого уравнения назвать соответствующий способ решения.

2) (х 2 +3х ) 2 +2 (х 2 +3х ) — 120=0

6) (х 2 +х+6)(х 2 +х-4)=144

7) х 5 — х 4 -2х 3 +2х 2 -3х +3=0

9) 2х 4 +х 3 — 3х 2 +х +2=0.

Учащиеся в фронтальном опросе предлагают соответствующий способ решения каждого уравнения, возможно даже не один.

1. Использование монотонности функции.

2. Замена переменной.

3. Графический способ или использование монотонности функции.

4. Замена переменной или использование четности функции.

5. Умножение меньшего множителя на больший и умножение двух средних множителей с последующей заменой переменной.

6. Разложение на множители.

8) Подбор коня и деление многочленов столбиком.

9) Деление на x 4 или подбор коня и деление многочленов столбиком

5. Задания для самостоятельной работы

Решите уравнение, выбирая подходящий метод или используя разные способы.

х 4 +2х 3 – 6х 2 +2х+1=0.

Ю.Н. Макарычев и др., Просвещение, 2011г.

У.И. Сахарчук, Л.С. Сагателова, Решение уравнений высших степеней: Волгоград, 2007.

Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ.

Виноградов И.М. (главный редактор) Математическая энциклопедия.

Б.М. Ивлев и др. Задачи повышенной трудности по алгебре и началам анализа 1990г.

Приемы решения целых уравнений

Цели урока:

учебная: систематизация и обобщение, расширение и углубление знаний обучающихся по решению целых уравнений с одной переменной высших степеней; подготовка учащихся к применению знаний в нестандартной ситуации.

развивающая: развитие личности обучающегося через самостоятельную творческую работу, развитие инициативы обучающихся; обеспечивать устойчивую мотивационную среду, интерес к изучаемой теме; развивать умение обобщать, правильно отбирать способы решения уравнения;

воспитательная: развитие интереса к изучению математики, подготовка обучающихся к применению знаний в нестандартной ситуации; воспитывать волю и настойчивость для достижения конечных результатов

Просмотр содержимого документа
«Приемы решения целых уравнений 9»

Открытое занятие по математике

в 9 классе по теме:

Приемы решения целых уравнений

Иванова Рина Юсуповна

учебная: систематизация и обобщение, расширение и углубление знаний обучающихся по решению целых уравнений с одной переменной высших степеней; подготовка учащихся к применению знаний в нестандартной ситуации.

развивающая: развитие личности обучающегося через самостоятельную творческую работу, развитие инициативы обучающихся; обеспечивать устойчивую мотивационную среду, интерес к изучаемой теме; развивать умение обобщать, правильно отбирать способы решения уравнения;

воспитательная: развитие интереса к изучению математики, подготовка обучающихся к применению знаний в нестандартной ситуации; воспитывать волю и настойчивость для достижения конечных результатов.

Мотивация изучения темы.

Актуализация знаний по теме «Целые уравнения»

Систематизация и обобщение знаний – сообщения обучающихся о стандартных приемах решения уравнений.

Расширение и углубление знаний – сообщение учителя о нестандартных приемах решения уравнений.

Домашнее задание: примеры на осмысление, закрепление новых знаний.

1.Организационный момент – ставятся цели и задачи урока.

Ребята! Вам предстоит итоговая аттестация по математике.

Уравнение — это самая простая и распространенная математическая задача. Вы накопили некоторый опыт решения разнообразных уравнений и нам нужно привести свои знания в порядок, разобраться в приемах решения нестандартных уравнений.

Стандартные приемы и методы решения элементарных алгебраических уравнений являются составной частью решения всех типов уравнений.

В простейших случаях решение уравнения с одним неизвестным распадается на два шага: преобразование уравнения к стандартному и решение стандартного уравнения. Полностью алгоритмизировать процесс решения уравнений нельзя, однако полезно запомнить наиболее употребительные приемы, общие для всех типов уравнений. Многие уравнения при применении нестандартных приемов решаются гораздо короче и проще.

2. Мотивация изучения темы.

Предлагаются задания повышенной трудности из учебника алгебры и заданий ГИА.

(написать на доске).

Для уравнений высшей степени известны формулы корней, но они очень сложные. Иногда приходится решить, применяя специальные приемы.

3. Повторение материала, изучаемого на предыдущих занятиях:

Виды целых уравнений и способы решения уравнений 1-ой и 2-ой степени

Уравнения 1-ой степени решаются с помощью арифметических операций, уравнения 2-ой степени – с помощью формул корней.