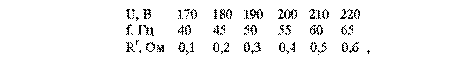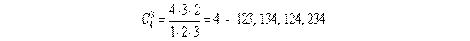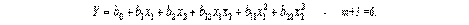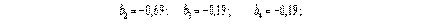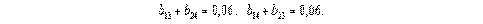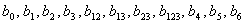Какими уравнениями описываются результаты активного эксперимента

Реферат: Математическое моделирование при активном эксперименте

Министерство образования РФ

Волгоградский государственный технический университет

Кафедра «САПР и ПК»

«Математическое моделирование при активном эксперименте»

Выполнил: студент II -го курса

Проверил: Фоменков С.А.

Основные положения теории планирования эксперимента.

Различают физическое и математическое моделирование. При физическом моделировании исследование объекта происходит при его воспроизведении в ином масштабе. Здесь возможен количественный перенос результатов эксперимента с модели на оригинал. Однако для анализа сложных объектов и процессов, каковыми являются большинство электронных схем, конструкций и технологических процессов производства радиоэлектронной техники, приборостроения, машиностроения и других промышленных отраслей, применение физического моделирования затруднительно, поскольку приходится использовать большое число критериев и ограничений, которые могут быть несовместимы, а зачастую и невыполнимы.

Математическое моделирование является методом качественного или количественного описания объектов или процессов, при этом реальный объект, процесс или явление упрощается, схематизируется и описывается определенным уравнением. В большинстве случаев математическая модель представляет собой уравнение регрессии, то есть геометрическое место точек математических ожиданий условных распределений целевой функции. Простейшим примером такой модели является уравнение парной корреляции, где на целевую функцию воздействует один фактор. На практике в реальном производстве на целевую функцию воздействуют много факторов и искомое уравнение регрессии становится многомерным.

Существует много методов отыскания уравнения регрессии, которые можно условно разделить на два класса: методы активного и методы пассивного эксперимента. Под активным экспериментом будем понимать эксперимент, предварительный план которого составлен так, чтобы получить максимальную информацию о целевой функции при минимальной ее дисперсии и проведении минимального числа опытов (эффективный план). Такой план (например, полный факторный эксперимент) требует искусственного одновременного варьирования всеми факторами в довольно широких пределах. Методы активного эксперимента довольно хорошо разработаны в специальном разделе математической статистики, который называется «Теория планирования эксперимента».

Под математической теорией планирования эксперимента будем понимать науку о способах составления экономных экспериментальных планов, которые позволяют извлекать наибольшее количество информации об объекте, о способах проведения эксперимента, о способах обработки экспериментальных данных, о способах использования полученных результатов для оптимизации исследуемых объектов (например, технологических процессов производства массовой продукции). Математический аппарат теории планирования эксперимента построен на сочетании методов математической статистики и методов решения экстремальных задач.

В настоящее время выделяют два основных направления теории планирования эксперимента:

1. планирование экстремальных экспериментов;
2. планирование экспериментов по выявлению механизма явлений.

В этой курсовой работе описываются в основном методы первого направления.

Любое экспериментальное исследование содержит три этапа:

1. этап постановки задачи;
2. этап планирования и проведения эксперимента;
3. анализ и интерпретация результатов.

Главной трудностью на этапе постановки задачи является переход с языка специальности на язык планирования эксперимента, на язык математики.

Построение математической модели технологического процесса в зависимости от поставленной задачи может преследовать следующие цели: минимизировать расход материала на единицу выпускаемой продукции при сохранении качества, произвести замену дорогостоящих материалов на более дешевые или дефицитных на распространение; сократить время обработки в целом или на отдельных операциях, перевести отдельные режимы в некритические зоны, снизить трудовые затраты на единицу продукции и т.п.; улучшить частные показатели и общее количество готовой продукции, повысить однородность продукции, улучшить показатели надежности и т.п.; увеличить надежность и быстродействие управления, увеличить эффективность контроля качества, создать условия для автоматизации процесса управления и т.п.

Прежде всего, необходимо выбрать зависимую переменную Y, которую впредь будем называть целевой функцией или параметром оптимизации, за который принимают один из показателей качества продукции либо по каждой технологической операции отдельно, либо по всему технологическому процессу сразу. Параметр оптимизации должен соответствовать следующим требованиям:

• параметр должен измеряться при любом изменении (комбинации) режимов технологического процесса;
• параметр должен быть статистически эффективным, то есть измеряться с наибольшей точностью;
• параметр должен быть информационным, то есть всесторонне характеризовать технологический процесс (операцию);
• параметр должен иметь физический смысл, то есть должна быть возможность достижения полезных результатов при соответствующих условиях процесса;
• параметр должен быть однозначным, то есть должно минимизироваться или максимизироваться только одно свойство изделия.

За фактор принимают контролируемую величину объекта (изделия, процесса, операции), то есть величину, характеризующую то или иное свойство объекта или режим технологического оборудования. Эта величина, числовое значение которой измеряется в пределах (границах) изменения, должна влиять на параметр оптимизации.

При определении величин количественных оценок во внимание должны приниматься только те факторы, которые имеют четкий метрологический смысл (возможность измерения фактора с определенной точностью).

Описание исследуемого объекта нельзя получить в виде точной формулы функции, справедливой во всем диапазоне существования аргументов. Оно может быть лишь приближенным и на небольшом участке в окрестностях выбранной базовой точки. Аппроксимация искомой математической зависимости представляет собой некоторый полином — отрезок ряда Тейлора, в который разлагается неизвестная зависимость:

(1)

В силу наличия неуправляемых и даже неконтролируемых входных переменных Xi изменение величины Y носит случайный характер, а потому уравнение (1) не дает нам точной связи между входом и выходом объекта и является лишь условным математическим ожиданием случайной величины Y, т.е. уравнением регрессии.

Чтобы отыскать коэффициенты уравнения регрессии по результатам экспериментов в N точках факторного пространства (что является типичной задачей регрессионного анализа), необходимо выполнение следующих предпосылок:

1. Результаты наблюдений Y 1 , Y 2 . Y n выходной величины в N точках факторного пространства представляют собой независимые, нормально распределенные случайные величины.
2. Выборочные дисперсии опытов однородны, т.е. статистически неразличимы. Это требование означает независимость выборочной дисперсии от местоположения точки факторного пространства, в которой проводится конкретный опыт (ротатабельность).
3. Независимые переменные X 1 , X 2 . X n измеряются с ошибкой много меньшей, чем величина возможного отклонения выходного параметра Y под влиянием неучтенных факторов.

Тогда задача отыскания коэффициентов уравнения регрессии сводится к решению системы так называемых нормальных уравнений:

(2)

где Y g — экспериментальные значения выходного параметра, полученные в g-й точке факторного пространства;
— значение выходного параметра, найденные по уравнению регрессии в тех же точках;
d — количество членов в уравнении регрессии.

Выражение (2) является основным критерием проверки правильности найденного уравнения регрессии.

Чтобы система нормальных уравнений, которая может быть представлена в виде матрицы, имела единственное решение, необходимо, чтобы матрица была невырожденной, т.е. чтобы вектор – столбцы были линейно – независимы. Чтобы величины коэффициентов уравнения регрессии не зависели от числа членов матрицы, нужно на нее наложить дополнительное условие ортогональности вектор столбцов.

1. Полный факторный эксперимент

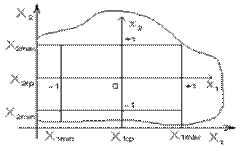
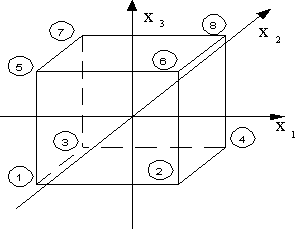
Полным факторным экспериментом (ПФЭ) называется эксперимент, реализующий все возможные повторяющиеся комбинации уровней независимых переменных, каждая из которых принудительно варьируется на двух уровнях (Рис 1)

Рис. 1 Схема перехода в относительные координаты

Число этих комбинаций N=2 n определяет тип планирования.

Для гарантированного получения единственного решения системы нормальных уравнений необходимо иметь ортогональную матрицу планирования, что невозможно обеспечить в абсолютной системе единиц факторов X i , то есть тогда, когда факторы именованные (например, трудно представить 17 километров ортогональными к 12 килограммам). Поэтому необходимо провести предварительное преобразование каждого фактора — его перевод в систему относительных координат. Такое преобразование легко сделать с помощью переноса начала координат в базовую точку X * и выбора единицы отсчета D X i по каждой координате X i .

(3)

Это дает возможность легко построить ортогональную матрицу планирования и значительно облегчает дальнейшие расчеты, так как в этом случае верхние и нижние уровни варьирования X iв и X iн в относительных единицах будут равны соответственно x iв = +1 и x iн = -1.

Шаг варьирования по каждой переменной выбирается таким, чтобы приращение величины выходного параметра Y к базовому значению Y * при реализации шага можно было выделить на фоне «шума» при небольшом числе параллельных опытов. Если нет никаких указаний на величину шага D X i , то в первом приближении можно выбрать D X i = 0,15X * i , т.е. принять за шаг 15%-ное отклонение от базового уровня X * i . Такой шаг дает достаточную гарантию того, что фактор X i вызовет заметную реакцию Y, если связь между ними существует.

Матрица планирования должна отвечать следующим условиям:

1. Ортогональность

2. Условие нормированости

3. Симметричность относительно центра экстремума

4. Ротатабельность, т.е. координаты точек факторного пространства в матрице планирования подстраиваются так, что точность предсказания значения параметра оптимизации одинакова на равных расстояниях от центра эксперимента (базовой точки) и не зависит от направления.

Матрица планирования составляется по следующим правилам:

1. Каждая g-я строка матрицы представляет собой набор координат точки g , в которой производится эксперимент;

2. Поскольку переменные x gi принимают лишь значения +1 и -1, то все остальные переменные могут принимать те же значения, что позволяет в целях упрощения записывать в таблицу вместо +1 и -1 их знаки + и -;

3. Первая строка 1 выбирается так, чтобы управляемые переменные находились на нижнем уровне, т.е. x i1 = -1. Последующие строки при составлении матрицы планирования набираются по правилу: при построчном переборе всех вариантов частота смены знака управляемых переменных для каждой последующей переменной вдвое меньше, чем для предыдущей (см. табл. 1)

Следует отметить, что суть матрицы не изменится, если первая строка 1 будет выбрана так, чтобы управляемые переменные находились на верхнем уровне, т.е. x i1 = +1.

Матрицы планирования любого другого типа, например, 2 4 , 2 5 и т.д. могут быть получены описаным выше способом.

Поскольку изменение выходной величины Y носит случайный характер, необходимо в каждой точке g (т.е. в точке с координатами, записаными в g-й строке) проводить m параллельных опытов и результаты наблюдений Y 1g ,Y 2g . Y mg усреднять

(4)

Величина m может быть любой, но не меньше m=3. Тогда эксперимент делится на m серий опытов, в каждой из которых полностью реализуется матрица планирования (т.е. эксперимент проводится в N=2 n точках факторного пространства).

Одним из важнейших положений современной теории планирования эксперимента является рандомизация . План эксперимента составляется так, чтобы рандомизировать, т.е. сделать случайными те систематически действующие факторы, которые трудно поддаются учету и контролю, для того, чтобы рассматривать их как случайные величины и учитывать статистически.

Перед реализацией плана на объекте необходимо произвести рандомизацию — с помощью таблицы равномерно распределенных случайных чисел (табл.П.6) определить последовательность реализации матрицы планирования в каждой из m серий опытов. Для этого в качестве начала выбирается любое число из табл.П.6 и записывается в столбец k 1 из табл.2 на место g=1. Остальные места этого столбца заполняют числа от 1 до N, следующие по порядку из табл.П.6 за выбранным начальным. Следует обращать внимание на то, чтобы числа в столбцах табл.2 не повторялись дважды. Пусть, например, при g=4 k 14 =8, это значит, что в первой серии испытаний точка 4 реализуется восьмой по порядку.

Аналогично рандомизируются испытания в каждой из оставшихся серий экспериментов; порядок реализации записывается в столбцах k 2 ,k 3 . k m . Результаты эксперимента в каждой из серий испытаний записываются в столбцах Y 1 ,Y 2 . Y m .

Проверка воспроизводимости — это проверка на выполнение второй предпосылки регрессионного анализа об однородности выборочных дисперсий S 2 g . Задача состоит в проверке гипотезы о равенстве дисперсий s 2 =s 2 =. s 2 при экспериментах соответственно в точках 1 ,2 . g . N .

Оценки дисперсий находятся по формуле

(5)

Так как все дисперсии получены по выборкам одинакового объема m, то число степеней свободы для всех дисперсий одинаково и равно

Для проверки гипотезы об однородности оценок дисперсий следует пользоваться критерием Кохрена, который основан на законе распределения отношения максимальной эмперической дисперсии к сумме всех дисперсий, т.е.

(7)

Если вычисленное значение критерия G окажется меньше табличного значения G кр , найденного для q%-ного уровня значимости, v зн = v 2 = N — числа степеней свободы знаменателя (например для q=5%; v числ = 3 — 1 = 2; v зн =8, G кр = 0,5157, см. табл.П.5), то гипотеза об однородности дисперсий принимается. При этом всю группу дисперсий S 2 g можно считать оценкой S 2 одной и той же генеральной дисперсии воспроизводимости s 2 , откуда

(8)

Если проверка на воспроизводимость дала отрицательный результат, то остается признать либо невоспроизводимость эксперимента относительно управляемых переменных вследствие наличия флуктуаций неуправляемых и неконтролируемых переменных, создающих на выходе большой уровень «шума», либо наличие грубого промаха в строке, откуда взята дисперсия max. В первом случае следует увеличить число параллельных опытов, во втором — найти грубый промах и заменить его на результат доброкачественного измерения при соответствующей комбинации факторов. Если это по каким-то причинам невозможно, то, чтобы не нарушать предпосылки использования критерия Кохрена, на место грубого промаха следует поместить среднюю арифметическую величину g данной строки.

Следует также отметить, что критерий Кохрена можно применять не к любой группе выборок, а только к группе выборок одинакового объема, что как раз и имеет место при полном факторном эксперименте.

Легко заметить, что исходный план (табл.1) содержит много больше строк, чем столбцев и, следовательно, из результатов эксперимента согласно условию решения нормальных уравнений (2) можно получить дополнительную информацию, т.е. расширить модель. Безусловно, это относится к средней арифметической всего эксперимента, т.е. к отклику в базовой точке b 0 , для расчета которого можно ввести фиктивную переменную x од = +1 для всех строк. Оставшиеся свободными столбцы можно использовать для нахождения оценок коэффициентов при парных взаимодействиях и т.п. При этом соответствующие величины x i x j , x i x j x l получаются простым перемножением соответствующих столбцов исходного плана.

Тогда математическая модель объекта, получающаяся в результате ПФЭ может быть представлена в виде

Однако вследствие того, что из ограниченного числа опытов нельзя получить точные значения коэффициентов b i , а только их независимые оценки b i , вся математическая модель становится оценочной

= b 0 + b 1 x 1 +. + b n x n + b 12 x 1 x 2 + b 1. n x 1 . x n

(10)

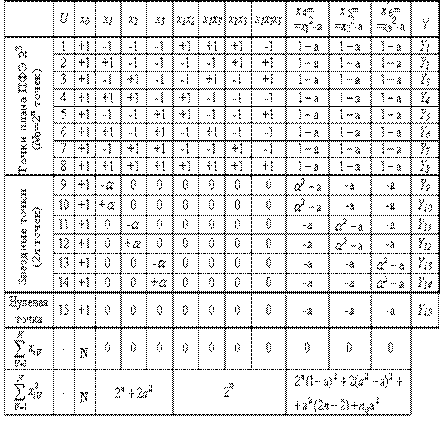
Пример матрицы планирования, принцыпа ее реализации и последующей обработки экспериментальных данных приведен в табл.2 на базе трехфакторного эксперимента. В разделе «Матрица планирования эксперимента» включены не только относительные переменные x i , сочетание которых и является собственно настоящей матрицей планирования, ни и их парные и тройные взаимодействия, знание которых необходимо лишь на этапе обработки экспериментальных данных.

Порядок реализации опытов					Матрица планирования эксперимента								Результаты эксперимента					Первичная обра ботка результатов		Проверка адекватности
l					z 0	z 1	z 2	z 3	z 4	z 5	z 6	z 7	Y g1	.	Y gl	.	Y gm	g	S 2 g	g	(g —g ) 2
k 1	.	k l	.	k m	x 0	x 1	x 2	x 3	x 1 x 2	x 1 x 3	x 2 x 3	x 1 x 2 x 3
1	1	.	6	.	8	+	—	—	—	+	+	+	—
2	7	.	5	.	4	+	+	—	—	—	—	+	+
3	3	.	7	.	6	+	—	+	—	—	+	—	+
4	8	.	2	.	7	+	+	+	—	+	—	—	—
5	6	.	3	.	2	+	—	—	+	+	—	—	+
6	4	.	4	.	1	+	+	—	+	—	+	—	—
7	2	.	1	.	5	+	—	+	+	—	—	+	—
8	5	.	8	.	3	+	+	+	+	+	+	+	+

Для удобства расчетов и представления формул каждый столбец может быть представлен в виде новой переменной Z ig . Тогда оценки коэффициентов уравнения регрессии легко найти по формуле

(11)

Легко заметить, что матрица планирования является ортогональной с линейно независимыми вектор-столбцами; отсюда следует диагональность матрицы нормальной системы уравнений, а следовательно, и взаимная независимость оценок коэффициентов уравнения регрессии.

Необходимо отметить, что получаемая модель не дает членов типа x 2 ii и, таким образом, является неполной. В большинстве случаев это не отражается на качестве модели, так как чаще всего b ii =0. Однако в случаях, когда b ii ¹ 0, модель становится неточной (неадекватной), тогда следует от ПФЭ переходить к другим принципам планирования (как правило, это случается в окрестностях частного или глобального экстремума целевой функции).

После определения оценок коэффициентов регрессии необходимо проверить гипотезу о значимости коэффициентов b i . Лучше всего это сделать в виде нуль-гипотезы, т.е. гипотезы о равенстве b i = 0. Если она подтвердилась, то коэффициент b i следует признать статистически незначимым и отбросить из искомой модели; если гипотеза не подтвердилась, то соответствующий коэффициент b i следует признать значимым и включить в модель.

Проверка гипотезы проводится с помощью t — критерия Стъюдента, который при проверка нуль-гипотезы формируется в виде

(12)

где S 2 — дисперсия ошибки определения коэффициента b i . При полном и дробном факторном планировании для всех i

(13)

Если вычисленная величина параметра t i превышает табличное значение t кр , найденное для q%-ного уровня значимости и v з =N(m-1) числа степеней свободы (например для q = 5%; v з = 16; t кр = 2,199, см.табл.П.2) то нуль-гипотеза отвергается и коэффициент считается незначимым и его следует отбросить, не включая в искомую модель.

Статистическая незначимость коэффициента b i может быть обусловлена следующими причинами:

1. уровень базового режима * близок к точке частного экстремума по переменной X i или по произведению переменных;
2. шаг варьирования D X i выбран малым;
3. данная переменная (или произведение переменных) не имеет функциональной связи с выходным параметром Y;
4. велика ошибка эксперимента вследствие наличия неуправляемых и неконтролируемых переменных.

Поскольку ортогональное планирование позволяет определять доверительные границы для каждого из коэффициентов регрессии в отдельности, то, если какой-либо из коэффициентов окажется незначимым, он может быть отброшен без пересчета всех остальных. После этого математическая модель объекта составляется в виде уравнения связи выходного параметра Y и переменных x i , включающего только значимые коэффициенты.

Чтобы проверить гипотезу об адекватности представления результатов эксперимента найденному уравнению связи (иными словами, чтобы проверить, насколько найденное уравнение соответствует экспериментальным результатам), достаточно оценить отклонение выходной величины Y g , предсказанное уравнением регрессии, от результатов экспериментов g в точках факторного пространства.

Рассеяние результатов эксперимента вблизи уравнения связи, аппроксимирующего искомую функциональную зависимость, можно охарактеризовать с помощью дисперсии неадекватности s 2 ад , оценка которой S 2 ад находится по формуле

(14)

с числом степеней свободы v ад = N-d, где d — число членов аппроксимирующего полинома.

Проверка адекватности состоит в выяснении соотношения между дисперсией неадекватности s 2 ад и дисперсией воспроизводимости s 2 . Если s 2 ад не превышает дисперсии опыта, то полученная математическая модель адекватно представляет результаты эксперимента, если же s 2 ад > s 2 , то описание считается неадекватным объекту.

Проверка гипотезы об адекватности проводится с использованием F-критерия Фишера.

Критерий Фишера позволяет проверить нуль-гипотезу о равенстве двух генеральных дисперсий s 2 ад и s 2 . В связи с тем, что самих генеральных дисперсий мы не знаем, F-критерий формируется как отношение

(15)

Если вычисленное по формуле (15) значение критерия F меньше табличного F кр , найденного для q%-ного уровня значимости, v числ = v ад = v 4 = N-d числа степеней свободы числителя и v зн = v з = N(m-1) числа степеней свободы знаменателя, то нуль-гипотеза принимается. В противном случае она отвергается и описание (модель) признается неадекватным объекту. Некоторые значения F кр (q=5%;v 4 ;v з ) приведены в табл.П.4

В ходе работы может возникнуть ситуация, когда выборочная дисперсия неадекватности S 2 ад не превосходит оценки дисперсии воспроизводимости S 2 (т.е. когда S 2 ад £ S 2 ). Тогда соотношение (15) будет равно F £ 1 и неравенство F 0. Число вариантов варьирования плана ПФЭ равно числу оцениваемых коэффициентов регрессии уравнения связи (N = d). Следовательно, не остается степеней свободы (v ад = 0) для проверки нуль-гипотезы об адекватности представления экспериментальных данных выбранной формой аппроксимирующего полинома. Если же некоторые коэффициенты регрессии оказались незначимыми или ими можно пренебречь в силу их малости, то число членов проверяемого уравнения в этом случае будет меньше числа вариантов варьирования (d 0) останется для проверки гипотезы адекватности.

Если гипотеза адекватности отвергается, то модель признается неадекватной экспериментальным данным. Неадекватность модели не означает ее неправильности! Неадекватность модели может означать, что не весь перечень влияющих факторов был принят во внимание, или что необходимо перейти к более сложной форме уравнения связи, или выбрать другой шаг варьирования по одному или нескольким факторам и т.п. Однако все достижения неадекватной модели: отсев незначимых факторов, оценка дисперсии эксперимента и др. остаются в силе.

Пример 1. Методом ПФЭ найти математическую модель процесса напыления резисторов.

После консультации с экспертами и некоторых предварительных исследований было определено, что на величину сопротивления напыляемых резисторов могут оказывать влияние следующие факторы:

1. Состояние испарителя — «чистое», т.е. порошок для напыления сыпется в стакан испарителя впервые после промывки его сторон, или «грязное», т.е. порошок сыпется в испаритель, в котором осталось некоторое его количество от предыдущего цикла напыления; обозначим этот фактор как x 1 , причем величина x 1 = +1соответствует «чистому», а величина x 1 = -1 соответствует «грязному» состоянию испарителя;
2. Температура подогрева подложки x 2 , причем x 2 = +1 соответствует верхней допустимой по техпроцессу температуре, а x 2 = -1 — нижней;
3. Температура испарителя x 3 , причем x 3 = +1 соответствует верхней допустимой по техпроцессу температуре, а х 3 = -1 — нижней.

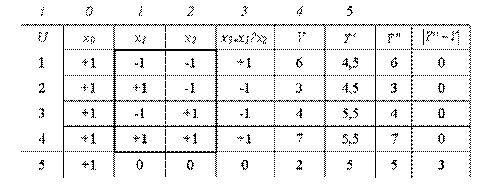
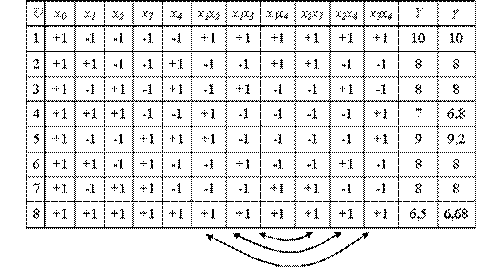
План эксперимента, его пятикратная реализация с учетом рандомизации и первичная обработка результатов представлена в таблице.

Циклыz 0z ₁z ₂z ₃z ₄z ₅z ₆z ₇Результаты, кOмОбработкаАдекватностьgS 2 gg(g —g ) 2k 1k 2k 3k 4k 5x 0x 1x 2x 3x 1 x 2x 1 x 3x ₂ x ₃x ₁ x ₂ x ₃Y g1Y _g2Y _g3Y _g4Y _g5142368+———+++—11,410,513,814,012,112,362,30312,100,0676233625++————++18,117,415,216,819,217,342,22817,080,0676386241+—+——+—+10,89,311,612,19,810,721,38710,980,0676461716+++—+———18,829,622,022,820,721,382,75221,640,0676558134+——++——+12,912,813,615,214,013,700,95013,980,0784625572++—+—+——12,011,614,213,412,512,741,11813,000,0676717487+—++——+—15,114,816,818,117,016,361,91316,100,0676874853++++++++13,511,914,317,016,214,584,22714,320,0676å119,1816,878—0,5410

При первичной обработке результатов экспериментов пользуемся формулами (4) и (5), а затем проверяем воспроизводимость опытов по (7)

Таким образом, подтверждена воспроизводимость опытов (отсутствие в данных грубых промахов), что позволяет, в свою очередь, найти среднюю дисперсию строчных выборок (дисперсию опытов) по (8)

C

v 3 = 8·(5-1) = 32 степенями свободы

Оценки коэффициентов уравнения регрессии ищутся по формуле (11)

и т.д. Аналогично находим b 3 = -0,55; b 12 = +0,61; b 13 = -2,30; b 23 = +0,26; b 123 = -0,81

Проверяем значимость оценок коэффициентов по критерию Стьюдента по формуле (12), предварительно найдя дисперсию оценок по формуле (13)

				;
Тогда		;				;

Табличное значение критерия t i (табл.П.2) t кр (5%;v 3 =32) = 2,046, поэтому все найденные оценки коэффициентов, кроме b 23 , признаются значимыми и должны войти в модель

= 14,90 + 1,61x 1 + 0,86x 2 -0,55x 3 + 0,61x 1 x 2 -2,30x 1 x 3 — 0,81x 1 x 2 x 3

Для определения дисперсии адекватности по формуле (14) необходимо сначала найти числовые значения модели g для каждой g-ой строки матрицы планирования, а затем подсчитать сумму квадратов разностей между модельным значением и средним арифметическим g той же строки

Тогда критерий Фишера (15) дает

что доказывает адекватность найденной модели. Ее можно использовать для управления технологическим процессом испытания резисторов

2. Дробный факторный эксперимент

Полный факторный эксперимент целесообразно использовать при сравнительно небольшом числе независимых факторов (обычно не больше 5), в противном случае число вариантов варьирования N = 2 n становится непомерно большим и реализация эксперимента затрудняется. В то же время в большинстве практических задач взаимодействия внешних порядков, начиная с третьего (а то и второго), отсутствуют или пренебрежимо малы, вследствие чего излишне много степеней свободы остается на проверку гипотезы адекватности. Если заранее пренебречь взаимодействиями высших порядков, то имеется возможность получить математическую модель при меньшем числу опытов, реализовав не весь план ДФЭ, а только его часть (дробную реплику).

Эксперимент, реализующий часть (дробную реплику) полного факторного эксперимента, называется дробным факторным экспериментом (ДФЭ). ДФЭ позволяет получить приближение искомой функциональной зависимости Y = f(X 1 . X n ) в некоторой небольшой окрестности точки базового режима при минимуме опытов.

Так, для решения трехфакторной задачи можно ограничиться четырьмя вариантами (N = 4), если в планировании ПФЭ типа 2 2 произведение x 1 x 2 приравнять к третьей независимой переменной x 3 . Такое планирование, представленное матрицей табл 3, позволяет оценить свободный член b 0 и три коэффициента регрессии при линейных членах b 1 ,b 2 ,b 3 (из четырех опытов нельзя получить более четырех коэффициентов).

Применение ДФЭ всегда связано со смешиванием, т.е. совместной оценкой нескольких коэффициентов уравнения связи. В нашем примере, если коэффициенты регрессии b ij при парных произведениях отличны от нуля, то каждый из найденных коэффициентов будет оценкой двух теоретических коэффициентов:

b 0 ® b 0 + b 123 ; b 2 ® b 2 + b 13 ;

b 1 ® b 1 + b 23 ; b 3 ® b 3 + b 12 .

Действительно, указанные коэффициенты в таком планировании не могут быть найдены раздельно, поскольку столбцы матрицы для линейных членов и парных произведений совпадают (полностью скоррелированы). Рассмотренный план ДФЭ представляет половину плана ДФЭ типа 2 3 и называется «полурепликой» от ПФЭ типа 2 3 или планированием типа N = 2 3-1 .

При большом числе переменных можно построить дробные реплики высокой степени дробности (1/4, 1/8, 1/16 и т.д.). Дробная реплика обозначается через 2 n-p , если p переменных приравнены к соответствующим произведениям переменных.

Для правильного планирования ДФЭ необходимо использовать все полученные ранее сведения об объекте теоретического и интуитивного характера и выделить из них те переменные и произведения переменных, влияние которых на процесс минимально. При этом смешивание нужно производить так, чтобы основные оценки b 0 ,b 1 . b n были смешаны с взаимодействиями, о которых заранее известно, что они не оказывают влияния на объект. Следовательно, произвольное разбиение матрицы планирования 2 3 на две части выделения полуреплики типа 2 3-1 недопустимо.

Генерирующее соотношение служит для построения дробной реплики. Так, в рассмотренном планировании 2 3-1 мы задавали полуреплику типа 2 3 с помощью генерирующего соотношения x 3 = x 1 x 2 .

Определяющим контрастом (ОК) называется соотношение, задающее элемент первого столбца матрицы планирования для фиктивной переменной (все они равны 1). Выражение ОК в нашем примере получается умножением левой и правой частей приведенного генерирующего соотношения на его левую часть x 3

так как всегда x 2 ig = 1.

Знание ОК позволяет определить всю систему совместных оценок не изучая матрицу планирования ДФЭ. Соотношения, задающие эти оценки, можно найти, последовательно перемножив независимые переменные на ОК

x 1 = x 2 x 3 ; x 2 = x 1 x 3 ; x 3 = x 1 x 2 .

Отсюда легко находим смешиваемые теоретические коэффициенты регрессии и их оценки

b 1 ® b 1 + b 23 ; b 2 ® b 2 + b 13 ; b 3 ® b 3 + b 12 .

Разрешающая способность дробных реплик определяется генерирующими соотношениями. Она тем выше, чем выше порядок взаимодействий, с которыми смешаны линейные коэффициенты, и увеличивается с ростом числа независимых переменных.

Для четверти реплики в пятифакторном планировании типа 25-2 могут быть заданы, например генерирующее соотношение

x 4 = x 1 x 2 x 3 ; x 5 = x 1 x 2

заранее полагая, что b 123 = b 12 = 0, т.е. что пара x 1 x 2 и тройка x 1 x 2 x 3 не дает значимого эффекта взаимодействия. Определяющими контрастами для этой четверть-реплики согласно вышеприведенным правилам будут соотношения

1 = x 1 x 2 x 3 x 4 ; 1 = x 1 x 2 x 5 .

Если у дробной реплики имеются два и более определяющих контраста, их необходимо перемножить между собой, используя все возможные комбинации. В случае четвертьреплики получается одна комбинация

Обобщающий определяющий контраст , построенный на основе всех полученных определяющих контрастов, полностью характеризует разрешающую способность реплик высокой степени дробности

1 = x 1 x 2 x 3 x 4 = x 1 x 2 x 5 = x 3 x 4 x 5 .

Совместные оценки здесь будут определяться соответствиями

x 0 = x 1 x 2 x 3 x 4 = x 1 x 2 x 5 = x 3 x 4 x 5 ;
x 1 = x 2 x 3 x 4 = x 2 x 5 = x 1 x 3 x 4 x 5 ;
x 2 = x 1 x 3 x 4 = x 1 x 5 = x 2 x 3 x 4 x 5 ;
x 3 = x 1 x 2 x 4 = x 1 x 2 x 3 x 5 =x 4 x 5 ;
x 4 = x 1 x 2 x 3 = x 1 x 2 x 4 x 5 =x 3 x 5 ;
x 5 = x 1 x 2 x 3 x 4 x 5 = x 1 x 2 = x 3 x 4 ;
x 1 x 3 = x 2 x 4 = x 2 x 3 x 5 = x 1 x 4 x 5 ;
x 2 x 3 = x 1 x 4 = x 1 x 3 x 5 =x 2 x 4 x 5 ;

Эти соотношения позволяют установить, оценкой каких теоретических коэффициентов является тот или иной коэффициент регрессии, полученный при обработке результатов эксперимента

b 0 = b 0 + b 1234 + b 125 + b 345 ;
b 1 = b 1 + b 234 + b 25 + b 1345 ;
b 2 = b 2 + b 134 + b 15 + b 2345 ;
b 3 = b 3 + b 124 + b 1235 + b 45 ;
b 4 = b 4 + b 123 + b 1245 + b 35 ;
b 5 = b 5 + b 12345 + b 12 + b 34 ;
b 13 = b 13 + b 24 + b 235 + b 145 ;
b 23 = b 23 + b 14 + b 135 + b 245 ;

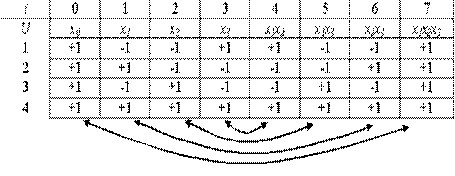
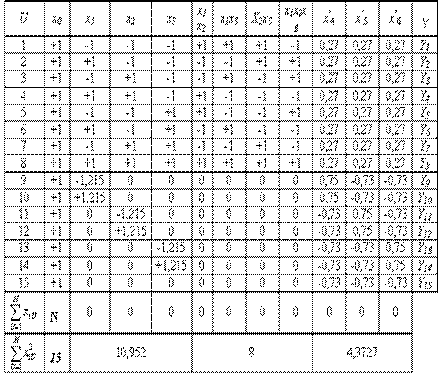
Разрешающая способность этой четверти реплики невысокая, так как все линейные коэффициенты смешаны с парными взаимодействиями. Матрица планирования такой четверти реплики представлена в табл.4.

Следует иметь в виду, что ДФЭ всегда можно дополнить до ПФЭ, реализовав недостающие дробные реплики.

Вся дальнейшая работа по реализации матрицы планирования ДФЭ, проверке воспроизводимости полученных результатов, определению оценок коэффициентов регрессии и их значимости, проверке адекватности полученной математической модели не отличается от соответствующих процедур в ПФЭ.

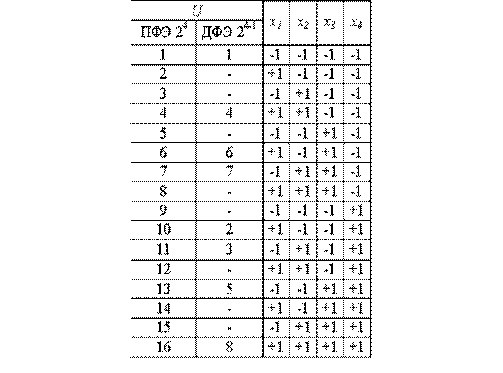
Четверть реплики от ПФЭ типа 2 5 (планирование типа 2 5-2 )

Пример 2. Методом ДФЭ найти математическую модель процесса напыления резисторов.

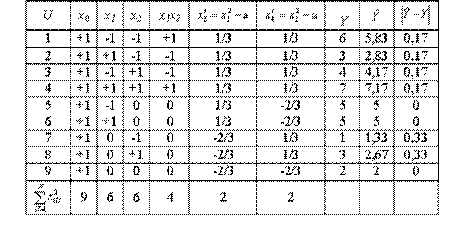
Воспользуемся результатами Примера 1 и положим в качестве генерирующего соотношения равениство x 1 = x 2 x 3 (т.к. b 23 = 0). Тогда матрица планирования и результаты эксперимента (опуская промежуточные данные) будут выглядеть так

g	x 0	x 1	x 2	x 3		S 2 g		(—) 2
1	+	+	—	—	17,34	2,228	17,41	0,0049
2	+	—	+	—	10,72	1,387	10,77	0,0025
3	+	—	—	+	13,70	0,950	13,65	0,0025
4	+	+	+	+	14,58	4,227	14,53	0,0025

Проверим воспроизводимость опытов

откуда следует, что результаты опытов получены правильно, дисперсия строчных выборок равна S 2 = 8,792 / 4 = 2,198 с числом степеней свободы v 3 = 4·4 = 16.

Оценки коэффициентов уравнения регрессии

;

аналогично b 2 = -1,44; b 3 = 0,05.

Проверка значимости полученных оценок начинается с определения их СКО

;

;

Табличные значения критерия t кр (5%;16) = 2,131, следовательно, модель найдена в виде

= 14,09 + 1,88x 1 — 1,44x 2 .

Проверка адекватности модели дает

, откуда

,

т.е. модель признается адекватной экспериментальным данным.

Сравнение моделей примера 1 и примера 2 показывает, что они имеют совершенно разный вид, а по некоторым факторам — противоположные по смыслу оценки коэффициентов. Отсюда можно сделать несколько общих выводов и рекомендаций (без подробного обоснования), пригодных для использования в рамках теории планирования экспериментов:

1. по одним и тем же экспериментальным данным можно построить несколько математических моделей, каждая из которых будет адекватна для своего набора оценок коэффициентов регрессии;
2. из всех моделей наилучшей признается та, у которой меньше членов и меньше критерий Фишера (или, если угодно, меньше дисперсия адекватности);
3. при большом числе факторов работу по математическому моделированию следует начинать с ДФЭ возможно большей дробности. Если модель получилась неадекватной, ее всегда можно достроить до следующей реплики вплоть до ПФЭ. Это сэкономит количество опытов, время, затраты и т.п.

Применение описанных выше методов математического моделирования полностью оправдало себя в условиях с небольшим числом факторов. Но при очень большом числе факторов и привлечение их к составлению математического описания исследуемого объекта методами ПФЭ или ДФЭ может потребовать увеличения объема экспериментальной работы, что редко может выполняться из-за экономических, технологических и прочих ограничений. Таким образом, возникает необходимость в предварительном отсеивании несущественных и выделении тех факторов процесса, которые оказывают наиболее заметное влияние на целевую функцию. Другим существенным затруднением для применения ПФЭ или ДФЭ в производственных условиях является метод получения оценок коэффициентов регрессии. Оценки вида (11) считаются оптимальными в смысле эффективности (минимума дисперсии), поскольку их вычисление базируется на методе наименьших квадратов, однако предварительным условием такой оптимальности являются требования независимости факторов, ортогональности и симметричности плана эксперимента, а также требование равенства дисперсий условных распределений плотности вероятности f(y/x k ). В свою очередь симметричность плана требует равного количества наблюдений, соответствующих положительным и отрицательным значениям k-го фактора.

На практике в производственных условиях требования симметричности плана и равенства дисперсий условных распределений плотности вероятности f(y/x k ) эксперимента, как правило, нарушаются, особенно в случаях, когда исследователь пытается построить модель по результатам, зафиксированными для случайной системы комбинаций производственных факторов. При этом всегда имеется выбор: либо нарушить одно из требований факторного анализа, либо потерять часть информации, пытаясь выбрать из нее только то, что согласуется с правилами ведения ПФЭ (ДФЭ).

Какими уравнениями описываются результаты активного эксперимента

Эти данные могут дать важную информацию для планирования активных экспериментов. [c.157]

Активные эксперименты предполагают влияние на изменение факторов исследователя, который может изменять их по своей воле. [c.157]

Активные эксперименты характеризуются одновременным варьированием всех факторов, действующих на целевую функцию. При этом могут быть решены следующие задачи [c.157]

При пассивных экспериментах уровни факторов берутся в произвольном порядке. При активных экспериментах уровни факторов выбираются в определенном порядке, что позволяет значительно сократить число опытов. Поэтому можно сказать, что активные эксперименты представляют собой процедуру выбора уровней факторов, их числа и условий проведения эксперимента, необходимых и достаточных для получения математической модели явления с заданной точностью. При проведении активных экспериментов существенно [c.160]

Погрешности при фиксации условий наблюдения (активные эксперименты). Во многих экспериментах i-e наблюдение проводится при условиях Xit несколько отличных от желаемых XQi Xt = Xoi + e i, где гхг — случайные величины (погрешности фиксации). Таким образом, экспериментатору доступны величины Yt = i i + ef и ХоЬ связанные между собой соотношением [c.235]

Мультиколлинеарность в основном появляется в задачах пассивного эксперимента, когда исследователь, собирая данные, не может влиять на значения объясняющих переменных. В активном эксперименте матрица данных X планируется (см. [ 1361), причем таким образом, что либо матрица S хорошо обусловлена, либо априори точно известны линейные зависимости, имеющие место между строками (столбцами матрицы X), и, следовательно, ее ранг. [c.253]

Активный эксперимент проводится главным образом в лабораторных условиях, где экспериментатор имеет возможность изменять входные характеристики по заранее намеченному плану. Такой эксперимент быстрее приводит к цели, и именно к нему применимы идеи планирования экстремального эксперимента. [c.245]

В каких случаях проводится активный эксперимент [c.279]

В основном в экономических науках опытная проверка теорий и моделей осуществляется на основе их сопоставления с данными учета. Активное экспериментирование, т. е. активное вмешательство в ход экономического процесса с целью получения информации, является скорее исключением из правила, чем правилом. Существует мнение, что активные эксперименты в экономической науке вообще невозможны. [c.6]

Лабораторным экспериментом определяются выход продукции, степень превращения, расход реагентов, выбор и активность катализатора, пределы изменения параметров процесса. [c.42]

Проведение тренировочных занятий по контролю готовности рабочих к распределению и переключению внимания и действий необходимо начинать с простейших экспериментов и по мере приобретения навыков усложнять задачи. Активное формирование этих профессионально необходимых качеств практически целесообразно начинать с использования корректурного теста Бурдона и метода черно-красной цифровой таблицы. [c.264]

Под экспериментом понимается изучение объекта, основанное на активном целенаправленном воздействии на него путем создания искусственных условий, позволяющих выявить рассматриваемые свойства, характеристики, зависимости объекта. Сделать поведение экспериментатора целенаправленным, организованным, повысить производительность его труда и надежность получаемых результатов позволяют современные методы статистического планирования многофакторных экспериментов. [c.48]

Второй вопрос, возникающий при изучении данного нами определения модели а зачем нужно использовать какие-то вспомогательные объекты (т. е. модели) и затем сталкиваться со сложнейшей проблемой о возможности переноса результатов исследования моделей на объект вместо того, чтобы исследовать интересующий нас объект непосредственно Прежде всего бросается в глаза причина практическая модели выбираются таким образом, чтобы они были значительно проще для исследования, чем интересующие нас объекты. Более того, некоторые объекты вообще не удается исследовать активно (т. е. провести с ними эксперимент). Невозможно, например, ставить на экономике страны эксперимент, имеющий чисто познавательное значение. Однако моделирование имеет и другое, более важное для науки значение поскольку в модели воспроизводятся лишь некоторые наиболее важные в данном исследовании стороны исходного объекта, моделирование позволяет выявить существенные факторы, ответственные за те или иные свойства изучаемых объектов. Моделирование как познавательный прием, как форма отражения действительности, зародилось еще в античную эпоху одновременно с возникновением научного познания. Сейчас трудно назвать ту область науки, где оно не используется. [c.21]

За триста лет совместной активной деятельности многих поколений физиков и математиков удалось построить стройное здание — систему математических моделей физических процессов. Это здание состоит из многих этажей. В его фундаменте лежат принципы, служащие основой моделей физических явлений. Эти принципы являются продуктом долгого развития науки, в них воплощен опыт воздействия человека на окружающую его природу, т. е. практики (в философском смысле этого слова), важное место в которой в естественных науках занимает натурный эксперимент. Три принципа механики, сформулированные Исааком Ньютоном, служат достаточной основой для построения математических моделей в механике в том случае, когда интересующие нас объекты можно с достаточной степенью точности описать в виде материальных точек и скорости их далеки от скорости света. К объектам такого рода относится широкий класс изучаемых явлений, начиная от колебаний маятника до управляемого полета космического корабля. Добавив к трем ньютоновским принципам принципы описания деформации твердого тела, мы сможем уже описать взаимодействие твердых тел, имеющих конечные размеры. Добавив к принципам Ньютона принцип рассмотрения жидкости как непрерывной, сплошной среды (т. е. пренебрегая ее молекулярным строением), принцип описания связи между плотностью и давлением, а также принцип сохранения массы, имеющей вид уравнения сплошности среды, мы получим математическую модель жидкости. [c.26]

Подчеркнем, что главная особенность имитационного исследования состоит в том, что в этом исследовании проводятся эксперименты, но только не с объектом, а с его математической моделью. Такое представление об имитации появилось в 60-х годах нашего столетия. Имитационные исследования используются для анализа сложных систем в таких непохожих областях науки, как исследование ядерных реакторов и изучение психологии человека, моделирование боевых действий и анализ биологических систем в природе, изучение распространения эпидемий и моделирование исторических процессов, автоматизированное проектирование сложных технических систем и оценка воздействия лечебных процедур на организм человека. Особенно важное место имитационные исследования занимают в анализе экономических процессов. В экономических исследованиях имитация используется в широком диапазоне задач, от отдельных вопросов массового обслуживания и оперативного планирования производства до изучения перспектив развития экономики нашей планеты в целом. Такое разнообразие задач затрудняет выработку каких-то единых, универсальных рекомендаций (тем более, что имитационные методы еще крайне молоды — они используются всего лишь около двадцати лет и сейчас бурно развиваются). Имитационное исследование в значительной степени остается задачей, требующей большой творческой активности и самостоятельности человека, их осуществляющего. Тем не менее, уже сейчас возможно выделить основные принципы проведения имитационных экспериментов, которым и будет посвящен этот раздел книги. [c.233]

Следующий шаг состоит в переходе от базового описания к основной модели изучаемого объекта. В этой модели отдельные блоки (подмодели) должны быть согласованы и обеспечены исходной информацией, что позволит проводить на ее основе имитационные эксперименты с различными вариантами решений ЛПР. Переход от базового описания к математической модели имитационного уровня осуществляется при активном участии ЛПР — именно ЛПР берет на себя ответственность за внесение тех упрощающих предположений, которые дают возможность построить согласованную и обеспеченную исходной информацией математическую модель. Процесс такого перехода является сложным шагом, требующим многочисленных и продолжительных дискуссий исследователя с ЛПР. [c.328]

Обобщая методы и приемы современной науки, процесс познания широко использует такие важнейшие инструменты. как анализ и синтез, эксперимент, моделирование. Активно-составляющим здесь выступает человеческое мышление, которое представляет собой наивысшую аналитико-синтетическую [c.9]

Активными называют эксперименты, при которых на изучаемую систему оказывают определенные, предусмотренные планом эксперимента воздействия. [c.40]

Заметим, что при любом методе проведения статистическое наблюдение пассивно статистика хочет как можно точнее зарегистрировать данные без какого-либо влияния на наблюдаемый процесс. Принципиально иным способом собирания данных является эксперимент. В этом случае статистику принадлежит активная роль он должен не только наблюдать, а полностью контролировать ситуацию, планировать эксперимент и реализовать свой план. Эксперимент позволяет выявить влияние каких-либо установленных ограничений или нагрузок на поведение людей. Например, влияние на скорость реакций человека пребывания без сна в течение одних, двух, трех суток. Эксперимент традиционно входил в круг методов биологической, медицинской статистики, приложений статистического метода в естественных науках. В настоящее время все большее распространение получают идеи социального эксперимента . [c.29]

Здесь могут быть наблюдения, полученные как с участием исследователя, так и без его участия (в условиях активного или пассивного эксперимента). [c.22]

Теория риска в применении к инвестиционному анализу начала интенсивно развиваться за рубежом с 50-х гг. нашего столетия. Наибольшее число исследований, посвященных анализу риска, принадлежит американским ученым, но эта проблема активно изучалась и в западноевропейских странах. В то же время в нашей стране происходило серьезное развитие математического аппарата анализа рисков применительно к теории планирования эксперимента в технических и естественных областях знаний. [c.202]

С тех пор как работа Налогового управления США был перестроена на принципах тотального управления качеством, уровень обслуживания клиентов и активность его служащих значительно выросли. В стремлении к абсолютному качеству Налоговое управление США предложило региональным отделениям провести эксперимент по внедрению различных методов командной работы. В семи региональных отделениях управления было создано более 400 межфункциональных групп. [c.113]

Вычислительный эксперимент показал заметное влияние (изменение характеристик на величину в пределах до 10 %) действующей помехи на активную аппаратуру при обработке сигнала. Отсутствие учёта влияния помех на базе известной математической модели (4) и (5) приводило к неверным результатам. Незначительное изменение конструктивных параметров аппаратуры (до значений Ё = f, А = А и т » = [c.88]

На этом месте я прекращаю свой эксперимент в режиме реального времени, поскольку я более не являюсь активным участником событий. Эти события представляют собой наглядную и довольно страшную иллюстрацию многих положений, которые я пытаюсь изложить в. настоящей книге в более абстрактной форме. Меня особенно страшит то, что в Министерстве финансов США действовала отличная команда, а в России было наилучшее правительство во всей ее постсоветской истории тем не менее кризис нельзя было предотвратить. Я также недоволен собственной ролью. [c.108]

Совсем нет. Я активно занимался управлением финансовыми делами. Это было время, когда я занимался экспериментом в реальном времени. Описание этого эксперимента стало частью Алхимии финансов. Это было определенно намного важнее для меня. Работа фонда во многом оставалась побочным делом, невзирая на то что я глубоко лично участвовал в ней. Я не отождествлял себя с фондом и не искал признания. Я чувствовал, что фонд принадлежит венграм в этом был секрет его успеха. Мы были абсолютно неизвестны, что внесло дополнительный вклад в успех фонда. «Агитпроп» коммунистической партии Венгрии решил, что средства массовой информации должны игнорировать деятельность фонда. Следовательно, никаких репортажей в прессе не было, хотя нам разрешалось рекламировать свои программы. Большинство узнавало о том, что мы делали, от других людей. Это была единственная организация в Венгрии, которая действительно делала что-то стоящее, не разговаривая об этом, в то время как все официальные организации много говорили о том, чего они в действительности не выполняли. Поэтому, в некотором смысле, образ фонда был создан благодаря его неизвестности, и я четко решил не ставить это себе в заслугу, поскольку я чувствовал, что люди, управлявшие фондом, действительно стояли на переднем крае, а я лишь предоставлял им необходимые средства. Я чрезвычайно высоко ценил их достижения, так что в действительности все это было создано ими, а не мной. [c.141]

Социально-экономическая статистика изучает совокупности од-нокачественных явлений в конкретных условиях места и времени. Таким образом, статистика располагает всегда ограниченным числом данных. Каждое явление возникает как результат множества факторов. В естественных науках можно проследить интересующие взаимосвязи с помощью специально проведенных лабораторных экспериментов, которые называют активными экспериментами, так как исследователь практически полностью контролирует ход экспе-р имента и может выделить в более или менее чистом виде влияние каждого из выбранных факторов, элиминируя влияние остальных. Иная ситуация в социально-экономических исследованиях. При анализе экономических форм нельзя пользоваться ни микроскопом, ни химическими реактивами. То и другое должна заменить сила абстракции , — писал К.Маркс (Маркс К., Энгельс Ф. Соч.- Изд. 2-е. -Т. 23.- С. 4). Применяя различные методы анализа, мы проводим пассивный эксперимент, причем ни один метод не позволяет определить чистый вклад каждого из факторов по отдельности в совокупный результат. [c.16]

При проведении активных экспериментов применяются различные виды планирования ортогональное, рототабельное, уни-формрототабельное, Д-оптимальное, симплекс-планирование и др. [c.162]

Пример В.1. Анализируется поведение двумерной случайной величины ( , -q), где (руб.) — среднедушевой доход и ц (руб.) — среднедушевые денежные сбережения в семье, случайно извлеченной из рассматриваемой совокупности семей, однородной по своему потребительскому поведению (см., например, [128]). В табл. В.1 и на рис. В.2 представлены исходные статистические данные вида (В.1), характеризующие среднедушевые величины дохода (xit руб.) и денежных сбережений (j/fl руб.) за определенный отрезок времени, а именно за месяц, в каждой (/-и, / = 1,2,. . п) обследованной семье рассматриваемой совокупности семей (в данном условном примере объем п статистически обследованной совокупности семей равнялся 40). В этом примере имелась возможность при отборе исходных данных (выборки) контролировать значения предик-торной переменной Е (условия активного эксперимента [14, с. 121]), что позволило, в частности, разбить статистически обследованные семьи на четыре равные по объему группы по доходам. [c.12]

И наконец, если при сборе исходной статистической информации мы находимся в условиях активного эксперимента [14, с. 12), то как, при заданных затратах на наблюдения, оптимально выбрать матрицу плана [14, с. 26, 68), т. е. как определить те значения объясняющих (предикторных) переменных и то распределение заданного общего числа наблюдений между этими значениями, которые являются в некотором смысле наиболее выгодными с точки зрения достижения наивысшей точности наших статистических выводов [c.13]

Разделы многомерного статистического анализа, составляющие математический аппарат статистического исследования зависимостей, формировались и развивались с учетом специфики анализируемых моделей, обусловленной в первую очередь природой исследуемых переменных. Так, изучение зависимостей между количественными переменными обслуживается регрессионным и корреляционным анализами и анализом временных рядов (гл. 1 —12, 14), изучение зависимостей количественного результирующего показателя от неколичественных или разнотипных объясняющих переменных — дисперсионным и ковариационным анализами, моделями типологической регрессии (гл. 13) для исследования зависимостей в условиях активного эксперимента служит теория оптимального планирования экспериментов [2, 3, 136] наконец, для исследования системы зависимостей, в которых одни и те же [c.54]

Модифицированный мнк для схемы активного эксперимента. Обратимся вначале к регрессирнной задаче (7.83), которая наиболее близка к классическому случаю. [c.236]

Ортогональное планирование эксперимента (по сравнению с неортогональным) уменьшает число опытов и существенно упрощает расчеты при получении уравнения регрессии. Однако такое планирование осуществимо только при возможности проведения активного эксперимента. [c.278]

ЭКСПЕРИМЕНТ (лат. experimentum) — проба, опыт, метод познания, при помощи которого в контролируемых и управляемых условиях исследуются явления действительности. Отличаясь от наблюдения активным оперированием изучаемым объектом, Э. осуществляется на основе теории, определяющей постановку задач и интерпритацию его результатов. Нередко задачей Э. служит проверка гипотез и [c.438]

Внешний контроль, являющийся специфической формой контроля качества измерений, организует метрологическая служба 1федприятия, государственная или ведомственная метрологическая службы либо организация, ответственная за качество измерений в отрасли. Внешний контроль подразделяют на активный и пассивный. Активный контроль основан на проведении контрольных проверок и межлабораторных экспериментов с применением СО. При этом могут быть оценены уровень освоения новых МКХА качество работы отдельной лаборатории выполнение указаний и предписаний [c.43]

Качество исходной информации в значительной степени определяется также способом получения необходимых данных. По этому признаку информация, как известно, делится на экспериментальную и неэкспериментальную [32, 36, 53]. Первая формируется в процессе управления протекающим явлением (экспериментом) по заранее составленной программе. В данном случае исследователь получает возможность активно [c.15]

Имитационные эксперименты на компьютере приобрели широкую популярность, поскольку активные экономические экспери- [c.41]

Совместно с Центром подготовки космонавтов исследовано влияние экстремальных факторов на процессы свободно-радикального окисления и возможность коррекции негативных последствий психоэмоционального стресса и высокой физической нагрузки с помощью пищевых добавок, содержащих антиоксиданты. В эксперименте на животных было показано, что факторы космического полета вызывают нарушение процессов свободно-радикального окисления в организме, что сопровождается нарушением двигательной активности, физиологических, биохимических, иммунологических показателей. Введение в пищевой рацион продуктов, содержащих естественные антиоксиданты лекарственных трав, продуктов пчеловодства — сдерживало развитие психо-эмоционального стресса, нормализировало поведенческие реакции, биохимические и иммунологические показатели. Полученные результаты послужили основой для использования природных анти-оксидантов при предполетной подготовке космонавтов, во время полета и после полетной реабилитации. [c.176]

Индикатор OBV — эффективное и удобное средство анализа, однако и у него есть свои недостатки. С одной стороны, не совсем уместно присваивать показателю полнодневного объема положительный или отрицательный знак. Предположим, что закрытие рынка отмечается незначительным увеличением — всего в один или два тика. Как можно в такой ситуации утверждать, что общий показатель дневной активности положителен Предположим также, что рынок весь день находился на подъеме, а затем закрылся несколько ниже, чем в предыдущий день. Должны ли мы считать, что в этом случае полный дневной объем — величина отрицательная Чтобы ответить на эти вопросы, было проведено множество экспериментов с индикатором OBV. В частности, были сделаны попытки определить реальные показатели объемов, присущие росту и падению цен. [c.165]

Трудность анализа цикла подъем — спад деловой активности состоит в том, что этот цикл представляет собой динамичную систему. Как отмечалось в предисловии, эта книга явилась продолжением моей статьи в февральском номере журнала Atlanti Monthly за 1997 г., озаглавленной Угроза капитализму . Первый вариант этой главы был написан весной 1998 г. В последующих главах описаны более поздние события. Когда кризис в России уже вступил в завершающую фазу, я проводил эксперимент в реальном времени и вел дневник с 9 по 31 августа. Остальную часть анализа я завершил уже в сентябре. Поэтому в последующих главах приводятся более точные прогнозы. [c.71]

Представление результатов экспериментов

Основные понятия и определения

Под экспериментом будем понимать совокупность операций совершаемых над объектом исследования с целью получения информации о его свойствах. Эксперимент, в котором исследователь по своему усмотрению может изменять условия его проведения, называется активным экспериментом. Если исследователь не может самостоятельно изменять условия его проведения, а лишь регистрирует их, то это пассивный эксперимент.

Важнейшей задачей методов обработки полученной в ходе эксперимента информации является задача построения математической модели изучаемого явления, процесса, объекта. Ее можно использовать и при анализе процессов и при проектировании объектов. Можно получить хорошо аппроксимирующую математическую модель, если целенаправленно применяется активный эксперимент. Другой задачей обработки полученной в ходе эксперимента информации является задача оптимизации, т.е. нахождения такой комбинации влияющих независимых переменных, при которой выбранный показатель оптимальности принимает экстремальное значение.

Опыт – это отдельная экспериментальная часть.

План эксперимента – совокупность данных определяющих число, условия и порядок проведения опытов.

Планирование эксперимента – выбор плана эксперимента, удовлетворяющего заданным требованиям, совокупность действий направленных на разработку стратегии экспериментирования (от получения априорной информации до получения работоспособной математической модели или определения оптимальных условий). Это целенаправленное управление экспериментом, реализуемое в условиях неполного знания механизма изучаемого явления.

В процессе измерений, последующей обработки данных, а также формализации результатов в виде математической модели, возникают погрешности и теряется часть информации, содержащейся в исходных данных. Применение методов планирования эксперимента позволяет определить погрешность математической модели и судить о ее адекватности. Если точность модели оказывается недостаточной, то применение методов планирования эксперимента позволяет модернизировать математическую модель с проведением дополнительных опытов без потери предыдущей информации и с минимальными затратами.

Цель планирования эксперимента – нахождение таких условий и правил проведения опытов при которых удается получить надежную и достоверную информацию об объекте с наименьшей затратой труда, а также представить эту информацию в компактной и удобной форме с количественной оценкой точности.

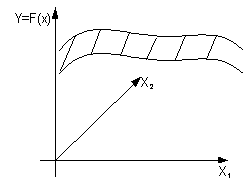
Пусть интересующее нас свойство (Y) объекта зависит от нескольких (n) независимых переменных (Х₁, Х₂, …, Х_n) и мы хотим выяснить характер этой зависимости — Y=F(Х₁, Х₂, …, Х_n), о которой мы имеем лишь общее представление. Величина Y – называется “отклик”, а сама зависимость Y=F(Х₁,Х₂, …, Х_n) – “функция отклика”.

Отклик должен быть определен количественно. Однако могут встречаться и качественные признаки Y. В этом случае возможно применение рангового подхода. Пример рангового подхода — оценка на экзамене, когда одним числом оценивается сложный комплекс полученных сведений о знаниях студента.

Независимые переменные Х₁, Х₂, …, Х_n – иначе факторы, также должны иметь количественную оценку. Если используются качественные факторы, то каждому их уровню должно быть присвоено какое-либо число. Важно выбирать в качестве факторов лишь независимые переменные, т.е. только те которые можно изменять, не затрагивая другие факторы. Факторы должны быть однозначными. Для построения эффективной математической модели целесообразно провести предварительный анализ значимости факторов (степени влияния на функцию), их ранжирование и исключить малозначащие факторы.

Диапазоны изменения факторов задают область определения Y. Если принять, что каждому фактору соответствует координатная ось, то полученное пространство называется факторным пространством. При n=2 область определения Y представляется собой прямоугольник, при n=3 – куб, при n >3 — гиперкуб.

При выборе диапазонов изменения факторов нужно учитывать их совместимость, т.е. контролировать, чтобы в этих диапазонах любые сочетания факторов были бы реализуемы в опытах и не приводили бы к абсурду. Для каждого из факторов указывают граничные значения

, i=1. n.

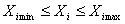
Регрессионный анализ функции отклика предназначен для получения ее математической модели в виде уравнения регрессии

, (1.1)

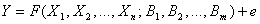
где В₁, …, В_m – некоторые коэффициенты; е – погрешность.

Среди основных методов планирования, применяемых на разных этапах исследования, используют:

планирование отсеивающего эксперимента, основное значение которого выделение из всей совокупности факторов группы существенных факторов, подлежащих дальнейшему детальному изучению;

планирование эксперимента для дисперсионного анализа, т.е. составление планов для объектов с качественными факторами;

планирование регрессионного эксперимента, позволяющего получать регрессионные модели (полиномиальные и иные);

планирование экстремального эксперимента, в котором главная задача – экспериментальная оптимизация объекта исследования;

планирование при изучении динамических процессов и т.д.

Инициатором применения планирования эксперимента является Рональд А. Фишер, другой автор известных первых работ – Френк Йетс. Далее идеи планирования эксперимента формировались в трудах Дж. Бокса, Дж. Кифера. В нашей стране — в трудах Г.К. Круга, Е.В. Маркова и др.

В настоящее время методы планирования эксперимента заложены в специализированных пакетах, широко представленных на рынке программных продуктов, например: StatGrapfics, Statistica, SPSS, SYSTAT и др.

Представление результатов экспериментов

При использовании методов планирования эксперимента необходимо найти ответы на 4 вопроса:

Какие сочетания факторов и сколько таких сочетаний необходимо взять для определения функции отклика?

Как оценить точность представления функции отклика?

Как использовать полученное представление для поиска оптимальных значений Y?

Геометрическое представление функции отклика в факторном пространстве Х₁, Х₂, …, Х_n называется поверхностью отклика (рисунок 1).

Рисунок 1 – Поверхность отклика

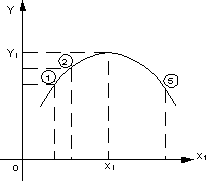
Если исследуется влияние на Y лишь одного фактора Х₁, то нахождение функции отклика — достаточно простая задача. Задавшись несколькими значениями этого фактора, в результате опытов получаем соответствующие значения Y и график Y =F(X) (рисунок 2).

Рисунок 2 – Построение функции отклика одной переменной по опытным данным

По его виду можно подобрать математическое выражение функции отклика. Если мы не уверены, что опыты хорошо воспроизводятся, то обычно опыты повторяют несколько раз и получают зависимость с учетом разброса опытных данных.

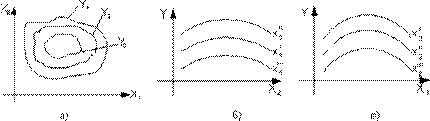
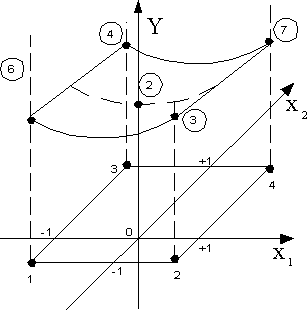
Если факторов два, то необходимо провести опыты при разных соотношениях этих факторов. Полученную функцию отклика в 3 х -мерном пространстве (рисунок 1) можно анализировать, проводя ряд сечений с фиксированными значениями одного из факторов (рисунок 3). Вычлененные графики сечений можно аппроксимировать совокупностью математических выражений.

Рисунок 3 – Сечения поверхности отклика при фиксированных откликах (а) и переменных (б,в)

При трех и более факторах задача становится практически неразрешимой. Если и будут найдены решения, то использовать совокупность выражений достаточно трудно, а часто и не реально.

Например, пусть необходимо исследовать влияние U, f и R r на М_пи P₂ асинхронного двигателя (АД) (рисунок 4).

Рисунок 4. Исследование влияния U, f и R r на М_пи P₂ АД

Если в диапазоне изменения каждого фактора взять хотя бы по пять точек

то для того чтобы выполнить опыты при всех возможных сочетаниях значений факторов (их три) необходимо выполнить 5 3 =125 опытов и сформировать по 5 2 =25 кривых для каждой из двух функций отклика. Если мы хотим хотя бы продублировать опыты чтобы снизить погрешность, то число опытов пропорционально возрастает, поэтому произвольное выполнение опытов при числе факторов более двух и использование их результатов — практически нереально.

Лекция 2. Разложение функции отклика в степенной ряд, кодирование факторов

Если заранее не известно аналитическое выражение функции отклика, то можно рассматривать не саму функцию, а ее разложение, например в степенной ряд в виде полинома

Разложение в степенной ряд функции возможно в том случае, если сама функция является непрерывной и гладкой. На практике обычно ограничиваются числом членов степенного ряда и аппроксимируют функцию полиномом некоторой степени.

Факторы могут иметь разные размерности (А, В, Вт, об/мин) и резко отличаться количественно. В теории планирования эксперимента используют кодирование факторов.

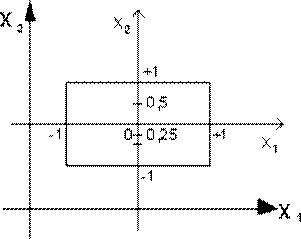
Рисунок 5 – Пространство кодированных факторов

Эта операция заключается в выборе нового масштаба для кодированных факторов (рисунок 5), причем такого, чтобы минимальное значение кодированных факторов соответствовало “-1”, а максимальное значение “+1”, а также в переносе начала координат в точку с координатами Х_1ср, Х_2ср, …, Х_nср

. (2.2)

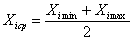
Текущее значение кодированного фактора

, (2.3)

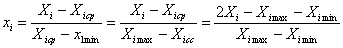
где Х_i – именованное (абсолютное) значение фактора; x_i – кодированное значение фактора; X_icp -X_imin =X_imax-X_icp — интервал варьирования фактора.

Граница совместимости факторов указана на рисунке 5 в виде кривой линии.

Если фактор изменяется дискретно, например он является качественным, то каждому уровню этого кодированного фактора присваиваются числа в диапазоне от +1 до –1. Так при двух уровнях это +1 и –1, при трех уровнях +1, 0, -1 и т.д.

Функция отклика может быть выражена через кодированные факторы Y=f(x₁,…, х_n) и записана в полиномиальном виде

Очевидно, что 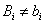, но

Для полинома, записанного в кодированных факторах, степень влияния факторов или их сочетаний на функцию отклика определяется величиной их коэффициента b_i. Для полинома в именованных факторах величина коэффициента В_i еще не говорит однозначно о степени влияния этого фактора или их сочетаний на функцию отклика.

Степенной вид полинома может быть записан в более компактной форме

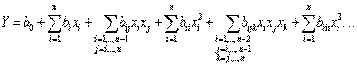(2.5)

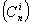
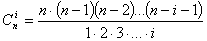При определении общего числа членов степенного ряда количество парных сочетаний для n факторов в полиноме, тройных сочетаний, i-ных сочетаний при n>i находится по соотношению

(2.6)

Например, для набора четырех чисел (n=4) — 1, 2, 3, 4 число тройных сочетаний составляет

Если считать, что существует фактор х₀ всегда равный 1, то

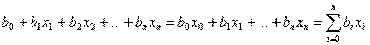(2.7)

Если дополнительно все двойные, тройные и т.д. сочетания факторов, а также квадраты факторов и все соответствующие им коэффициенты обозначить через х_i и b_i, для i=n+1, …, m, то степенной ряд можно записать в виде

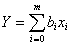(2.8)

Здесь m+1 общее число рассматриваемых членов степенного ряда.

Для линейного полинома с учетом всех возможных сочетаний факторов

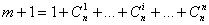(2.9)

Полный квадратичный полином выглядит следующим образом:

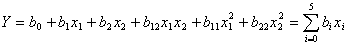(2.10)

Матричные преобразования при обработке результатов эксперимента

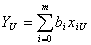
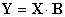
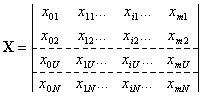При матричной записи результатов различных N опытов для полиномиального представления результата будем иметь

; Х — матрица сочетаний факторов.

(2.11)

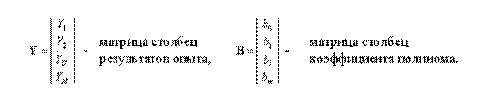
Здесь 0,1, …,i,…, m – номера членов уравнения; 1,…,U,…,

N … – номера опытов. Матрица Х — прямоугольная, содержащая m + 1 столбец и N строк.

Если учесть, что в матрице Х элементы 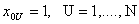, то матрицу Х можно записать

(2.12)

Домножим левую и правую часть этого уравнения на одну и туже матрицу X_t – транспонированную матрицу Х

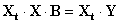(2.13)

Транспонированная матрица – это матрица, у которой по отношению к исходной столбцы и строки поменяны местами.

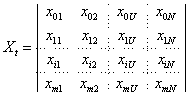(2.14)

строка

— матрица, получившаяся в результате произведения транспонированной матрицы на исходную. Она является квадратной матрицей, содержащей m +1 строку и m + 1 столбец.

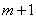
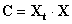
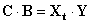(2.15)

Для того чтобы получить в общем виде матрицу-столбец коэффициентов В необходимо домножить обе части последнего матричного уравнения слева на матрицу С -1 – матрицу обратную матрице С.

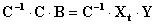(2.16)

Обратная матрица строится так (используется процедура обращения матрицы), что при умножении ее на исходную матрицу получается единичная матрица – Е, у которой на главной диагонали расположены 1, а вне ее — 0.

.

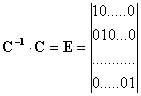
Окончательно в общем виде матрица-столбец коэффициентов полинома

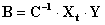(2.17)

Рассмотрим в качестве простого примера полином в виде

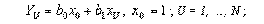(2.18)

формируемого по результатам N опытов.

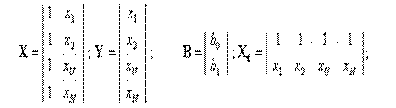	(2.19)
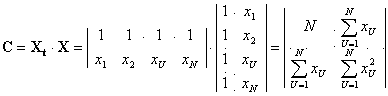	(2.20)

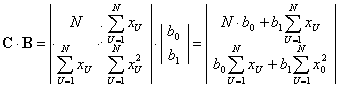	(2.21)
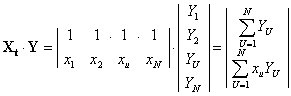	(2.22)
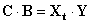	(2.23)
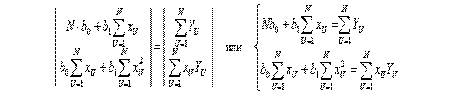	(2.24)

Откуда решение системы относительно коэффициентов b₀ и b₁

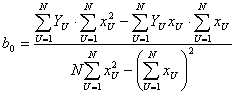	(2.25)
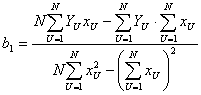	(2.26)

Этот результат полностью совпадает с соотношениями для такого же полинома при использовании метода наименьших квадрантов, где используется численный показатель минимальности суммы квадрантов отклонений во всех N опытах. Следовательно, построенный таким образом полином будет проходить самым ближайшим образом к результатам эксперимента.

Лекция 3. Ортогональное планирование эксперимента

Структура матрицы С играет важную роль в реализации алгоритма определения коэффициентов аппроксимирующего полинома. Структура матрицы С зависит от выбора значений факторов в N опытах. Поэтому желательно особым образом выбирать значения факторов в опытах.

Элемент С_ii на главной диагонали матрицы С (i-тая строка, i-тый столбец) представляется суммой квадратов значений i-того столбца сочетаний факторов матрицы Х в N опытах

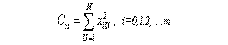(3.1)

Элементы матрицы симметрично расположенные относительно главной диагонали равны между собой, то есть матрица С — симметричная.

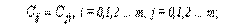(3.2)

где первый индекс указывает номер столбца матрицы Х, второй индекс — номер строки.

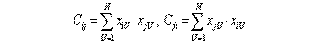(3.3)

Чтобы существовала матрица С -1 , матрица С размера (1+m; 1+m) должна быть невырожденной, то есть ее определитель должен быть отличен от нуля. Это условие выполняется, если все m+1 столбцов матрицы Х линейно независимы. Кроме того, необходимо, чтобы число различных сочетаний факторов в матрице Х (число опытов N) должно быть не меньше чем m+1. Это условие исходит из того, что для определения m+1 коэффициента полинома необходимо не менее m+1 уравнений (опытов).

Полученные коэффициенты B позволяют сформировать уравнение функции отклика при m+1 членах уравнения. Если точность этого уравнения оказалась недостаточной, то требуется взять уравнение с большим числом членов и начать все заново так как все коэффициенты B оказываются зависимыми друг от друга. Это возникает при использовании пассивного эксперимента. Однако если целенаправленно использовать активный эксперимент и особым образом построить матрицу сочетаний факторов в опытах Х, использовать планирование эксперимента, то коэффициенты полинома определяются независимо друг от друга.

Стратегия применения планов заключается в принципе постепенного планирования – постепенного усложнения модели. Начинают с простейшей модели, находятся для нее коэффициенты, определяется ее точность. Если точность не удовлетворяет, то планирование и модель постепенно усложняются.

Задача планирования заключается в том как нужно строить матрицу Х, чтобы матрица С легко обращалась и коэффициенты B определялись независимо друг от друга. Эти требования выполняется если матрица С является диагональной, то есть все элементы расположенные не на главной диагонали матрицы равны нулю

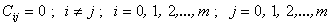(3.4)

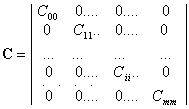(3.5)

Тогда обратная матрица определяется как

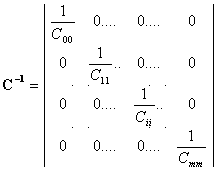(3.6)

В этом случае система уравнений распадается на m+1 независимых уравнения и коэффициенты полинома определяются как

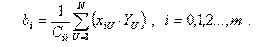(3.7)

Если учесть, что С_ii определяется как сумма квадратов значений факторов

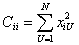(3.8)

то коэффициенты определяются как

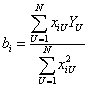(3.9)

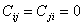
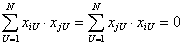Требование выполнения условия заключается в выполнении условия

(3.10)

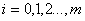
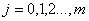
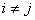
где i, j — номера столбцов в матрице Х; ; ; при .

Каждый столбец матрицы Х можно представить в виде вектора

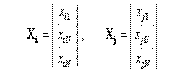(3.11)

если ,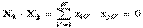

то это означает что скалярное произведение двух векторов Х_i и Х_j равняется нулю, то есть векторы Х_i и Х_j — ортогональны.

Так как любое скалярное произведение двух различных столбцов в матрице Х должно быть равно нулю, то это условие называется условием ортогональности матрицы Х, а соответствующее планирование эксперимента (определение сочетаний факторов) называется ортогональным планированием.

Для ортогонального планирования при учете того что

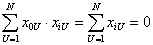(3.12)

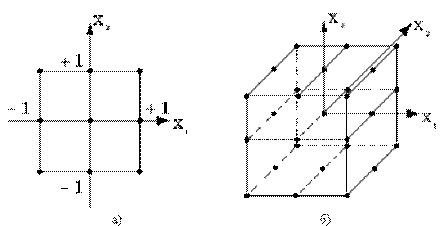
Таким образом, при ортогональном планировании сумма элементов любого столбца матрицы Х, кроме первого столбца должно быть равна нулю. Это правило используется при построении плана эксперимента, то есть при определении каким образом нужно менять значения факторов в опытах. Это правило показывает, что в ортогональном планировании при четном числе уровней, на которых фиксируется каждый фактор, то эти уровни должны быть симметрично расположены относительно центральной точки х=0, при нечетном числе уровней должна использоваться и центральная точка (рисунок 6).

Кроме свойства ортогональности план может обладать свойствам насыщенности, рототабельности и др. План является насыщенным, если общее число опытов N равняется числу неизвестных коэффициентов полинома m+1.

Рисунок 6 – Выбор уровней варьирования при ортогональном планировании

План называется рототабельным, если дисперсия отклика одинакова на одном расстоянии от центра плана при любом направлении в факторном пространстве. В упрощенном виде это означает, что все точки плана лежат на окружности (сфере, гиперсфере).

Лекция 4. Планы полного факторного эксперимента 2 n (планы ПФЭ 2 n )

Планы ПФЭ 2 n являются простейшими планами первого порядка. Основание 2 означает, что принято два уровня варьирования, на которых фиксируются факторы. n – число факторов.

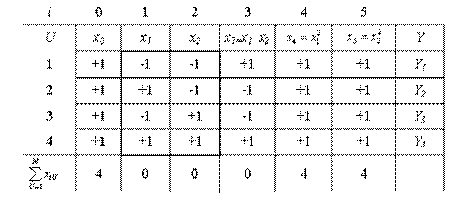
Для плана ПФЭ 2 2 число факторов равно двум (n=2) и число уровней фиксирования факторов также 2. Значения кодированных факторов выбираются в виде +1 и –1. Полное число возможных сочетаний значений n факторов (число опытов, а значит и число строк плана) N=2 2 =4. Составляется план, в котором число столбцов факторов и их сочетаний равняется числу членов уравнения. Так для уравнения

План ПФЭ 2 2 для этого уравнения представляется в следующем виде

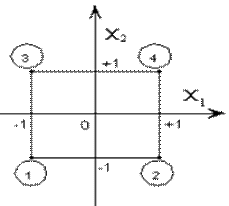
В первый столбец (i=0) во все четыре ячейки заносятся +1. Во второй столбец (i=1) заносятся единицы с чередующими знаками (начинаем с -1). В этом случае сумма элемента столбца равняется нулю. Третий столбец заполняем единицами с чередующимися через 2 элемента знаками. Сумма элементов также равняется нулю. Геометрическое отображение плана ПФЭ 2 2 с указанием номеров точек плана в факторном пространстве представлено на рисунке 7. Точки плана располагаются в вершинах квадрата.

Рисунок 7 – Геометрическое отображение плана ПФЭ 2 2 в факторном пространстве

Элементы столбцов соответствующих произведениям факторов получаются путем перемножения элементов предыдущих столбцов. Такое правило позволяет гарантировать, что мы не пропустили ни одного возможного сочетания факторов в опытах и в то же время не будет повторений одинаковых сочетаний. Последние два столбца факторов, соответствующие квадратам факторов, состоят только из +1. Столбцы, обведенные утолщенной рамкой, образуют план эксперимента. Столбец х₁х₂, не обведенный утолщенной рамкой, при проведении опытов носит вспомогательный характер.

Особенности плана ПФЭ 2 2 :

1. Различных столбцов в таблице получилось лишь четыре. Столбцы, соответствующие квадратам факторов неотличимы от столбца х₀ — это общий результат для плана ПФЭ 2 n . Это не позволяет определить отдельно коэффициенты при квадратах факторов. Поэтому планы ПФЭ 2 n называют планами первого порядка. Для определения коэффициентов при квадратах факторов используют планы второго порядка. В дальнейшем в планах ПФЭ 2 n столбцы квадратов факторов изображаться не будут.

2. Число различных столбцов равняется числу различных сочетаний факторов, то есть числу строк плана — числу опытов N. Это тоже общий результат для этих планов, то есть с помощью планов ПФЭ 2 n можно определить все коэффициенты линейного полинома со всеми возможными сочетаниями факторов, включая коэффициенты b_12…n , отражающие максимальное взаимодействие факторов вида х₁х₂…х_n.

3. В плане ПФЭ 2 2 сумма квадратов элементов любого столбца

,

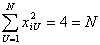
Поэтому для планов ПФЭ 2 n

.

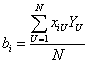
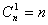
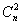
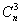
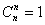
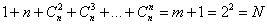Таким образом, с помощью планов ПФЭ 2 n можно определить свободный член уравнения b₀, коэффициентов b_i, коэффициентов при различных взаимодействиях двух факторов b_ij , коэффициентов тройных взаимодействий факторов b_ijk , …. коэффициент b_12…n. максимального взаимодействия факторов. Общее число определяемых коэффициентов

(4.1)

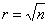
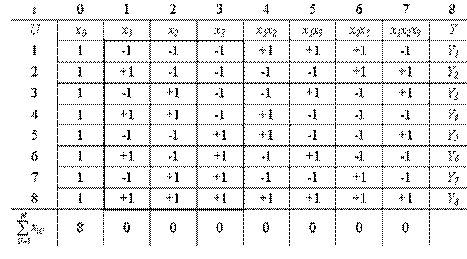
План ПФЭ 2 n может являться насыщенным, при выборе числа членов уравнения m+1=N, ненасыщенным, при выборе числа членов уравнения и соответственно числа столбцов плана m+1 n является также рототабельным, так как все точки плана лежат на окружности (сфере, гиперсфере) с радиусом относительно центра плана.

Для плана ПФЭ 2 3 число факторов n = 3. Выполняется N = 2 3 = 8 опытов. Уравнение может содержать до восьми членов

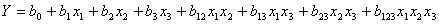(4.2)

Таким образом формируется план из восьми строк и восемь столбцов. В четвертом столбце (i=3) записываются единицы с чередующимися знаками через четыре элемента. План составляется аналогичным образом плану ПФЭ 2 2 .

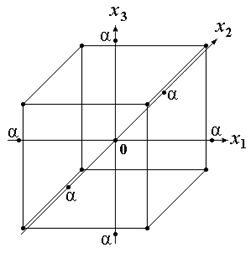
Столбцы, обведенные утолщенной рамкой, образуют план эксперимента. Столбцы, не обведенные утолщенной рамкой, при проведении опытов носят вспомогательный характер. Геометрическое отображение плана ПФЭ 2 3 с указанием номеров точек плана в факторном пространстве представлено на рисунке 8. Точки плана располагаются в вершинах куба.

Рисунок 8 – Геометрическое отображение плана ПФЭ 2 3 в факторном пространстве

Пример применения плана ПФЭ 2 2 . Пусть в результате проведения экспериментов по плану ПФЭ 2 2 , то есть при изменении двух факторов, мы получили опытные значения Y₁, Y₂, Y₃, Y₄. Поверхность, уравнение которой нас интересует, имеет вид рисунке 9.

Рисунок 9 – Поверхность функции отклика

Составляем план ПФЭ 2 2 .

Вначале найдем коэффициенты сокращенного линейного полинома вида

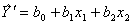(4.4)

и результаты вычислений 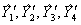по нему.

Рассчитываем коэффициенты полинома.

;

;

.

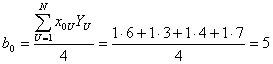
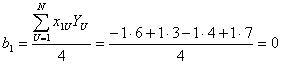
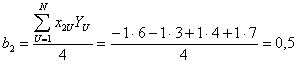
Полином имеет вид

.

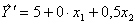
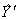
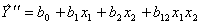Результаты расчета по нему приведены в соответствующем столбце плана. Наблюдаются расхождения между Y и . Если точность сокращенного полинома не удовлетворяет, то по тем же результатам опытов можно сформировать более полный полином вида

(4.5)

При этом ранее определенные коэффициенты остаются без изменений. Определим коэффициент при дополнительном члене полинома

.

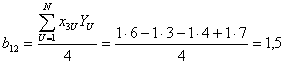
Полином имеет вид

.

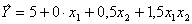
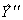
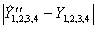
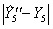
По нему рассчитываем предсказанные значения отклика в точках плана (столбец ). Поверхность, построенная по полученному полиному, проходит точно через четыре точки плана ( =0), по которым определены коэффициенты. Однако в других точках области определения функции, например в центре плана (точка 5 в плане, х₁=0, х₂=0), предсказанные и действительные значения, могут не совпадать ( =3).

Лекция 5. Планы дробного факторного эксперимента (планы ДФЭ)

При многофакторном эксперименте, особенно когда число факторов больше шести (n > 6), число опытов планов ПФЭ 2 n (N = 2 n ) становится чрезмерным. Если нам не требуется определение всех коэффициентов неполного квадратичного полинома, то переходят к дробному факторному эксперименту (ДФЭ) – части полного факторного эксперимента. Так, например, если требуется определить лишь коэффициенты при самих факторах

,

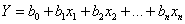(5.1)

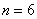
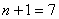
то план ПФЭ 2 n дает избыточную информацию. Так при , в этом случае требуется определить коэффициентов, тогда как по плану ПФЭ необходимо провести N = 2 6 =64 опыта.

Хотя эта избыточная информация не является бесполезной, она позволяет более точно определить коэффициенты, но все же часто используют планы ДФЭ 2 n-k , где k – показатель дробности плана ПФЭ. При k = 1 число опытов в плане ДФЭ в два раза меньше, чем в плане ПФЭ, поэтому такие планы называют полуреплика плана ПФЭ. Так при k=1 для плана ДФЭ 2 6-1 N =2 6-1 = 32, при k=2 для плана ДФЭ 2 6-2 N =2 6-2 = 16 и такой план называют четвертьрепликой, при k=3 для плана ДФЭ 2 6-3 N =2 6-3 = 8. При выборе дробности плана k необходимо учитывать, что число опытов должно быть больше числа членов уравнения. В рассматриваемом случае величина k должна быть такой, что бы удовлетворялось условие

.

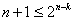(5.2)

План ДФЭ строится, как и для плана ПФЭ, но с меньшим числом факторов. Оставшиеся факторы варьируются не произвольно, а так чтобы сохранялась ортогональность плана. Это обеспечивается, если оставшиеся факторы варьируются по выбранному генерирующему соотношению, например как произведение каких-либо факторов из первой группы. Но это приводит к тому, что в матрице Х будут существовать одинаковые столбцы. Следовательно, мы не сможем найти в чистом виде все коэффициенты неполного квадратичного полинома, а лишь определим совместную величину коэффициентов для одинаковых столбцов.

Рассмотрим построение плана ДФЭ 2 3-1 . Здесь n = 3, к =1, N=2 3-1 =4. Первые два фактора варьируем как и ранее для плана ПФЭ 2 2 , а для третьего фактора выбираем генерирующее соотношение в виде .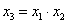

Для неполного квадратичного полинома

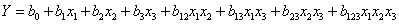(5.3)

количество столбцов плана составляет восемь.

План является ортогональным, но в нем оказались четыре пары одинаковых столбцов. Поэтому можно определить только четыре коэффициента, отражающие совместные влияния двух одинаковых столбцов

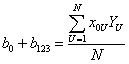(5.4)

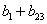
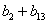
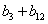
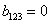
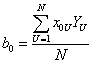Суммарные значения коэффициентов ; ; определяются аналогично. Это следствие того, что мы пытаемся определить полное количество коэффициентов – 8 по недостаточному числу опытов — 4. Однако, если заранее известно, что некоторые из членов уравнения равны нулю (пренебрежимо малы) или имеется априорная информация о величинах некоторых коэффициентов, то полученные коэффициенты могут быть вычленены. Так если , то

(5.5)

Если можно допустить, что коэффициенты из их смешанной оценки сопоставимы, то для рассмотренного плана

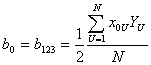(5.6)

Графическое изображение планов ПФЭ 2 3 и ДФЭ 2 3-1 в факторном пространстве (для трех факторов — трехмерное пространство) представлено на рисунке 10. План ПФЭ 2 3 представлен кубом с восемью узлами (точками плана), а возможные планы ДФЭ 2 3-1 – проекциями этого куба на три плоскости. То есть из восьми узлов выбираются четыре (рисунок 10, а). Из куба можно также выбрать четыре точки из восьми, не лежащие в одной плоскости, и сформировать план ДФЭ 2 3-1 (рисунок 10, б).

Рисунок 10 – Графическое изображение планов ПФЭ 2 3 и ДФЭ 2 3-1 в факторном пространстве

Планы ДФЭ, как и планы ПФЭ, являются рототабельными. Планы ДФЭ могут быть как насыщенными так и ненасыщенными.

Достоинство планов ДФЭ заключается и в том, что если построенный на его основе неполный полином не удовлетворяет требованиям по точности, то план ДФЭ легко достраиваются до плана ПФЭ, без потери информации прежних опытах, с формированием более точного полинома.

Пример построения плана ДФЭ.

Построить план ДФЭ 2 4-1 и определить полином

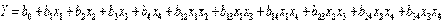(5.7)

Число факторов – 4. Нужно найти 8 коэффициентов полинома. Выбираем 8 из 16 опытов плана ПФЭ 2 4 таким образом, чтобы были определены независимые коэффициенты при самих факторах, смешанные коэффициенты при парных сочетаниях факторов и в пренебрежении тройными и четверным сочетаниями факторов и при этом сохранялась ортогональность плана.

Такой выбор позволяет сформировать план ДФЭ 2 4-1 как и план ПФЭ 2 3 , но с х₄=х₁х₂х₃ . План ДФЭ 2 4-1 представляется в виде

Значения коэффициентов полинома составляют:

.

;

;

;

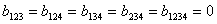
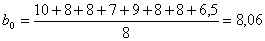
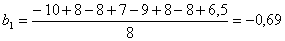
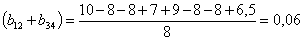
Если принять, что

,

,

,

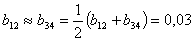
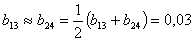
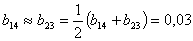
то полином имеет вид

.

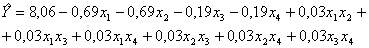
Значения полинома в точках плана приведены в последнем столбце плана ДФЭ 2 4-1 . В нашем случае точность его достаточно высокая.

Лекция 6. Насыщенные планы первого порядка.

Насыщенным планом первого порядка – называется план, содержащий n+1 точку (опыт). Например, при n = 4, N=n + 1 = 5.

То есть полином формируется в виде

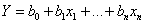(6.1)

Таким образом, насыщенный план – это предельно минимальный случай плана ДФЭ. Такие планы называются симплекс-планы. Для симплекс-плана при n = 1 N = 2 его геометрическое изображение представлено на рисунке 11, а; при n=2, N=3 – на рисунке 11, б; при n=3, N=4 – на рисунке 11, в. Симплекс-планы обычно используются на стадии предварительного исследования.

Симплекс-план не всегда является ортогональным. Симплекс-план называется правильным, если расстояние между двумя любыми точками плана одинаковое. Симплекс-план называется центрированным, если

,

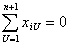
Применимость планов ПФЭ и пути повышения точности полиномов

По каким же признакам можно судить о допустимости использования неполного квадратичного полинома, построенного на основе планов ПФЭ 2 n ?

Такие полиномы дают поверхность отклика, которая проходит точно через все экспериментальные точки, по которым определяются коэффициенты. Так как точки планов ПФЭ располагаются на границах диапазонов варьирования факторов, то это означает, что поверхность отклика проходит через граничные точки. В любом сечении поверхности отклика, полученной по такому полиному, плоскостью при фиксированных всех факторах кроме одного и параллельной оси Y получается след в виде прямой линии.

Возможны случаи, когда реальная поверхность отклика определяется полиномами второго и выше порядков В этом случае поверхность плана ПФЭ, совпадая с реальной поверхностью в граничных точках, может отличаться в других точках факторного пространства, например в центральной точке плана, т.е. 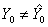. Поэтому одним из признаков неудовлетворительной аппроксимации полиномами по плану ПФЭ является расхождение результатов функции отклика с реальной функцией в центральной точке плана.

Однако при многофакторном эксперименте возможны случаи, когда в реальности функция отклика зависит, в том числе, от квадратов факторов, у которых коэффициенты имеют разные знаки, например, для “седловидной” поверхности. При этом, несмотря на то, что эта поверхность явно нелинейная, результат опыта в центральной точке может оказаться достаточно близким к полученному результату по неполному квадратичному полиному плана ПФЭ. Однако расхождения будут возникать во всех других точках плана эксперимента. Поэтому нецелесообразность использования плана ПФЭ определяется нелинейностью каких-либо сечений поверхности отклика. 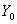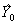Косвенным признаком может служить расхождение и в центральной точке плана.

Если не удается получить полином по плану ПФЭ, хорошо аппроксимирующей реальную поверхность, то какие пути можно предложить для повышения точности полиномов?

Уменьшение диапазона варьирования факторов или его разбиение на поддиапазоны, для каждого из которых строится свой план ПФЭ и определяется свой полином. Путь достаточно трудоемок, но погрешность семейства планов ПФЭ снижается.

Выделение фактора, порождающий нелинейность, и построение для оставшихся n–1 факторов k планов ПФЭ, в каждом из которых выделенный фактор зафиксирован при некотором значении. На основе полученных k полиномов можно попытаться сформировать общий полином, коэффициенты которого являются функциями выделенного фактора. Этот путь также достаточно трудоемок.

Переход к плану ПФЭ с большим числом уровней варьирования факторов, например к планам с варьированием факторов на трех уровнях — планам ПФЭ 3 n (рисунок 12). В этом случае происходит резкое увеличение количества точек по сравнению с планом ПФЭ 2 n . Так при n = 2 для ПФЭ 2 n N=4, для ПФЭ 3 n N=9; при n = 3 для ПФЭ 2 n N=8, для ПФЭ 3 n N=27; при n = 4 для ПФЭ 2 n N=16, для ПФЭ 3 n N=81 и т.д.

Рисунок 12 – Планы ПФЭ 3 2 (а) и ПФЭ 3 3 (б)

Достраивание планов ПФЭ 2 n до планов более высокого порядка (чаще всего второго) и построение полных квадратичных полиномов (с наличием квадратов факторов).

Преобразование метрики матричного пространства, то есть переход к новым факторам функционально связанным с прежними факторами, но не порождающими нелинейности.

Лекция 7. Планы второго порядка

Они позволяют сформировать функцию отклика в виде полного квадратичного полинома, который содержит большее число членов, чем неполный квадратичный полином, сформированный по планам первого порядка, и поэтому требуют большего числа выполняемых опытов. Полный квадратичный полином при n =2 содержит 6 членов

,

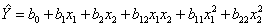(7.1)

при n = 3 — 11 членов

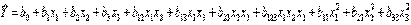(7.2)

Известно, что для получения квадратичной зависимости каждый фактор должен фиксироваться как минимум на трех уровнях.

Для планов второго порядка область планирования может:

Быть естественной, то есть включать область планирования планов первого порядка и дополнительные точки (такие планы называются композиционными). Дополнительные точки могут выходить за область плана первого порядка – единичного гиперкуба. В этом случае опыты в них реализуются при установлении факторов за пределами варьирования. Это надо учитывать при определении области совместимости факторов.

Не выходить за пределы единичного гиперкуба, то есть для всех точек плана выполняется условие .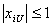

Не выходить за пределы единичного гипершара, определяемую соотношением таких значений факторов в плане, что .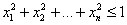

Во втором и третьем случаях используют специальные приемы выполнения приведенных соотношений в плане. План с одной областью планирования можно перестроить в план другой областью планирования.

Если уже был ранее сформирован план ПФЭ, но точность его функции отклика не удовлетворяет, то мы можем достроить этот план до плана второго порядка (композиционный план) и сформировать функцию отклика в виде полного квадратичного полинома, без потери информации о ранее сделанных опытах.

Ортогональный центрально-композиционный план второго порядка

Ортогональным планом называется такой план, у которого матрица планирования Х строится так, что бы матрица С=Х_tХ оказалась диагональной. Используем этот подход и при построении планов второго порядка. План называется центральным, если все точки расположены симметрично относительно центра плана. ОЦКП – центральный симметричный ортогональный композиционный план.

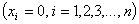
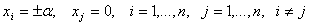
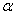
В ОЦКП входят: ядро — план ПФЭ с N₀= 2 n точками плана, n₀ (одна для этого плана) центральная точка плана и по две “звездные” точки для каждого фактора

.

– плечо “звездных” точек.

При этом в каждой плоскости, содержащей ось Y и координатную ось i-того фактора (проходящей через центр плана), оказываются три значения фактора х_i 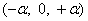и три соответствующих значения Y.

Общее количество точек в плане ОЦКП составляет

,

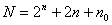(7.3)

При n > 2 в ОЦКП оказывается меньшее количество точек, чем в плане ПФЭ 3 n .

Число точек в плане

Графическое представление ОЦКП для n=3 приведено на рисунке 13.

Рисунок 13 – ОЦКП при n=3

Для ортогонального плана необходимо, чтобы выполнялось соотношение

.

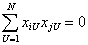(7.4)

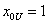
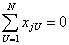Так как , то для столбцов j=1, 2,…., m+1 должно выполняться условие

.

(7.5)

Это означает необходимость выполнения требования, чтобы сумма элементов любого столбца (кроме j=0), включая столбцы, соответствующие квадратам фактора, должна быть равна нулю. Это возможно, если члены столбцов, соответствующих квадратам факторов, преобразованы, иначе сумма квадратов факторов не может быть равна нулю.

Преобразование элементов этих столбцов осуществляется в виде

,

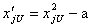(7.6.)

где а – величина, зависящая от числа факторов.

Сумма элементов столбца, соответствующего квадратам факторов

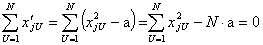(7.7)

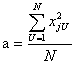(7.8)

В общем случае ортогональный центрально-композиционный план при трех (n) факторов имеет следующий вид

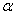
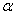
В ОЦКП каждый фактор фиксируется, в общем случае, на пяти уровнях (- , -1, 0, 1, + ).

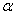
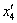
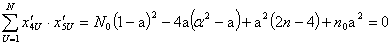Для определения неизвестных “а” и “ ” нужно сформировать и решить систему из двух уравнений. Одно из них для “а” мы записали раннее. Другое уравнение получим из условия ортогональности для столбцов и

(7.9)

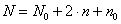
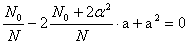После простейших преобразований с учетом того, что – общее число опытов в плане, получаем соотношение

(7.10)

Соотношение для а при j=1, 2 или 3 может быть записано как (см. план)

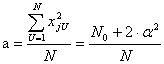(7.11)

Подставив его в последнее уравнение получаем

,

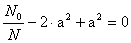
откуда константа преобразования а

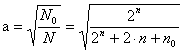(7.12)

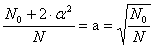(7.13)

и плечо звездных точек

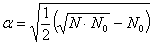(7.14)

Например, для ОЦКП при числе факторов n=3 имеем следующие параметры плана

,

,

.

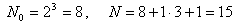
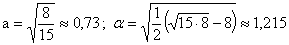
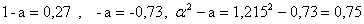
Сам план принимает вид

Очевидно, что план является ортогональным. В отличие от планов ПФЭ для ОЦКП сумма квадратов факторов разных столбцов не является одинаковой.

По результатам опытов плана формируется полином

.

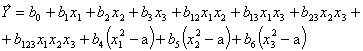
Коэффициенты полинома

.

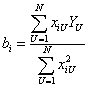
Можно преобразовать полином к виду

,

.

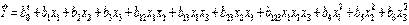
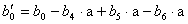
Значения параметров ОЦКП при числе факторов n

При n =2 ОЦКП совпадает с планом ПФЭ 2 3 . Звездные точки ОЦКП в этом случае лежат на границах варьирования факторов. Если точки плана ПФЭ 2 n всегда лежат на окружности (поверхности шара, гипершара), то точки плана ОЦКП не лежат на какой-либо одной окружности (поверхности шара, гипершара). План ОЦКП не является насыщенным. Так, например, для n = 3 полином имеет одиннадцать членов со своими коэффициентами, но для их определения используются пятнадцать опытов.

Пример плана ОЦКП для n = 2.

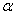
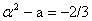
Параметры плана N₀=4, N=9, = 1, а = 2/3, 1-а=1/3, -а=-2/3, .

Использован рассмотренный ранее план ПФЭ 2 2 с добавленными опытами 5-9.

Коэффициенты полинома составляют

;

;

;

;

;

.

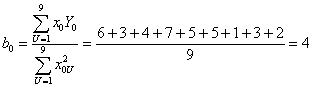
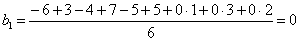
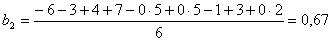
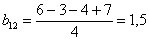
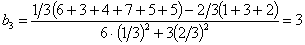
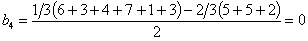
Полином принимает вид

.

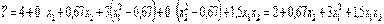
(Ранее по плану ПФЭ 2 2 был сформирован полином ).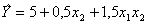

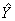
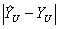
Рассчитанные значения по полиному приведены в плане. Также приведены величины , подтверждающие достаточно высокую точность полинома. Так в центральной точке плана, в отличие от случая применения плана ПФЭ 2 2 , расхождений нет.

Лекция 8. Рототабельные планы

Рототабельные планы – это планы, у которых точки плана располагаются на окружностях (сферах, гиперсферах). У рототабельного плана первого порядка точки плана располагаются на одной окружности (сфере, гиперсфере) с радиусом R

,

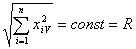(8.1)

где V=1,…, N — номер точки плана, i =1,…, n – номер фактора.

В таком случае точность оценивания функции отклика по любому направлению факторного пространства (для всех точек плана) одинаковая.

Рототабельный план может быть симметричным, когда точки плана располагаются симметрично друг друга. Рассмотренный ранее план ПФЭ 2 n – рототабельный симметричный план первого порядка.

У рототабельных планов второго порядка точки плана располагаются на двух концентрических гиперсферах с радиусами R₁ и R₂ . В таких планах

,

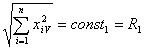(8.2.)

,

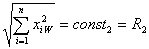(8.4)

где V и W – текущие номера точек плана в двух подмножествах опытов N₀ и n₀ из их общего количества N, относящихся к двум разным концентрическим сферам. Одна из сфер может быть вырожденной, когда R₂=0. Рассмотренный ранее ортогональный центрально-композиционный план второго порядка (ОЦКП) не является рототабельным планом, так как его точки лежат на трех концентрических окружностях (сферах, гиперсферах). При n=2 это очевидно из рисунка 14. “Звездные” точки плана и точки плана ПФЭ 2 n лежат на разных окружностях.

Рисунок 14 – Расположение точек ОЦКП на трех окружностях

Рототабельный план может быть ортогональным, если выполняется условие

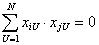(8.5)

Дата добавления: 2016-02-20 ; просмотров: 826 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ