Какое самое сложное математическое уравнение в мире

7 математических загадок тысячелетия. Просто о сложном

Только для мыслящих людей!

«Я знаю только то, что ничего не знаю, но другие не знают и этого»
(Сократ, древнегреческий философ)

НИКОМУ не дано владеть вселенским разумом и знать ВСЁ. Тем не менее, у большинства ученых, да и тех, кто просто любит размышлять и исследовать, всегда есть стремление узнать больше, разгадать загадки. Но остались ли еще неразгаданные темы у человечества? Ведь, кажется, все уже ясно и нужно только применять полученные веками знания?

НЕ стоит отчаиваться! Еще остались нерешенные проблемы из области математики, логики, которые в 2000 году эксперты Математического института Клэя в Кембридже (Массачусетс, США) объединили в список, так называемые, 7 загадок тысячелетия (Millennium Prize Problems). Эти проблемы волнуют ученых всей планеты. С тех пор и по сей день любой человек может заявить, что нашел решение одной из задач, доказать гипотезу и получить от бостонского миллиардера Лэндона Клэя (в честь которого и назван институт) премию. Он уже выделил на эти цели 7 миллионов долларов. К слову сказать, на сегодняшний день одна из проблем уже решена.

Итак, вы готовы узнать о математических загадках?

Уравнения Навье — Стокса (сформулированы в 1822 году)

Уравнения о турбулентных, воздушных потоках, а также течении жидкостей известны как уравнения Навье — Стокса. Если, к примеру, плыть по озеру на чем-либо, то неизбежно вокруг возникнут волны. Это касается и воздушного пространства: при полете на самолете в воздухе также будут образовываться турбулентные потоки.
Данные уравнения как раз производят описание процессов движения вязкой жидкости и являются стержневой задачей всей гидродинамики. Для некоторых частных случаев уже найдены решения, в которых части уравнений отбрасываются, как не влияющие на конечный результат, но в общем виде решения этих уравнений не найдены.
Необходимо найти решение уравнениям и выявить гладкие функции.

Гипотеза Римана (сформулирована в 1859 году)

Область: теория чисел

Известно, что распределение простых чисел (Которые делятся только на себя и на единицу: 2,3,5,7,11…) среди всех натуральных чисел не подчиняется никакой закономерности.
Над этой проблемой задумался немецкий математик Риман, который сделал свое предположение, теоретически касающееся свойств имеющейся последовательности простых чисел. Уже давно известны так называемые парные простые числа — простые числа-близнецы, разность между которыми равна 2, например 11 и 13, 29 и 31, 59 и 61. Иногда они образуют целые скопления, например, 101, 103, 107, 109 и 113.
Если такие скопления будут найдены и выведен определенный алгоритм, то это приведет к революционному изменению наших знаний в области шифрования и к невиданному прорыву в области безопасности Интернета.

Проблема Пуанкаре (сформулирована в 1904 году. Решена в 2002 году.)

Область: топология или геометрия многомерных пространств

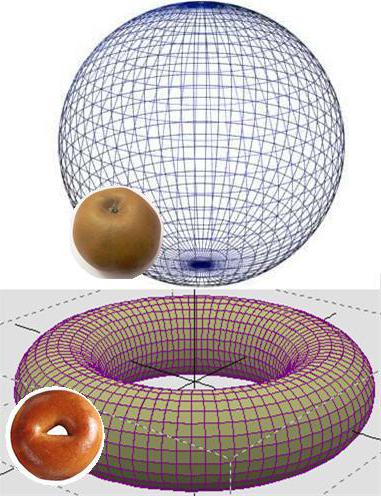
Суть проблемы заключается в топологии и состоит в том, что если натягивать резиновую ленту, к примеру, на яблоко (сферу), то будет теоретически возможным сжать ее до точки, медленно перемещая без отрыва от поверхности ленту. Однако если эту же ленту натянуть вокруг бублика (тора), то сжать ленту без разрыва ленты или разлома самого бублика не представляется возможным. Т.е. вся поверхность сферы односвязна, в то время как тора – нет. Задача состояла в том, чтобы доказать, что односвязной является только сфера.

Представитель ленинградской геометрической школы Григорий Яковлевич Перельман является лауреатом премии тысячелетия математического института Клэя (2010 г.) за решение проблемы Пуанкаре. От знаменитой Фильдсовской премии он отказался.

Гипотеза Ходжа (сформулирована в 1941 году)

Область: алгебраическая геометрия

В реальности существуют множество как простых, так и куда более сложных геометрических объектов. Чем сложнее объект, тем труднее его изучать. Сейчас учеными придуман и вовсю применяется подход, основанный на использовании частей одного целого («кирпичики») для изучения этого объекта, как пример — конструктор. Зная свойства «кирпичиков», становится возможным подступиться и к свойствам самого объекта. Гипотеза Ходжа в данном случае связана с некоторыми свойствами как «кирпичиков», так и объектов.
Это очень серьезная проблема алгебраической геометрии: найти точные пути и методы анализа сложных объектов с помощью простых «кирпичиков».

Уравнения Янга — Миллса (сформулированы в 1954 году)

Область: геометрия и квантовая физика

Физики Янг и Миллс описывают мир элементарных частиц. Они, обнаружив связь между геометрией и физикой элементарных частиц, написали свои уравнения в области квантовой физики. Тем самым был найден путь к объединению теорий электромагнитного, слабого и сильного взаимодействий.
На уровне микрочастиц возникает «неприятный» эффект: если на частицу действуют несколько полей сразу, их совокупный эффект уже нельзя разложить на действие каждого из них поодиночке. Это происходит по причине того, что в этой теории друг к другу притягиваются не только частицы материи, но и сами силовые линии поля.
Хотя и уравнения Янга — Миллса приняты всеми физиками мира, экспериментально теория, касающаяся предсказывания массы элементарных частиц, не доказана.

Гипотеза Берча и Свиннертон-Дайера (сформулирована в 1960 году)

Область: алгебра и теория чисел

Гипотеза связана с уравнениями эллиптических кривых и множеством их рациональных решений. В доказательстве теоремы Ферма эллиптические кривые заняли одно из важнейших мест. А в криптографии они образуют целый раздел имени себя, и на них основаны некоторые российские стандарты цифровой подписи.
Задача в том, что нужно описать ВСЕ решения в целых числах x, y, z алгебраических уравнений, то есть уравнений от нескольких переменных с целыми коэффициентами.

Проблема Кука (сформулирована в 1971 году)

Область: математическая логика и кибернетика

Ее еще называют «Равенство классов P и NP», и она является одной из наиболее важных задач теории алгоритмов, логики и информатики.
Может ли процесс проверки правильности решения какой-либо задачи длиться дольше, чем время, затраченное на само решение этой задачи (независимо от алгоритма проверки)?
На решение одной и той же задачи, порой, нужно разное количество времени, если изменить условия и алгоритмы. К примеру: в большой компании вы ищете знакомого. Если вы знаете, что он сидит в углу или за столиком — то вам понадобится доли секунд, чтобы его увидеть. Но если вы не будете знать точно, где находится объект, то затратите больше времени на его поиски, обходя всех гостей.
Основным вопросом является: все или не все задачи, которые можно легко и быстро проверить, можно также легко и быстро решить?

Математика, как может показаться многим, не так далека от реальности. Она является тем механизмом, с помощью которого можно описать наш мир и многие явления. Математика всюду. И прав был В.О. Ключевский, который изрек: «Не цветы виноваты, что слепой их не видит».

Математические уравнения, которые изменили мир

Для большинства людей математика — это что-то скучное и совершенно ненужное в обычной жизни. Глядя на все эти цифры, сложно понять, что в них такого. На самом деле математика, наравне с физикой — самые важные предметы, ведь она по сути раскрывает секреты мироздания.

В этой статье мы расскажем о математических уравнениях, которые изменили мир. И, может быть, в очередной раз взглянув на эти цифры, ты уже будешь думать о них не просто как о наборе символов, а как о чем-то, что помогло человечеству продвинуться вперед.

Теорема Пифагора

Вряд ли кто-то не слышал или не видел этой теоремы, даже если он плохо учился в школе. Она говорит о том, что сумма квадратов длин катетов равна квадрату гипотенузы. Если говорить простыми словами, то это отношение длин сторон прямоугольного треугольника.

Казалось бы, одна из самых простых формул, глядя на которую, глаза не начинают слезиться от огромного количества символов, но она сделала для человечества очень много. Помимо архитектуры и других инженерных дисциплин, теорема Пифагора применяется в навигации, картографии и других важных для человечества науках.

Теорему Пифагора применяют в таком большом количестве точных наук, что проще сказать, где она не используется. Несмотря на то, что теорема была открыта несколько тысячелетий назад, она до сих пор служит на благо человечества.

Закон всемирного тяготения Ньютона

Эта формула выглядит чуть сложнее, чем предыдущая, и она принесла не меньше благ человечеству. Исаак Ньютон, одна из самых выдающихся личностей в науке, открыл этот закон около 1666 года и буквально перевернул им мир.

Эта формула позволила лучше понять движение различных физических объектов и явлений. Причем Ньютон своим законом заложил основы для более сложных научных теорий, таких как Общая теория относительности и Квантовая гравитация.

Логарифмы

Пожалуй, самые нелюбимые формулы у школьников, ведь мало кто понимает их суть и необходимость. Может сейчас важность логарифмов и не так велика, но в прошлом, до появления цифровых компьютеров, они являлись наиболее быстрым способом умножения больших чисел.

Ну, и что такого, спросишь ты, умножать стали быстрее, как же это повлияло на мир? А так, что теперь ученые смогли сосредоточиться на воплощении своих теорий в жизнь, а не на долгих и нудных подсчетах.

Второй закон термодинамики

Второй закон термодинамики говорит о том, что в закрытой системе энтропия всегда постоянна и возрастает. Звучит непонятно, если не разобраться. Если сказать просто, то в системе, которая первоначально находится в упорядоченном неравномерном состоянии, например, горячая рядом с холодной, они будут стремиться к выравниванию, то есть к стабилизации температур, пока они не станут одинаковыми. Кроме того, уравнение говорит, что каждый раз, когда энергия изменяется или перемещается, она становится менее полезной.

Казалось бы, и что здесь такого, и чем это поменяло мир? А тем, что благодаря этому закону началось развитие двигателей внутреннего сгорания, современной металлургии, эффективного производства электроэнергии и других сфер деятельности.

Преобразование Фурье

Французский математик Жан-Батист Жозеф Фурье сформулировал свое уравнение интегралов еще в начале 19 века, но они до сих пор используются в науке. Если говорить простым языком, то преобразования Фурье необходимы для понимания более сложных волновых структур, например, человеческой речи, позволяя разбить беспорядочную функцию на комбинацию простых волн. Это значительно упрощает анализ сигналов.

Для каких сфер она несет пользу? Для астрономии, акустики, радиотехники и для других, работающих со звуком. Ты сталкиваешься с преобразованием Фурье каждый раз, когда слушаешь музыку или голосовое сообщение, включаешь радио в машине и так далее.

Концепция эквивалентности массы и энергии

Думаем, ты слышал об уравнении Альберта Эйнштейна, сформулированном им в 1905 году, хотя на самом деле оно было предложено еще до знаменитого ученого. Казалось бы, что в нем особенного, ведь оно куда короче всего того, что преподают на математике даже на гуманитарных факультетах. Но с этой концепцией человечество вступило в новую эпоху.

Опираясь на эту формулу, ученые изучают космос, строят ускорители частиц, стараются понять природу субатомного мира. Концепция стала настолько известной, что, наравне со значком атома, является одним из главных символов науки.

Уравнения Максвелла

Британский физик, математик и механик Джеймс Клерк Максвелл был весьма плодовит в плане науки и заложил основы современной классической электродинамики, а также ввел несколько понятий в физику, которые используются и по сей день.

Одним из главных трудов Максвелла стала система из 20 уравнений, описывающих работу электрических и магнитных полей, а также их взаимодействие. В настоящее время уравнения Максвелла представляют собой систему из четырех уравнений, которые можно описать следующими словами:

1. Электрический заряд является источником электрической индукции.
2. Магнитные заряды не обнаружены.
3. Изменение магнитной индукции порождает вихревое электрическое поле.
4. Электрический ток и изменение электрической индукции порождают вихревое магнитное поле.

Выглядит как китайская грамота для гуманитарных умов, но поверь, без этих четырех уравнений ты бы, возможно, не пользовался сейчас благами цивилизации вроде компьютеров, смартфонов и другой техники, работающей на электричестве, или, как минимум, они выглядели бы иначе.

Уравнение Шредингера

Многие знают ученого Эрвина Шредингера только по мысленному эксперименту «кота Шредингера». Но этот австрийский ученый сделал для науки куда больше, чем простой мысленный эксперимент, выведя уравнение, описывающее, как состояние квантовой системы изменяется со временем и определяет поведение атомов и субатомных частиц в квантовой механике.

Эта сложная формула открыла человечеству путь к атомной энергетике, микрочипам, квантовым вычислениям и другим важным для современного общества дисциплинам.

Нерешаемые задачи: уравнения Навье-Стокса, гипотеза Ходжа, гипотеза Римана. Задачи тысячелетия

Нерешаемые задачи — это 7 интереснейших математических проблем. Каждая из них была предложена в свое время известными учеными, как правило, в виде гипотез. Вот уже много десятилетий над их решением ломают головы математики во всем мире. Тех, кто добьется успеха, ждет вознаграждение в миллион американских долларов, предложенное институтом Клэйя.

Предыстория

В 1900 году великий немецкий математик-универсал Дэвид Гильберт, представил список из 23-х проблем.

Исследования, осуществленные с целью их решения, оказали огромное влияние на науку 20 века. На данный момент большинство из них уже перестали быть загадками. В числе нерешенных или решенных частично остались:

• проблема непротиворечивости арифметических аксиом;
• общий закон взаимности на пространстве любого числового поля;
• математическое исследование физических аксиом;
• исследование квадратичных форм при произвольных алгебраических числовых коэффициентах;
• проблема строгого обоснования исчислительной геометрии Федора Шуберта;
• и пр.

Институт Клэйя

Под таким названием известна частная некоммерческая организация, штаб-квартира которой находится в Кембридже, штат Массачусетс. Она была основана в 1998 году гарвардским математиком А. Джеффи и бизнесменом Л. Клэйем. Целью деятельности института является популяризация и развитие математических знаний. Для ее достижения организация выдает премии ученым и спонсирует многообещающие исследования.

В начале 21 столетия Математический институт Клэйя предложил премию тем, кто решит проблемы, которые известны, как самые сложные нерешаемые задачи, назвав свой список Millennium Prize Problems. Из «Списка Гильберта» в него вошла только гипотеза Римана.

Задачи тысячелетия

В список института Клэйя изначально входили:

• гипотеза о циклах Ходжа;
• уравнения квантовой теории Янга — Миллса;
• гипотеза Пуанкаре;
• проблема равенства классов Р и NP;
• гипотеза Римана;
• уравнения Навье Стокса, о существовании и гладкости его решений;
• проблема Берча — Свиннертон-Дайера.

Эти открытые математические проблемы представляют огромный интерес, так как могут иметь множество практических реализаций.

Что доказал Григорий Перельман

В 1900 году известный ученый-философ Анри Пуанкаре предположил, что всякое односвязное компактное 3-мерное многообразие без края гомеоморфно 3-мерной сфере. Ее доказательство в общем случае не находилось в течение века. Лишь в 2002-2003 годах петербургский математик Г. Перельман опубликовал ряд статей с решением проблемы Пуанкаре. Они произвели эффект разорвавшейся бомбы. В 2010 году гипотеза Пуанкаре была исключена из списка «Нерешенные задачи» института Клэйя, а самому Перельману было предложено получить полагающееся ему немалое вознаграждение, от которого последний отказался, не объяснив причин своего решения.

Самое понятное объяснение того, что удалось доказать российскому математику, можно дать, представив, что на бублик (тор), натягивают резиновый диск, а затем пытаются стянуть края его окружности в одну точку. Очевидно, что это невозможно. Другое дело, если произвести этот эксперимент с шаром. В таком случае вроде бы трехмерная сфера, получившаяся из диска, окружность которого стянули в точку гипотетическим шнуром, будет трехмерной в понимании обычного человека, но двумерной с точки зрения математики.

Пуанкаре предположил, что трехмерная сфера является единственным трехмерным «предметом», поверхность которой можно стянуть в одну точку, а Перельману удалось это доказать. Таким образом, список «Нерешаемые задачи» сегодня состоит из 6 проблем.

Теория Янга-Миллса

Эта математическая проблема была предложена ее авторами в 1954-м году. Научная формулировка теории имеет следующий вид: для любой простой компактной калибровочной группы квантовая пространственная теория, созданная Янгом и Милльсом, существует, и при этом имеет нулевой дефект массы.

Если говорить на языке, понятном для обычного человека, взаимодействия между природными объектами (частицами, телами, волнами и пр.) делятся на 4 типа: электромагнитное, гравитационное, слабое и сильное. Уже много лет физики пытаются создать общую теорию поля. Она должна стать инструментом для объяснения всех этих взаимодействий. Теория Янга-Миллса — это математический язык, с помощью которого стало возможно описать 3 из 4-х основных сил природы. Она не применима к гравитации. Поэтому нельзя считать, что Янгу и Миллсу удалось создать теорию поля.

Кроме того, нелинейность предложенных уравнений делает их крайне сложными для решения. При малых константах связи их удается приближенно решить в виде ряда теории возмущений. Однако пока непонятно, как можно решить эти уравнения при сильной связи.

Уравнения Навье-Стокса

С помощью этих выражений описываются такие процессы, как воздушные потоки, течение жидкостей и турбулентность. Для некоторых частных случаев аналитические решения уравнения Навье-Стокса уже были найдены, однако сделать это для общего пока никому не удалось. В то же время, численное моделирование для конкретных значений скорости, плотности, давления, времени и так далее позволяет добиться прекрасных результатов. Остается надеяться, что у кого-нибудь получится применить уравнения Навье-Стокса в обратном направлении, т. е. вычислить с их помощью параметры, либо доказать, что метода решения нет.

Задача Берча — Свиннертон-Дайера

К категории «Нерешенные задачи» относится и гипотеза, предложенная английскими учеными из Кембриджского университета. Еще 2300 лет назад древнегреческий ученый Эвклид дал полное описание решений уравнения x2 + y2 = z2.

Если для каждого из простых чисел посчитать количество точек на кривой по его модулю, получится бесконечный набор целых чисел. Если конкретным образом «склеить» его в 1 функцию комплексной переменной, тогда получится дзета-функция Хассе-Вейля для кривой третьего порядка, обозначаемая буквой L. Она содержит информацию о поведении по модулю всех простых чисел сразу.

Брайан Берч и Питер Свиннертон-Дайер выдвинули гипотезу относительно эллиптических кривых. Согласно ей, структура и количество множества ее рациональных решений связаны с поведением L-функции в единице. Недоказанная на данный момент гипотеза Берча — Свиннертон-Дайера зависит от описания алгебраических уравнений 3 степени и является единственным сравнительно простым общим способом расчета ранга эллиптических кривых.

Чтобы понять практическую важность этой задачи, достаточно сказать, что в современной криптографии на эллиптических кривых основан целый класс асимметричных систем, и на их применении основаны отечественные стандарты цифровой подписи.

Равенство классов p и np

Если остальные «Задачи тысячелетия» относятся к чисто математическим, то эта имеет отношение к актуальной теории алгоритмов. Проблема, касающаяся равенства классов р и np, известная также, как проблема Кука-Левина, понятным языком может быть сформулирована следующим образом. Предположим, что положительный ответ на некий вопрос можно проверить достаточно быстро, т. е. за полиномиальное время (ПВ). Тогда правильно ли утверждение, что ответ на него можно довольно быстро отыскать? Еще проще эта задача звучит так: действительно ли решение задачи проверить не труднее, чем его найти? Если равенство классов р и np будет когда-либо доказано, то все проблемы подбора можно будет решать за ПВ. На данный момент многие специалисты сомневаются в истинности этого утверждения, хотя не могут доказать обратное.

Гипотеза Римана

Вплоть до 1859 года не было выявлено какой-либо закономерности, которая описывала бы, как распределяются простые числа среди натуральных. Возможно, это было связано с тем, что наука занималась другими вопросами. Однако к середине 19 столетия ситуация изменилась, и они стали одними из наиболее актуальных, которыми начала заниматься математика.

Гипотеза Римана, появившаяся в этот период — это предположение о том, что в распределении простых чисел существует определенная закономерность.

Сегодня многие современные ученые считают, что если она будет доказана, то придется пересмотреть многие фундаментальные принципы современной криптографии, составляющие основу значительной части механизмов электронной коммерции.

Согласно гипотезе Римана, характер распределения простых чисел, возможно, существенно отличается от предполагаемого на данный момент. Дело в том, что до сих пока не было обнаружено какой-либо системы в распределения простых чисел. Например, существует проблема «близнецов», разность между которыми равна 2. Этими числами являются 11 и 13, 29. Другие простые числа образуют скопления. Это 101, 103, 107 и др. Ученые давно подозревали, что подобные скопления существуют и среди очень больших простых чисел. Если их найдут, то стойкость современных криптоключей окажется под вопросом.

Гипотеза о циклах Ходжа

Эта нерешенная до сих пор задача сформулирована в 1941 году. Гипотеза Ходжа предполагает возможность аппроксимации формы любого объекта путем «склеивания» вместе простых тел большей размерности. Этот способ был известен и успешно применяется достаточно давно. Однако не известно, до какой степени можно производить упрощение.

Теперь вы знаете, какие нерешаемые задачи существуют на данный момент. Они являются предметом исследования тысяч ученых во всем мире. Остается надеяться, что в ближайшее время они будут решены, а их практическое применение поможет человечеству выйти на новый виток технологического развития.