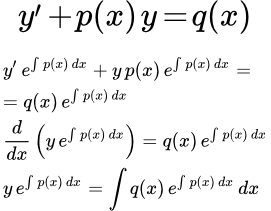Какое уравнение называется линейным дифференциальным уравнением первого порядка

Решение линейных дифференциальных уравнений первого порядка

Определения и методы решений

Линейное дифференциальное уравнение первого порядка – это уравнение вида
,
где p и q – функции переменной x .

Линейное однородное дифференциальное уравнение первого порядка – это уравнение вида
.

Линейное неоднородное дифференциальное уравнение первого порядка – это уравнение вида
.

Член q ( x ) называется неоднородной частью уравнения.

Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:
(1) .
Существует три способа решения этого уравнения:

Решение линейного дифференциального уравнения с помощью интегрирующего множителя

Рассмотрим метод решения линейного дифференциального уравнения первого порядка с помощью интегрирующего множителя.
Умножим обе части исходного уравнения (1) на интегрирующий множитель
:
(2)
Далее замечаем, что производная от интеграла равна подынтегральной функции:

По правилу дифференцирования сложной функции:

По правилу дифференцирования произведения:

Подставляем в (2):

Интегрируем:

Умножаем на . Получаем общее решение линейного дифференциального уравнения первого порядка:

Пример решения линейного дифференциального уравнения первого порядка

Разделим обе части исходного уравнения на x :
(i) .
Тогда
;
.
Интегрирующий множитель:

Знак модуля можно опустить, поскольку интегрирующий множитель можно умножать на любую постоянную (в том числе на ± 1 ).
Умножим (i) на x 3 :
.
Выделяем производную.
;
.
Интегрируем, применяя таблицу интегралов:
.
Делим на x 3 :
.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 22-07-2012 Изменено: 25-02-2015

Линейные дифференциальные уравнения первого порядка

Дифференциальное уравнение называется линейным, если в нём функция и все её производные содержатся только в первой степени, отсутствуют и их произведения.

Общий вид линейного дифференциального уравнения первого порядка таков:

,

где и — непрерывные функции от x.

Как решить линейное дифференциальное уравнение первого порядка?

Интегрирование такого уравнения можно свести к интегрированию двух двух дифференциальных уравнений первого порядка с разделяющимися переменными. Великие математики доказали, что нужную функцию, то есть решение уравнения, можно представить в виде произведения двух неизвестных функций u(x) и v(x). Пусть y = uv, тогда по правилу дифференцирования произведения функций

и линейное дифференциальное уравнения первого порядка примет вид

. (*)

Выберем функцию v(x) так, чтобы в этом уравнении выражение в скобках обратилось в нуль:

,

то есть в качестве функции v берётся одно из частных решений этого уравнения с разделяющимися переменными, отличное от нуля. Разделяя в уравнении переменные и выполняя затем его почленное интегрирование, найдём функцию v. Так как функция v — решение уравнения, то её подстановка в уравнение даёт

.

Таким образом, для нахождения функции u получили дифференциальное уравнение первого порядка с разделяющимися переменными. Найдём функцию u как общее решение этого уравнения.

Теперь можем найти решение исходного линейного дифференциального уравнения первого порядка. Оно равно произведению функций u и v, т. е. y = uv. u и v уже нашли.

Пример 1. Решить линейное дифференциальное уравнение первого порядка

.

Решение. Как было показано в алгоритме, y = uv. Подставляя выражения для и y в уравнение вида (*), получим

(* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

или .

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

и, интегрируя находим u:

Теперь можно записать общее решение данного линейного дифференциального уравнения первого порядка:

Как видим, всё решение выполняется точным следованием алгоритму, приведённому в начале статьи. Меняются лишь виды функций в уравнениях. Степени, корни, экспоненты и т.д. Это чтобы алгоритм отпечатался в памяти и был готов к разным случаям, которые только могут быть на контрольной и экзамене. А кому стало скучно, наберитесь терпения: впереди ещё примеры с интегрированием по частям!

Важное замечание. При решении заданий не обойтись без преобразований выражений. Для этого требуется открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.

Пример 2. Решить линейное дифференциальное уравнение первого порядка

.

Решение. Подставляя выражения для и y в уравнение вида (*), получим

(* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

.

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные:

и, интегрируя находим u:

Теперь можно записать общее решение данного линейного дифференциального уравнения первого порядка:

В следующем примере — обещанная экспонента.

Пример 3. Решить линейное дифференциальное уравнение первого порядка

.

Решение. Подставляя выражения для и y в уравнение вида (*), получим

(* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

или .

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находимu:

Записываем общее решение данного линейного дифференциального уравнения первого порядка:

Любители острых ощущений дождались примера с интегрированием по частям. Таков следующий пример.

Пример 4. Решить линейное дифференциальное уравнение первого порядка

.

Решение. В этом случае сначала нужно добиться, чтобы производная «игрека» ни на что не умножалась. Для этого поделим уравнение почленно на «икс» и получим

.

Подставляя выражения для и y в уравнение вида (*), получим

(* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

или .

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируем по частям.

В интеграле , .

Тогда .

Интегрируем и находим u:

Записываем общее решение данного линейного дифференциального уравнения первого порядка:

И уж совсем странной статья о дифференциальных уравнениях была бы без примера с тригонометрическими функциями.

Пример 5. Решить линейное дифференциальное уравнение первого порядка

.

Решение. Подставляя выражения для и y в уравнение вида (*), получим

(* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

или .

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находим u:

Записываем общее решение данного линейного дифференциального уравнения первого порядка:

В последних двух примерах требуется найти частное решение уравнения.

Пример 6. Найти частное решение линейного дифференциальное уравнение первого порядка

при условии .

Решение. Чтобы производная «игрека» ни на что не умножалась, разделим уравнение почленно на и получим

.

Подставляя выражения для и y в уравнение вида (*), получим

(* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

или .

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находим u:

Записываем общее решение данного линейного дифференциального уравнения первого порядка:

Найдём частное решение уравнения. Для этого в общее решение подставим и и найдём значение C:

Подставляем значение C и получаем частное решение данного линейного дифференциального уравнения первого порядка:

.

Пример 7. Найти частное решение линейного дифференциального уравнения первого порядка

при условии .

Перенесём функцию «игрека» в левую часть и получим

.

Подставляя выражения для и y в уравнение вида (*), получим

(* *).

Выберем функцию v(x) так, чтобы выполнялось равенство

или .

После разделения переменных это уравнение принимает вид

.

Почленное интегрирование даёт

Подставив найденное значение функции v в равенство (* *), получим

.

Это уравнение с разделяющимися переменными для нахождения функции u. Разделяем переменные и, интегрируя, находим u:

.

Первый интеграл равен , второй находим интегрированием по частям.

В нём , .

Тогда , .

Находим второй интеграл:

.

В результате получаем функцию u:

Записываем общее решение данного линейного дифференциального уравнения первого порядка:

Найдём частное решение уравнения. Для этого в общее решение подставим и и найдём значение C:

Подставляем значение C и получаем частное решение данного линейного дифференциального уравнения первого порядка:

.

Выводы. Алгоритм решения линейных дифференциальных уравнений первого порядка достаточно однозначен. Трудности чаще всего возникают при интегрировании и это означает, что следует повторить этот обширный раздел математического анализа. Кроме того, что особенно видно из примеров ближе к концу статьи, очень важно владеть приёмами действий со степенями и дробями, а это школьные темы, и если они подзабыты, то их тоже следует повторить. Совсем простых «демо»-примеров ждать на контрольной и на экзамене не стоит.

Линейные дифференциальные уравнения 1-го порядка
и уравнение Бернулли

Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и её производной. Оно имеет вид

где и — заданные функции от , непрерывные в той области, в которой требуется проинтегрировать уравнение (1).

Если , то уравнение (1) называется линейным однородным . Оно является уравнением с разделяющимися переменными и имеет общее решение

Общее решение неоднородного уравнения можно найти методом вариации произвольной постоянной , который состоит в том, что решение уравнения (1) ищется в виде

Пример 1. Решить уравнение .

Решение. Применим метод вариации постоянной. Рассмотрим однородное уравнение , соответствующее данному неоднородному уравнению. Это уравнение с разделяющимися переменными. Его общее решение имеет вид .

Общее решение неоднородного уравнения ищем в виде , где — неизвестная функция от . Подставляя, получаем , откуда . Итак, общее решение неоднородного уравнения будет , где — постоянная интегрирования.

Замечание. Может оказаться, что дифференциальное уравнение линейно относительно как функция от . Нормальный вид такого уравнения

Пример 2. Решить уравнение .

Решение. Данное уравнение является линейным, если рассматривать как функцию от :

Применяем метод вариации произвольной постоянной. Сначала решаем соответствующее однородное уравнение

которое является уравнением с разделяющимися переменными. Его общее решение имеет вид .

Общее решение уравнения ищем в виде , где — неизвестная функция от . Подставляя, получаем

Отсюда, интегрируя по частям, будем иметь

Исходное уравнение может быть проинтегрировано также следующим образом. Полагаем

где и — неизвестные функции от , одна из которых, например , может быть выбрана произвольно.

Подставляя в , после преобразования получаем

Определяя из условия , найдем затем из функцию , а следовательно, и решение уравнения . В качестве можно взять любое частое решение уравнения .

Пример 3. Решить задачу Коши: .

Решение. Ищем общее решение уравнения в виде ; имеем . Подставляя выражение для и в исходное уравнение, будем иметь

Функцию находим из условия . Беря любое частное решение последнего уравнения, например , и подставляя его, получаем уравнение , из которого находим функцию . Следовательно, общее решение уравнения будет

Используя начальное условие , получаем для нахождения уравнение , откуда ; так что решением поставленной задачи Коши будет функция .

Пример 4. Известно, что между силой тока и электродвижущей силой в цепи, имеющей сопротивление и самоиндукцию , существует зависимость , где и — постоянные. Если считать функцией времени , то получим линейное неоднородное уравнение для силы тока :

Найти силу тока для случая, когда и .

Решение. Имеем . Общее решение этого уравнения имеем вид . Используя начальное условие (13), получаем из , так что искомое решение будет

Отсюда видно, что при сила тока стремится к постоянному значению .

Пример 5. Дано семейство интегральных кривых линейного неоднородного уравнения .

Показать, что касательные в соответственных точках к кривым , определяемым линейным уравнением, пересекаются в одной точке (рис. 13).

Решение. Рассмотрим касательную к какой-либо кривой в точке .Уравнение касательной в точке имеет вид

По определению, в соответственных точках является постоянным, а переменным. Беря любые две касательные к линиям в соответственных точках, для координат точки их пересечения, получаем

Отсюда видно, что все касательные к кривым в соответственных точках ( фиксировано) пересекаются в одной и той же точке

Исключая в системе аргумент , получаем уравнение геометрического места точек .

Пример 6. Найти решение уравнения , удовлетворяющее условию: ограничено при .

Решение. Общее решение данного уравнения . Любое решение уравнения, получаемое из общего решения при , будет неограниченно, так как при функция ограничена, а . Отсюда следует, что данное уравнение имеет единственное решение , ограниченное при , которое получается из общего решения при .

Уравнение Бернулли

Дифференциальное уравнение Бернулли имеет вид

С помощью замены переменной уравнение Бернулли приводится к линейному уравнению и интегрируется как линейное.

Пример 7. Решить уравнение Бернулли .

Решение. Делим обе части уравнения на :

Делаем замену переменной , откуда . После подстановки последнее уравнение обратится в линейное уравнение

Замечание. Уравнение Бернулли может быть проинтегрировано также методом вариации постоянной, как и линейное уравнение, и с помощью подстановки .

Пример 8. Решить уравнение Бернулли .

Решение. Применим метод вариации произвольной постоянной. Общее решение соответствующего однородного уравнения имеет вид . Общее решение уравнения ищем в виде , где — новая неизвестная функция. Подставляя в исходное уравнение, будем иметь

Для нахождения функции получим уравнение с разделяющимися переменными, из которого, разделяя переменные и интегрируя, найдем

Итак, общее решение исходного уравнения .

Некоторые нелинейные уравнения первого порядка с помощью удачно найденной замены переменных сводятся к линейным уравнениям или к уравнениям Бернулли.

Пример 9. Решить уравнение .

Решение. Запишем данное уравнение в виде .

Деля обе части уравнения на , получаем .

Замена приводит это уравнение к линейному , общее решение которого .

Заменяя его выражением через , получаем общий интеграл данного уравнения .

В некоторых уравнениях искомая функция может находиться под знаком интеграла. В этих случаях иногда удается путем дифференцирования свести данное уравнение к дифференциальному.

Пример 10. Решить уравнение 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAUQAAABNBAMAAAAsvACJAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAAUbAgWgQITGh8LHQkeBuUEPaAAAHI0lEQVRo3u1afWxTVRQ/97XvtbUbvG6OwJxrmcMpzHRjgBLULQRJEGTFMBMRWQMaiSBrMBJCjBtEQSdmi5sJEc0o4hAXQ8N3gnEDEwxfo3HxD8jIhMlfRnHdxjYm1HPfu+36um4QPCRN2E229vX1nv7u+fj9zr0twNh4AIcyxZfsEFfl/ZLsEF+DBckO8RBMpTZpca0ntTcD3CotQjYl/6KHGCK1F4OVa1xJDhGWA2lg6mEFOcSvFS9l4uTDZWKA1r6rMiVEmPTbEeqCPr/gV1qLG+8Dk7Ex1U7C4Uh6k9bOWmqE1s4CUnubXt5NDXHd3G9J7X35SC81xNI3ekhZbMDyCjXlNCnzKe1lhBhxpwNpxGFJv0Fez7Z+WnsVJ8ghZvpp7bnJKQdqaCmHdXioEbLyElp7F6rIvdhM2nODElbJvbifdmcudZM70XqTdtWPDsS69Cj//+5oLbM1MMINU3RWRnccRFlL9x33TIuxUmXSkkgSKOSiBJW0PSF+C846Fbmw3xp2mqAJtwj/tNl3yJOcuBU6QzEXC/ENT4CjXjgM035LvIGTCeXkIFp9KXKVLcTlzQj+RrTlgbQW/fK9AVBGYRE29fLVOFrsi4nzd/iHLqgWnurwQmecAbkldomy/mD+k4e2MlIklaHodF1skIPsu4BdE9nfC7auUXqG3bDMZ+SwGCUwt+j6mqLzGjsH1viOJduw/nSB18Eh2oQGMLcA0CrucuzOALAV+rW5D8YNU7TPoqhsu8AZNNxriFECDi0VvWrWLaBD5VC8cPgSQWQcohxZbOmVyHR9LMabbk90rukKVAaHEcvsiOFxhZCOBt6ZIc8Qxq/r7/70GKS5KlxgXtxTAhLvLJS2L0LmRT3z44RD5bNXPifKKxbiRNE8sGKt3NIWDM5V2lzwEcwBWFpc74NMj1aDNbW5DfURckdbevVIRZNFcSDELlCeyfrD7RLMrUVOmTUH3euugpXuAy6wcN9VLym/Ibmn87etz+Ejj7+xTgXlWNbpak+cF/k/USUsrOWJdVooz5bbBT+pewC2nMnxQjpmgvLzW/s9W4pzRJoikogtS52O0V3Imy97lcnfrOueFNYezZMHmduDLmI8IvzDlCZ46ATUaNNz5/Exlz8twmRxmRobXMMDzUTeWsP6zawT8KR9F2vir7NB7nPMKXsjdPhYZ6Tm0NYNYQssXy3RIBaAKYSF6KxdLSpE1z8Zk67DV4rPO3z6h9lCUBGE8hgB550vQ4gSZAb4bHnevMWI3BuFuEeUeVhPK5yeV1Er9fIFS9zDpkIEEGTPq5aeIUrILlgdORewtLuiEJmWvTrNCiWw+1mryhOtVfgj088wF5rjWJRDdAjfZowAMVXXPz4dyl3mfg7R3C8gNrjYgKEIK4e6ImURh1ih5SIWXaR+skXZZQaUAX4WqnA95BArC5HX2DfazQ8NgQbhW4eaONDp3UO02Kya/Px1k18PNCtWOS3GNPrl0a4IA839mVkIWX5YU3JGFdadvZHFICFiuaT1WgJauVSUsHOTNvYoLcZyaVPBFmxWs9QEuShMZepQWSuqchGMD3DvOgPpWC7Ijc8iq5Vlt9iqZM1JMbYsdTpYJHlnLbh3dMMLQlwEU1SUmPrA6cIYmKpAQm4cF7QNrpVCtrjWD3PBfeQ2LI2j7n8dWCYho7h0o9b/COUeOI4QS3BGJsb0ElT/c9QZfB3cjdrHz/pe2JLqJus5KYUAU2Rd+/ttQkDKhRLIP7RegfQSmNCEImxG6rT+NfPSAeXs4TiKRaVY255fFzRANIfDWMWyMOUWYby00wvVO69XcVWxncYZNZgfq45/vi+Yuq8WNmkLSWnP3xnUqTvqi2Vl/JxgM9ssrjsi4rIS81bmAuhVIYXPmqhafCB5EwjgZtgaL4AO9KItYBAXsCAiR16rLoDb8AVNADfAau2KaamNtjZoj58MqZalzCjRxbo/LE3wohcm7B0S1RGGbNg5ZRi2ksIPzUMdZUoXZxubiNg1g6XCEVsdI4swQbNSr8wPdsSXRPWjdHMnR7QW+YbpwlCn4Sz4oFZvxvhn/G4Q5eDdnpYImlUOnvVpZK+p66lRZmwfqSW3njKuWm+KZ/KHV/WW1rCPs3nvdudyW431h/L0nTcGI2277SI7pNj9mn7OKGugj93btuDhAfLNlZxgv/Z/tlt28nM7SO2htZfdTw7RFCI+c/KTQ3R2PWhnTlBKfubERZl0FHvJITbQHmOJfpDU5N+k5rZJ5JzzsYWUc6w3J1EXNAtn7CU9Wrz1tosa4r51tCe0y6+Rfym7/DniNav01UJPEWMjGYeS60t2iCmPT092iI+Jg22q8dShuipiiBdpfzulBKeOp+Zu4h/JKd6F5IFGiLTMOPN+QKT0otQSSqUWgzbaH2zK5w+VUXtxO/HPXrdayXk29fCspJeXjTA2kmX8B/XH3ORQKCpxAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />.

Решение. Дифференцируя обе части этого уравнения по , получаем

Дифференцируя еще раз по , будем иметь линейное однородное уравнение относительно

Разделяя переменные и интегрируя, найдем . Это решение, как легко проверить, удовлетворяет исходному уравнению.