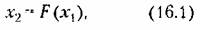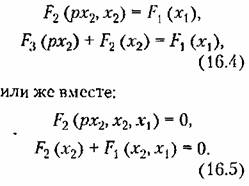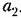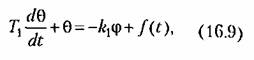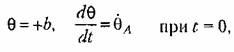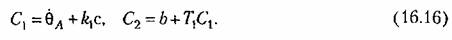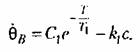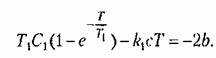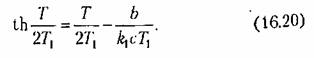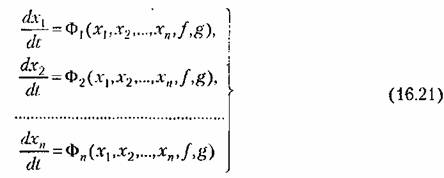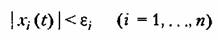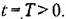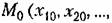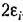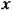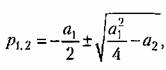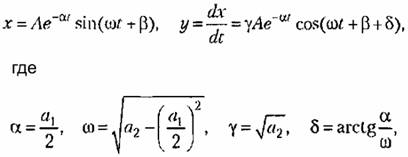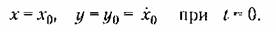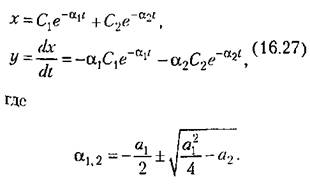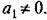Нелинейные системы автоматического управления
СОСТАВЛЕНИЕ УРАВНЕНИЙ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Нелинейной системой автоматического управления называется такая система, которая содержит хотя бы одно звено, описываемое нелинейным уравнением. Перечислим виды нелинейных звеньев:
звено релейного тина (рис. 1.12);
звено с кусочно-линейной характеристикой (рис. 1.10, д и др.);
звено с криволинейной характеристикой любого очертания;
звено, уравнение которого содержит произведение переменных или их производных и другие их комбинации;
нелинейный импульсный элемент;
звенья, описываемые кусочно-линейными дифференциальными уравнениями, в том числе неременной структуры.
Различают статические и динамические нелинейности. Первые описываются нелинейными алгебраическими уравнениями, а вторые представляются в виде нелинейных дифференциальных уравнений.
Общий метод составления уравнений для нелинейных систем состоит в следующем. Сначала по правилам §3.1 производится линеаризация уравнений всех звеньев системы, для которых это допустимо, кроме существенно нелинейных звеньев (чате всего одпого-двух). Затем составляются уравнения этих последних звеньев со всеми допустимыми упрощениями их характеристик.
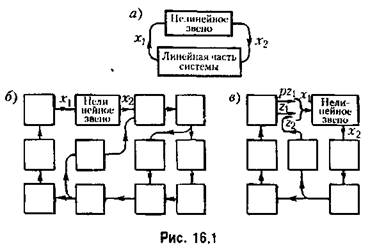
В результате получается система линейных уравнений, к которым добавляется одно-два (иногда более) нелинейных. В соответствии с этим обобщенную структурную схему любой нелинейной системы в случае одного нелинейного звена можно представить в виде рис. 16.1, а, где линейная часть может иметь структуру любой сложности (с обратными связями и т. п„ как, например, на рис. 16.1, били в). В случае двух нелинейных
звеньев могут быть разные комбинации, в зависимости от того, в какие цепи системы они холят (см., например, рис. 16.2).
Часто при исследовании нелинейных систем удается выделить нелинейность так, чтобы она описывалась непосредственно зависимостью между выходной и входной величинами
которая может иметь любую форму (релейного типа, кусочно-линейного или криволинейного). Но иногда, как будет показано в следующих параграфах, не удается этого сделать и приходится исследовать нелинейные дифференциальные зависимости вида
Встречаются и более сложные случаи, когда обе величины (входная и выходная) оказываются под знаком нелинейной функции раздельно:
Разделим все нелинейные системы на два больших класса.
1 . К первому классу отнесем такие, в которых Уравнение нелинейного звена приводится к любому из видов (16.1)-(16.3), т. е. когда под знаком нелинейной функции стоит только входная величина (и ее производные) либо только выходная величина (и ее производные). При этом имеется в виду, что схема системы в целом может быть приведена к виду рис. 16.1 с одним нелинейным звеном. К этому классу сводится также случай с двумя нелинейными звеньями, указанный на рис. 16.2, я, так как там они могут быть объединены в одно нелинейное звено. Сюда же относится и случаи, покапанный на рис. 16.2, г, где имеются два нелинейных звена (если их уравнения содержат под знаком нелинейности только входную величину х, например, вида (16.1) или (16.2)).
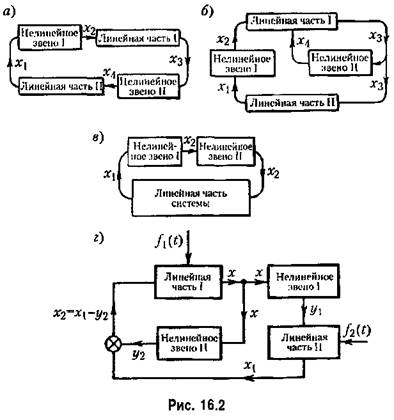
2 . Второй к л а с с нелинейных систем включает системы с любым числом нелинейных звеньев, когда под знаки нелинейных функций входят различные переменные, связанные между собой линейной передаточной функцией. Так будет в случае системы с одним нелинейным звеном вида (16.4) или (16.5), а также в системе с двумя нелинейными звеньями (рис. 16.2, а или г), если в нервом из них под знак нелинейности входит входная величина, а во втором — выходная. Система же рис, 16.2, б относится ко второму классу, если под знаки нелипейпоетей входят в обоих звеньях либо только входные, либо только выходные величины нелинейных звеньев.
Ко второму класcу нелинейных систем относятся также системы с двумя и более нелипейноетями, в уравнениях которых под знаки нелинейных функций входят разные переменные, связанные между собой нелинейными дифференциальными уравнениями (т. е. связанные через линейные части и нелинейные звенья). К таким системам относятся, например, система на рис. 16,2, а, если в ее уравнения х под знаками нелинейных функций находятся входные (пли выходные) величины обоих нелинейных звеньев, и многие другие системы.
Системы с логическими устройствами относятся обычно к нелинейным системам второго класса.
Заметим, что во всех случаях, когда под знак нелинейной функции входит какая-либо линейная комбинация разных переменных, их следует обозначать одной буквой, а данную линейную комбинацию учесть при составлении общего уравнения линейной части системы. Это бывает, например, в тех случаях, когда на вход нелинейного звена подаются производные или включается обратная связь. Так. если для рис. 16.1,6
можно привести уравнение нелинейного звена к виду (16.1 )
Из всех уравнений линейных звеньев, а также добавочных линейных выражений типа (16.6), получаемых при выделении нелинейности, составляется общее уравнение линейной части системы
Составление уравнений будет проиллюстрировано ниже на примерах.
Процессы в нелинейных системах автоматического управления имеют целый ряд весьма существенных особенностей, которые не встречаются в линейных системах.
Благодаря этим существенным особенностям даже вопрос об устойчивости системы становится здесь более сложным. Кроме структуры системы и значений ее параметров для устойчивости того или иного установившегося процесса в отличие от линейных систем имеют значение также и начальные
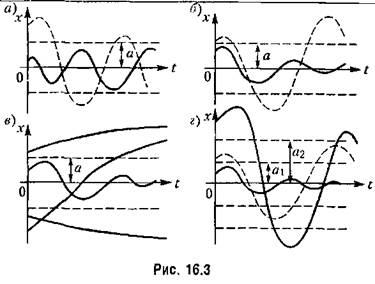
условия. Возможен новый вид установившегося процесса — автоколебания, т. е. устойчивые собственные колебания с постоянной амплитудой при отсутствии внешних колебательных воздействий. Когда в системе возникают автоколебания, то установившееся состояние, соответствующее постоянному значению управляемой величины, становится невозможным.
Следовательно, в общем случае на плоскости параметров системы могут быть не два вида областей (устойчивости и неустойчивости), как в линейных системах, а больше: 1) область устойчивости равновесного состояния с постоянным значением управляемой величины; 2) область автоколебаний; 3) область неустойчивости системы; 4) области, соответствующие другим, более сложным случаям.
устойчиво в малом, т. е. при начальных условиях, не выводящих отклонения в переходном процессе за определенную величину а, и неустойчиво в большом, т. е. при начальных условиях, выводящих отклонение в переходном процессе за пределы величины а. Здесь граничным процессом является неустойчивый периодический процесс собственного движения системы с амплитудой а (переходные процессы расходятся от него и обе стороны).
II р и м е р. Для иллюстрации особенностей нелинейной системы исследуем переходный процесс и автоколебания в релейной системе стабилизации температуры. Для этого составим сначала уравнения управляемого объекта и управляющего устройства.
Пусть объект представляет собой некоторую камеру. Учитывая инерционность процесса нагрева и охлаждения запишем его уравнение в виде
Следовательно, уравнение управляющего устройства запишется следующим образом:
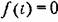
На участке ЛВ уравнение управляющего устройства согласно рис. 16.4, в будет
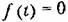
а на участке BD
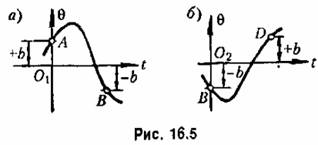
Условимся для простоты отсчитывать время Сот начала участка AВ (рис. 16.5, а). Тогда начальные условия будут
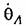
Аналогично для участка ВО согласно (16.13), отсчитывая время г тоже от начала этого участка (рис. 16.5, б), получим решение
Все остальные участки кривой переходного процесса будут определяться, очевидно,
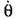
будет задана величина 6 в начальной точке первого участка процесса, то все вышена-писанное решение для переходного процесса в системе станет определенным. Такой метод решения задачи называется методом припасоаывапия.
Выясним теперь, возможны ли в данной системе автоколебания, т. е, устойчивое периодическое решение. Для этого нужно, очевидно, чтобы в конце D одного периода
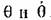
начале его А, Легко заметит!), что при этом оба полупериода (AB и BD) должны быть одинаковыми вследствие симметрии характеристики (рис. 16.4, а). Поэтому для определения автоколебаний достаточно рассмотреть только один участок АВ и потребовать, чтобы
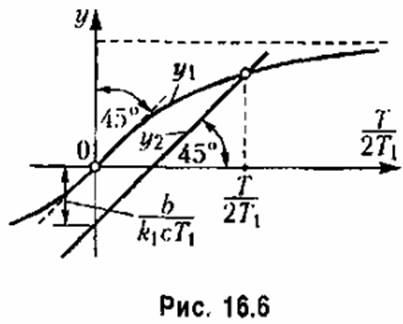
Обозначив период искомых автоколебаний через 2Г. а длительность участка AB, через Т, из (16.14) найдем
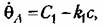

Это трансцендентное уравнение для легко решается графически (рис. 16.6) пересечением двух кривых:
Если найдено вещественное положительное значение для У, то это свидетельствует о наличии периодического решения
в дайной системе. Чтобы доказать, что это соответствует автоколебаниям, нужно исследовать их устойчивость, т. е. показать, что в переходном процессе система ведет себя, как изображено на рис. 16.3, я, по не так, как на рис. 16.3,6. Это будет показано ниже.
(рис. 16.5, а) путем исследования функции (16.15) па максимум обычным путем.
Фазовое пространство. Для наглядного представления о сложных нелинейных процессах управления часто прибегают к понятию фазового пространства, которое заключается в следующем. Дифференциальное уравнение замкнутой системы я-го порядка можно преобразовать к системе п дифференциальных уравнений первого порядка в виде
с начальными условиями
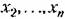

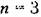

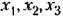

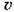
482 Нелинейные системы автоматического управления
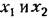
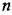
Итак, фазовое пространство и фазовые траектории представляют собой лишь геометрический образ процессов, протекающих в системе. В этом геометрическом представлении участвуют координаты и исключено время. Фазовая траектория сама по себе дает лишь качественное представление о характере поведения системы. Чтобы определить количественно положение изображающей точки (а значит, и состояние системы) в любой момент времени, нужно найти решение заданных дифференциальных уравнений (16.21) во времени.
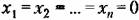
Отсюда вытекает, что фазовые траектории устойчивой линейной системы будут асимптотически приближаться к началу координат при неограниченном увеличении времени. Фазовые траектории неустойчивой линейной системы будут неограниченно удаляться от начала координат.
Для нелинейной системы вследствие ряда особенностей процессов, отмечавшихся выше, фазовые траектории могут принимать самые разнообразные очертания. Если имеется асимптотическая устойчивость для определенного круга начальных условий, то все фазовые траектории, которые начинаются внутри определенной области Г), окружающей начало координат фазового пространства (рис. 16.7, б), будут асимптотически приближаться к началу координат. Если устойчивость неасимптотическая, то фазовые траектории, начинающиеся внутри области Т| могут иметь любые очертания, но не будут выходить за пределы некоторой определенной области е, окружающей начало координат (рис. 16.7, б).
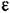

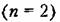
В формулировке Ляпунова содержится требование сколь угодной малости указанных областей. Однако практически это определение, так же как и теоремы Ляпунова, которые будут приведены ниже, применяется и тогда, когда эти области имеют определенные конечные размеры.
Фазовые траектории для обыкновенных линейных систем. Пусть переходный процесс в некоторой системе описывается уравнением второго порядка
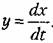
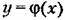
стоянной определяет собой некоторое семейство так называемых интегральных кривых на фазовой плоскости (х,у), каждая из которых соответствует одному определенному значению произвольной постоянной.
Вся совокупность интегральных кривых представит собой все возможные фазовые траектории, а значит, и все возможные виды переходного процесса в дайной системе при любых начальных условиях.
Рассмотрим отдельно различные случаи. Уравнению (16.23) соответствуют корни характеристического уравнения
причем возможны шесть случаев:
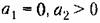



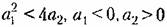
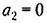
Случай 1. В первом случае получаются, как известно, незатухающие колебания (рис. 16.8, а)
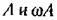
причем Л — произвольная постоянная
Итак, периодическим колебаниям системы (рис. 16.8, а) соответствует движение изображающей точки по замкнутой кривой (рис. 16.8,6).
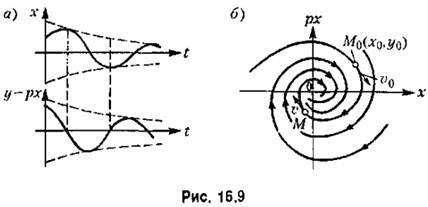
Случай 2. В этом случае (комплексные корни с отрицательными вещественными частями), как известно, имеют место затухающие; колебания (рис. 16 9 а)
а произвольные постоянные A и (B определяются из начальных условий:

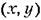
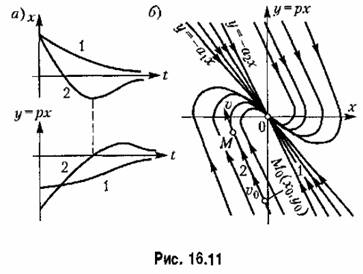
оборот не возвращается в прежнюю точку М0, а подходит ближе к началу координат.
Итак, затухающим колебаниям системы (рис 16.9, а) отвечают фазовые траектории в виде спиралей, по которым изображающая точка приближается к началу координат (рис. 16.9,6).
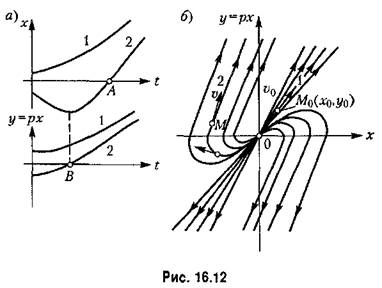
С л уча и 3. Этот случай (комплексные корни с положительными вещественными частями) соответствует расходящимся колебаниям (рис. 16.10, а). Рассуждая аналогично предыдущему, получим всю совокупность возможных фазовых траекторий тоже в виде спиралей, но только изображающая точка будет двигаться но ним не к началу координат, а от него (рис. 16.10,6).
С л у ч а и 4. Этот случай (вещественные отрицательные корпи) соответствует апериодическому процессу


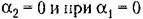
В отличие от прежнего здесь все фазовые траектории вливаются непосредственно в начало координат О фазовой плоскости. Однако изображающая точка Мне попадает в начало координат в конечное время, а приближается асимптотически.
Итак, затухающим апериодическим процессам в системе отвечают фазовые траектории, вливающиеся в начало координат.



Интегрирование последних аналогично случаю 1 дает
Направления движения изображающей точки М по фазовым траекториям, показанные на рис 16.13, б, легко определяются в

Итак, расходящимся апериодическим процессам в системе отвечают фазовые траектории тина рис. 16.12, били типа рис. 16.13,6, причем изображающая точка, двигаясь по ним, в конечном итоге удаляется от начала координат.
Особые точки. В точках, которые соответствуют установившемуся состоянию, получаем согласно (16.25) неопределенное выражение
т. е. неопределенное направление касательных к интегральным кривым (фазовым траекториям). Такие точки называются особыми точками, причем для них существует следующая классификация:
а) особые точки типа точки О на рис. 16.8, б называются центрами,
б) особые точки типа рис. 16.9, б называются устойчивыми фокусами,
в) особые точки типа рис. 16.10, б называются неустойчивыми фокусами,
г) особые точки типа рис. 16.11, б называются устойчивыми узлами,
д) особые точки тина рис. 16.12, б называются неустойчивыми узлами,
е) особые точки типа рис. 16.13, б называются седлами (седло всегда неустойчиво).
2. Математическое описание систем автоматического управления
Публикую первую часть второй главы лекций по теории автоматического управления.
В данной статье рассматриваются:
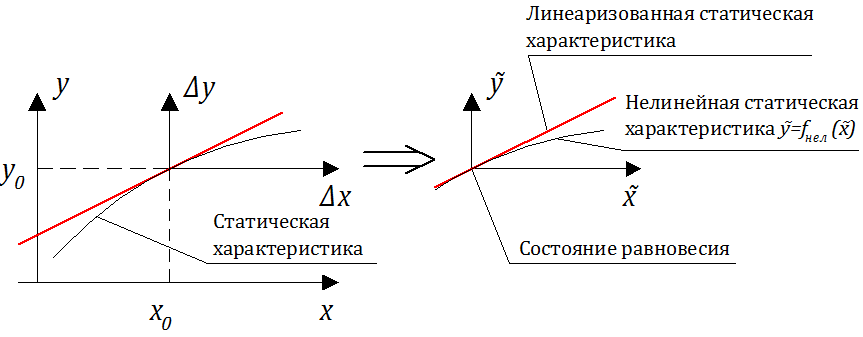
2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
2.3. Классический способ решения уравнений динамики
Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.
Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.
2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
При составлении уравнений, описывающих нестационарные процессы в САУ (САР) и которые в дальнейшем будем называть уравнениями динамики, система “разбивается” на отдельные элементы (звенья), для каждого из которых не существует проблем в записи соответствующего уравнения динамики.
На рис. 2.1.1 представлено схематичное представление САУ (звена) в переменных «вход-выход», где x(t) (или u(t)) — входное воздействие, а y(t) — выходное воздействие, соответственно. Нередко входное воздействие будет называться управляющим, а выходное воздействие — регулируемой величиной (переменной).
При составлении уравнений динамики используются фундаментальные законы сохранения из разделов “Механики”, “Физики”, “Химии” и др.
Например, при описании перемещения узла какого-то механизма силового привода используются законы сохранения: момента, энергии, импульса и др… В теплофизических (теплогидравлических) системах используются фундаментальные законы сохранения: массы (уравнение неразрывности), импульса (уравнение движения), энергии (уравнение энергии) и др
Уравнения сохранения в общем случае содержат постоянные и нестационарные члены, причем при отбрасывании нестационарных членов получают так называемые уравнения статики, которые соответствуют уравнениям равновесного состояния САУ (звена). Вычитанием из полных уравнений сохранения стационарных уравнений получают нестационарные уравнения САУ в отклонениях (от стационара).
где: — стационарные значения входного и выходного воздействий;
— отклонения от станционара, соотвесвенно.
В качестве примера рассмотрим «технологию» получения уравнений динамики для механического демпфера, схематическое изображение которого представлено на рис. 2.1.2.
Согласно 2-му закону Ньютона, ускорение тела пропорционально сумме сил, действующих на тело:
где, m — масса тела, Fj — все силы воздействующие на тело (поршень демпфера)
Подставляя в уравнение (2.1.1) все силы согласно рис. 2.2, имеем:
где — сила тяжести;
— сила сопротивления пружины,
— сила вязконо трения (пропорциональна скорости поршеня)
Размерности сил и коэффициентов, входящих в уравнение (2.1.2):
Предполагая, что при t ≤ 0 поршень демпфера находился в равновесии, то есть
перейдем к отклонениям от стационарного состояния:
Пусть при t>0 . Тогда, подставляя эти соотношения в уравнение (2.1.2), получаем:
если , то уравнение принимает вид:
Соотношение (2.1.4) – уравнение звена (демпфера) в равновесном (стационарном) состоянии, а соотношение (2.1.5) – статическая характеристика звена – демпфера (см. рисунок 2.1.3).
Вычитая из уравнения (2.1.3) уравнение (2.1.4), получаем уравнение динамики демпфера в отклонениях:
тогда, разделив на k, имеем:
Уравнение (2.1.6) — это уравнение динамики в канонической форме, т.е. коэффициент при Δy(t) равен 1.0!
«Легко» видеть, что коэффициенты перед членами, содержащими производные, имеют смысл (и размерность!) постоянных времени. В самом деле:
Таким образом, получаем, что:
— коэффициент перед первой производной имеет размерность [c] т.е. смысл некоторой постоянной времени;
— коэффициент перед второй производной: [];
— коэффициент в правой части (): [
].
Тогда уравнение (2.1.6) можно записать в операторной форме:
, что эквивалентно
где: — оператор диффренцирования;
-линейный дифференциальный оператор;
— линейный дифференциальный оператор, вырожденный в константу, равную
.
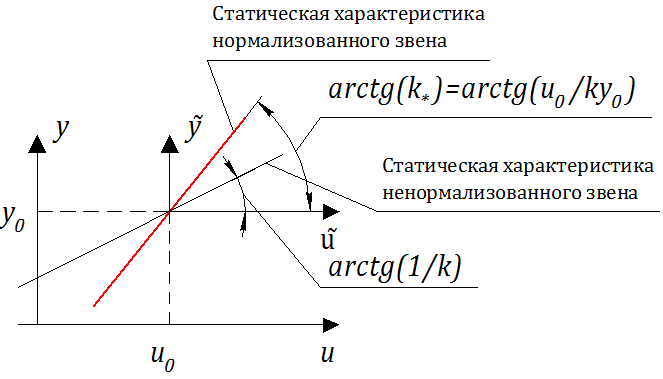
Анализ уравнения (2.1.6.а) показывает, что такое уравнение имеет размерные переменные, а также размерными являются все коэффициенты уравнения. Это не всегда удобно. Кроме того, если реальная САР (САУ) состоит из многих звеньев, выходными воздействиями которых являются различные физические переменные (скорость, температура, нейтронный поток, тепловой поток и т.д.), то значения коэффициентов могут различаться на большое число порядков, что ставит серьезные математические проблемы при численном решении уравнений динамики на компьютере (поскольку числа в компьютере всегда представляются с какой-то точностью). Одним из наилучших способов избежать численных трудностей является принцип нормализации, т.е. переход к безразмерным отклонениям, которые получены нормированием отклонения на стационарное значение соответствующей переменной.
Введем новые нормированные (безразмерные) переменные:
Подставляя эти соотношения в уравнение (2.1.2), имеем:
Поддчеркнутые члены выражения в сумме дают 0 (см. 2.1.4) Перенося в левую часть члены, содержащие , и, разделив на
, получаем:
где: — коэффициент усиления, причем безразмерный.
Проверим размерность коэффициента
Использованный выше «технический» прием позволяет перейти к безразмерным переменным, а также привести вид коэффициентов в уравнении динамики к легко интерпретируемому виду, т.е. к постоянным времени (в соответствующей степени) или к безразмерным коэффициентам усиления.
На рис. 2.1.4 представлены статические характеристики для механического демпфера:
Процедура нормировки отклонений позволяет привести уравнения динамики к виду:
где дифференциальные операторы.
Если дифференциальные операторы — линейные, а статическая характеристика САУ (звена) – тоже линейна, то выражение (2.1.8) соответствует линейному обыкновенному дифференциальному уравнению (ОДУ).
А если – нелинейные дифференциальные операторы, или
, то уравнение динамики — нелинейное. Под нелинейными действиями понимаются все математические действия, кроме сложения (+) и вычитания (-).
Пример создания модели демпфера можно посмотереть здесь: «Технология получения уравнений динамики ТАУ»
2.2. Линеаризация уравнений динамики САУ (САР)
Практически все реальные системы автоматического управления (САУ) являются нелинейными, причем нелинейность САУ может определяться различными причинами:
- Нелинейностью статической характеристики.
- Нелинейностью динамических членов в уравнениях динамики.
- Наличием в САУ принципиально нелинейных звеньев.
Если в замкнутой САУ (САР) нет принципиально нелинейных звеньев, то в большинстве случаев уравнения динамики звеньев, входящих в систему, могут быть линеаризованы. Линеаризация основана на том, что в процессе регулирования (т.е. САУ с обратной связью) все регулируемые величины мало отклоняются от их программных значений (иначе система регулирования или управления не выполняла бы своей задачи).
Например, если рассмотреть управление мощностью энергетического ядерного реактора, то главная задача САР — поддержание мощности на заданном (номинальном) уровне мощности. Существующие возмущения (внутренние и внешние) “отрабатываются” САР и поэтому параметры ядерного реактора незначительно отличаются от стационарных. На рис. 2.2.1 представлена временная зависимость мощности ядерного реактора, где нормированные отклонения мощности ΔN /N0 Рис. 2.2.1 – Пример изменения мощности реактора
Рассмотрим некоторое звено (или САР в целом), описание динамики которого можно представить в переменных “вход-выход”:
Предположим, что динамика данного звена описывается обыкновенным дифференциальным уравнением n-го порядка:
Перенесем в левую часть уравнения и запишем уравнение в виде%
где -– функция регулируемой переменной и ее производных, а также управляющего (входного) воздействия и его производных, причем F – обычно нелинейная функция.
Будем считать, что при t ≤ 0 САУ (звено) находилось в равновесии (в стационарном состоянии). Тогда уравнение (2.2.2) вырождается в уравнение статической характеристики:
Разложим левую часть уравнения (2.2.2) в ряд Тейлора в малой окрестности точки равновесного состояния .
Напомним, что разложение в ряд Тейлора трактуется следующим образом: если , то «простое» разложение функции в ряд Тейлора в окрестности точки
будет выглядеть так:
C учетом вышеприведенного разложение принимает вид:
Предполагая, что отклонения выходных и входных воздействий незначительны, (т.е.:), оставим в разложении только члены первого порядка малости (линейные). Поскольку
, получаем:
Подставляя соотношение (2.2.4) в уравнение (2.2.2), и перенося множители при у и u в разные части получаем уравнения:
Коэффициенты — постоянные коэффициенты, поэтому уравнения 2.2.5 — линейное дифференциальное с постоянными коэффициентами.
В дальнейшем нами будет часто использоваться операторная форма записи уравнений динамики:
где – оператор дифференцирования;
— линейный дифференциальный оператор степени n;
— линейный дифференциальный оператор степени m, причем обычно порядок оператора
выше порядка оператора
:
Уравнения (2.2.5) и (2.2.6) — уравнения динамики системы (звена) в отклонениях.
Если исходное уравнение (2.2.1) — дифференциальное уравнение в физических переменных (температура, скорость, поток и т.д.), то размерность коэффициентов может быть произвольной (любой).
Переход к нормализованным отклонениям позволяет “упорядочить” размерность коэффициентов. В самом деле, разделив уравнение (2.2.5) на начальные условия (значения в нулевой момент времени) и выполнив некоторые преобразования, получаем:
Приведение уравнения динамики САУ (звена) к нормализованному виду позволяет “унифицировать” размерность коэффициентов уравнений: ==>
Если вынести в правой части (2.2.7) коэффициент за общую скобку и разделить все уравнение на
, то уравнение принимает вид:
или в операторном виде:
Линеаризация уравнений динамики и нормализация переменных позволяют привести уравнения динамики САУ (звена) к виду, наиболее удобному для использования классических методов анализа, т.е. к нулевым начальным условиям.
Пример
Выполнить линеаризацию уравнения динамики некоторой «абстрактной» САР в окрестности состояния (x0, y0), если полное уравнение динамики имеет вид:
Нелинейность полного уравнения динамики проявляется в следующем:
• во-первых, в нелинейности статической характеристики:
• во-вторых, слагаемое в левой части — чисто нелинейное, так как действие умножения является нелинейным.
Выполним процесс линеаризации исходного уравнения, динамики без разложения я ряд Тейлора, основываясь на том, что в окрестности состояния (x0, y0) нормированные отклонения управляющего воздействия и регулируемой величины намного меньше 1.
Преобразования выполним в следующей последовательности:
- Перейдем к безразмерным переменным (нормализованным);
- Выполним линеаризацию, отбросив нелинейные члены 2-го и выше порядков малости.
Перейдем к новым безразмерным переменным:
Заметим, что: .
Подставляя значения x(t) и y(t) в исходное уравнение:
Удаляем полученного уравнения уравнения стационара: , а так же пренебрегая слагаемыми второго прядка малости:
, получаем следующее уравнение:
Вводим новые обозначения:
Получаем уравнения в «почти» классическом виде:
Если в правой части вынести за общую скобку и разделить все уравнение на
, то уравнение (линеаризованное) принимает вид:
Процедура нормализации позволяет более просто линеаризовать уравнение динамики, так как не требуется выполнять разложение в ряд Тейлора (хотя это и не сложно).
2.3. Классический способ решения уравнений динамики
Классический метод решения уравнений динамики САУ (САР) применим только для линейных или линеаризованных систем.
Рассмотрим некоторую САУ (звено), динамика которой описывается линейным дифференциальным уравнением вида:
Переходя к полной символике, имеем:
Выражение (2.3.2) — обыкновенное дифференциальное уравнение (ОДУ), точнее неоднородное ОДУ, так как правая часть ≠ 0.
Известно входное воздействие x(t), коэффициенты уравнения и начальные условия (т.е. значения переменных и производных при t = 0).
Требуется найти y(t) при известных начальных условиях.
где: — решение однородного дифференциального уравнения
y_<част.>(t) $inline$ — частное решение. $inline$
Будем называть решение однородного дифференциального уравнения , собственным решением, так как его решение не зависит от входного воздействия, а полностью определяется собственными динамическими свойствами САУ (звена).
Вторую составляющую решения (2.3.3) будем называть , вынужденным, так как эта часть решения определяется внешним воздействием
, поэтому САУ (САР или звено) “вынуждена отрабатывать” это воздействие:
Напомним этапы решения:
1) Если имеется уравнение вида , то сначала решаем однородное дифференциальное уравнение:
2) Записываем характеристическое уравнение:
3) Решая уравнение (2.3.5), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения
4) Тогда собственное решение записывается в виде:
если среди нет повторяющихся корней (кратность корней равна 1).
Если уравнение (2.3.5) имеет два совпадающих корня, то собственное решение имеет вид:
Если уравнение (2.3.5) имеет k совпадающих корней (кратность корней равна k), то собственное решение имеет вид:
5) Вынужденную часть решения можно найти различными способами, но наиболее распространены следующие способы:
а) По виду правой части.
б) Методом вариации постоянных.
в) Другие методы…
Если вид правой части дифференциального уравнения – относительно несложная функция времени, то предпочтительным является способ а): подбор решения. .
6) Суммируя полученные составляющие (собственную и вынужденную), имеем:
7) Используя начальные условия (t = 0), находим значения постоянных интегрирования .
Обычно получается система алгебраических уравнений.
Решая систему, находим значения постоянных интегрирования
Пример
Найти аналитическое выражение переходного процесса на выходе звена, если
Решение. Запишем однородное ОДУ:
Характеристическое уравнение имеет вид: ; Решая, имеем:
тогда:
где — неизвестные (пока) постоянные интегрирования.
По виду временной функции в правой части запишем как:
Подставляя в исходное уравнение, имеем:
Суммируя , имеем:
Используя 1-е начальное условие (при t = 0), получаем: , а из 2-го начального условия имеем:
Решая систему уравнений относительно и
, имеем:
Тогда окончательно:
Что бы проверить результ, выполним моделирование процесса в SimInTech, для этого преобразуем исходное уравнение к виду:
Создадим модель SimInTech, содержащую исходное динамическое уравнение и полученное аналитическое решение, и выведем результаты на один график (см. рис. 2.3.1).
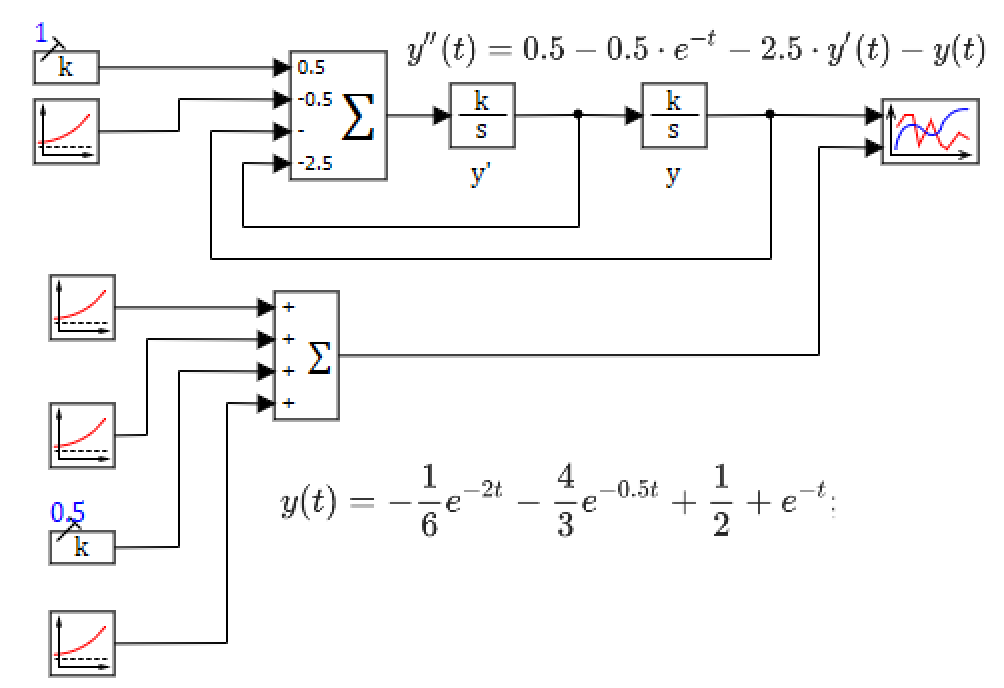
Рис. 2.3.1 – структурная схема для проверки решения
На рис. 2.3.2 приведено решение по вышеприведенному соотношению и численное решение задачи в среде SimInTech (решения совпадают и линии графиков «наложены» друг на друга).
Лекция 11. Нелинейные САУ
Большинство характеристик реальных устройств в общем случае являются нелинейными и некоторые из них не могут быть линеаризованы, т.к . имеют разрывы второго рода и к ним кусочно-линейная аппроксимация неприменима. Работу реальных звеньев (устройств) могут сопровождать такие явления, как насыщение, гистерезис, люфт, наличие зоны нечувствительности и т.д. Нелинейности могут быть естественными и искусственными (преднамеренно вводимые). Естественные нелинейности присущи системам в силу нелинейного проявления физических процессов и свойств у отдельных устройств. Например, механическая характеристика асинхронного двигателя. Искусственные нелинейности вводятся разработчиками в системы, чтобы обеспечить требуемое качество работы: для оптимальных по быстродействию систем применяют релейное управление, наличие нелинейных законов в поисковых и безпоисковых экстремальных системах, системы с переменной структурой и т.д.
Нелинейной системой называется такая система, в состав которой входит хотя бы один элемент, линеаризация которого невозможна без потери существенных свойств системы управления в целом. Существенными признаками нелинейности являются: если некоторые координаты или их производные по времени входят в уравнение в виде произведений или степени, отличной от первой; если коэффициенты уравнения являются функциями некоторых координат или их производных. При составлении дифференциальных уравнений нелинейных систем сначала составляют дифференциальные уравнения для каждого устройства системы. При этом характеристики устройств, допускающих линеаризацию, линеаризуются. Элементы, не допускающие линеаризации, называются существенно нелинейными. В результате получают систему дифференциальных уравнений, в которой одно или несколько уравнений нелинейные. Устройства, допускающие линеаризацию, образуют линейную часть системы, а устройства, которые не могут быть линеаризованы, составляют нелинейную часть. В простейшем случае структурная схема САУ нелинейной системы представляет собой последовательное соединение безынерционного нелинейного элемента и линейной части, охваченное обратной связью (рис.7.1). Так как для нелинейных систем не применим принцип суперпозиции, то, проводя структурные преобразования нелинейных систем, единственным ограничением по сравнению со структурными преобразованиями линейных систем, является то, что нельзя переносить нелинейные элементы через линейные и наоборот.

Рис. 7.1. Функциональная схема нелинейной системы:
НЭ — нелинейный элемент; ЛЧ — линейная часть; Z(t) и X(t)
соответственно выход и вход нелинейного элемента.
Классификация нелинейных звеньев возможна по различным признакам. Наибольшее распространение получила классификация по статическим и динамическим характеристикам. Первые представляются в виде нелинейных статических характеристик, а вторые — в виде нелинейных дифференциальных уравнений. Примеры таких характеристик приведены в [2,6]. На рис.7.2. приведены примеры однозначных (без памяти) и многозначных (с памятью) нелинейных характеристик. В этом случае учитывается направление (знак) скорости сигнала на входе.

Рис.7.2. Статические характеристики нелинейных элементов
Поведение нелинейных систем при наличии существенных нелинейностей имеет ряд особенностей, отличных от поведения линейных САУ [2,6,13 ]:
1. выходная величина нелинейной системы непропорциональна входному воздействию, т.е. параметры нелинейных звеньев зависят от величины входного воздействия;
2. переходные процессы в нелинейных системах зависят от начальных условий (отклонений). В связи с этим, для нелинейных систем введены понятия устойчивости «в малом», «в большом», «в целом». Система устойчива «в малом», если она устойчива при малых (бесконечно малых) начальных отклонениях. Система устойчива «в большом», если она устойчива при больших (конечных по величине) начальных отклонениях. Система устойчива «в целом», если она устойчива при любых больших (неограниченных по величине) начальных отклонениях. На рис.7.3 приведены фазовые траектории систем: устойчивой «в целом» (а) и системы устойчивой «в большом» и неустойчивой «в малом» (б);

Рис.7.3. Фазовые траектории нелинейных систем
3. для нелинейных систем характерен режим незатухающих периодических колебаний с постоянной амплитудой и частотой (автоколебаний), возникающий в системах при отсутствии периодических внешних воздействий;
4. при затухающих колебаниях переходного процесса в нелинейных системах возможно изменение периода колебаний.
Эти особенности обусловили отсутствие общих подходов при анализе и синтезе нелинейных систем. Разработанные методы позволяют решать лишь локальные нелинейные задачи. Все инженерные методы исследования нелинейных систем разделяются на две основные группы: точные и приближенные. К точным методам относится метод А.М.Ляпунова, метод фазовой плоскости, метод точечных преобразований, частотный метод В.М.Попова. Приближенные методы основаны на линеаризации нелинейных уравнений системы с применением гармонической или статистической линеаризации. Границы применимости того или иного метода буду рассмотрены ниже. Следует заметить, что в обозримом будущем имеется необходимость дальнейшего развития теории и практики нелинейных систем.
Мощным и эффективным методом исследования нелинейных систем является моделирование, инструментарием которого служит компьютер. В настоящее время многие сложные для аналитического решения теоретические и практические вопросы сравнительно легко могут быть решены с помощью вычислительной техники.
Основными параметрами, характеризующими работу нелинейных САУ, являются:
1. Наличие или отсутствие автоколебаний. Если автоколебания имеются, то необходимо определить их амплитуду и частоту.
2. Время выхода регулируемого параметра в режим стабилизации (быстродействие).
3. Наличие или отсутствие скользящего режима.
4. Определение особых точек и особых траекторий движения.
Это далеко не полный перечень исследуемых показателей, сопровождающих работу нелинейных систем. Системы экстремальные, самонастраивающиеся, с переменными параметрами требуют оценки и дополнительных свойств.
| Метод гармонического баланса |
Идея метода гармонической линеаризации принадлежит Н.М. Крылову и Н.Н. Боголюбову и базируется на замене нелинейного элемента системы линейным звеном, параметры которого определяются при гармоническом входном воздействии из условия равенства амплитуд первых гармоник на выходе нелинейного элемента и эквивалентного ему линейного звена. Метод является приближенным и может быть использован только в случае, когда линейная часть системы является фильтром низких частот, т.е. отфильтровывает все возникающие на выходе нелинейного элемента гармонические составляющие, кроме первой гармоники. При этом линейная часть может быть описана дифференциальным уравнением любого порядка, а нелинейный элемент может быть как однозначным, так и многозначным.
В основе метода гармонической линеаризации (гармонического баланса) лежит предположение, что на вход нелинейного элемента подается гармоническое воздействие с частотой ω и амплитудой А, т.е. x = А sinωt. В предположении, что линейная часть является фильтром низких частот, спектр выходного сигнала линейной части ограничивается только первой гармоникой, определяемой рядом Фурье (в этом и заключается приближенность метода, т.к. высшие гармоники выбрасываются из рассмотрения). Тогда связь между первой гармоникой выходного сигнала и входным гармоническим воздействием нелинейного элемента представляется в виде передаточной функции [2,4,13]:

Уравнение (7.1) называется уравнением гармонической линеаризации, а коэффициенты q и q’ — коэффициентами гармонической линеаризации, зависящие от амплитуды А и частоты ω входного воздействия. Для различных видов нелинейных характеристик коэффициенты гармонической линеаризации сведены в таблицу [2,4,13]. Следует заметить. что для статических однозначных коэффициент q'(А)=0. Подвергнув уравнение (7.1) преобразованию по Лапласу при нулевых начальных условиях с последующей заменой оператора p на jω (p = jω ), получим эквивалентный комплексный коэффициент передачи нелинейного элемента
Wнэ(jω,A) = q + jq’. (7.2)
После того, как проведена гармоническая линеаризация, для анализа и синтеза нелинейных САУ возможно применение всех методов, применяемых для исследования линейных систем, в том числе и использование различных критериев устойчивости. При исследовании нелинейных систем на основе метода гармонической линеаризации в первую очередь решают вопрос о существовании и устойчивости периодических (автоколебательных) режимов. Если периодический режим устойчив, то в системе существуют автоколебания с частотой ω0 и амплитудой А0. Рассмотрим нелинейную систему, включающую в себя линейную часть с передаточной функцией

и нелинейный элемент с эквивалентным комплексным коэффициентом передачи (7.2). Расчетная структурная схема нелинейной системы приобретает вид рис.7.5.

Рис.7.5. Структурная схема нелинейной САУ
Для оценки возможности возникновения автоколебаний в нелинейной системе методом гармонической линеаризации необходимо найти условия границы устойчивости, как это делалось при анализе устойчивости линейных систем. Если линейная часть описывается передаточной функцией (7.3), а нелинейный элемент (7.2), то характеристическое уравнение замкнутой системы будет иметь вид
d(p) + k(p)(q(ω,A) + q'(ω,A)) = 0 (7.4)
На основании критерия устойчивости Михайлова границей устойчивости будет прохождение годографа Михайлова через начало координат. Из выражений (7.4) можно найти зависимость амплитуды и частоты автоколебаний от параметров системы, например, от коэффициента передачи k линейной части системы. Для этого необходимо в уравнениях (7.4) коэффициент передачи k считать переменной величиной, т.е. это уравнение записать в виде:
где ωo и Ao — возможные частота и амплитуда автоколебаний.
Тогда, приравнивая к нулю действительную и мнимую части уравнения (7.5)

можно построить границу устойчивости (D-разбиение) по интересующему нас параметру k (рис.7.6).

Рис.7.6. D-разбиение плоскости параметра К нелинейной САУ
Анализируя рис.7.6 можно заключить, что в области 1 автоколебания невозможны и критический коэффициент равен ккр, а в области 2 колебания сходятся к величине амплитуды Ao и частоты ωo (автоколебательный режим) в зависимости от начальных условий. По графику рис.7.6 можно выбрать коэффициент передачи k, при котором амплитуда и частота возможных автоколебаний имеет допустимые значения или вообще отсутствует.
Чаще на практике используется графоаналитический метод определения возможных амплитуд и частот автоколебаний в нелинейных системах. В соответствии с критерием устойчивости Найквиста незатухающие колебания в линейной системе возникают в том случае, когда амплитудно-фазовая характеристика разомкнутой системы проходит через точку с координатами [ 1, j0]. Данное условие является также условием существования автоколебаний в гармонически линеаризованной нелинейной системе (рис.7.5), т.е.
Решение уравнения (7.8) относительно частоты и амплитуды автоколебаний можно получить графически, как точку пересечения годографа частотной характеристики линейной части системы Wлч(jω) и годографа обратной характеристики нелинейной части -1/Wнэ(jω,А) (рис7.7). Если эти годографы не пересекаются, то режим автоколебаний в исследуемой системе не существует.

Рис. 7.7. Годографы линейной и нелинейной частей системы
Для устойчивости автоколебательного режима с частотой ω0 и амплитудой А0 требуется, чтобы точка на годографе нелинейной части М, соответствующая увеличенной амплитуде А0+ ΔА по сравнению со значением в точке пересечения годографов, не охватывалась годографом частотной характеристики линейной части системы, в противном случае автоколебания неустойчивые. На рис. 7.7 дан пример расположения годографов для случая, когда в нелинейной системе существуют устойчивые автоколебания. Параметры автоколебаний на входе нелинейного элемента определяются в точке пересечения годографов: частота из Wлч(jω), а амплитуда из Wнэ -1 (A). Исследование нелинейных систем возможно по логарифмическим частотным характеристикам (метод шаблонов) [2]. Метод гармонического баланса позволяет вести синтез нелинейных САУ на обеспечение требуемых показателей качества меняя параметры или линейной части, или нелинейного элемента.
| Методы фазовой плоскости |
Метод фазового пространства относится к наиболее ранним точным аналитическим методам теории нелинейных систем. К ним относится метод фазовой плоскости, впервые введенный в ТАУ А.А.Андроновым, и метод точечных преобразований [2,13]. Фазовым пространством называется пространство, по осям координат которого отложены переменные, характеризующие состояние динамической системы. Если движение системы описывается дифференциальным уравнением n-го порядка, то состояние этой системы в любой момент времени можно характеризовать некоторой точкой n-мерного фазового пространства, по осям которого отложены координата системы и (n-1) ее производных. Точка, характеризующая состояние системы в фазовом пространстве, называется изображающей точкой. При движении системы изображающая точка описывает в фазовом пространстве некоторую кривую, называемую фазовой траекторией. Каждому определенному переходному процессу в фазовом пространстве соответствует определенная фазовая траектория. Начальное положение изображающей точки определяется начальными условиями. В установившемся равновесном состоянии системы все производные рассматриваемой переменной равны нулю. Соответствующие этому точки фазового пространства находятся в покое и называются особыми точками. Совокупность фазовых траекторий для всевозможных начальных отклонений называется фазовым портретом системы. По виду фазового портрета системы определяют особые точки и особые траектории, исследуют устойчивость системы и оценивают качество процесса управления.
Метод фазовой плоскости используется для исследования нелинейных систем, линейная часть которых описывается дифференциальным уравнением не выше второго порядка, а нелинейный элемент может быть любым. Метод заключается в том, что из уравнений состояния исключается время и определяются уравнения фазовых кривых. Задача значительно упрощается, если нелинейный элемент обладает кусочно-линейной характеристикой. Тогда фазовое пространство разбивается на ряд областей, где работа нелинейной системы описывается обыкновенными линейными уравнениями, на основании которых строятся фазовые траектории. Непрерывность движения изображающей точки на фазовом пространстве (переход из одной области в другую) обеспечивается «сшиванием» по линиям переключения в соответствии с видом нелинейности. При исследовании нелинейных систем высокого порядка их аппроксимируют системами второго порядка с эквивалентным запаздыванием. Уравнение фазовой траектории может быть получено из уравнений состояния

где: x1, x2 — координата системы и ее производная; f(x1;x2) — нелинейная функция.
Разделив второе из уравнений (7.9) на первое, получим уравнение фазовой траектории, в котором отсутствует время t в явном виде:

Решение уравнения (7.10) x2 = F(x1) изображается на фазовой плоскости (x1;x2). По оси абсцисс откладывается сама координата x1, а по оси ординат откладывается ее первая производная x2. Каждой совокупности начальных условий (x10, x20) соответствует свое решение и своя фазовая траектория. Семейство фазовых траекторий характеризует все возможные виды переходных процессов в данной системе управления при любых начальных условиях и образует ее фазовый портрет.
Основные свойства фазовых траекторий вытекают из выражения (7.10):
1) если F(x1;x2) определена и непрерывна в некоторой области и имеет непрерывные частные производные по своим аргументам, то через каждую точку фазовой плоскости, за исключением особых точек, проходит единственная фазовая траектория. Это означает, что фазовые траектории не пересекаются между собой;
2) при x2= 
3) в точках, где x2 = 0 и F(x1;x2) не равно 0, фазовые траектории пересекают ось абс-цисс под прямым углом. Ось ординат фазовые траектории могут пересекать под любым углом.
В большинстве своем решение уравнения (7.10) может быть получено простым интегрированием, но если переменные x1 и x2 не разделяются, то фазовые траектории можно построить приближенным графоаналитическим методом, например, методом изоклин [2,4].
Изоклиной называется такая линия, во всех точках пересечения которой с фазовыми траекториями, последние наклонены под одним и тем же углом αi к оси абсцисс, т.е. сi =dx2/dx1 и arctg ci = αi. Уравнение изоклины получается из уравнения (7.10) подстановкой
из которого получается уравнение изоклины x2 = φ(x1, ci ). Задавая различные значения сi наклона касательных к фазовым траекториям, пересекающим эти изоклины, строят семейство изоклин, которые используются для построения фазовых траекторий (рис. 7.9). В качестве примера на рис. 7.8 на изоклинах отмечены наклоны фазовых траекторий к оси абсцисс и построена фазовая траектория, исходящая из точки Мо.

Рис. 7.9. Фазовая траектория нелинейной САУ
Особенностью фазовых траекторий нелинейных САУ является то, что кроме особых точек на фазовом портрете могут появляться особые траектории [2,3,6,13]. На рис.7.3 показаны предельные циклы: неустойчивый и устойчивый. К этим предельным циклам стремятся изображающие точки при различных начальных отклонениях по различным фазовым траекториям. Устойчивый предельный цикл соответствует автоколебаниям системы. Размеры предельного цикла представляют амплитуды колебаний самой величины x1 и скорости ее изменения x2. Пересечение траектории устойчивого предельного цикла с осью абсцисс определяет амплитуду автоколебаний Ао, а пересечение с осью ординат определяет величину произведения амплитуды на частоту колебаний Аоωо.
| Учет чистого запаздывания в нелинейных САУ |
Для учета чистого запаздывания в нелинейных САУ расчетная структурная схема приводится к виду Рис.7.12.

Рис. 7.12. Расчетная схема нелинейной системы
со звеном чистого запаздывания
Определить возможную амплитуду и частоту автоколебаний можно методом гармонического баланса, если построить годографы:
Wлч(jω)*e -jωτ — а.ф.х. эквивалентной линейной части;
Wнэ -1 (A) — обратная а.ф.х. нелинейного элемента.
В случае пересечения этих годографов определяются параметры и устойчивость автоколебаний по приведенной выше методике.
| Коррекция нелинейных систем |
При коррекции нелинейных автоматических систем обычно решаются две основные задачи [2,5]:
— обеспечение устойчивости системы;
— получение автоколебаний с заданной амплитудой и частотой.
Коррекция осуществляется с помощью включения как линейных, так и нелинейных корректирующих устройств, а также компенсацией влияния нелинейностей. В качестве линейных корректирующих устройств используются главным образом неединичные главные обратные связи и местные обратные связи, охватывающие нелинейные элементы. Нелинейные корректирующие устройства включаются или последовательно, или в обратные связи.
При расчете корректирующих устройств структурную схему нелинейной системы необходимо привести к эквивалентной одноконтурной схеме с нелинейным элементом и эквивалентной линейной частью (рис.7.1). И методом шаблонов [2] или методом гармонического баланса подбирается передаточная функция линейного корректирующего устройства и параметры нелинейности с тем, чтобы избежать возникновение автоколебаний в системе или ограничить их приемлемыми амплитудой и частотой автоколебаний.
При компенсации нелинейностей нелинейную систему можно рассматривать как линейную относительно определенных входных воздействий. Линеаризация заданной нелинейности F(x) заключается во включении последовательно или параллельно компенсирующего нелинейного элемента (КЭ) с обратной нелинейной характеристикой F -1 (x). При этом получаем эквивалентный линейный элемент. На рис. 7.14 приведен пример линеаризации усилителя с насыщением путем включения параллельно с ним усилителя с зоной нечувствительности.

Рис. 7.14. Схема включения параллельно компенсирующей нелинейности
Целью вибрационной компенсация нелинейностей является приближение свойств нелинейной системы к линейной САУ. Этого можно достичь за счет того, что на вход нелинейного элемента наряду с сигналом рассогласования Δ(t) подается высокочастотная периодическая составляющая u(t) (рис. 7.15).

Рис. 7.15. Вибрационная компенсация нелинейности
Сигнал рассогласования Δ(t) смещает эти колебания относительно нелинейной характеристики. Средние времена состояний оказываются неодинаковыми, и в определенном диапазоне среднее значение сигнала на выходе НЭ будут примерно пропорциональным Δ(t). Колебания u(t) вводятся от специального генератора. Если частота этих колебаний достаточно велика, чтобы можно было приближенно считать рассогласованиеΔ(t) неизменным в пределах периода T=2π/ω, то постоянная составляющая выходного сигнала нелинейного элемента определится выражением (рис.7.15,б)
Достаточно часто проводят линеаризацию нелинейных систем применяя высокочастотные автоколебания рис.7.16.

Рис.7.16. Линеаризация автоколебаниями
Для получения таких автоколебаний НЭ (чаще всего релейный) охватывают отрицательной обратной связью, в цепь которой включено апериодическое звено (рис.7.16,а) — запаздывающая обратная связь, или применяют скоростную обратную связь (рис.7.16,б). В этих случаях нелинейные системы обычно работают в скользящем режиме.
http://habr.com/en/post/506984/
http://poisk-ru.ru/s8227t8.html