Какова вероятность что корни уравнения разных знаков

Какова вероятность того, что корни этого уравнения будут действительными числами?

Коэффициенты р и q квадратного уравнения х 2 + рх + q = 0 выбирают наудачу на отрезке [0; 2]. Какова вероятность того, что корни этого уравнения будут действительными числами?

Решение. Обозначим событие: А – корни данного уравнения бу­дут действительными числами. Найдем вероятность события А, применив формулу р(А) = mesD / mesΩ. Пусть коэффициенты р и q квадратного уравнения ‒ наудачу взятые числа. Их воз­можные значения: 0 2 – 4q > 0, откуда следует, что q ≤ р 2 / 4.

Построим границы области, которой принадлежат точки плоскости, удовлетворяющие условиям:

Граничные прямые р = 0, р = 2, q = 0, q = 2 являются сторонами квадрата, ограничивающего область возможных значений р и q. Граничная кривая q = р 2 /4 представляет собой параболу. Решениями состав­ленной системы неравенств являются координа-ты всех точек плоскости, расположенных на рис. 1.14 заштрихованной области, то есть между граничными линиями р = 0, q = 2, q = р 2 /4 и на самих этих линиях. Точки плоскости, принадлежащие заштрихованной области, характеризуют исхо­ды испытания, благоприятст-вующие событию А. Площадь заштрихованной области равна

Таким образом, вероятность события А равна р(А) = S_g / S_G = 1 / 6.

Какова вероятность что корни уравнения разных знаков

КВАДРАТНЫЙ ТРЕХЧЛЕН III

§ 53. Исследование знаков корней квадратного уравнения по его коэффициентам

Используя теорему Виета, можно, не решая уравнения x 2 + px + q = 0. определить, какими будут его корни: положительными или отрицательными. Но при этом, конечно, нужно быть уверенным в том, что рассматриваемое уравнение имеет корни. Если же корней нет, то говорить о знаках корней не имеет смысла. Поэтому на протяжении всего этого параграфа мы будем предполагать, что рассматриваемое приведенное квадратное уравнение x 2 + px + q = 0 имеет корни, то есть дискриминант его неотрицателен.

1) Пусть q > 0; тогда оба корня имеют одинаковые знаки, поскольку x₁ • х₂= q > 0.
Если к тому же р 0, значит, оба корня положительны.
Если р > 0, то x₁ + х₂ = — р 0, то x₁ + х₂ = — р 0. Это возможно только тогда, когда положительный корень больше абсолютной величины отрицательного корня.
При р = 0 x₁ + х₂ = 0, откуда x₁= — х₂ в этом случае корни равны по абсолютной величине и противоположны по знаку.

3) Осталось рассмотреть случай, когда q = 0. Тогда x₁ • х₂ = 0, поэтому хотя бы один из корней равен нулю.
Пусть для определенности x₁ = 0, тогда другой корень найдется из условия x₁ + х₂ = — р, откуда х₂ = — р. Значит, в этом случае один корень равен нулю, а другой представляет собой число, противоположное коэффициенту р.
Если же и р = 0, то уравнение имеет , два равных корня: x₁= х₂ = 0.

Полученные результаты исследования знаков корней представлены в таблице .

Еще раз отметим, что приведенные здесь рассуждения верны лишь в предположении, что исследуемое уравнение имеет действительные корни, то есть его дискриминант неотрицателен.

Рассмотрим несколько примеров на исследование знаков корней квадратных уравнений.

1) x 2 — 8х — 9 = 0. Дискриминант этого уравнения равен D = 64 + 36 = 100 > 0. Поэтому уравнение имеет два различных действительных корня.
Вследствие того, что x₁ • х₂ = — 9, корни должны иметь разные знаки,
а так как x₁ + х₂ = 8, то абсолютная величина отрицательного корня меньше положительного корня.

2) x 2 + 7х + 10 = 0. Дискриминант этого уравнения равен D = 49 — 40 = 9 > 0. Поэтому уравнение имеет два различных действительных корня.
Так как x₁ • х₂ = 10 > 0, то корни имеют одинаковые знаки.
Кроме того, x₁ + х₂ = —7, значит, оба корня отрицательны.

3) x 2 — х + 1 = 0. Для данного уравнения

D = (—1) 2 — 4 = — 3 2 + bx + c = 0 . Для этого сначала нужно посредством деления на а привести данное уравнение к приведенному квадратному уравнению x 2 + b /_a х + c /_a = 0, а затем для этого уравнения провести описанные выше рассуждения.

Пусть, например, нужно исследовать знаки корней уравнения —3x 2 + 5х — 2 == 0. Дискриминант этого уравнения равен D = 25 — 24 = 1 > 0. Поэтому оно имеет два различных действительных корня.

Разделив обе части уравнения на — 3, получим: x 2 — 5 /₃х + 2 /₃ = 0. Отсюда видно, что корни данного уравнения имеют одинаковые знаки, так как x₁ • х₂ = 2 /₃ > 0. Кроме того, x₁ + х₂ = 5 /₃ > 0. Следовательно, оба корня положительны.

Не решая данных уравнений (№ 391—400), определить знаки их корней:

Проверить себя, да и вообще исследовать квадратные уравнения полные и приведенные можно, с помощью соответствующих алгоритмов в программе EXCEL. Алгоритм можно усовершенствовать для отображения промежуточных результатов вычислений.

401. При каких значениях а корни уравнения

имеют одинаковые знаки и при каких — разные?

402. При каких значениях а корни уравнения

имеют одинаковые знаки и при каких — разные?

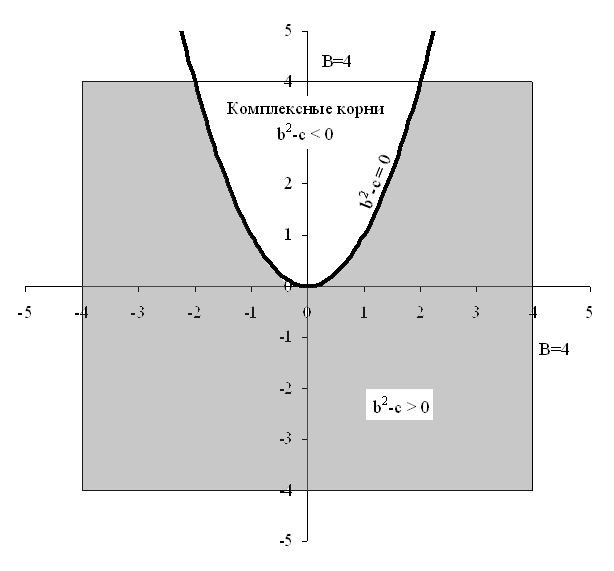
Случайное квадратное уравнение

Какова вероятность того, что корни квадратного уравнения x 2 + 2bx + c = 0 вещественны?

Для того чтобы вопрос задачи имел смысл, предположим, что точка (b, c) равномерно распределена на квадрате с центром в начале координат и стороной 2B (рис. 1). Решим задачу при фиксированном B, а затем устремим B к бесконечности, так что b и c могут принимать любые значения.

Рис. 1. Серая область отвечает случаю вещественных корней

Для того чтобы уравнение имело вещественные корни, необходимо и достаточно, чтобы
b 2 — c ≥ 0.

На приведенном рисунке изображена парабола b 2 = c и показана область, где наше уравнение имеет вещественные корни для B = 4.

Нетрудно подсчитать, что площадь незаштрихованной области равна 4/3∙B 3/2 (при B ≥ 1), а площадь всего квадрата, конечно, равна 4B 2 . Следовательно, вероятность того, что корни комплексные, равна 1/3∙√ B . При B = 4 ответ равен 1/6. С ростом B 1/√ B стремится к нулю, так что вероятность того, что корни вещественные, стремится к 1.

Следует заметить, что эта задача отличается от такой же задачи, связанной с уравнением ax 2 + 2bx + c = 0. Конечно, можно разделить на a, но если a, b и c были независимы и равномерно распределены в некотором кубе, то b/a и c/a уже зависимы и распределены неравномерно.

Публикуется по работе: Пятьдесят занимательных вероятностных задач с решениями. Ф.Мостеллер, перев. с англ., издание второе. М. Наука, 1975, 112 с.

Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката

Отсутствие ссылки на использованный материал является нарушением заповеди «Не укради»