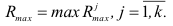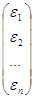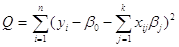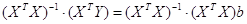Отбор важнейших факторов многофакторных регрессионных моделей
Отбор важнейших факторов многофакторных регрессионных моделей
Проблема выбора существенных переменных (факторов) для включения их в модель тесно связана с исходными предпосылками регрессионного анализа. При построении модели два момента вступают в противоречие. В модель должны войти все переменные, которые с экономической точки зрения оказывают влияние на зависимую переменную. Но большое количество переменных, включенных в модель, требует большого числа наблюдений. Невыполнение первого требования может привести к неадекватности модели из-за того, что не учтены некоторые существенные факторы, а также к нарушению нормальности распределения случайной компоненты £ из-за того, что ее вариация будет обусловлена не только случайными факторами, но и систематически действующими, т.е. к нарушению гомоскедастичности. Дж. У. Юл и М. Дж. Кендалл считают, что максимальное число переменных, включенных в модель, не должно превышать десяти.
Сокращение числа переменных, входящих в модель, можно производить путем отсеивания менее существенных факторов в процессе построения регрессионной модели или путем замены исходного набора переменных меньшим числом эквивалентных переменных, полученных в результате преобразований исходного набора.
Процедура отсева несущественных факторов в процессе построения регрессионной модели называется многошаговым регрессионным анализом. Этот метод основан на построении нескольких промежуточных уравнений регрессии, в результате анализа которых получается конечная модель, включающая только факторы, оказывающие существенное влияние на исследуемый показатель. При этом выделяется три подхода.
- Строится уравнение регрессии по максимально возможному количеству факторов, предположительно оказавших влияние на исследуемый показатель. Затем с помощью
— критерия исключаются несущественные факторы. - Строится парная регрессия по одному значимому фактору, а затем в уравнение регрессии последовательно вводятся по одному все значимые факторы. Этот метод называет методом пошаговой регрессии.
- Строится несколько уравнений регрессии, затем с помощью определенного критерия выбирается наилучшее.
Кратко охарактеризуем эти методы построения регрессионных моделей.
Применение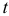 
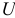
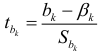
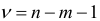
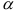
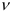
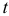
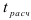
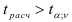
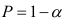
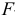
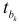
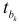
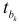
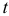
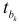
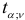
-критерия для отбора существенных факторов основано на предположении о нормальном распределении остатков 
. Если это условие выполняется, то величина 
распределена по закону Стьюдента с 
степенями свободы. Задавая уровень значимости 
по числу степеней свободы 
, находят квантиль -распределения, с которым сравнивают 
. При 
коэффициент регрессии признается статистически значимым с вероятностью 
. Если все коэффициенты регрессии признаны значимыми, то уравнение регрессии считается окончательным и при общей проверке его адекватности по 
-критерию принимается в качестве модели исследуемого экономического процесса. Если же среди коэффициентов регрессии имеются незначимые, то соответствующие факторы следует исключить из уравнения регрессии, предварительно проранжировав коэффициенты регрессии по значению 
. В первую очередь исключается фактор, для которого значение наименьшее. Исключив один фактор с наименьшим значением , строят уравнение регрессии без исключенного фактора и снова производят оценку коэффициентов регрессии по -критерию. Изложенную процедуру повторяют до тех пор, пока все коэффициенты регрессии в уравнении не окажутся значимыми. При этом на каждом шаге, кроме формальной статистической проверки значимости коэффициентов регрессии, проводят экономический анализ несущественных факторов и устанавливают порядок их исключения. В некоторых случаях, исходя из профессиональных соображений, оставляют фактор, для которого , незначительно меньше 
.
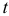
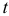
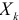
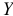
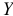
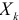
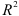
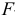
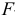
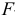
Отметим, что не существенность коэффициента регрессии по -критерию не всегда является основанием для исключения фактора из дальнейшего анализа. Т. Андерсон рекомендовал исключать переменную из уравнения регрессии лишь в том случае, когда средняя квадратичная ошибка коэффициента регрессии превышает абсолютную величину вычисленного коэффициента, т.е. в случае, если значение -критерия меньше единицы. При этом предполагается, что нет веских оснований для того, чтобы оставить переменную в модели. При пошаговом построении уравнения регрессии выбирают фактор 
имеющий наибольший коэффициент парной корреляции с 
, и строят уравнение парной регрессии. Затем находят частные коэффициенты корреляции между и остальными переменными при исключении выбранной переменной . Переменную с максимальным значением частного коэффициента корреляции включают в уравнение регрессии и вычисляют 
и частный -критерий, который показывает, существенный ли вклад вносит в уравнение эта переменная по сравнению с уже введенными. Указанная процедура проводится до тех пор, пока расчетное значение -критерия становится меньше табличного. Подчеркнем, что на каждом шаге с добавлением новой переменной определяется значимость не только новой переменной, но и переменных, уже включенных в модель. И если какие-то из них окажутся незначимыми, они исключаются из уравнения. Значимость определяется значением частного -критерия для всех переменных модели.
В многошаговом регрессионном анализе, основанном на методе случайного поиска с адаптацией, разработанным Г.С. Лбовым, применяют «поощрение» или «наказание» отдельных переменных исходя из их «ценности». В качестве критерию «ценности» используют коэффициент множественной корреляции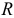 
.
В начале поиска задают равные вероятности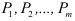 
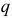
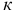
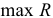
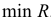
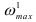
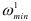
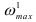
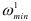
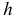
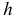
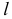
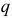
для каждого из факторов. Затем случайным образом выбирают 
групп по 
факторов и в этой системе определяют 
и 
. Векторы факторов в первой системе 
и 
запоминают. Вероятность попадания в систему увеличивается, а в уменьшается на 
( — произвольное число). Так образовывают 
систем по групп в каждой. За эффективную принимают ту группу, при которой
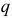
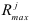
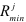
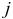
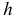
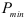
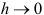
При переборе ряда групп вероятность выбора факторов, часто встречающихся в удачных сочетаниях, становится большей, и именно этот набор факторов повторяется гораздо чаще остальных. Число выбирают так, чтобы между значениями 
и 
данной системы 
была заключена основная часть сочетаний, а величину шага — такой, чтобы вероятность выбора фактора, если он будет встречаться на каждом этапе, оставалась большей или равной установленной вероятности 
. При увеличении шага растет и доля случаев, когда эффективное сочетание факторов не будет найдено. При 
эффективный поиск сводится к методу Монте-Карло. В этом методе отсутствует статистическая проверка значимости коэффициентов регрессии.
Из предложенных подходов построения регрессионной модели выделяют первый, основанный на оценке значимости коэффициентов регрессии по критерию Стьюдента.
Эта лекция взята со страницы предмета «Эконометрика»
Эти страницы возможно вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Отсеивание менее существенных факторов в процессе построения регрессионной модели;
1. отсеивание менее существенных факторов в процессе построения регрессионной модели;
2. замена исходного набора переменных меньшим числом эквивалентных факторов, полученных в результате преобразований исходного набора.
Процедура отсева несущественных факторов в процессе построения регрессионной модели и получила название многошагового регрессионного анализа.
Этот метод основан на вычислении нескольких промежуточных уравнений регрессии, в результате анализа которых получают конечную модель, включающую только факторы, оказывающие статистически существенное влияние на исследуемую зависимую переменную. Различные сочетания одних и тех же факторов оказывают разное влияние на зависимую переменную. Вследствие этого появляется необходимость выбора наилучшей модели, т.к. перебирать все возможные варианты сочетания факторов и строить множество уравнений регрессии (количество которых может быть очень велико) просто не имеет смысла.
Таким образом методы пошагового регрессионного анализа позволяют избежать столь громоздких расчетов и получить достаточно надежную и полную модель зависимости исследуемого признака от ряда объясняющих переменных.
Как было сказано выше, основой многошагового регрессионного анализа является построение уравнения регрессии. Рассмотрим более подробно его систему и основные понятия.
Многомерный регрессионный анализ
В общем виде многомерная линейная регрессионная модель зависимости y от объясняющих переменных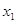 
, 
,…, 
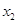
имеет вид:
.
Для оценки неизвестных параметров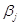 
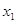
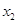
взята случайная выборка объема n из (k+1)–мерной случайной величины (y, ,,…,).
В матричной форме модель имеет вид:
,
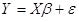
где 
, 
, 
, ε=
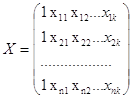
— вектор-столбец фактических значений зависимой переменной размерности n;
— матрица значений объясняющих переменных размерности n*(k+1);
— вектор-столбец неизвестных параметров, подлежащих оценке, размерности (k+1);
— вектор-столбец случайных ошибок размерности n с математическим ожиданием ME=0 и ковариационной матрицей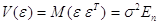 
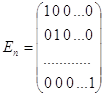
соответственно, при этом
-единичная матрица размерности (nxn).
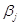
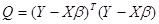
Оценки неизвестных параметров находятся методом наименьших квадратов, минимизируя скалярную сумму квадратов 
по компонентам вектора β.
Далее подставив выражение
в ,
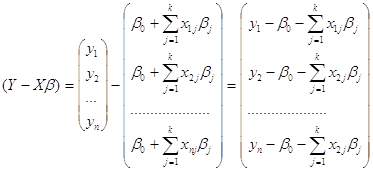
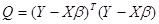
получаем скалярную сумму квадратов 
Условием обращения полученной суммы в минимум является система нормальных уравнений:
, (j=0,1,2,…,k) .
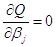
В результате дифференцирования получается:
.
При замене вектора неизвестных параметров β на оценки, полученные методом наименьших квадратов, получаем следующее выражение:
.
Далее умножив обе части уравнения слева на матрицу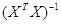 
, получим
Так как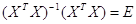 
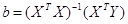
, тогда 
.
Полученные оценки вектора b являются не смещенными и эффективными.
Ковариационная матрица вектора b имеет вид:
, где 
— остаточная дисперсия.
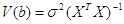
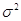
Элементы главной диагонали этой матрицы представляют собой дисперсии вектора оценок b. Остальные элементы являются значениями коэффициентов ковариации:
, где 
, 
.
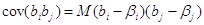
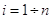
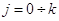
Таким образом, оценка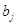 
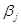
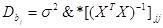
— это линейная функция от зависимой переменной. Она имеет нормальное распределение с математическим ожиданием 
и дисперсией 
.
Несмещенная оценка остаточной дисперсии определяется по формуле:
, где n – объем выборочной совокупности;
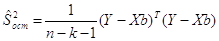
k – число объясняющих переменных.
Для проверки значимости уравнения регрессии используют F-критерий дисперсионного анализа, основанного на разложении общей суммы квадратов отклонений на составляющие части:
, где 
— сумма квадратов отклонений (от нуля), обусловленная регрессией;
— сумма квадратов отклонений фактических значений зависимой переменной от расчетных 
, т.е. сумма квадратов отклонений относительно плоскости регрессии, обусловленное воздействием случайных и неучтенных в модели факторов.
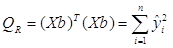
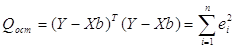
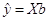
Для проверки гипотезы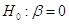 
используется величина 
, которая имеет F-распределение Фишера-Снедекора с числом степеней свободы 
и 
. Если 
, то уравнение регрессии значимо, т.е. в уравнении есть хотя бы один коэффициент регрессии, отличный от нуля.
В случае значимости уравнения регрессии проверяется значимость отдельных коэффициентов регрессии. Для проверки нулевой гипотезы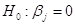 
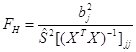
используется величина
, которая имеет F-распределение Фишера-Снедекора с числом степеней свободы 
и ; 
— соответствующий элемент главной диагонали ковариационной матрицы.
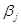
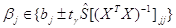
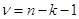
Коэффициент регрессии считается значимым, если . Для значимых коэффициентов регрессии можно построить доверительные интервалы, используя формулу
, где 
находится по таблице распределения Стьюдента для уровня значимости 
и числа степеней свободы 
.
В многошаговом регрессионном анализе наиболее известны три подхода:
1. Метод случайного поиска с адаптацией. Осуществляется путем построения нескольких уравнений регрессии на основе формально разработанного принципа включения факторов и последующего выбора лучшего уравнения с точки зрения определенного критерия.
2. Метод включения переменных, основанный на построении уравнения регрессии по одному значимому фактору и последовательном добавлении всех остальных статистически значимых переменных путем расчета частных коэффициентов корреляции и F-критерия при проверке значимости вводимого в модель фактора.
3. Метод отсева факторов по t-критерию. Данный метод заключается в построении уравнений регрессии по максимально возможному количеству объясняющих переменных и последующем исключении статистически не существенных факторов.
Метод отсева факторов по t-критерию
Наиболее оправданным является использование многошагового регрессионного анализа, основанного на оценке значимости коэффициентов регрессии с помощью t-критерия Стьюдента. Данный метод и был использован при анализе продолжительности жизни населения стран Африки в данной курсовой работе, потому что его применение четко формализовано, и в то же время на различных стадиях построения модели можно производить качественный экономический анализ. Рассмотрим его более подробно.
Итак, на первом этапе строится уравнение регрессии по переменным, предположительно влияющим на исследуемую зависимую переменную. Затем с помощью определенных критериев исключаются те переменные, которые оказывают статистически несущественное влияние. На этом подходе основан метод отсева факторов по t-критерию в многошаговом регрессионном анализе.
Применение t-критерия при отборе существенных факторов основано на следующей предпосылке регрессионного анализа: если выполняется условие, что Ei распределены нормально, то величина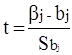 
распределена по закону Стьюдента с n = n-k-1 степенями свободы. По этому критерию можно проверить гипотезу о существенном отличии от нуля коэффициента регрессии bj при некотором заданном уровне значимости и n-k-1 степенях, то коэффициент регрессии bj признается значимым.
Простейшая схема проверки сводится к построению доверительного интервала для каждого коэффициента регрессии и проверке гипотезы о том, находится ли нуль внутри построенного интервала. Если это так, то данный коэффициент регрессии признается незначимым или же его значимость подвергается сомнению и выявляется на следующих этапах анализа.
Схема отбора значимых факторов в уравнение регрессии с помощью t-критерия выглядит следующим образом. Если все коэффициенты регрессии значимы, то уравнение регрессии признается окончательным и принимается в качестве модели исследуемого признака для последующего анализа. Если же среди коэффициентов регрессии имеются незначимые, то соответствующие объясняющие переменные следует исключить из уравнения.
Однако предварительно следует проранжировать коэффициенты регрессии по величине tH и в первую очередь отсеять тот фактор, для которого коэффициент регрессии незначим и tH имеет наименьшее значение. Затем уравнение регрессии пересчитывается снова (уже без исключенного фактора), и производится оценка коэффициентов регрессии по t-критерию. Такую процедуру повторяют до тех пор, пока все коэффициенты регрессии в уравнении не окажутся значимыми.
При этом на каждом шаге, кроме формальной статистической проверки значимости коэффициентов регрессии, проводится экономический анализ несущественных факторов и устанавливается порядок их исключения. В некоторых случаях значение tH находится вблизи tкр, и, с точки зрения содержательности модели, этот фактор можно оставить для последующей проверки его значимости в сочетании с другим набором факторов. Возможность такого экономического анализа при формальной статистической процедуре отсеивания незначимых факторов по t-критерию является большим преимуществом этого метода многошагового регрессионного анализа.
Вместе с тем следует отметить, что несущественность коэффициента регрессии по t-критерию не всегда является надежным основанием для исключения переменной из дальнейшего анализа. Поэтому в ряде случаев для проведения многошагового регрессионного анализа с помощью t-критерия предполагается использовать некоторые дополнительные эмпирические процедуры. Например, исключать переменную из уравнения регрессии лишь в том случае, когда средняя квадратическая ошибка коэффициента регрессии превышает абсолютный размер вычисленного коэффициента, то есть когда tH по абсолютной величине меньше единицы. При этом предполагается, что нет достаточных логических оснований для того, чтобы оставлять такую переменную в модели.
Практическая часть. Вариационные характеристики.
Для изучения корреляционного и регрессионного анализа в более подробном разрезе была взята совокупность стран Африки.
Задачей проводимого исследования является выявление и изучение зависимости данных экономических явлений.
При проведении данного исследования была взята совокупность, состоящая из 25 стран Африки:
Алжир, Ангола, Генин, Ботсвана, Бурунди, Буркина Фасо, Габон, Гамбия, Гана, Гвинея, Гвинея-Бисау, Джибути, Египет, Заир, Замбия, Зимбабве, Кабо-Верде, Кения, Коморские острова, Конго, Кот-д’Ивуар, Лесото, Либерия, Ливия.
Характеризующими являются следующие признаки: средняя продолжительность жизни (лет), численность населения (тыс. человек), доля городского населения (%), число медицинских работников на 10 тысяч населения (чел.), доля неграмотных (%), среднегодовой индекс роста производства продовольствия (%).
Но для упрощения проведения расчетов и всего исследования, а также выявления связи стоит разделить вышеописанные признаки на факторный и результативные и заменить их условными переменными (у, х1, х2, х3, х4, х5):
результативный признак (у) представляет собой среднюю продолжительность жизни (лет);
факторные признаки (х):
х1: численность населения (тыс. человек);
х2: доля городского населения (%);
х3: число медицинских работников на 10 тысяч населения (чел.);
х5: среднегодовой индекс роста производства продовольствия (%).
Начальные данные представлены в таблице:
│ N │ y │ x1 │ x2 │ x3 │ x4 │ x5 │
│ 1 │ 63.00 │ 23102.00 │ 60.85 │ 32.70 │ 55.30 │ 87.00 │
│ 2 │ 44.50 │ 9226.00 │ 21.00 │ 12.70 │ 97.00 │ 58.00 │
│ 3 │ 46.00 │ 4304.00 │ 30.80 │ 7.50 │ 75.20 │ 108.00 │
│ 4 │ 56.50 │ 1169.00 │ 29.50 │ 35.80 │ 59.30 │ 71.00 │
│ 5 │ 48.50 │ 5001.00 │ 2.29 │ 3.80 │ 77.40 │ 101.00 │
│ 6 │ 47.20 │ 8305.00 │ 8.48 │ 8.10 │ 91.20 │ 92.00 │
│ 7 │ 51.00 │ 1058.00 │ 35.80 │ 22.30 │ 87.60 │ 98.00 │
│ 8 │ 37.00 │ 670.00 │ 18.50 │ 15.10 │ 85.20 │ 62.00 │
│ 9 │ 54.00 │ 13704.00 │ 35.86 │ 37.60 │ 69.80 │ 73.00 │
│ 10 │ 42.20 │ 6380.00 │ 19.07 │ 4.20 │ 80.00 │ 91.00 │
│ 11 │ 45.00 │ 925.00 │ 23.80 │ 38.60 │ 71.60 │ 83.00 │
│ 12 │ 64.50 │ 372.00 │ 73.95 │ 72.20 │ 80.00 │ 75.00 │
│ 13 │ 60.60 │ 50740.00 │ 45.37 │ 47.90 │ 56.50 │ 89.00 │
│ 14 │ 52.00 │ 32461.00 │ 39.50 │ 12.60 │ 42.10 │ 86.00 │
│ 15 │ 53.30 │ 7563.00 │ 40.40 │ 18.50 │ 56.00 │ 91.00 │
│ 16 │ 57.80 │ 8640.00 │ 19.60 │ 16.60 │ 29.20 │ 94.00 │
│ 17 │ 53.00 │ 10822.00 │ 34.60 │ 14.40 │ 59.50 │ 102.00 │
│ 18 │ 61.50 │ 348.00 │ 5.80 │ 18.80 │ 63.10 │ 83.00 │
│ 19 │ 53.30 │ 22936.00 │ 14.17 │ 11.20 │ 50.40 │ 93.00 │
│ 20 │ 52.00 │ 472.00 │ 11.53 │ 15.30 │ 41.60 │ 91.00 │
│ 21 │ 48.50 │ 1837.00 │ 37.27 │ 31.70 │ 84.40 │ 83.00 │
│ 22 │ 52.30 │ 11142.00 │ 37.62 │ 13.50 │ 58.80 │ 102.00 │
│ 23 │ 50.60 │ 1619.00 │ 4.52 │ 0.50 │ 48.00 │ 78.00 │
│ 24 │ 51.00 │ 2349.00 │ 32.94 │ 11.30 │ 74.60 │ 91.00 │
│ 25 │ 60.80 │ 4083.00 │ 52.40 │ 64.80 │ 49.90 │ 151.00 │
Реализация алгоритма многомерного регрессионного анализа начинается с расчета важнейших статистических характеристик исходной информации и матрицы выборочных парных коэффициентов корреляции.
Рассмотрим более подробно вариационные характеристики переменной у:
. число наблюдений 25
. среднее значение 52.2440
. верхняя оценка среднего 54.5134
. нижняя оценка среднего 49.9746
. среднеквадратическое отклонение 6.6138
. дисперсия (несмещ. оценка) 45.5651
. среднекв. откл. (несмещ. оценка) 6.7502
. среднее линейное отклонение 5.0938
. 2-го поpядка 2773.1780
. 3-го поpядка 1.4943e+05
. 4-го поpядка 8.1668e+06
. 3-го поpядка -2.1613e+01
. 4-го поpядка 5.1166e+03
. несмещенная оценка -0.0796
. среднекв. отклонение 0.4637
. несмещенная оценка 0.2846
. среднекв. отклонение 0.9017
. по pазмаху 0.5264
. сpеднему линейному откл. 0.0975
. сpеднеквадp. откл. 0.1266
. минимальное значение 37.0000
. максимальное значение 64.5000
Средняя продолжительность жизни в странах Африки – 52,244 года. Она вычисляется по формуле средней арифметической невзвешенной:
где n – объем исследуемой совокупности.
Дисперсия в нашем случае равна 43,7425. Она представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формуле:
σ 2 = Σ (у I – у ) 2 / n
Среднее квадратическое отклонение представляет собой корень второй степени из дисперсии, и в нашем случае σ = 6,6138, то есть значение продолжительности жизни в среднем отклоняется на 6,6138 лет.
А среднее линейное отклонение вычисляется по формуле:
которое в нашем случае равно 5,0938 и представляет собой среднюю величину из отклонений вариантов признака от их средней.
Коэффициент вариации среднеквадратического отклонения в исследуемой нами совокупности равен Vσ = 0,1266 или 12,66%, который вычисляется по формуле:
Коэффициент вариации характеризует не только сравнительную оценку вариации, но и дает характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%, то есть наша совокупность является однородной.
Мода – значение признака, наиболее часто встречающегося в совокупности. Она рассчитывается по формуле:
То есть по Африке наиболее часто встречающееся значение продолжительности жизни равно 48,5 лет.
Медиана – значение признака, приходящегося на середину ранжированной (упорядоченной) совокупности.
Таким образом, в нашем случае в половине стран Африки население имеет среднюю продолжительность жизни менее 52 лет, а в другой половине – более 52 лет.
Начальным моментом порядка k случайной величины х называют математическое ожидание величины х к :
в частности ν1 = М (х), ν2 = М (х 2 ).
начальные моменты равны:
. 2-го поpядка 2773.1780
. 3-го поpядка 1.4943e+05
. 4-го поpядка 8.1668e+06
Центральным моментом порядка k случайной величины х называют математическое ожидание величины (х – (М (х)) к , в частности
μ1 = М[х – М (х)] = 0; μ2 = М[ ( х – М (х)) 2 ] = D (х).
В нашем случае центральные моменты равны:
. 3-го поpядка -2.1613e+01
. 4-го поpядка 5.1166e+03
Теперь рассмотрим нашу совокупность на предмет симметрии.
Симметричным называется распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой. В статистике для характеристики асимметрии используют показатели асимметрии и эксцесса.
Так как видно, что наша совокупность асимметричная, найдем степень асимметрии. Сперва используем коэффициент асимметрии:
что свидетельствует о наличии незначительной правосторонней асимметрии (Аs>0).
Теперь рассчитаем показатель эксцесса:
ЕК = μ4/ σ 4 – 3, где μ4 – центральный момент четвертого порядка.
ЕК = 0,9017, следовательно, распределение стран Африки по продолжительности жизни является островершинным (ЕК>0).
Кроме того, взглянув на нашу совокупность, можно увидеть, что максимальная продолжительность жизни жителей стран Африки равна уmax=64,5 лет, а минимальная у min=37 лет.
Размах данной совокупности равен уmax — у min = 27,5 лет.
Многошаговый регрессионный анализ.
Построим корреляционную модель из исследуемых шести переменных:y,, 
,
,
,
.
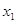
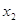
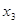
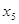
Присвоим для облегчения обозначений всем переменным порядковые номера: у-1, х1-2, х2-3, x3-4,x4-5,x5-6.
Предварительно, с целью анализа взаимосвязи показателей построена таблица парных коэффициентов корреляции R.
│ │ y │ x1 │ x2 │ x3 │ x4 │ x5 │
│ y │ 1.00 │ 0.30 │ 0.53 │ 0.60 │ -0.51 │ 0.26 │
│ x1 │ 0.30 │ 1.00 │ 0.27 │ 0.10 │ -0.33 │ 0.02 │
│ x2 │ 0.53 │ 0.27 │ 1.00 │ 0.74 │ -0.04 │ 0.17 │
│ x3 │ 0.60 │ 0.10 │ 0.74 │ 1.00 │ -0.03 │ 0.15 │
│ x4 │ -0.51 │ -0.33 │ -0.04 │ -0.03 │ 1.00 │ -0.31 │
│ x5 │ 0.26 │ 0.02 │ 0.17 │ 0.15 │ -0.31 │ 1.00 │
Анализ матрицы парных коэффициентов корреляции показывает, что результативный показатель наиболее тесно связан с показателем x3 – числом медицинских работников на 10 тысяч населения (ryx3=0.60).
Одним из основных препятствий эффективного применения регрессионного анализа, является мультиколлинеарность (наличие сильной корреляции между независимыми переменными, входящими в уравнение регрессии x1,x2,x3,x4,x5). Наиболее распространенный метод выявления коллинеарности основан на анализе парных коэффициентов корреляции. Он состоит в том, что две или несколько переменных признаются коллинеарными (мультиколлинеарными), если парные коэффициенты корреляции больше определенной величины. На практике наиболее часто считают, что два аргумента коллинеарны, если парный коэффициент корреляции между ними по абсолютной величине больше 0,8.
В данном примере ни один парный коэффициент корреляции не превышает величины 0,8, что говорит об отсутствии явления мультиколлинеарности.
Приступим непосредственно к регрессионному анализу.
Построим регрессионную модель по следующим факторам: х1, х2, х3, х4 и х5. Для расчета параметров уравнения регрессии используем стандартную программу многошагового регрессионного анализа с последовательным отсевом факторов.
На первом шаге построения модели в уравнение линейной регрессии вводятся все указанные выше переменные. В результате получена следующая модель:
Прежде чем осуществлять проверку значимости уравнения регрессии и коэффициентов регрессии, следует убедиться, что выполняется необходимое для этого условие, а именно следует проверить, является ли распределение остатков (т.е. отклонений эмпирических значений зависимой переменной от расчетных) нормальным. Для проверки данного условия используем критерий согласия Пирсона 
, рассчитанные значения которого приведены ниже:
Проверка нормального закона распределения
.число степеней свободы 3
.хи-квадpат pасчетное 1.571
веpоятн. хи-квадpат заключение
уpовень теоpетическое о гипотезе
0.900 6.226 не отвеpгается
0.950 7.795 не отвеpгается
0.990 11.387 не отвеpгается
Таким образом, можно сделать вывод, что гипотеза о нормальности распределения остатков не отвергается с доверительной вероятностью 0.95 (=7.795).
Проверка значимости уравнения регрессии показала, что оно значимо на уровне доверительной вероятности 0,95. (см. приложение 3.1)
Уровень множественного коэффициента детерминации (0,625) свидетельствует о том, что воздействием включенных в модель факторов обусловлено 62,5% вариации средней продолжительности жизни в странах Африки.
Далее осуществляется проверка значимости отдельных коэффициентов регрессии на основе t-критерия Стьюдента. Для определения 
, используем таблицу распределения Стьюдента: =2,093 (α=0,05 и ν=n-k-1=25-5-1=19).
По нижеприведенной таблице (гр.5 t-значения) статистически существенными оказались только два коэффициента регрессии при переменных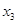 
и 
(|t|>).
Оценки коэффициентов линейной регрессии
│ N │ Значение │ Дисперсия │ Средне- │ t — │ Нижняя │ Верхняя │
│ │ │ │ квадатическое │ значение │ оценка │ оценка │
│ 
│ 57.70 │ 59.12 │ 7.69 │ 7.50 │ 44.37 │ 71.03 │
│ 
│ 0.00 │ 0.00 │ 0.00 │ 0.36 │ -0.00 │ 0.00 │
│ 
│ 0.06 │ 0.01 │ 0.08 │ 0.66 │ -0.09 │ 0.20 │
│ 
│ 0.17 │ 0.01 │ 0.08 │ 2.21 │ 0.04 │ 0.31 │
│ 
│ -0.18 │ 0.00 │ 0.06 │ -2.96 │ -0.29 │ -0.08 │
│ 
│ 0.01 │ 0.00 │ 0.06 │ 0.12 │ -0.09 │ 0.11 │
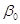
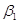
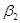
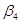
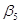
Среди незначимых коэффициентов регрессии наименее существенно по значению t-критерия является коэффициент регрессии при переменной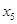 
(среднегодовой индекс роста производства продовольствия), t=0.12. Этот фактор и подлежит исключению из модели в первую очередь.
Исключив указанный фактор, на втором шаге получаем уравнение регрессии следующего вида:
Величина коэффициента детерминации на этом шаге не изменилась и составляет 0,625, гипотеза о значимости уравнения также не отвергается с вероятностью 0,95 (см. приложение 3.2).
Т.к. значение степеней свободы на каждом этапе построения модели изменяется (в связи с уменьшением числа объясняющих переменных), то также меняется. Тогда при α=0,05 и
ν=n-k-1=25-4-1=20, =2,086. Таким образом, значимыми являются коэффициенты регрессии при факторах и , а среди оставшихся незначимых наименьшее значение t-критерия, которое равно 0,35, принадлежит коэффициенту регрессии при переменной 
. Поэтому фактор (численность населения) из дальнейшего процесса исключается.
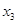
На третьем шаге уравнение регрессии имеет следующий вид:
Воздействием включенных в модель переменных объясняется 62,2% вариации средней продолжительности жизни. Проверка на значимость уравнения регрессии показала, что оно значимо (на уровне значимости α=0,05). На этом шаге =2,080 (α=0,05 и ν=n-k-1=25-3-1=21), таким образом, статистически существенными оказались все коэффициенты регрессии, кроме коэффициента при объясняющей переменной , который и подлежит исключению по t-критерию из уравнения регрессии (t=0,87).
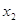
На последнем шаге регрессионного анализа получено значимое уравнение следующего вида:
Все коэффициенты регрессии значимы (см. приложение).
В результате моделирования зависимости средней продолжительности жизни в странах Африки можно сделать следующие выводы.
Уровень множественного коэффициента детерминации 0,609 свидетельствует о том, что 60,9% вариации зависимой переменной объясняется вариацией двух факторов:
x3 — число медицинских работников на 10 тыс. населения,
x4 — доля неграмотных.
Указанный уровень влияния достаточно высок, поэтому можно сделать вывод, что все факторы, оказывающие существенной влияние на среднюю продолжительность жизни, включены в модель, поскольку уровень остаточной вариации составляет 39.1%, объясняется воздействием случайных и неучтенных в модели факторов.
В рассматриваемом уравнении регрессии с изменением каждого фактора на одну единицу собственного измерения (при постоянном значении остальных факторов, вошедших в модель) зависимая переменная изменяется на соответствующий коэффициент регрессии βj отражает среднее приращение функции за счет единичного приращения j-го аргумента, независимое от изменения остальных учтенных в модели аргументов. Интерпретируемый таким образом коэффициент регрессии используется в экономико-статистическом анализе как средняя оценка эффективности влияния j-го аргумента на функцию.
Значение коэффициента регрессии βj зависит от принятых единиц измерения величин у и хj. Если единица измерения хj велика, то увеличение хj на единицу соответствует меньшее изменение среднего значения у, то есть βj мало. Если единица измерения у велика, то соответствующее изменение у выражается большим количеством единиц хj, следовательно, βj велико.
Анализируя полученную модель, можно сказать, что при увеличении числа медицинских работников на 1 человека средняя продолжительность жизни жителей стран Африки повышается в среднем на 0.215 лет; при увеличении доли неграмотных на 1% средняя продолжительность жизни уменьшится на 0.192 лет (обратная зависимость).
Однако с помощью коэффициентов регрессии нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени колеблемости. Поэтому для устранения таких различий при интерпретации применяется целая система показателей: средние частные коэффициенты эластичности, бета-коэффициенты или коэффициенты регрессии в стандартизированном масштабе и дельта-коэффициенты.
Средний частный коэффициенты эластичности рассчитывается по формуле:
В рассматриваемой модели при изменении на 1% числа медицинских работников на 10 тысяч населения и доли неграмотных среди жителей исследуемых стран Африки средняя продолжительность жизни изменяется следующим образом: увеличивается на 0.094% и уменьшается на 0.241% соответственно (частные коэффициенты эластичности). — см. приложение.
Однако средний частный коэффициент эластичности не учитывает степени колеблемости факторов, которая может значительно различаться у отдельных факторов. Поэтому для устранения различий в измерении и степени колеблемости факторов используется другой показатель — коэффициент регрессии в стандартизированном масштабе (бета-коэффициент). Он показывает, на какую часть величины среднего квадратического отклонения изменяется среднее значение зависимой переменной с изменением соответствующей независимой переменной на одно среднее квадратическое отклонение при фиксированном на постоянном уровне значении остальных независимых переменных.
Бета-коэффициенты, рассчитанные для нашей модели, показывают, что при увеличении на одно среднее квадратическое отклонение числа медработников на 10 тысяч населения и доли неграмотных, средняя продолжительность жизни в среднем увеличивается на 0.587 и уменьшается на 0.495 средних квадратических отклонений соответственно. — см. приложение.
С помощью частных коэффициентов эластичности и с помощью бета-коэффициентов можно проранжировать факторы по степени их влияния на зависимую переменную, то есть сопоставить их между собой по величине этого влияния. Но с помощью бета-коэффициентов нельзя непосредственно оценить долю влияния каждого фактора в суммарном влиянии всех факторов. Для этой цели используются дельта-кэффициенты.
В практических задачах при корректно проведенном анализе величины дельта-коэффициентов положительны, то есть все коэффициенты регрессии имеют тот же знак, что и соответствующие парные коэффициенты корреляции. В этих случаях сумма величин вкладов независимых переменных равна коэффициенту множественной детерминации. Вместе с тем, в некоторых исследованиях отдельные коэффициенты регрессии имеют знак, противоположный знаку соответствующего коэффициента парной корреляции, вследствие чего величина дельта-коэффициента будет отрицательной. Не менее важно, что случаи с отрицательными вкладами могут иметь место только при значительной коррелированности объясняющих переменных.
В нашей модели наибольшее влияние на среднюю продолжительность жизни оказывает число медработников на 10 тысяч населения — 58.2%, а доля неграмотных оказывает влияние в размере 41.8%.
В настоящей курсовой работе был рассмотрен один из наиболее популярных в настоящее время методов математико-статистического моделирования экономических процессов, который позволяет строить достаточно адекватные и легко экономически интерпретируемые модели. Но легко заметить, что все вышеприведенные вычисление очень трудоемки и занимают немало времени. Поэтому, кроме вычислений вручную, а также для упрощения исследования, была проведена работа в пакете прикладных программ «ОЛИМП» — совокупность программных средств, ориентированных на решение задач экономического анализа и прогнозирования с помощью различных методов математической статистики. Полученные результаты приведены в Приложении.
Просмотр начальных данных
│ N │ y │ x1 │ x2 │ x3 │ x4 │ x5 │
│ 1 │ 63.00 │ 23102.00 │ 60.85 │ 32.70 │ 55.30 │ 87.00 │
│ 2 │ 44.50 │ 9226.00 │ 21.00 │ 12.70 │ 97.00 │ 58.00 │
│ 3 │ 46.00 │ 4304.00 │ 30.80 │ 7.50 │ 75.20 │ 108.00 │
│ 4 │ 56.50 │ 1169.00 │ 29.50 │ 35.80 │ 59.30 │ 71.00 │
│ 5 │ 48.50 │ 5001.00 │ 2.29 │ 3.80 │ 77.40 │ 101.00 │
│ 6 │ 47.20 │ 8305.00 │ 8.48 │ 8.10 │ 91.20 │ 92.00 │
│ 7 │ 51.00 │ 1058.00 │ 35.80 │ 22.30 │ 87.60 │ 98.00 │
│ 8 │ 37.00 │ 670.00 │ 18.50 │ 15.10 │ 85.20 │ 62.00 │
│ 9 │ 54.00 │ 13704.00 │ 35.86 │ 37.60 │ 69.80 │ 73.00 │
│ 10 │ 42.20 │ 6380.00 │ 19.07 │ 4.20 │ 80.00 │ 91.00 │
│ 11 │ 45.00 │ 925.00 │ 23.80 │ 38.60 │ 71.60 │ 83.00 │
│ 12 │ 64.50 │ 372.00 │ 73.95 │ 72.20 │ 80.00 │ 75.00 │
│ 13 │ 60.60 │ 50740.00 │ 45.37 │ 47.90 │ 56.50 │ 89.00 │
│ 14 │ 52.00 │ 32461.00 │ 39.50 │ 12.60 │ 42.10 │ 86.00 │
│ 15 │ 53.30 │ 7563.00 │ 40.40 │ 18.50 │ 56.00 │ 91.00 │
│ 16 │ 57.80 │ 8640.00 │ 19.60 │ 16.60 │ 29.20 │ 94.00 │
│ 17 │ 53.00 │ 10822.00 │ 34.60 │ 14.40 │ 59.50 │ 102.00 │
│ 18 │ 61.50 │ 348.00 │ 5.80 │ 18.80 │ 63.10 │ 83.00 │
│ 19 │ 53.30 │ 22936.00 │ 14.17 │ 11.20 │ 50.40 │ 93.00 │
│ 20 │ 52.00 │ 472.00 │ 11.53 │ 15.30 │ 41.60 │ 91.00 │
│ 21 │ 48.50 │ 1837.00 │ 37.27 │ 31.70 │ 84.40 │ 83.00 │
│ 22 │ 52.30 │ 11142.00 │ 37.62 │ 13.50 │ 58.80 │ 102.00 │
│ 23 │ 50.60 │ 1619.00 │ 4.52 │ 0.50 │ 48.00 │ 78.00 │
│ 24 │ 51.00 │ 2349.00 │ 32.94 │ 11.30 │ 74.60 │ 91.00 │
│ 25 │ 60.80 │ 4083.00 │ 52.40 │ 64.80 │ 49.90 │ 151.00 │
*** Вариационные характеристики переменной y ***
. число наблюдений 25
. среднее значение 52.2440
. верхняя оценка среднего 54.5134
. нижняя оценка среднего 49.9746
. среднеквадратическое отклонение 6.6138
. дисперсия (несмещ. оценка) 45.5651
. среднекв. откл. (несмещ. оценка) 6.7502
. среднее линейное отклонение 5.0938
. 2-го поpядка 2773.1780
. 3-го поpядка 1.4943e+05
. 4-го поpядка 8.1668e+06
. 3-го поpядка -2.1613e+01
. 4-го поpядка 5.1166e+03
. несмещенная оценка -0.0796
. среднекв. отклонение 0.4637
. несмещенная оценка 0.2846
. среднекв. отклонение 0.9017
. по pазмаху 0.5264
. сpеднему линейному откл. 0.0975
. сpеднеквадp. откл. 0.1266
. минимальное значение 37.0000
. максимальное значение 64.5000
**** Характеристики интеpвального pяда *****
. среднее значение 52.4000
. среднеквадратическое отклонение 6.5949
. коэффициент асимметpии -0.0815
. коэффициент эксцесса -0.2092
N инт. Начало Сеpедина Конец Частота Частость
1 34.7083 37.0000 39.2917 1.0 0.0400
2 39.2917 41.5833 43.8750 1.0 0.0400
3 43.8750 46.1667 48.4583 4.0 0.1600
4 48.4583 50.7500 53.0417 9.0 0.3600
5 53.0417 55.3333 57.6250 4.0 0.1600
6 57.6250 59.9167 62.2083 4.0 0.1600
7 62.2083 64.5000 66.7917 2.0 0.0800
Пpовеpка ноpмального закона pаспpеделения
.число степеней свободы 3
.хи-квадpат pасчетное 1.571
веpоятн. хи-квадpат заключение
уpовень теоpетическое о гипотезе
0.900 6.226 не отвеpгается
0.950 7.795 не отвеpгается
0.990 11.387 не отвеpгается
222222222222222 ОТЧЕТ 2222222222222222222222222222222222
0,990 11,387 не отвергается
не отвергается с вероятностью 0,950
│ N │ 1 │ 2 │ 3 │ 4 │ 5 │ 6 │
│ y │ 1.00 │ 0.30 │ 0.53 │ 0.60 │ -0.51 │ 0.26 │
│ x1 │ 0.30 │ 1.00 │ 0.27 │ 0.10 │ -0.33 │ 0.02 │
│ x2 │ 0.53 │ 0.27 │ 1.00 │ 0.74 │ -0.04 │ 0.17 │
│ x3 │ 0.60 │ 0.10 │ 0.74 │ 1.00 │ -0.03 │ 0.15 │
│ x4 │ -0.51 │ -0.33 │ -0.04 │ -0.03 │ 1.00 │ -0.31 │
│ x5 │ 0.26 │ 0.02 │ 0.17 │ 0.15 │ -0.31 │ 1.00 │
Какой фактор является незначимым в уравнении регрессии
Регрессионный анализ позволяет приближенно определить форму связи между результативным и факторными признаками, а также решить вопрос о том, значима ли эта связь. Вид функции, с помощью которой приближенно выражается форма связи, выбирают заранее, исходя из содержательных соображений или визуального анализа данных. Математическое решение задачи основано на методе наименьших квадратов.
Суть метода наименьших квадратов. Рассмотрим содержание метода на конкретном примере. Пусть имеются данные о сборе хлеба на душу населения по совокупности черноземных губерний. От каких факторов зависит величина этого сбора? Вероятно, определяющее влияние на величину сбора хлеба оказывает величина посева и уровень урожайности. Рассмотрим сначала зависимость величины сбора хлеба на душу населения от размера посева на душу ( столбцы 1 и 2 табл .4 ) Попытаемся представить интересующую нас зависимость с помощью прямой линии. Разумеется, такая линия может дать только приближенное представление о форме реальной статистической связи. Постараемся сделать это приближение наилучшим. Оно будет тем лучше, чем меньше исходные данные будут отличаться от соответствующих точек, лежащих на линии. Степень близости может быть выражена величиной суммы квадратов отклонении, реальных значений от, расположенных на прямой. Использование именно квадратов отклонений (не просто отклонений) позволяет суммировать отклонения различных знаков без их взаимного погашения и дополнительно обеспечивает сравнительно большее внимание, уделяемое большим отклонениям. Именно этот критерий (минимизация суммы квадратов отклонений) положен в основу метода наименьших квадратов.
В вычислительном аспекте метод наименьших квадратов сводится к составлению и решению системы так называемых нормальных уравнений. Исходным этапом для этого является подбор вида функции, отображающей статистическую связь.
Тип функции в каждом конкретном случае можно подобрать путем прикидки на графике исходных данных подходящей, т. е. достаточно хорошо приближающей эти данные, линии. В нашем случае связь между сбором хлеба на душу и величиной посева на душу может быть изображена с помощью прямой линии ( рис. 14 ) и записана в виде
где у—величина сбора хлеба на душу (результативный признак или зависимая переменная); x—величина посева на душу (факторный признак или независимая переменная); a o и a 1 — параметры уравнения, которые могут быть найдены методом наименьших квадратов.
Для нахождения искомых параметров нужно составить систему уравнений, которая в данном случае будет иметь вид
Полученная система может быть решена известным из школьного курса методом Гаусса. Искомые параметры системы из двух нормальных уравнений можно вычислить и непосредственно с помощью последовательного использования нижеприведенных формул:
где y i — i-e значение результативного признака; x i — i-e значение факторного признака; и — средние арифметические результативного и факторного признаков соответственно; n— число значений признака y i , или, что то же самое, число значений признака x i .
Пример 9. Найдем уравнение линейной связи между величиной сбора хлеба (у) и размером посева (х) по данным табл. 4. Проделав необходимые вычисления, получим из (6.17):
Таким образом, уравнение связи, или, как принято говорить, уравнение регрессии, выглядит следующим образом:
Интерпретация коэффициента регрессии. Уравнение регрессии не только определяет форму анализируемой связи, но и показывает, в какой степени изменение одного признака сопровождается изменением другого признака.
Коэффициент при х, называемый коэффициентом регрессии, показывает, на какую величину в среднем изменяется результативный признак у при изменении факторного признака х на единицу.
В примере 9 коэффициент регрессии получился равным 24,58. Следовательно, с увеличением посева, приходящегося на душу, на одну десятину сбор хлеба на душу населения в среднем увеличивается на 24,58 пуда.
Средняя и предельная ошибки коэффициента регрессии. Поскольку уравнения регрессии рассчитываются, как правило, для выборочных данных, обязательно встают вопросы точности и надежности полученных результатов. Вычисленный коэффициент регрессии, будучи выборочным, с некоторой точностью оценивает соответствующий коэффициент регрессии генеральной совокупности. Представление об этой точности дает средняя ошибка коэффициента регрессии ( ), рассчитываемая по формуле
у i , — i-e значение результативного признака; ŷ i — i-e выравненное значение, полученное из уравнения (6.15); x i —i-e значение факторного признака; σ x —среднее квадратическое отклонение х; n — число значений х или, что то же самое, значений у; m—число факгорных признаков (независимых переменных).
В формуле (6.18), в частности, формализовано очевидное положение: чем больше фактические значения отклоняются от выравненных, тем большую ошибку следует ожидать; чем меньше число наблюдений, на основе которых строится уравнение, тем больше будет ошибка.
Средняя ошибка коэффициента регрессии является основой для расчета предельной ошибки. Последняя показывает, в каких пределах находится истинное значение коэффициента регрессии при заданной надежности результатов. Предельная ошибка коэффициента регрессии вычисляется аналогично предельной ошибке средней арифметической (см. гл. 5), т. е. как t где t—величина, числовое значение которой определяется в зависимости от принятого уровня надежности.
Пример 10. Найти среднюю и предельную ошибки коэффициента регрессии, полученного в примере 9.
Для расчета прежде всего подсчитаем выравненные значения ŷ i для чего в уравнение регрессии, полученное в примере 9, подставим конкретные значения x i :
ŷ i = 17,6681 +24,5762*0,91 = 40,04 и т. д.
Затем вычислим отклонения фактических значений у i , от выравненных и их квадраты
Далее, подсчитав средний по черноземным губерниям посев на душу ( =0,98), отклонения фактических значений x i от этой средней, квадраты отклонений и среднее квадратическое отклонение , получим все необходимые составляющие формул (618) и (619):
Таким образом, средняя ошибка коэффициента регрессии равна 2,89, что составляет 12% от вычисленного коэффициента
Задавшись уровнем надежности, равным 0,95, найдем по табл. 1 приложения соответствующее ему значение t=1,96, рассчитаем предельную ошибку 1,96*2,89=5,66 и пределы коэффициента регрессии для принятого уровня надежности ( В случае малых выборок величина t находится из табл. 2 приложения. ). Нижняя граница коэффициента регрессии равна 24,58-5,66=18,92, а верхняя граница 24,58+5,66=30,24
Средняя квадратическая ошибка линии регрессии. Уравнение регрессии представляет собой функциональную связь, при которой по любому значению х можно однозначно определить значение у. Функциональная связь лишь приближенно отражает связь реальную, причем степень этого приближения может быть различной и зависит она как от свойств исходных данных, так и от выбора вида функции, по которой производится выравнивание.
На рис. 15 представлены два различных случая взаимоотношения между двумя признаками. В обоих случаях предполагаемая связь описывается одним и тем же уравнением, но во втором случае соотношение между признаками х и у достаточно четко выражено и уравнение, по-видимому, довольно хорошо описывает это соотношение, тогда как в первом случае сомнительно само наличие сколько-нибудь закономерного соотношения между признаками. И в том, и в другом случаях, несмотря на их существенное различие, метод наименьших квадратов дает одинаковое уравнение, поскольку этот метод нечувствителен к потенциальным возможностям исходного материала вписаться в ту или иную схему. Кроме того, метод наименьших квадратов применяется для расчета неизвестных параметров заранее выбранного вида функции, и вопрос о выборе наиболее подходящего для конкретных данных вида функции в рамках этого метода не ставится и не решается. Таким образом, при пользовании методом наименьших квадратов открытыми остаются два важных вопроса, а именно: существует ли связь и верен ли выбор вида функции, с помощью которой делается попытка описать форму связи.
Чтобы оценить, насколько точно уравнение регрессии описывает реальные соотношения между переменными, нужно ввести меру рассеяния фактических значений относительно вычисленных с помощью уравнения. Такой мерой служит средняя квадратическая ошибка регрессионного уравнения, вычисляемая по приведенной выше формуле (6.19).
Пример 11. Определить среднюю квадратическую ошибку уравнения, полученного в примере 9.
Промежуточные расчеты примера 10 дают нам среднюю квадратическую ошибку уравнения. Она равна 4,6 пуда.
Этот показатель аналогичен среднему квадратическому отклонению для средней. Подобно тому, как по величине среднего квадратического отклонения можно судить о представительности средней арифметической (см. гл. 5), по величине средней квадратической ошибки регрессионного уравнения можно сделать вывод о том, насколько показательна для соотношения между признаками та связь, которая выявлена уравнением. В каждом конкретном случае фактическая ошибка может оказаться либо больше, либо меньше средней. Средняя квадратическая ошибка уравнения показывает, насколько в среднем мы ошибемся, если будем пользоваться уравнением, и тем самым дает представление о точности уравнения. Чем меньше σ y.x , тем точнее предсказание линии регрессии, тем лучше уравнение регрессии описывает существующую связь. Показатель σ y.x позволяет различать случаи, представленные на рис. 15. В случае б) он окажется значительно меньше, чем в случае а). Величина σ y.x зависит как от выбора функции, так и от степени описываемой связи.
Варьируя виды функций для выравнивания и оценивая результаты с помощью средней квадратической ошибки, можно среди рассматриваемых выбрать лучшую функцию, функцию с наименьшей средней ошибкой. Но существует ли связь? Значимо ли уравнение регрессии, используемое для отображения предполагаемой связи? На эти вопросы отвечает определяемый ниже критерий значи-мости регрессии.
Мерой значимости линии регрессии может служить следующее соотношение:
где ŷ i —i-e выравненное значение; —средняя арифметическая значений y i ; σ y.x —средняя квадратическая ошибка регрессионного уравнения, вычисляемая по формуле (6.19); n—число сравниваемых пар значений признаков; m—число факторных признаков.
Действительно, связь тем больше, чем значительнее мера рассеяния признака, обусловленная регрессией, превосходит меру рассеяния отклонений фактических значений от выравненных.
Соотношение (6.20) позволяет решить вопрос о значимости регрессии. Регрессия значима, т. е. между признаками существует линейная связь, если для данного уровня значимости вычисленное значение F ф [m,n-(m+1)] превышает критическое значение F кр [m,n-(m+1)], стоящее на пересечении m-го столбца и [n—(m+1)]-й строки специальной таблицы ( см. табл. 4 приложения ).
Пример 12. Выясним, связаны ли сбор хлеба на душу населения и посев на душу населения линейной зависимостью.
Воспользуемся F-критерием значимости регрессии. Подставив в формулу (6.20) данные табл. 4 и результат примера 10, получим
Обращаясь к таблице F-распределения для Р=0,95 (α=1—Р=0,5) и учитывая, что n=23, m =1, в табл. 4А приложения на пересечения 1-го столбца и 21-й строки находим критическое значение F кр , равное 4,32 при степени надежности Р=0,95. Поскольку вычисленное значение F ф существенно превосходит по величине F кр , то обнаруженная линейная связь существенна, т. е. априорная гипотеза о наличии линейной связи подтвердилась. Вывод сделан при степени надежности P=0,95. Между прочим, вывод в данном случае останется прежним, если надежность повысить до Р=0,99 (соответствующее значение F кр =8,02 по табл. 4Б приложения для уровня значимости α=0,01).
Коэффициент детерминации. С помощью F-критерия мы Установили, что существует линейная зависимость между величиной сбора хлеба и величиной посева на душу. Следовательно, можно утверждать, что величина сбора хлеба, приходящегося на душу, линейно зависит от величины посева на душу. Теперь уместно поставить уточняющий вопрос — в какой степени величина посева на душу определяет величину сбора хлеба на душу? На этот вопрос можно ответить, рассчитав, какая часть вариации результативного признака может быть объяснена влиянием факторного признака.
Оно показывает долю разброса, учитываемого регрессией, в общем разбросе результативного признака и носит название коэффициента детерминации. Этот показатель, равный отношению факторной вариации к полной вариации признака, позволяет судить о том, насколько «удачно» выбран вид функции ( Отметим, что по смыслу коэффициент детерминации в регрессионном анализе соответствует квадрату корреляционного отношения для корреляционной таблицы (см. § 2). ). Проведя расчеты, основанные на одних и тех же исходных данных, для нескольких типов функций, мы можем из них выбрать такую, которая дает наибольшее значение R 2 и, следовательно, в большей степени, чем другие функции, объясняет вариацию результативного признака. Действительно, при расчете R 2 для одних и тех же данных, но разных функций знаменатель выражения (6.21) остается неизменным, а числитель показывает ту часть вариации результативного признака, которая учитывается выбранной функцией. Чем больше R 2 , т. е. чем больше числитель, тем больше изменение факторного признака объясняет изменение результативного признака и тем, следовательно, лучше уравнение регрессии, лучше выбор функции.
Наконец, отметим, что введенный ранее, при изложении методов корреляционного анализа, коэффициент детерминации совпадает с определенным здесь показателем, если выравнивание производится По прямой линии. Но последний показатель (R 2 ) имеет более широкий спектр применения и может использоваться в случае связи, отличной от линейной ( см. § 4 данной главы ).
Пример 13. Рассчитать коэффициент детерминации для уравнения, полученного в примере 9.
Вычислим R 2 , воспользовавшись формулой (6.21) и данными табл. 4:
Итак, уравнение регрессии почти на 78% объясняет колебания сбора хлеба на душу. Это немало, но, По-видимому, можно улучшить модель введением в нее еще одного фактора.
Случай двух независимых переменных. Простейший случай множественной регрессии. В предыдущем изложении регрессионного анализа мы имели дело с двумя признаками — результативным и факторным. Но на результат действует обычно не один фактор, а несколько, что необходимо учитывать для достаточно полного анализа связей.
В математической статистике разработаны методы множественной регрессии ( Регрессия называется множественной, если число независимых переменных, учтенных в ней, больше или равно двум. ), позволяющие анализировать влияние на результативный признак нескольких факторных. К рассмотрению этих методов мы и переходим.
Возвратимся к примеру 9. В нем была определена форма связи между величиной сбора хлеба на душу и размером посева на душу. Введем в анализ еще один фактор — уровень урожайности (см. столбец З табл. 4). Без сомнения, эта переменная влияет на сбор хлеба на душу. Но в какой степени влияет? Насколько обе независимые переменные определяют сбор хлеба на душу в черноземных губерниях? Какая из переменных — посев на душу или урожайность — оказывает определяющее влияние на сбор хлеба? Попытаемся ответить на эти вопросы.
После добавления второй независимой переменной уравнение регрессии будет выглядеть так:
где у—сбор хлеба на душу; х 1 —размер посева на душу; x 2 —урожай с десятины (в пудах); а 0 , а 1 , а 2 —параметры, подлежащие определению.
Для нахождения числовых значений искомых параметров, как и в случае одной независимой переменной, пользуются методом наименьших квадратов. Он сводится к составлению и решению системы нормальных уравнений, которая имеет вид
Когда система состоит из трех и более нормальных уравнений, решение ее усложняется. Существуют стандартные программы расчета неизвестных параметров регрессионного уравнения на ЭВМ. При ручном счете можно воспользоваться известным из школьного курса методом Гаусса.
Пример 14. По данным табл. 4 описанным способом найдем параметры a 0 , а 1 , а 2 уравнения (6.22). Получены следующие результаты: a 2 =0,3288, a 1 =28,7536, a 0 =-0,2495.
Таким образом, уравнение множественной регрессии между величиной сбора хлеба на душу населения (у), размером посева на душу (x 1 ) и уровнем урожайности (х 2 ) имеет вид:
у=-0,2495+28,7536x 1 +0,3288x 2 .
Интерпретация коэффициентов уравнения множественной регрессии. Коэффициент при х 1 в полученном уравнении отличается от аналогичного коэффициента в уравнении примера 9.
Коэффициент при независимой переменной в уравнении простой регрессии отличается от коэффициента при соответствующей переменной в уравнении множественной регрессии тем, что в последнем элиминировано влияние всех учтенных в данном уравнении признаков.
Коэффициенты уравнения множественной регрессии поэтому называются частными или чистыми коэффициентами регрессии.
Частный коэффициент множественной регрессии при х 1 показывает, что с увеличением посева на душу на 1 дес. и при фиксированной урожайности сбор хлеба на душу населения вырастает в среднем на 28,8 пуда. Частный коэффициент при x 2 показывает, что при фиксированном посеве на душу увеличение урожая на единицу, т. е. на 1 пуд с десятины, вызывает в среднем увеличение сбора хлеба на душу на 0,33 пуда. Отсюда можно сделать вывод, что увеличение сбора хлеба в черноземных губерниях России идет, в основном, за счет расширения посева и в значительно меньшей степени—за счет повышения урожайности, т. е. экстенсивная форма развития зернового хозяйства является господствующей.
Введение переменной х 2 в уравнение позволяет уточнить коэффициент при х 1 . Конкретно, коэффициент оказался выше (28,8 против 24,6), когда в изучаемой связи вычленилось влияние урожайности на сбор хлеба.
Однако выводы, полученные в результате анализа коэффициентов регрессии, не являются пока корректными, поскольку, во-первых, не учтена разная масштабность факторов, во-вторых, не выяснен вопрос о значимости коэффициента a 2 .
Величина коэффициентов регрессии изменяется в зависимости от единиц измерения, в которых представлены переменные. Если переменные выражены в разном масштабе измерения, то соответствующие им коэффициенты становятся несравнимыми. Для достижения сопоставимости коэффициенты регрессии исходного уравнения стандартизуют, взяв вместо исходных переменных их отношения к собственным средним квадратическим отклонениям. Тогда уравнение (6.22) приобретает вид
Сравнивая полученное уравнение с уравнением (6.22), определяем стандартизованные частные коэффициенты уравнения, так называемые бета-коэффициенты, по формулам:
где β 1 и β 2 —бета-коэффициенты; а 1 и а 2 —коэффициенты регрессии исходного уравнения; σ у , , и — средние квадратические отклонения переменных у, х 1 и х 2 соответственно.
Вычислив бета-коэффициенты для уравнения, полученного в примере 14:
видим, что вывод о преобладании в черноземной полосе россии экстенсивной формы развития хозяйства над интенсивной остается в силе, так как β 1 значительно больше, чем β 2 .
Оценка точности уравнения множественной регрессии.
Точность уравнения множественной регрессии, как и в случае уравнения с одной независимой переменной, оценивается средней квадратической ошибкой уравнения. Обозначим ее , где подстрочные индексы указывают, что результативным признаком в уравнении является у, а факторными признаками х 1 и x 2 . Для расчета средней квадратической ошибки уравнения множественной регрессии применяется приведенная выше формула (6.19).
Пример 15. Оценим точность полученного в примере 14 уравнения регрессии.
Воспользовавшись формулой (6.19) и данными табл. 4, вычислим среднюю квадратическую ошибку уравнения:
Оценка полезности введения дополнительной переменной. Точность уравнения регрессии тесно связана с вопросом ценности включения дополнительных членов в это уравнение.
Сравним средние квадратические ошибки, рассчитанные для уравнения с одной переменной х 1 (пример 11) и для уравнения с двумя независимыми переменными х 1 и х 2 . Включение в уравнение новой переменной (урожайности) уменьшило среднюю квадратическую ошибку почти вдвое.
Можно провести сравнение ошибок с помощью коэффициентов вариации
где σ f —средняя квадратическая ошибка регрессионного уравнения; —средняя арифметическая результативного признака.
Для уравнения, содержащего одну независимую переменную:
Для уравнения, содержащего две независимые переменные:
Итак, введение независимой переменной «урожайность» уменьшило среднюю квадратическую ошибку до величины порядка 7,95% среднего значения зависимой переменной.
Наконец, по формуле (6.21) рассчитаем коэффициент детерминации
Он показывает, что уравнение регрессии на 81,9% объясняет колебания сбора хлеба на душу населения. Сравнивая полученный результат (81,9%) с величиной R 2 для однофакторного уравнения (77,9%), видим, что включение переменной «урожайность» заметно увеличило точность уравнения.
Таким образом, сравнение средних квадратических ошибок уравнения, коэффициентов вариации, коэффициентов детерминации, рассчитанных до и после введения независимой переменной, позволяет судить о полезности включения этой переменной в уравнение. Однако следует быть осторожными в выводах при подобных сравнениях, поскольку увеличение R 2 или уменьшение σ и V σ не всегда имеют приписываемый им здесь смысл. Так, увеличение R 2 может объясняться тем фактом, что число рассматриваемых параметров в уравнении приближается к числу объектов наблюдения. Скажем, весьма сомнительными будут ссылки на увеличение R 2 или уменьшение σ, если в уравнение вводится третья или четвертая независимая переменная и уравнение строится на данных по шести, семи объектам.
Полезность включения дополнительного фактора можно оценить с помощью F-критерия.
Частный F-критерий показывает степень влияния дополнительной независимой переменной на результативный признак и может использоваться при решении вопроса о добавлении в уравнение или исключении из него этой независимой переменной.
Разброс признака, объясняемый уравнением регрессии (6.22), можно разложить на два вида: 1) разброс признака, обусловленный независимой переменной х 1 , и 2) разброс признака, обусловленный независимой переменной x 2 , когда х 1 уже включена в уравнение. Первой составляющей соответствует разброс признака, объясняемый уравнением (6.15), включающим только переменную х 1 . Разность между разбросом признака, обусловленным уравнением (6.22), и разбросом признака, обусловленным уравнением (6.15), определит ту часть разброса, которая объясняется дополнительной независимой переменной x 2 . Отношение указанной разности к разбросу признака, регрессией не объясняемому, представляет собой значение частного критерия. Частный F-критерий называется также последовательным, если статистические характеристики строятся при последовательном добавлении переменных в регрессионное уравнение.
Пример 16. Оценить полезность включения в уравнение регрессии дополнительной переменной «урожайность» (по данным и результатам примеров 12 и 15).
Разброс признака, объясняемый уравнением множественной регрессии и рассчитываемый как сумма квадратов разностей выравненных значений и их средней, равен 1623,8815. Разброс признака, объясняемый уравнением простой регрессии, составляет 1545,1331.
Разброс признака, регрессией не объясняемый, определяется квадратом средней квадратической ошибки уравнения и равен 10,9948 (см. пример 15).
Воспользовавшись этими характеристиками, рассчитаем частный F-критерий
С уровнем надежности 0,95 (α=0,05) табличное значение F (1,20), т. е. значение, стоящее на пересечении 1-го столбца и 20-й строки табл. 4А приложения, равно 4,35. Рассчитанное значение F ф значительно превосходит табличное, и, следовательно, включение в уравнение переменной «урожайность» имеет смысл.
Таким образом, выводы, сделанные ранее относительно коэффициентов регрессии, вполне правомерны.
Важным условием применения к обработке данных метода множественной регрессии является отсутствие сколько-нибудь значительной взаимосвязи между факторными признаками. При практическом использовании метода множественной регрессии, прежде чем включать факторы в уравнение, необходимо убедиться в том, что они независимы.
Если один из факторов зависит линейно от другого, то система нормальных уравнений, используемая для нахождения параметров уравнения, не разрешима. Содержательно этот факт можно толковать так: если факторы х 1 и x 2 связаны между собой, то они действуют на результативный признак у практически как один фактор, т. е. сливаются воедино и их влияние на изменение у разделить невозможно. Когда между независимыми переменными уравнения множественной регрессии имеется линейная связь, следствием которой является неразрешимость системы нормальных уравнений, то говорят о наличии мультиколлинеарности.
На практике вопрос о наличии или об отсутствии мультиколлинеарности решается с помощью показателей взаимосвязи. В случае двух факторных признаков используется парный коэффициент корреляции между ними: если этот коэффициент по абсолютной величине превышает 0,8, то признаки относят к числу мультиколлинеарных. Если число факторных признаков больше двух, то рассчитываются множественные коэффициенты корреляции. Фактор признается мультиколлинеарным, если множественный коэффициент корреляции, характеризующий совместное влияние на этот фактор остальных факторных признаков, превзойдет по величине коэффициент множественной корреляции между результативным признаком и совокупностью всех независимых переменных.
Самый естественный способ устранения мультиколлинеарности — исключение одного из двух линейно связанных факторных признаков. Этот способ прост, но не всегда приемлем, так как подлежащий исключению фактор может оказывать на зависимую переменную особое влияние. В такой ситуации применяются более сложные методы избавления от мультиколлинеарности ( См.: Мот Ж. Статистические предвидения и решения на предприятии. М., 1966; Ковалева Л. Н. Многофакторное прогнозирование на основе рядов динамики. М., 1980. ).
Выбор «наилучшего» уравнения регрессии. Эта проблема связана с двойственным отношением к вопросу о включении в регрессионное уравнение независимых переменных. С одной стороны, естественно стремление учесть все возможные влияния на результативный признак и, следовательно, включить в модель полный набор выявленных переменных. С другой стороны, возрастает сложность расчетов и затраты, связанные с получением максимума информации, могут оказаться неоправданными. Нельзя забывать и о том, что для построения уравнения регрессии число объектов должно в несколько раз превышать число независимых переменных. Эти противоречивые требования приводят к необходимости компромисса, результатом которого и является «наилучшее» уравнение регрессии. Существует несколько методов, приводящих к цели: метод всех возможных регрессий, метод исключения, метод включения, шаговый регрессионный и ступенчатый регрессионный методы.
Метод всех возможных регрессий заключается в переборе и сравнении всех потенциально возможных уравнений. В качестве критерия сравнения используется коэффициент детерминации R 2 . «Наилучшим» признается уравнение с наибольшей величиной R 2 . Метод весьма трудоемок и предполагает использование вычислительных машин.
Методы исключения и включения являются усовершенствованными вариантами предыдущего метода. В методе исключения в качестве исходного рассматривается регрессионное уравнение, включающее все возможные переменные. Рассчитывается частный F-критерий для каждой из переменных, как будто бы она была последней переменной, введенной в регрессионное уравнение. Минимальная величина частного F-критерия (F min ) сравнивается с критической величиной (F кр ), основанной на заданном исследователем уровне значимости. Если F min >F кр , то уравнение остается без изменения. Если F min кр , то переменная, для которой рассчитывался этот частный F-критерий, исключается. Производится перерасчет уравнения регрессии для оставшихся переменных, и процедура повторяется для нового уравнения регрессии. Исключение из рассмотрения уравнений с незначимыми переменными уменьшает объем вычислений, что является достоинством этого метода по сравнению с предыдущим.
Метод включения состоит в том, что в уравнение включаются переменные по степени их важности до тех пор, пока уравнение не станет достаточно «хорошим». Степень важности определяется линейным коэффициентом корреляции, показывающим тесноту связи между анализируемой независимой переменной и результативным признаком: чем теснее связь, тем больше информации о результирующем признаке содержит данный факторный признак и тем важнее, следовательно, введение этого признака в уравнение.
Процедура начинается с отбора факторного признака, наиболее тесно связанного с результативным признаком, т. е. такого факторного признака, которому соответствует максимальный по величине парный линейный коэффициент корреляции. Далее строится линейное уравнение регрессии, содержащее отобранную независимую переменную. Выбор следующих переменных осуществляется с помощью частных коэффициентов корреляции, в которых исключается влияние вошедших в модель факторов. Для каждой введенной переменной рассчитывается частный F-критерий, по величине которого судят о том, значим ли вклад этой переменной. Как только величина частного F-критерия, относящаяся к очередной переменной, оказывается незначимой, т. е. эффект от введения этой переменной становится малозаметным, процесс включения переменных заканчивается. Метод включения связан с меньшим объемом вычислений, чем предыдущие методы. Но при введении новой переменной нередко значимость включенных ранее переменных изменяется. Метод включения этого не учитывает, что является его недостатком. Модификацией метода включения, исправляющей этот недостаток, является шаговый регрессионный метод.
Шаговый регрессионный метод кроме процедуры метода включения содержит анализ переменных, включенных в уравнение на предыдущей стадии. Потребность в таком анализе возникает в связи с тем, что переменная, обоснованно введенная в уравнение на ранней стадии, может оказаться лишней из-за взаимосвязи ее с переменными, позднее включенными в уравнение. Анализ заключается в расчете на каждом этапе частных F-критериев для каждой переменной уравнения и сравнении их с величиной F кр , точкой F-распределения, соответствующей заданному исследователем уровню значимости. Частный F-критерий показывает вклад переменной в вариацию результативного признака в предположении, что она вошла в модель последней, а сравнение его с F кр позволяет судить о значимости рассматриваемой переменной с учетом влияния позднее включенных факторов. Незначимые переменные из уравнения исключаются.
Рассмотренные методы предполагают довольно большой объем вычислений и практически неосуществимы без ЭВМ. Для реализации ступенчатого регрессионного метода вполне достаточно малой вычислительной техники.
Ступенчатый регрессионный метод включает в себя такую последовательность действий. Сначала выбирается наиболее тесно связанная с результативным признаком переменная и составляется уравнение регрессии. Затем находят разности фактических и выравненных значений и эти разности (остатки) рассматриваются как значения результативной переменной. Для остатков подбирается одна из оставшихся независимых переменных и т. д. На каждой стадии проверяется значимость регрессии. Как только обнаружится незначимость, процесс прекращается и окончательное уравнение получается суммированием уравнений, полученных на каждой стадии за исключением последней.
Ступенчатый регрессионный метод менее точен, чем предыдущие, но не столь громоздок. Он оказывается полезным в случаях, когда необходимо внести содержательные правки в уравнение. Так, для изучения факторов, влияющих на цены угля в Санкт-Петербурге в конце XIX— начале XX в., было получено уравнение множественной регрессии. В него вошли следующие переменные: цены угля в Лондоне, добыча угля в России и экспорт из России. Здесь не обосновано появление в модели такого фактора, как добыча угля, поскольку Санкт-Петербург работал исключительно на импортном угле. Модели легко придать экономический смысл, если независимую переменную «добыча» заменить независимой переменной «импорт». Формально такая замена возможна, поскольку между импортом и добычей существует тесная связь. Пользуясь ступенчатым методом, исследователь может совершить эту замену, если предпочтет содержательно интерпретируемый фактор.
§ 4. Нелинейная регрессия и нелинейная корреляция
Построение уравнений нелинейной регрессии. До сих пор мы, в основном, изучали связи, предполагая их линейность. Но не всегда связь между признаками может быть достаточно хорошо представлена линейной функцией. Иногда для описания существующей связи более пригодными, а порой и единственно возможными являются более сложные нелинейные функции. Ограничимся рассмотрением наиболее простых из них.
Одним из простейших видов нелинейной зависимости является парабола, которая в общем виде может быть представлена функцией (6.2):
Неизвестные параметры а 0 , а 1 , а 2 находятся в результате решения следующей системы уравнений:
Дает ли преимущества описание связи с помощью параболы по сравнению с описанием, построенным по гипотезе линейности? Ответ на этот вопрос можно получить, рассчитав последовательный F-критерий, как это делалось в случае множественной регрессии (см. пример 16).
На практике для изучения связей используются полиномы более высоких порядков (3-го и 4-го порядков). Составление системы, ее решение, а также решение вопроса о полезности повышения порядка функции для этих случаев аналогичны описанным. При этом никаких принципиально новых моментов не возникает, но существенно увеличивается объем расчетов.
Кроме класса парабол для анализа нелинейных связей можно применять и другие виды функций. Для расчета неизвестных параметров этих функций рекомендуется использовать метод наименьших квадратов, как наиболее мощный и широко применяемый.
Однако метод наименьших квадратов не универсален, поскольку он может использоваться только при условии, что выбранные для выравнивания функции линейны по отношению к своим параметрам. Не все функции удовлетворяют этому условию, но большинство применяемых на практике с помощью специальных преобразований могут быть приведены к стандартной форме функции с линейными параметрами.
Рассмотрим некоторые простейшие способы приведения функций с нелинейными параметрами к виду, который позволяет применять к ним метод наименьших квадратов.
Функция не является линейной относительно своих параметров.
Прологарифмировав обе части приведенного равенства
получим функцию, линейную относительно своих новых параметров:
Кроме логарифмирования для приведения функций к нужному виду используют обратные величины.
с помощью следующих переобозначений:
может быть приведена к виду
Подобные преобразования расширяют возможности использования метода наименьших квадратов, увеличивая число функций, к которым этот метод применим.
Измерение тесноты связи при криволинейной зависимости. Рассмотренные ранее линейные коэффициенты корреляции оценивают тесноту взаимосвязи при линейной связи между признаками. При наличии криволинейной связи указанные меры связи не всегда приемлемы. Разберем подобную ситуацию на примере.
Пример 17. В 1-м и 2-м столбцах табл. 5 приведены значения результативного признака у и факторного признака х (данные условные). Поставив вопрос о тесноте связи между ними, рассчитаем парный линейный коэффициент корреляции по формуле (6.3). Он оказался равным нулю, что свидетельствует об отсутствии линейной связи. Тем не менее связь между признаками существует, более того, она является функциональной и имеет вид
Для измерения тесноты связи при криволинейной зависимости используется индекс корреляции, вычисляемый по формуле
где у i —i-e значение результативного признака; ŷ i —i-e выравненное значение этого признака; —среднее арифметическое значение результативного признака.
Числитель формулы (6.27) характеризует разброс выравненных значений результативного признака. Поскольку изменения выравненных, т. е. вычисленных по уравнению регрессии, значений признака происходят только в результате изменения факторного признака х. то числитель измеряет разброс результативного признака, обусловленный влиянием на него факторного признака. Знаменатель же измеряет разброс признака-результата, который определен влиянием на него всех факторов, в том числе и учтенного. Таким образом, индекс корреляции оценивает участие данного факторного признака в общем действии всего комплекса факторов, вызывающих колеблемость результативного признака, тем самым определяя тесноту зависимости признака у от признака х. При этом, если признак х не вызывает никаких изменений признака у, то числитель и, следовательно, индекс корреляции равны 0. Если же линия регрессии полностью совпадает с фактическими данными, т. е. признаки связаны функционально, как в примере 17, то индекс корреляции равен 1. В случае линейной зависимости между х и у индекс корреляции численно равен линейному коэффициенту корреляции г. Квадрат индекса корреляции совпадает с введенным ранее (6.21) коэффициентом детерминации. Если же вопрос о форме связи не ставится, то роль коэффициента детерминации играет квадрат корреляционного отношения η 2 y/x (6.12).
Таковы основные принципы и условия, методика и техника применения корреляционного и регрессионного анализа. Их подробное рассмотрение обусловлено тем, что они являются высокоэффективными и потому очень широко применяемыми методами анализа взаимосвязей в объективном мире природы и общества. Корреляционный и регрессионный анализ широко и успешно применяются и в исторических исследованиях.
http://kazedu.com/referat/117633/1
http://masters.donntu.org/2005/kita/tokarev/library/linreg.htm