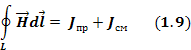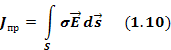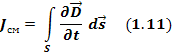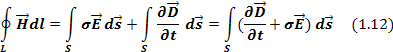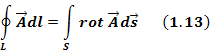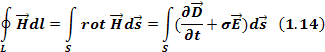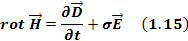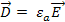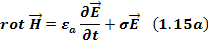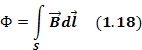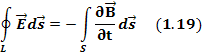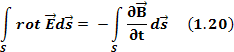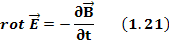Какой из перечисленных законов выражает первое уравнение максвелла

Первое уравнение Максвелла.

Первое уравнение Максвелла — это обобщение закона Ампера и Био-Саварра для токов смещения. Звучит следующим образом: циркуляция вектора напряженности магнитного поля по замкнутому контуру равна полному току, пронизывающему этот контур.

В современном обозначении записывается

Т.о. физический смысл первого уравнения Максвелла состоит в том, что магнитное поле в некоторой области пространства связано не только с токами проводимости, протекающими в этой области, но и с изменением электрического поля во времени в этой области(токами смещения).

Это означает, что циркуляция вектора 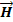по контуру L равна сумме токов проводимости и смещения.

Подставляя 1.10, 1.11 в 1.9, получим

Уравнение 1.12 называют первым уравнением Максвелла в интегральной форме.

Получим дифференциальную форму уравнения Максвелла. Для этого воспользуемся уравнением Стокса, которое преобразует контурный интеграл в поверхностный:

Применим уравнение 1.13 к левой части уравнения 1.12. Получим

Уравнение 1.14 справедливо, если равны подынтегральные функции, то есть

Уравнение 1.15 есть первое уравнение Максвелла в дифференциальной форме.

Для изотропных сред

Подставим в 1.15

Дифференциальная форма первого уравнения Максвелла используется в том случае, когда производные поля по координатам пространства непрерывны. Интегральная форма 1.12 такого ограничения не имеет.

§1.3. Второе уравнение Максвелла.

Второе уравнение Максвелла— это обобщение закона индукции Фарадея для диэлектрической среды в свободном пространстве

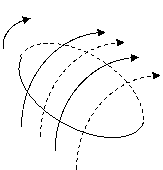
где Ф – поток магнитной индукции, пронизывающий проводящий контур и создающий в нем ЭДС. ЭДС создается не только в проводящем контуре, но и в некотором диэлектрическом контуре в виде электрического тока смещения.

(1.17)

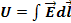
Физический смысл второго уравнения Максвелла состоит в том, что электрическое поле в некоторой области пространства связано с изменением магнитного поля во времени в этой области. То есть переменное магнитное поле возбуждает вихревое электрическое поле.

Получим второе уравнение Максвелла в интегральной форме

Уравнение 1.19 – второе уравнение Максвелла в интегральной форме.

Воспользуемся уравнением Стокса 1.13, преобразуем левую часть уравнения 1.19:

Уравнение 1.20 есть второе уравнение Максвелла в дифференциальной форме.

Уравнения Максвелла

Уравнения Максвелла — это 4 уравнения, которые описывают, как электрические и магнитные поля распространяются и взаимодействуют; т.е. эти уравнения (правила или даже законы) описывают процессы/взаимодействия электромагнетизма.

Эти правила описывают, как проходит управление поведением электрических и магнитных полей. Уравнения Максвелла показывают, что электрический заряд (положительный и отрицательный):

1. Порождает электрическое поле (также если заряд изменяется со временем, то он вызывает появление электрического поля).
2. В дальнейшем он вызывает появление магнитного поля.

Уравнения Максвелла в дифференциальной форме

Уравнение 1: Закон Гаусса или Теорема Гаусса

Дивергенция электрического поля равняется плотности заряда. Существует вязь между электрическим полем и электрическим зарядом.

Дивергенция в физике показывает, насколько данная точка пространства является источником или потребителем потока поля.

Очень кратко: Электрические поля расходятся от электрических зарядов: электрический заряд создаёт поле вокруг себя и, таким образом, действует как источник электрических полей. Это можно сравнить с краном, который является источником воды.

Ещё закон Гаусса говорит о том, что отрицательные заряды действуют как сток для электрических полей (способ, как вода стекает через отверстие стока). Это означает, что линии электрического поля имеют начало и поглощаются при электрическом заряде.

Заряды с одинаковым знаком отталкиваются друг от друга, а противоположные заряды притягиваются друг к другу (если есть два положительных заряда, они будут отталкиваться; а если есть один отрицательный и один положительный, они будут притягиваться друг к другу).

Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

Можно создать электрическое поле, изменив магнитное поле.

Очень кратко: Закон Фарадея гласит, что изменяющееся магнитное поле внутри контура вызывает индуцированный ток, который возникает из-за силы или напряжения внутри контура. Это значит:

1. Электрический ток порождает магнитные поля, а эти магнитные поля (вокруг цепи) вызывают электрический ток.
2. Изменяющееся во времени магнитное поле вызывает распространение электрического поля.
3. Циркулирующее во времени электрическое поле вызывает изменение магнитного поля во времени.

Уравнение 3: Закон Гаусса для магнетизма

Дивергенция магнитного потока любой замкнутой поверхности равна нулю. Магнитного монополя не существует.

Закон Гаусса для магнетизма утверждает (очень кратко):

1. Магнитных монополей не существует.
2. Расхождение полей B или H всегда равно нулю в любом объёме.
3. На расстоянии от магнитных диполей (это круговой ток) магнитные поля текут по замкнутому контуру.

Уравнение 4: Закон Ампера

Магнитное поле создаётся с помощью тока или изменяющегося электрического поля.

Очень кратко: Электрический ток порождает магнитное поле вокруг тока. Изменяющийся во времени электрический поток порождает магнитное поле.

Уравнения Максвелла в интегральной и дифференциальной форме

Вспомним сначала в дифференциальной форме и следом будет в интегральной форме.

Уравнение 1: Закон Гаусса (Теорема Гаусса)

Это же уравнение в интегральной форме:

Поток вектора электрической индукции D через любую замкнутую поверхность равняется сумме свободных зарядов, охваченных этой поверхностью. Электрическое поле создаётся нескомпенсированными электрическими зарядами (это те, что создают вокруг себя своё собственное электрическое поле).

Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Е вихревого электрического поля (по любому замкнутому контуру) равняется скорости изменения магнитного потока через площадь контура (S) с противоположным знаком.

Уравнение 3: Закон Гаусса для магнетизма

И это же уравнение в интегральной форме:

Силовые линии магнитного поля замкнуты, т.к. поток вектора индукции В магнитного поля через любую замкнутую поверхность равняется нулю.

Уравнение 4: Закон Ампера

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Н магнитного поля по замкнутому контуру равняется алгебраической сумме токов, которые пронизывают этот контур. Магнитное поле создаётся не только током проводимости, но и переменным электрическим полем.

Уравнения Максвелла. Первое уравнение Максвелла

Для описания электромагнитного поля было введено шесть векторов Е, Р, D, В, М и Н. Так как векторы электрического поля Е, Р, D связаны соотношением (1.4), а векторы магнитного поля В, М, Н – соотношением (1.15), то для определения электромагнитного поля можно ограничиться нахождением четырех векторов. Обычно в качестве таких векторов используют векторы Е, D, В и Н. В линейных изотропных средах, для которых справедливы соот­ношения (1.5) и (1.17), электромагнитное поле может быть пол­ностью определено двумя векторами (обычно Е и Н).

Все электромагнитные процессы, относящиеся к макроскопи­ческой электродинамике, подчиняются законам, впервые сформу­лированным в виде дифференциальных уравнений Дж.К. Макс­веллом, которые были опубликованы им в 1873 г. Эти уравнения были получены в результате обобщения накопленных к тому времени экспериментальных данных и называются уравнениями Максвелла.

Первое уравнение Максвелла является обобщением закона полного тока (закона Ампера). В домаксвелловской формулировке это уравнение могло быть сформулировано следующим образом: циркуляция вектора напряженности Н магнитного поля по замк­нутому контуру Г равна току I, пронизывающему данный контур:

(1.25)

где dl= τ0·dl– элемент контура Г, направленный по касательной к Г; τ0 – орт этой касательной, положительное направление кото­рого выбирается в соответствии с обходом контура Г. В каче­стве контура Г может быть взят любой одновитковый замкнутый контур.

До Максвелла под током I понимали только ток проводимости. В общем случае распределение тока I внутри контура Г может быть неравномерным. При этом

(1.26)

где j – вектор плотности тока проводимости; S – произвольная поверхность, опирающаяся на контур Г; dS = n0dS, a n0 – орт нормали к поверхности S (рис. 1.6). Направление вектора n0 определяется направлением обхода контура Г. Пусть для оп­ределенности все точки поверхности S расположены с одной стороны относительно контура Г. Тогда, если смотреть вдоль вектора n0, обход контура Г будет идти по часовой стрелке. Такую взаимосвязь направлений вектора n0 и обхода контура для краткости будем условно называть правовинтовой системой. Подставляя (1.26) в (1.25), получаем

(1.27)

Рис. 1.6. Орт нормали к поверхности S

Уравнение (1.27), справедливое при постоянном токе, ока­зывается неверным в случае переменных процессов. Дейст­вительно, рассмотрим конденсатор, включенный в цепь пере­менного тока (рис. 1.7). Пусть Г – замкнутый контур, охваты­вающий провод, по которому течет переменный ток. Правая часть уравнения (1.27) представляет собой интеграл от плотности тока проводимости j по произвольной поверхности S, опирающейся на контур Г. Эту поверхность можно провести так, чтобы она либо пересекла провод (поверхность S1 на рис. 1.7), либо прошла между обкладками конденсатора (поверхность S2). Интеграл в правой части уравнения (1.27) в первом случае равен току I, а во втором обращается в нуль. В то же время циркуляция напряженности магнитного поля по контуру Г (левая часть уравнения) не зависит от того, как проведена поверхность S. Это противоречие сви­детельствует о непригодности уравнения (1.27) для описания переменных полей.

Рис. 1.7. Конденсатор, включенный в цепь пере­менного тока

Максвелл дал обобщенную формулировку закона полного тока. Он ввел фундаментальное понятие тока смещения и, ос­новываясь на работах Фарадея, предположил, что в случае переменных полей ток смещения с точки зрения образования магнитного поля равноценен току проводимости. Примером эле­ктрической системы, в которой преобладают токи смещения, может служить рассмотренный выше конденсатор в цепи пе­ременного тока. Переменный ток может циркулировать между обкладками конденсатора даже в том случае, когда они разделены идеальным диэлектриком или находятся в вакууме и, следо­вательно, образование тока проводимости невозможно. Соеди­нительный провод, по которому течет ток проводимости, окружен кольцевыми линиями магнитного поля, которые как бы образуют «оболочку» вокруг всего провода. Максвелл предположил, что эта «оболочка» не обрывается у пластин конденсатора, а образует непрерывную поверхность, т.е. изменяющееся электрическое поле конденсатора также окружено кольцевыми линиями магнитного поля. Таким образом, переменное электрическое поле, так же как и ток проводимости, сопровождается появлением магнитного поля. Это дало основание ввести понятие о новом виде тока, получившем название тока смещения. Плотность тока смещения определяется формулой:

. (1.28)

Как и плотность тока проводимости, она измеряется в А/м2.

Подчеркнем, что ток проводимости и ток смещения в вакууме имеют различную физическую сущность. Ток проводимости – это упорядоченное движение свободных электрических зарядов. Ток смещения в вакууме соответствует только изменению электри­ческого поля и не сопровождается каким-либо движением электрических зарядов. В вакууме D = ε0Е и уравнение (1.28) принимает вид .Ток смещения в вакууме не сопровождается выделением тепла.

Рассмотрим общий случай, когда ток смещения возникает в какой-либо среде. Вектор электрического смещения связан с векторами Е и Р соотношением (1.4). Подставляя это соотношение в (1.28), получаем

.

Первое слагаемое в правой части этой формулы совпадает с выражением для плотности тока смещения в вакууме, т.е. определяет как бы «чистый» ток смещения, не связанный непо­средственно с движением зарядов. Второе слагаемое определяет ток смещения, обусловленный движением зарядов, связанных с атомами вещества, в результате действия переменного поля. Эту составляющую тока смещения можно рассматривать как свое­образный ток проводимости, так как она, по существу, обусловлена упорядоченным перемещением связанных зарядов. На ее под­держание в реальной среде затрачивается некоторая часть энергии электромагнитного поля.

Вернемся к закону полного тока. Как уже указывалось, Макс­велл предположил, что уравнение (1.25) имеет частный характер, так как не учитывает токов смещения. Для того чтобы оно было справедливым и в случае переменных полей, нужно в его правую часть помимо тока проводимости I ввести ток смещения Iсм:

. (1.29)

Ток смещения выражается через плотность тока смещения jcмсоотношением:

. (1.30)

Подставляя формулы (1.26) и (1.30) в (1.29), получаем

. (1.31)

Уравнение (1.31) сформулировано применительно к контуру конечных размеров. Оно представляет собой первое уравнение Максвелла в интегральной форме.

Максвеллом этот закон был сформулирован также в диф­ференциальной форме. Для перехода к дифференциальной фор­ме воспользуемся теоремой Стокса (П. 20). Заменяя в уравнении (1.31) циркуляцию вектора Н интегралом от rot H по поверхности S, получаем

. (1.32)

Так как S-произвольная поверхность, то равенство (1.32) возможно только в том случае, если

. (1.33)

Равенство (1.33) называют первым уравнением Максвелла. Векторное уравнение (1.33) эквивалентно трем скалярным урав­нениям, которые в декартовой системе координат х, у, z имеют вид