Какой вид имеет уравнение бернулли в виде давлений

Основы гидравлики

Уравнение Бернулли — фундамент гидродинамики

Бернулли — вне всякого сомнения — имя, знакомое и специалистам, и обывателям, которые хоть немного интересуются науками. Этот человек оставил ослепительный след в истории познавания человечеством окружающего мира, как физик, механик, гидравлик и просто общепризнанный гений, Даниил Бернулли навсегда останется в памяти благодарных потомков за свои идеи и выводы, которые долгое время существования человечества были покрыты мраком неизведанного.
Открытия и законы, которыми Бернулли осветил путь к познанию истины, являются фундаментальными, и придали ощутимый импульс развитию многих естественных наук. К таковым относится и уравнение Бернулли в Гидравлике, которое он вывел почти три века назад. Данное уравнение является основополагающим законом этой сложной науки, объясняющим многие явления, описанные даже древними учеными, например, великим Архимедом.

Попробуем уяснить несложную суть закона Бернулли (чаще его называют уравнением Бернулли), описывающего поведение жидкости в той или иной ситуации.

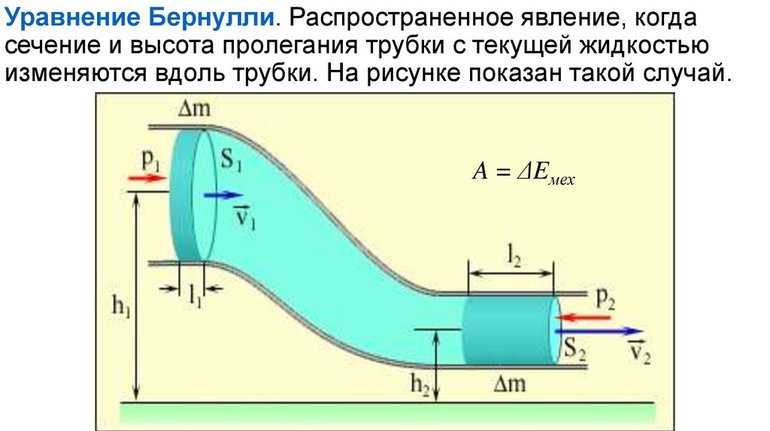
Выделим в стационарно текущей идеальной жидкости трубку тока, которая ограничена сечениями S₁ и S₂ , (рис. 1) .
(Понятие идеальной жидкости абстрактно, как и понятие всего идеального. Идеальной считается жидкость, в которой нет сил внутреннего трения, т. е. трения между отдельными слоями и частицами подвижной жидкости).
Пусть в месте сечения S₁ скорость течения ν₁ , давление p₁ и высота, на которой это сечение расположено, h₁ . Аналогично, в месте сечения S₂ скорость течения ν₂ , давление p₂ и высота сечения h₂ .

За бесконечно малый отрезок времени Δt жидкость переместится от сечения S₁ к сечению S₁‘ , от S₂ к S₂‘ .

По закону сохранения энергии, изменение полной энергии E₂ — E₁ идеальной несжимаемой жидкости равно работе А внешних сил по перемещению массы m жидкости:

где E₁ и E₂ — полные энергии жидкости массой m в местах сечений S₁ и S₂ соответственно.

С другой стороны, А — это работа, которая совершается при перемещении всей жидкости, расположенной между сечениями S₁ и S₂ , за рассматриваемый малый отрезок времени Δt .
Чтобы перенести массу m от S₁ до S₁‘ жидкость должна переместиться на расстояние L₁ = ν₁Δt и от S₂ до S₂‘ — на расстояние L₂ = ν₂Δt . Отметим, что L₁ и L₂ настолько малы, что всем точкам объемов, закрашенных на рис. 1 , приписывают постоянные значения скорости ν , давления р и высоты h .
Следовательно,

где F₁ = p₁S₁ и F₂ = — p₂S₂ (сила отрицательна, так как направлена в сторону, противоположную течению жидкости; см. рис. 1).

Полные энергии E₁ и E₂ будут складываться из кинетической и потенциальной энергий массы m жидкости:

Подставляя (3) и (4) в (1) и приравнивая (1) и (2) , получим

Согласно уравнению неразрывности для несжимаемой жидкости, объем, занимаемый жидкостью, всегда остается постоянным, т. е.

Разделив выражение (5) на ΔV , получим

где ρ — плотность жидкости.

После некоторых преобразований эту формулу можно представить в другом виде:

Поскольку сечения выбирались произвольно, то в общем случае можно записать:

ρv 2 /2 +ρgh +p = const (6) .

Выражение (6) получено швейцарским физиком Д. Бернулли (опубликовано в 1738 г.) и называется уравнением Бернулли.

Даниил Бернулли (Daniel Bernoulli, 1700 — 1782), швейцарский физик, механик и математик, один из создателей кинетической теории газов, гидродинамики и математической физики. Академик и иностранный почётный член (1733) Петербургской академии наук, член Академий: Болонской (1724), Берлинской (1747), Парижской (1748), Лондонского королевского общества (1750).

Уравнение Бернулли по своей сути является интерпретацией закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Уравнение хорошо выполняется и для реальных жидкостей, для которых внутреннее трение не очень велико.

Величина р в формуле (6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела) , величина ρν 2 /2 — динамическим давлением, величина ρgh — гидростатическим давлением.

Статическое давление обусловлено взаимодействием поверхности жидкости с внешней средой и является составляющей внутренней энергии рассматриваемого элементарного объема жидкости (т. е. характеризуется взаимодействием внутренних частиц жидкости, вызванных внешним возмущением — давлением) , а гидростатическое – положением этого объема жидкости в пространстве (зависит от высоты над поверхностью Земли) .
Динамическое давление характеризует кинематическую составляющую энергии этого объема, поскольку зависит от скорости потока, в котором движется рассматриваемый элементарный объем жидкости.

Для горизонтальной трубки тока изменение потенциальной составляющей ρgh будет равно нулю (поскольку h2 – h1 = 0) , и выражение (6) примет упрощенный вид:

ρv 2 /2 + p = const (7) .

Выражение p + ρν 2 /2 называется полным давлением.

Таким образом, содержание уравнения Бернулли для элементарной струйки при установившемся движении можно сформулировать так: удельная механическая энергия при установившемся движении элементарной струйки идеальной жидкости, представляющая собой сумму удельной потенциальной энергии положения и давления и удельной кинетической энергии, есть величина постоянная.

Все члены уравнения Бернулли измеряются в линейных единицах.

В гидравлике широко применяют термин напор, под которым подразумевают механическую энергию жидкости, отнесенную к единице ее веса (удельную энергию потока или неподвижной жидкости) .
Величину v 2 /2g называют скоростным (кинетическим) напором, показывающим, на какую высоту может подняться движущаяся жидкость за счет ее кинетической энергии.
Величину h_п = p/ρg называют пьезометрическим напором, показывающим на какую высоту поднимается жидкость в пьезометре под действием оказываемого на нее давления.
Величину z называют геометрическим напором, характеризующим положение центра тяжести соответствующего сечения движущейся струйки над условно выбранной плоскостью сравнения.

Сумму геометрического и пьезометрического напоров называют потенциальным напором, а сумму потенциального и скоростного напора — полным напором.

На основании анализа уравнения Бернулли можно сделать вывод, что при прочих неизменных параметрах потока (жидкости или газа) величина давления в его сечениях обратно пропорциональна скорости, т. е. чем выше давление, тем меньше скорость, и наоборот.
Это явление используется во многих технических конструкциях и устройствах, например, в карбюраторе автомобильного двигателя (диффузор), в форме крыла самолета. Увеличение скорости воздушного потока в диффузоре карбюратора приводит к созданию разрежения, всасывающего бензин из поплавковой камеры, а специальная форма сечения самолетного крыла позволяет создавать на его нижней стороне зону повышенного давления, способствующего появлению подъемной силы.

Геометрическая интерпретация уравнения Бернулли

Поскольку напор измеряется в линейных величинах, можно дать графическую (геометрическую) интерпретацию уравнению Бернулли и его составляющим.

На графике (рис. 2) представлена горизонтальная плоскость сравнения 0-0 , относительно которой геометрический напор будет в каждом сечении равен вертикальной координате z центра тяжести сечения (линия геометрического напора проходит по оси струйки) .
Линия К-К , характеризующая потенциальный напор струйки, получена сложением геометрического и пьезометрического напора в соответствующих сечениях (т. е. разница координат точек линии К-К и соответствующих точек оси струйки характеризует пьезометрический напор в данном сечении) .
Полный напор характеризуется линией MN , которая параллельна плоскости сравнения О-О , свидетельствуя о постоянстве полного напора H’_e (удельной механической энергии) идеальной струйки в любом ее сечении.

При движении реальной жидкости, обладающей вязкостью, возникают силы трения между ограничивающими поток поверхностями и между слоями внутри самой жидкости. Для преодоления этих сил трения расходуется энергия, которая превращается в теплоту и рассеивается в дальнейшем движущейся жидкостью. По этой причине графическое изображение уравнения Бернулли для идеальной жидкости будет отличаться от аналогичного графика для реальной жидкости.
Если обозначить h_f потери напора (удельной энергии) струйки на участке длиной L , то уравнение Бернулли для реальной жидкости примет вид:

Для реальной жидкости полный напор вдоль струйки не постоянен, а убывает по направлению течения жидкости, т. е. его графическая интерпретация имеет вид не прямой линии, а некоторой кривой МЕ (рис. 3) . Заштрихованная область характеризует потери напора.

Падение напора на единице длины элементарной струйки, измеренной вдоль оси струйки, называют гидравлическим уклоном:

Гидравлический уклон положителен, если напорная линия снижается по течению жидкости, что всегда бывает при установившемся движении.

Для практического применения уравнения Бернулли необходимо распространить его на поток реальной жидкости:

где α₁ , α₂ — коэффициенты Кориолиса, учитывающие различие скоростей в разных точках сечения потока реальной жидкости.
На практике обычно принимают α₁ = α₂ = α : для ламинарного режима течения жидкости в круглых трубах α = 2, для турбулентного режима α = 1,04. 1,1.

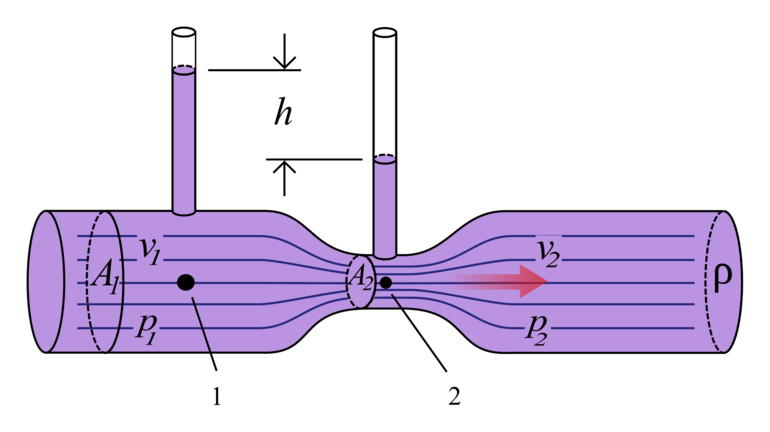
Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности ( S₁v₁Δt = S₂v₂Δt ) видно, что при течении жидкости по горизонтальной трубе, которая имеет различные сечения, скорость жидкости больше в более узких местах (где площадь сечения S меньше) , а статическое давление больше в более широких местах, т. е. там, где скорость меньше. Это можно увидеть, установив вдоль трубы ряд манометров.

Данный опыт показывает, что в манометрической трубке В , которая прикреплена к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С , которые прикреплены к широкой части трубы, что соответствует уравнению Бернулли.

Так как динамическое давление зависит от скорости движения жидкости (газа) , то уравнение Бернулли можно использовать для измерения скорости потока жидкости. Принципиально это свойство жидкости для определения скорости потока реализовано в так называемой трубке Пито – Прандтля (обычно ее называют трубкой Пито ) .

Трубка Пито – Прандтля ( см. рис. 2 ) состоит из двух тонких стеклянных трубок, одна из которых изогнута под прямым углом (Г-образно) , а вторая — прямая.
Одним из свободных концов каждая трубка присоединена к манометру.
Изогнутая трубка имеет открытый свободный конец, направленный против тока и принимающий напор потока жидкости, а вторая погружена в поток перпендикулярно току, и скорость потока на давление внутри трубки не влияет, т. е. внутри этой трубки действует лишь статическая составляющая давления жидкости.
Разница между давлением в первой трубке (полное давление) и второй трубке (статическое давление) , которую показывает манометр, является динамическим давлением, определяемым по формуле:

Определив с помощью трубки Пито — Прандтля динамическое давление в потоке жидкости, можно легко вычислить скорость этого потока:

Уравнение Бернулли также используют для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, с маленьким отверстием в боковой стенке на некоторой глубине ниже уровня жидкости.

Рассмотрим два сечения (на уровне h₁ свободной поверхности жидкости в сосуде и на уровне h₁ выхода ее из отверстия) и применим уравнение Бернулли:

Так как давления р₁ и р₂ в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. р₁ = р₂ , то уравнение будет иметь вид

Из уравнения неразрывности мы знаем, что ν₁/ν₂ = S₂/S₁ , где S₁ и S₂ — площади поперечных сечений сосуда и отверстия.
Если S₁ значительно превышает S₂ , то слагаемым ν₁ 2 /2 можно пренебречь и тогда:

Это выражение получило название формулы Торричелли.
Формулу Торричелли можно использовать для подсчета объемного (или массового) расхода жидкости, истекающего из отверстия в сосуде с поддерживаемым постоянно уровнем под действием атмосферного давления.
При этом используется формула Q = vS (для определения массового расхода – m = ρvS ) , по которой определяется расход жидкости за единицу времени.

Если требуется узнать расход жидкости за определенный промежуток времени t , то его определяют, умножив расход за единицу времени на время t .

Следует отметить, что такая методика расчета расхода реальной жидкости через отверстие в стенке сосуда дает некоторые погрешности, обусловленные физическими свойствами реальных жидкостей, поэтому требует применения поправочных коэффициентов (коэффициентов расхода) .

Пример решения задачи на определение расхода жидкости

Определить примерный объемный расход воды, истекающей из отверстия диаметром 10 мм, проделанном в вертикальной стенке широкого сосуда на высоте h = 1 м от верхнего, постоянно поддерживаемого, уровня воды за 10 секунд.
Ускорение свободного падения принять равным g = 10 м/с 2 .
Коэффициент расхода воды через отверстие — µ_s = 0,62.

По формуле Торричелли определим скорость истечения воды из отверстия:

v = √2gh = √2×10×1 ≈ 4,5 м/с.

Определим расход воды Q за время t = 10 секунд:

Q = µ_svSt = 0,62×4,5×3,14×0,012/4 × 10 ≈ 0,0022 м 3 ≈ 2,2 литра.

На практике расход жидкости в трубопроводах измеряют расходомерами, например, расходомером Вентури. Расходомер Вентури (см рис. 2) представляет собой конструкцию из двух конических патрубков, соединенных цилиндрическим патрубком. В сечениях основной трубы и цилиндрического патрубка устанавливают трубки-пьезометры, которые фиксируют уровень жидкости, обусловленный полным давлением в потоке.

При прохождении жидкости через сужающийся конический патрубок часть потенциальной энергии потока преобразуется в кинетическую, и, наоборот, – при прохождении потока по расширяющемуся коническому патрубку, кинетическая энергия уменьшается, а потенциальная растет. Это сказывается на скорости движения жидкости по рассматриваемым участкам. Перепад высоты уровня жидкости в пьезометрах позволяет рассчитать среднюю скорость потока жидкости на рассматриваемых участках и вычислить объемный расход по внутреннему сечению трубы.
В расходомерах учитываются потери напора в самом приборе при помощи коэффициента расхода прибора φ .

Уравнение Бернулли ( формула пример)

Уравнение Бернулли Статическое и динамическое давление

Силы притяжения между молекулами в жидкости больше, чем в газах, но значительно меньше, чем в твердых телах. Частицы жидкости легко взаимно смещаются и под действие тления легко перемещаются из области более высокого давления в сторону более низкого. Это называется тече нием жидкости.

Вследствие наличия сил притяжения взаимное смещение частиц жидкости сопровождается некоторым сопротивлением, которое подобно механическому трению между мелкими частицами твердого вещества и называется внутренним трением, или вязкостью, жидкости. Вязкость жидкости проявляется, например, сопротивлением при помешивании жидкости, замедлением при падении в жидкости предметов и т. д.

Рассмотрим вначале стационарное течение идеальной жидкости (идеальной называется несжимаемая жидкость, не имеющая вязкости; стационарным называется течение, при котором величина скорости в любой точке жидкости со временем не изменяется). Установим для этих условий соотношение между давлением р в жидкости, скоростью движения v ее частиц и положением их в поле силы тяжести, характеризуемое высотой Л над некоторым уровнем отсчета (рис. 2).

Уравнение Бернулли

В соответствии с законом сохранения энергии полная энергия некоторой массы m (имеющей объем V) идеальной жидкости при течении остается неизменной, так как в ней отсутствуют потери на внутреннее трение.

Полная энергия составляется из потенциальной энергии давления (Е_n = pV), потенциальной энергии тяжести (E«_п = mgh) и кинетической энергии (Е_к = m υ 2 /2). На основании сказанного: pV + mgh + (m υ 2 /2) = const.

Соответственно для каких-либо двух положений массы т идеальной жидкости, например в точках А и Б (рис. 2):

Если предпоследнее уравнение разделить почленно на объем V жидкости, то учитывая, что m/V есть плотность ρ жидкости, получим:

Это и есть уравнение Бернулли.

Для движения жидкости в горизонтальных трубках силу тяжести можно не учитывать и тогда уравнение Бернулли принимает вид:

Из этого уравнения следует вывод, называемый правилом Бернулли: давление невязкой жидкости, текущей по горизонтальной трубе, выше там, где скорость ее меньше, и наоборот.

Пример расчета по формуле

Рассмотрим течение жидкости по трубе с неодинаковым сечением. Течение называется непрерывным, если через любое сечение трубы в единицу времени протекает одинаковое количество (объем) жидкости. При этом скорость движения жидкости на участках трубы обратно пропорциональна площади их сечений.

Действительно не трудно доказать, что объем V₀ жидкости, протекающей в единицу времени через любое сечение трубы, может быть выражен произведением площади S сечения трубы на скорость υ течения жидкости: V₀=Sυ. По условию этот объем постоянен для любого сечения трубы, следовательно,

т. е. произведение скорости течения жидкости на поперечное сечение струи есть величина постоянная. Это соотношение называют уравнением неразрывности струи.

Если обозначить сечение и скорость движения на участках трубы соответственно S₁ и υ₁ S₂ и υ₂, то согласно сказанному:

Скорость течения жидкости в трубе с переменным сечением обратно пропорциональна площади этих сечений.

При этом в соответствии с правилом Бернулли на участках меньшего сечения трубы давление будет ниже, на участках большего сечения — выше (рис. , а). Поясним механизм этого явления. При переходе на участок трубы меньшего сечения (линия ab на рис. , б) частицы жидкости ускоряются, на что затрачивается часть силы Р₄, создающей давление на более широком участке (по условию равновесия частиц жидкости Р₁= Р₂+F_у, где Р₂ — сила, создающая давление на суженном участке, F_у — сила, обеспечивающая ускорение частиц).

Наоборот, при переходе на участок с большим сечением (линия cd на рис. 82, б) частицы жидкости набегают на лежащую впереди и более медленно двигающуюся массу жидкости и, затормаживаясь, создают дополнительную силу F_т, повышающую давление на более широком участке (аналогично P₃=P₂ + F_т).

Можно подобрать условия, при которых давление жидкости в сужен ном участке трубы станет ниже атмосферного и тогда в этом месте струя будет обладать всасывающим действием. Всасывающее действие струи газа, пара или воды, выходящей из суженного отверстия с большой скоростью, используется в ряде приборов, применяемых в медицинской практике (ингалятор, водоструйный насос и др.).

Паровой ингалятор

Это прибор для вдыхания жидких лекарственных веществ в распыленном виде. Он состоит из кипятильника В, стакана К с лекарственной жидкостью и вставленной в него тонкой трубкой Т и направляющего патрубка С. Струя пара выходит из трубки кипятильника с большой скоростью. Вследствие этого давление около ее отверстия падает и лекарственная жидкость, всасываясь по трубке Т, поступает в струю, распыляется и, смешиваясь с паром, вдыхается больным через патрубок С

Водоструйный насос состоит из стеклянного сосуда Н, в который впаяно три трубки. Трубка имеет на конце коническое сужение. Насос присоединяется к водоводу и колбе К, из которой производится отсасывание. Вода, имеющая достаточно высокое давление, выходит из суженного конца трубки 1 с большей скоростью. Давление у отверстия трубки резко снижается и в сосуд А через трубку 2 засасывается воздух или жидкость, которые вместе с водой удаляются через трубку 3. Водоструйный насос удобен тем, что он не имеет вращающихся частей, требующих смазки, бесшумен и гигиеничен. Поэтому он часто применяется в лабораториях, операционных и т. п.

В уравнении Бернулли давление р называется статическим давлением р_с жидкости. Оно может быть измерено обычным манометром, который двигается вместе с жидкостью, или практически при помощи неподвижной манометрической трубки, плоскость отверстия которой расположена параллельно направлению движения жидкости.

Второй член уравнения Бернулли (ρυ₂/2)также имеет размерность давления и называется динамическим давлением р_д в жидкости. Сумма статического и динамического давлений называется полным давлением р в жидкости:

Для измерения его применяют манометрическую трубку, изогнутую под прямым углом и помещенную отверстием навстречу движению жидкости. Частицы жидкости, заходящие в отверстие трубки полностью тормозятся в ней: скорость υ₂ частиц жидкости в отверстии рав няется нулю: υ ₂=0. Тогда по уравнению Бернулли

Следовательно, давление р₂ в трубке:

где р₁ — давление и υ₁ — скорость движущейся жидкости

Если в струю жидкости поставить рядом две такие трубки, то разность уровней в трубках будет соответствовать динамическому давлению. На этом основан способ измерения скорости движения жидкости или газа В струю погружают две скрепленные вместе измерительные трубки, прямую и изогнутую (подобное устройство называется трубкой Пито), которые соединяются с U= образным манометром. Манометр покажет динамическое давление, по величине которого, пользуясь приведенной выше формулой, вычисляют искомую скорость:

Статья на тему Уравнение Бернулли

Уравнение Бернулли — вывод формулы, физический смысл, примеры использования

Исследования учёного

Даниил Бернулли родился в Голландии в 1700 году. В 1725 году он начал работать на кафедре физиологии, где увлёкся основами теоретической физики. Через 25 лет он возглавил кафедру экспериментальной физики, которой и руководил до конца своих дней. Основным его трудом считается создание теории гидродинамической зависимости, известной как Закон Бернулли. Открытие учёного предвосхитило зарождение молекулярно-кинетического учения поведения газов.

Причиной открытия принципа стало изучение действия закона сохранения энергии в различных ситуациях. Бернулли установил, что давление жидкости в замкнутом пространстве зависит от сечения объекта, в котором она находится. Чем меньше сечение трубы, тем ниже будет созданное давление в пропускаемом через неё жидком веществе.

Этот факт был доказан экспериментально и описан математически.

Правило в математической формулировке имеет вид (pv 2 / 2) + p * g * h + ρ = const, где:

p — количество жидкости на единицу объёма;
v — скорость движения потока;
h — уровень, на который поднят элемент жидкости;
ρ — сила, действующая на единицу площади;
g — ускорение, придаваемое жидкости под действием притяжения Земли.

Чтобы понять физический смысл уравнения Бернулли, нужно рассмотреть трубу переменного сечения, в которой существует точка А и Б. Первая располагается в широкой части, а вторая — в узкой. В соответствии с уравнением непрерывности скорость V1 в части трубы, имеющей большее сечение, будет меньше, чем скорость жидкости V2 в узком сечении. Если в жидкость поместить прибор для измерения давления, он покажет какое-то значение P1 в точке A и P2 в точке Б. При этом там, где скорость движения жидкости медленнее, давление будет больше.

Объясняется это следующим образом: если V1 больше V2, значит, при движении происходит изменение скорости течения. Представив, что в жидкости находится точка, можно утверждать о её движении с ускорением. Это означает, что на неё действуют силы.

Одна из них совпадает с направлением течения, тем самым ускоряя движение. Обусловлена эта сила разностью давления.

Так как движение происходит от точки А к Б, то и давление возле А будет больше, чем около Б. Эта разность давлений и приводит к ускорению.

Условия действия

Закон применим для условия, при котором соблюдается неразрывность струи воздуха или жидкости. В тех участках потока, где скорость течения больше, давление будет меньше и наоборот. Это утверждение и называется теоремой Бернулли. По сути, закон позволяет установить связь между давлением, скоростью, высотой.

Пусть имеется труба переменного сечения с изменяющейся высотой. Внизу она широкая, а затем сужается. По ней течёт жидкость. Площадь сечения можно обозначить как S1 и S2, а давление участков и скорость движения на них P1, P2, V1, V2. Высота внизу будет равняться S1, а вверху S2.

Выделив участок в трубе с жидкостью, можно сказать, что она движется слева направо и через некоторое время полностью сдвинется в область S2. Изменение положения слева будет равно расстоянию дельта L1, а справа — дельта L2.

Течение является:

ламинарным — находящаяся в трубке жидкость перемешивается слоями без хаотических изменений давления и скорости, турбулентность отсутствует;
стационарным — распределение скоростей не изменяется с течением времени;
скоростным — в движении принимает участие такой параметр, как ускорение;
идеальным с несжимаемой жидкостью.

Последнее обозначает, что нет вязкости. Поэтому на жидкость действует только сила упругости и тяжести, а силы трения нет. Система не является замкнутой, а значит закон сохранения энергии применительно к рассматриваемому участку использовать нельзя. Зато вполне можно применить теорему о кинетической энергии.

Для газов уравнение можно использовать лишь в том случае, если их плотность изменяется незначительно. Но касаемо аэродинамики учитывается и то, что изменение давления воздуха гораздо меньше атмосферного. Поэтому уравнение можно применять в аэродинамических расчётах.

Согласно ему, сумма действующих всех сил на тело (рассматриваемый кусок жидкости) равняется изменению кинетической энергии объекта: ΣAi = ΔEk. На нижний участок действует сила давления, выполняющая положительную работу, а на верхний — отрицательную. Кроме этого, действует и сила тяжести. Так как жидкость поднимается, она имеет тоже отрицательный знак. Сила бокового давления перпендикулярна любой точке в системе, поэтому никакого влияния она не оказывает.

Количественная сторона

Исходя из сил, действующих на тело, изменение кинетической энергии можно описать выражением: ΔEk = Ap1 +Ap2 +Ag. Чтобы найти работу, необходимо силу умножить на пройденное расстояние. Поэтому работа силы давления равна произведению самой силы F на модуль перемещения ΔL и косинусу угла между ними: Ap1 = F1* ΔL *1.

Чтобы найти силу, нужно давление умножить на площадь. Значит: Ap1 = p 1 * S1 * ΔL1 = p1V1. Таким же образом находится работа для второго состояния: Ap2 = F1* ΔL2 *(-1) = — p2 * S2 * ΔL2 = -p2 * V2. Жидкость несжимаемая, следовательно: V1=V2=V.

Работу силы тяжести можно вычислить исходя из того, что рассматриваемый кусок жидкости является относительным, то есть он, хотя и не статический, в любом месте будет подвергаться воздействию одинаковой силы тяжести. Верным будет выражение: Ag = — ΔEp = — (m2 * g * h2 — m1 * g * h1) = m1 * g * h1 — m2 * g * h2. Так как жидкость несжимаемая, её плотность не изменится. Отсюда можно утверждать: Ag = ρ * V * g * h1 — ρ * V * g * h2.

Зная количественные показатели всех трёх работ, можно найти изменение кинетической энергии. Из физики известно, что оно равно разнице конечной и начальной энергии. Течение стационарное, значит, скорость с течением времени не изменится. Следовательно, кинетическая энергия будет определяться разницей появившейся энергии в верхней части и ушедшей из нижней области: ΔEk = (m2 * v2 2 )/2 — (m1 * v1 2 ) / 2.

Воспользовавшись тем, что масса равняется произведению плотности на объём, формулу можно привести к виду: ΔEk = (ρ * V * v2 2 )/2 — (ρ * V * v1 2 ) / 2. Теперь найденные выражения для работ нужно подставить в теорему о кинетической энергии. Получится следующее равенство: p1V — p2V + ρ * V * g * h1 — ρ * V * g * h2 = (ρ * V * v2 2 ) / 2 — (ρ * V * v1 2 ) / 2. Разделив левую и правую часть на объём, выражение можно упростить до вида: p1 — p2 + ρ * g * h1 — ρ * g * h2 = (ρ * v2 2 )/2 — (ρ * v1 2 ) / 2 .

То место, где давление p1, некая точка внутри трубки, пусть будет обозначено цифрой один, а там, где p2, — цифрой два. Всё что относится к единице можно записать в левой части, а к двойке — в правой: ρ1 * g * h1 + (ρ * v1 2 ) / 2 = ρ * g * h2 + (ρ * v2 2 ) / 2. Полученная формула показывает, что при переходе в пределе одной линии скорость, давление и высота изменяются. Поэтому в любой точке будет справедливым выражение: ρ1+ ρ * g * h + (ρ * v1) / 2 = const. Это и есть количественное описание уравнения Бернулли для идеальной жидкости.

Применение в гидравлике

Наиболее типичным примером использования уравнения является решение заданий по нахождению скорости вытекания жидкости из отверстия в широком сосуде. Такой ёмкостью называют систему, в которой диаметр сосуда значительно больше размера отверстия. Необходимо найти скорость вытекающей жидкости U1. Известно, что высота столба жидкости, на который действует сила тяжести g, равна h.

Пусть в жидкости, находящейся сверху, имеется точка один. Через некоторое время она окажется внизу в положении два. На верх жидкости давит атмосферное давление, поэтому p1=pатм. Высота в точке один равна h. Скорость U1 считают равной нулю. Давление p2 в точке два будет также равно атмосферному. Так как жидкость опустится на дно, то высота h2 станет нулевой.

Все эти величины следует подставить в уравнение Бернулли. Получится выражение: pатм + ρ * g * h + 0 = pатм + (ρ * U 2 ) / 2 + 0. Атмосферное давление взаимно уничтожается: ρ * g * h = (ρ * U 2 ) / 2. В левой и правой части стоит плотность, на которую можно сократить. Отсюда получается, что вид жидкости значения не имеет. Это может быть: вода, ртуть, расплавленный металл. Эффект от этого не поменяется. Из формулы можно выразить искомое U2. Оно будет равно: U2 = (2 * g * h) ½ .

Интересным фактом является то, что полученный ответ при решении задачи называется формулой Торричелли. Она показывает, что скорость, с которой вытекает жидкость из широкого сосуда, равна скорости тела при свободном падении с той же высоты.

Используя уравнение, можно легко рассчитать давление жидкости на дно и стенки сосуда. В этом случае закон Бернулли является обобщением для формулы гидростатического давления. Пусть имеется сосуд с жидкостью высотой h. Точка, находящаяся наверху, характеризуется давлением p1 = pатм., высотой h1 равной h и скоростью U1. Для точки на дне параметры будут следующие: p2 = p, h2 = 0, U2 = 0. Скорости принимаются равными нулевому значению, так как рассматриваемая жидкость находится в состоянии покоя.

Данные следует подставить в уравнение. В итоге получится равенство: pатм + ρ * g * h + 0 = p + 0 + 0. Из него несложно найти неизвестное: p = pатм + ρ * g * h. Полученный ответ является формулой гидростатического давления и подтверждает закон Паскаля.

Аналогично уравнение Бернулли для потока реальной жидкости используется при расчёте расхода в карбюраторе, пульверизаторе, учёте статического и динамического давления.

Подъёмная сила

Самолёт летает благодаря тому, что набегающий на крыло напор воздуха создаёт подъёмную силу. Её можно рассчитать и оценить с помощью уравнения. Геометрически крыло можно представить в виде плоскости с углом a (угол атаки). На него действует поток воздуха со скоростью U. Частица воздуха ударяет в твёрдую поверхность и отражается от неё. Угол отражения равен углу атаки, а её скорость равняется U’. Нужно рассчитать подъёмную силу. Для этого необходимо выполнить три шага:

рассмотреть изменение скорости воздуха;
узнать импульс частиц;
используя закон Ньютона, определить силу.

В результате получится, что на крыло действует сила, состоящая из двух компонентов: подъёмной силы Fy и аэродинамического сопротивления Fx. Fy = Cy * p * U 2 * S, а Fx = Cx * p * U 2 * S. В формулах С является коэффициентом, а S — площадью крыла.

Для расчёта используется уравнение Бернулли. Выглядеть оно будет следующим образом: Pп. к + (ρ * Uп. к) * 2 / 2 + ρ * g * hп. к = Pн. к + (ρ * Uн. к) * 2 / 2 + ρ * g * hн. к, где: п. к — под крылом, а н. к — над крылом. Это уравнение можно упростить, приняв, что давления над и под крылом примерно одинаковые, поэтому плотность будет также одинаковая. Кроме того, высота крыла довольно маленькая. Исходя из этого, формулу можно упростить, и она примет вид: pп. к-pн.к = (ρ * (Uн.к + Uп. к) * (Uн.к — Uп. к)) / 2 = 2 * U1 * U2. Теперь можно найти подъёмную силу. Для этого разность давлений нужно умножить на площадь крыла: Fy = (pп.к-pн. к) * S.

Таким образом, используя метод, можно рассчитать подъёмную силу, обусловленную эффектом Бернулли. Например, пусть дано, что площадь крыла равна 50 м². Скорость потока воздуха над крылом и под ним соответственно равны: U1 = 320 м/с, U2 = 290 м/с. Найти грузоподъёмность. Для решения задания нужно знать дифференциальную плотность воздуха. Это справочная величина, равная 1,29 кг/м3.

Используя уравнение Бернулли, можно записать: pп. к-pн.к = ρ * (U2н.к — U2п. к). Подъёмная сила равна площади крыла, умноженной на разность давления. Подставив одно выражение в другое, получим рабочую формулу: Fy = ρ * (U2н.к — U2п. к) * S / 2. После выполнения расчёта получится ответ 590 кН. То есть грузоподъёмность самолёта составит порядка 59 тонн.

Реальные вычисления для таких задач довольно сложные, поэтому часто используют онлайн-калькуляторы.

источники: