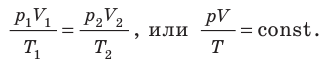Термическое и калорическое уравнения состояния. Термическое уравнение состояние идеального газа
Второй постулат ТД приводит к существованию функциональных соотношений, называемых уравнения состояния, устанавливающих связь между внешними параметрами, температурой и каким-либо внутренним параметром состояния макросистемы. Т.е. параметры системы не могут принимать произвольное значение. Для любой системы они связаны некоторым функциональным соотношением.
Если этим внутренним параметром является внутренняя энергия 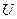
Если внутренним параметром является какая-либо обобщенная сила, то уравнение называется термическим уравнение состояния.
Общее число термических и калорического уравнений состояния системы равно числу ее степеней свободы, т.е. числу независимых параметров, характеризующих состояние системы. Если все эти уравнения состояния известны, то с помощью начал термодинамики можно определить все термодинамические свойства системы.
Вывести сами уравнения состояния на основе начал ТД нельзя. Для каждой конкретной системы они определяются эмпирически, т.е. берутся из опыта, или находятся методами статистической физики. Так что в рамках ТД они считаются заданными при определении системы.
До сих пор не существует удовлетворительной общей теории уравнений состояния, кроме случаев особых простых систем: идеального газа и совершенных кристаллов. Для жидкостей и твердых тел соотношения между параметрами состояния до сих пор получают эмпирически.
Ограничимся рассмотрением простых систем, систем с постоянным числом частиц, состояние которых определяется только одним внешним параметром и температурой.
Термическое уравнение состояния такой системы, записанное в общем виде:

Калорическое уравнение состояния, записанное в общем виде:
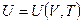
для идеального газа уравнение состояния (термическое) — это уравнение
Менделеева-Клапейрона 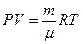
для модели реального газа уравнение состояния — это уравнение Ван-дер-Ваальса
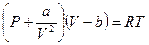
Если известны два параметра, то третий находится из уравнения состояния

Например: 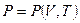
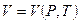
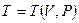
Уравнение состояния изображается в условном пространстве 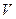
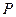
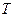
Калорическое уравнение состояния для идеального газа
Из основных положений статистической механики следует, что термодинамические свойства классической системы, состоящей из N одинаковых частиц и занимающей объем V при температуре T, полностью определяются канонической статистической суммой (статистическим интегралом):
Z(T,V,N) = 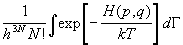
где H(p,q) — классическая функция Гамильтона системы, dГ = d 3N p d 3N q — элемент фазового объема (d 3N p =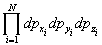
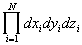
Статистическая сумма содержит в себе всю термодинамическую информацию о системе. Если удалось теоретически рассчитать статистическую сумму (как это сделать — отдельный вопрос), то можно определить все термодинамические функции и вывести термическое и калорическое уравнения состояния. Так, свободная энергия Гельмгольца связана со статистической суммой соотношением:
Энтропия и давление системы связаны с производными статистической суммы по температуре и объему, соответственно:
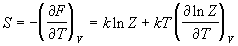
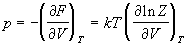
Последнее соотношение дает давление как функцию температуры и объема, т.е. термическое уравнение состояния. Калорическое уравнение состояния, т.е. зависимость внутренней энергии от температуры и объема дается соотношением:
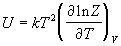
Таким образом, основная задача классической статистической термодинамики состоит в расчете статистической суммы (2.1).
Формулы (2.2) – (2.5), выражающие связь между термодинамикой и статистической механикой, справедливы для любых термодинамических систем. Формула (2.1) справедлива только для классических систем, в которых квантовые эффекты несущественны, в частности для систем, состоящих из частиц, не имеющих внутренней структуры. Многие такие системы (например, газы и жидкости) описываются гамильтонианом вида
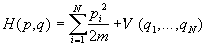
где m — масса частиц, V — потенциальная энергия их взаимодействия друг с другом. В гамильтониане (2.6) координаты и импульсы разделены, поэтому интегрирование по ним можно провести независимо. Подставляя (2.6) в (2.1) и вычисляя интегралы по N импульсам
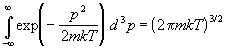
получаем статистическую сумму в виде
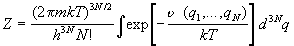
Интеграл по координатам в формуле (2.7) называют конфигурационным интегралом:
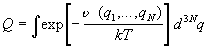
Именно он определяет зависимость статистической суммы от объема и содержит в себе описание всех отклонений системы от идеального поведения. Давление системы определяется только конфигурационным интегралом:
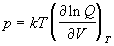
2.2. Статистическая термодинамика идеального одноатомного газа
Для идеального газа потенциал взаимодействия частиц равен нулю. Кроме того, в этой модели частицы не имеют собственного объема, поэтому интегрирование по координатам проводится по всему объему системы и конфигурационный интеграл равен
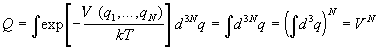
Статистическая сумма имеет вид:
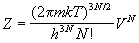
Все термодинамические функции выражаются через логарифм статистической суммы:
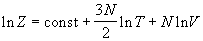
Подставляя (2.11) в (2.4), находим термическое уравнение состояния идеального одноатомного газа (зависимость давления от температуры и объема):
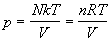
где n = N / NA — число молей, R = kЧ NA — универсальная газовая постоянная. Калорическое уравнение состояния (зависимость внутренней энергии от температуры и объема) получается при подстановке (2.11) в (2.5):
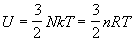
Наконец, из (2.10) и (2.3) можно получить уравнение Закура-Тетроде для энтропии одного моля одноатомного идеального газа:
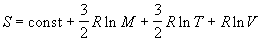
где M = mЧ NA — молярная масса газа. Значение постоянной в этом уравнении зависит от размерностей величин, стоящих под знаком логарифма [4, с. 210].
Таким образом, на примере идеального газа мы реализовали схему, демонстрирующую связь микроскопических свойств (гамильтониана) системы с ее макроскопическими (т.е., термодинамическими) свойствами:
| Гамильтониан | Статистическая сумма | Термодинамические функции, уравнение состояния |


Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору
Уравнение состояния идеального газа — основные понятия, формулы и определение с примерами
Содержание:
Уравнение состояния идеального газа:
Уравнения Клапейрона и Менделеева — клапейрона; законы Шарля, Гей-Люссака, Бойля — Мариотта, Авогадро, Дальтона, — пожалуй, такого количества «именных» законов нет ни в одном разделе физики. за каждым из них — кропотливая работа в лабораториях, тщательные измерения, длительные аналитические размышления и точные расчеты. нам намного проще. Мы уже знаем основные положения теории, и «открыть» все вышеупомянутые законы нам не составит труда.
Уравнение состояния идеального газа
Давление газа полностью определяется его температурой и концентрацией молекул: p=nkT. Запишем данное уравнение в виде: pV = NkT. Если состав и масса газа известны, число молекул газа можно найти из соотношения
Произведение числа Авогадро 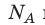
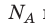
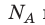
Обратите внимание! Состояние данного газа некоторой массы однозначно определяется двумя его макроскопическими параметрами; третий параметр можно найти из уравнения Менделеева — Клапейрона.
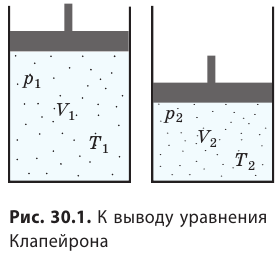
Уравнение Клапейрона
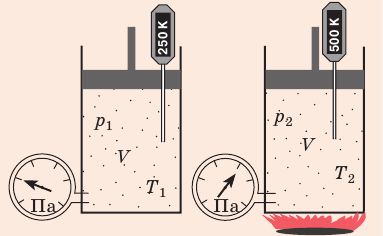
С помощью уравнения Менделеева — Клапейрона можно установить связь между макроскопическими параметрами газа при его переходе из одного состояния в другое. Пусть газ, имеющий массу m и молярную массу М, переходит из состояния (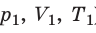
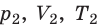
Для каждого состояния запишем уравнение Менделеева — Клапейрона: 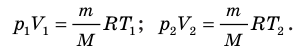
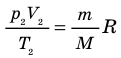
Для данного газа некоторой массы отношение произведения давления на объем к температуре газа является неизменным.
Изопроцессы
Процесс, при котором один из макроскопических параметров данного газа некоторой массы остается неизменным, называют изопроцессом. Поскольку состояние газа характеризуется тремя макроскопическими параметрами, возможных изопроцессов тоже три: происходящий при неизменной температуре; происходящий при неизменном давлении; происходящий при неизменном объеме. Рассмотрим их.
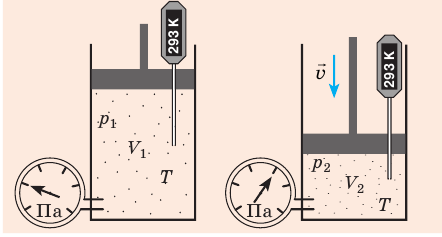
Какой процесс называют изотермическим. Закон Бойля — Мариотта
Пузырек воздуха, поднимаясь со дна глубокого водоема, может увеличиться в объеме в несколько раз, при этом давление внутри пузырька падает, поскольку вследствие дополнительного гидростатического давления воды (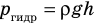
Рис. 30.2. Изотермическое сжатие газа. Если медленно опускать поршень, температура газа под поршнем будет оставаться неизменной и равной температуре окружающей среды. Давление газа при этом будет увеличиваться
Изотермический процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменной температуре.
Пусть некий газ переходит из состояния (
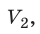
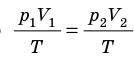
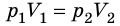
Закон Бойля — Мариотта:
Для данного газа некоторой массы произведение давления газа на его объем остается постоянным, если температура газа не изменяется:
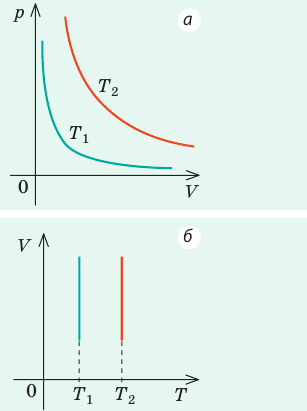
Графики изотермических процессов называют изотермами. Как следует из закона Бойля — Мариотта, при неизменной температуре давление газа данной массы обратно пропорционально его объему: 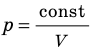
Какой процесс называют изобарным. Закон Гей-Люссака
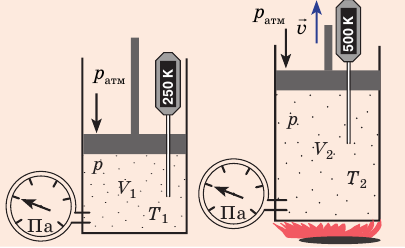
Изобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном давлении.
Пусть некий газ переходит из состояния (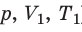
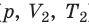
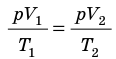
Рис. 30.4. Изобарное расширение газа. Если газ находится под тяжелым поршнем массой M и площадью S, который может перемещаться практически без трения, то при увеличении температуры объем газа будет увеличиваться, а давление газа будет оставаться неизменным и равным p
Закон Гей-Люссака
Для данного газа некоторой массы отношение объема газа к температуре остается постоянным, если давление газа не изменяется:
Графики изобарных процессов называют изобарами. Как следует из закона Гей-Люссака, при неизменном давлении объем газа данной массы прямо пропорционален его температуре: V = const⋅T. График данной зависимости — прямая, проходящая через начало координат (рис. 30.5, а). По графику видно, что с приближением к абсолютному нулю объем идеального газа должен уменьшиться до нуля. Понятно, что это невозможно, поскольку реальные газы при низких температурах превращаются в жидкости. В координатах p, V и p, T изобары перпендикулярны оси давления (рис. 30.5, б, в).
Изохорный процесс. Закон Шарля
Если газовый баллон сильно нагреется на солнце, давление в нем повысится настолько, что баллон может взорваться. В данном случае имеем дело с изохорным нагреванием.
Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном объеме.
Пусть некий газ переходит из состояния (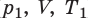
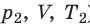
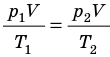
Рис. 30.6. Изохорное нагревание газа. Если газ находится в цилиндре под закрепленным поршнем, то с увеличением температуры давление газа тоже будет увеличиваться. Опыт показывает, что в любой момент времени отношение давления газа к его температуре неизменно:
Закон Шарля
Для данного газа некоторой массы отношение давления газа к его температуре остается постоянным, если объем газа не изменяется:
Графики изохорных процессов называют изохорами. Из закона Шарля следует, что при неизменном объеме давление газа данной массы прямо пропорционально его температуре: p T = ⋅ const . График этой зависимости — прямая, проходящая через начало координат (рис. 30.7, а). В координатах p, V и V, T изохоры перпендикулярны оси объема (рис. 30.7, б, в).
Пример №1
В вертикальной цилиндрической емкости под легкоподвижным поршнем находится 2 моль гелия и 1 моль молекулярного водорода. Температуру смеси увеличили в 2 раза, и весь водород распался на атомы. Во сколько раз увеличился объем смеси газов?
Анализ физической проблемы. Смесь газов находится под легкоподвижным поршнем, поэтому давление смеси не изменяется:
Решение:
Воспользуемся уравнением состояния идеального газа: pV = νRT. Запишем это уравнение для состояний смеси газов до и после распада: 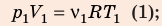
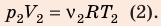

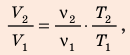
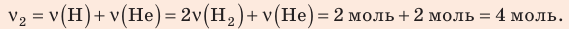
Ответ: примерно в 2,7 раза.
Пример №2
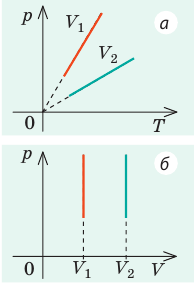
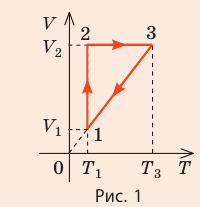
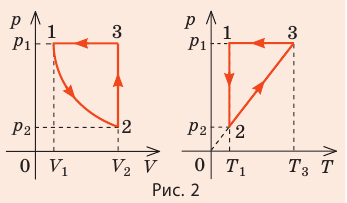
На рис. 1 представлен график изменения состояния идеального газа неизменной массы в координатах V, T. Представьте график данного процесса в координатах p, V и p, T.
Решение:
1. Выясним, какой изопроцесс соответствует каждому участку графика (рис. 1).
Зная законы, которым подчиняются эти изопроцессы, определим, как изменяются макроскопические параметры газа. Участок 1–2: изотермическое расширение; T = const, V ↑, следовательно, по закону Бойля — Мариотта p ↓. Участок 2–3: изохорное нагревание; V = const, T ↑, следовательно, по закону Шарля p ↑ . Участок 3–1: изобарное охлаждение; p = const , T ↓, следовательно, по закону Гей-Люссака V ↓ .
2. Учитывая, что точки 1 и 2 лежат на одной изотерме, точки 1 и 3 — на одной изобаре, а точки 2 и 3 на одной изохоре, и используя результаты анализа, построим график процесса в координатах p, V и p, T (рис. 2)
- Из соотношения p=nkT можно получить ряд важных законов, большинство из которых установлены экспериментально.
- Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):
— универсальная газовая постоянная.
- Уравнение Клапейрона:
- Законы, которым подчиняются изопроцессы, то есть процессы, при которых один из макроскопических параметров данного газа некоторой массы остается неизменным:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://www.chem.msu.su/rus/teaching/realgases/chap2(1-2).html
http://www.evkova.org/uravnenie-sostoyaniya-idealnogo-gaza
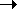
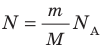
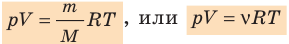
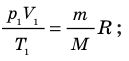
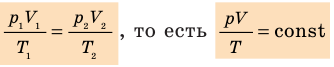
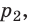
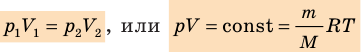

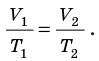
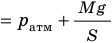
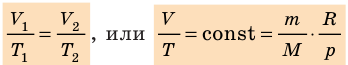
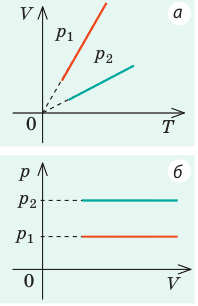

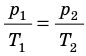
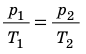
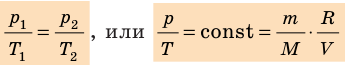

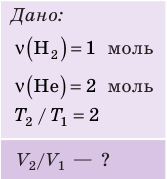
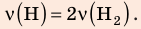

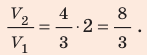
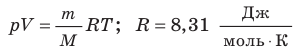 — универсальная газовая постоянная.
— универсальная газовая постоянная.