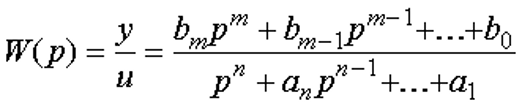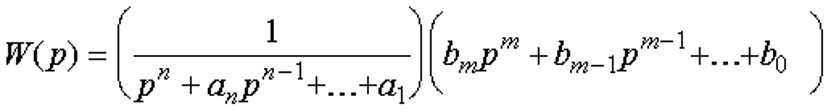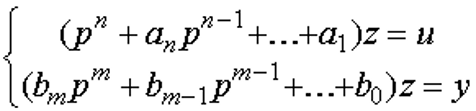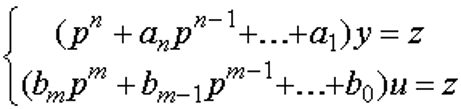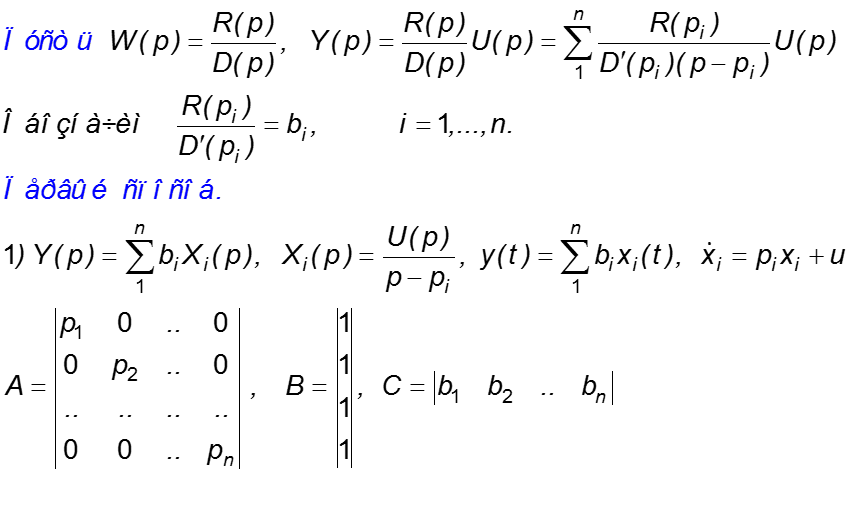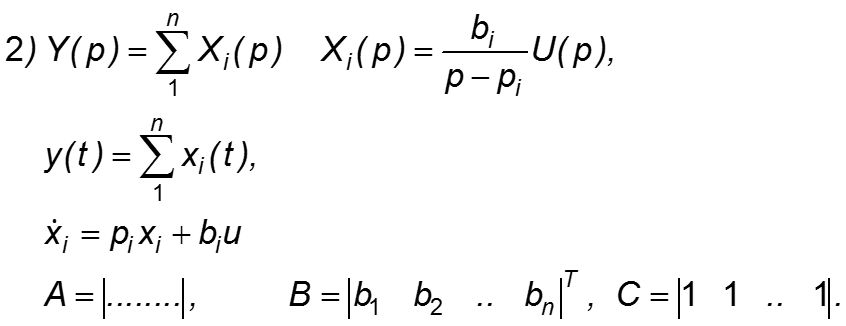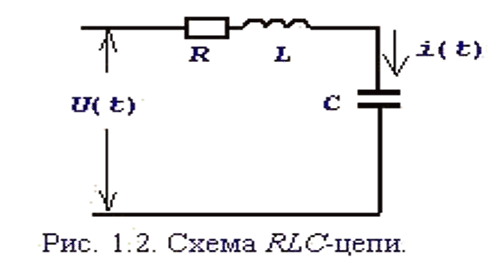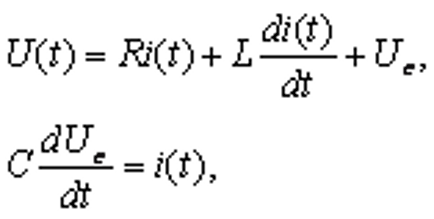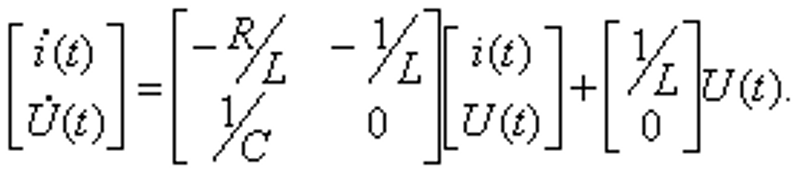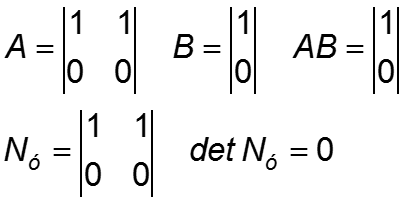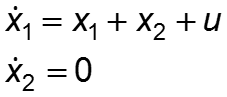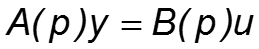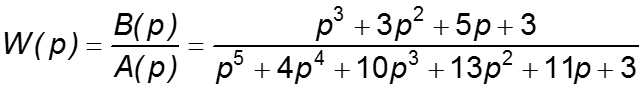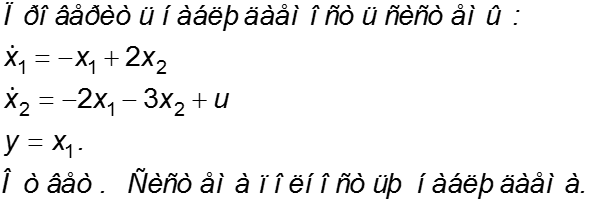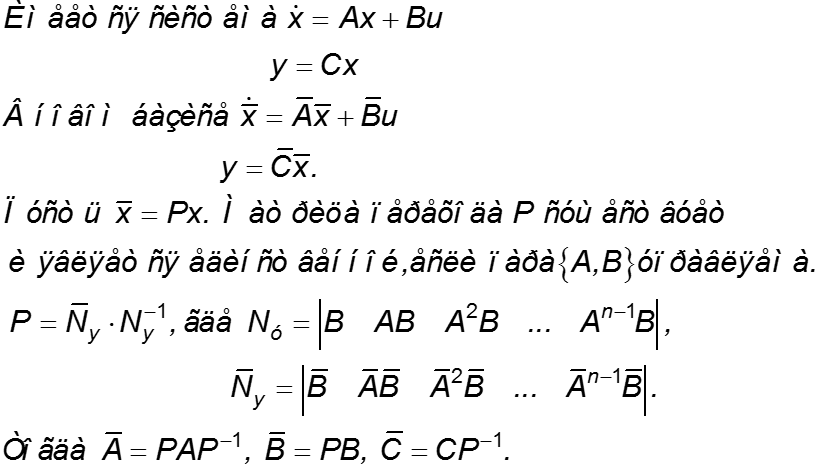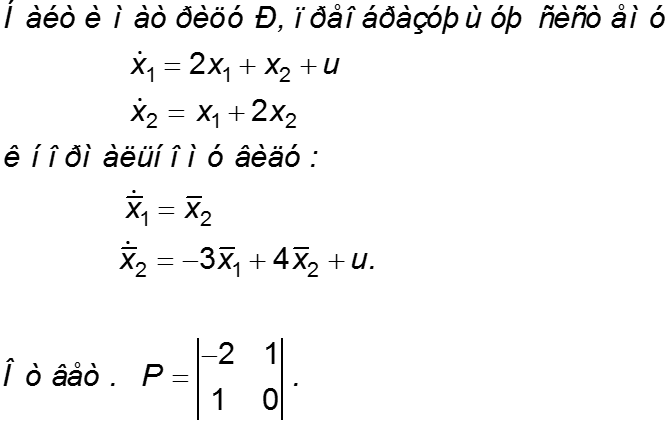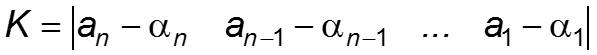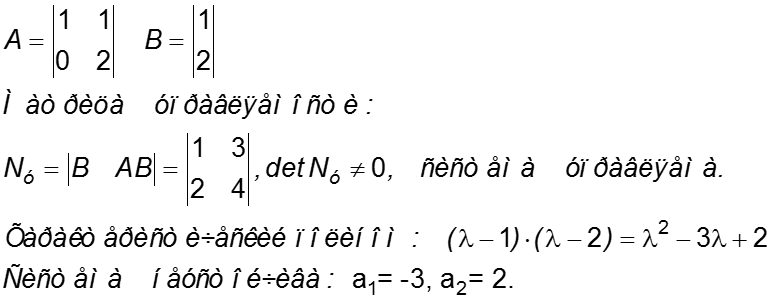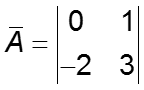Канонические формы уравнений в пространстве состояний

Канонические формы уравнений в пространстве состояний

Тема: «Канонические формы уравнений состояния»

Математические модели объектов управления первоначально получаются на основе расчетных данных и физического поведения объекта. В этом случае переменные состояния представляют собой физические переменные объекта, и описания в пространстве состояний объективно связываются с физической реальностью.

В некоторых случаях, однако, полезно ввести переменные состояния, которые формально определяются как линейная комбинация различных физических переменных. Такое преобразование выполняется в целях получения определенных канонических форм уравнений состояния, что облегчает обнаружение некоторых свойств объекта и системы или позволяет описать их с помощью меньшего числа параметров, а также установить для односвязных систем (с одним входом и одним выходом) непосредственную связь векторно-матричных моделей с моделями типа “вход — выход”.

Рассмотрим n-мерный вектор — допустимый вектор состояния некоторой системы и невырожденную матрицу T (n x n). Тогда вектор z=Tx — также возможный вектор состояния рассматриваемой системы.

Реальная система с вектором состояния x описывается следующими уравнениями при D=0:

Эта же система с вектором состояния z:

Подставляя выражение x=T — 1 z в (5.1) , получим

Умножая первое уравнение (5.3) слева на T, получим

Сравнивая (5.4) и (5.2), легко установим, что

Таким образом, матрицы А, В, С зависят от используемого координатного базиса.

Интерес представляют инварианты, полученные после преобразования.

Теорема 5.6. Характеристическое уравнение непрерывной и дискретной систем является инвариантом, если новые состояния вводятся через невырожденную матрицу Т.

Для доказательства теоремы запишем характеристический полином матрицы z A:

Таким образом, характеристическое уравнение матрицы состояния и ее собственное значение не зависят от базиса пространства состояний.

Следовательно, можно утверждать, что свойства систем не изменяются при изменении базиса пространства состояний.

Например, ранг матрицы управляемости не изменяется, так как

или в краткой форме

Ранг матрицы наблюдаемости также не изменится, поскольку

Из (5.8) и (5.10) могут быть получены полезные соотношения для поиска соответствующей матрицы преобразования:

Особый интерес представляют так называемые канонические формы, названные в силу их простоты и непосредственной связи элементов матрицы состояния с коэффициентами характеристического уравнения или для односвязных систем с коэффициентами полиномов передаточной функции.

Каноническая форма управляемости

Здесь и далее остановимся на рассмотрении только односвязных динамических систем.

Предположим, что характеристическое уравнение матрицы А имеет вид

и матрица управляемости не вырождена. Тогда существует такое преобразование, при котором преобразованная система имеет вид

или в компактной форме

Соответствующая передаточная функция системы, описываемой уравнениями состояния (5.13), имеет вид

Матрица преобразования ВММ в каноническую форму управляемости может быть найдена по уравнениям (5.11). Однако этот процесс трудоемкий, поэтому можно использовать другие существующие способы ее определения.

Первый способ основан на использовании так называемой матрицы Фробениуса [14], которая представляет собой матрицу состояния системы в не рассматриваемой здесь канонической форме достижимости, или

— матрица управляемости размером n x n, а₀, а₁. а_n-1 — коэффициенты характеристического уравнения (5.12), которые могут быть найдены в результате расчета матрицы Фробениуса.

Матрица преобразования v T вычисляется с помощью следующего выражения

Таким образом, алгоритм преобразования ВММ к канонической форме управляемости (5.14) включает в себя следующие операции:

1. Вычисление матрицы управляемости Q_у согласно (5.17).

2. Вычисление матрицы Фробениуса F по формуле (5.16), транспонирование F для определения v A=F T .

3. Вычисление матрицы v Q линейного преобразования по формуле (5.18).

4. Вычисление матрицы выхода, определяющей выходную переменную y по новому вектору состояния z:

Второй способ позволяет вычислить матрицу преобразования v Q рекуррентно по столбцам q_i

Действительно, на основании приведенных выше рассуждений можно записать:

Так как вектор v B известен, то мы можем сначала вычислить

и далее продолжить вычисления по отдельным столбцам справа налево:

Последняя строка может служить для контроля.

Коэффициенты a_i, i=0,1,2. n-1, матрицы v А можно определить с помощью определителя .

Пример 5.1. Выполним переход к канонической форме управляемости для непрерывной ВММ электродвигателя постоянного тока.

В пространстве состояния получим

Запишем характеристическое уравнение системы

из которого следует, что матрицы состояния и управления в новом координатном базисе будут иметь следующий вид

Определим матрицу преобразования Q.

Первый способ. Используем выражение (5.18) , которое для нашего примера запишется следующим образом

Такой же результат получается и по второму способу. Из выражения (5.20) получаем

Теперь определим матрицу v C в новом координатном базисе

Таким образом, ВММ нашего объекта в канонической форме управляемости принимает следующий вид

Каноническая форма наблюдаемости

Если желательно иметь матрицу в простейшей форме, то можно воспользоваться так называемой канонической формой наблюдаемости:

или в компактной форме

Как видно из выражений (5.13) и (5.22), матрицы состояний обеих канонических форм идентичны, то есть .

Для канонической формы наблюдаемости матрица наблюдаемости — единичная матрица, то есть

Для нахождения матрицы N B= N TB= N Q -1 B матрица N Т может быть вычислена согласно выражению (5.11):

Так как в нашем случае , получаем, что матрица преобразования ВММ в каноническую форму наблюдаемости (5.22) соответствует матрице наблюдаемости исходной системы

В таком случае выражение для вычисления матрицы N B принимает следующий вид:

Пример 5.2. Выполним переход к канонической форме наблюдаемости для непрерывной ВММ электродвигателя постоянного тока (5.21).

Здесь нам необходимо только определить новое содержание матрицы N B. Для этого воспользуемся выражением (5.26)

Таким образом, ВММ нашего объекта в канонической форме наблюдаемости принимает следующий вид

Основные свойства объектов и систем управления можно оценить в автоматизированном режиме с помощью подсистемы Анализ Компьютерного комплекса функционального проектирования динамических систем (FuncPro 1.0). На рис. 5.1 приведено основное окно подсистемы, в котором раскрыто меню «Анализ»

Рис. 5.1. Основное окно подсистемы «Анализ»

Контрольные вопросы к лекции № 5.

1. Какие свойства и характеристики системы изменятся после преобразования ее векторно-матричной модели к новому координатному базису с помощью невырожденной матрицы Т.

2. Допустим, что нам необходимо привести ВММ непрерывной системы с одним входом и одним выходом

к канонической форме управляемости. Предварительно определены коэффициенты характеристического уравнения системы и матрица преобразования . Для вычисления какой матрицы преобразованной системы будет использована матрица Q.

3. Допустим, что нам необходимо привести ВММ непрерывной системы с одним входом и одним выходом

к канонической форме наблюдаемости. Предварительно определены коэффициенты характеристического уравнения системы и матрица преобразования . Для вычисления какой матрицы преобразованной системы будет использована матрица Q.

4. Какова будет матрица наблюдаемости непрерывной системы

ОТВЕТЫ

внутреннее содержание матриц состояния А(Ф), управления по состоянию В(Г), выхода С.

матрицы выхода по состоянию

матрицы управления ;

Электронный учебник по ТАУ (теория автоматического управления)

ТАУ Модели «вход – состояние – выход»

ТАУ предлагает два основных подхода к анализу и синтезу линейных САУ. Первый базируется на структурных схемах и ПФ отдельных элементов и всей системы. В связи с этим его часто называют операторно—структурным. Другой его особенностью является использование физических величин в качестве переменных. Подробно этот подход рассмотрен при изучении ММ типа «вход – выход» (см. п. 2.1).

Второй подход отличается описанием САУ системой ОДУ первого порядка, составленных относительно переменных состояния. Переменные состояния при таком описании САУ аналогичны обобщенным координатам, используемым в теоретической механике. Сам подход к исследованию САУ получил название метода пространства состояний или метода переменных состояния.

Понятие пространства состояний

Согласно методу пространства состояний (МПС) все переменные величины, характеризующие САУ, разделяют на три группы:

1) входные переменные или входные (управляющие) воздействия u m ;

2) выходные переменные y p , характеризующие реакцию САУ на входные воздействия;

3) переменные (координаты) состояния x n , характеризующие динамическое поведение САУ.

Взаимосвязь названных переменных поясняют схемой САУ, на которой систему изображают в виде «черного ящика» в соответствии с рисунком 2.29.

Отдельные части САУ характеризуют ПФ W 1 (s) и W 2 (s). Как следует из схемы, переменные состояния x n являются промежуточными величинами. Их относят к содержимому «черного ящика». Следовательно, они скрыты от прямого наблюдения. Кроме того, переменные состояния

y 2 ( t )

u 1 ( t )

u 2 ( t )

u m ( t )

x 1 ( t )

x 2 ( t )

x n ( t )

y 1 ( t )

y n ( t )

W 1 ( s )

W 2 ( s )

не всегда являются физическими величинами. Иногда для удоб­ства математического моделиро­вания САУ целенаправленно отказываются от физического содержания переменных состоя­ния. Поэтому в общем случае x n (t) являются абстрактными переменными. Однако они должны однозначно выражаться через физические величины y p (t).

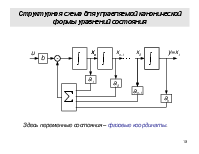
В общем случае исследуемую САУ считают многомерной (рисунок 2.29). Для упрощения работы с многомерными величинами их представляют в векторно-матричном виде. Так, совокупность входных переменных представляют в виде вектора входа совокупность выходных переменных – в виде вектора выхода а совокупность переменных состояния – в виде вектора состояния

Согласно МПС множество всех значений, которые может принять вектор входа U в момент времени t, образует пространство входа исследуемой САУ. Аналогично, множество всех значений, которые может принять вектор выхода Y в момент времени t, образует пространство выхода, а множество всех значений, которые может принять вектор состояния X в момент времени t, образует пространство состояний САУ.

Как было отмечено, векторно-матричные уравнения (2.82) описывают многомерную САУ. Эта же совокупность уравнений служит ММ одномерной САУ, т.е. системы с одним входом и одним выходом. При использовании МПС такие САУ часто называют системами со скалярным входом и выходом, так как входная и выходная величины являются скалярными. Уравнения состояния и выхода одномерной системы имеют вид

Канонические формы уравнений состояния

Разработано множество эквивалентных форм (представлений) уравнений состояния, различающихся между собой видом матриц A , B и C . Одни из форм используются чаще, так как обладают в некоторых случаях известными преимуществами перед другими. Такие формы записи уравнений состояния называются каноническими. Считают, что удобство канонических форм заключается в следующем. Во-первых, канонические представления матриц обеспечивают минимальное количество ненулевых элементов, что заметно упрощает вычисления. Во-вторых, канонические представления приводят к простым алгоритмам синтеза оптимальных регуляторов замкнутых САУ /3/.

Таким образом, в результате приведения уравнений к канонической форме более простую структуру принимают две из трех матриц: A и B (управляемые формы) или A и C (наблюдаемые формы). Управляемые канонические формы используют при синтезе регулятора, а наблюдаемые канонические формы – при синтезе наблюдателя /23/.

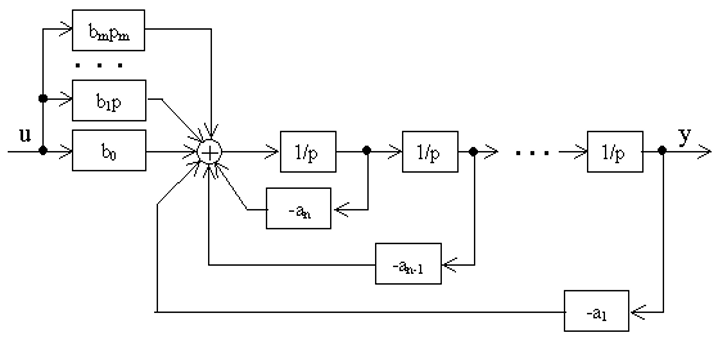
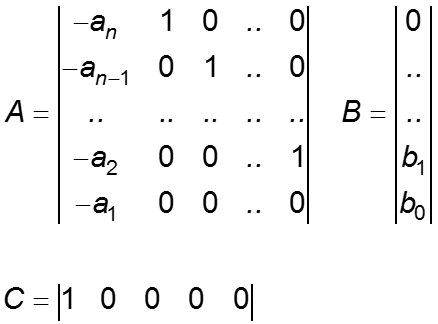
Первая управляемая каноническая форма

Первой управляемой канонической формой называют специальные матрицы

Очевидно, что коэффициенты характеристического полинома A(s) составляют последний столбец матрицы A. Матрицы такого вида называют матрицами Фробениуса. Элементы таких матриц определяют без вычислений. Характеристический многочлен A(s) совпадает со знаменателем ПФ системы управления. Корни данного многочлена определяют устойчивость и качество переходных процессов в САУ.

Матрица входа B рассматриваемого канонического представления также имеет специальный вид. Вследствие скалярного входного воздействия матрица B представляет собой вектор-столбец, элементы которого также не требуется вычислять.

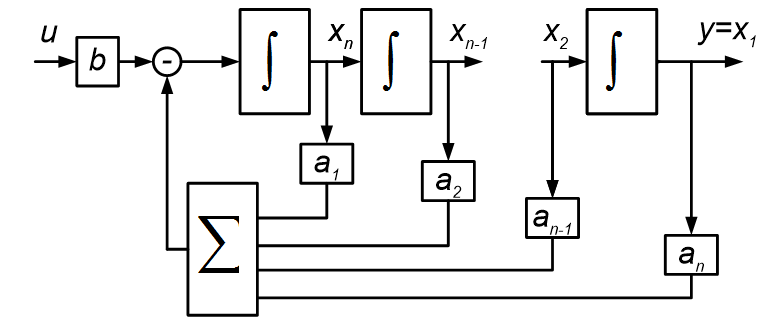
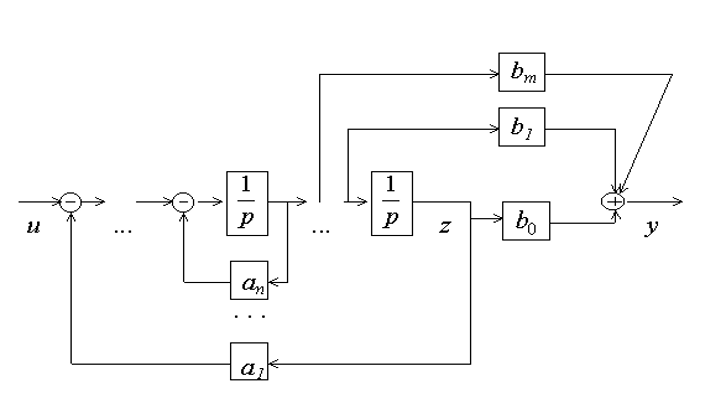
Полученная ММ системы управления может быть изображена в виде структурной схемы, представленной на рисунке 2.31.

Принятые переменные состояния являются выходными сигналами интеграторов.

Первую управляемую каноническую форму называют также канонической формой дуальной фазовой переменной /20/.

Методы переменных состояния в теории автоматического управления. Современная теория автоматического управления

Страницы работы

Фрагмент текста работы

Характеристическое уравнение располагается в последней строке.

Структурная схема для управляемой канонической формы уравнений состояния

Здесь переменные состояния – фазовые координаты.

Другая форма: в правой части уравнения содержатся производные от входного воздействия

Введем переменные состояния:

Здесь координаты состояния xi – абстрактные переменные.

Этим уравнениям соответствует структура:

Возможно другое представление:

Структурная схема может быть преобразована к виду:

Тогда матрицы A, B, C в уравнениях состояния будут:

Это — наблюдаемая каноническая форма уравнений состояния.

Таким образом, переход от передаточной функции к описанию в переменных состояния является неоднозначным.

Другие канонические формы уравнений состояния.

В двух последних формах матрица А – диагональная.

• Преимущества структурной модели :
• наглядное представление понятия «состояние систем»,
• однозначно представляется структура взаимодействий
• между переменными в виде системы с обратными связями,
• структурные модели полезны при моделировании САУ
• на аналоговых или цифровых вычислительных машинах.

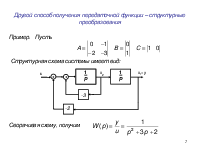
Пример получения уравнений состояния

П р и м е р. Система описывается дифференциальным уравнением Составим уравнения состояния и структурную схему

Свойства объектов и систем управления. Управляемость .

Определение. Система полностью управляема, если она может быть переведена из любого начального состояния x(0) в начало координат (0, 0,…,0) под действием управления u(t) за конечное время. Теорема Калмана об управляемости. Состояние непрерывной системы управляемо, если и только если ранг матрицы NУ = [B | AB | A2B | . | An-1B] равен размерности пространства состояний n.

Пример 1. Проверим, управляема ли система:

Пример 2. Также проверим управляемость системы:

Т.к. rangNy = 1 , система управляема неполностью. Порядок управляемой части равен 1.

В такой системе есть “висячая” часть на входе.

В случае представления объекта управления моделью типа “вход — выход” условием его управляемости является отсутствие общих корней полиномов А(p) и B(p): Т.е. система управляема, если алгебраические уравнения A(p)=a0pn+a1pn-1+…+an = 0, B(p)=b0pm+b1pm-1+…+bm = 0 не имеют общих корней.

Пример 2. Определим управляемость системы, имеющей передаточную функцию

Прямой расчет корней числителя и знаменателя дает результаты, приведенные в табл.

Таким образом, числитель и знаменатель передаточной функции W(p) имеют два общих корня (-1 -j1.414) и ( -1+j 1.414). Значит, система не управляема. Изменение значений корней для этих пар в числителе или знаменателе переведет систему в ранг управляемых.

• Для осуществления управления необходимо иметь информацию о текущем состоянии системы, т.е. о значениях вектора состояния x(t) в каждый момент времени.
• Однако некоторые из переменных состояния являются абстрактными, не имеют физических аналогов в реальной системе или же не могут быть измерены. Измеряемыми и наблюдаемыми являются физические выходные переменные y(t).
• Таким образом, возникает вопрос: можно ли определить вектор состояния по измеряемому вектору выхода и вектору входа?

• Определение. Система называется полностью наблюдаемой, если по результатам измерения входных u(t) и выходных y(t) переменных можно однозначно определить все составляющие вектора x(t) на конечном интервале времени.
• Теорема Калмана о наблюдаемости. Система наблюдаема, если и только если ранг матрицы
• Nн = [CT | ATCT | (AT)2CT | . | (AT)n-1CT].
• равен размерности пространства состояний.

Изменение базиса в уравнениях состояния

О синтезе системы

• Синтез системы — это направленный расчет, цель
• которого :
• построение рациональной структуры системы;
• нахождение оптимальных значений параметров отдельных звеньев.
• Качество управления можно описать двумя способами.
• Первый способ предусматривает или непосредственное задание динамических характеристик выходных координат системы при типовых воздействиях, или задание совокупности прямых и косвенных показателей качества (значение перерегулирования, времени регулирования, статической ошибки, частоты среза, полосы пропускания и т.д.).
• Второй способ основан на введении некоторого обобщенного функционала, определяемого всеми переменными системы управления u(t), x(t), y(t).
• В теории линейных систем управления широко используются оба указанных способа.

• Если передаточная функция системы не имеет нулей, то при выборе ее желаемого полинома D(p) можно руководствоваться стандартными формами (фильтрамиЧебышева, Баттерворта и др.)
• Стандартные формы определяют коэффициенты характеристического полинома , обеспечивающие в системе переходные и частотные характеристики с известными показателями качества.
• Если же система характеризуется наличием нулей, стандартные формы могут служить в качестве исходного материала для поиска своего оптимального расположения корней.
• Одним из основных методов проектирования детерминированных систем управления в пространстве состояний является метод расположения полюсов.

Распределение полюсов системы управления

• Рассмотрим систему с одним входом и одним выходом.
• Требуемое качество процессов может быть достигнуто заданием распределения полюсов замкнутой системы на комплексной плоскости.
• Для системы
• полюса системы — это собственные значения матрицы А или корни ее характеристического уравнения

• Если уравнения объекта заданы в нормальной форме (Фробениуса), то матрица обратных связей по состоянию
• Покажем это:

Нормальная форма матрицы А:

Пусть желаемые полюсы : λ1= -3, λ2= -2 Желаемый характеристический полином: φ=(λ+3)(λ+1)= λ 2+4 λ +3; α1=4, α2=3. Тогда k1 = a2 — α2 = 2 — 3 = -1, k2 = a1- α1 = -3 — 4 = -7. K = |-1 -7| Следовательно: v = u — x1 -7×2 Вычислив матрицу перехода P от исходной к нормальной форме можно получить матрицу обратной связи для исходного представления