Канонические уравнения плоскости через точку перпендикулярно вектору

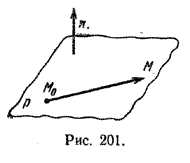
Уравнение плоскости, проходящей через точку перпендикулярно вектору

Пусть дана некоторая точка M₀ и ненулевой вектор n. Через точку M₀ можно провести только одну плоскость р перпендикулярную вектору n (рис. 201).

Выведем уравнение плоскости р. Пусть М — произвольная точка пространства. Очевидно, что точка М принадлежит плоскости р тогда и только тогда, когда вектор \(\overrightarrowM>\) перпендикулярен вектору n. Как известно, необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения. Поэтому уравнение плоскости, проходящей через точку M₀ перпендикулярно вектору n, может быть записано в виде

Вектор n в уравнении (1) называется нормальным вектором плоскости. В качестве нормального вектора можно взять любой вектор, перпендикулярный плоскости.

Пусть точка M₀ и вектор n заданы своими координатами в некоторой прямоугольной системе координат:

Обозначим координаты произвольной точки М плоскости р через х, у и z. Тогда вектор \(\overrightarrowM>\) имеет координаты х — х₀, у — у₀ и z — z₀, а уравнение (1) в координатах записывается следующим образом:

Это уравнение называется уравнением плоскости, проходящей через точку (х₀; у₀; z₀) перпендикулярно вектору (А; В; С).

Задача 1. Найти уравнение плоскости, проходящей через точку М₀(-3; 4; 7) перпендикулярно вектору n = (1; —2; 6).

В данном случае х₀ = -3, у₀ = 4, z₀ = 7; А = 1, В = -2, С = 6. Подставив эти значения в уравнение (2), получим искомое уравнение

3адачa 2. Даны точки M₁ (2; -1; 3) и M₂(4; 5; 0). Написать уравнение плоскости, проходящей через точку М₂ перпендикулярно вектору \(\overrightarrowM_2>\).

За нормальный вектор плоскости можно взять вектор n = \(\overrightarrowM_2>\) = (2; 6; -3). После подстановки координат нормального вектора и координат точки М₀ = М₂(4; 5; 0) в уравнение (2) получим

Задача 3. В треугольнике с вершинами в точках А₁<-5; 2; 7), А₂(5; 0; 6), А₃(0; -1; 2) проведена медиана А₁М₀. Найти уравнение плоскости, проходящей через точку М₀ перпендикулярно медиане А₁М₀.

За нормальный вектор плоскости можно принять вектор n = \(\overrightarrowM_0>\). Определим его координаты. Точка М₀ — середина отрезка А₂А₃, поэтому, если (х₀; у₀; z₀) — ее координаты, то

Координаты нормального вектора n = (А; В; С), следовательно, равны

A = 5 /₂ + 5 = 15 /₂, В = — 1 /₂ — 2 = — 5 /₂, С = 4 — 7 = — 3.

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости онлайн

С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через данную точку и перпендикуляной данной плоскости. Дается подробное решение с пояснениями. Для построения уравнения прямой введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости

Наша цель построить уравнение прямой, проходящей через данную точку M₀ и перпендикулярной к данной плоскости Ax+By+Cz+D=0.

Общее уравнение плоскости имеет вид:

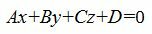(1)

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

(2)

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

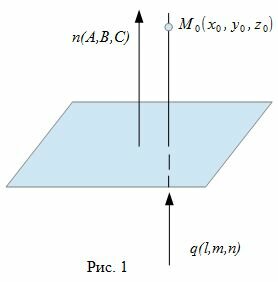Таким образом, уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и ортогональный плоскости (1) имеет следующий вид:

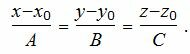(3)

Пример 1. Построить прямую, проходящую через точку M₀(5, -4, 4) и перпендикулярной плоскости

Общее уравнение плоскости имеет вид (1), где :

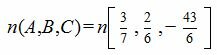(4)

Подставляя координаты точки M₀(5, -4, 4) и координаты нормального вектора плоскости (4) в (3), получим:

Канонические уравнения плоскости через точку перпендикулярно вектору

Пусть в декартовой системе координат дан вектор n = и точка М 0 =( x 0 , y 0 , z 0 ).

Построим плоскость Π, проходящую через т. М 0 , перпендикулярную вектору n (этот вектор называют нормальным вектором или нормалью плоскости).

Утверждение 1: М Π ó М 0 М n .

М 0 М= < x-x 0 , y-y 0 , z-z 0 > n ó A( x-x 0 )+B( y-y 0 )+C( z-z 0 )=0. (*)

Каноническое уравнение плоскости в пространстве:

Аx+By+Cz+D=0, где D = -A x 0 -B y 0 -C z 0 .

Замечание 1: формула (*) используется при непосредственном решении задач, после упрощения получается искомое каноническое уравнение плоскости.

Пример 1. Написать каноническое уравнение плоскости, перпендикулярной вектору n= <3,1,1>и проходящей через точку М(2,-1,1).

Пример 2. Написать каноническое уравнение плоскости, содержащей точки K(2,1,-2), L(0,0,-1), M(1,8,1).

Пусть в декартовой системе координат дан вектор a =и точка М 0 =( x 0 , y 0 , z 0 ).

Построим прямую l , проходящую через т. М 0 , параллельную вектору a (этот вектор называют направляющим вектором прямой).

Утверждение 2: М l ó М 0 М || a .

М 0 М= < x-x 0 , y-y 0 , z-z 0 >|| a ó t R , т.ч. М 0 М=t ·a =>

Параметрические уравнения прямой в пространстве:

(**)

Вы никогда не сталкивались с параметрическим заданием кривых? Поясним на примере: представьте себе, что по заранее намеченному маршруту с известной скоростью движется турист (автомобиль, самолёт, подводная лодка, как Вам больше понравится). Тогда, зная точку начала его путешествия, мы в любой момент времени знаем, где он находится. Таким образом, его положение на маршруте определяется всего одним параметром – временем.

В нашем случае турист движется по бесконечной прямой в пространстве, в момент времени t 0 =0 он находится в точке М 0 , в любой другой момент времени t его координаты в пространстве вычисляются по формулам (**).

Теперь несколько преобразуем формулы (**).

Выразим из каждой строчки параметр t:

Канонические уравнения прямой в пространстве:

Замечание 2: Эта компактная запись на самом деле содержит три уравнения.

Замечание 3: Это формальная запись и выражение вида в данном случае допустимо.

Замечание 4: Надо понимать, что для уравнения плоскости (прямой) играет роль именно направление перпендикулярного (направляющего) вектора, а не он сам. Т.о. вполне допустимо из каких-либо соображений заменять данный (или полученный в ходе решения) вектор на пропорциональный ему. Целесообразно также упрощать полученное уравнение, деля все его коэффициенты на общий множитель.

Пример 3. Написать канонические и параметрические уравнения прямой, параллельной заданной прямой и проходящей через заданную точку.

Пример 4. Написать канонические уравнения прямой, заданной пересечением двух плоскостей.

Пример 5. Найти точку пересечения прямой и плоскости.

Пусть в декартовых координатах плоскость Π задана уравнением: Ax+By+Cz+D=0, а точка М 1 =(x 1 ,y 1 ,z 1 ).

Утверждение 3: расстояние от точки М 1 до плоскости Π вычисляется по формуле:

Пример 6. Найти расстояние от точки до плоскости.

Пусть в декартовой системе координат М 1 =(x 1 ,y 1 ,z 1 ), М 2 =(x 2 ,y 2 ,z 2 ) .

Утверждение 4: Координаты т. М, т.ч. М 1 М=λ∙ММ 2 , находятся по следующим формулам:

.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter