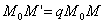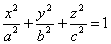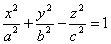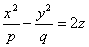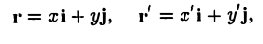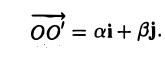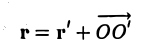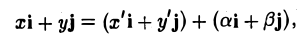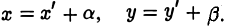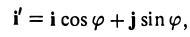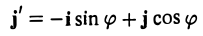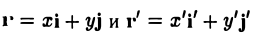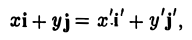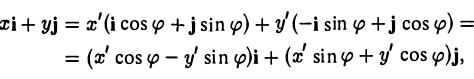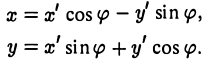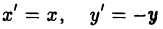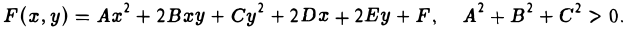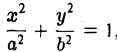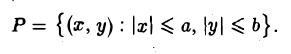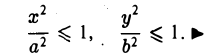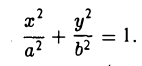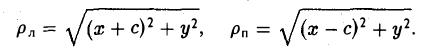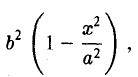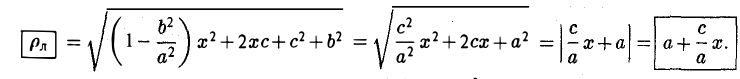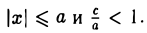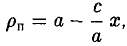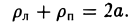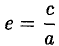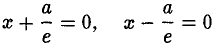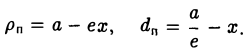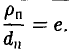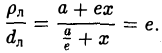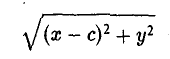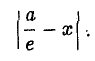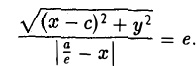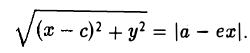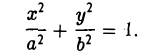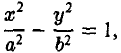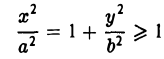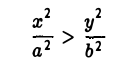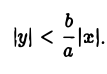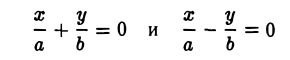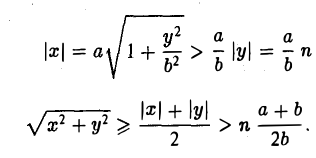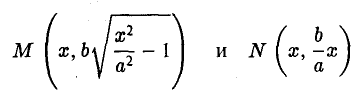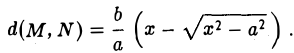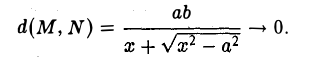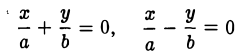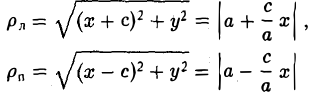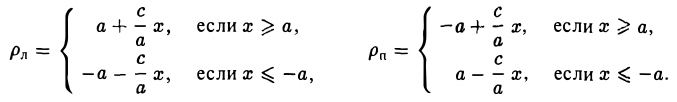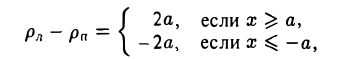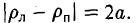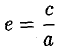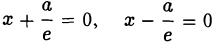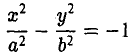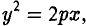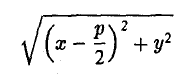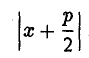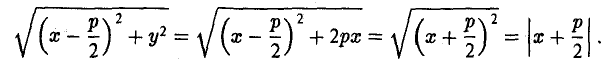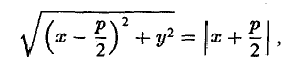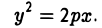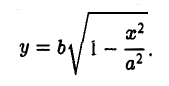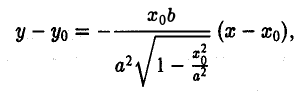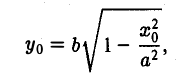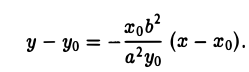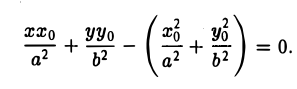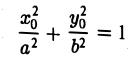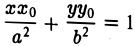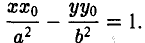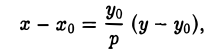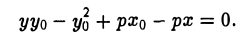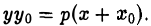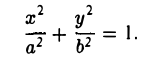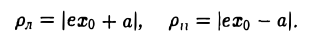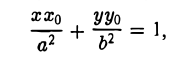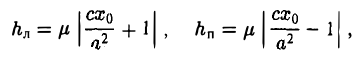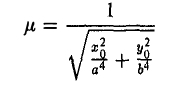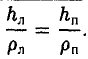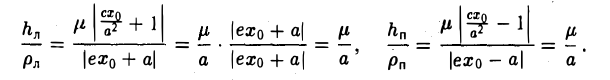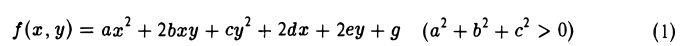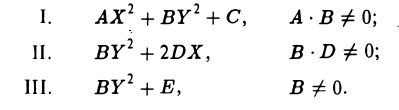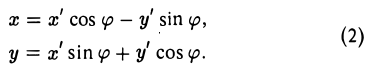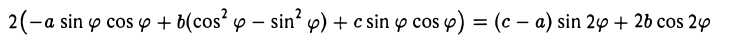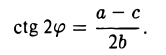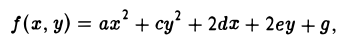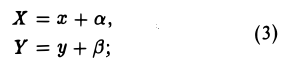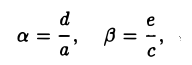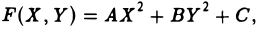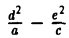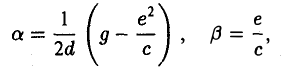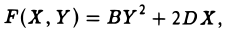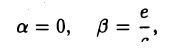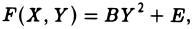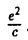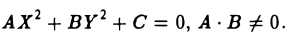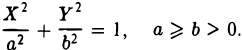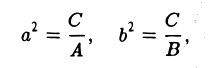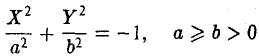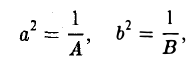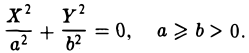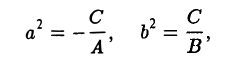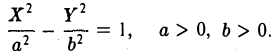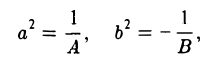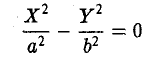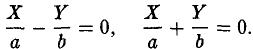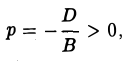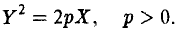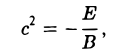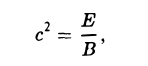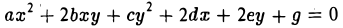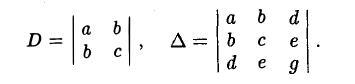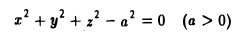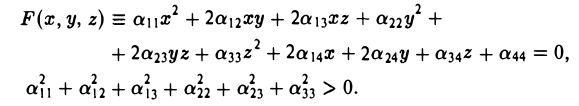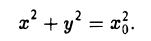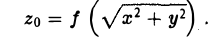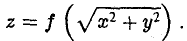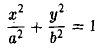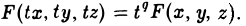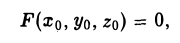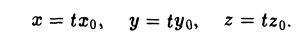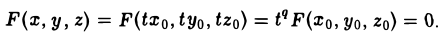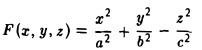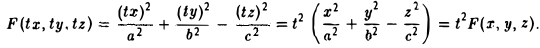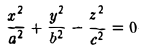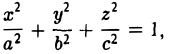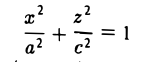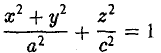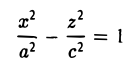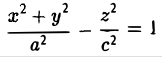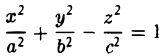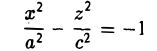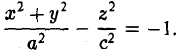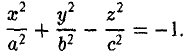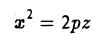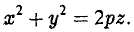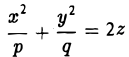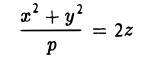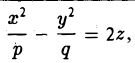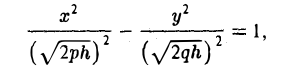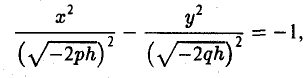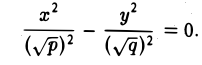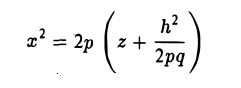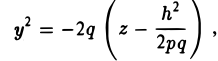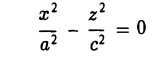Каноническое уравнение эллипсоида второго порядка

Глава 46. Поверхности второго порядка

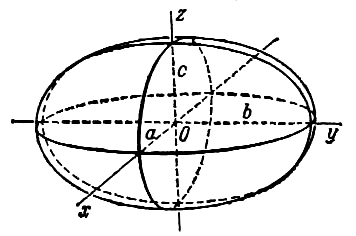
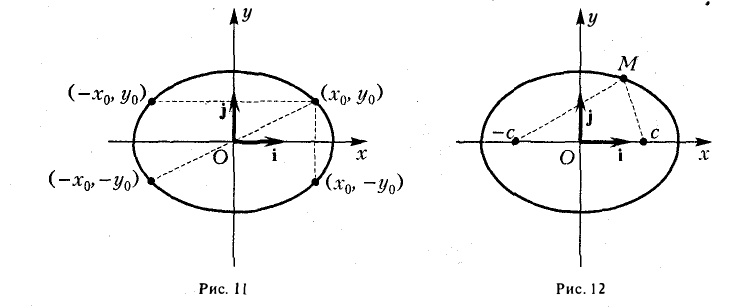
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

(1).

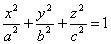
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.

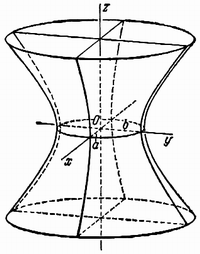
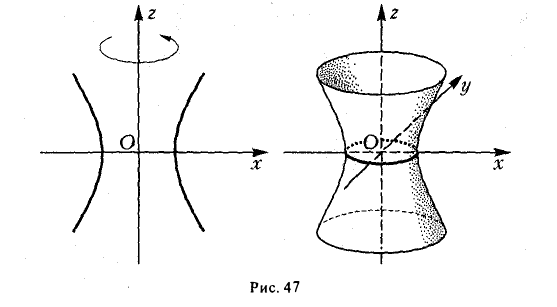
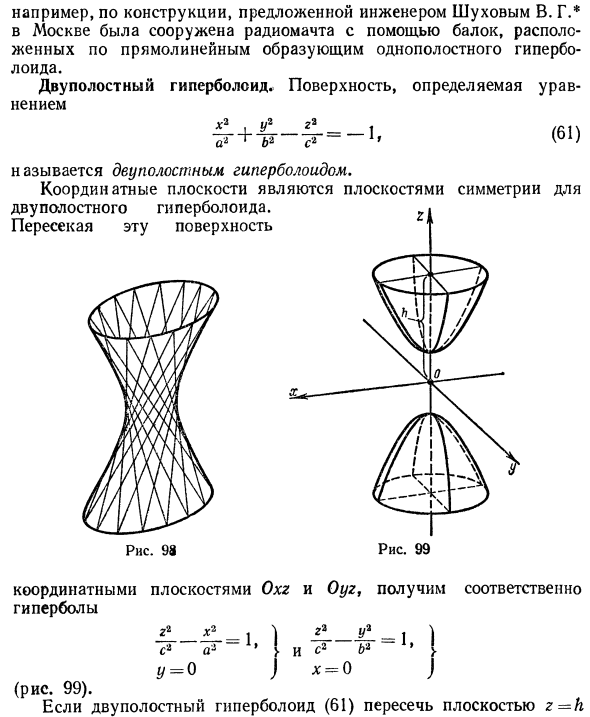
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (2)

. (3)

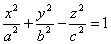
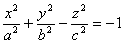
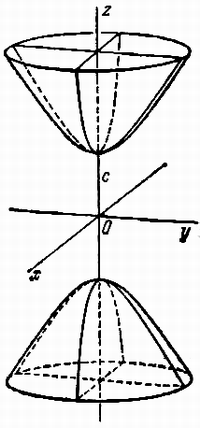
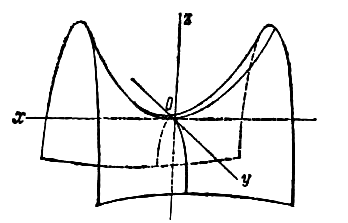
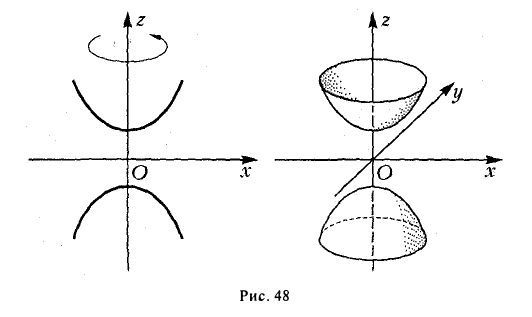
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), — двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.

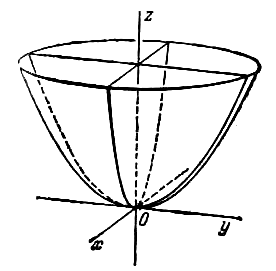
Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (4)

, (5)

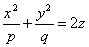
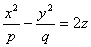
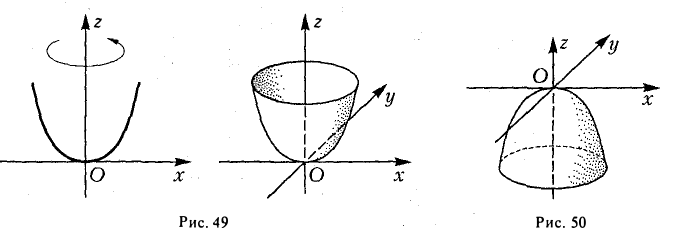
где p и q — положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), — гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).

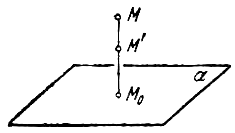
Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).

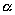
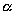
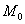
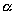
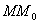
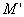
Выберем какую-нибудь плоскость; обозначим ее буквой . Зададим, кроме того, некоторое положительное число q . Пусть М — произвольная точка пространства, не лежащая на плоскости , — основание перпендикуляра, опущенного на плоскость из точки М. Переместим точку М по прямой в новое положение так, чтобы имело место равенство

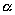
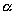
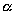
и чтобы после перемещения точка осталась с той же стороны от плоскости , где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости ; точки, которые расположены на плоскости , оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости , переместятся; при этом расстояние от каждой точки до плоскости изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости ; число q носит название коэффициента сжатия.

Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).

ПРИМЕР. Доказать, что произвольный трехосный эллипсоид

может быть получен из сферы

в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия и к плоскости Oxz с коэффициентом сжатия .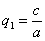

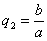
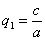
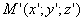
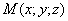
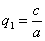
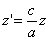
ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом и пусть — точка, в которую переходит при этом точка . Выразим координаты x’, y’, z ’ точки М’ через координаты x, y, z точки М. Так как прямая MM ’ перпендикулярна к плоскости Oxy , то x’=x, y’=y . С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число , то .

Таким образом, мы получаем искомые выражения:

, , (6)

, , (7)

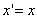
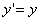
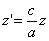
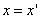
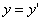
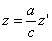
Предположим, что M(x; y; z ) — произвольная точка сферы

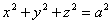
Заменим здесь x, y, z их выражениями (7); получим

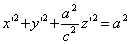
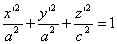
Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам

, , ;

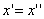
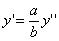
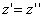
тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.

Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.

имеет две системы прямолинейных образующих, которые определяются уравнениями:

, ;

, ,

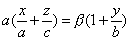
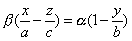
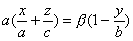
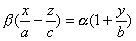
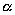
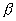
где и — некоторые числа, не равные одновременно нулю. Гиперболический параболоид

также имеет две системы прямолинейных образующих, которые определяются уравнениями

, ;

, .

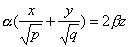
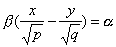
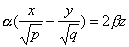
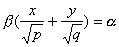
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L — направляющей.

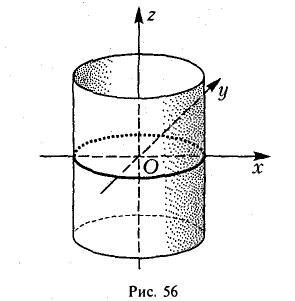
Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).

Кривые и поверхности второго порядка в математике с примерами решения и образцами выполнения

Кривая второго порядка — геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида.

Кривые второго порядка используются при решении задач по аналитической геометрии, кривые других порядков используются при решении задач математического анализа в разделе вычисления кратных, криволинейных и поверхностных интегралов.

Кривые и поверхности второго порядка

Преобразование координат на плоскости

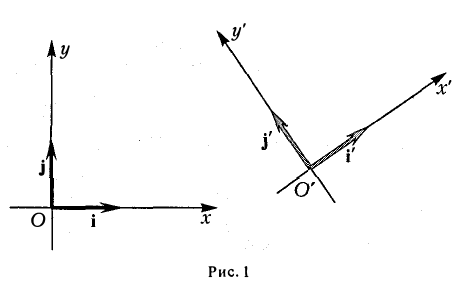
Пусть на плоскости заданы две прямоугольные декартовы системы координат, Оху и О’х’у’ (рис. 1). Произвольная точка М относительно одной из этих координатных систем определяется парой чисел х и у, а относительно другой — парой чисел x’ и у’. Ясно, что между парами (х,у) и (x’, у’) имеется связь. Найдем ее.

Параллельный перенос

Предположим, что соответствующие координатные оси параллельны и сонаправлены, а точки начала отсчета различны. Это означает, что орты координатных осей соответственно равны (рис. 2).

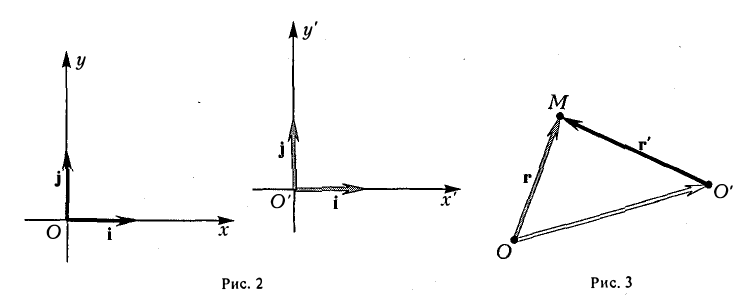
Пусть г и г’ — радиусы-векторы точки М, т.е.

и а, β — координаты точки О’ относительно системы координат Оху, т. е.

Поворот

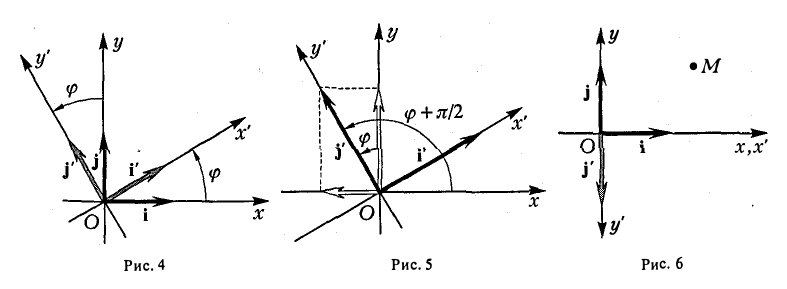
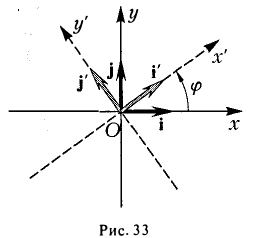
Предположим, что координатные оси одной системы координат получаются из координатных осей другой системы поворотом на угол φ, а начальные точки совпадают (рис.4). Координатами единичного вектора i’ являются косинусы углов φ и 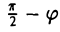, образованных этим вектором с осями Ох и Оу:

а координатами единичного вектора j’ служат косинусы углов 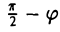и φ:

(рис. 5). Так как радиус-векторы

произвольной точки М в рассматриваемом случае равны,

то, заменяя векторы i’ и j’ их выражениями, получаем, что

Зеркальное отражение

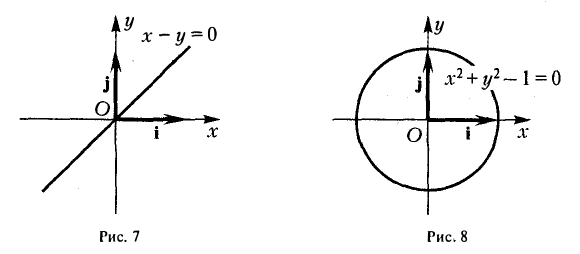
В случае, когда оси абсцисс Ох и Ох’ координатных систем совпадают, а оси ординат Оу и Оу’ направлены противоположно, координаты (х, у) и (х’,у’) произвольной точки М связаны равенствами

Справедливо следующее утверждение.

Любое преобразование прямоугольных декартовых координат (с сохранением масштаба) можно представить в виде последовательного выполнения переноса, поворота и <если необходимо) зеркального отражения.

Кривые второго порядка

Пусть на плоскости задана прямоугольная декартова система координат Оху. Множество точек плоскости, координаты х и у которых удовлетворяют равенству

F(x, у) = 0,

где F(x, у) — некоторая функция двух переменных, называется плоской кривой, или плоской линией само равенство называется уравнением данной линии (кривой).

Например, равенство х — у = 0 есть уравнение прямой — биссектрисы первого и третьего координатных углов (рис. 7). Равенство x 2 + y 2 — 1 = 0 — уравнение окружности единичного радиуса с центром в начале координат (рис. 8).

Рассмотрим многочлен второй степени от двух переменных х и у:

F(x,y) = 0

будем называть уравнением линии (кривой) второго порядка.

Если линиями первого порядка являются именно прямые и только они, то множество кривых второго порядка заметно разнообразней. Поэтому исследованию общего уравнения кривой второго порядка естественно предпослать изучение некоторых частных, но важных случаев.

Эллипс

Эллипсом называется кривая, уравнение которой в некоторой прямоугольной декартовой системе координат Оху имеет вид (1)

Система координат Оху, в которой уравнение эллипса имеет вид (1), называется канонической (для данного эллипса); само уравнение (!) называется каноническим уравнением эллипса. Окружность

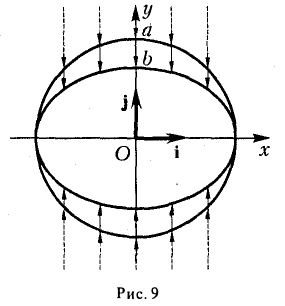
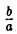
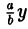
является частным случаем эллипса (при а = b). Это позволяет несложным способом определить форму эллипса: эллипс (1) получается из окружности (2) путем ее равномерного сжатия» к оси Ох (с коэффициентом), т.е. заменой в уравнении x 2 + y 2 = a 2 координаты у на (рис.9).

Свойства эллипса

Эллипс (I) содержится в прямоугольнике

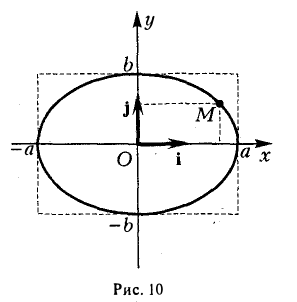
В этом легко убедиться, заметив, что, если точка М(х, у) принадлежит эллипсу (1), то (рис. 10)

Точки (±а, 0), (0, ±b) называются вершинами эллипса.

2. Координатные оси Ох и Оу канонической системы являются осями симметрии эллипса, а начало координат О — его центром симметрии. Это означает, что если точка Мо(хo, yо) принадлежит эллипсу, то точки (-хо, yо), (-xо, -yо) и (хо, -yо) также ему принадлежат (рис. 11).

3. Если эллипс не является окружностью, то координатные оси канонической системы — единственные оси симметрии.

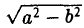
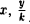
Положим с = . Ясно, что с 0 называется преобразование, переводящее произвольную точку М(х, у) окружности в точку М’ ().

Пусть сначала М(х, у) — произвольная точка эллипса

Вычислим ее расстояния от фокусов эллипса (рис. 12). Имеем

Заменяя y 2 его выражением

после несложных преобразований получаем, что

Последнее равенство вытекает из того, что

Легко убедиться в том, что

Доказательство того, что точки, обладающие указанным свойством, принадлежат эллипсу, было проведено ранее (см. раздел «Простейшие задачи аналитической геометрии» Введения, задача 2).

называется эксцентриситетом эллипса (I). Ясно, что 0

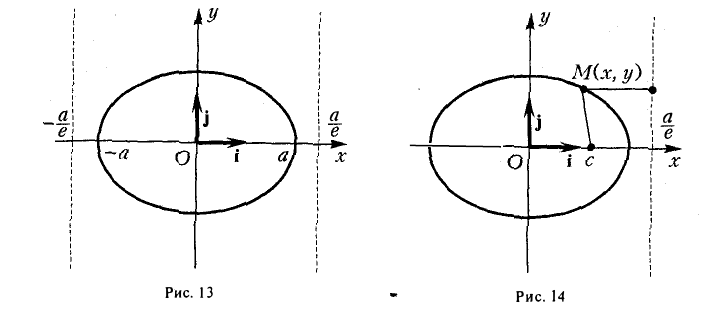
называются директрисами эллипса. У каждого эллипса две директрисы — левая и правая (рис. 13).

5. Эллипс есть множество точек плоскости, отношение расстояний от которых до данной точки (фокуса эллипса) и доданной прямой (одноименной с фокусом директрисы эллипса) постоянно (равно эксцентриситету эллипса).

Пусть сначала М(х,у) — произвольная точка эллипса (1). Вычислим расстояния от нее до правого фокуса и до правой директрисы (рис. 14). Имеем соответственно

Откуда легко получаем требуемое

Аналогично проверяется, что

Рассмотрим теперь на плоскости точку (с, 0) и прямую х =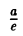(с = ае). Возьмем произвольную точку М(х, у) и вычислим расстояния от нее до выбранной точки (с, 0) —

— и до выбранной прямой —

Возведем обе части последнего соотношения в квадрат и, положив 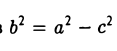и учтя равенство с = ае, после простых преобразований получим

Тем самым, точка М(х,у) лежит на эллипсе (1).

Гипербола

Гиперболой называется кривая, уравнение которой в некоторой прямоугольной системе координат Оху имеет вид (1)

Система координат Оху, в которой уравнение гиперболы имеет вид (1), называется канонической (для данной гиперболы); само уравнение (1) называется каноническим уравнением гиперболы.

Свойства гиперболы

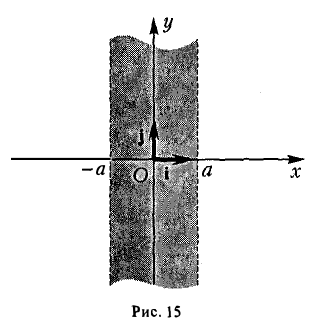
Гипербола (1) лежит вне полосы |x|

и, значит, |x| ≥ а (рис. 15).

Точки (±а, 0) называются вершинами гиперболы.

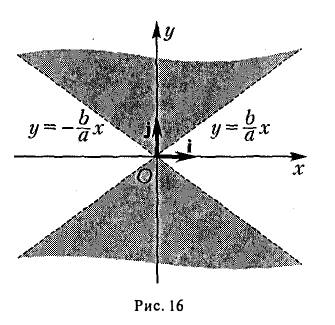
2. Гипербола (1) лежит в вертикальных углах, образованных прямыми у = ±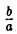х и содержащих точки оси Ох (рис. 16).

вытекает, что если точка М(х, у) лежит на гиперболе (1), то

Таким образом, гипербола состоит из двух частей — ветвей гиперболы, левой и правой. Прямые

называются асимптотами гиперболы.

3, На гиперболе лежат точки, сколь угодно далекие от начала координат O(0, 0).

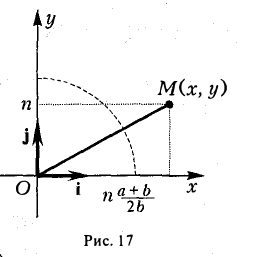
Пусть, например, точка М(х, у) лежит на гиперболе (1) и \у\ = n, где n — произвольное положительное число (рис. 17).

Возьмем в первой четверти две точки: точку гиперболы (1) и точку ее асимптоты 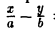= 0 с одинаковой абсциссой х > а —

соответственно — и вычислим расстояние между ними. Имеем

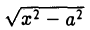
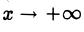
Умножив и разделив полученное выражение на сумму х +и перейдя затем к пределу при получим

Тем самым, установлен следующий факт.

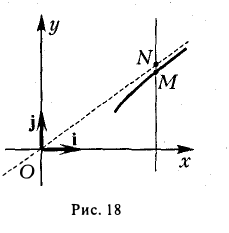
4. Если текущая точка асимптоты неограниченно удаляется от начала координат, т.е. \х\ —» + ∞, то на гиперболе можно указать соответствующую ей точку так, чтобы расстояние между ними стремилось к нулю (рис. 18).

Верно и обратное.

стремится к нулю.

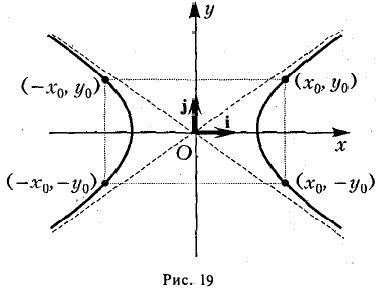
6. Оси канонической координатной системы являются осями симметрии гиперболы, а начало координат — ее центром симметрии (рис. 19).

Координатные оси канонической системы — единственные оси симметрии гиперболы.

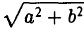
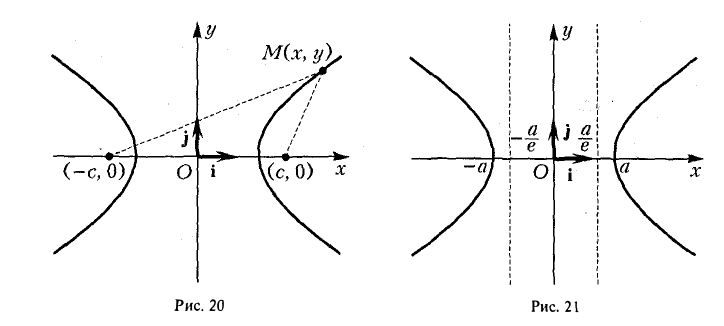
Положим с = . Ясно, что с > 0. .Точки (-с, 0) и (с, 0) называются фокусами гиперболы, 2с — фокусное расстояние.

Гипербола есть множество точек, абсолютная величина разности расстояний от которых до двух данных точек (фокусов гиперболы) постоянна (равна заданному числу).

Доказательство этого свойства проводится так же, как и доказательство свойства 4 эллипса. Покажем, например, что каждая точка гиперболы обладает указанным свойством. Если М(х, у) — точка гиперболы (1), то расстояния от нее до фокусов соответственно равны

(рис. 20). Так как 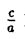> 1, то

Отсюда нетрудно вычислить, что

называется эксцентриситетом гиперболы (1). Ясно, что е > 1. Прямые

называются директрисами гиперболы (рис. 21). У каждой гиперболы две директрисы — левая и правая.

Практически также, как и для эллипса, доказывается следующий факт.

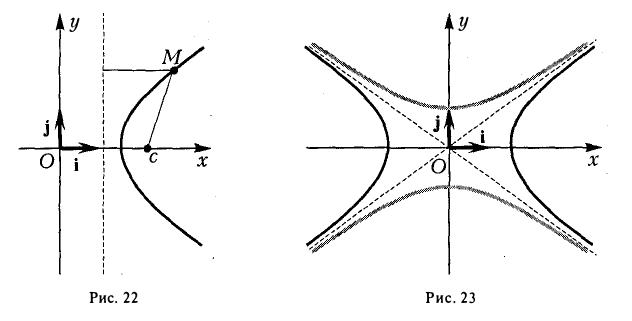
8. Гипербола есть множество точек, отношение расстояний от которых до данной точки (фокуса гиперболы) и доданной прямой (одноименной с фокусом директрисы) постоянно (равно эксцентриситету гиперболы) (рис. 22).
Гипербола (2)

называется сопряженной гиперболе (1). Взаимное расположение гипербол (1) и (2) указано на рис. 23.

Парабола

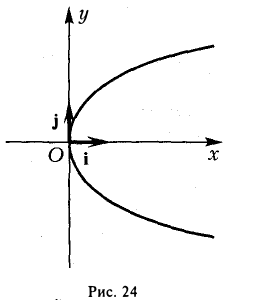
Параболой называется кривая, уравнение которой в некоторой прямоугольной декартовой системе координат Оху имеет вид (1)

Система координат Оху, в которой уравнение параболы имеет вид (1), называется канонической (для данной параболы); уравнение (]) называется каноническим уравнением параболы.

Свойства параболы

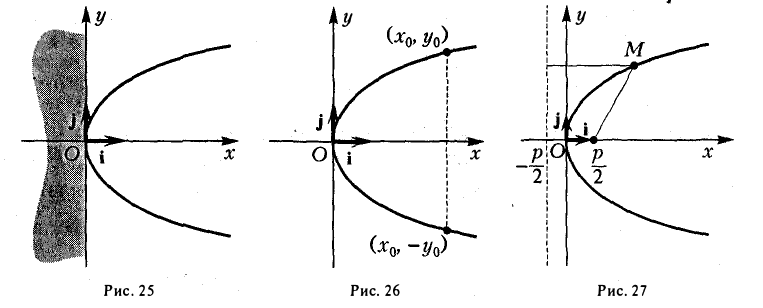
Все точки параболы лежат в правой полуплоскости: х ≥ 0 (рис. 25). Точка 0(0, 0) лежит на параболе и называется ее вершиной.
На параболе лежат точки, сколь угодно далеко расположенные от начала координат О(0, 0).
Ось абсцисс канонической координатной системы является (единственной) осью симметрии параболы (рис. 26).

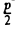
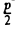
Ось симметрии параболы называется осью параболы. Число р называется фокальным параметром параболы; точка (; 0) — фокус параболы; прямая х = — директриса параболы.

4. Парабола есть множество точек, равноудаленных отданной точки (фокуса параболы) и от данной прямой (директрисы параболы) (рис. 27).

Пусть точка М(х, у) лежит на параболе (1). Вычислим расстояния от нее до фокуса (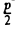;0)

и до директрисы х = —

Заменяя у 2 его выражением 2рх, легко убеждаемся в том, что

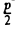
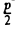
Верно и обратное. Если для некоторой точки М(х, у) расстояния от нее до точки (; 0) и до прямой х = — равны —

то, возводя в квадрат, после простых преобразований получаем, что эта точка лежит на параболе:

Оптическое свойство кривых второго порядка

Касательные к эллипсу и гиперболе

Если кривая задана уравнением

y = f(x)

то уравнение касательной к ней, проходящей через точку (хо,у0)> где Уо = f(xо), можно записать в следующем виде

Пусть Мо(хо, yо) — точка эллипса

Предположим для определенности, что точка М0 лежит в первой четверти, т. е. хо > 0, yо > 0. Тогда часть эллипса, лежащую в первой четверти, можно описать уравнением

Пользуясь формулой (1), получаем уравнение касательной к эллипсу в точке Мо

а так как точка (х0, у о) лежит на эллипсе, то

Полученное соотношение после несложных преобразований можно записать так:

Отсюда с учетом тождества

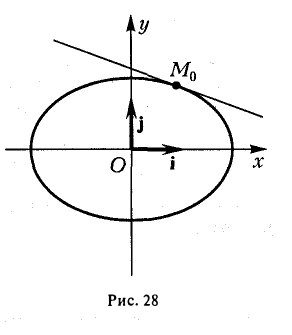
приходим к уравнению

(рис. 28). Полученное соотношение является уравнением касательной к эллипсу, проходящей через его точку (х0, yо), и в общем случае ее произвольного расположения, т. е. при любых знаках хо и уо.

Уравнение касательной к гиперболе выводится аналогично и имеет следующий вид

Подчеркнем, что точка (хо, yо) лежит на гиперболе.

Касательные к параболе

Если кривая задана уравнением

х = g(у),

то уравнение касательной к ней, проходящей через точку (хo,уo), где х0 = g (уо), можно записать в следующем виде

Пусть М0(х0, у0) — точка параболы. Пользуясь формулой (I), получаем уравнение касательной к параболе

Отсюда в силу равенства 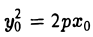приходим к уравнению касательной вида

Замечание:

Сопоставляя канонические уравнения эллипса, гиперболы и параболы с уравнениями касательных к этим кривым, нетрудно заметить, что для получения последних не требуется специальных вычислений. В самом деле, заменяя у 2 на уу ₀ , а х 2 на хх ₀ (в случае параболы 2х нужно заменить на x + х ₀ ). приходим к уравнению соответствующей касательной. Еще раз отметим, что сказанное справедливо лишь в том случае, когда точка (x ₀ . y ₀ ) лежит на кривой.

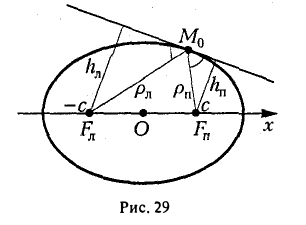
Оптическое свойство эллипса

Пусть М ₀ — произвольная точка эллипса

Как уже отмечалось, расстояния от нее до фокусов F_л и F _n — фокальные радиусы — равны соответственно

Проведем через точку М ₀ касательную к эллипсу,

и вычислим, на каком расстоянии от этой касательной лежат фокусы F_л (-c, 0) и F_n (c; 0) (напомним, что для этого следует воспользоваться формулой (10).

— нормирующий множитель (рис. 29). Нетрудно проверить, что

Обратившись к рис.29, заметим, что вычисленные отношения равны синусам углов, образованных касательной и фокальными радиусами точки касания. Из того, что синусы этих углов равны, вытекает равенство и самих углов. Тем самым доказано оптическое свойство эллипса: касательная к эллипсу образует равные углы с фокальными радиусами точки касания.

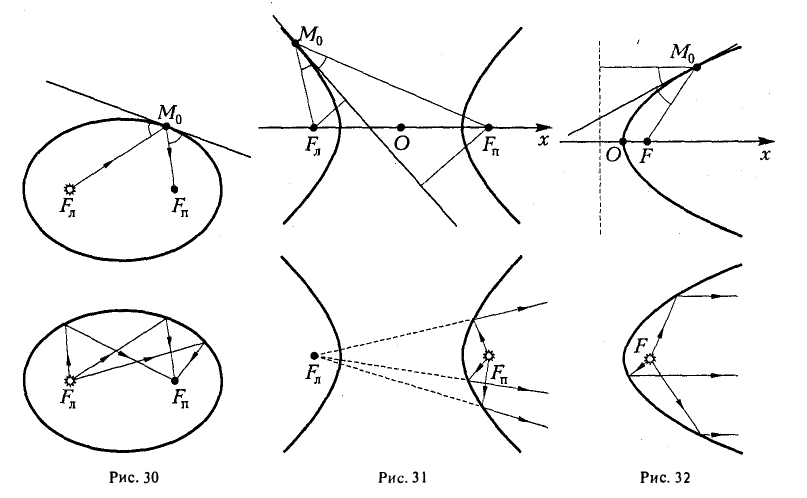
Это свойство называется оптическим по следующей причине: если поместить в один из фокусов эллипса с зеркальной «поверхностью» точечный источник света, то все лучи после отражения от «поверхности» эллипса сойдутся в другом его фокусе (рис. 30).

Оптическое свойство гиперболы

Устанавливается аналогичными выкладками и заключается в следующем.

Если поместить в один из фокусов гиперболы точечный источник света, то каждый луч после отражения от зеркальной «поверхности» гиперболы видится исходящим из другого фокуса (рис. 31).

Оптическое свойство параболы

Если в фокус параболы помещен точечный источник света, то все лучи, отраженные от зеркальной «поверхности» параболы, будут направлены параллельно оси параболы (рис. 32).

Классификация кривых второго порядка

Многочлены второй степени на плоскости

Теорема:

Пусть на плоскости введена прямоугольная декартова система координат Оху и пусть

— многочлен второй степени от переменных х и у.

Тогда на плоскости можно построить прямоугольную дека ртов у систему координат O’XY так, что после замены переменных х и у на переменные X и Y исходный многочлен f(x, у) приведется к многочлену F(X, Y) одного из следующих трех видов:

1-й шаг. Поворотом координатных осей на подходящим образом выбранный угол всегда можно добиться того, чтобы коэффициент при произведении разноименных координат обратился в нуль.

Пусть b ≠ 0 (при 6 = 0 этот шаг не нужен). Повернем оси координат вокруг точки О. Эта операция описывается следующими формулами

При этом координатные оси исходной системы Оху поворачиваются на угол φ (рис.33).

Заменим переменные х и у в формуле (1) их выражениями (2) через x’ и у’ и вычислим коэффициент 2b’ при произведении х’у’. Он равен

и обращается в нуль, если

Так как полученное уравнение разрешимо относительно φ, то указанным преобразованием всегда можно добиться обращения в нуль нужного коэффициента.

Приступая ко второму этапу преобразования, будем считать, что исходный многочлен f(x,у) уже имеет вид

где а 2 + с 2 >0. Для определенности положим с ≠ 0 (это не ограничивает общности наших рассуждений, так как заменой х, у в случае необходимости этого всегда можно добиться).

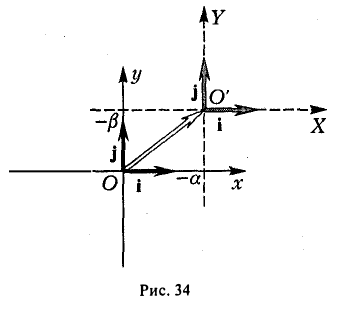
2-й шаг. Переносом начала координат можно достичь дальнейшего упрощения вида многочлена f(x,y). Эта операция описывается следующими формулами:

координатные оси новой системы O’XY получаются из координатных осей исходной системы Оху параллельным переносом в точку (-а, — β) (рис. 34).

Укажем конкретные значения а и β. Возможны три случая

I. а ≠ 0, с ≠ 0. Тогда, полагая

где А = а, В = с, С = g —

II. а = 0, d ≠ 0. Тогда, полагая

III. а = d = 0. Тогда, полагая

где В = с, Е = g —

Канонические уравнения кривых второго порядка

Если многочлен второй степени F(X, У) приравнять к нулю, то получим уравнение линии второго порядка

F(X, У) = 0.

Рассмотрим каждый из трех полученных выше случаев I, II, III отдельно.

Э. А • В > 0. Домножением обеих частей уравнения на — 1 и заменой X на У, а У на X (в случае необходимости) всегда можно добиться того, чтобы В ≥ А > 0.

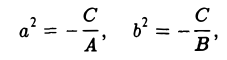
(мнимый эллипс)2). На действительной плоскости нет ни одной точки (X, Y), координаты которой обращали бы это уравнение в тождество.

Точка (0, 0) является единственной точкой плоскости, координаты которой удовлетворяют этому уравнению; точку (0,0) можно мыслить как действительную точку пересечения двух мнимых пересекающихся прямых 3).

Г. А • В 0, В

— пару пересекающихся прямых:

2) Название можно объяснить некоторым сходством этого уравнения с уравнением эллипса.
3) Название можно объяснить некоторым сходством этого уравнения с уравнением пары пересекающихся
прямых.

II. BY 2 + 2DX = О, В • D ≠ 0.

Всегда можно добиться того, чтобы В • D

III. BY 2 + Е = 0, В ≠ 0. Можно считать, что В > 0.

1. Е

Y 2 — с 2 = 0, с > 0

— пару параллельных прямых.

Y 2 — с 2 = 0, с 2 = 0

— пара совпадающих прямых.

Чтобы определить тип кривой второго порядка, не обязательно проводить все указанные выше преобразования. Достаточно вычислить знаки некоторых выражений, составленных из коэффициентов уравнения.

— уравнение линии второго порядка. Введем следующие обозначения

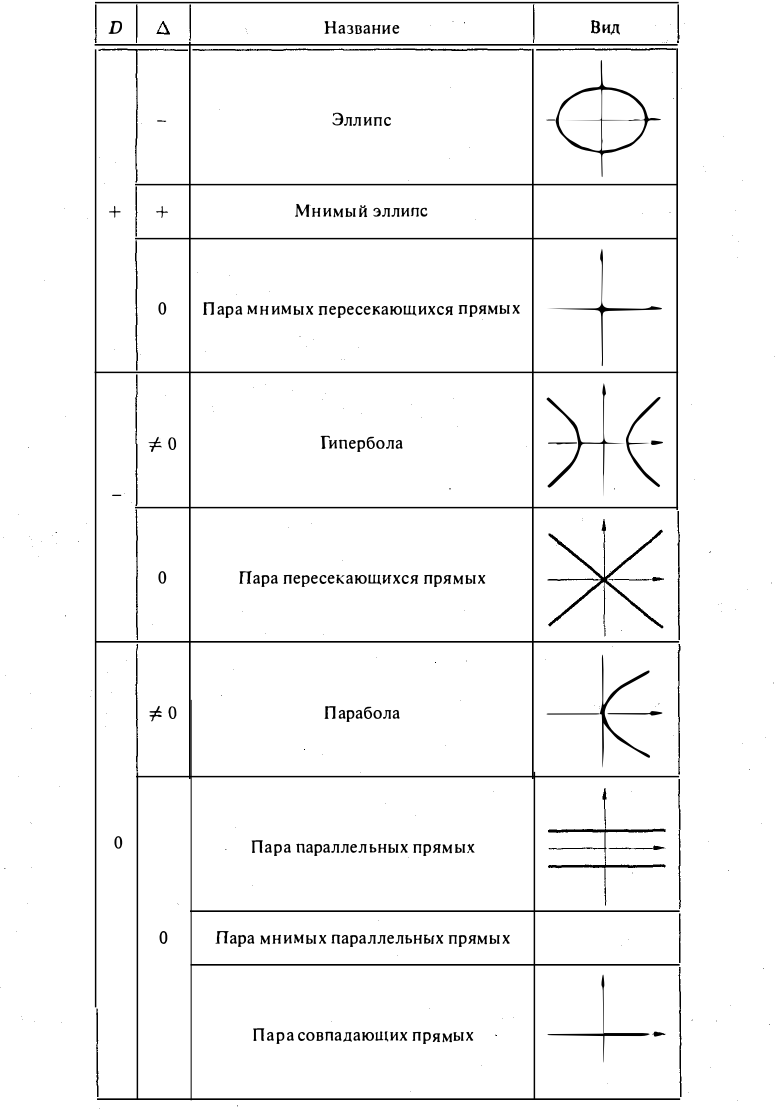
Числа D и ∆ не зависят от выбора системы координат на плоскости и называются инвариантами. Из приводимой таблицы видно, какому сочетанию знаков определителей D и ∆ соответствует та или иная линия второго порядка.

Задача:

Убедитесь в том, что D и ∆ при рассмотренных преобразованиях системы координат действительно остаются неизменными.
4) Название можно объяснить некоторым сходством этого уравнения с уравнением пары параллельных прямых.

Поверхности второго порядка

Пусть в пространстве задана прямоугольная декартова система координат Oxyz. Множество точек пространства, координаты х, у и z которых удовлетворяют равенству

F(x, у, z) = О,

называется поверхностью; равенство (*) называется уравнением этой поверхности.

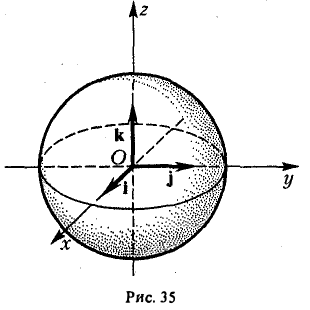
Пример:

— уравнение сферы радиуса о с центром в точке (0,0,0) (рис. 35).

Рассмотрим многочлен второй степени от трех переменных х, у и z

Уравнение

F(x, y, z) = 0

будем называть уравнением поверхности второго порядка.

Исследование общего уравнения поверхностей второго порядка оказывается зна-чительноболее сложным, чем исследование общего уравнения кривых второго порядка, требует разработки соответствующего математического аппарата и будет проведено в конце главы VI.

В оставшихся параграфах этой главы мы сначала остановимся на изучении геометрических свойств некоторых важных классов общих поверхностей; затем используем их для рассмотрения канонических уравнений основных поверхностей второго порядка и исследования структуры этих поверхностей.

Некоторые классы поверхностей

Поверхности вращения

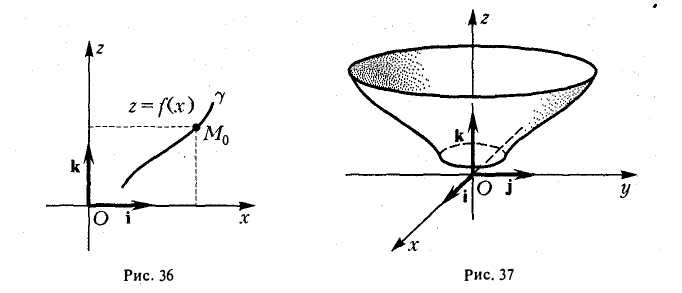
Рассмотрим на плоскости Oxz кривую γ, заданную уравнением

г = f(x), х ≥ 0

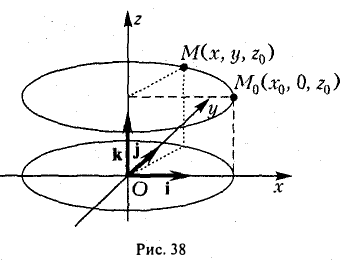
(рис. 36). При вращении кривой γ вокруг оси Oz она будет заметать некоторую поверхность, называемую поверхностью вращения (рис. 37). Найдем уравнение этой поверхности, т. е. равенство, которому должны удовлетворять координаты точек построенной поверхности и только они.

Тем самым, координаты х, у и z0 любой точки М этой окружности связаны следующим равенством

В силу произвольности выбора точки М0 на кривой γ искомое уравнение полученной поверхности вращения имеет вид

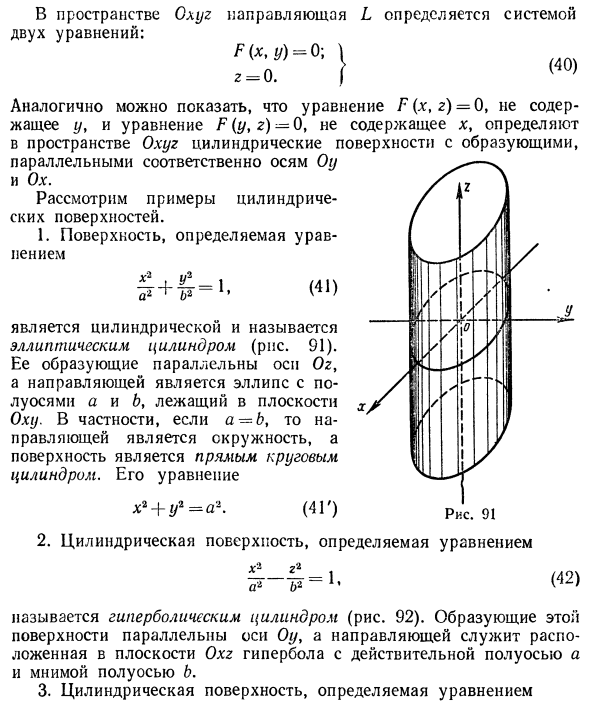
Цилиндрические поверхности

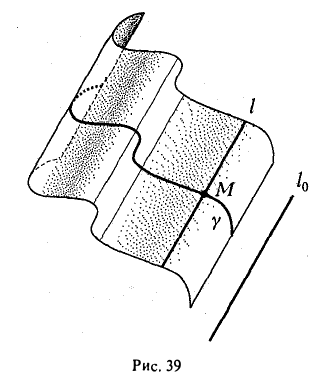
Через каждую точку некоторой заданной кривой γ проведем прямую l параллельно заданной прямой l0. Множество точек, лежащих на так построенных прямых, назовем цилиндрической поверхностью (рис. 39); кривая γ называется направляющей цилиндрической поверхности, а прямая l — ее образующей.

Найдем уравнение, описывающее цилиндрическую поверхность.

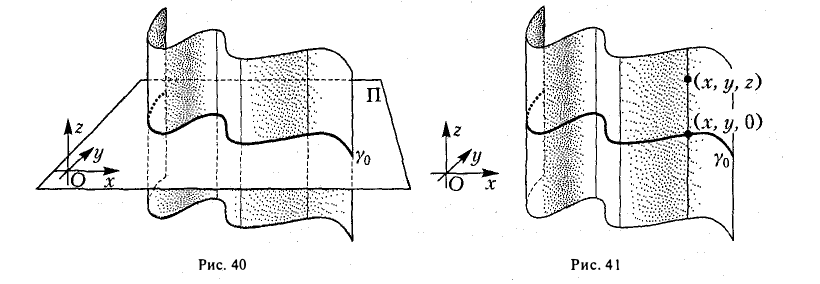
Возьмем произвольную точку О и проведем через нее плоскость П, перпендикулярную образующей I. Построим в пространстве прямоугольную координатную систему Oxyz, взяв за ось Oz прямую, перпендикулярную плоскости П. Тогда плоскость П будет координатной плоскостью Оху (рис.40). Плоскость П пересекает цилиндрическую поверхность по направляющей γ0.

F(x,y) = 0

— уравнение этой направляющей. Убедимся в том, что последнее соотношение можно считать уравнением искомой цилиндрической поверхности.

самом деле, пусть (х, у, z) — точка цилиндрической поверхности (рис. 41). Тогда точка (х, у, 0) лежит на γ0 и, значит, удовлетворяет уравнению

F(x,y)=0.

Но координаты точки (х, у, z) также обращают это уравнение в тождество. Последнее обстоятельство и позволяет считать соотношение F(x,y) = 0 искомым уравнением.

Пример:

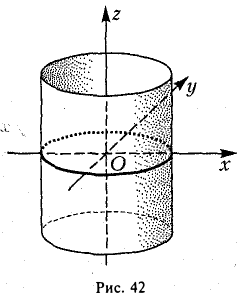
Введем в пространстве прямоугольные декартовы координаты Охуz. Соотношение

является уравнением цилиндрической поверхности (эллиптического цилиндра) (рис. 42).

Замечание:

F(y, z) = 0

описывает цилиндрическую поверхность с образующей, параллельной координатной оси Оx, а уравнение

F(x,z) = 0

— цилиндрическую поверхность с образующей, параллельной оси Oy.

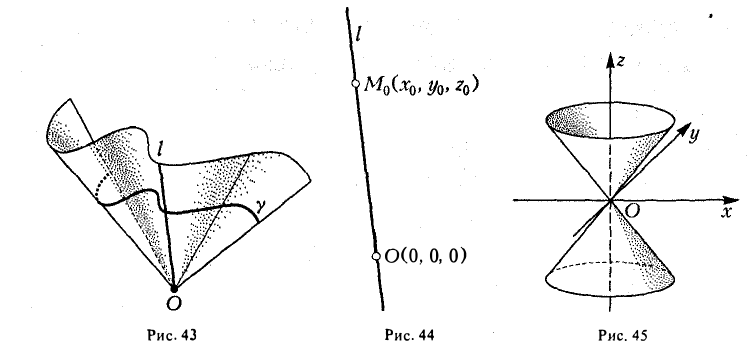
Конические поверхности

Пусть γ — произвольная кривая и О — точка вне eе. Через каждую точку кривой γ и точку О проведем прямую l. Множество точек, лежащих на построенных таким образом прямых, называется конической поверхностью (рис.43); кривая γ — направляющая конической поверхности, l — ее образующая, точка О — вершина. Рассмотрим функцию

F (x, у, z)

переменных х, у и z. Функция F(x, у, z) называется однородной функцией степени q, если для любого t > 0 выполняется равенство

Покажем, что если F(x, у, z) однородная функция, то F
является уравнением конической поверхности.

В самом деле, пусть

т.е. точка М0(xo, уо, zо) лежит на этой поверхности. Будем считать, что 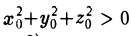. Проведем через эту точку и точку 0(0,0, 0) (считая, что F(0,0, 0) = 0) прямую I (рис. 44). Ее параметрические уравнения имеют вид

Подставляя полученные выражения для х, у и z в функцию F(x, у, z), видим, что

Это означает, что вся прямая l лежит на поверхности, определяемой уравнением F(x,y,z) = 0, которое, следовательно, и описывает коническую поверхность.

Пример:

является однородной функцией второй степени:

— уравнение конической поверхности (конуса второго порядка) (рис.45).

Воспользуемся теперь полученными выше результатами для исследования геометрической формы поверхностей второго порядка.

Эллипсоид. Гиперболоиды. Параболоиды. Цилиндры и конус второго порядка

Эллипсоид

Эллипсоидом называется поверхность, уравнение которой в некоторой прямоугольной декартовой системе координат Oxyz имеет вид

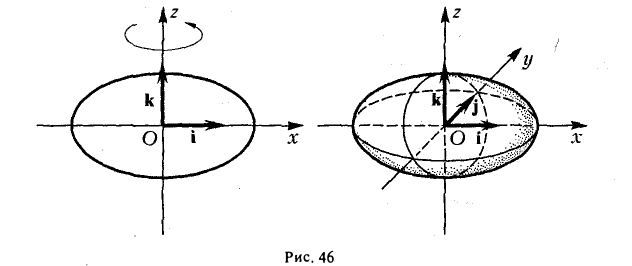
где а ≥ b ≥ с > 0. Для того, чтобы выяснить, как выглядит эллипсоид, поступим следующим образом. Возьмем на плоскости Oxz эллипс

и будем вращать его вокруг оси Oz (рис. 46).

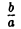
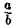
— эллипсоид вращения — уже дает представление о том, как устроен эллипсоид общего вида. Чтобы получить его уравнение, достаточно равномерно сжать эллипсоид вращения . вдоль оси Оу с коэффициентом — ≤ 1, т. с. заменить в его уравнении у на y 5).

Гиперболоиды

вокруг оси Oz (рис. 47), получим поверхность, называемую однополостным гиперболоидом вращения. Его уравнение имеет вид

получается тем же способом, что и в случае эллипсоида вращения.

5) Эллипсоид вращения («) можно получить равномерным сжатием сферы х 2 + у 2 + z 2 = а 2 вдоль оси Оz с коэффициентом — 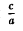≤ 1.

Путем равномерного сжатия этой поверхности вдоль оси Оу с коэффициентом 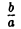≤ 1 получим однополостный гиперболоид общего вида. Его уравнение

получается тем же способом, что и в разобранном выше случае эллипсоида. Путем вращения вокруг оси Oz сопряженной гиперболы

получим двуполостный гиперболоид вращения (рис.48). Его уравнение

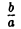
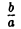
Путем равномерного сжатия этой поверхности вдоль оси Оу с коэффициентом ≤ 1 приходим к двуполостному гиперболоиду общего вида. Заменой у на у получаем его уравнение

Эллиптический параболоид

вокруг оси Oz (рис.49), получаем параболоид вращения. Его уравнение имеет вид

Путем сжатия параболоида вращения вдоль оси Оу с коэффициентом 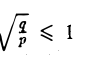получаем эллиптический параболоид. Его уравнение

получается из уравнения параболоида вращения

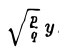
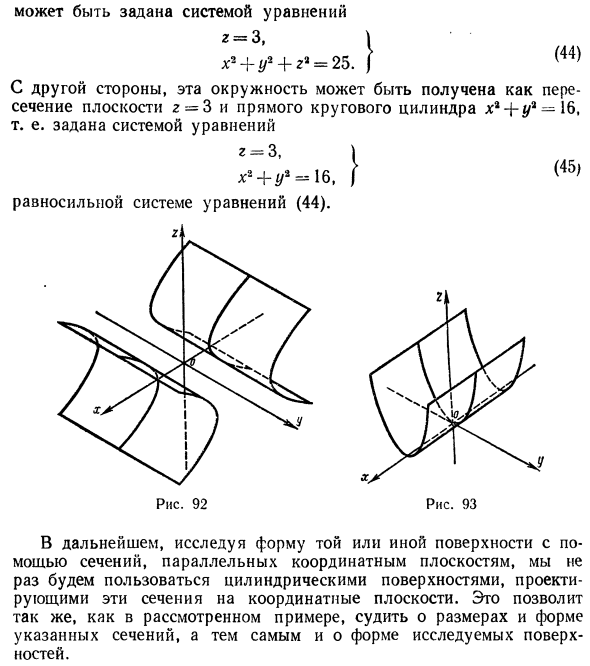
путем замены у на . Если р Гиперболический параболоид

Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой прямоугольной декартовой системе координат Oxyz имеет вид

где р > 0, q > 0. Вид этой поверхности определим, применив так называемый метод сечений, который заключается в следующем: параллельно координатным плоскостям проводятся плоскости, пересекающие исследуемую поверхность, и по изменению конфигурации возникающих в результате плоских кривых делается вывод о структуре самой поверхности.

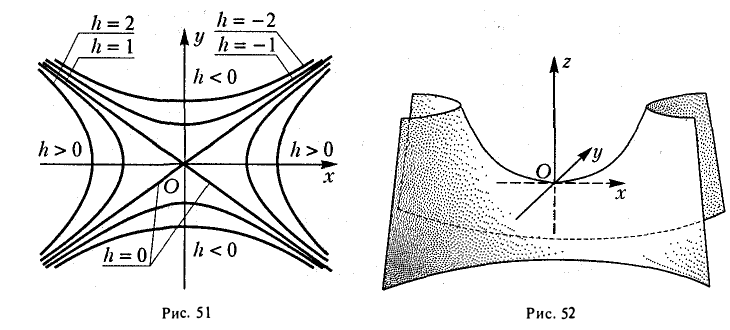
Начнем с сечений плоскостями z = h = const, параллельными координатной плоскости Оху. При h > 0 получаем гиперболы

при h

при h = 0 — пару пересекающихся прямых

Заметим, что эти прямые являются асимптотами для всех гипербол (т. е. при любом h ≠ 0). Спроектируем получаемые кривые на плоскость Ох у. Получим следующую картину (рис. 51). Уже это рассмотрение позволяет сделать заключение о седлообразном строении рассматриваемой поверхности (рис. 52).

Рассмотрим теперь сечения плоскостями

у = h.

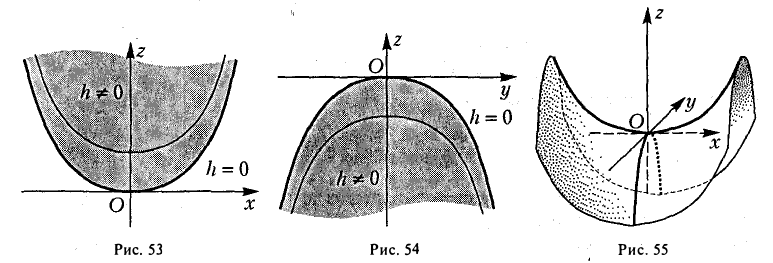
Заменяя в уравнении поверхности у на h, получаем уравнения парабол (рис.53).

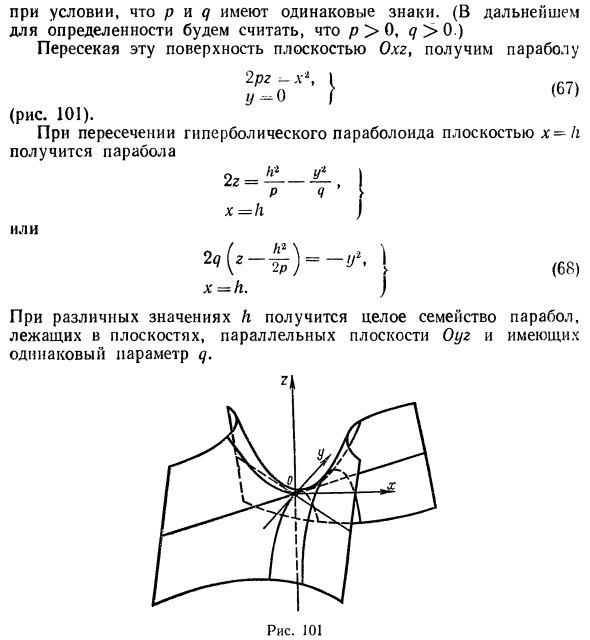
Аналогичная картина возникает при рассечении заданной поверхности плоскостями

х = h.

В этом случае также получаются параболы

ветви которых направлены вниз (а не вверх, как для сечения плоскостями у = h) (рис. 54).

Используя последние два типа сечений, приходим к заключению, что гиперболический параболоид можно получить путем параллельного переноса параболы х2 = 2pz вдоль параболы у2 = -2qz, или наоборот (рис. 55).

Замечание:

Методом сeчeний можно разобраться в строении и всех ранее рассмотренных поверхностей второго порядка. Однако путем вращения кривых второго порядка и последующего равномерного сжатия к пониманию их структуры можно прийти проще и значительно быстрее.

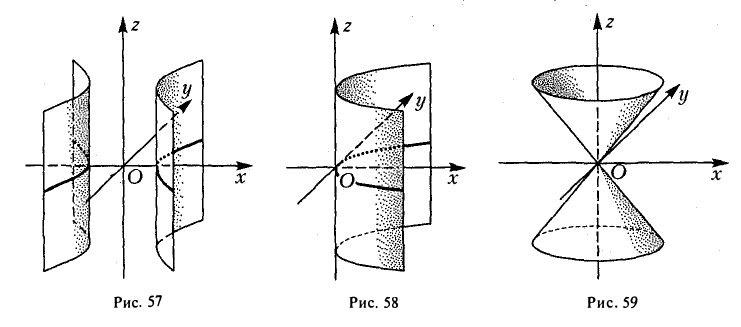
Оставшиеся поверхности второго порядка по существу уже рассмотрены ранее. Это цилиндры:

представление о котором можно получить либо путем вращения пары пересекающихся прямых

вокруг оси Oz и последующего сжатия, либо методом сечений. Конечно, в обоих случаях получим, что исследуемая поверхность имеет вид, указанный на рис. 59.

Дополнение к поверхностям второго порядка

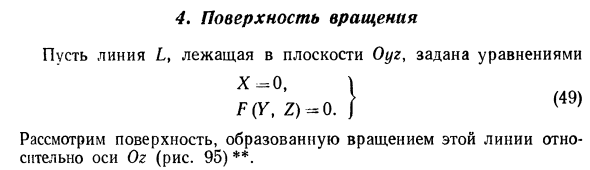
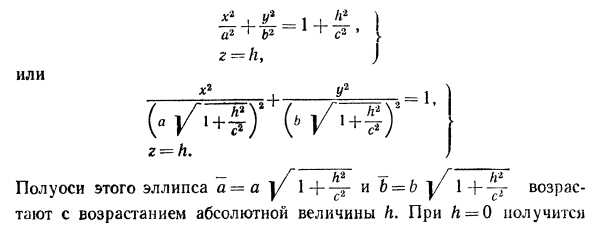
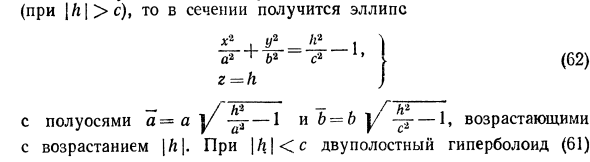
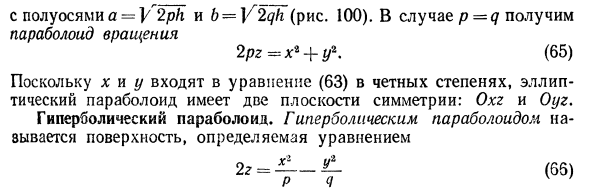
Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Поверхности второго порядка: их виды, уравнения, примеры

Общее уравнение поверхности второго порядка и инварианты поворота и переноса декартовой прямоугольной системы координат

Общее уравнение поверхности второго порядка имеет вид

Для определения вида поверхности второго порядка по общему уравнению и приведения общего уравнения к каноническому, нам понадобятся выражения, которые называются инвариантами. Инварианты — это определители и суммы определителей, составленные из коэффициентов общего уравнения, которые не меняются при переносе и повороте системы координат. Эти инварианты следующие:

Следующие два выражения, называемые семиинвариантами, являются инвариантами поворота декартовой прямоугольной системы координат:

В случае, если I 3 = 0 , K 4 = 0 , семиинвариант K 3 будет также и инвариантом переноса; в случае же I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 семиинвариант K 2 = 0 будет также и инвариантом переноса.

Виды поверхностей второго порядка и приведение общего уравнения поверхности второго порядка к каноническому

I. Если I 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 , λ 2 , λ 3 — корни характеристического уравнения

В зависимости от того, какие знаки у чисел λ 1 , λ 2 , λ 3 и K 4 /I 3 , определяется вид поверхности второго порядка.

Эллипсоид

Если числа λ 1 λ 2 , λ 3 одного знака, а K 4 /I 3 имеет знак им противоположный, то общее уравнение поверхности второго порядка определяет эллипсоид.

После решения характеристического уравнения общее уравнение можно переписать в следующем виде:

Тогда полуоси эллипсоида будут

, , .

Поэтому каноническое уравнение эллипсоида имеет вид

Мнимый эллипсоид

Если числа λ 1 λ 2 , λ 3 и K 4 /I 3 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллипсоид.

После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого эллипсоида:

, , .

Мнимый конус

Если числа λ 1 λ 2 , λ 3 , а K 4 = 0 , то общее уравнение поверхности второго порядка определяет мнимый конус.

После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого конуса:

, , .

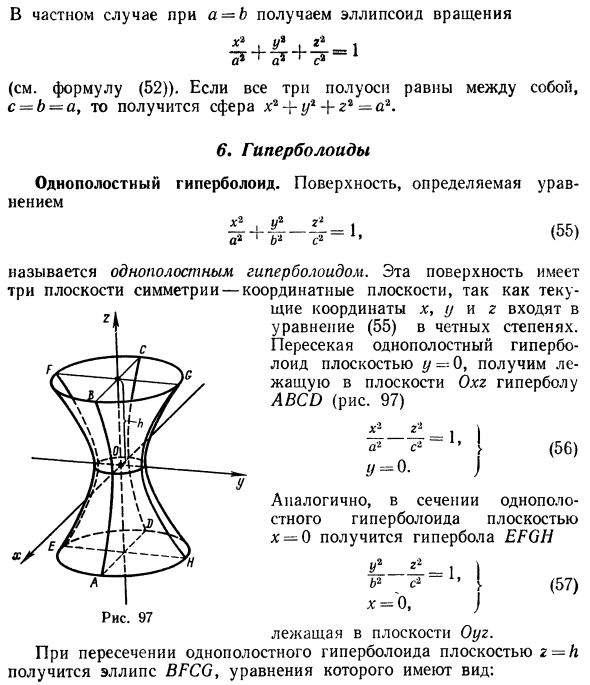
Однополостный гиперболоид

Если два корня характеристического уравнения имеют один знак, а третий корень и K 4 /I 3 имеют знак, им противоположный, то общее уравнение поверхности второго порядка определяет однополостный гиперболоид.

Обозначая в этом случае через λ 1 и λ 2 корни характеристического уравнения, имеющие один знак, общее уравнение можно переписать в виде:

, , ,

то каноническое уравнение однополостного гиперболоида будет иметь вид

Двуполостный гиперболоид

Если два корня характеристического уравнения и K 4 /I 3 имеют один и тот же знак, а третий корень характеристического уравнения им противоположный, то общее уравнение поверхности второго порядка определяет двуполостный гиперболоид.

Обозначая в этом случае через λ 1 и λ 2 корни, имеющие один знак, общее уравнение можно переписать в виде:

Последняя запись и есть каноническое уравнение двуполостного гиперболоида.

Конус

Если два корня характеристического уравнения имеют один знак, третий корень имеет знак, им противоположный, а K 4 = 0 , то общее уравнение поверхности второго порядка определяет конус.

Считая, что одинаковый знак имеют корни λ 1 и λ 2 , общее уравнение можно переписать в виде:

известном как каноническое уравнение конуса.

II. Если I 3 = 0 , а K 4 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.

Эллиптический параболоид

Если λ 1 и λ 2 имеют один знак, то общее уравнение поверхности второго порядка определяет эллиптический параболоид.

Общее уравнение можно переписать в виде:

Выбирая перед корнем знак, противоположный знаку λ 1 и λ 2 , и полагая

получим каноническое уравнение эллиптического параболоида:

Гиперболический параболоид

Если λ 1 и λ 2 имеют разные знаки, то общее уравнение поверхности второго порядка определяет гиперболический параболоид.

Обозначая через λ 1 положительный корень, а через λ 2 — отрицательный и беря перед корнем знак минус, переписываем уравнение в виде:

, ,

получим каноническое уравнение гиперболического параболоида:

III. Если I 3 = 0 , а K 4 = 0 , I 2 ≠ 0 то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.

Эллиптический цилиндр

Если λ 1 и λ 2 одного знака, а K 3 /I 2 имеет знак, им противоположный, то общее уравнение поверхности второго порядка определяет эллиптический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

, ,

получим каноническое уравнение эллиптического цилиндра:

Мнимый эллиптический цилиндр

Если λ 1 , λ 2 и K 3 /I 2 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллиптический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

Последняя запись — каноническое уравнение мнимого эллиптического цилиндра.

Мнимые пересекающиеся плоскости

Если λ 1 и λ 2 имеют один знак, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две мнимые пересекающиеся плоскости.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

, ,

получим каноническое уравнение мнимых пересекающихся плоскостей:

Гиперболический цилиндр

Если λ 1 и λ 2 имеют разные знаки, а K 3 ≠ 0 , то общее уравнение поверхности второго порядка определяет гиперболический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

, .

Таким образом, каноническое уравнение гиперболического цилиндра:

Пересекающиеся плоскости

Если λ 1 и λ 2 имеют разные знаки, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две пересекающиеся плоскости.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

, .

Таким образом, пересекающихся плоскостей:

IV. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 = I 1 — отличный от нуля корень характеристического уравнения.

Параболический цилиндр

Уравнение, получившееся после решения характеристического уравнения, можно переписать в виде:

Это уравнение параболического цилиндра, в каноническом виде оно записывается так:

V. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду: