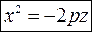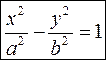Гиперболический параболоид
Каноническое уравнение имеет вид 
,
где 
и 
— это параметры параболоида, 
; 
,
Строим методом сечений.
1) Находим линию пересечения с плоскостью 
.
Решаем систему уравнений
— это уравнение параболы, симметричной относительно оси 
.
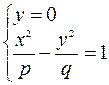
2) Находим линию пересечения с плоскостью 
.
Решаем систему уравнений
— это уравнение параболы,
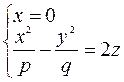
симметричной относительно оси .
3) Находим линии пересечения с плоскостями, параллельными
плоскости 
.
а) Решаем систему уравнений
— это уравнение гиперболы, у которой
— действительная полуось, а 
— мнимая полуось.
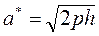
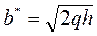
б) Решаем систему уравнений
( знак левой части изменился, так как 
по условию)
— это уравнение гиперболы, у которой 
— действительная полуось, а 
— мнимая полуось.
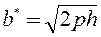
4) Находим линию пересечения с плоскостью .
Решаем систему уравнений
— это уравнение двух прямых, проходящих через точку 
.
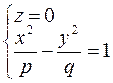
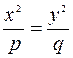
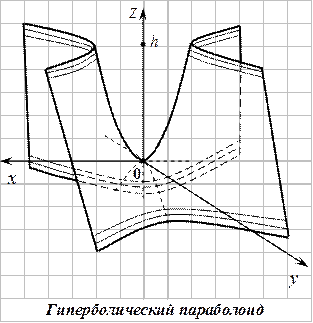
Гиперболический параболоид–это поверхность, имеющая вид седла.
Конус второго порядка
Каноническое уравнение имеет вид 
Строим методом сечений.
1) Находим линию пересечения с плоскостью 
.
Решаем систему уравнений
— это уравнение точки 
.
2) Находим линии пересечения с плоскостями параллельными 
.
Решаем систему уравнений
— это уравнение эллипса
с полуосями 
и 
.
3) Находим линию пересечения с плоскостью 
.
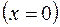
Решаем систему уравнений
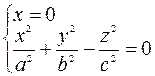
— это уравнение двух прямых, проходящих через начало координат.
4) Находим линию пересечения с плоскостью 
.
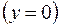
Решаем систему уравнений
— это уравнение двух прямых, проходящих через начало координат.
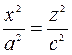
Цилиндрические поверхности
; образующая параллельна оси ;
; образующая параллельна оси 
;
; образующая параллельна оси 
;
1. Эллиптический цилиндр
образующая параллельна оси
2. Параболический цилиндр
образующая параллельна оси
3. Гиперболический цилиндр
образующая параллельна оси .
Пример 1. Построить поверхность
заданную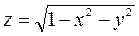 
.
¦ Из уравнения следует, что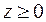 
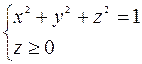
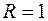
. Возведем обе части уравнения в квадрат 
полусфера, 
,
с центром в точке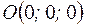 
.
Пример 2. Построить тело, ограниченное поверхностями
.
¦ Определим вид поверхностей.
— параболический цилиндр ;
— плоскость;
— координатные плоскости.
ЛИТЕРАТУРА
1. Шипачев В.С. Основы высшей математики [Текст]: Учебное пособие / В.С.Шипачев, 2002. — 479с.
2. Ильин В.А. Аналитическая геометрия [Текст]: Учебник / В.А.Ильин, Э.Г. Позняк, 2002. — 240с.
3. Зимина О.В. Линейная алгебра и аналитическая геометрия [Текст]: Учебный комплекс: Учебное пособие / О.В.Зимина; Под ред. А.И.Кириллова, 2000. – 328с.
4. Сборник задач по математике для втузов. В 4-х ч [Текст]: Учебное пособие для втузов. Ч.1 / Ред. А.В.Ефимов, Ред. А.С.Поспелов, 2003. – 288с.
5. Данко П.Е. Высшая математика в упражнениях и задачах [Текст]: Учебное пособие в 2-х ч. Ч.2 / П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова, 2005. – 404с.
6. Руководство к решению задач по высшей математике [Текст]: Учебное пособие в 2-х ч. Ч.1 /Е.И.Гурский, В.П.Домашов, В.К.Кравцов, А.П.Сильванович; Под общ. Ред. Е.И.Гурского, 1989. – 349 с.
Параболоиды: определение, виды, сечения
Определение параболоида
Эллиптическим параболоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением
Гиперболическим параболоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением
В уравнениях (4.51) и (4.52) и — положительные параметры, характеризующие параболоиды, причем для эллиптического параболоида .
Начало координат называют вершиной каждого из параболоидов ((4.50) или (4.51)).
Плоские сечения эллиптического параболоида
Плоскость пересекает эллиптический параболоид (4.51) по линии, имеющей в этой плоскости уравнение , которое равносильно уравнению параболы с фокальным параметром . Сечение параболоида плоскостью получаем, подставляя в уравнение (4.51): . Это уравнение равносильно уравнению параболы с фокальным параметром . Эти сечения называются главными параболами эллиптического параболоида (4.51).
Рассмотрим теперь сечение эллиптического параболоида плоскостями, параллельными плоскости . Подставляя , где — произвольная постоянная (параметр), в уравнение (4.51), получаем
При уравнение не имеет действительных решений, т.е. плоскость при не пересекает параболоид (4.51). При уравнению (4.51) удовлетворяет одна вещественная точка — вершина параболоида. При 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» /> уравнение определяет эллипс с полуосями . Следовательно, сечение эллиптического параболоида плоскостью (при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» />) представляет собой эллипс, центр которого лежит на оси аппликат, а вершины — на главных параболах.
Таким образом, эллиптический параболоид можно представить как поверхность, образованную эллипсами, вершины которых лежат на главных параболах (рис.4.46,а).
Параболоид вращения
Эллиптический параболоид, у которого , называется параболоидом вращения . Такой параболоид является поверхностью вращения. Сечения параболоида вращения плоскостями (при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» />), представляют собой окружности с центрами на оси аппликат (рис.4.46,б). Его можно получить, вращая вокруг оси параболу , где .
Плоские сечения гиперболического параболоида
Сечения гиперболического параболоида координатными плоскостями и представляют собой параболы (главные параболы) или с параметрами или соответственно. Поскольку оси симметрии главных парабол направлены в противоположные стороны, гиперболический параболоид называют седловой поверхностью .
Рассмотрим теперь сечения гиперболического параболоида плоскостями, параллельными плоскости . Подставляя , где — произвольная постоянная (параметр), в уравнение (4.52), получаем При 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» /> уравнение равносильно уравнению гиперболы полуосями , то есть сечение гиперболического параболоида плоскостью при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» /> представляет собой гиперболу с центром на оси аппликат, вершины которой лежат на главной параболе . При получаем уравнение сопряженной гиперболы с полуосями , т.е. сечение гиперболического параболоида плоскостью при представляет собой сопряженную гиперболу с центром на оси аппликат, вершины которой лежат на главной параболе . При получаем уравнение пересекающихся прямых , т.е. сечение гиперболического параболоида плоскостью представляет собой пару пересекающихся в начале координат прямых.
Таким образом, гиперболический параболоид можно представить как поверхность, образованную гиперболами (включая и «крест» из их асимптот), вершины которых лежат на главных параболах (рис.4.47,а).
Сечение параболоида плоскостью , где — произвольная постоянная, представляет собой параболу
равную главной параболе с параметром , вершина которой лежит на другой главной параболе с параметром . Поэтому гиперболический параболоид можно представить как поверхность, получающуюся при перемещении одной главной параболы так, чтобы ее вершина «скользила» по другой главной параболе (рис.4.47,б).
1. Гиперболический параболоид является линейчатой поверхностью, т.е. поверхностью, образованной движением прямой (рис.4.47,в).
2. Ось аппликат канонической системы координат является осью симметрии параболоида, а координатные плоскости — плоскостями симметрии параболоида.
В самом деле, если точка принадлежит параболоиду (эллиптическому или гиперболическому), то точки с координатами при любом выборе знаков также принадлежат параболоиду, поскольку их координаты удовлетворяют уравнению (4.51) или (4.52) соответственно. Поэтому параболоид симметричен относительно координатных плоскостей и координатной оси .
Гиперболический параболоид: определение, свойства и примеры
Гиперболический параболоид: определение, свойства и примеры — Наука
Содержание:
А гиперболический параболоид — поверхность, общее уравнение которой в декартовых координатах (x, y, z) удовлетворяет следующему уравнению:
(за) 2 — (г / б) 2 — г = 0.
Название «параболоид» происходит от того факта, что переменная z зависит от квадратов переменных x и y. В то время как прилагательное «гиперболический» связано с тем, что при фиксированных значениях z мы имеем уравнение гиперболы. По форме эта поверхность похожа на конское седло.
Описание гиперболического параболоида
Чтобы понять природу гиперболического параболоида, будет проведен следующий анализ:
1.- Мы возьмем частный случай a = 1, b = 1, то есть декартово уравнение параболоида остается как z = x 2 — Y 2 .
2.- Плоскости считаются параллельными плоскости ZX, то есть y = ctte.
3.- При y = ctte остается z = x 2 — C, которые представляют параболы с ветвями вверх и вершиной ниже плоскости XY.
4.- При x = ctte остается z = C — y 2 , которые представляют собой параболы с ветвями вниз и вершиной над плоскостью XY.
5.- При z = ctte остается C = x 2 — Y 2 , которые представляют собой гиперболы в плоскостях, параллельных плоскости XY. Когда C = 0, есть две прямые (на + 45º и -45º по отношению к оси X), которые пересекаются в начале координат на плоскости XY.
Свойства гиперболического параболоида
1.- Четыре разные точки в трехмерном пространстве определяют один и только один гиперболический параболоид.
2.- Гиперболический параболоид — это двояковыпуклая поверхность. Это означает, что, несмотря на искривленную поверхность, две разные линии проходят через каждую точку гиперболического параболоида, полностью принадлежащего гиперболическому параболоиду. Другая поверхность, которая не является плоскостью и имеет двойную линейку, — это гиперболоид вращения.
Именно второе свойство гиперболического параболоида позволило широко использовать его в архитектуре, поскольку поверхность может быть образована балками или прямыми веревками.
Второе свойство гиперболического параболоида позволяет дать ему альтернативное определение: это поверхность, которая может быть образована движущейся прямой линией, параллельной фиксированной плоскости, и разрезает две фиксированные линии, которые служат в качестве направляющих.. Следующий рисунок поясняет это альтернативное определение гиперболического параболоида:
Примеры работы
— Пример 1
Покажите, что уравнение:г = ху, соответствует гиперболическому параболоиду.
Решение
Преобразование будет применено к переменным x и y, соответствующим повороту декартовых осей относительно оси Z на + 45º. Старые координаты x и y преобразуются в новые x ‘и y’ в соответствии со следующими соотношениями:
а координата z остается прежней, т. е. z = z ‘.
Подставляя в уравнение z = x, мы имеем:
Применяя заметное произведение разницы на сумму, равную разности квадратов, мы имеем:
что явно соответствует изначально данному определению гиперболического параболоида.
Пересечение плоскостей, параллельных оси XY, с гиперболическим параболоидом z = x и определение равносторонних гипербол, которые имеют в качестве асимптотов плоскости x = 0 и y = 0.
— Пример 2
Определить параметры к Y б гиперболического параболоида, проходящего через точки A (0, 0, 0); В (1, 1, 5/9); С (-2, 1, 32/9) и D (2, -1, 32/9).
Решение
По своим свойствам четыре точки в трехмерном пространстве определяют единый гиперболический параболоид. Общее уравнение:
г = (х / а) 2 — (г / б) 2
Подставляем указанные значения:
Для точки A имеем 0 = (0 / a) 2 — (0 / б) 2 , уравнение, которое удовлетворяется при любых значениях параметров a и b.
Подставляя точку B, получаем:
5/9 = 1 / год 2 — 1 млрд 2
А для пункта C остается:
32/9 = 4 / год 2 — 1 млрд 2
Наконец, для точки D получаем:
32/9 = 4 / год 2 — 1 млрд 2
Что идентично предыдущему уравнению. В конечном итоге необходимо решить систему уравнений:
5/9 = 1 / год 2 — 1 млрд 2
32/9 = 4 / год 2 — 1 млрд 2
Вычитание второго уравнения из первого дает:
27/9 = 3 / год 2 откуда следует, что a 2 = 1.
Аналогичным образом второе уравнение вычитается из четверки первого, получая:
(32-20) / 9 = 4 / а 2 — 4 / а 2 -1 млрд 2 + 4 / б 2
Что упрощается как:
12/9 = 3 / б 2 ⇒ b 2 = 9/4.
Короче говоря, гиперболический параболоид, который проходит через заданные точки A, B, C и D, имеет декартово уравнение, задаваемое следующим образом:
— Пример 3
Согласно свойствам гиперболического параболоида, через каждую точку параболоида проходят две прямые, которые полностью в нем содержатся. Для случая z = x ^ 2 — y ^ 2 найдите уравнение двух прямых, которые проходят через точку P (0, 1, -1), явно принадлежащих гиперболическому параболоиду, так что все точки этих прямых также принадлежат тем же.
Решение
Используя замечательное произведение разности квадратов, уравнение для гиперболического параболоида можно записать так:
(х + у) (х — у) = с z (1 / с)
Где c — ненулевая константа.
Уравнение x + y = c z и уравнение x — y = 1 / c соответствуют двум плоскостям с нормальными векторами п= и м= . Векторное произведение м х п = дает нам направление линии пересечения двух плоскостей. Тогда одна из прямых, проходящих через точку P и принадлежащих гиперболическому параболоиду, имеет параметрическое уравнение:
Чтобы определить c, подставляем точку P в уравнение x + y = c z, получая:
Аналогичным образом, но учитывая уравнения (x — y = k z) и (x + y = 1 / k), мы имеем параметрическое уравнение линии:
Итак, две строки:
Они полностью содержатся в гиперболическом параболоиде z = x 2 — Y 2 проходящий через точку (0, 1, -1).
В качестве проверки предположим, что t = 1, что дает нам точку (1,2, -3) в первой строке. Вы должны проверить, находится ли он также на параболоиде z = x 2 — Y 2 :
-3 = 1 2 – 2 2 = 1 – 4 = -3
Это подтверждает, что он действительно принадлежит поверхности гиперболического параболоида.
Гиперболический параболоид в архитектуре
Гиперболический параболоид использовался в архитектуре великими архитекторами-авангардистами, среди которых выделяются имена испанского архитектора Антонио Гауди (1852-1926) и, в частности, также испанского Феликса Канделы (1910-1997).
Ниже приведены некоторые работы, основанные на гиперболическом параболоиде:
-Часовня города Куэрнавака (Мексика) работы архитектора Феликса Канделы.
-Океанография Валенсии (Испания), также Феликс Кандела.
Ссылки
- Энциклопедия математики. Линейчатая поверхность. Получено с: encyclopediaofmath.org
- Ллера Рубен. Гиперболический параболоид. Получено с: rubenllera.wordpress.com
- Вайсштейн, Эрик В. «Гиперболический параболоид». Материал из MathWorld — веб-ресурса Wolfram. Получено с: mathworld.wolfram.com
- Википедия. Параболоид. Получено с: en.wikipedia.com
- Википедия. Параболоид. Получено с: es.wikipedia.com
- Википедия. Рифленая поверхность. Получено с: en.wikipedia.com
3 различия между пандемией и эпидемией (и примеры)
http://mathhelpplanet.com/static.php?p=paraboloid
http://ru1.warbletoncouncil.org/paraboloide-hiperbolico-6291