Каноническое уравнение ортогональной проекции прямой на плоскость

Задача 31787 Найти проекцию прямой (x–2)/5 = (y–3)/1.

Условие

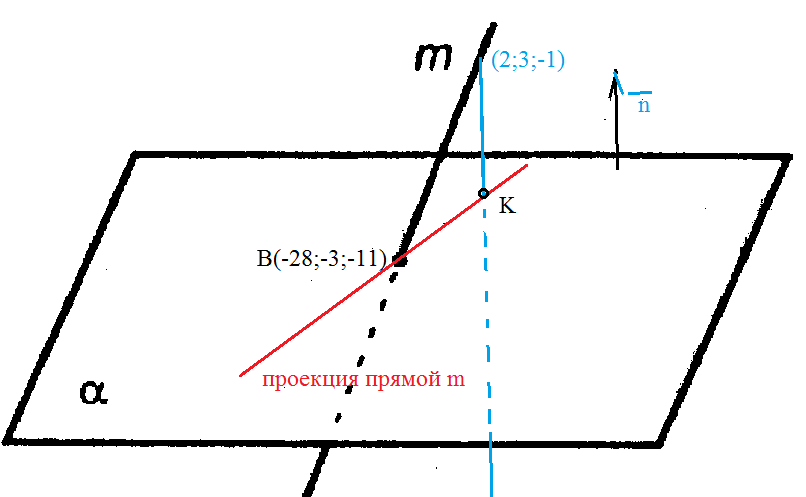
Найти проекцию прямой (x–2)/5 = (y–3)/1 = (z+1)/2 на плоскость x+4y–3z+7=0

Решение

Точка (2;3;-1) принадлежит данной прямой.
Составим уравнение прямой || нормальному вектору плоскости
vector=(1;4;-3)

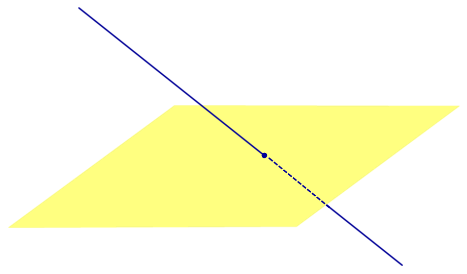
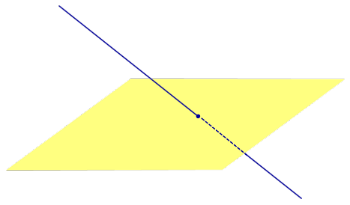
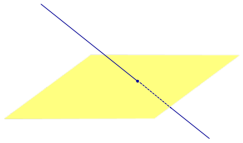
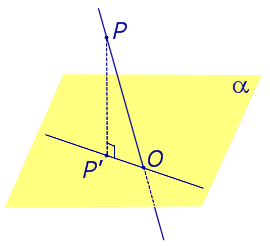
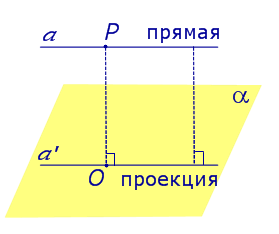
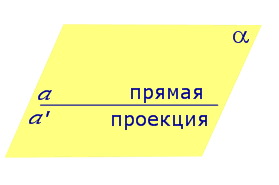
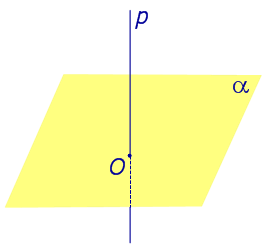
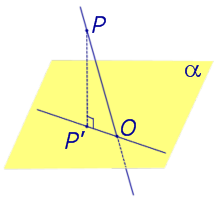
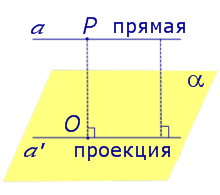
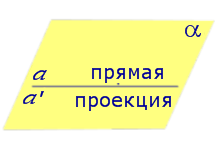
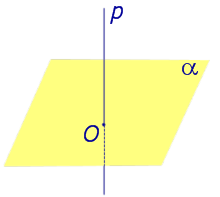
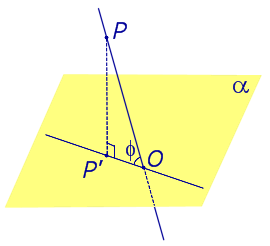
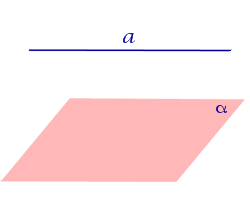
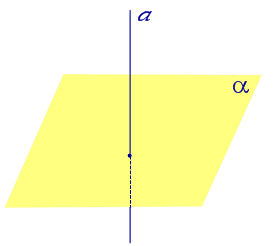
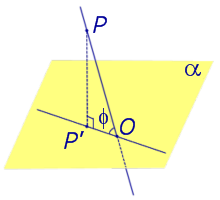
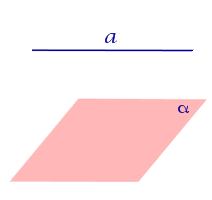
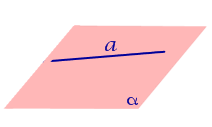
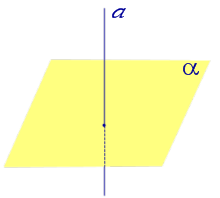
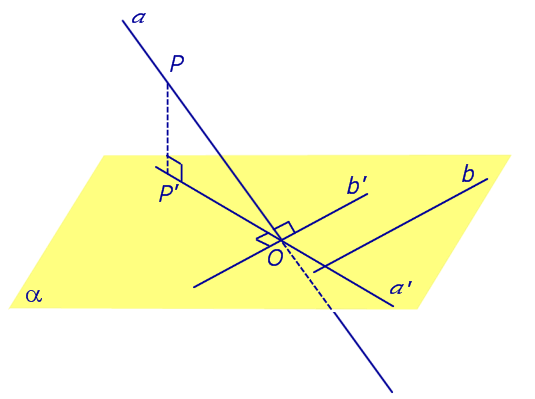
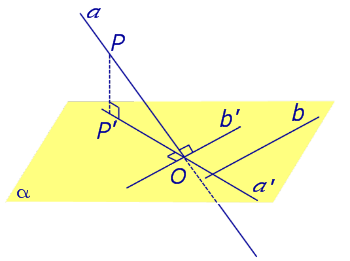
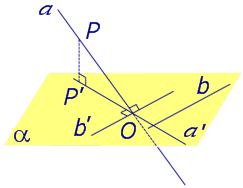
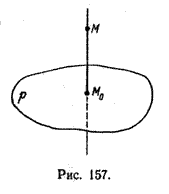
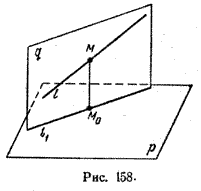
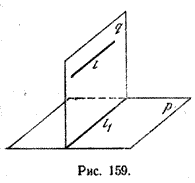
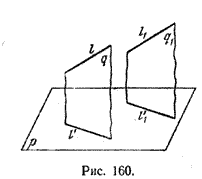
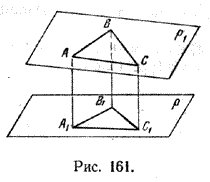
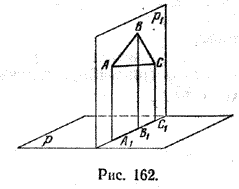
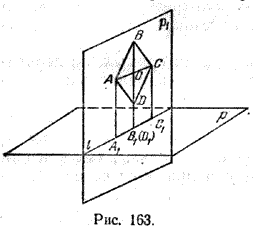
Найдем координаты точки K — точки пересечения этой прямой и плоскости
Решаем систему:
<(x-2)/1=(y-3)/4=(z-1)/(-3)

Обозначим отношение
(x-2)/1=(y-3)/4=(z-1)/(-3) = λ ⇒
получим параметрические уравнения прямой
x= λ +2
y= 4λ +3
z=-3 λ +1

подставим в уравнение плоскости

Найдем координаты точки В — точки пересечения данной прямой и данной плоскости.

Обозначим отношение
(x-2)/5=(y-3)/1=(z+1)/2=t ⇒
получим параметрические уравнения прямой
x=5t+2
y=t+3
z=2t+1

подставим в уравнение плоскости

Составляем уравнение прямой ВК, как уравнение прямой, проходящей через две точки

Ортогональнальная проекция прямой на плоскость.
Угол между прямой и плоскостью.
Теорема о трех перпендикулярах

Проекция точки на плоскость. Проекция прямой на плоскость

Угол между прямой и плоскостью

Теорема о трех перпендикулярах. Обратная теорема

Проекция прямой на плоскость

Определение 1. Ортогональной проекцией точки на плоскость называют основание перпендикуляра, опущенного из этой точки на плоскость.

Рассмотрим рисунок 1, на котором изображены прямая p, перпендикулярная к плоскости α и пересекающая плоскость α в точке O.

Точка O является ортогональной проекцией на плоскость α каждой точки прямой p.

Замечание 1. Рассматриваемый в данном разделе случай ортогонального проектирования точки на плоскость α представляет собой частный случай более общего понятия проектирования точки на плоскость параллельно некоторой прямой, необязательно перпендикулярной к плоскости. Такое проектирование используется в нашем справочнике при определении понятия «призма».

Замечание 2. Если это не приводит к разночтениям, для упрощения формулировок термин «ортогональная проекция на плоскость» часто сокращают до термина «проекция на плоскость».

Определение 2. Проекцией фигуры a на плоскость α называют фигуру a’, образованную проекциями всех точек фигуры a на плоскость α.

Определение 3. Прямую, пересекающую плоскость и не являющуюся перпендикуляром к плоскости, называют наклонной к этой плоскости (рис. 2).

Все возможные случаи, возникающие при ортогональном проектировании прямой на плоскость представлены в следующей таблице

Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α.

На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α.

Если прямая a параллельна плоскости α , то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO.

Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a .

Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O , то точка O и является проекцией этой прямой на плоскость α.

Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α.

На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α.

Если прямая a параллельна плоскости α , то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO.

Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a .

Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O , то точка O и является проекцией этой прямой на плоскость α.

Угол между прямой и плоскостью

Все возможные случаи, возникающие при определении понятия угла между прямой и плоскостью, представлены в следующей таблице.

Фигура	Рисунок	Свойство проекции
Наклонная к плоскости α
Прямая, параллельная плоскости
Прямая, лежащая на плоскости
Прямая, перпендикулярная к плоскости

Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P’O. )

На рисунке это угол φ

Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.

Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.

Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( радиан).

Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P’O )

На рисунке это угол φ

Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.

Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.

Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( радиан).

Теорема о трех перпендикулярах

Теорема о трех перпендикулярах. Если наклонная a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и проекция наклонной a’ на плоскость α перпендикулярна к прямой b.

Доказательство. Рассмотрим следующий рисунок 3.

На рисунке 3 буквой O обозначена точка пересечения наклонной a с плоскостью α. Точка P – произвольная точка на прямой a, а точка P’ – это проекция точки P на плоскость α. Проведем через точку O прямую b’, параллельную прямой параллельную прямой b. Если прямая b проходит через точку O, то прямая b’, совпадет с прямой b.

Поскольку PP’ – перпендикуляр к плоскости α, то прямая PP’ перпендикулярна к прямой b’. Прямая a перпендикулярна к прямой b’ по условию. Таким образом, прямая b’ перпендикулярна к двум пересекающимся прямым PO и PP’, лежащим в плоскости POP’. В силу признака перпендикулярности прямой и плоскости получаем, что прямая b’ перпендикулярна к плоскости POP’, откуда вытекает, что прямая b’ перпендикулярна и к прямой a’, лежащей на плоскости POP’.

Теорема, обратная теореме о трех перпендикулярах. Если проекция a’ наклонной a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и сама наклонная a перпендикулярна к прямой b.

Доказательство. Как и для доказательства прямой теоремы о трех перпендикулярах, воспользуемся рисунком 3.

Прямая a’ перпендикулярна к прямой b по условию обратной теоремы. Прямая PP’ перпендикулярна к прямой b’, поскольку PP’ – перпендикуляр к плоскости α. Таким образом, прямая b’, перпендикулярна к двум пересекающимся прямым P’O и PP’, лежащим в плоскости POP’. В силу признака перпендикулярности прямой и плоскости прямая b’ перпендикулярна к плоскости POP’. Тогда, в частности, прямая b’ перпендикулярна к прямой a, лежащей на плоскости POP’.

Ортогональные проекции прямых и отрезков

Рассмотрим некоторую плоскость р и точку М. Ортогональной проекцией точки М на плоскость р называется основание М₀ перпендикуляра к плоскости р, проведенного через точку М (рис. 157). Плоскость р называют в этом случае плоскостью проекции.

Существует единственный перпендикуляр к плоскости р, проведенный через данную точку. Поэтому для каждой точки пространства существует единственная ортогональная проекция М₀ этой точки на данную плоскость. В частности, если М \(\in\) р, то М₀ = М.

В дальнейшем для краткости, говоря об ортогональных проекциях, мы будем обычно употреблять термин «проекция», опуская слово «ортогональная».

Проекцией прямой l на плоскость р называется множество точек плоскости р, являющихся проекциями точек этой прямой.

Рассмотрим некоторые свойства проекций прямых на плоскость.

Если прямая l не перпендикулярна плоскости проекции, то ее проекция на эту плоскость есть прямая.

Если прямая l лежит в плоскости р, то это утверждение очевидное.

Пусть прямая l не лежит в плоскости р, и пусть М₀ — проекция точки М, принадлежащей l и не принадлежащей р, на плоскость р (рис. 158).

Через прямые l и М₀М проведем плоскость q. Плоскости р и q перпендикулярны по признаку перпендикулярности плоскостей. Следовательно, прямая l₁ = p \(\cap\) q является проекцией прямой l на плоскость р.

Отсюда следует, что проекции луча и отрезка (не перпендикулярных плоскости р) представляют собой соответственно луч и отрезок. Если l — перпендикуляр к р, то по определению проекцией l на р будет точка (точка пересечения прямой l и плоскости р).

Из этого свойства следует, что общее определение проекции прямой на плоскость не противоречит определению проекции наклонной к плоскости.

Если прямая l параллельна плоскости проекции, то она параллельна прямой l₁, являющейся ее проекцией.

Действительно, проведя через прямые l и l₁ плоскость q (рис. 159), получим l₁ = p \(\cap\) q Следовательно, l₁ || l.

Отсюда следует, что проекция отрезка, параллельного плоскости проекции, есть отрезок, конгруэнтный данному.

Проекции двух параллельных прямых, не перпендикулярных плоскости проекции, — параллельные прямые.

Пусть плоскость q проходит через прямую l и ее проекцию l&#146, a q₁ — через прямую l₁ и ее проекцию l&#146₁ (рис. 160). Плоскости q и q₁ параллельны, так как они перпендикулярны плоскости р и проходят через параллельные прямые l и l₁. Но тогда и l&#146 || l&#146₁ как прямые пересечения параллельных плоскостей q , q₁плоскостью р.

Отсюда следует, что проекции пересекающихся прямых (не лежащих в плоскости, перпендикулярной плоскости р) пересекаются.

Отношение длин проекций двух параллельных отрезков, не перпендикулярных плоскости проекции, на данную плоскость равно отношению длин проектируемых отрезков.

Вместо данных отрезков можно рассматривать конгруэнтные им отрезки, лежащие на одной прямой. А так как прямая и ее проекция принадлежат одной плоскости, то доказываемое утверждение следует из теоремы о пропорциональных отрезках на плоскости.

Проекцией фигуры F на плоскость р называется множество точек, являющихся проекциями точек фигуры F на эту плоскость.

Задача 1. Изобразить проекцию треугольника ABC на данную плоскость р.

Если плоскость \(\Delta\) АВС (p₁) не перпендикулярна плоскости р, то проекцией треугольника ABC на эту плоскость будет некоторый треугольник A₁B₁C₁ (проекция отрезка есть отрезок) (рис. 161).

Если p₁ ⊥ p, то проекцией данного треугольника ABC на плоскость р будет отрезок

Если p₁ || p , то проекцией \(\Delta\) АВС на плоскость р будет \(\Delta\) A₁B₁C₁ \(\cong\) \(\Delta\) АВС.

Задача 2. Одна из диагоналей ромба ABCD перпендикулярна данной плоскости р. Какова проекция данного ромба на эту плоскость?

Пусть [BD] ⊥ р (рис. 163).

Тогда плоскость ромба ABCD (p₁) перпендикулярна плоскости р, а проекция [A₁C₁] диагонали АС будет принадлежать l = p₁ \(\cap\) p .

По свойству ромба [AC] ⊥ [BD] , по условию (BD) ⊥ р; по определению прямой, перпендикулярной плоскости, (BD) ⊥ l. Тогда точки В, D и точка О пересечения диагоналей проектируются в точку В₁ (D₁) отрезка A₁C₁. Поэтому проекцией ромба ABCD на плоскость р является отрезок A₁C₁.

Фигура	Рисунок	Определение
Наклонная к плоскости α
Прямая, параллельная плоскости
Прямая, лежащая на плоскости
Прямая, перпендикулярная к плоскости