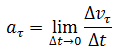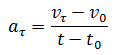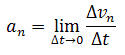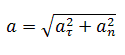Теоретическая механика:
Кинематика точки
Смотрите также решения задач по теме «Кинематика точки» в онлайн решебниках Яблонского, Мещерского, Чертова (с примерами и методичкой для заочников), Иродова и Савельева.
В этой главе в основном рассмотрены методы решения задач, в которых закон движения точки выражен так называемым естественным способом: уравнением s=f(t) по заданной траектории *.
* Решения задач, в которых закон движения задан координатным способом, рассмотрены в конце главы (§ 31).
В этом случае главными параметрами, характеризующими движение точки но заданной траектории, являются: s – расстояние от заданного начального положения и t – время.
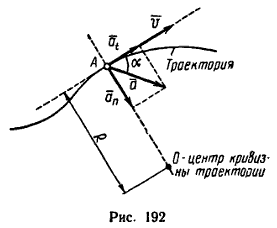
Величина, характеризующая в каждый данный момент времени направление и быстроту движения точки, называется скоростью (v на рис. 192). Вектор скорости всегда направлен вдоль касательной в ту сторону, куда движется точка. Числовое значение скорости в любой момент времени выражается производной от расстояния по времени:
v = ds/dt или v = f'(t).
Ускорение a точки в каждый данный момент времени характеризует быстроту изменения скорости. При этом нужно отчетливо понимать, что скорость – вектор, и, следовательно, изменение скорости может происходить по двум признакам: по числовой величине (по модулю) и по направлению.
Быстрота изменения модуля скорости характеризуется касательным (тангенсальным) ускорением at – составляющей полного ускорения a, направленной по касательной к траектории (см. рис. 192).
Числовое значение касательного ускорения в общем случае определяется по формуле
at = dv/dt или at = f»(t).
Быстрота изменения направления скорости характеризуется центростремительным (нормальным) ускорением an – составляющей полного ускорения a, направленного по нормали к траектории в сторону центра кривизны (см. рис. 192).
Числовое значение нормального ускорения определяется в общем случае по формуле
an = v 2 /R,
где v – модуль скорости точки в данный момент;
R – радиус кривизны траектории в месте, где находится точка в данный момент.
После того как определены касательное и нормальное ускорения, легко определить и ускорение a ( полное ускорение точки ).
Так как касательная и нормаль взаимно перпендикулярны, то числовое значение ускорения а можно определить при помощи теоремы Пифагора:
a = sqrt(at 2 + an 2 ).
Направление вектора a можно определить, исходя из тригонометрических соотношений, по одной из следующих формул:
sin α = an/a; cos α = at/a; tg α = an/at.
Но можно сначала определить направление полного ускорения a использовав формулу tg α = an/at,
а затем найти числовое значение a:
a = an/sin α или a = at/cos α.
Касательное и нормальное ускорения точки являются главными кинематическими величинами, определяющими вид и особенности движения точки.
Наличие касательного ускорения (at≠0) или его отсутствие (at=0) определяют соответственно неравномерность или равномерность движения точки.
Наличие нормального ускорения (an≠0) или его отсутствие (an=0) определяют криволинейность или прямолинейность движения точки.
Движение точки можно классифицировать так:
а) равномерное прямолинейное (at = 0 и an = 0);
б) равномерное криволинейное (at = 0 и an ≠ 0);
в) неравномерное прямолинейное (at ≠ 0 и an = 0);
г) неравномерное криволинейное (at ≠ 0 и an ≠ 0).
Таким образом, движение точки классифицируется по двум признакам: по степени неравномерности движения и по виду траектории.
Степень неравномерности движения точки задана уравнением s=f(t), а вид траектории задается непосредственно.
§ 27. Равномерное прямолинейное движение точки
Если at=0 и an=0, то вектор скорости остается постоянным (v=const), т. е. не изменяется ни по модулю, ни по направлению. Такое движение называется равномерным прямолинейным .
Уравнение равномерного движения имеет вид
(а) s = s0 + vt
или в частном случае, когда начальное расстояние s0=0,
(б) s = vt.
В уравнение (а) входит всего четыре величины, из них две переменные: s и t и две постоянные: s0 и v. Поэтому в условии задачи на равномерное и прямолинейное движение точки должны быть заданы три любые величины.
При решении задач необходимо выяснить все заданные величины и привести их к одной системе единиц. При этом нужно заметить, что как в системе МКГСС (технической), так и в СИ единицы всех кинематических величин одинаковы: расстояние s измеряется в м, время t – в сек, скорость v – в м/сек.
§ 28. Равномерное криволинейное движение точки
Если at = 0 и an ≠ 0, то модуль скорости остается неизменным (точка движется равномерно), но ее направление изменяется и точка движется криволинейно. Иначе, при равномерном движении по криволинейной траектории точка имеет нормальное ускорение, направленное по нормали к траектории и численно равное
an = v 2 /R,
где R – радиус кривизны траектории.
В частном случае движения точки по окружности (или по дуге окружности) радиус кривизны траектории во всех ее точках постоянный:
R = r = const,
а так как и числовое значение скорости постоянно, то
an = v 2 /r = const.
При равномерном движении числовое значение скорости определяется из формулы
v = (s — s0)/t или v = s/t.
Если точка совершит полный пробег по окружности, то путь s равен длине окружности, т. е. s = 2πr = πd (d = 2r – диаметр), а время равно периоду, т. е. t = T. Выражение скорости примет вид
v = 2πr/T = πd/T.
§ 29. Равнопеременное движение точки
Если вектор at=const (касательное ускорение постоянно как по модулю, так и по направлению), то an=0. Такое движение называется равнопеременным и прямолинейным .
Если же постоянным остается только числовое значение касательного уравнения
at = dv/dt = f'(t) = const,
то an≠0 и такое движение точки называется равнопеременным криволинейным .
При |at|>0 движение точки называется равноускоренным , а при |at| равнозамедленным .
Уравнение равнопеременного движения независимо от его траектории имеет вид
(1) s = s0 + v0t + att 2 / 2.
Здесь s0 – расстояние точки от исходного положения в момент начала отсчета; v0 – начальная скорость и at – касательное ускорение – величины численно постоянные, a s и t – переменные.
Числовое значение скорости точки в любой момент времени определяется из уравнения
(2) v = v0 + att.
Уравнения (1) и (2) являются основными формулами равнопеременного движения и они содержат шесть различных величин: три постоянные: s0, v0, at и три переменные: s, v, t.
Следовательно, для решения задачи на равнопеременное движение точки в ее условии должно быть дано не менее четырех величин (систему двух уравнений можно решить лишь в том случае, если они содержат два неизвестных).
Если неизвестные входят в оба основных уравнения, например, неизвестны at и t, то для удобства решения таких задач выведены вспомогательные формулы:
после исключения at из (1) и (2)
(3) s = s0 + (v + v0)t / 2;
после исключения t из (1) и (2)
(4) s = s0 + (v 2 — v0 2 ) / (2at).
В частном случае, когда начальные величины s0=0 и v0=0 (равноускоренное движение из состояния покоя), то получаем те же формулы в упрощенном виде:
(5) s = att 2 / 2;
(6) v = att;
(7) s = vt / 2;
(8) s = v 2 / (2at).
Уравнения (5) и (6) являются основными, а уравнения (7) и (8) – вспомогательными.
Равноускоренное движение из состояния покоя, происходящее под действием только силы тяжести, называется свободным падением . К этому движению применимы формулы (5)–(8), причем
at = g = 9,81 м/сек 2 ≈ 9,8 м/сек 2 .
§ 30. Неравномерное движение точки по любой траектории
§ 31. Определение траектории, скорости и ускорения точки, если закон ее движения задан в координатной форме
Если точка движется относительно некоторой системы координат, то координаты точки изменяются с течением времени. Уравнения, выражающие функциональные зависимости координат движущейся точки от времени, называют уравнениями движения точки в системе координат (см. § 51, п. 2 в учебнике Е. М. Никитина).
Движение точки в пространстве задается тремя уравнениями:
x = f1(t);
(1) y = f2(t);
z = f3(t);
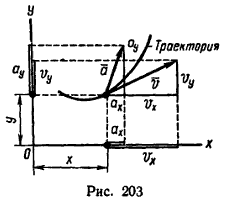
Движение точки в плоскости (рис. 203) задается двумя уравнениями:
(2) x = f1(t);
y = f2(t);
Системы уравнений (1) или (2) называют законом движения точки в координатной форме .
Ниже рассматривается движение точки в плоскости, поэтому используется только система (2).
Если закон движения точки задан в координатной форме, то:
а) траектория плоского движения точки выражается уравнением
y = F(x),
которое образуется из данных уравнений движения после исключения времени t;
б) числовое значение скорости точки находится из формулы
v = sqrt(vx 2 + vy 2 )
после предварительного определения проекции (см. рис. 203) скорости на оси координат
vx = dx/dt и vy = dy/dt;
в) числовое значение ускорения находится из формулы
a = sqrt(ax 2 + ay 2 )
после предварительного определения проекций ускорения на оси координат
ax = dvx/dt и ay = dvy/dt;
г) направления скорости и ускорения относительно осей координат определяются из тригонометрических соотношений между векторами скорости или ускорения и их проекциями.
§ 32. Кинематический способ определения радиуса кривизны траектории
При решении многих технических задач возникает необходимость знать радиус кривизны R (или 1/R – кривизну ) траектории. Если задано уравнение траектории, то радиус ее кривизны в любой точке можно определить при помощи дифференциального исчисления. Используя уравнения движения точки в координатной форме, можно определять радиус кривизны траектории движущейся точки без непосредственного исследования уравнения траектории. Определение радиуса кривизны траектории при помощи уравнений движения точки в координатной форме называется кинематическим способом. Этот способ основан на том, что радиус кривизны траектории движущейся точки входит в формулу
an = v 2 /R,
выражающую числовое значение нормального ускорения.
Скорость v точки определяется по формуле
(б) v = sqrt(vx 2 + vy 2 ).
Числовое значение нормального ускорения an входит в выражение полного ускорения точки
a = sqrt(an 2 + at 2 ),
откуда
(в) an = sqrt(a 2 — at 2 ),
где квадрат полного ускорения
(г) a 2 = ax 2 + ay 2
и касательное ускорение
(д) at = dv/dt.
Таким образом, если закон движения точки задан уравнениями
x = f1(t);
y = f2(t),
то при определении радиуса кривизны траектории рекомендуется произвести следующее:
1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:
vx = f1‘(t);
vy = f2‘(t).
2. Подставив в (б’) выражения vx и vy, найти v 2 .
3. Продифференцировав по t уравнение (б), полученное непосредственно из (б’), найти касательное ускорение at, а затем at 2 .
4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения
ax = f1»(t) = vx‘;
ay = f2»(t) = vy‘.
5. Подставив в (г) выражения ax и ay, найти a 2 .
6. Подставить в (в) значения a 2 и at 2 и найти an.
7. Подставив в (а) найденные значения v 2 и an, получить радиус кривизны R.
Техническая механика
Скорость и ускорение
Скорость точки
В предыдущей статье движение тела или точки определено, как изменение положения в пространстве с течением времени. Для того чтобы более полно охарактеризовать качественные и количественные стороны движения введены понятия скорости и ускорения.
Скорость – это кинематическая мера движения точки, характеризующая быстроту изменения ее положения в пространстве.
Скорость является векторной величиной, т. е. она характеризуется не только модулем (скалярной составляющей), но и направлением в пространстве.
Как известно из физики, при равномерном движении скорость может быть определена длиной пути, пройденного за единицу времени: v = s/t = const (предполагается, что начало отсчета пути и времени совпадают).
При прямолинейном движении скорость постоянна и по модулю, и по направлению, а ее вектор совпадает с траекторией.
Единица скорости в системе СИ определяется соотношением длина/время, т. е. м/с .
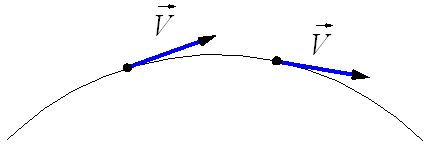
Очевидно, что при криволинейном движении скорость точки будет меняться по направлению.
Для того, чтобы установить направление вектора скорости в каждый момент времени при криволинейном движении, разобьем траекторию на бесконечно малые участки пути, которые можно считать (вследствие их малости) прямолинейными. Тогда на каждом участке условная скорость vп такого прямолинейного движения будет направлена по хорде, а хорда, в свою очередь, при бесконечном уменьшении длины дуги ( Δs стремится к нулю), будет совпадать с касательной к этой дуге.
Из этого следует, что при криволинейном движении вектор скорости в каждый момент времени совпадает с касательной к траектории (рис. 1а) . Прямолинейное движение можно представить, как частный случай криволинейного движения по дуге, радиус которой стремится к бесконечности (траектория совпадает с касательной) .
При неравномерном движении точки модуль ее скорости с течением времени меняется.
Представим себе точку, движение которой задано естественным способом уравнением s = f(t) .
Если за небольшой промежуток времени Δt точка прошла путь Δs , то ее средняя скорость равна:
Средняя скорость не дает представления об истинной скорости в каждый данный момент времени (истинную скорость иначе называют мгновенной). Очевидно, что чем меньше промежуток времени, за который определяется средняя скорость, тем ближе ее значение будет к мгновенной скорости.
Истинная (мгновенная) скорость есть предел, к которому стремится средняя скорость при Δt, стремящемся к нулю :
v = lim vср при t→0 или v = lim (Δs/Δt) = ds/dt .
Таким образом, числовое значение истинной скорости равно v = ds/dt .
Истинная (мгновенная) скорость при любом движении точки равна первой производной координаты (т. е. расстояния от начала отсчета перемещения) по времени.
При Δt стремящемся к нулю, Δs тоже стремится к нулю, и, как мы уже выяснили, вектор скорости будет направлен по касательной (т. е. совпадает с вектором истинной скорости v ). Из этого следует, что предел вектора условной скорости vп , равный пределу отношения вектора перемещения точки к бесконечно малому промежутку времени, равен вектору истинной скорости точки.
Ускорение точки в прямолинейном движении
В общем случае движение точки с изменяющейся во времени скоростью называют ускоренным, при этом считая ускорение, вызывающее уменьшение скорости, отрицательным. Иногда движение, в котором скорость с течением времени уменьшается, называют замедленным.
Ускорение есть кинематическая мера изменения скорости точки во времени. Другими словами — ускорение — это скорость изменения скорости.
Как и скорость, ускорение является величиной векторной, т. е. характеризуется не только модулем, но и направлением в пространстве.
При прямолинейном движении вектор скорости всегда совпадает с траекторией и поэтому вектор изменения скорости тоже совпадает с траекторией.
Из курса физики известно, что ускорение представляет собой изменение скорости в единицу времени. Если за небольшой промежуток времени Δt скорость точки изменилась на Δv , то среднее ускорение за данный промежуток времени составило: аср = Δv/Δt .
Среднее ускорение не дает представление об истинной величине изменения скорости в каждый момент времени. При этом очевидно, что чем меньше рассматриваемый промежуток времени, во время которого произошло изменение скорости, тем ближе значение ускорения будет к истинному (мгновенному).
Отсюда определение: истинное (мгновенное) ускорение есть предел, к которому стремится среднее ускорение при Δt , стремящемся к нулю:
а = lim аср при t→0 или lim Δv/Δt = dv/dt .
Учитывая, что v = ds/dt , получим: а = dv/dt = d 2 s/dt 2 .
Истинное ускорение в прямолинейном движении равно первой производной скорости или второй производной координаты (расстояния от начала отсчета перемещения) по времени.
Единица ускорения — метр, деленный на секунду в квадрате ( м/с 2 ).
Ускорение точки в криволинейном движении
При движении точки по криволинейной траектории скорость меняет свое направление, т. е вектор скорости является переменной величиной.
Представим себе точку М , которая за время Δt , двигаясь по криволинейной траектории, переместилась в положение М1 (рис. 1) .
Вектор приращения (изменения) скорости обозначим Δv , тогда: Δv = v1 – v .
Для нахождения вектора Δv перенесем вектор v1 в точку М и построим треугольник скоростей. Определим вектор среднего ускорения:
Вектор аср параллелен вектору Δv , так как от деления векторной величины на скалярную направление вектора не меняется.
Вектор истинного ускорения есть предел, к которому стремится отношение вектора приращения скорости к соответствующему промежутку времени, когда последний стремится к нулю:
а = lim Δv/Δt при t→0 .
Такой предел называют векторной производной.
Таким образом, истинное ускорение точки в криволинейном движении равно векторной производной скорости по времени .
Из рисунка 1 видно, что вектор ускорения в криволинейном движении всегда направлен в сторону вогнутости траектории.
Так как векторную производную непосредственно вычислять мы не умеем, то ускорение в криволинейном движении будем определять косвенными методами. Так, например, если движение точки задано естественным способом, то применяется теорема о проекции ускорения на касательную и нормаль. Чтобы понять суть этой теоремы, следует рассмотреть понятие кривизны кривых линий.
Понятие о кривизне кривых линий
Рассмотрим криволинейную траекторию точки М (рис. 2а) .
Угол Δφ между касательными к кривой в двух соседних точках называется углом смежности .
Кривизной кривой в данной точке называется предел отношения угла смежности Δφ к соответствующей длине Δs дуги, когда последняя стремится к нулю.
Обозначим кривизну буквой k , тогда:
k = lim Δφ/Δs при Δs → 0 .
Рассмотрим окружность радиуса R (см. рисунок 2б) .
Так как Δs = RΔφ , то:
k = lim Δφ/Δs = lim Δφ/RΔs = 1/R (при Δs → 0) .
Следовательно, кривизна окружности во всех точках одинакова и равна k = 1/R .
Для каждой точки данной кривой можно подобрать такую окружность, кривизна которой равна кривизне кривой в данной точке. Радиус ρ такой окружности называется радиусом кривизны кривой в данной точке, а центр этой окружности – центром кривизны .
Итак, кривизна кривой в данной точке есть величина, обратная радиусу кривизны в данной точке :
Очевидно, что кривизна прямой линии будет равна нулю, а поскольку радиус кривизны такой линии равен бесконечности.
Теорема о проекции ускорения на касательную и нормаль
Проекция ускорения на касательную к траектории называется касательным (тангенциальным) ускорением, а проекция ускорения на нормаль к этой касательной – нормальным ускорением.
Теорема: нормальное ускорение равно квадрату скорости, деленному на радиус кривизны траектории в данной точке; касательное ускорение – первой производной от скорости по времени .
Доказательство этой теоремы основывается на геометрических построениях с учетом приведенных ранее зависимостей перемещения, скорости и ускорения от времени. В данной статье доказательство теоремы не приводится; при необходимости, его можно рассмотреть в других источниках информации.
Итак, на основании теоремы об ускорениях, можно записать:
ап = v 2 /ρ; aτ = dv/dt .
Анализируя формулы касательного и нормального ускорения можно сделать вывод, что касательное ускорение характеризует изменение скорости только по модулю, а нормальное – только по направлению.
Зная величину нормального и касательного ускорения, можно вычислить полное ускорение точки, применив теорему Пифагора:
Направление ускорения: cos (aτ,a) = аτ/а .
Часто касательное и нормальное ускорения рассматривают не как проекции, а как составляющие полного ускорения, т. е. как векторные величины.
Вектор нормального ускорения всегда направлен к центру кривизны, поэтому нормальное ускорение иногда называют центростремительным .
Виды движения точки в зависимости от ускорения
Анализируя формулы касательного и нормального ускорений, можно выделить следующие виды движения точки:
ап = v 2 /ρ ≠ 0; aτ = dv/dt ≠ 0 , — неравномерное криволинейное (рис. 3а) ;
ап = v 2 /ρ ≠ 0; aτ = dv/dt = 0 , — равномерное криволинейное (рис. 3б) ;
ап = v 2 /ρ = 0; aτ = dv/dt ≠ 0 , — неравномерное прямолинейное (рис. 3в) ;
aτ = dv/dt = const ≠ 0; ап = v 2 /ρ ≠ 0 , — равнопеременное криволинейное (рис. 3г) ;
aτ = dv/dt = const ≠ 0, ап = v 2 /ρ = 0 , — равнопеременное прямолинейное (рис. 3д) ;
ап = v 2 /ρ = 0; aτ = dv/dt = 0 , — равномерное прямолинейное (движение без ускорения) (рис. 3е) .
Теоремы о проекциях скорости и ускорения на координатную ось
Если движение точки задано координатным способом, то путь (перемещение), скорость и ускорение за промежуток времени Δt можно найти, используя проекции этих величин на координатную ось. Очевидно, что приращение любой из координат при Δt стремящемся к нулю тоже стремится к нулю, и предел такого приращения может быть определен из дифференциальных отношений, устанавливаемых теоремами о проекциях скорости и ускорения:
Теорема: проекция скорости на координатную ось равна первой производной от соответствующей координаты по времени :
Теорема: проекция ускорения на координатную ось равна второй производной от соответствующей координаты по времени :
ax = d 2 x/Δt 2 ay = d 2 y/Δt 2 az = d 2 z/Δt 2 .
Зная проекции скорости или ускорения на координатные оси, можно определить модуль и направление вектора любой из этих величин, используя теорему Пифагора и тригонометрические соотношения.
Криволинейное движение
Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению.
Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).
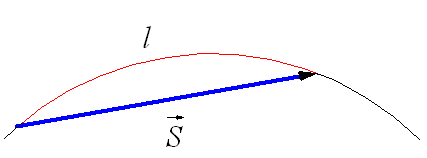
При движении по криволинейной траектории вектор перемещения 
Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – это тангенциальное ускорение:
Где vτ, v0 – величины скоростей в момент времени t0 + Δt и t0 соответственно.
Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.
Нормальное ускорение — это изменение скорости по направлению за единицу времени:
Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.
Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности.
Полное ускорение при равнопеременном криволинейном движении тела равно:
Движение тела по криволинейной траектории можно приближённо представить как движение по дугам некоторых окружностей (рис. 1.21).
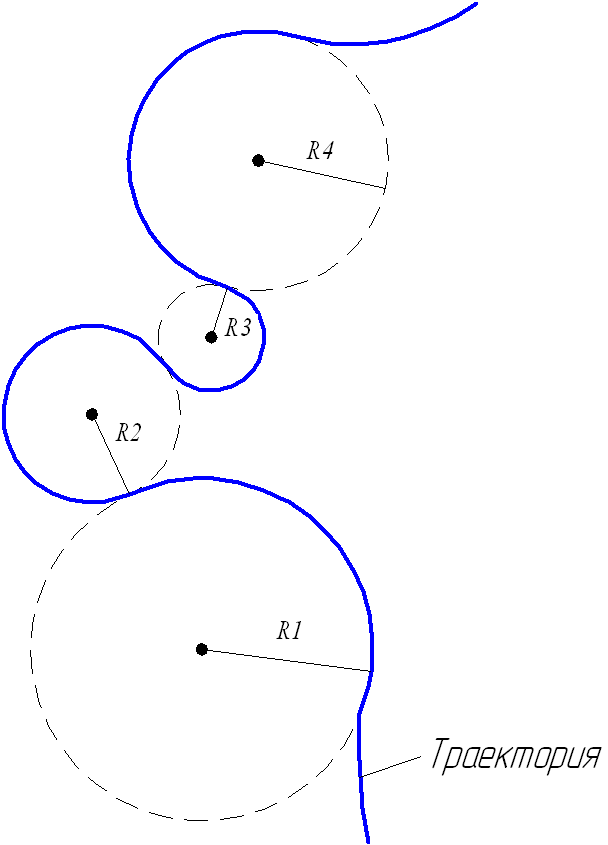
http://k-a-t.ru/tex_mex/12-kinematika_skor_uskor/index.shtml
http://av-mag.ru/physics/index.php/mechanics/kinematika/curvilinear-movement/