Плоскость как поверхность первого порядка.
Теорема. В декартовой прямоугольной системе координат каждая плоскость определяется уравнением первой степени.
Доказательство. Рассмотрим произвольную плоскость π и докажем, что эта плоскость определяется уравнением первой степени. Возьмем на плоскости p какую-нибудь точку М0(x0; y0; z0); выберем кроме этого, произвольный вектор (не нулевой) перпендикулярный к плоскости π. 





Условием перпендикулярности двух векторов является равенство нулю их скалярного произведения:




Это и есть искомое уравнение плоскости π, т.к. ему удовлетворяют координаты x; y; z точки М тогда и только тогда, когда М лежит на плоскости π.
Раскрывая скобки, представим уравнение (1) в виде Аx+Вy+Сz+(-Аx0-Вy0-Сz0)=0. Далее, обозначая число -Аx0-Вy0-Сz0 буквой D, получим:
Мы видим, что плоскость π действительно определяется уравнением первой степени. Теорема доказана.
Произвольный ненулевой вектор, перпендикулярный плоскости, называется нормальным к ней вектором. Употребляя это название, мы можем сказать, что уравнение А(x-x0)+В(y-y0)+С(z-z0)=0 есть уравнение плоскости, проходящей через точку М0(x0; y0; z0) и имеющей нормальный вектор 
называется общим уравнением плоскости.
Теорема. В декартовых координатах каждое уравнение первой степени определяет плоскость.
Доказательство. Рассмотрим произвольное уравнение первой степени Аx+Вy+Сz+D=0 (А, В, С одновременно не равны нулю).
Пусть x0, y0, z0 произвольная тройка чисел, удовлетворяющая уравнению (2):
Вычтем из уравнения (2) тождество (3), получим
которое по предыдущему представляет собой уравнение плоскости, проходящей через точку М0(x0;y0; z0) и имеющей нормальный вектор 
Докажем теперь следующее важное утверждение: если два уравнения А1x+В1y+С1z+D1=0 и А2x+В2y+С2z+D2=0 определяют одну и ту же плоскость, то коэффициенты их пропорциональны. Действительно 



Пусть М0(x0;y0; z0) — любая точка плоскости: ее координаты должны удовлетворять каждому из данных уравнений, таким образом А1x+В1y+С1z+D1=0 и А2x+В2y+С2z+D2=0. Умножим второе из этих равенств на m и вычтем из первого: получим
D1 — D2m=0 или D1= D2m и 
Плоскость и прямая в пространстве. Поверхности второго порядка.
Плоскость.
Рассмотрим в декартовом базисе произвольную плоскость Р и вектор нормали (перпендикулярный) к ней `n (А, В, С). Возьмем в этой плоскости произвольную фиксированную точку М0(х0, у0, z0) и текущую точку М(х, у, z). Очевидно, что 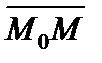
(см.(1.20) при j = p /2). Это уравнение плоскости в векторной форме. Переходя к координатам, получим общее уравнение плоскости
А(х – х0) + В(у – у0) + С(z – z0) = 0 ÞАх + Ву + Сz + D = 0 (1.54).
(D = –Ах0– Ву0 – Сz0; А 2 + В 2 + С 2 ¹ 0).
Можно показать, что в декартовых координатах каждая плоскость определяется уравнением первой степени и, обратно, каждое уравнение первой степени определяет плоскость, (т.е. плоскость есть поверхность первого порядка и поверхность первого порядка есть плоскость).
Рассмотрим некоторые частные случаи расположения плоскости, заданной общим уравнением:
А = 0 – параллельна оси Ох; В = 0 – параллельна оси Оу; С = 0 – параллельна оси Оz. (Такие плоскости, перпендикулярные одной из координатных плоскостей, называют проектирующими); D = 0 – проходит через начало координат; А = В = 0 – перпендикулярна оси Оz (параллельна плоскости хОу); А = В = D = 0 – совпадает с плоскостью хОу (z = 0). Аналогично анализируются все остальные случаи.
Если D ¹ 0, то, разделив обе части (1.54) на —D, можно привести уравнение плоскости к виду: 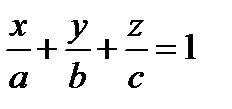
а = – D /А, b = –D/ В, с =–D /С. Соотношение (1.55) называетcя уравнением плоскости в отрезках; а, b, с – абсцисса, ордината и аппликата точек пересечения плоскости с осями Ох, Оу, Оz, а |a|, |b|, |c| – длины отрезков, отсекаемых плоскостью на соответствующих осях от начала координат.
Умножая обе части (1.54) на нормирующий множитель 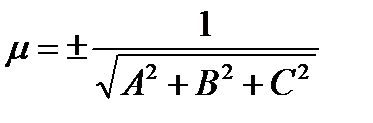
Тест 11.
1) Даны точки М1(0,-1,3) и М2(1,3,5). Написать уравнение плоскости, проходящей через точку М1 и перпендикулярной к вектору 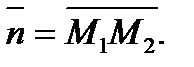
а) 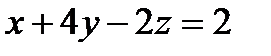
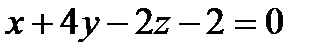
2) Найти угол между плоскостями 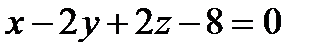
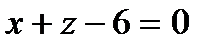
а) 135 о , б) 45 о
1.7.2. Прямая.Плоскости, нормали которых не коллинеарны, 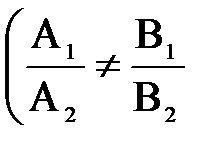
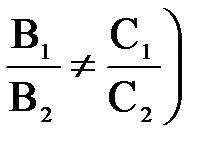
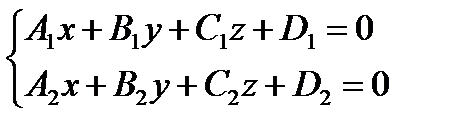
Через эту прямую можно провести бесконечно много плоскостей (пучок плоскостей (1.62)), в том числе и проектирующие ее на координатные плоскости. Чтобы получить их уравнения, достаточно преобразовать (1.63), исключив из каждого уравнения по одной неизвестной и приведя их, например, к виду 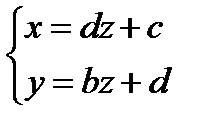
Поставим задачу – провести через точку М0(х0,у0,z0) прямую, параллельную вектору `S (l, m, n) (его называют направляющим). Возьмем на искомой прямой произвольную точку М(х,у,z). Векторы 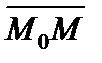
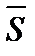
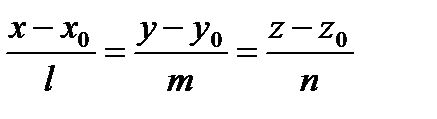
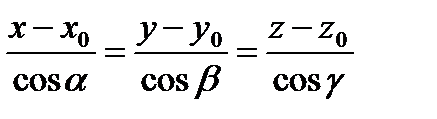
где cosa, cosb, cosg – направляющие косинусы вектора `S. Из (1.64) легко получить уравнение прямой, проходящей через заданные точки М1(х1, у1, z1) и М2(х2, у2, z2) (она параллельна 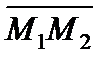
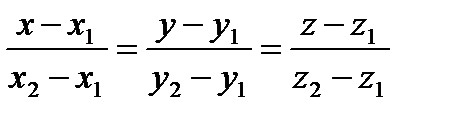
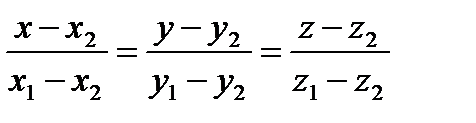
(Значения дробей в (1.64) равны для каждой точки прямой и могут быть обозначены через t, где t 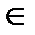
Каждому значению параметра tсоответствует набор координат х, у, z точки на прямой или (иначе) — значения неизвестных, удовлетворяющих уравнениям прямой).
Используя уже известные свойства векторов и операций над ними и канонические уравнения прямой легко получить следующие формулы:
Угол между прямыми: 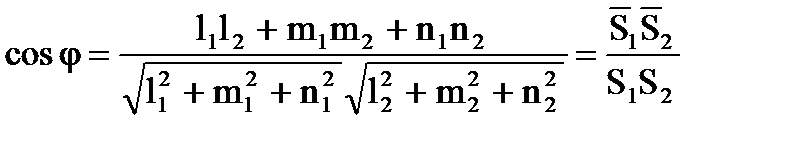
где `S1 и `S2 – направляющие векторы прямых.
Условие параллельности 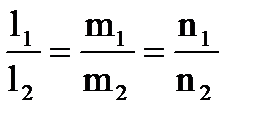
Угол между прямой и плоскостью (легко получить, найдя угол между прямой и нормалью к плоскости, составляющий в сумме с искомым p/2)
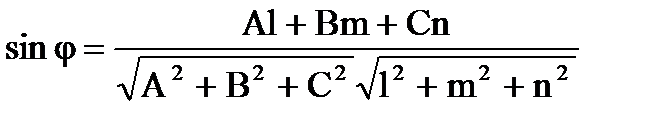
Из (1.66) получаем условие параллельности Al + Bm + Cn = 0 (1.69)
и перпендикулярности 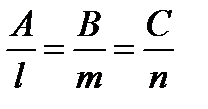

контрольные вопросы.
1) Каковы способы задания прямой линии в пространстве?
Тест 12.
1) Написать уравнения прямой, проходящей через точку А(4,3,0) и параллельной вектору 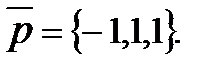
а) 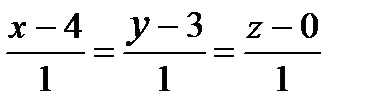
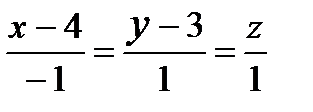
2) Написать уравнения прямой, проходящей через точки А(2,-1,3) и В(2,3,3). Указать верный ответ.
а) 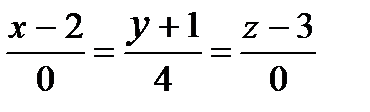
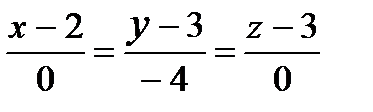
3) Найти точку пересечения прямой с плоскостью: 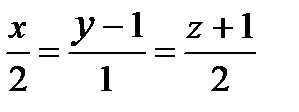
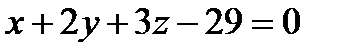
1.7.3. Поверхности второго порядка. Если линейное уравнение в трехмерном декартовом базисе однозначно определяет плоскость, любое нелинейное уравнение, содержащее х, у, z описывает какую – то иную поверхность. Если уравнение имеет вид
Ах 2 + Ву 2 + Cz 2 + 2Dxy + 2Exz + 2Fyz + 2Gx + 2Hy + 2Kz + L = 0,то оно описывает поверхность второго порядка (общее уравнение поверхности второго порядка). Выбором или преобразованием декартовых координат уравнение можно максимально упростить, приведя к одной из следующих форм, описывающих соответствующую поверхность.
1. Канонические уравнения цилиндров второго порядка, образующие которых параллельны оси Oz, а направляющими служат соответствующие кривые второго порядка, лежащие в плоскости хОу:

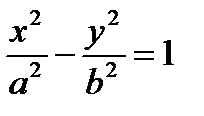
эллиптический, гиперболический и параболический цилиндры соответственно.
(Напомним, что цилиндрической называют поверхность, полученную перемещением прямой, называемой образующей, параллельно самой себе. Линию пересечения этой поверхности с плоскостью, перпендикулярной образующей, называют направляющей – она определяет форму поверхности).
По аналогии можно записать уравнения таких же цилиндрических поверхностей с образующими, параллельными оси Оу и оси Oх. Направляющую можно задать, как линию пересечения поверхности цилиндра и соответствующей координатной плоскости, т.е. системой уравнений вида:
2. Уравнения конуса второго порядка с вершиной в начале координат:
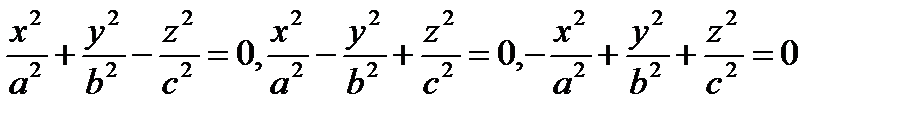
(осями конуса служат оси Oz, Oy и Ох соответственно)
3. Каноническое уравнение эллипсоида: 
Частными случаями являются эллипсоиды вращения, например 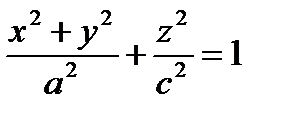

а > с эллипсоид сжат, при a 2 + у 2 + z 2 + = r 2 – уравнение сферы радиусаrс центром в начале координат).
4. Каноническое уравнение однополостногогиперболоида
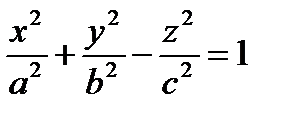
(знак “ – ” может стоять перед любым из трех слагаемых левой части – это изменяет только положение поверхности в пространстве). Частные случаи – однополостные гиперболоиды вращения, например 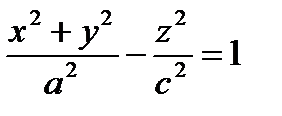

5. Каноническое уравнение двухполостного гиперболоида
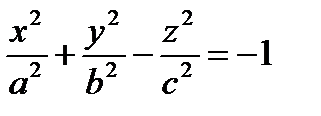
(знак “ – ” может стоять перед любым из трех слагаемых левой части).
Частные случаи – двухполостные гиперболоиды вращения, например 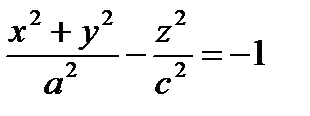
6. Каноническое уравнение эллиптического параболоида
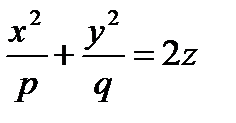
(переменная z может поменяться местами с любой из переменных х и у – изменится положение поверхности в пространстве).
7. Каноническое уравнение гиперболического параболоида
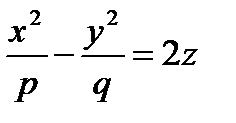
(переменная z может поменяться местами с любой из переменных х и у– изменится положение поверхности в пространстве).
Отметим, что представление об особенностях (форме) этих поверхностей легко получить, рассматривая сечения этих поверхностей плоскостями, перпендикулярными осям координат.
контрольные вопросы.
1) Какое множество точек в пространстве определяет уравнение 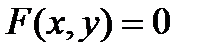
2) Каковы канонические уравнения цилиндров второго порядка; конуса второго порядка; эллипсоида; однополостного гиперболоида; двухполостного гиперболоида; эллиптического параболоида; гиперболического параболоида?
Тест 13.
1) Найти центр и радиус сферы 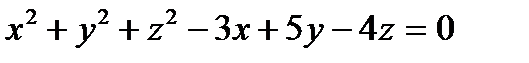
а) С(1,5;-2,5;2), 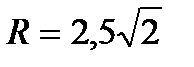
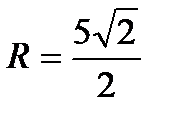
2) Определить вид поверхности, заданной уравнениями: 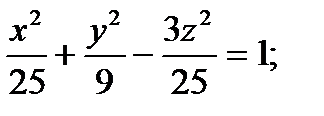
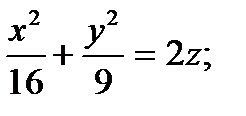
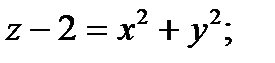
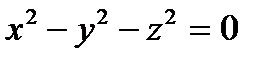
а) однополостный гиперболоид; гиперболический параболоид; эллиптический параболоид; конус.
б) двухполостный гиперболоид; гиперболический параболоид; эллиптический параболоид; конус.
Плоскость в R3.
Читайте также:
|
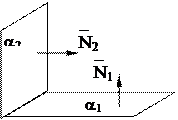 |
· 
· Угол 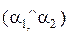


· Расстояние от точки М0(х0, у0, z0) до плоскости Ах + Ву + Сz +D = 0 находят по формуле

Вывод формулы аналогичен тому, как это было проделано для прямой на плоскости. Провести его самостоятельно.
Дата добавления: 2015-04-15 ; просмотров: 9 ; Нарушение авторских прав
http://helpiks.org/7-84376.html
http://lektsii.com/1-153472.html
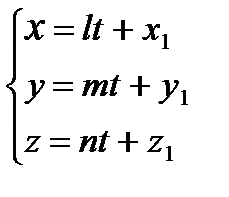
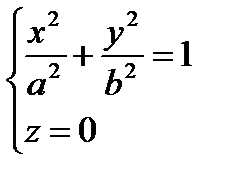
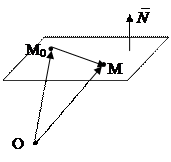 Рассмотрим ПДСК
Рассмотрим ПДСК  и`r0 =
и`r0 =  . Тогда
. Тогда 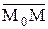 = `r –`r0, а точка МÎa тогда и только тогда, когда векторы `N и
= `r –`r0, а точка МÎa тогда и только тогда, когда векторы `N и  Как известно, через три точки можно провести единственную плоскость. Пусть М1(х1, у1, z1), М3(х2, у2, z2), М3(х3, у3, z3)Îa. Найдем уравнение этой плоскости. Согласно векторному уравнению (9), чтобы записать это уравнение, необходимо знать точку плоскости и нормальный вектор. Точка у нас есть (например М1). А в качестве нормального вектора подойдет любой вектор, перпендикулярный этой плоскости. Известно, что векторное произведение двух векторов перпендикулярно плоскости, в которой лежат эти векторы. Следовательно, векторное произведение векторов
Как известно, через три точки можно провести единственную плоскость. Пусть М1(х1, у1, z1), М3(х2, у2, z2), М3(х3, у3, z3)Îa. Найдем уравнение этой плоскости. Согласно векторному уравнению (9), чтобы записать это уравнение, необходимо знать точку плоскости и нормальный вектор. Точка у нас есть (например М1). А в качестве нормального вектора подойдет любой вектор, перпендикулярный этой плоскости. Известно, что векторное произведение двух векторов перпендикулярно плоскости, в которой лежат эти векторы. Следовательно, векторное произведение векторов 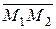 и
и  можно взять в качестве нормального вектора плоскости a:
можно взять в качестве нормального вектора плоскости a: .(
.(  , (11)
, (11) ,
, 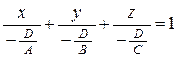 .
. Обозначив здесь
Обозначив здесь  ,
,  ,
,  , получим уравнение
, получим уравнение  , (13)
, (13)
 Для построения плоскости в системе координат, отметим на оси ОХ точку (6, 0, 0), на оси ОУ точку (0, -4, 0), на оси ОZ – (0, 0, 3), соединим их отрезками прямы (следы плоскости). Полученный треугольник есть часть искомой плоскости, заключенная между осями координат.
Для построения плоскости в системе координат, отметим на оси ОХ точку (6, 0, 0), на оси ОУ точку (0, -4, 0), на оси ОZ – (0, 0, 3), соединим их отрезками прямы (следы плоскости). Полученный треугольник есть часть искомой плоскости, заключенная между осями координат.
