Кинематические уравнения для радиус вектора

Кинематика материальной точки

Основные формулы кинематики материальной точки

Приведем основные формулы кинематики материальной точки. После чего дадим их вывод и изложение теории.

Радиус-вектор материальной точки M в прямоугольной системе координат Oxyz :
,
где – единичные векторы (орты) в направлении осей x, y, z .

Скорость точки:
;
;
;
Единичный вектор в направлении касательной к траектории точки:
.
Вектор можно выбрать двумя способами во взаимно противоположных направлениях. Обычно его выбирают в направлении увеличения дуговой координаты. Тогда, наряду с модулем скорости , вводят алгебраическую величину скорости . При , вектор скорости сонаправлен с . При – имеет противоположное с направление.

Скорость и ускорение точки M

Тангенциальное (касательное) ускорение:
;
;
.
Здесь, как и для скорости, – это алгебраическое касательное ускорение, . Если , то вектор касательного ускорения сонаправлен с . При – имеет противоположное с направление.

Единичный вектор, направленный к центру кривизны траектории точки (вдоль главной нормали):
.

Радиус кривизны траектории:
.

Далее приводится вывод этих формул и изложение теории кинематики материальной точки.

Радиус-вектор и траектория точки

Рассмотрим движение материальной точки M . Выберем неподвижную прямоугольную систему координат Oxyz с центром в некоторой неподвижной точке O . Тогда положение точки M однозначно определяются ее координатами ( x, y, z ) . Эти координаты являются компонентами радиус-вектора материальной точки.

Радиус-вектор точки M – это вектор , проведенный из начала неподвижной системы координат O в точку M .
,
где – единичные векторы в направлении осей x, y, z .

При движении точки, координаты изменяются со временем . То есть они являются функциями от времени . Тогда систему уравнений
(1)
можно рассматривать как уравнение кривой, заданной параметрическими уравнениями. Такая кривая является траекторией точки.

Траектория материальной точки – это линия, вдоль которой происходит движение точки.

Если движение точки происходит в плоскости, то можно выбрать оси и системы координат так, чтобы они лежали в этой плоскости. Тогда траектория определяется двумя уравнениями

В некоторых случаях, из этих уравнений можно исключить время . Тогда уравнение траектории будет иметь зависимость вида:
,
где – некоторая функция. Эта зависимость содержит только переменные и . Она не содержит параметр .

Скорость материальной точки

Согласно определению скорости и определению производной:

Производные по времени, в механике, обозначают точкой над символом. Подставим сюда выражение для радиус-вектора:
,
где мы явно обозначили зависимость координат от времени. Получаем:

,
где
,
,

– проекции скорости на оси координат. Они получаются дифференцированием по времени компонент радиус-вектора
.

Таким образом
.
Модуль скорости:
.

Касательная к траектории

С математической точки зрения, систему уравнений (1) можно рассматривать как уравнение линии (кривой), заданной параметрическими уравнениями. Время , при таком рассмотрении, играет роль параметра. Из курса математического анализа известно, что направляющий вектор для касательной к этой кривой имеет компоненты:
.
Но это есть компоненты вектора скорости точки. То есть скорость материальной точки направлена по касательной к траектории.

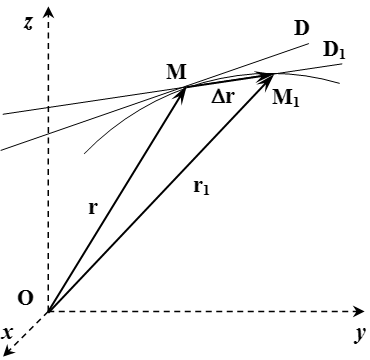
Все это можно продемонстрировать непосредственно. Пусть в момент времени точка находится в положении с радиус-вектором (см. рисунок). А в момент времени – в положении с радиус-вектором . Через точки и проведем прямую . По определению, касательная – это такая прямая , к которой стремится прямая при .
Введем обозначения:
;
;
.
Тогда вектор направлен вдоль прямой .

При стремлении , прямая стремится к касательной , а вектор – к скорости точки в момент времени :
.
Поскольку вектор направлен вдоль прямой , а прямая при , то вектор скорости направлен вдоль касательной .
То есть вектор скорости материальной точки направлен вдоль касательной к траектории.

Введем направляющий вектор касательной единичной длины:
.
Покажем, что длина этого вектора равна единице. Действительно, поскольку
, то:
.

Здесь мы направили вектор по направлению к вектору скорости, поскольку это более удобно. Но могут возникнуть случаи, когда точка останавливается и движется по той же траектории в обратном направлении. Чтобы не вводить для одной и той же точки траектории два единичных касательных вектора, нужно охватить случай, когда направлен противоположно скорости. Для этого вводят алгебраическую величину скорости:
.
Если направления векторов и совпадают, то . Если они противоположны, то .
– это проекция скорости на направление единичного вектора . Она равна скалярному произведению этих векторов:
.

Абсолютную величину (модуль) вектора скорости мы обозначаем символом с прямыми скобками, или символом без стрелки:
;
Алгебраическая величина скорости:
.

Тогда вектор скорости точки можно представить в следующем виде:
.

Ускорение материальной точки

Аналогично предыдущему, получаем компоненты ускорения (проекции ускорения на оси координат):
;
;
;
.
Модуль ускорения:
.

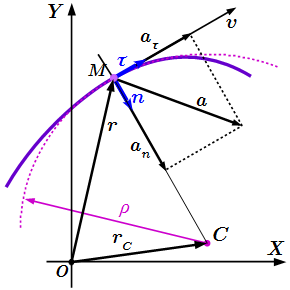
Тангенциальное (касательное) и нормальное ускорения

Теперь рассмотрим вопрос о направлении вектора ускорения по отношению к траектории. Для этого применим формулу:
.
Дифференцируем ее по времени, применяя правило дифференцирования произведения:
.

Вектор направлен по касательной к траектории. В какую сторону направлена его производная по времени ?

Чтобы ответить на этот вопрос, воспользуемся тем, что длина вектора постоянна и равна единице. Тогда квадрат его длины тоже равен единице:
.
Здесь и далее, два вектора в круглых скобках обозначают их скалярное произведение. Продифференцируем последнее уравнение по времени:
;
;
.
Поскольку скалярное произведение векторов и равно нулю, то эти векторы перпендикулярны друг другу. Так как вектор направлен по касательной к траектории, то вектор перпендикулярен к касательной.

Скорость, касательное и нормальное ускорение точки M

Первую компоненту называют тангенциальным или касательным ускорением:
.
Вторую компоненту называют нормальным ускорением:
.
Тогда полное ускорение:
(2) .
Эта формула представляет собой разложение ускорения на две взаимно перпендикулярные компоненты – касательную к траектории и перпендикулярную к ней.

Тангенциальное (касательное) ускорение

Также как и для скорости, введем алгебраическую величину вектора касательного ускорения :
.
Если , то вектор касательного ускорения сонаправлен с . Если , то эти векторы противоположны. Абсолютную величину касательного ускорения будем обозначать прямыми скобками: . Тогда
.

Умножим обе части уравнения (2) скалярно на :
.
Поскольку , то . Тогда
;
.
Здесь мы положили: .
Отсюда видно, что алгебраическая величина тангенциального ускорения равна проекции полного ускорения на направление касательной к траектории. Она также равна производной по времени алгебраической величины скорости точки: .

Подставив , имеем:
.
Здесь мы учли, что .

Найдем производную по времени модуля скорости . Применяем правила дифференцирования:

;
.

Итак,
.
Отсюда следует, что если между векторами ускорения и скорости острый угол: , то движение ускоренное. Абсолютное значение скорости возрастает. Если между ними тупой угол: , то движение замедленное. Абсолютное значение скорости убывает.

Выразим ускорение через тангенциальное и нормальное: , и учтем, что . Получим:
.
Тогда предыдущую формулировку можно выразить посредством тангенциального ускорения. Если векторы касательного ускорения и скорости направлены в одну сторону, то движение ускоренное. Если их направления противоположны, то движение замедленное.

Радиус кривизны траектории

Теперь исследуем вектор .

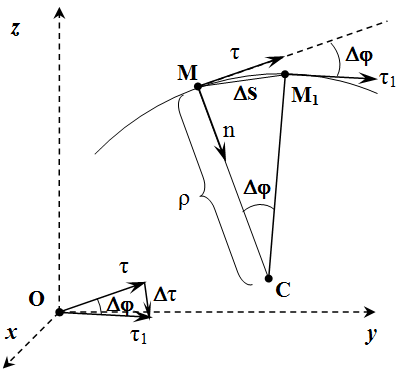
Рассмотрим вектор в два момента времени – в момент времени t и в момент t ₁ . Введем обозначения: . По определению производной:
.
Пусть в момент времени t , точка находится в положении M , а в момент t ₁ – в положении M ₁ (см. рисунок).

Рассмотрим случай, когда алгебраическая скорость положительна: . То есть направления векторов и совпадают. Тогда точка M ₁ находится справа от M . Через точки и проведем плоскости, перпендикулярные векторам и . Пересечение этих плоскостей образует прямую. Она проходит через точку C перпендикулярно плоскости рисунка. MC – это перпендикуляр, опущенный из точки M на эту прямую.

При , точка стремится к точке , а длина отрезка CM стремится к радиусу кривизны траектории ρ . Поскольку и , то угол между отрезками и равен углу между векторами и . Отложим их для наглядности из одного центра.

Абсолютное значение производной:
.
Здесь мы учли, что .

Вектор , как указывалось выше, перпендикулярен . В данном случае он направлен вдоль единичного вектора главной нормали , направленной к центру кривизны C траектории. Поэтому при имеем:
.

Теперь рассмотрим случай, когда алгебраическое значение скорости отрицательно: . В этом случае, вектор скорости противоположен . Получается тот же рисунок, только точка располагается слева от M . В результате абсолютное значение производной остается прежней:
.
Но ее направление меняется на противоположное:
.
Поскольку , то формула сохраняет прежний вид и в этом случае:
.

Нормальное ускорение

Теперь находим нормальное ускорение:
.
Перепишем результат в следующем виде:
,
где ; – единичный вектор в направлении главной нормали траектории – то есть вектор, направленный к мгновенному центру кривизны перпендикулярно касательной к траектории. Поскольку , то также является модулем нормального ускорения. Для него не нужно вводить алгебраическое значение, как мы это делали для скорости и касательного ускорения.
Нормальное ускорение всегда направлено к центру кривизны траектории.

Из формулы (2) имеем:
(4) .
Из формулы (3) находим модуль нормального ускорения:
.

Умножим обе части уравнения (2) скалярно на :
(2) .
.
Поскольку , то . Тогда
;
.
Отсюда видно, что модуль нормального ускорения равен проекции полного ускорения на направление главной нормали.

Выпишем еще раз следующую формулу:
.
Отсюда видно, что нормальное ускорение вызывает изменение направления скорости точки, и оно связано с радиусом кривизны траектории.

Радиус кривизны траектории:
.

И в заключении заметим, что формулу (4) можно переписать в следующем виде:
.
Здесь мы применили формулу для векторного произведения трех векторов:
,
в которую подставили
.

Итак, мы получили:
;
.
Приравняем модули левой и правой частей:
.
Но векторы и взаимно перпендикулярны. Поэтому
.
Тогда
.
Это известная формула из дифференциальной геометрии для кривизны кривой.

Автор: Олег Одинцов . Опубликовано: 09-02-2016 Изменено: 27-01-2020

Кинематические уравнения движения (уравнения для скорости и радиус-вектора).

Для движения точки с постоянным ускорением

а = du/dt = const, ее скорость определится интегрированием соотношения du = а×dt:

òdu = òа×dt Þ u — u_о = аt Þ u = u_о + аt

Аналогично, зная скорость u= dr/dt, найдём радиус-вектор r, определяющий местоположение тела. Интегрируя соотношение dr = udt, получим:

òdr = òudt = ò(u_о + аt)dt Þ r – r_о = u_оt + аt 2 /2 Þ r = r_о + u_оt + аt 2 /2

Кроме ускорения а, решение основной задачи механики, т. е. определение скорости u
и местонахождения r точки, требует знания начального сос­тояния движения точки, т. е. значений скорости u_о и положения r_о точки в начальный момент времени t = 0. Задача нахождения ускорения тела решается в следующем за кинематикой разделе механики — динамике.

На практике полученные векторные уравнения для скорости и радиус — век­тора используют обычно в скалярной форме, т. е. в виде проекций на оси координат:х = х_о + u_охt + а_хt 2 /2; у = у_о + u_оуt + а_уt 2 /2; z = z_о + u_оzt + а_zt 2 /2;

В прямолинейном одномерном движении можно записать следующие формулы для скорости и пути:

u = u_о + аt и S = u_оt + аt 2 /2, где путь S в однонаправленном движении равен модулю разности координат конечного и начального положений тела.

3. Абсолютно твердое тело. Виды движения абсолютно твердого тела. Кинематика вращательного движения. Угловая скорость. Угловое ускорение. Связь между линейными и угловыми характеристиками движения.

В тех ситуациях, когда размерами и формой движущегося тела нельзя пренебречь, его часто можно смоделировать твёрдым телом – совокупностью материальных точек с неизменными расстояниями между ними. При этом про­извольное движение такого тела обычно может быть разложено на такие бо­лее простые, независимые движе­ния, как поступательное и вращательное.

Под поступательным движением твёрдого тела понимают такое движение, при котором любая прямая, проведённая в теле, остаётся при его движении параллельной самой себе (Поступательным является, прежде всего, прямолинейное движение, а также и такие виды криволинейного движения, движение в кабине колеса обозрения . ). Существенно, что при поступательном движении все точки тела дви­жутся

эквивалентно, т. е. по идентичным траекториям с одинаковыми мгновенными скоростями и ускорениями.

Поэтому механика поступательного дви­жения твёрдого тела в целом не содержит в себе принципиальных отличий от механики точки и по существу сводится к ней. В качестве некоторой выделенной точки твердого тела выбирают его центр масс, который еще называют центром инерции.

Иначе обстоит дело с вращательным движением. Простейший его вид — вращение вокруг неподвижной оси. В нем все точки тела движутся по окружностям, центры которых лежат
на одной прямой, называемой осью вра­щения. Во вращательном движении разные точки тела (разно удалённые от оси вращения) за одно и тоже время Dt совершают разные линейные перемещения Dr и, соответственно, обла­дают разными линейными скоростями и ускорениями. Одинаковыми же для всех точек вращающегося вокруг оси тела будут не линейные, а угловые кинема­тические характеристики (скорости и пути, перемещения). Они и будут адекватными (и удобными) характеристиками вращательного движения тела в целом. Вращающееся вокруг неподвижной оси тело имеет одну степень свободы. Линейное перемещение Dr (или dr) пропорционально расстоянию R до оси вращения. Угло­вое же перемещение Dj (или dj), равное линейному Dr, делённому на радиус R соответствующей окружности, то есть dj = dr/R, не зависит от R.

Соответственно и быстрота w = dj/dt [рад/с = с -1 ] углового перемещения (или изменения утла поворота j), называемая угловой скоростью, и быстрота её изменения e = dw/dt [рад/с 2 = с -2 ], называемая угловым ускорением, не зависят от радиуса окружности, то есть являются оди­наковыми для всех точек вращающегося тела.

Линейные и угловые характеристики точки, вращающейся по окружности радиуса R взаи­мосвязаны следующим образом:

w= dj/dt = (dr/R)/dt = u/R; Þ u = wR.

e = dw/dt = d/dt(u/R) = (1/R)du/dt = а_t/R Þ а_t = eR

а_n = u 2 /R = (wR)2/R = w 2 R;

а = Ö(а_t 2 + а_n 2 ) = Ö(e 2 R 2 + w 4 R 2 ) = [Ö(e 2 + w 4 )]/R .

Так как dr = Rdj = rsin q×dj, то в векторной форме dr = [dj, r]. Поделив полученное равенство на dt, получим: dr/dt = u = [dj/dt, r] = [w, r] Þ u = [w, r].

а = du/dt = d/dt[w, r] = [dw/dt, r] + [w, dr/dt] = [e, r] + [w, u] = а_t + [w, [w, r]] =а_t + а_n, где

а_t = [e, r] и а_n=[w, [w, r]] = —w 2 R.

Направление векторов dj и w определяется правилом правого винта (буравчика), совпа­дая с его поступательным перемещением при вращении рукояти в направ­лении вращения тела.
Угловое же ускорение e = dw/dt совпадает, по направ­лению с элементарным приращением dw
угловой скорости:e­­dw . Оно, таким образом, направ­лено по направлению w при ускоренном
(dw/dt > 0) вращении и против направ­ления w при замедленном (dw/dt

Векторный характер w и e позволяет характеризовать с их помощью не только быстроту вращения, но и ориентацию оси вращения в пространстве, и направление вращения.

Так же, как и для линейных, для угловых кинематических характеристик справедливы аналогичные уравнения для скорости и перемещения во враще­нии с постоянным ускорением:
w = w_о ± et и j = j_о + w_оt ± et 2 /2 , где знак ²плюс ² — для ускоренного вращения, а ²минус² — для замедленного вращения.

Также как и в поступательном движении, для решения основной задачи механики вращательного движения (определе­ния угловой скорости и положения в любой момент времени) необходимо знать начальное состояние движения (характеристики j_о и w_о), а также угловое ускорение e. Задача определения ускорения движущегося тела ре­шается в следующем за кинематикой разделе механики, называемом динамикой. В практических задачах на анализ вращательного движения часто исполь­зуют такие
характеристика, как число оборотов N, связанное с угловым путем j очевидным соотношением
N = j/2p, и частота вращения n = dN/dt или для равномерного вращения n = N/t:

n = (dj/dt)/2p = w/2p Þ w = 2pn; j = 2pN.

Время одного оборота Т = 1/n называется периодом вращения:w = 2p/Т или Т = 2p/w.

4.Динамика материальной точки.Масса.Сила. Импульс(количество движения).Законы Ньютона.

Первый закон Ньютона, утвер­ждает, что свободно движущееся тело, т. е. тело, на которое не действуют другие тела (или действие их взаимно скомпенсировано), относительно некоторых систем отсчета движется с неиз­менной скоростью (иногда говорят — движется по инерции). Первый закон Ньютона выделяет определенный класс систем отсчета, называемых инерциальными, в которых движение свободного тела имеет наиболее простой вид (происходит равномерно и прямолинейно, в частном случае – покоится),
и в которых только и верна механика Ньютона. Иногда его и формулируют в виде утверждения
о сущест­вовании инерциальных систем отсчёта (ИСО). Если известна хотя бы одна ИСО, то все ИСО, движущиеся относительно неё с постоянной скоростью, также будут инерциальными.

Обычно в качестве ИСО выбирают систему отсчёта, связанную с Землёй — геоцентрическую систему отсчёта. Её инерциальность приближенная, нарушаемая суточным вращением Земли вокруг своей оси. Большей степенью инерциальности обладает гелиоцентрическая СО, связываемая с Солнцем. На практике же, достаточной долей инерциальности обладает лабораторная система отсчета, связываемая с конкретным телом на Земле.

Согласно принципу относительности Галилея, все ИСО являются равноправными в отображении механических явлений, то есть все законы механики во всех ИСО имеют одинаковый вид и никакими механическими опытами, проводимыми внутри ИСО, нельзя обнаружить движется она или покоится.

В ИСО все наблюдаемое ускорение тела объясняется воздействием на него состороны конкретных, окружающих его тел.В качестве меры этого воздейст­вия, вызывающего ускорения тел в ИСО, в механике Ньютона выбирается величина, называемая силой F. Сила F является векторной функцией положения и/или скорости тела относи­тельно ИСО, то есть F = F(r, u), и она прямо пропорциональна сообщаемому ею ускорению а тела:F(r, u)

а или а

F

Если на тело действует несколько сил, их можно заменить геометрической результирующей F_S = SF_i — принцип суперпозиции сил (независимого наложения, сложения) сил.

Одна и та же сила сообщает разным телам разные ускорения. Таким образом, ускорение, приобретаемое телом, зависит не только от внешних воздействий, но и от внутрен­них свойств тела, мерой которых в механике Ньютона выбрана величина, названная массой (Под массой тела Ньютон понимал величину, пропорциональную его плотности и объему, то есть: m = ρV.) m тела. Очевидно, что более массивные тела, обладающие большей массой, должны приобретать меньшие ускорения при одинаковых воздействиях (силах).

В результате можно связать ускорение с силой и массой в следующем виде: а = F_S/m и утверждать, что ускорение а,приобретаемое точечным телом в ИСО прямо пропорционально действующей на него (или, как ещё говорят — приложенной к нему) результирующей силе F_Sи обратно пропорцио­нально массе m тела. Это утверждение и представляет собой основной закон динамики материальной точки (и поступательного движения твёрдого тела) — второй закон Ньютона.

В механике Ньютона имеет место однозначная линейная взаимосвязь между мерами движения и взаимодействия, порождающая однозначную причинность и предсказуемость движения, называемую еще лапласовским или механистическим детерминизмом.

Такая динамическая характеристика тела, как его масса, выступает, мерой его инертности, неподатливости к изме­нению скорости, к изменению состояния движения. Чем больше масса тела, тем меньшее ускорение оно приобретает при воздействии одной и той же силы, т. е. тем медленнее изменяется его скорость. Инертность и выража­ет собой невозможность мгновенного изменения скорости тела, растяну­тость этого изменения во времени, т. е. замедленность изменения скорости тела. Измерение массы как меры инертности тела может быть осуществлено путём измерения и сравнения приобретаемых разными телами ускорений при воздействии на них одной и той же силы. Выбрав одно из тел за эталон массы, можно через его массу выразить массы других тел. Единица массы — килограмм (кг) является основной в СИ. Масса является аддитивной характеристикой тела, т. е. масса m_S совокупности тел, частиц равна сумме масс этих тел (частиц) по отдельности: m_S = Sm_i.

Сила, как векторная мера взаимодействия тел, измеряется производи­мым ею эффектом, численно равным произведению массы тела на его ускорение: F = mа.
Единица силы в СИ — ньютон — сила, сообщающая телу массой в 1 кг ускорение в 1 м/с 2 .

При решении конкретных задач динамики 2-ой закон Ньютона записывают обычно в скалярной форме,т. е.в виде проекций на оси координат соответствующей ИСО:

а = F/m Þ а_у = F_у/m или mа_у = F_у

При этом предполагается справедливость принципа суперпозиции (независимости действия и векторного характера сложения) сил, согласно которому результирующее ускорение, равно векторной сумме ускорений, сообщаемых телу действующими на него силами по отдельности.

2-ой закон Ньютона позволяет рассчитать ускорение а тела массой m, если известен
характер действующих на него сил, то есть их зависимость от координат и скорости.
В зависимости от характера этой зависимости различают ряд следующих видов сил:

F = mg — направлена вертикально вниз и, так как она прямо пропорциональна массе тела, сообщает всем телам одинаковое ускорение g » 9,8 м/с 2 (ускорение свободного падения); масса m здесь уже не инертная, а тяжелая- мера силы тяжести.

— сила гравитационного взаимодействия

F_гр = G×m₁m₂/r 2 — опре­деляет притяжение двух тел
с массами m₁ и m₂, разделённых расстоя­нием r. Коэффициент G = 6,67×10 -11 Н×м 2 /кг 2 – называется гравитационной постоянной. Масса здесь также тяжелая, выступающая в роли гравитационного заряда (двоякий смысл массы — мера инертности и мера гравитации).

F_у = — kх, где х – вектор линейной деформацииупругого тела (вектор приращения длины относительно ее недеформированного, равновесного значе­ния), а k — коэффициент упругости или в применении к пружине — жёст­кость пружины.

— сила вязкого сопротивления

F = — r×u, где u — скорость тела в вязкой среде, r — коэффициент сопротивления среды (обычно жидкой или газо­образной).

Кроме названных выше сил большое значение в решении задач механики имеют такие силы, как вес тела и сила трения, которые не имеют явного выражения через коорди­наты или скорости:

— весом тела Р называют силу, с которой тело действует на подвес или опору;

— силой трения скольжения F_тр называют силу, прямо пропорциональную силе F_нд нормального давления (Обычно ее заменяют на численно равную ей силу N реакции опоры, то есть Fтр = μN.), т. е. составляющей веса тела, нормальной к поверхности опоры: F_тр = mF_нд, где m — коэффициент трения скольжения тела о поверхность. Сила трения скольжения направлена против перемещения тела и является составляющей силы реакции опоры.

Исторически исходной (ньютоновской) формулировкой 2 — го закона Ньютона была следующая: F = dР/dt, где Р = mu — импульс тела. Эта форма записи второго закона Ньютона является более общей, сводящейся к известной ранее F = mа при условии независимости массы m тела от скорости u его движения. F = dР/dt = d(mu)/dt = m×du/dt = mа.

Третий закон Ньютона утверждает, что силы взаимодействия двух материальных точек в инерциальной системе отсчета: равны по модулю;
противоположны по направлению; и действуют вдоль прямой, соединяющей точки

F₁₂ = — F₂₁

F₁₂ — сила, действующая на первое тело со стороны второго тела; F₂₁ — сила, действующая на второе тело со стороны первого тела. Этот закон вместе с первыми двумя законами Ньютона, позволяет осуществить переход от динамики точки к динамике системы точек.

5. Система материальных точек. Силы внешние и внутренние. Импульс системы материальных точек. Закон сохранения импульса.

Рассмотрим простейшую замкнутую (Замкнутой называют такую систему тел, на которую не действуют внешние тела (силы), и тела которой взаимодействуют лишь между собой, посредством сил, называемых внутренними.) систему из двух материальных точек. Исходя из смысла силы как быстроты изменения импульса, третий закон Ньютона можно записать в виде:

dР₁/dt = — dР₂/dt Þ dР₁ = — dР₂Þ d(Р₁ + Р₂) = 0 Þ Р₁ + Р₂ = const

Полученное равенство выражает собой закон сохранения импульса (ЗСИ) замкнутой системы из двух материальных точек, т. е. точек, взаимодействующих лишь между собой. Общий (суммарный, результирующий) импульс двух тел остается при их движении постоянным, и может при их движении лишь перераспределяться между ними.

Движение может лишь передаваться от одних тел к другим, так что общее его количество в замкнутой системе тел остается неизменным, то есть сохраняется. Полученный выше для двух точек закон сохранения импульса легко обобщается на замк­нутую систему из произвольного числа N материальных точек, и его можно сформулировать так: при любом движении замкнутой системы материальных точек полный её импульс остаётся неизменным: SР_i = const; внутри системы воз­можны лишь перераспределения импульса между отдельными точками.

Рассмотрим систему из n материальных точек. Запишем второй закон Ньютона для i — ой точки: dР_i/dt = F_i. Результирующую силу F_i, действующую на i — ую точку системы представим в виде суммы внешних и внутренних сил: F_i = F_{i внеш} + SF_ik , где F_ik – внутренняя сила, дейст­вующая на i — ую точку системы со стороны ее k – ой точки. Полученное равенство dР_i/dt = F_{i внеш} + SF_ik, выражающее второй закон Ньютона для i — ой точки системы, просуммируем по всем ее n точкам: SdР_i/dt = SF_{i внеш} + SSF_ik. По третьему закону Ньютона силы воздействия i — ой и k – ой точек друг на друга равны по величине и противоположны по направлению, то есть F_ik = — F_ki. Поэтому при суммировании внутренних сил по всем точкам системы они взаимно скомпенсируют друга, так что SSF_ik = 0. Тогда второй закон Ньютона для системы материальных точек запишется в виде: SdР_i/dt = d/dtSР_i = dР_S/dt = SF_{i внеш} = F_{S внеш}. Или окончательно dР_S/dt = F_{S внеш}

Если система замкнута, то есть результирующая действующих на нее внешних сил равная нулю: F_{S внеш} = 0, то dР_S/dt = 0, откуда следует Р_S = SР_i= const – закон сохранения импульса замкнутой системы материальных точек.

Сохране­ние импульса — величины векторной — означает сохранение и любой его состав­ляющей, проекции на любую ось, любое направление в пространстве. В конкретных задачах
динамики векторный закон сохранения импульса за­писывают в скалярной форме, проецируяего на соответствующие направления.

Закон сохранения импульса является эффективным средством, методом реше­ния основ­ной задачи механики (ОЗМ), т. к. он выражает собой взаимосвязь мер (коли­честв) движения взаимодействующих тел. Особенно плодотворнымего применение оказывается для кратковре­менных взаимодействий типа удара, взрыва-разрыва, выброса тел, где труд­но задать характер сил, то есть использовать под­ход к решению ОЗМ с непосредственным использованием законов Ньютона. Зная, например, импульсы Р₁ и Р₂ двух тел до удара и импульс Р_i ¢ одного из тел после удара, можно, пользуясь законом сохранения импульса, рассчитать импульс другого тела после удара.

6. Система материальных точек. Центр масс. Движение центра масс замкнутой системы.

При поступательном движении системы материальных точек /твёрдого тела/ все точки системы движутся с одинаковыми мгновенными линейными скоростями и ускорениями,
и движение всей системы /тела/ эквивалентно движению любой её точки. Обычно в качестве точки, моделирующей движе­ние всей системы, выбирается точка С, называемая центром масс системы. Она задаётся радиусом — вектором r_С, определяемым через радиус — векторы r_i материальных точек системы, об­ладающих массами m_i, следующим выражением:

r_С = Sm_ir_i/М , где М = Sm_i — полная масса системы из N точек.

Скорость u_с движения центра масс равна:

u_с = dr_С/dt = d/dt(Sm_idr_i/М) = Sm_iu_i/М = Р_С/М,

где Р_С = Sm_iu_i — полный импульс системы.

Закон изменения скорости центрамасс системы (или уравнение движения центра масс) — естественное обобщение основ­ного уравнения динамики точки на систему частиц, твёрдое тело:

а_с = du_с/dt = (1/М)×dР_С/dt = F_{S внеш}/М –

— центр масс механической системы движется как материа­льная точка, масса которой равна массе М системы, под действием результирующейF_{S внеш} внешних сил, приложенных к системе. Эта теорема о движении центра масс показывает, что при поступательном движении твердого тела можно не учитывать его размеры и форму, т.к. все его точки движутся идентично. Если результирующая внешних сил равна нулю: F_{S внеш}=0, то центр масс системы точек движется с постоянной скоростью, сохраняя состояние своего движения, в частном случае – покоя. Внутренние взаимодействия не меняют положения центра масс; это утверждение часто используется при решении задач механики замкнутой системы тел.

7. Работа. Мощность. Работа постоянной и переменной силы.

Наряду с векторным подходом к решению основной задачи механики, в физике широко используется и более общий скалярно-энергетический под­ход. В нём в качестве динамической меры движения выступает более уни­версальная величина, не имеющая уже векторного характера, называемая кинетической энергией Е_к.

Если элементарное изменение импульса dР точечного (твердого) тела определялось действием силы F на вре­менном интервале dt, а именно — импульсом силы Fdt, то элементарное
изменение кине­тической энергии dE_к определяется действием силы на пространственном
интервале dr, называемом работой силы dА = Fdr.

Кинетическая энергия, как и работа, измеряется в джоулях: 1 Дж = 1 Н×м.

Работа силы — величина скалярная, но алгебраическая, т. е. имеющая знак. Если она ускоряет тело, увеличивает его кинетическую энергию — она положительна. Если же она тормозит тело, то её значение будет отри­цательным; такова работы сил трения, сопротивления. Если при действии силы на тело, его скорость не изменяется по модулю, работа си­лы равна нулю.

Элементарная работа силы dA = Fdr = Fdr×cos (Fdr) = F×dr_F зависит от угла между силой F и перемещением dr тела. Сила, перпендикулярная перемещению dr (и скорости u = dr/dt) тела, работыне совершает, она изменяет лишь направление скорости, сообщая телу вращательное движение.

Постоянная сила F, действующая под углом a к перемещению тела и его скорости, на прямолинейном пути s совершает работу равную:

Нa графике F/x/ работа пропорциональна площади фигуры между кривой F(х) и осью х.

Быстрота совершения работы (быстрота изменения кинетической энергии) называется мощностью N силы и она равна: N = dЕ_к/dt = dА/dt = Fdr/dt = Fu = Fu×cos (F^dr). [Н×м/с = Дж/с = Вт].

Мгновенная мощность численно равна работе, совершаемой за единицу времени при равномерном совершении работы. Средняя же мощность численно равна отношению работы А
ко времени t ее совершения, то есть:

Имеет место аналогия: силы — как быстроты изменения импульса тела F = dР/dt и мощности N = dЕ_к/dt, как быстроты изменения кинетической энергии. Импульс Р и кинетическая энергия Е_к, являющиеся соответственно векторной и скалярной динамическими мерами движения, также просто взаимосвязаны:

Р = mu; Е_к = mu 2 /2 = m 2 u 2 /2m = Р 2 /2m. Итак,

8. Энергия. Виды механической энергии. Кинетическая энергия. Вывод формулы кинетической энергии.

Энергия – физическая клоичественнная вел-на, характеризующая движение и взаимодействие материй. (яднрная, мех-я, тепл-я, атомная, эл.магнитная)

Потенциальная энергия – мех энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.

Кинетическая энергия механической системы – это энергия механического движения этой системы.

Кинетическая энергия – энергия упорядоченного движения тела.

Сила F,действуя на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа dA силы F на пути, который прошло тело за время возрастания скорости от 0 до v, идет на увеличение кинетической энергии dT тела dA=dT. Используя закон Ньютона F=m(dv/dt) и уможая обе части равенства на перемещение dr, получим

F dr=m(dv/dt)dr = dA

Т.к. v=dr/dt то dA=mv dv=mvdv = dT,

Р = mu; Е_к = mu 2 /2 = m 2 u 2 /2m = Р 2 /2m.

Итак, Е_к = Р 2 /2m и Р = Ö2mЕ_к.

9. Консервативные и неконсервативные силы. Связь между силой и потенциальной энергией. Градиент потенциальной энергии. Условие равновесия системы.

Силы, работа которых не зависит от формы траектории и характера движения при переходе системы из начального состояния в конечное, а определяется только взаимным положением тел системы, называются консервативными.Работа консервативных сил по замкнутой траектории равняется нулю.Все силы, работа которых по замкнутому контуру не равняется нулю, называются неконсервативными.К неконсервативным относятся диссипативные силы. Суммарная работа всех внутренних диссипативных сил системы на любом участке траектории отрицательна в любой произвольно выбранной ИСО. Диссипативными являются силы трения, сопротивления. К диссипативным относятся все силы, которые могут быть представлены в виде:

F = -h(υ)·υ,
где υ — относительная скорость движения тел;
h(υ) — положительный коэффициент, который в общем случае
может зависеть от скорости

Физика

План урока:

Механическое движение. Система отсчёта. Закон относительности движения

Механическим движением в физике называется изменение с течением времени положения тела (или его частей) в пространстве относительно других тел.

То есть, чтобы сказать, что тело или система совершает механическое движение, нам необходимо: 1) наблюдать его во времени; 2) сравнивать его положение с положением какого-то другого тела (относительно этого тела).

Например, пассажир в едущем автомобиле неподвижен относительно кресла, на котором он сидит, но он движется относительно людей, стоящих на автобусной остановке и самой остановки. А сама автобусная остановка неподвижна относительно стоящих людей, ждущих автобус (см. рисунок 1). Однако она движется относительно проезжающих мимо машин. В первом случае наблюдаемым объектом был человек в машине, а точкой отсчета кресло и люди на остановке. Во втором случае наблюдаемой была автобусная остановка, а точками отсчета – люди на остановке и проезжающие мимо машины.

Рисунок 1 – Иллюстрация к примеру

Из примеров можно сделать вывод, что важно, какой именно объект находится под наблюдением и относительно какого объекта – тела отсчета – рассматривается его движение. Отсюда можно сформулировать закон относительности движения: характер движения тела зависит от того, относительно какого объекта мы рассматриваем данное движение.

Тело (или точка) отсчета, связанная с ним система координат и часы, вместе образуют систему отсчета. То есть все сказанное выше можно переформулировать в одно предложение: для наблюдения механического движения важно в какой системе отсчета будет происходить наблюдение.

Рисунок 2 – Пример системы отсчета (наблюдаемы объект – летящий мяч, тело отсчета – камень, лежащий в начале координат, система координат и секундомер для отсчета времени)

Однако объекты могут быть очень сложными для наблюдения. Например, автомобиль едет по прямой несколько километров и необходимо описать его движение относительно камня на обочине. Казалось бы, все просто. Но как именно описать движение автомобиля, если корпус его движется по прямой, а колеса совершают вращательные движения.

Для удобства решения подобных задач принято упрощение: если размер и форма тела в данной задаче не играют важной роли для наблюдателя, можно считать это тело за материальную точку.

Материальная точка – это такое тело, размером и формой которого в условиях данной задачи можно пренебречь.

Приведем пример: когда автобус едет из города А в город Б, его можно рассматривать как материальную точку. Когда пассажир идет из одного конца этого автобуса в другой, считать автобус материальной точкой нельзя. В общем случае можно сказать, что тело можно считать материальной точкой, если его размеры значительно меньше расстояния, на которое оно перемещается.

Уравнения движения. Радиус-вектор. Проекция вектора

Для описания движения тела необходимо уметь рассчитывать его положение в каждый момент времени. Как это сделать?

Самый очевидный способ – координатный. Если вернуться к примеру на рисунке 2, можно увидеть, что летящий мяч в каждый момент времени имеет три координаты по осям OX, OY и OZ. Эти координаты являются функциями времени (т.е. они зависят от времени), а значит, их можно записать в виде системы:

Вид этих уравнений будет зависеть от многих вещей: от того, с какой силой бросили мяч в начале, от массы мяча, под каким углом его бросили и так далее. В любом случае, если эти уравнения заданы, можно найти координаты (то есть положение) тела в любой момент времени. Поиск этих уравнений – основная задача кинематики.

Эта система является кинематическими уравнениями движения тела или материальной точки, записанными в координатной форме. Повторим: если вид уравнений движения задан, можно узнать координату движущейся точки в любой момент времени.

В общем случае, координат три, но иногда можно обойтись двумя или даже одной координатой. Например, для описания движения бильярдного шара достаточно двух координат (так как шар не может двигаться вверх и вниз), а для описания движения шарика, катящегося по прямому горизонтальному желобку достаточно одной координаты (шарик не может двигаться вверх-вниз и вправо-влево).

Еще один способ описания движения – векторный.

*Перед дальнейшим прочтением данной статьи желательно вспомнить основную теорию по теме «Векторы» и «Метод координат»

Вектор, проведенный из начала координат к материальной точке, называется радиус-вектором (см. рисунок 3).

Рисунок 3 – Радиус-вектор (серой линией изображены траектория движения материальной точки, r₁ и r₂* радиус-векторы, проведенные к этой материальной точке в разные моменты времени)

Радиус-вектор проведенный к материальной точке в разные моменты времени будет разным. Значит, его тоже можно представить, как функцию времени:

r = r(t)

Такая функция и будет уравнением движения в векторной форме. Если ее вид задан, можно описать движение тела с той же полнотой, как и при координатной записи.

Еще раз обозначим отличия: при записи уравнения движения в координатной форме в каждый момент времени наблюдающий будет знать три координаты тела; при записи в векторной форме в каждый момент времени известен радиус-вектор (его модуль и направление). Обе записи равносильны.

*На письме векторы обычно обозначаются стрелкой сверху, над величиной. Однако в печатном тексте не всегда удобно нагромождать формулы дополнительными знаками, поэтому в печати векторные величины пишут просто жирным шрифтом. В данной статье далее жирным шрифтом будут написаны только векторные величины.

Покажем, что векторная и координатная записи равносильны. Для этого необходимо вспомнить, как построить проекцию вектора на ось (см. рисунок 4).

Рисунок 4 – Построение проекции вектора на ось

Чтобы построить проекцию вектора на ось, необходимо опустить перпендикуляра из начала и конца вектора на эту ось. Длина получившегося отрезка между проекциями начала и конца вектора, взятая со знаком «+», если вектор а сонаправлен с осью Х, или со знаком «-», если вектор а противонаправлен оси Х, — это и есть искомая проекция.

Если вектор выходит из начала координат, задача облегчается – необходимо опустить перпендикуляр только из конца вектора.

Напоминания из геометрии:

два вектора равны, если они параллельны или лежат на одной прямой, сонаправлены, а их модули равны;

проекции равных векторов равны.

Рассмотрим пример (см. рисунок 5)

Рисунок 5 – Задача на нахождение проекции векторов

Предлагаем читателю самому подумать, а затем сравнить свои рассуждения с приведенными ниже.

Итак, вектор а: его начала соответствует координате х_н=1, а конец х_к = 4. Значит a_x = х_к – х_н = 4-1 = 3. Вектор b: его начало лежит в точке х_н=2, а конец х_к =0. Значит b_x = х_к – х_н = 0-2 = -2.

В двумерном случае, проецировать нужно на две оси, но принцип остается тем же.

Иногда еще нужно находить составляющие компоненты вектора а_х и а_у. Рассмотрим пример, для простоты возьмем вектор, выходящий из начал координат (см. рисунок 6).

Сумма векторов а_х и а_у равна а. Модули векторов а_х и а_у численно равны координатам точек, куда попали перпендикуляры, опущенные из конца вектора а на оси ОХ и ОУ.

Еще следует отметить, что, если известен угол β между вектором а и осью ОХ, воспользовавшись основами тригонометрии, можно найти величины проекций:

Если бы вектор а совпадал с радиус-вектором какой-нибудь точки, то величины а_х и а_у совпадали бы с координатами тела по осям ОХ и ОY.

Способ с использованием тригонометрических функций удобен, когда координата конца вектора попадает в нецелое число и опустив перпендикуляр на ось его трудно найти точно. В физических задачах такое часто случается.

Рисунок 6 – Нахождение компонент вектора а

Рассмотрим пример (см. рисунок 7). Модуль вектора r равен 2. Сам вектор направлен под углом в 45 градусов к оси ОХ. Необходимо найти величины проекций (они же координаты) этого вектора на оси ОХ и ОУ.

Рисунок 7 – Задача на нахождение проекций вектора в двумерном пространстве

В общем случае радиус-вектор находится в трехмерном пространстве (см. рисунок 8). Построение проекции осуществляется по тому же принципу, что и в рассмотренных выше примерах. Когда строятся проекции на оси ОХ и ОУ, перпендикуляр сначала опускается на плоскость, в которой лежат оси ОХ и ОУ, а затем точка, в которую упал перпендикуляр к плоскости, проецируется на оси ОХ и ОУ.

Точки, в которые попал перпендикуляры к осям – r_x, r_y, r_z – это и есть координаты x, y, z тела в текущий момент времени.

Следует оговориться, что большинство задач 10-го класса будут ограничиваться двумерным пространством.

Рисунок 8 – Построение проекций радиус-вектора

Траектория. Путь. Перемещение

Траектория – это линия, вдоль которой движется тело.

Траектория движения может быть прямолинейной, если тело движется по прямой линии, и криволинейной, если тело движется по кривой.

Путь (S), пройденный телом, равен длине траектории.

Перемещение (r)* – это вектор, проведенный из начала пути в конец.

В случае прямолинейного движения путь и модуль перемещения тела совпадают (см. рисунок 9а). В случае криволинейного – путь и перемещение различаются (см. рисунок 9б), так как длина линии движения тела больше длины вектора, соединяющего начало и конец траектории.

Рисунок 9 – Путь (S) и перемещение (r) при прямолинейном (а) и криволинейном (б) движении

*Иногда перемещение так же, как и путь, называют буквой S — (на письме с вектором над ней, при печати — жирным шрифтом, так как это векторная величина). В данной статье, чтобы не путаться, перемещение называется только буквой r. В целом, обозначения равноправны, поэтому при решении задач можно использовать то, которое удобнее. Однако не стоит забывать отмечать, что именно обозначено под той или иной буквой.

Равномерное прямолинейное движение: скорость и уравнение движения

Путь и перемещение при равномерном прямолинейном движении

Прямолинейное равномерное движение уже рассматривалось в курсе физики ранее, однако приведем основные определения.

Прямолинейное движение – это движение по прямой линии. Равномерное движение – такое, в процессе которого тело за равные временные промежутки проходит один и тот же путь. Если объединить эти два определения получится третье:

• равномерное прямолинейное движение – это такое движение, в ходе которого 1) тело совершает движение по прямой линии; 2) за одинаковые временные промежутки проходит одинаковый путь.

Зная определения пути и перемещения, это определение можно упростить: прямолинейное равномерное движение тела – это такое движение, в процессе которого тело за одинаковые временные промежутки совершает равные перемещения.

Важной характеристикой является скорость механического движения. Предположим, что при равномерном прямолинейном движении тело за промежуток времени △t перемещается из точки А в точку Б (см. рисунок 8). Радиус-вектор, проведенный в точку A обозначим r₀, а радиус-вектор в точку Б обозначим r₁. Изменение радиус-вектора назовем △r – нетрудно заметить, что это есть перемещение тела за время △t.

Рисунок 8 – Поиск перемещения тела через радиус-векторы при равномерном прямолинейном движении

Тогда скорость движения (v) будет вычисляться по формуле:

Так как △r – вектор, △t – скаляр, скорость v тоже будет вектором, сонаправленным перемещению.

Если тело начинает двигаться в момент начала отсчета, то △t = t*. Из правила сложения векторов следует, что △r = r₁ — r₀. Тогда выражение для скорости можно переписать в виде:

Из этого выражения следует:

Это выражение можно применить к любому произвольно взятому моменту времени, поэтому можно опустить индекс в левой части и переписать:

Данное уравнение является уравнением движения при прямолинейном равномерном движении.

*Напоминание: символом △ (дельта) обозначают изменение какой-нибудь величины. Например △t = t – t₁, где t – конечный момент времени, t₁ – начальный. Если же начальный момент времени совпадает с началом отсчета t₁ = 0, то △t = t – 0 = t_.

Фактически уравнение равномерного прямолинейного движения означает, что радиус-вектор в произвольный момент времени t можно посчитать, сложив начальный радиус-вектор и приращение v*t.

Найдя проекции радиус-вектора и вектора скорости, можно разложить уравнение движения тела на три составляющие вдоль осей ОX, ОY и ОZ.

В этих выражениях r_0x, r_0y, r_0z и v_x, v_y, v_z – это компоненты изначальных векторов r₀ и v вдоль осей ОХ, ОY и ОZ соответственно. И теперь можно перейти к скалярному виду:

Стоит отметить, что при проецировании какие-то компоненты вектора могут стать отрицательными, тогда знаки в выражениях поменяются на противоположные.

В рассмотренном выше примере движение происходит только вдоль оси ОХ (остальные координаты не изменяются). На рисунке 9 приведены проекции начальной (х₀) и конечной (х₁) точки на ось ОХ.

Рисунок 9 – Перемещение тела в координатном представлении

Уравнение координаты (х) движения будет выглядеть:

А это уже похоже на знакомую из прошедшего курса физики формулу для нахождения пути:

Если точка начала двигаться из начала отсчета S₀ = 0, можно переписать эту формулу в виде:

Отсюда следуют известные уже формулы для нахождения скорости и времени при равномерном прямолинейном движении:

Приведем последний в этой статье пример: известно, что тело движется вдоль оси ОХ, начиная из точки x₀ = 3 см. Скорость тела равна v = 5 м/с и направлена вдоль оси ОХ. Необходимо записать уравнение движения по координате х для этого тела.

Итак, для начала приведем все единицы измерения к СИ:

Теперь можно записывать уравнение для координаты х:

Из этого уравнения можно найти координату тела в любой момент времени. Например, через 2 секунды после начала отсчета тело находилось в точке:

x(2) = 0,03 + 5*2 = 10, 03.

А какой путь прошло тело к этому моменту? В начале оно находилось в точке x(2) = 0,03 м, а через 2 секунды оно стало находиться в точке x(2) = 10, 03. Значит за 2 секунды тело прошло:

S = x(2) – x₀ = 10, 03 – 0,03 = 10 м.

А если скорость тела была направлена противоположно оси ОХ, как тогда выглядело бы уравнение движения?

Тогда проекция вектора скорости на ось ОХ была бы отрицательной и в уравнении знак перед скоростью поменялся бы на противоположный: