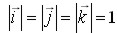Кинематические уравнения движения материальных точек

Уравнение движения материальной точки

Движение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени.

Имеет смысл говорить только о движении в некоторой системе отсчета.

Система отсчета. Системы координат

Точки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки.

В теории используется декартова прямоугольная система координат, где определение точки возможно при наличии радиус-вектора r и трех проекций x , y , z – ее координат. Могут быть применены другие:

• сферическая система с положением точек и ее радиус-вектором, определенных координатами r , υ , φ ;
• цилиндрическая система с координатами p , z , α ;
• на полярной плоскости с параметрами r , φ .

В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений.

Кинематическое уравнение движения материальной точки

Любая система отсчета или координат предполагает определение координат материальной точки в любой момент времени.

При условии положения и определения материальной точки в данной системе отсчета считается, что ее движение задано или описано.

Это возможно при использовании кинематического уравнения движения:

Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения.

Ее перемещение по уравнению ( 1 ) определено, если имеется указанное положение в любой момент времени t . Для этого следует задавать декартовы координаты точки в качестве однозначных и непрерывных функций времени:

x ( t ) = x , y ( t ) = y , z ( t ) = z ( 2 ) .

Прямоугольные декартовы координаты x , y , z — это проекции радиус-вектора r ¯ , проведенного из начала координат. Очевидно, что длину и направление r ¯ можно найти из соотношений, где a , β , γ являются образованными радиус-вектором углами с координатными осями.

Равенства ( 2 ) считают кинематическими уравнениями движения материальной точки в декартовых координатах.

Они могут быть записаны в другой системе координат, которая связана с декартовой взаимно однозначным преобразованием. Если движение точки происходит в плоскости О х у , тогда применимы полярные координаты r , φ , относящиеся к декартовым преобразованиям. Данный случай подразумевает использование уравнения движения точки следующего вида:

r = r ( t ) , φ = φ ( t ) ( 3 ) .

Кинематическое уравнение движения точки в криволинейных координатах q 1 , q 2 , q 3 , связанных с декартовыми преобразованиями вида x = x ( q 1 , q 2 , q 3 ) , y = y ( q 1 , q 2 , q 3 ) , z = z ( q 1 , q 2 , q 3 ) ( 4 ) , записывается как

q 1 = q 1 ( t ) , q 2 = q 2 ( t ) , q 3 = q 3 ( t ) ( 5 ) .

Кривая радиус-вектора, описываемая концом вектора r при движении точки, совпадает с ее траекторией. Параметрическое уравнение траектории с t представлено кинематическими уравнениями ( 2 ) , ( 5 ) . Чтобы получить координатное уравнение траектории следует исключить время из кинематических уравнений.

Определение движения точки возможно с помощью задания траектории и мгновенного положения точки на ней. Ее положение на кривой определяется с помощью указания только одной величины: расстояния вдоль кривой от некоторой начальной точки с положительным направлением:

Это и есть уравнение движения точки по траектории. Способ его задания относят к естественному или траекторному.

Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи.

Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов.

Дано уравнение движения материальной точки x = 0 , 4 t 2 . Произвести запись формулы зависимости υ x ( t ) , построить график зависимости скорости от времени. На графике отметить площадь, численно равную пути, пройденному точкой за 4 секунды, произвести вычисление.

Дано: x = 0 , 4 t 2 , t = 4 c

Найти: υ x ( t ) , S — ?

Решение

При решении необходимо учитывать зависимость скорости от времени:

υ x = υ 0 x + a x t .

Зависимость координаты от времени и сравнение уравнения с заданным принимает вид:

x = x 0 + υ 0 x t + a x t 2 2 , x = 0 , 4 t 2 .

Очевидно, что x 0 = 0 , υ 0 x = 0 , a x = 0 , 8 м / с 2 .

После подстановки данных в уравнение:

Определим точки, изобразим график:

υ x = 0 , t = 0 , υ x = 4 , t = 5

Путь, по которому двигалось тело, равняется площади фигуры, ограниченной графиком, и находится с помощью формулы:

Кинематические уравнения движения

Кинематика материальной точки

Кинематика изучает движение тел, не интересуясь причинами, обусловливающими это движение.

Всякое движение относительно, так как понятие перемещение в пространстве или движение имеет строго определенное содержание только при указании, относительно каких именно тел перемещается рассматриваемый объект.

Совокупность тела или системы тел, условно принятых за неподвижные, относительно которых определяется положение остальных тел, и прибора для отсчета времени (синхронизированных часов) называется пространственно-временной системой отсчета.

Для того, чтобы иметь возможность изучать конкретные движения тел, необходимо зафиксировать некоторую точку тела, принятого условно за неподвижное, то есть выбрать так называемое начало отсчета, относительно которого и будет производиться отсчет положения движущихся тел. Далее, для определения положения данного тела относительно начала отсчета необходимо выбрать масштаб отсчета расстояний и направления отчета положения. Обычно для этого пользуются тремя взаимно перпендикулярными осями декартовых координат или так называемыми обобщенными криволинейными координатами, к числу которых относятся полярные, цилиндрические и сферические системы координат. Часто выбор системы координат определяется постановкой самой задачи. Например, при изучении движения жидкости по цилиндрической трубе наиболее удобными оказываются цилиндрические координаты, в случае исследования обтекания сферы жидкостью или газом — сферические.

Наконец, поскольку движение тел совершается с течением времени, то для его описания необходимо выбрать начало отсчета времени и масштаб времени.

Итак, элементами системы отсчета, необходимыми для описания движений, являются: начало отсчета, масштабы отсчета расстояний, три направления отсчета положения тел, начало отсчета времени, масштаб времени.

Очевидно, что одно и то же движение в различных системах отсчета, движущихся относительно друг друга, будет выглядеть по-разному. Так, скорость, ускорение, направление и траектория движения пассажира, идущего от передней к задней стенке вагона, ускоренно движущегося по криволинейному железнодорожному пути, будут различными, если это движение рассматривать в системах отсчета, связанных: а) с движущимся вагоном; б) с Землей; в) с Солнцем и т.д.

Кинематические уравнения движения

Если с выбранными телами отсчета мы связали какую-либо систему координат, то движение тела можно изучать относительно этой системы координат.

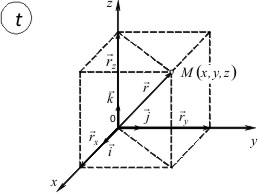
Для определения положения тела в пространстве обычно пользуются декартовой системой координат x,y,z (рис. 1.1).

Положение точки M относительно системы отсчета можно задать с помощью трех ее декартовых координат x,y,z представляющими собой расстояния от этой точки до координатных плоскостей yz, zx, xy соответственно.

Три координаты x,y,z можно объединить в один направленный отрезок или радиус-вектор r, проведенный из начала координат в рассматриваемую точку. Координаты x,y,z являются его проекциями на координатные оси, а потому

(1.1)

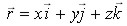
где i,j,k — координатные орты, то есть единичные векторы, направленные вдоль положительного направления координатных осей x,y,z соответственно, то есть

Геометрически вектор представляется диагональю параллелепипеда, построенного на трех взаимно перпендикулярных векторах r_x=xi, r_y=yj, r_z=zk и по величине (по модулю) равен

(1.2)

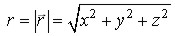
Будем пользоваться правой координатной системой, различать которую можно с помощью правила буравчика. Ввинчивая буравчик с правой нарезкой, вращая его ручку в плоскости xy кратчайшим путем от положительного конца оси x к положительному концу оси y, получим поступательное перемещение буравчика, совпадающее с положительным направлением оси z.

Движение точки будет описано полностью, если будет известно ее положение в любой момент времени относительно выбранной системы отсчета.

При движении материальной точки M ее координаты z,y,z и радиус-вектор r изменяются с течением времени t. В механике время считается аргументом, то есть независимым переменным, поэтому для задания закона движения материальной точки необходимо указать либо вид функциональной зависимости всех ее трех координат от времени

(1.3)

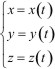
либо зависимость от времени ее радиус-вектора

Уравнения (1.3) и (1.4) называют кинематическими уравнениями движения материальной точки.

Геометрическое место точек концов радиус-вектора r называют траекторией точки M. Уравнения движения задают траекторию точки в параметрической форме. Роль параметра играет время t. Если надо получить уравнение траектории из кинематических уравнений движения исключают время, получая уравнение траектории, указывающее связь между тремя координатами любой точки.

Кинематические уравнения движения материальных точек

В соответствии с (2.2.4) эти уравнения эквивалентны векторному уравнению

Уравнения (1.2.8) и (1.2.9) называются кинематическими уравнениями движения материальной точки.

Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы.

Если материальная точка движется в пространстве, то она имеет три степени свободы (координаты х, у, z); если она движется на плоскости — две степени свободы; если вдоль линии — одну степень свободы.

При движении материальной точки А из положения 1 в положение 2 (рис. 1.2.3) её радиус-вектор изменяется и по величине, и по направлению, т. е. r зависит от времени t.

Геометрическое место точек концов r называется траекторией точки. Длина траектории есть путь Δs. Если точка движется по прямой, то приращение |Δr| равно пути Δs.

Рис. 1.2.3. Перемещение точки А в пространстве из положения 1 в положение 2: вектор перемещения Δr = r2 — r1

Пусть за время Δt точка А переместилась из точки 1 в точку 2. Вектор перемещения Δr есть приращение r за время Δt: