Кинематические уравнения движения центра масс летательного аппарата

ЛЕКЦИЯ 3 ТЕМА: УРАВНЕНИЯ ДВИЖЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА КАК ТВЕРДОГО ТЕЛА. ПРОДОЛЬНОЕ И БОКОВОЕ ДВИЖЕНИЕ

Евгений Перхуров 5 лет назад Просмотров:

1 1 Направления подготовки: Авионика Аэронавигация Системная инженерия Бортовые системы управления Дисциплина: Курс, семестр, уч. год: 3, весенний, 11/1 Кафедра: 31 СУЛА Руководитель обучения: ассистент Копысов Олег Эдуардович ЛЕКЦИЯ 3 ТЕМА: УРАВНЕНИЯ ДВИЖЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА КАК ТВЕРДОГО ТЕЛА. ПРОДОЛЬНОЕ И БОКОВОЕ ДВИЖЕНИЕ Движение ЛА, как твѐрдого тела в связанной системе координат описывается уравнениями Эйлера (шесть нелинейных дифференциальных уравнений второго порядка). Силы и моменты, входящие в эти уравнения, сложным образом зависят от высоты, скорости и режима полѐта и меняются во времени, г. к. изменяются условия полѐта, например из-за изменения массы и момента инерции ЛА в результате расхода топлива или сброса груза. При аналитическом исследовании процессов управления ЛА его уравнения движения, как правило, упрощают, рассматривая два независимые друг от друга движения: продольное и боковое. К продольному относят поступательные движения ЛА вдоль осей ОХ и ОY и вращательное движение вокруг оси O. К боковому движению относят поступательное вдоль оси O и вращательные движения вокруг осей ОХ и ОY. Продольное движение. Обобщенная математическая модель При продольном движении ЛА вектор V линейной скорости его центра масс находится в вертикальной плоскости. Внешние силы, действующие на ЛА: Р сила тяги двигателей, вектор которой направлен вдоль оси ОХ: Х а сила лобового сопротивления, вектор которой направлен против вектора V, т.е. в отрицательную сторону оси ОХ а Y а подъѐмная сила, вектор которой перпендикулярен вектору V mg вес ЛА (m масса ЛА, g ускорение свободного падения). Вращение ЛА в плоскости

2 Х а Y а возможно под действием момента М, действующего вокруг оси O а, который называется аэродинамическим моментом тангажа. В соответствии с рис. 3.1 имеют место кинематические соотношения:, (3.1) где ϑ угол тангажа θ угол наклона траектории движения центра масс (ЦМ) ЛА ω угловая скорость тангажа. Рисунок 3.1 Внешние силы, действующие на ЛА в продольном движении Вращательное движение ЛА вокруг оси O а описывается уравнением: I, (3.) где I момент инерции ЛА относительно оси O а М момент аэродинамических сил, который можно представить в виде: mba S V, (3.3) где т коэффициент момента b а — хорда крыла ρ плотность воздуха S площадь крыльев. Коэффициент т можно представлять состоящим из суммы трех слагаемых, два из которых зависят от статических параметров (α, V, δ в ) и определяют статический момент, а третий от динамических параметров ( ), и определяет демпфирующий момент.

3 3 Спроектируем силы, действующие на ЛА, на касательную к траектории полѐта (ось X) и на нормаль к ней (ось Y). Сумма проекций сил на касательную к траектории: dv m mv P cos X a mg sin. dt (3.4) При определении проекций сил на нормаль к траектории нужно иметь в виду, что при движении ЛА по искривленной траектории с радиусом кривизны r, на него действует центробежная сила инерции mv траектории), a ds = Vdt, то / mv mv mv d r. Так как r = ds/dθ (s длина дуги mv mv. r ds / d Vdt / d dt Следовательно, сумма проекций сил на нормаль к траектории: mv Y Psin mg cos. a (3.5) Сила тяги Р зависит от параметров двигателя, от внешних условий, характеризуемых скоростью полѐта V, высотой полѐта Н и параметра управления двигателем δ р, т. е. в общем виде Р = Р(V, Н, δ р ). Аэродинамические силы Х а и Y а зависят от угла атаки α, скорости полѐта V, плотности воздуха ρ и угла отклонения руля высоты δ в. Так как угол δ в практически не влияет на величины Х а и Y а, то этим влиянием пренебрегают и представляют их обычно в виде: где X a CxaS V Ya CyaS V, (3.6) C xa, C ya коэффициенты лобового сопротивления и подъемной силы, зависящие от угла атаки и скорости полета. Система нелинейных дифференциальных уравнений (3.), (3.4), (3.5) с учѐтом (3.1), (3.3), (3.6) является математической моделью продольного движения ЛА. Известно, что для пилотируемых ЛА самолетной схемы практически для всех компоновок и большинства режимов полета, собственное движение ЛА состоит из двух колебательных движений, отличающихся частотой и степенью затухания. Эти движения называются короткопериодическими и длиннопериодическими или фуго-

4 идными. Причиной возникновения короткопериодических движений является нарушение равновесия моментов вокруг оси O a, что приводит к вращению ЛА относительно ЦМ и изменению углов α и ϑ. Скорость невозмущѐнного линейного движения при этом практически не изменяется. Причиной возникновения длиннопериодических движений является нарушение внешних сил, действующих в продольной плоскости симметрии ЛА, следствием чего является изменение скорости его полета. 4 Линеаризованные уравнения продольного движения ЛА Применяя к уравнениям (3.), (3.4), (3.5) метод малых возмущений, могут быть получены линейные уравнения продольного движения ЛА. Предположим, что на исследуемом участке полета невозмущенное движение ЛА характеризуется постоянными силами X, Y, P, и параметрами V, α, ϑ, θ, H и ω z =, а параметры управления δ В, δ р также постоянны. Если исследуется участок полета, на котором параметры движения существенно меняются, его разбивают на несколько участков, на которых параметра движения можно считать постоянными. Уравнения невозмущѐнного движения ЛА на участке с постоянными параметрами следуют из уравнений (3.), (3.4), (3.5): P cos X mg sin Y P sin mg cos. Из первых двух уравнений системы следует отношение: P cos X tg, P sin Y (3.7) из которого можно заключить, что при P cos X ЛА летит горизонтально, при P cos X набирает высоту ( ), а при P cos X уменьшает высоту ( ).

5 Если в некоторый момент времени параметры движения и управления изменились на величины V. то соответствующие параметры P возмущѐнного движения принимают вид: V V V P P P. При изучении продольного углового движения ЛА в области малых изменений параметров движения первое уравнение системы (3.7) из рассмотрения можно исключить, т.к. оно представляет сумму проекций сил на ось ОХ a (рис. 3.1), не влияющих на угловое движение ЛА. При линеаризации второго уравнения системы (3.7) полагают, что проекция силы тяжести на ось OY a не оказывает влияния на угловое движение ЛА, и этой составляющей можно пренебречь. В результате известных процедур линеаризации могут быть получены простейшие уравнения продольного движения ЛА: mv Y I (3.8), где постоянные коэффициенты соответствуют исходному невозмущѐнному движению и определяются следующим образом: Y Y ( Pcos ) ( ) ( ) ( ). 5

6 Рассмотрим аэродинамические моменты в уравнениях (3.8), определяющих короткопериодическое движение ЛА. При >, что обычно имеет место, момент называется моментом продольной статической устойчивости, который является следствием воздействия набегающего воздушного потока на хвостовое горизонтальное оперение, от размеров и формы которого главным образом и зависит. При невозмущѐнном движении ЛА угол атаки и аэродинамический момент относительно поперечной оси отсутствует. Восходящие или нисходящие потоки воздуха приводят к изменению угла атаки на величину например изменения центровки ЛА. Величина, который может измениться и из-за других причин, приводит к увеличению подъѐмной силы крыльев, следствием чего является изменение высоты полѐта ЛА, и к увеличению на Y подъѐмной силы горизонтального хвостового оперения, которая приложена в центре давления (ЦД) на плече L ГО, что и создаѐт момент Y L ГО, возвращающий ЛА к прежнему углу атаки, т.е. (рис. 3.). Таким образом, момент обеспечивает продольную устойчивость ЛА, если центр давления аэродинамических сил находится за центром масс ЛА в сторону хвостового оперения. Если ЦМ и ЦД совпадают, то 6 = (нейтральный ЛА), если ЦД находится впереди ЦМ, то 7 еѐ увеличение средствами аэродинамики приводит к увеличению воздействия на ЛА аэродинамических возмущений. 7 Рисунок 3. Определение момента продольной статической устойчивости Рисунок 3.3 Определение момента демпфирования тангажа Управляющий момент появляется при отклонении руля высоты хвостового горизонтального оперения, вследствие чего изменяется его угол атаки. Физическая картина воздействия этого момента на ЛА аналогична влиянию момента продольной статической устойчивости (статической устойчивости тангажа). На руль высоты, отклонѐнный от нейтрального положения на угол, действует аэродинамическая сила Y РВ, направленная перпендикулярно набегающему потоку воздуха и приложенная в ЦД рулевой поверхности (рис. 3.4), который, как правило, не совпадает с ее осью вращения (ОВ). Сила Y РВ относительно оси вращения создает так называемый шарнирный момент, который является основным нагрузочным моментом для привода, осуществляющего разворот руля высоты. В точке, соответствующей ОВ, можно приложить две противоположно направленных силы Y РВ, равных по модулю Y РВ.

8 8 Рисунок 3.4 Определение управляющего момента по высоте Тогда можно записать равенство, Y ‘ L Y ‘ l Y L из которого P P P P следует, что управляющий момент, приложенный к ЛА, состоит из суммы шарнирного момента, действующего относительно ОВ руля и момента силы Y РВ на плече L относительно ЦМ ЛА. Вернемся к уравнениям системы (3.8) и перепишем их в переменных приращений углов тангажа где и атаки : I mv ( ) Y F. Y (3.9), F Y возмущающие момент и сипа, действующие соответственно относительно оси O а и вдоль оси OY а. Уравнения системы (3.9) перепишем в виде: где a1 a a3 a a a a a 5 a F, 6 Y Y. a I I I 4 1, a 1 5, a6. I mv mv (3.1) (3.11) Постоянные коэффициенты в (3.11), соответствующие невозмущѐнному движению, определяются следующим образом:

9 m qsb m qsl m qsb Y c, yqs (3.1) где q V / скоростной напор b хорда крыла. 9 Боковое движение Аэродинамические силы и моменты, действующие на ЛА Боковое движение ЛА включает вращение вокруг продольной оси ОХ, нормальной оси ОY и линейное перемещение вдоль оси O. Рассмотрим основные аэродинамические силы и моменты, действующие на ЛА (рис. 3.5). Предположим, что вследствие какого-либо возмущения ЛА относительно нормальной системы координат ОХ g Y g g получил крен на угол γ, после чего возмущение исчезло. Угол γ определяет положение связанной системы координат ОХY, причѐм т. О совпадает с центром масс ЛА самолѐтной схемы. Плоскости крыльев относительно плоскости Х располагаются под углом φ. При положительном крене (на правое крыло) вдоль оси O появляется составляющая mg sin силы веса ЛА, под действием которой возникает скольжение ЛА со скоростью V VXtg ( V X продольная составляющая скорости V, β угол скольжения). Вследствие скольжения нарушается симметрия обтекания крыльев воздушным потоком. Для иллюстрации указанного обстоятельства на концах правого и левого крыльев построены треугольники воздушных скоростей ( V к составляющая скорости V набегающего воздушного потока вдоль крыльев V I — составляющая, перпендикулярная вектору скорости V ), из которых следует VI V tg. Так как скорости V 1 на правом и левом крыльях направлены в разные стороны, происходит изменение их углов атаки, что иллюстрируется построением треугольников скоростей на векторах скоростей V X и V I, из которых следует V / V. При этом на правом крыле имеет место положительное приращение I X угла атаки (+ ), а на другом отрицательное ( ).

10 1 Рисунок 3.5 Определение моментов статической устойчивости крена и пути Соответственно подъемная сила правого крыла увеличится на ΔY, а левого уменьшится на ΔY. В результате относительно оси ОХ образуется момент поперечной статической устойчивости или момент статической устойчивости крена, первопричиной которого является скольжение и который обозначается в виде, х М где ( х ) х. Очевидно, что этот момент тем больше, чем больше изменение угла, величина которого в соответствии с приведенными выше соотношениями, может быть представлена в виде: VI Vtg Vxtgtg, V V V x x x откуда следует, что чем больше угол φ, тем больше момент поперечной устойчивости. Стреловидность крыльев в плане также приводит к появлению момента поперечной устойчивости. Изменение углов атаки приводит к изменению сил лобового сопротивления на крыльях: на правом крыле эта сила увеличится на величину ΔХ, а на левом умень-

11 шится на ΔХ. С появлением угла β возникает также сила Δ на вертикальном оперении. Следствием указанных сил является возникновение флюгерного момента, или момента статической устойчивости пути, который старается развернуть ЛА в сторону набегающего воздушного потока. Этот момент обеспечивает устойчивость по углу скольжения, стремясь так развернуть ЛА, чтобы установился угол скольжения, имевший место до возмущения. Момент статической устойчивости пути обозначается в виде, где ( М y ) y y. 11 Используя литературные источники, найти графические зависимости коэффициента продольного момента от угла атаки и отклонения руля высоты, зависимость коэффициентов С ха, С уа от угла атаки. Термины для занесения в тезаурус: продольное движение, боковое движение, коэффициент лобового сопротивления, коэффициент подъемной силы, невозмущенное движение летательного аппарата, момент статической устойчивости, шарнирный момент.

УРАВНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА. МАСС САМОЛЕТА

Уравнение движения центра масс в векторной форме

Положение и движение самолета в полете определяют относительно поверхности Земли. Поэтому за основную систему отсчета, принимают геоцентрическую неинерциальную систему ко­ординат, связанную с Землей и совершающую вместе с ней суточное

вращение с угловой скоростью со3 (земная система отсчета).

Движение центра масс самолета описывается динамическим

уравнением (1.7), которое после подстановки FBIi = RA + mgr примет вид

m^^P + RA + mgr + F’ + F*, (1.32)

где 1/к — вектор скорости движения центра масс самолета относи-

тельно Земли и gr — вектор гравитационного ускорения.

Переносную и кориолисову силы инерции, связанные с враще­нием Земли, определяют известными из теоретической механики выражениями

Fe — — mWe == — m[iо3 х (со3 X r)]

KK = — m#K = — 2m(to3 x VK), . (1.33)

где r —- радиус-вектор, проведенный из начала геоцентрической си­стемы отсчета 0° в центр масс самолета; We и И7К — переносное и кориолисово ускорения центра масс, обусловленные вращением выбранной геоцентрической системы отсчета относительно инер­циальной. ‘ . .

Поскольку в справочных таблицах обычно приводятся значения ускорения свободного падения с учетом переносной силы инерции в зависимости от высоты, то в правой части уравнения (1.32) можно

геометрическую сумму сил гравитационного притяжеция. mgr и переносной силы инерции F1 заменить силой тяжести G:

G = mgt + Fe — mg. (1-34)

В (1.34) g—вектор результирующего ускорения свободного паде­ния и центробежной силы,.

Векторное уравнение (1,32) с учетом (1.34) запишем в виде

Как было указано в § 1.1, при практическом применении вектор­ное уравнение движения проектируется на оси прямоугольной си­стемы координат. Выбор систёмы координат для составления-диф­ференциальных уравнений движения центра масс самолета опреде­ляется задачей исследования. При исследовании траекторий обычно применяют траекторные оси. В то же время задачи устойчивости и управляемости удобнее рассматривать в связанной системе коор­динат.

Уравнения движения центра масс в траекторией системе координат

Наиболее простую и удобную форму система динамиче­ских уравнений движения центра масс самолета (поступательного движения) примет, если векторное уравнение (1.35) спроектировать на оси траекторной системы координат.

Применяя формулы (1.9) для проектирования левой части урав­нения (1.35) и учитывая, что 1/*„ = VI:, Vm = Vzi: =0, получим

Ь Р*к‘> тыг^Ук — Р!,к г Уi; b G,;K — F(1.36) — тыугУК — РZK “Ь

где (оун, согк — проекции на траекторные оси вектора угловой ско-

рости (о„ вращения траекторной системы координат относительно Земли; в правой части приведены проекции соответствующих сил на траекторные оси.

Для написания этих уравнений в развернутом виде необходимо

найти проекции угловой скорости сок, а также проекции кориоли-

совой силы инерции FK на траекторные оси. Проекции внешних сил и тяги на эти оси были определены в § 1.6.

Угловую скорость со„ можно представить в виде суммы переносной

угловой скорости сокр нормальной системы 0XgYgZg в системе от-

счета O^X^YqZq и угловой скорости сок& вращения скоростной си­стемы относительно нормальной:

сон = соКр -|- coKg. (1.37)

Переносная угловая скорость сокр, в свою очередь, может быть представлена суммой угловых скоростей:

где К — угловая скорость поворота меридиональной плоскости,

содержащей центр масс О, вокруг оси вращения Земли; ф — угловая скорость поворота радиуса-вектора центра масс в меридиональной плоскости вокруг оси, лежащей в плоскости экватора (см. рис. 1.4).

Угловая скорость coKg также может быть представлена в виде

суммы угловой скорости Фг вокруг ОСИ OYg и угловой скорости 0 вокруг оси OZg (см. рис. 1.5):

Используя табл. I (см. приложение) направляющих косинусов, находим проекции вектора сок на оси OY„ и OZK траекторной системы

co^j, = Я (sin ер cos 0 — cos ф sin Y sin 0) ф sin Y sin 0 + !F cos 0;

согк = Я, cos ф sin V — ф cos V

которые после подстановки выражений (1.21) в результате неслож­ных преобразований будут иметь вид

gj,(K = ¥ cos 0 V sin 4r cos20 tg ф/(/?з — f Я);

co2K = 0 — И cos Q/(R3 + Я). (1.41)

Найдем теперь проекции кориолисовой силы инерции на траек — торные оси. Вектор кориолисовой силы инерции определяется из­вестной из механики формулой

— mwK = — 2т(и3 х Кк) (1-42)

и перпендикулярен (03 и Ук.

Проекции кориолисовой силы инерции на оси траекторной системы выражаются формулами

Кк = 0; FyK = 2ma>aVR cos ф cos

F*к = 2mcoaVK (sin ф cos 0 — cos ф sin ‘P sin 0).

Подставляя в (1.36) выражения для проекций угловых скоростей, определенные формулами (1.41), проекции тяги, аэродинамической силы, силы тяжести (см. формулы (1.27) и (1.28), а также (1.30)) и проекции кориолисовой силы инерции, выраженные формулами (1.43), получим систему динамических уравнений движения центра масс самолета относительно сферической вращающейся Земли в про­екциях на оси траекторной системы координат (при отсутствии ветра ук = V, ¥ = фи):

mV — Р cos (а + ф,) cos р — Ха — mg sin 0; (1.44)

— Zu sin y„ — mg cos 0 — j0$mu>3V cos ф sin ‘P — f mV^cos 0/(/?3 Я);

— mV cos 0 *P = P [sin (а + Ф/ ) sin ya — cos (a ф^ зіп p cos yj -|-

-j — Ya sin yu + Za cos ya -1- 2/ж.>зV (sin ф cos 0 — cos ф cos lP sin 0) —

— mV2 cos2 0 sin Y tg ф/(/?8 + Я). (1.46)

Эти уравнения называют уравнениями поступательного движения.

Приведем некоторые оценки величин членов правых частей уравнений (1.44) … (1.46), связанных с суточным вращением Земли и кривизной ее поверхности. Кориолисова сила, связанная с вра­щением Земли, пропорциональна скорости полета. При скоростях полета свыше 2000 … 3000 м/с кориолисово ускорение составит 2 … 3 % от ускорения свободного падения. Центростремительное
ускорение, обусловленное кривизной Земли, пропорционально ква­драту скорости полета и при скорости 1000 м/с достигает около 1,6 % от ускорения свободного падения. При расчете траекторий самолетов, летающих со скоростями до 1000 м/с, кориолисову силу инерции и силу инерции, связанную с кривизной поверхности Земли, обычно не учитывают.

В динамические уравнения движения центра масс входит масса самолета, заметно меняющаяся у некоторых типов самолетов в про­цессе полета. Э общем случае характер изменения массы самолета из-за выгорания топлива зависит от скорости, высоты полета и режима работы двигателя:

Перегрузка. Уравнения движения центра масс в безразмерной форме

При исследовании многих задач динамики полета исполь­зуется понятие перегрузки. Перегрузкой называется отношение суммы векторов тяги и полной аэродинамической силы к величине силы тяжести

• —^ . P + RA . ■mg » title=»УРАВНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА. МАСС САМОЛЕТА» align=»left» width=»58″ height=»45 src=»http://ooobskspetsavia.ru/2015/11/06/uravneniya-dvizheniya-centra-mass-samoleta/style=»margin-left:-70px; margin-right:70px»/>(1.48)

. Вектор перегрузки характеризует маневренность самолета, по­скольку он учитывает величину и направление сил, изменяя кото­рые, можно управлять полетом.

Проектируя вектор перегрузки на оси координат, получим составляющие перегрузки по осям. Проекции перегрузки на оси скоростной системы координат равны:

^ cos ( sin(a 4-фр) +FJ; ‘ (1.49)

«;« = -^[—Р COS (a — f фя) sin р + ZJ

и называются соответственно тангенциальной, нормальной’скорост­ной и боковой перегрузками.

Проекции вектора перегрузки на оси траекторной системы координат составят (при отсутствии ветра):

пхк = і cos (« + Фи)cos Р — *a] = пха

п1т = Р fsln (« + COS Уа + cos (о — f Фя) Stalin уа1 +

В (1.49) и (1.50) аэродинамические силы определены в скорост­ной системе осей координат. .

‘ Разделив левые и правые части уравнений (1.44) … (1.46) на О = mg, получим динамические уравнения движения центра масс в перегрузках

-jr ё = tlya COS Yu — «za Sin Yu — COS 0 |-

f — cos ф sin ¥ (/?з + //)’. (1.51)

——— — і = nya sin Yu — «70 cos Ya H — — C0B к (simp cos 0 —

— cos ф cos ¥ sin 0) — Vі cosE0 sin ¥ tg

‘При рассмотрении частных случаев движения самолета выра­жения для проекций перегрузки значительно упрощаются.

Для]) полета без скольжения (ft == О, Za = 0) с малыми углами атаки, когда можно принять sin (a + фР) « а + фР, cos (os + + Фр) » 1, формулы (1.49) и (1.50) примут вид

Р-Ха. .. Р(а + Фр) + Ко. ха

и, без ветра, » ‘ 1 ‘ ■

«зса» пу* =.■«№COS Yu’.. «Лі = «j/аSin Yu — (15 )

В проекциях на связанные оси вектор перегрузки может быть представлен составляющими пх, пу и nz, которые называются продольной, нормальной и поперечной перегрузкой соответственно. Используя таблицу направляющих косинусов, получим

Пх = пха COS a COS Р + пиа sin о — nzu cos os Sin Р; 4

пу — — пха sin a cos Р -)- пуа cos a + пга sin a sin P; (1-54) «г = nxa Si» P + «га cos P-

§ 1.8. ДИНАМИЧЕСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ САМОЛЕТА ОТНОСИТЕЛЬНО ЦЕНТРА МАСС

Исследование движения самолета относительно центра масс (вращательного,- илн углового) удобно выполнять, если ис­пользовать динамические уравнения в проекциях на оси связанной системы координат 0XYZ. При изучении углового движения само-

лета так же, как и при определении траекторий центра масс, при­меняют в качестве системы отсчета неинерциальную систему, свя­занную с Землей.

Проектируя векторное уравнение (1.8) на оси связанной системы координат и применяя формулы (1.9) для вычисления проекций производных по времени от вектора кинетического момента самолета, получим систему скалярных уравнений движения самолета относи­тельно центра масс (вращательного, или углового движения)

-j — агКх ьзхКг = Мру’, (1.55)

-rff — •+ ЫхКу — Ь)1/Кх = Мрг,

где К. х, К у, Кг — проекции вектора кинетического момента са­молета на связанные оси координат; (ох, ыу, (oz — проекции век­тора угловой скорости самолета относительно Земли на те же оси; MRx, MRu, MRz — проекции результирующего момента аэроди­намических сил и тяги относительно центра масс на те же оси. Сле­дует иметь в виду, что момент массовых сил (сил тяжести, центро­бежных и кориолисовых сил инерции) вокруг центра масс самолета равен нулю.

Угловая скорость самолета относительно Земли является сум­мой векторов угловой скорости самолета относительно нормальной

системы координат и угловой скорости (о«р вращения нормальной системы координат относительно Земли вследствие кривизны по­верхности Земли, Для реальных условий полета самолета последняя

составляющая ы„р мала и ею можно пренебречь.

Проекции кинетического момента К на произвольные подвижньЙ! оси записываются в теоретической механике^как /’V-;

Кх JХ^Х ‘ /xytoy /хг(0г)

где /ж, Jy, Jz осевые, а 7*„, Jxz, uJyZ — центробежные моменты инерции, которые определяются формулами:

Jx = J (уг + z[5]) dm Jy — J (Xі — f z-) dm)

Jz = j (Xі + Уъ) dm; Jay = jxy dm

Jxi = j xz dm) Jyz = j t/z dm.

Моменты инерции самолетов с заметно изменяющейся в полете массой являются функциями времени.

Поскольку основная плоскость OXY связанной системы коорди­нат является плоскостью симметрии самолета, то в связанных осях центробежные моменты инерции, содержащие координаты г, равны нулю: Jxz — Juz — — 0.

С учетом этого упрощения, используя выражения (1.56), урав­нения (1.55), запишем в виде

Jх^х ^ху®у і г ^ у) ^ ху^х^у == рх)

Jу®У ^ху®х (/ж ‘ *^г) ®жВ)г Jx^z == ^Ry’i

Jг Ь (^у ^х) ^[>х^[)у Jxy (Щ* Wp) = Аі рг.

Подробнее выражения для проекций результирующего момента MRx, MRy и MRz будут рассмотрены во второй части книги при анализе углового движения самолета.

Уравнения движения центра масс самолета

Самолет движется в воздухе по действием аэродинамической силы 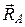, силы тяги двигателей и силы тяжести . С аэродинамической силой и ее проекциями на оси различных систем координат мы познакомились при изучении основ аэродинамики. Сила тяги создается силовой установкой самолета. Вектор обычно располагается в базовой плоскости самолета и образует некоторый угол с осью 0X связанной системы координат, но для простоты мы будем полагать, что этот угол равен нулю, а сам вектор приложен в центре масс.

Полет самолета можно условно разбить на несколько этапов: взлет, набор высоты, горизонтальный полет, снижение и посадка. Самолет также может совершать вираж и другие маневры. На некоторых этапах полета движение самолета может быть как установившимся, так и неустановившимся. При установившемся движении самолет летит с постоянной скоростью, при неизменных углах атаки, крена и скольжения. Ниже мы будем рассматривать только установившееся движение на этапах горизонтального полета, набора высоты и снижения.

Установившийся горизонтальный полет – это прямолинейный полет с постоянной скоростью на постоянной высоте (см. рис. 39). Уравнения движения центра масс самолета запишутся в этом случае следующим образом:

(48)

Поскольку угол атаки a мал (при этом cos a » 1, а sin a » 0), то можно записать:

(49)

Рис. 39. Схема сил, действующих на самолет в установившемся

Если первое из этих равенств не будет выполняться, то скорость самолета будет либо увеличиваться, либо уменьшаться, т.е. не будет выполняться условие установившегося движения. Если же подъемная сила не равна силе тяжести, то самолет будет либо подниматься, либо снижаться, а это значит, что не будет выполняться условие горизонтального полета. Из этого равенства, зная формулу подъемной силы (35), можно получить величину скорости, необходимую для выполнения горизонтального полета V_г.п.

Учитывая, что G = mg (где m – масса самолета, а g – ускорение свободного падения), можно записать:

, (50)

(51)

Из этой формулы видно, что скорость горизонтального полета зависит от массы самолета, плотности воздуха r (которая зависит от высоты полета), площади крыла S_кр и коэффициента подъемной силы C_ya. Поскольку C_ya напрямую зависит от угла атаки a, то каждому значению скорости горизонтального полета будет соответствовать единственное значение угла атаки. Поэтому для обеспечения установившегося горизонтального полета с требуемой скоростью летчик задает определенную тягу двигателей и величину угла атаки.

Установившийся набор высоты – прямолинейное движение самолета вверх с постоянной скоростью. Схема сил, действующих на самолет при установившемся наборе высоты с углом наклона траектории q, показана на рис. 40.

Рис. 40. Схема сил, действующих на самолет при установившемся

наборе высоты (угол атаки принят малым и не показан)

В этом случае уравнения движения примут вид:

(52)

Необходимо отметить, что при наборе высоты тяга двигателей P уравновешивает не только силу лобового сопротивления X_a, как в горизонтальном полете, но и составляющую силы тяжести Gsinq. Подъемная сила Y_a при этом требуется меньшая, поскольку Gcosq