Кинематические уравнения вращательного движения тела

Если тело совершает вращения около неподвижной оси, то $\vec \varepsilon$ имеет направление вдоль оси вращения тела.

Если угловая скорость вращения тела увеличивается (вращение ускоренное), то вектор углового ускорения и вектор угловой скорости сонаправлены.

При замедленном вращении векторы углового ускорения и угловой скорости имеют противоположные направления.

Тангенциальная и нормальная компоненты линейного ускорения

По определению, составляющая линейного ускорения ($a_<\tau>$), которая отвечает за изменение величины скорости движения тела (тангенциальное ускорение) равна:

Принимая во внимание выражение (2), мы получим:

Ускорение, отвечающее за изменение направления скорости движения при криволинейном перемещении – это нормальное (или центростремительное ускорение) ($a_n$) равно:

Использовав формулу (2), имеем:

Мы получили связи между линейными параметрами движения:

• длиной пути ($s$) пройденным, материальной точкой по дуге окружности радиуса $R$;
• линейной скоростью перемещения точки $v$;
• тангенциальным ускорением $a_<\tau>$;
• нормальным ускорением $a_n$

и угловыми величинами:

• углом поворота $\varphi$;
• угловой скоростью $\omega$;
• угловым ускорением $varepsilon$.

$s=R\Delta \varphi$, $v=R\omega$, $a_<\tau>=R\varepsilon$, $a_n=\omega^2R.$

Вращение с постоянным угловым ускорением

Если вращение материальной точки происходит с постоянным угловым ускорением ($\varepsilon = const$,), то его называют равнопеременным.

В таком случае это движение можно описывать при помощи следующих уравнений. Для угловой скорости имеют место равенства:

$\omega = \omega _0+\varepsilon t (13) $

при вращении с положительным ускорением (равноускоренное движение) и

$\omega = \omega _0-\varepsilon t (14) $

при равнозамедленном вращении. В формулах (13) и (14) $\omega_0$ — начальная скорость вращения.

Угол поворота материальной точки при равноускоренном движении задает формула:

$\varphi= \varphi_0 + \omega _0 t +\frac<\varepsilon t^2> <2>(15)$

при равноускоренном движении

$\varphi= \varphi_0 + \omega _0 t — \frac<\varepsilon t^2> <2>(16)$

при равнозамедленном движении. В уравнениях (15) и (16) $\varphi_0 $ — начальный угол поворота.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 08 05 2021

Кинематика твердого тела

Содержание:

Кинематика твёрдого тела (от др.-греч. κίνημα — движение) — раздел кинематики, изучающий движение абсолютно твёрдого тела, не вдаваясь в вызывающие его причины.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Кинематика твердого тела

В кинематике твердого тела определяются закон движения и кинематические характеристики абсолютно твердого тела, а также кинематические характеристики точек тела.

Абсолютно твердым телом называется материальное тело, в котором расстояния между любыми двумя его точками остается постоянным.

Простейшие движения твердого тела

После рассмотрения кинематики материальной точки перейдем к изучению движения твердого тела. Рассмотрим сначала его простейшие виды — поступательное и вращательное.

Поступательное движение твердого тела

Поступательным называется такое движение твердого тела, при котором произвольная прямая, проведенная на этом теле, перемещается, всегда оставаясь параллельной самой себе.

Примерами поступательного движения твердого тела может быть: движение планки мотовила зерноуборочного комбайна при прямолинейном его движении; движение клавиши соломотряса (шарнирного параллелограмма O₁ABO₂ рис. 2.10, а), который осуществляет круговое поступательное движение; поступательное движение штанги кулачкового механизма (рис. 2.10, б), которой осуществляет обратнопоступательное движение; движение педали велосипеда относительно рамы, поршня двигателя
относительно цилиндра, движение кузова автомобиля при прямолинейном движении и т. п.

Таким образом, траектории движения точек тела при поступательном движении могут быть как прямая линия, так и любые кривые. Термин «поступательное движение» касается только тела, а не точки.

Каким же образом определяются кинематические характеристики движения твердого тела при поступательном движении? Рассмотрим теорему

«При поступательном движении тела все его точки движутся по тождественных траекториях и имеют в каждый момент времени одинаковые скорости и ускорения».

Доказательство: Пусть есть тело, которое движется поступательно и которое за некоторый промежуток времени перешло из одного положения в другое (рис. 2.11). Прямая AB, проведена через произвольные точки А и В тела осталась параллельной
самой себе и заняла новое положение A´B´. Выберем за начало отсчета произвольную точку О. Проведем из точки О радиусы — векторы , двух произвольных точек тела А и В. Из треугольника ОАВ, что создано на рис. 2.11, следует, что

Согласно определению поступательного движения тела вектор , соединяющий
точки А и В и перемещается параллельно самому себе является постоянным вектором,
потому что точки А и В принадлежат твердому телу:

То есть, при поступательном движении тела радиусы — векторы и произвольных точек А и В, изменяясь по направлению, будут отличаться согласно формуле на один и тот же постоянный вектор .

Итак, из этого следует, что траекторию движения точки В можно получить, сместив траекторию точки А по направлению вектора на расстояние AB, и поэтому эти траектории будут тождественными, конгруэнтными (совмещаются при наложении).

Определим скорости точек A и B тела. Для этого продифференцируем по времени выражение:

Вторая составляющая правой части этого выражения будет равна нулю:

поскольку = const, то окончательно имеем:

а это скорости точек А и В:

= .

Таким образом, скорости точек А и В движущегося тела постепенно, равны по величине и имеют одинаковое направление, поскольку они расположены на касательных к одинаковым траекториям движения и направлены в одну и ту же сторону.

Определим ускорение точек А и В. После второго дифференцирования по времени выражения имеем:

Как и в предыдущем случае имеем поскольку = const. Тогда окончательно:

= .

Таким образом, поступательное движение тела вполне определяется движением
какой-либо одной его точки.

Окончательно можно сделать следующие вывод: определение поступательного
движения твердого тела сводится к определению движения только одной его точки,
поскольку все точки тела движутся одинаково. При этом скорость и ускорения, которые являются общими для всех точек тела, называются скоростью и ускорением поступательного движения тела, а уравнения движения любой его точки является уравнением поступательного движения тела.

Таким образом, в результате полного тождества движения всех точек тела, движется поступательно, большинство задач по кинематике такого движения тела решается методами кинематики материальной точки.

Вращательное движение твердого тела вокруг неподвижной оси

Вращательное движение вокруг неподвижной оси — это движение твердого тела, при котором все его точки, двигаясь в параллельных плоскостях, описывают окружности с центрами, лежащими на одной неподвижной прямой, называемой осью вращения.

Закон вращательного движения

Кроме поступательного движения твердого тела в простых относится вращательное движение. Вращательное движение тел наиболее распространено используется в технике. Рассмотрим его сущность и сначала сформулируем его определение.

Вращательным движением твердого тела называется такое движение, при котором все точки тела движутся по кругам, центры которых лежат на одной прямой, которая называется осью вращения.

Ось вращения может находиться, как внутри самого тела, так и быть снаружи его.

Для того, чтобы осуществить вращательное движение твердого тела, необходимо закрепить неподвижно две любые точки этого тела, например, в подшипниках, тогда прямая, проходящая через все точки будет осью вращения и будет оставаться при вращении тела неподвижной.

Определим положение тела, вращающегося вокруг неподвижной оси.

Представим твердое тело, вращающееся вокруг неподвижной оси z (рис. 2.12).

Проведем через ось вращения z две полуплоскости, одна из которых есть
неподвижной полуплоскостью, а вторая полуплоскость неизменно сопряжена с
телом и вращается вместе с ним. Тогда положение тела в любой момент времени t однозначно определяется двугранным углом φ между полуплоскостями и , взятыми с соответствующим знаком, называется углом поворота тела φ.

При вращении тела вокруг неподвижной оси z угол поворота φ является непрерывной и однозначной функцией времени:

Выражение называется законом вращательного движения тела или кинематическим уравнением вращательного движения.

Если есть эта функция, то положение тела будет полностью определено. То есть каждому значению параметра времени t имеем в соответствии только единую величину угла φ.

Угол поворота φ тела вокруг неподвижной оси имеет знак. Так, угол φ будет
положительным (φ > 0), если смотреть с положительного конца оси z видеть вращения
подвижной плоскости в направлении против часовой стрелки. И наоборот, будет отрицательным (φ 0 , то тело в данный момент времени вращается в положительном направлении, и, наоборот, если ω 0), то вращение тела будет ускоренным, а если уменьшается (ε 2 . Определить угловую скорость вала в конце 15 секунды. Определить также, сколько оборотов сделает вал за эти 15 секунд.

Решение.

По условию примера угловое ускорение вала есть постоянная положительная
величина, а потому его вращательное движение будет равноускоренным. Для
определения угловой скорости ω и угла поворота φ вала можно воспользоваться выражениями соответственно, используемые при рассмотрении равноускоренного движения:

Следует сразу заметить, что, поскольку вал начинает вращаться из состояния покоя, то его начальная угловая скорость равна нулю. Начальный угол поворота равен нулю, поскольку совмещаем начало отсчета угла поворота с началом движения. То есть:

Подставим дальше в выражение для угловой скорости значение углового ускорения ε и времени t₁ = 15 c. Тогда угловая скорость ω после пятнадцатой секунды будет равна:

Подставим в выражение для угла поворота φ вала известные величины, получаем его значение за 15 секунд:

Для нахождения общего числа оборотов вала воспользуемся таким выражением:

Отсюда число оборотов N вала за 15 с равно:

Кинематические характеристики точек тела, вращающегося вокруг неподвижной оси

Кроме общих кинематических характеристик вращающегося тела вокруг неподвижной оси — угловой скорости ω и углового ускорения ε — рассмотрим кинематические характеристики отдельных точек вращающегося тела. К этим характеристикам относятся линейные или круговые скорости точек и линейные или круговые ускорения точек тела.

Линейная скорость

Рассмотрим тело, вращающееся вокруг неподвижной оси z (рис. 2.13). Направление вращения показано стрелкой. Выберем в теле любую точку M, которая размещается на расстоянии R от оси вращения z. при вращении тела точка M описывает окружность радиуса R, плоскость которого перпендикулярна оси z вращения, а центр C расположен на самой оси z.

За некоторый промежуток времени dt происходит элементарный поворот тела на угол dφ, при этом точка M осуществит вдоль своей траектории перемещение в положение M₁ на такую величину:

Определим линейную скорость точки M. По известному выражению она будет равняться

= ωR.

Эта скорость носит название линейной или круговой скорости точки, принадлежит телу, которое вращается вокруг неподвижной оси.

Таким образом, линейная скорость точки твердого тела, вращается вокруг неподвижной оси, численно равна произведению угловой скорости тела на радиус вращения (расстояние от данной точки до оси вращения).

Направление вектора линейной скорости — по касательной в круг (перпендикулярно радиусу вращения), которое описывается точкой М во время движения и всегда направлено в сторону вращения.

Поскольку для всех точек тела угловая скорость ω в данный момент времени имеет одно и то же значение, то линейные скорости точек тела, которое вращается, пропорциональные их расстояниям до оси вращения.

Если есть тело, вращающееся вокруг оси, перпендикулярной плоскости рисунка, то для диаметра KL будет иметь место эпюра распределения скоростей точек, которая имеет линейный характер (рис. 2.14).

Линейное ускорение

Определим далее ускорение точки М, принадлежащее телу, которое вращается вокруг неподвижной оси (см. рис. 2.14). Для этого можно воспользоваться полученными ранее уравнениями, а именно:

В данном случае ρ = R, тогда, подставляя значения, будем иметь значение крутящего, касательного ускорения

и центростремительного, нормального ускорения

Направления векторов полученных составляющих ускорений будут направлены так. Касательное ускорение всегда направлено по касательной к траектории движения точки M, то есть перпендикулярно радиусу R. Причем, если вращение тела будет ускоренным, то направление будет в сторону вектора скорости , если замедленное — то против. Нормальное ускорение всегда положительное и его вектор направлен к центру окружности, по которой движется точка M.

Определим полное ускорение a точки M. Оно будет равняться геометрической сумме составляющих касательного a и нормального a_n ускорений. По модулю это ускорение равно:

Определим направление вектора полного ускорения , для этого рассмотрим движение материальной точки M по кругу с угловой скоростью ω и угловым ускорением ε, что осуществляется в плоскости рисунка, направления которых показаны на рис. 2.15. Покажем направления векторов касательного , нормального и полного ускорений. Тогда отклонения вектора полного ускорения от нормали n к траектории движения точки определяется углом φ, который может быть вычислен по такому выражению:

Следует заметить, что поскольку угловая скорость ω и угловое ускорение ε имеют в данный момент времени для всего тела одно и то же значение, то из выражений для полного ускорения и для угла отклонение φ следует, что ускорение всех точек вращающегося тела вокруг неподвижной оси, пропорциональные их расстояниям от оси вращения и образуют одинаковый угол φ с радиусами кругов, описывающих различные точки тела, который равен

не зависит от радиуса и в данный момент одинаков для всех точек тела.

Безусловно, что линейные скорости и линейные ускорения точек, расположены на оси вращения, равны нулю.

Векторы угловой скорости и углового ускорения вращающегося тела

Угловую скорость ω вращающегося тела можно представить как вектор.

Вектор угловой скорости вращающегося тела расположен на оси вращения и направлен так, что, смотря на него с конца, можно видеть вращения тела против направления движения часовой стрелки.

Это так называемое «правило буравчика».

Угловое ускорение ε вращающегося тела можно представить как вектор.

Вектор углового ускорения вращающегося тела расположен на оси вращения и направлен в ту же сторону, что и вектор угловой скорости если вращение ускоренное, и в направлении, которое противоположно направлению вектора угловой скорости, если вращение замедлено.

Если рассматривать различные случаи вращения твердого тела вокруг неподвижной оси и разное их использование, то направления векторов и будут такими, как показано на (рис. 2.16).

Как видим, могут быть два варианта, когда векторы угловой скорости и направлены в одну сторону (рис. 2.16 а), или указанные векторы, которые направленные в разные стороны (рис. 2.16 б). Направления вращения тела показаны стрелками.

Векторы угловой скорости и углового ускорения являются векторами скользящими, а это значит, что за их начало можно взять любые точки тела, расположенные на оси оборота.

Задание векторов и полностью характеризует и определяет вращательное движение тела, направление вращения, а также численные значения угловой скорости и углового ускорения, учитывая длину векторов и масштабные коэффициенты.

Векторное выражение линейной скорости точки тела, вращающегося вокруг неподвижной оси

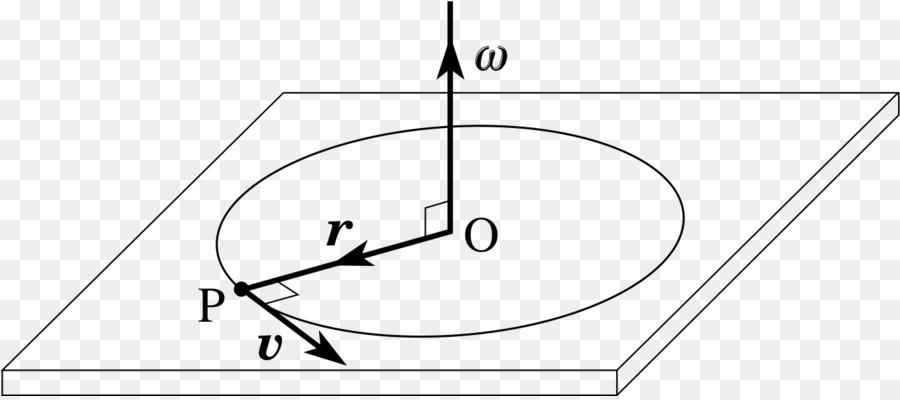
Линейную скорость точки вращающегося тела можно представить в виде векторного произведения. Докажем это.

Представляем тело, вращающееся вокруг неподвижной оси z в направлении, что показано стрелкой (рис. 2.17). Возьмем в теле произвольную точку M и покажем траекторию ее движения и радиус R. Покажем далее на оси вращения z с любой произвольной точки O вектор угловой скорости и с этой же точки проведем радиус — вектор , который определяет положение данной точки M тела.

Общеизвестно, что векторным произведением двух векторов и , угол между которыми составляет α есть третий вектор ( = х ), модуль которого равен:

Направлен этот вектор перпендикулярно плоскости, в которой расположены векторы и , в сторону, откуда кратчайший поворот от вектора к вектору происходит против направления хода часовой стрелки.

Теперь определим модуль линейной скорости точки М. На основании формулы будем иметь:

= ωR.

Из схемы рис. 2.17 видим, что

= ω · R = ω · rsinα,

где — радиус-вектор точки М относительно центра О; α — угол между векторами и .

Если сравнить предыдущее выражение с векторным произведением двух векторов, то по модулю имеем третий вектор, которым и является вектор .

Покажем направление вектора линейной скорости точки M, который будет расположен на касательной к окружности, образованное траекторией движения точки M, или по перпендикуляру к плоскости треугольника OMC.

Далее определим модуль векторного произведения х :

| х | = ω rsinα.

Направление векторного произведения, как результирующего вектора, показанный
на рис. 2.17, он также перпендикулярен плоскости ΔОМС. Из этого можно сделать вывод, что не только совпадают модули линейной скорости и векторного произведения, но совпадают и их направления. Отсюда:

= х .

Таким образом, линейная скорость любой точки тела, вращается вокруг неподвижной оси, равна векторному произведению двух векторов: угловой скорости и радиус-вектора этой точки относительно произвольной точки оси вращения.

Определим линейную скорость точки M тела, ось вращения которого произвольно расположена в пространстве относительно декартовой системы отсчета Oxyz (рис. 2.18). Координаты точки M — x, y, z, проекции вектора угловой скорости — ω_x ω_y ω_z; проекции радиус-вектора — такие же координаты x, y, z.

Выразим линейную скорость с помощью определителя векторного произведения:

Как известно, вектор можно записать через его проекции:

Тогда, сравнивая последние два выражения, проекции линейной скорости на оси координат равны:

Выражения получены Эйлером в 1765 г.

Для случая на рис. 2.17:

откуда, пользуясь выражением, будем иметь:

Пример:

Вращения маховика двигателя в пусковой период определяется уравнением , где t — в секундах, φ — в радианах. Определить модуль и направление ускорения точки, расположенной на расстоянии 50 см от оси вращения, в момент, когда ее скорость равна ₁ = 8 м/с .

Решение.

Для определения ускорения движения материальной точки можно использовать выражение:

Угловые скорость и ускорение движения маховика двигателя определим использовав выражения:

Определим момент времени, в который нужно определить ускорение точки. Для этого, на основании предыдущего выражения, определим угловую скорость вращения маховика:

Поскольку определена ранее угловая скорость равна ω = t 2 , то можем определить время t₁:

В определенное выше угловое ускорение, равное ε = 2t, подставим значение времени t₁, получим его значение

Подставим окончательно значение ω₁ и ε₁ в выражение для полного ускорения, получим искомый результат

Направление вектора определим по выражению:

где φ — угол между радиусом вращения и вектором ускорения .

Векторное выражение нормального и тангенциального ускорений

Для определения векторного выражения линейной скорости произвольной точки тела, вращающейся вокруг неподвижной оси, составим расчетную схему (рис. 2.19). Также, как и в случае векторного выражения линейной скорости точки тела, рассматриваем произвольную точку M на теле, которое вращается вокруг неподвижной оси z. Направление вращения тела показано стрелкой. Точка M движется по траектории, созданной кругом с центром С, расположенным на оси вращения z и радиусом R. С любой точки O на оси вращения z проведен к точке M радиус — вектор . Поскольку вращения тела вокруг оси z является ускоренным, то с точки O отложены векторы угловой скорости и углового ускорения . С точкой M связан вектор линейной скорости , который направлен по касательной, проведенной через точку M в круг, образованного траекторией ее движения. На этой же касательной показан вектор касательной составляющей линейного ускорения точки M, направленный в ту же сторону, что и вектор . Вдоль радиуса R окружности, описываемой траекторией движения точки M, показанный
вектор — нормальной составляющей линейного ускорения.

Для получения векторных формул нормального и тангенциального ускорений возьмем производную по времени от выражения выше, подставляя в него выражение:

Анализируя выражение и рассматривая рис. 2.19, можно записать, что — вектор углового ускорения, который направляется аналогично вектора угловой скорости , а — вектор линейной скорости.

Подставим последние значения в выражение, получим

= х + х = х + х ( х ).

Выражение называют формулой Ривальса.

Проведем анализ выражения.

Модуль первого векторного произведения будет равен:

| х | = εr sin α.

Модуль тангенциального ускорения будет равен:

a = εR = εr sin α.

Как видно из последних выражений совпадают не только их модули, но и направления (┴ΔОМС), поэтому

= х .

Тангенциальное ускорение точки твердого тела, вращающегося вокруг неподвижной оси, равно векторному произведению вектора углового ускорение на радиус-вектор этой точки относительно произвольной точки оси вращения.

Модуль нормального ускорения будет равен:

a_n = ω 2 R = ω .

Модуль векторного произведения | х | = поскольку

Сопоставляя значения модулей векторов , х и их направления, можно сделать вывод, что

= х = х ( х ).

Нормальное ускорение точки твердого тела, вращающегося вокруг неподвижной оси, равно векторному произведению вектора угловой скорости на вектор линейной скорости этой точки.

Передача вращательного движения

Передача вращательного движения осуществляется с помощью зубчатых, ременных, цепных передач, колес трения и т. д.

Рассмотрим передачу вращательного движения с помощью зубчатой передачи (или фрикционной передачи) (рис. 2.20), которая состоит из двух колес, вращающихся вокруг неподвижных осей. Назовем первое колесо (меньшего диаметра) ведущим. Направление его вращения показано стрелкой. Оно имеет такие физические и кинематические параметры: радиус — r₁, количество зубов — z₁, угловая скорость — ω₁ или частота вращения — n₁. Второе колесо, которое является ведомым, имеет следующие параметры: радиус — r₂, количество зубов — z₂, угловая скорость — ω₂ или частота вращения — n₂. Направление вращения второго колеса также показано стрелкой.

Теперь, если передача вращательного движения осуществляется без проскальзывания в месте контакта колес, то линейная скорость точки контакта (точка А), которая принадлежит одновременно двум колесам, должна быть одинаковой. Найдем линейные скорости точки A начала для первого колеса, а затем для второго колеса и приравняем их. Линейная скорость точки А для первого колеса равна:

_А = ω₁ · r₁ ,

а линейная скорость точки А для второго колеса будет равна:

_А = ω₂ · r₂ .

Приравняв выражения, будем иметь:

Преобразуем выражение следующим образом:

= .

Если считать, что передаточное отношение, это = u, то можно окончательно написать:

Таким образом, передаточное отношение, это отношение угловой скорости ведущего колеса к угловой скорости ведомого колеса, которое равно отношению радиуса (или числа зубьев) ведомого колеса к радиусу ведущего колеса.

В технике есть такое понятие, как передаточное число.

Передаточное число —это отношение большей угловой скорости до меньшей.

Указанные основные положения о передаче вращательного движения между двумя колесами полностью пригодны для определения передаточного отношения для ременной или цепной передач. На рис. 2.21 показана схема ременной (цепной) передачи с указанием физических и кинематических параметров. Для определения передаточного отношения этой передачи необходимо использовать выражение (2.64).

Передаточное отношение может быть больше единицы или меньше.

Если передача вращательного движения осуществляется с помощью, так называемой червячной передачи (рис. 2.22), то передаточное отношение определяется формулой:

где z_k — число зубьев червячного колеса; h — число заходов червяка.

Услуги по теоретической механике:

Учебные лекции:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Вращательное движение твердого тела: уравнение, формулы

В природе и технике мы часто сталкиваемся с проявлением вращательного движения твердых тел, например, валов и шестерен. Как в физике описывают этот тип движения, какие формулы и уравнения для этого применяются, эти и другие вопросы освещаются в данной статье.

Что такое вращение?

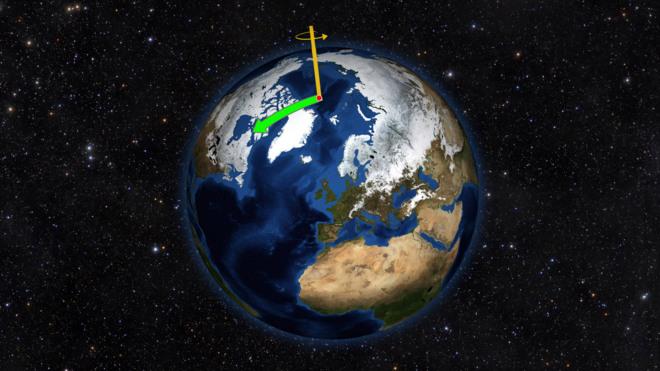
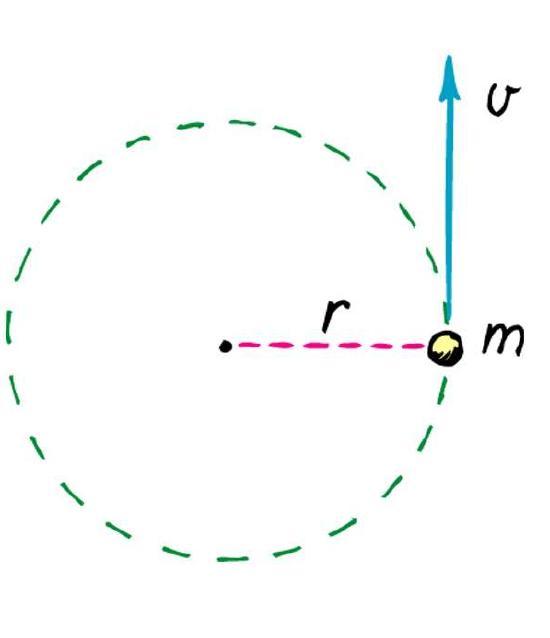
Каждый из нас интуитивно представляет, о каком движении пойдет речь. Вращение — это процесс, при котором тело или материальная точка движется по круговой траектории вокруг некоторой оси. С геометрической точки зрения ось вращения твердого тела — это прямая, расстояние до которой в процессе перемещения остается неизменным. Это расстояние называют радиусом вращения. Далее будем обозначать его буквой r. Если ось вращения проходит через центр масс тела, то ее называют собственной осью. Примером вращения вокруг собственной оси является соответствующее движение планет Солнечной системы.

Вам будет интересно: Афронт — это ситуация, в которой не хочется оказаться

Чтобы вращение происходило, должно существовать центростремительное ускорение, которое возникает за счет центростремительной силы. Эта сила направлена от центра масс тела к оси вращения. Природа центростремительной силы может быть самой разной. Так, в космическом масштабе ее роль выполняет гравитация, если тело закреплено нитью, то сила натяжения последней будет центростремительной. Когда тело вращается вокруг собственной оси, роль центростремительной силы играет внутреннее электрохимическое взаимодействие между составляющими тело элементами (молекулами, атомами).

Вам будет интересно: Декабрист Оболенский Евгений Петрович: биография. Декабристские организации

Необходимо понимать, что без присутствия центростремительной силы тело будет двигаться прямолинейно.

Описывающие вращение физические величины

Во-первых, это динамические характеристики. К ним относятся:

• момент импульса L;
• момент инерции I;
• момент силы M.

Во-вторых, это кинематические характеристики. Перечислим их:

• угол поворота θ;
• скорость угловая ω;
• ускорение угловое α.

Кратко опишем каждую из названных величин.

Момент импульса определяется по формуле:

Где p — линейный импульс, m — масса материальной точки, v — ее линейная скорость.

Момент инерции материальной точки рассчитывается с помощью выражения:

Для любого тела сложной формы величина I рассчитывается, как интегральная сумма моментов инерции материальных точек.

Момент силы M вычисляется так:

Здесь F — внешняя сила, d — расстояние от точки ее приложения до оси вращения.

Физический смысл всех величин, в названии которых присутствует слово «момент», аналогично смыслу соответствующих линейных величин. Например, момент силы показывает возможность приложенной силы сообщить угловое ускорение системе вращающихся тел.

Кинематические характеристики математически определяются следующими формулами:

Как видно из этих выражений, угловые характеристики аналогичны по своему смыслу линейным (скорости v и ускорению a), только они применимы для круговой траектории.

Динамика вращения

В физике изучение вращательного движения твердого тела осуществляется с помощью двух разделов механики: динамики и кинематики. Начнем с динамики.

Динамика изучает внешние силы, действующие на систему вращающихся тел. Сразу запишем уравнение вращательного движения твердого тела, а затем, разберем его составные части. Итак, это уравнение имеет вид:

Момент силы, который действует на систему, обладающую моментом инерции I, вызывает появление углового ускорения α. Чем меньше величина I, тем легче с помощью определенного момента M раскрутить систему до больших скоростей за малые промежутки времени. Например, металлический стержень легче вращать вдоль его оси, чем перпендикулярно ей. Однако, тот же стержень легче вращать вокруг оси, перпендикулярной ему, и проходящей через центр масс, чем через его конец.

Закон сохранения величины L

Выше была введена эта величина, она называется моментом импульса. Уравнение вращательного движения твердого тела, представленное в предыдущем пункте, часто записывают в иной форме:

Если момент внешних сил M действует на систему в течение времени dt, то он вызывает изменение момента импульса системы на величину dL. Соответственно, если момент сил равен нулю, тогда L = const. Это и есть закон сохранения величины L. Для нее, используя связь между линейной и угловой скоростью, можно записать:

L = m*v*r = m*ω*r2 = I*ω.

Таким образом, при отсутствии момента сил произведение угловой скорости и момента инерции является постоянной величиной. Этот физический закон используют фигуристы в своих выступлениях или искусственные спутники, которые необходимо повернуть вокруг собственной оси в открытом космосе.

Центростремительное ускорение

Выше, при изучении вращательного движения твердого тела, уже была описана эта величина. Также была отмечена природа центростремительных сил. Здесь лишь дополним эту информацию и приведем соответствующие формулы для расчета этого ускорения. Обозначим его ac.

Поскольку центростремительная сила направлена перпендикулярно оси и проходит через нее, то момента она не создает. То есть эта сила не оказывает совершенно никакого влияния на кинематические характеристики вращения. Тем не менее, она создает центростремительное ускорение. Приведем две формулы для его определения:

Таким образом, чем больше угловая скорость и радиус, тем большую силу следует приложить, чтобы удержать тело на круговой траектории. Ярким примером этого физического процесса является занос автомобиля во время поворота. Занос возникает, если центростремительная сила, роль которой играет сила трения, становится меньше, чем центробежная сила (инерционная характеристика).

Кинематика вращения

Три основные кинематические характеристики были перечислены выше в статье. Кинематика вращательного движения твердого тела формулами следующими описывается:

θ = ω*t => ω = const., α = 0;

θ = ω0*t + α*t2/2 => ω = ω0 + α*t, α = const.

В первой строке приведены формулы для равномерного вращения, которое предполагает отсутствие внешнего момента сил, действующего на систему. Во второй строке записаны формулы для равноускоренного движения по окружности.

Отметим, что вращение может происходить не только с положительным ускорением, но и с отрицательным. В этом случае в формулах второй строки следует перед вторым слагаемым поставить знак минус.

Пример решения задачи

На металлический вал в течение 10 секунд действовал момент силы 1000 Н*м. Зная, что момент инерции вала равен 50 кг*м2, необходимо определить угловую скорость, которую придал валу упомянутый момент силы.

Применяя основное уравнение вращения, вычислим ускорение вала:

Поскольку это угловое ускорение действовало на вал в течение времени t = 10 секунд, то для вычисления угловой скорости применяем формулу равноускоренного движения:

Здесь ω0 = 0 (вал не вращался до действия момента сил M).

Подставляем в равенство численные значения величин, получаем:

ω = 1000/50*10 = 200 рад/с.

Чтобы это число перевести в привычные обороты в секунду, необходимо его поделить на 2*pi. Выполнив это действие, получаем, что вал будет вращаться с частотой 31,8 об./с.