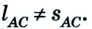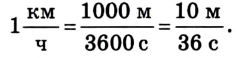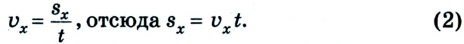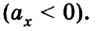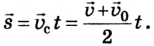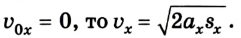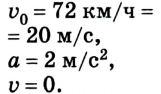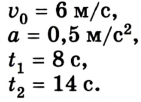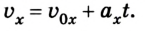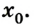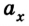Кинематика
Механика — это раздел физики, изучающий механическое движение тел.
Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.
Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если
- расстояние, которое проходит тело, много больше его размера;
- расстояние от данного тела до другого тела много больше его размера;
- тело движется поступательно.
Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.
Важно!
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.
Основная задача механики — определить положение тела в пространстве в любой момент времени.
Механическое движение и его виды
Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение может быть:
1. по характеру движения
- поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
- вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
- колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;
2. по виду траектории
- прямолинейным — это движение, траектория которого прямая линия;
- криволинейным — это движение, траектория которого кривая линия;
- равномерным — движение, при котором скорость тела с течением времени не изменяется;
- неравномерным — это движение, при котором скорость тела с течением времени изменяется;
- равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
- равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.
Относительность механического движения
Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.
Правило сложения перемещений
Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:
где \( S \) — перемещение тела относительно неподвижной системы отсчета;
\( S_1 \) — перемещение тела относительно подвижной системы отсчета;
\( S_2 \) — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.
Правило сложения скоростей
Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:
где \( v \) — скорость тела относительно неподвижной системы отсчета;
\( v_1 \) — скорость тела относительно подвижной системы отсчета;
\( v_2 \) — скорость подвижной системы отсчета относительно неподвижной системы отсчета.
Относительная скорость
Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.
Пусть \( v_1 \) — скорость первого тела, а \( v_2 \) — скорость второго тела.
Определим скорость первого тела относительно второго \( v_ <12>\) :
Определим скорость второго тела относительно первого \( v_ <21>\) :
Следует помнить, что траектория движения тела и пройденный путь тоже относительны.
Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:
Если скорости направлены под углом \( \alpha \) друг к другу, то относительная скорость рассчитывается по теореме косинусов:
Скорость
Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.
Обозначение — \( v \) , единицы измерения — м/с (км/ч).
Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:
Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:
Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.
Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.
Ускорение
Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.
Обозначение — \( a \) , единица измерения — м/с 2 .
В векторном виде:
где \( v \) – конечная скорость; \( v_0 \) – начальная скорость;
\( t \) – промежуток времени, за который произошло изменение скорости.
В проекциях на ось ОХ:
где \( a_n \) – нормальное ускорение, \( a_ <\tau>\) – тангенциальное ускорение.
Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:
Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:
Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.
Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если \( a_ <\tau>\) ≠ 0, \( a_n \) = 0, то тело движется по прямой;
если \( a_ <\tau>\) = 0, \( a_n \) = 0, \( v \) ≠ 0, то тело движется равномерно по прямой;
если \( a_ <\tau>\) = 0, \( a_n \) ≠ 0, тело движется равномерно по кривой;
если \( a_ <\tau>\) = 0, \( a_n \) = const, то тело движется равномерно по окружности;
если \( a_ <\tau>\) ≠ 0, \( a_n \) ≠ 0, то тело движется неравномерно по окружности.
Равномерное движение
Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.
Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:
Проекция вектора скорости на ось ОХ:
Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:
График скорости (проекции скорости)
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью \( t \) , тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью \( t \) , тело движется против оси ОХ.
Перемещение при равномерном движении – это величина, равная произведению скорости на время:
Проекция вектора перемещения на ось ОХ:
График перемещения (проекции перемещения)
График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:
График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью \( t \) , тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью \( t \) , тело движется против оси ОХ.
По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время \( t \) . Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Координата тела при равномерном движении рассчитывается по формуле:
График координаты представляет собой зависимость координаты от времени: \( x=x(t) \) .
График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:
График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:
Прямолинейное равноускоренное движение
Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:
При движении с ускорением скорость может как увеличиваться, так и уменьшаться.
Скорость тела при равноускоренном движении рассчитывается по формуле:
При разгоне (в проекциях на ось ОХ):
При торможении (в проекциях на ось ОХ):
График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:
График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, \( a_x \) > 0.
График 2 лежит под осью t, тело тормозит, \( a_x \) \( v_ <0x>\) > 0, \( a_x \) > 0.
График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, \( v_ <0x>\) > 0, \( a_x \) \( v_ <0x>\) \( a_x \) \( t_2-t_1 \) . Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Перемещение при равноускоренном движении рассчитывается по формулам:
Перемещение в \( n \) -ую секунду при равноускоренном движении рассчитывается по формуле:
Координата тела при равноускоренном движении рассчитывается по формуле:
Свободное падение (ускорение свободного падения)
Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.
Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).
Обозначение – \( g \) , единицы измерения – м/с 2 .
Важно! \( g \) = 9,8 м/с 2 , но при решении задач считается, что \( g \) = 10 м/с 2 .
Движение тела по вертикали
Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:
Если тело падает вниз без начальной скорости, то \( v_0 \) = 0.
Время падения рассчитывается по формуле:
Тело брошено вверх:
Если брошенное вверх тело достигло максимальной высоты, то \( v \) = 0.
Время подъема рассчитывается по формуле:
Движение тела, брошенного горизонтально
Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали со скоростью \( v_0=v_ <0x>\) ;
- равноускоренного движения по вертикали с ускорением свободного падения \( g \) и без начальной скорости \( v_<0y>=0 \) .
Скорость тела в любой момент времени:
Угол между вектором скорости и осью ОХ:
Движение тела, брошенного под углом к горизонту (баллистическое движение)
Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали;
- равноускоренного движения по вертикали с ускорением свободного падения.
Скорость тела в любой момент времени:
Угол между вектором скорости и осью ОХ:
Время подъема на максимальную высоту:
Максимальная высота подъема:
Максимальная дальность полета:
Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость \( v_0 \) , с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол \( \alpha \) , под которым тело брошено, будет равен углу, под которым оно упадет.
При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:
Это облегчает решение задач:
Движение по окружности с постоянной по модулю скоростью
Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.
Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.
Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – \( a_ <цс>\) , единицы измерения – м/с 2 .
Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – \( T \) , единицы измерения – с.
где \( N \) – количество оборотов, \( t \) – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – \( \nu \) , единицы измерения – с –1 (Гц).
Период и частота – взаимно обратные величины:
Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – \( v \) , единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:
Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – \( \omega \) , единицы измерения – рад/с .
Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:
Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:
Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:
Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью \( v_1 \) , и все точки обода колеса движутся относительно его центра с такой же линейной скоростью \( v_1 \) , то относительно дороги мгновенная скорость разных точек колеса различна.
Мгновенная скорость нижней точки \( (m) \) равна нулю, мгновенная скорость в верхней точке \( (n) \) равна удвоенной скорости \( v_1 \) , мгновенная скорость точки \( (p) \) , лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке \( (c) \) – по теореме косинусов.
Кинематическое уравнение движения для пути и скорости
лЙОЕНБФЙЛБ ЙЪХЮБЕФ ТБЪМЙЮОЩЕ НЕИБОЙЮЕУЛЙЕ ДЧЙЦЕОЙС ФЕМ ВЕЪ ТБУУНПФТЕОЙС РТЙЮЙО ЧЩЪЩЧБАЭЙИ ЬФЙ ДЧЙЦЕОЙС.
1.1.1 лЙОЕНБФЙЛБ РПУФХРБФЕМШОПЗП ДЧЙЦЕОЙС
рТЙ РПУФХРБФЕМШОПН ДЧЙЦЕОЙЙ ФЕМБ ЧУЕ ФПЮЛЙ ФЕМБ ДЧЙЦХФУС ПДЙОБЛПЧП, Й, ЧНЕУФП ФПЗП ЮФПВЩ ТБУУНБФТЙЧБФШ ДЧЙЦЕОЙЕ ЛБЦДПК ФПЮЛЙ ФЕМБ, НПЦОП ТБУУНБФТЙЧБФШ ДЧЙЦЕОЙЕ ФПМШЛП ПДОПК ЕЗП ФПЮЛЙ.
пУОПЧОЩЕ ИБТБЛФЕТЙУФЙЛЙ ДЧЙЦЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ: ФТБЕЛФПТЙС ДЧЙЦЕОЙС, РЕТЕНЕЭЕОЙЕ ФПЮЛЙ, РТПКДЕООЩК ЕА РХФШ, ЛППТДЙОБФЩ, УЛПТПУФШ Й ХУЛПТЕОЙЕ.
мЙОЙА, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ Ч РТПУФТБОУФЧЕ, ОБЪЩЧБАФ ФТБЕЛФПТЙЕК.
рЕТЕНЕЭЕОЙЕН НБФЕТЙБМШОПК ФПЮЛЙ ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ОБЪЩЧБЕФУС ЧЕЛФПТ РЕТЕНЕЭЕОЙС ∆r=r-r0, ОБРТБЧМЕООЩК ПФ РПМПЦЕОЙС ФПЮЛЙ Ч ОБЮБМШОЩК НПНЕОФ ЧТЕНЕОЙ Л ЕЕ РПМПЦЕОЙА Ч ЛПОЕЮОЩК НПНЕОФ.
уЛПТПУФШ НБФЕТЙБМШОПК ФПЮЛЙ РТЕДУФБЧМСЕФ УПВПК ЧЕЛФПТ, ИБТБЛФЕТЙЪХАЭЙК ОБРТБЧМЕОЙЕ Й ВЩУФТПФХ РЕТЕНЕЭЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ ПФОПУЙФЕМШОП ФЕМБ ПФУЮЕФБ. чЕЛФПТ ХУЛПТЕОЙС ИБТБЛФЕТЙЪХЕФ ВЩУФТПФХ Й ОБРТБЧМЕОЙЕ ЙЪНЕОЕОЙС УЛПТПУФЙ НБФЕТЙБМШОПК ФПЮЛЙ ПФОПУЙФЕМШОП ФЕМБ ПФУЮЕФБ.
1.1.2 тБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ
тБЧОПНЕТОЩН РТСНПМЙОЕКОЩН ДЧЙЦЕОЙЕН ОБЪЩЧБЕФУС ФБЛПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ, РТЙ ЛПФПТПН НБФЕТЙБМШОБС ФПЮЛБ (ФЕМП) ДЧЙЦЕФУС РП РТСНПК Й Ч МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ УПЧЕТЫБЕФ ПДЙОБЛПЧЩЕ РЕТЕНЕЭЕОЙС.
чЕЛФПТ УЛПТПУФЙ ТБЧОПНЕТОПЗП РТСНПМЙОЕКОПЗП ДЧЙЦЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ ОБРТБЧМЕО ЧДПМШ ЕЕ ФТБЕЛФПТЙЙ Ч УФПТПОХ ДЧЙЦЕОЙС. чЕЛФПТ УЛПТПУФЙ РТЙ ТБЧОПНЕТОПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ ТБЧЕО ЧЕЛФПТХ РЕТЕНЕЭЕОЙС ЪБ МАВПК РТПНЕЦХФПЛ ЧТЕНЕОЙ, РПДЕМЕООПНХ ОБ ЬФПФ РТПНЕЦХФПЛ ЧТЕНЕОЙ:
рТЙНЕН МЙОЙА, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ, ЪБ ПУШ ЛППТДЙОБФ пи, РТЙЮЕН ЪБ РПМПЦЙФЕМШОПЕ ОБРТБЧМЕОЙЕ ПУЙ ЧЩВЕТЕН ОБРТБЧМЕОЙЕ ДЧЙЦЕОЙС ФПЮЛЙ. фПЗДБ, УРТПЕГЙТПЧБЧ ЧЕЛФПТЩ r Й v, ОБ ЬФХ ПУШ, ДМС РТПЕЛГЙК ∆rx = |∆r| Й ∆vx = |∆v| ЬФЙИ ЧЕЛФПТПЧ НЩ НПЦЕН ЪБРЙУБФШ:

ф.Л. РТЙ ТБЧОПНЕТОПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ S = |∆r|, НПЦЕН ЪБРЙУБФШ: Sx = vx · t. фПЗДБ ДМС ЛППТДЙОБФЩ ФЕМБ Ч МАВПК НПНЕОФ ЧТЕНЕОЙ ЙНЕЕН:
ЗДЕ И0 — ЛППТДЙОБФБ ФЕМБ Ч ОБЮБМШОЩК НПНЕОФ t = 0.
рТЙНЕТ 1. хТБЧОЕОЙЕ ДЧЙЦЕОЙС ФЕМБ ДБОП Ч ЧЙДЕ И = 4 — 3t. пРТЕДЕМЙФШ ОБЮБМШОХА ЛППТДЙОБФХ ФЕМБ, УЛПТПУФШ ДЧЙЦЕОЙС Й РЕТЕНЕЭЕОЙС ФЕМБ ЪБ 2 УЕЛХОДЩ.
тЕЫЕОЙЕ: уТБЧОЙН ДБООПЕ ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ФЕМБ У ХТБЧОЕОЙЕН ДЧЙЦЕОЙС Ч ПВЭЕН ЧЙДЕ: И = И0 + vx t Й И = 4 — 3t.
пЮЕЧЙДОП, ЮФП И0 = 4Н, vx = — 3Н/У (ЪОБЛ «-» ПЪОБЮБЕФ, ЮФП ОБРТБЧМЕОЙЕ УЛПТПУФЙ ОЕ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ПУЙ пи, Ф.Е. ПОЙ РТПФЙЧПРПМПЦОП ОБРТБЧМЕОЩ). рЕТЕНЕЭЕОЙЕ ФЕМБ ОБКДЕН РП ЖПТНХМЕ: S = И — И0. лПОЕЮОХА ЛППТДЙОБФХ И НПЦОП ПРТЕДЕМЙФШ, РПДУФБЧМСС Ч ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ЧТЕНС t1: И = 4 — 3t1. ч ПВЭЕН ЧЙДЕ ЖПТНХМБ РЕТЕНЕЭЕОЙС: S = 4 — 3t1 — И0 = 4 — 3t1 — 4 = — 3t1 = -3 · 2 = — 6 Н (фЕМП ДЧЙЦЕФУС Ч ПФТЙГБФЕМШОПН ОБРТБЧМЕОЙЙ ПУЙ пи).
рТЙНЕТ 2.мПДПЮОЙЛ РЕТЕЧПЪЙФ РБУУБЦЙТПЧ У ПДОПЗП ВЕТЕЗБ ОБ ДТХЗПК ЪБ ЧТЕНС t =10 НЙО. РП ФТБЕЛФПТЙЙ бч. уЛПТПУФШ ФЕЮЕОЙС ТЕЛЙ vТ = 0,3 Н/У, ЫЙТЙОБ ТЕЛЙ 240 Н. у ЛБЛПК УЛПТПУФША v ПФОПУЙФЕМШОП ЧПДЩ Й РПД ЛБЛЙН ХЗМПН α Л ВЕТЕЗХ ДПМЦОБ ДЧЙЗБФШУС МПДЛБ, ЮФПВЩ ДПУФЙЮШ ДТХЗПЗП ВЕТЕЗБ ЪБ ХЛБЪБООПЕ ЧТЕНС?
t = 10 НЙО = 660 У.
v’ — ? α — ?

тЕЫЕОЙЕ: рТЙНЕН ВЕТЕЗ ЪБ ОЕРПДЧЙЦОХА УЙУФЕНХ ПФУЮЕФБ. фПЗДБ ПФОПУЙФЕМШОП ВЕТЕЗБ УЛПТПУФШ МПДЛЙ ТБЧОБ:
ьФБ УЛПТПУФШ (ТЙУХОПЛ 1.1), СЧМСЕФУС УХННПК ДЧХИ УЛПТПУФЕК: УЛПТПУФЙ МПДЛЙ ПФОПУЙФЕМШОП ЧПДЩ v’ (УЛПТПУФЙ ПФОПУЙФЕМШОП РПДЧЙЦОПК УЙУФЕНЩ ПФУЮЕФБ) Й УЛПТПУФЙ ТЕЛЙ vТ (УЛПТПУФЙ УБНПК РПДЧЙЦОПК УЙУФЕНЩ ПФУЮЕФБ ПФОПУЙФЕМШОП ОЕРПДЧЙЦОПК). рП ЪБЛПОХ УМПЦЕОЙС УЛПТПУФЕК: v =vТ + v’. фБЛ ЛБЛ РП ХУМПЧЙА ЪБДБЮЙ УЛПТПУФШ МПДЛЙ ПФОПУЙФЕМШОП ВЕТЕЗБ ОБРТБЧМЕОБ ЧДПМШ бч, Б УЛПТПУФШ ТЕЛЙ РЕТРЕОДЙЛХМСТОП бч, ФП УЛПТПУФШ МПДЛЙ ПФОПУЙФЕМШОП ЧПДЩ(РП ФЕПТЕНЕ рЙЖБЗПТБ):
йУЛПНЩК ХЗПМ НПЦОП ОБКФЙ ЙЪ ЧЩТБЦЕОЙС:

пФЧЕФ: v’ = 0.5 Н /У, α = arctg ≈ 53 0 .
1.1.3 оЕТБЧОПНЕТОПЕ ДЧЙЦЕОЙЕ
дЧЙЦЕОЙЕ, РТЙ ЛПФПТПН ЪБ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ФЕМП УПЧЕТЫБЕФ ОЕТБЧОЩЕ РЕТЕНЕЭЕОЙС ОБЪЩЧБАФ ОЕТБЧОПНЕТОЩН ЙМЙ РЕТЕНЕООЩН. уТЕДОЕК УЛПТПУФША vУТ ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА РЕТЕНЕЭЕОЙС ФЕМБ ∆r ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ЬФПНХ РТПНЕЦХФЛХ:
нПДХМШ УТЕДОЕК УЛПТПУФЙ ПРТЕДЕМСЕФУС ЛБЛ ПФОПЫЕОЙЕ РХФЙ ∆S, РТПКДЕООПЗП ФЕМПН ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ, Л ЬФПНХ РТПНЕЦХФЛХ:
оБРТБЧМЕОЙЕ ЧЕЛФПТБ УТЕДОЕК УЛПТПУФЙ vУТ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ∆r (ТЙУХОПЛ 1.2).
рТЙ ОЕПЗТБОЙЮЕООПН ХНЕОШЫЕОЙЙ ∆t, vУТ УФТЕНЙФУС Л РТЕДЕМШОПНХ ЪОБЮЕОЙА, ЛПФПТПЕ ОБЪЩЧБЕФУС НЗОПЧЕООПК УЛПТПУФША. йФБЛ, НЗОПЧЕООБС УЛПТПУФШ v ЕУФШ РТЕДЕМ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОСС УЛПТПУФШ vУТ, ЛПЗДБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ДЧЙЦЕОЙС УФТЕНЙФУС Л ОХМА:
йЪ ЛХТУБ НБФЕНБФЙЛЙ ЙЪЧЕУФОП, ЮФП РТЕДЕМ ПФОПЫЕОЙС РТЙТБЭЕОЙС ЖХОЛГЙЙ Л РТЙТБЭЕОЙА БТЗХНЕОФБ, ЛПЗДБ РПУМЕДОЙК УФТЕНЙФУС Л ОХМА РТЕДУФБЧМСЕФ УПВПК РЕТЧХА РТПЙЪЧПДОХА ЬФПК ЖХОЛГЙЙ РП ДБООПНХ БТЗХНЕОФХ. рПЬФПНХ:
нЗОПЧЕООБС УЛПТПУФШ v ЕУФШ ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС РЕТЧПК РТПЙЪЧПДОПК ТБДЙХУБ — ЧЕЛФПТБ ДЧЙЦХЭЕКУС ФПЮЛЙ РП ЧТЕНЕОЙ. фБЛ ЛБЛ УЕЛХЭБС Ч РТЕДЕМЕ УПЧРБДБЕФ У ЛБУБФЕМШОПК, ФП ЧЕЛФПТ УЛПТПУФЙ v ОБРТБЧМЕО РП ЛБУБФЕМШОПК Л ФТБЕЛФПТЙЙ Ч УФПТПОХ ДЧЙЦЕОЙС (ТЙУХОПЛ 1.2).
рП НЕТЕ ХНЕОШЫЕОЙЕ ∆t РХФШ ∆S ЧУЕ ВПМШЫЕ ВХДЕФ РТЙВМЙЦБФШУС Л |∆r|, РПЬФПНХ НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ:
фБЛЙН ПВТБЪПН, НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ v ТБЧЕО РЕТЧПК РТПЙЪЧПДОПК РХФЙ РП ЧТЕНЕОЙ :
рТЙ ОЕТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФЕМБ ЕЗП УЛПТПУФШ ОЕРТЕТЩЧОП ЙЪНЕОСЕФУС. лБЛ ВЩУФТП ЙЪНЕОСЕФУС УЛПТПУФШ ФЕМБ, РПЛБЪЩЧБЕФ ЧЕМЙЮЙОБ, ЛПФПТБС ОБЪЩЧБЕФУС ХУЛПТЕОЙЕН. уТЕДОЙН ХУЛПТЕОЙЕН ОЕТБЧОПНЕТОПЗП ДЧЙЦЕОЙС Ч ЙОФЕТЧБМЕ ПФ t ДП t + ∆t ОБЪЩЧБЕФУС ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА ЙЪНЕОЕОЙС УЛПТПУФЙ ∆v Л ЙОФЕТЧБМХ ЧТЕНЕОЙ ∆t:
нЗОПЧЕООЩН ХУЛПТЕОЙЕН Б Ч НПНЕОФ ЧТЕНЕОЙ t ВХДЕФ РТЕДЕМ УТЕДОЕЗП ХУЛПТЕОЙС:
фБЛЙН ПВТБЪПН, ХУЛПТЕОЙЕ ∆Б ЕУФШ ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС РЕТЧПК РТПЙЪЧПДОПК УЛПТПУФЙ РП ЧТЕНЕОЙ. ч ДБООПК УЙУФЕНЕ ПФУЮЕФБ ЧЕЛФПТ ХУЛПТЕОЙС НПЦЕФ ВЩФШ ЪБДБО РТПЕЛГЙСНЙ ОБ УППФЧЕФУФЧХАЭЙЕ ЛППТДЙОБФОЩЕ ПУЙ (РТПЕЛГЙСНЙ БИ, БХ, Бz).
уПУФБЧМСАЭБС Бτ ЧЕЛФПТБ ХУЛПТЕОЙС, ОБРТБЧМЕООБС ЧДПМШ ЛБУБФЕМШОПК Л ФТБЕЛФПТЙЙ Ч ДБООПК ФПЮЛЕ, ОБЪЩЧБЕФУС ФБОЗЕОГЙБМШОЩН (ЛБУБФЕМШОЩН) ХУЛПТЕОЙЕН. фБОЗЕОГЙБМШОПЕ ХУЛПТЕОЙЕ ИБТБЛФЕТЙЪХЕФ ЙЪНЕОЕОЙЕ ЧЕЛФПТБ УЛПТПУФЙ РП НПДХМА. чЕЛФПТ Бτ ОБРТБЧМЕО Ч УФПТПОХ ДЧЙЦЕОЙС ФПЮЛЙ РТЙ ЧПЪТБУФБОЙЙ ЕЕ УЛПТПУФЙ (ТЙУХОПЛ 1.3 — Б) Й Ч РТПФЙЧПРПМПЦОХА УФПТПОХ — РТЙ ХВЩЧБОЙЙ УЛПТПУФЙ (ТЙУХОПЛ 1.3 — В).
 Б) |  В) | ||||||
 тЕЫЕОЙЕ: рХУФШ ПУШ пи УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ДЧЙЦЕОЙС РЕТЧПЗП ЧЕМПУЙРЕДЙУФБ, Б ОБЮБМП ЛППТДЙОБФ У ФПЮЛПК O, Ч ЛПФПТПК ПО ОБИПДЙМУС Ч НПНЕОФ ЧТЕНЕОЙ t = 0 (ТЙУХОПЛ 1.4). фПЗДБ ХТБЧОЕОЙС ДЧЙЦЕОЙС ЧЕМПУЙРЕДЙУФБ ФБЛПЧЩ : ч НПНЕОФ ЧУФТЕЮЙ Ч ФПЮЛЕ б: t = t1; x1 = x2. фПЗДБ РПМХЮЙН ТБЧЕОУФЧП:
пРТЕДЕМЙН РЕТЕНЕЭЕОЙЕ ЛБЦДПЗП ДП ЧУФТЕЮЙ. 1.1.5 уЧПВПДОПЕ РБДЕОЙЕ ФЕМ. дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП ЧЕТФЙЛБМШОП ЧЧЕТИуЧПВПДОЩН РБДЕОЙЕН ОБЪЩЧБЕФУС ДЧЙЦЕОЙЕ, ЛПФПТПЕ УПЧЕТЫЙМП ВЩ ФЕМП ФПМШЛП РПД ДЕКУФЧЙЕН УЙМЩ ФСЦЕУФЙ ВЕЪ ХЮЕФБ УПРТПФЙЧМЕОЙС ЧПЪДХИБ. рТЙ УЧПВПДОПН РБДЕОЙЙ ФЕМБ У ОЕВПМШЫПК ЧЩУПФЩ h ПФ РПЧЕТИОПУФЙ ъЕНМЙ (h ≪RЪ, ЗДЕ RЪ — ТБДЙХУ ъЕНМЙ) ПОП ДЧЙЦЕФУС У РПУФПСООЩН ХУЛПТЕОЙЕН g, ОБРТБЧМЕООЩН ЧЕТФЙЛБМШОП ЧОЙЪ. хУЛПТЕОЙЕ g ОБЪЩЧБЕФУС ХУЛПТЕОЙЕН УЧПВПДОПЗП РБДЕОЙС. пОП ПДОП Й ФПЦЕ ДМС ЧУЕИ ФЕМ Й ЪБЧЙУЙФ МЙЫШ ПФ ЧЩУПФЩ ОБД ХТПЧОЕН НПТС Й ПФ ЗЕПЗТБЖЙЮЕУЛПК ЫЙТПФЩ. еУМЙ Ч НПНЕОФ ОБЮБМБ ПФУЮЕФБ ЧТЕНЕОЙ (t0 = 0) ФЕМП ЙНЕМП УЛПТПУФШ v0, ФП РП ЙУФЕЮЕОЙЙ РТПЙЪЧПМШОПЗП РТПНЕЦХФЛБ ЧТЕНЕОЙ ∆t = t — t0 УЛПТПУФШ ФЕМБ РТЙ УЧПВПДОПН РБДЕОЙЙ ВХДЕФ: v = v0 + g·t. рХФШ h, РТПКДЕООЩК ФЕМПН Ч УЧПВПДОПН РБДЕОЙЙ, Л НПНЕОФХ ЧТЕНЕОЙ t: нПДХМШ УЛПТПУФЙ ФЕМБ РПУМЕ РТПИПЦДЕОЙС Ч УЧПВПДОПН РБДЕОЙЙ РХФЙ h ОБИПДЙФУС ЙЪ ЖПТНХМЩ: рТПДПМЦЙФЕМШОПУФШ ∆t УЧПВПДОПЗП РБДЕОЙС ВЕЪ ОБЮБМШОПК УЛПТПУФЙ (v0 = 0) У ЧЩУПФЩ h: рТЙНЕТ 1. фЕМП РБДБЕФ ЧЕТФЙЛБМШОП ЧОЙЪ У ЧЩУПФЩ 20 Н ВЕЪ ОБЮБМШОПК УЛПТПУФЙ. пРТЕДЕМЙФШ: 1) РХФШ h, РТПКДЕООЩК ФЕМПН ЪБ РПУМЕДОАА УЕЛХОДХ РБДЕОЙС, 2) УТЕДОАА УЛПТПУФШ РБДЕОЙС vУТ, 3) УТЕДОАА УЛПТПУФШ ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ vУТ2. |  тЕЫЕОЙЕ: оБРТБЧЙН ПУШ Х ЧЕТФЙЛБМШОП ЧОЙЪ, Й РХУФШ ОБЮБМП ЛППТДЙОБФ УПЧРБДБЕФ У ОБЮБМШОЩН РПМПЦЕОЙЕН ФЕМБ (ТЙУХОПЛ 1.5). 1) уПЗМБУОП ЖПТНХМЕ: ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ЪБРЙЫЕФУС Ч ЧЙДЕ: Ч НПНЕОФ РБДЕОЙС ОБ ЪЕНМА Х = h0. пФУАДБ ЧТЕНС ДЧЙЦЕОЙС ФЕМБ: ъБ ЧТЕНС ( t — ∆t) ФЕМП РТПЫМП РХФШ рХФШ ЪБ РПУМЕДОАА УЕЛХОДХ ТБЧЕО: 2) фЕМП РТПЫМП РХФШ h0. чТЕНС ДЧЙЦЕОЙС
3) дМС ПРТЕДЕМЕОЙС УТЕДОЕК УЛПТПУФЙ ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ, ОЕПВИПДЙНП ХЪОБФШ ЧТЕНС, ЪБ ЛПФПТПЕ ЬФБ ЮБУФШ РХФЙ РТПКДЕОБ. чТЕНС ДЧЙЦЕОЙС ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ ТБЧОП РПМОПНХ ЧТЕНЕОЙ РПМЕФБ t НЙОХУ ЧТЕНС t1, ЪБФТБЮЕООПЕ ОБ РТПИПЦДЕОЙЕ РЕТЧПК РПМПЧЙОЩ РХФЙ. чТЕНС t1 ОБИПДЙФУС ЙЪ ХТБЧОЕОЙС: | ,Ф.Е. |  |
 |
 |
рТЙ ДЧЙЦЕОЙЙ ФЕМБ ЧЕТФЙЛБМШОП ЧЧЕТИ У ОБЮБМШОПК УЛПТПУФША v0, ХУЛПТЕОЙЕ ФЕМБ ТБЧОП ХУЛПТЕОЙА УЧПВПДОПЗП РБДЕОЙС g. оБ ХЮБУФЛЕ ДП ОБЙЧЩУЫЕК ФПЮЛЙ РПДЯЕНБ ДЧЙЦЕОЙЕ ФЕМБ СЧМСЕФУС ТБЧОПЪБНЕДМЕООЩН, Б РПУМЕ ДПУФЙЦЕОЙС ЬФПК ФПЮЛЙ — УЧПВПДОЩН РБДЕОЙЕН ВЕЪ ОБЮБМШОПК УЛПТПУФЙ.
уЛПТПУФШ ФЕМБ Ч РТПЙЪЧПМШОЩК НПНЕОФ ЧТЕНЕОЙ t ПФ ОБЮБМБ ДЧЙЦЕОЙС ОЕЪБЧЙУЙНП ПФ ФПЗП, ТБУУНБФТЙЧБЕФУС МЙЫШ РПДЯЕН ФЕМБ ЙМЙ ЕЗП ПРХУЛБОЙЕ РПУМЕ ДПУФЙЦЕОЙС ОБЙЧЩУЫЕК ФПЮЛЙ, ТБЧОБ v = v0 + g·t.
чЕЛФПТ РЕТЕНЕЭЕОЙС ∆r ФЕМБ ЪБ РТПЙЪЧПМШОЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t0, РТЙ ХУМПЧЙЙ t0 = 0, ТБЧЕО:
ч НПНЕОФ ЧТЕНЕОЙ tРПД, УППФЧЕФУФЧХАЭЙК ОБЙВПМШЫЕНХ РПДЯЕНХ ФЕМБ ОБД ФПЮЛПК ВТПУБОЙС (ЛПЗДБ Х = ХНБИ ЙМЙ ЧЩУПФБ РПДЯЕНБ ФЕМБ НБЛУЙНБМШОБ h = hmax = Хmax — Х0) УЛПТПУФШ ФЕМБ УФБОЕФ ТБЧОБ ОХМА: v = v0 — g·tРПД = 0, ПФЛХДБ tРПД = v0/g, Ч ЬФПФ НПНЕОФ ОБРТБЧМЕОЙЕ ДЧЙЦЕОЙС ФЕМБ ЙЪНЕОСЕФУС ОБ РТПФЙЧПРПМПЦОПЕ.
нБЛУЙНБМШОБС ЧЩУПФБ РПДЯЕНБ ФЕМБ ОБД ФПЮЛПК ВТПУБОЙС:
1.1.6 дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП РПД ХЗМПН Л ЗПТЙЪПОФХ Й ВТПЫЕООПЗП ЗПТЙЪПОФБМШОП У ОЕЛПФПТПК ЧЩУПФЩ
дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП У ОЕЛПФПТПК ЧЩУПФЩ, НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ ОЕЪБЧЙУЙНЩИ ДЧЙЦЕОЙС: ТБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ, РТПЙУИПДСЭЕЕ Ч ЗПТЙЪПОФБМШОПН ОБРТБЧМЕОЙЙ УП УЛПТПУФША υИ , ТБЧОПК ОБЮБМШОПК УЛПТПУФЙ ВТПУБОЙС υ0 (υИ = υ0), Й УЧПВПДОПЕ РБДЕОЙЕ У ЧЩУПФЩ, ОБ ЛПФПТПК ОБИПДЙМПУШ ФЕМП Ч НПНЕОФ ВТПУБОЙС, У ХУЛПТЕОЙЕН g. дМС ПРЙУБОЙС ЬФПЗП ДЧЙЦЕОЙС ЧЩВЙТБАФ РТСНПХЗПМШОХА УЙУФЕНХ ЛППТДЙОБФ ИпХ. фТБЕЛФПТЙС ДЧЙЦЕОЙС СЧМСЕФУС ЧЕФЧШ РБТБВПМЩ (ТЙУХОПЛ 1.6).
хТБЧОЕОЙЕ ДЧЙЦЕОЙС РП ПУСН пИ Й пХ:
уЛПТПУФШ ФЕМБ Ч МАВПК ФПЮЛЕ ФТБЕЛФПТЙЙ НПЦОП ПРТЕДЕМЙФШ РП ЖПТНХМЕ:
рТЙ ЬФПН ЧТЕНС РПМЕФБ УЧСЪБОП У ЧЕТФЙЛБМШОПК УПУФБЧМСАЭЕК ДЧЙЦЕОЙС. дБМШОПУФШ РПМЕФБ — У ЗПТЙЪПОФБМШОПК.
рТЙНЕТ 1. у ВБЫОЙ ЧЩУПФПК о = 25 Н ЗПТЙЪПОФБМШОП ВТПЫЕО ЛБНЕОШ УП УЛПТПУФША υ0 = 15 Н/У. оБКФЙ: УЛПМШЛП ЧТЕНЕОЙ ЛБНЕОШ ВХДЕФ Ч ДЧЙЦЕОЙЙ; ОБ ЛБЛПН ТБУУФПСОЙЙ Sx ПФ ПУОПЧБОЙЙ ВБЫОЙ ПО ХРБДЕФ ОБ ЪЕНМА; У ЛБЛПК УЛПТПУФША υ ПО ХРБДЕФ ОБ ЪЕНМА; ЛБЛПК ХЗПМ φ УПУФБЧЙФ ФТБЕЛФПТЙС ЛБНОС У ЗПТЙЪПОФПН Ч ФПЮЛЕ ЕЗП РБДЕОЙС ОБ ЪЕНМА.
рЕТЕНЕЭЕОЙЕ ВТПЫЕООПЗП ЗПТЙЪПОФБМШОП ЛБНОС НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ (ТЙУХОПЛ 1.7): ЗПТЙЪПОФБМШОПЕ Sx Й ЧЕТФЙЛБМШОПЕ Sy.
рТЙНЕОСС ЪБЛПО ОЕЪБЧЙУЙНПУФЙ ДЧЙЦЕОЙС, ЙНЕЕН:


1)

2) Sx = L = v0·t = 15 · 2,26 = 33,9 Н;
3) vХ = g · t = 9,81 · 2,26 = 22,1 Н/У,
4)

дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП РПД ХЗМПН Л ЗПТЙЪПОФХ, ФБЛЦЕ НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ ОЕЪБЧЙУЙНЩИ ДЧЙЦЕОЙС: ТБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ, РТПЙУИПДСЭЕЕ Ч ЗПТЙЪПОФБМШОПН ОБРТБЧМЕОЙЙ У ОБЮБМШОПК УЛПТПУФША v0И = v0·Cosα Й УЧПВПДОПЕ РБДЕОЙЕ У ОБЮБМШОПК УЛПТПУФША v0Х = v0·Sinα, (ТЙУХОПЛ 1.8). зДЕ α — ХЗПМ НЕЦДХ ОБРТБЧМЕОЙСНЙ ЧЕЛФПТБ УЛПТПУФЙ υ0 Й ПУША пИ. фТБЕЛФПТЙЕК ФБЛПЗП ДЧЙЦЕОЙС СЧМСЕФУС РБТБВПМБ. хТБЧОЕОЙС ДЧЙЦЕОЙС РТЙНХФ ЧЙД:
уЛПТПУФШ ФЕМБ Ч МАВПК ФПЮЛЕ ФТБЕЛФПТЙЙ:
рТЙНЕТ 2. фЕМП ВТПЫЕОП РПД ХЗМПН α Л ЗПТЙЪПОФХ У ОБЮБМШОПК УЛПТПУФША υ0. пРТЕДЕМЙФШ ЧТЕНС РПМЕФБ t, НБЛУЙНБМШОХА ЧЩУПФХ о РПДЯЕНБ Й ДБМШОПУФШ L РПМЕФБ.
тЕЫЕОЙЕ: лБЛ ПВЩЮОП ЪБДБЮБ ОБЮЙОБЕФУС У ЧЩСЧМЕОЙС УЙМ, ДЕКУФЧХАЭЙИ ОБ ФЕМП. оБ ФЕМП ДЕКУФЧХЕФ ФПМШЛП УЙМБ ФСЦЕУФЙ, РПЬФПНХ Ч ЗПТЙЪПОФБМШОПН ОБРТБЧМЕОЙЙ ПОП РЕТЕНЕЭБЕФУС ТБЧОПНЕТОП, Б Ч ЧЕТФЙЛБМШОПН — ТБЧОПРЕТЕНЕООП У ХУЛПТЕОЙЕН g.
вХДЕН ТБУУНБФТЙЧБФШ ЧЕТФЙЛБМШОХА Й ЗПТЙЪПОФБМШОХА УПУФБЧМСАЭЙЕ ДЧЙЦЕОЙС ФЕМБ РП ПФДЕМШОПУФЙ, ДМС ЬФПЗП ТБЪМПЦЙН ЧЕЛФПТ ОБЮБМШОПК УЛПТПУФЙ ОБ ЧЕТФЙЛБМШОХА ( υ0·Sinα ) Й ЗПТЙЪПОФБМШОХА ( υ0·Cosα ) УПУФБЧМСАЭЙЕ (ТЙУХОПЛ 1.9).
оБЮОЕН ТБУУНБФТЙЧБФШ ЧЕТФЙЛБМШОХА УПУФБЧМСАЭХА ДЧЙЦЕОЙС. чТЕНС РПМЕФБ t = t1 + t2, ЗДЕ t1 — ЧТЕНС РПДЯЕНБ (ФЕМП ДЧЙЦЕФУС РП ЧЕТФЙЛБМЙ ТБЧОПЪБНЕДМЕООП), t2 — ЧТЕНС УРХУЛБ (ФЕМП ДЧЙЦЕФУС РП ЧЕТФЙЛБМЙ ТБЧОПХУЛПТЕООП).
чЕТФЙЛБМШОБС УЛПТПУФШ ФЕМБ Ч ОБЙЧЩУЫЕК ФПЮЛЕ ФТБЕЛФПТЙЙ (РТЙ t = t1) ТБЧОБ ПЮЕЧЙДОП ОХМА. у ДТХЗПК УФПТПОЩ, ЬФБ УЛПТПУФШ НПЦЕФ ВЩФШ ЧЩТБЦЕОБ РТЙ РПНПЭЙ ЖПТНХМЩ ЪБЧЙУЙНПУФЙ УЛПТПУФЙ ТБЧОПЪБНЕДМЕООПЗП ДЧЙЦЕОЙС ПФ ЧТЕНЕОЙ.
пФУАДБ, РПМХЮБЕН: 0 = υ0Sinα — g·t1 ЙМЙ
рПДУФБЧЙН (1.1) Ч (1.2)
чТЕНС УРХУЛБ t2 НПЦОП ЧЩЮЙУМЙФШ, ТБУУНПФТЕЧ РБДЕОЙЕ ФЕМБ У ЙЪЧЕУФОПК ЧЩУПФЩ о ВЕЪ ОБЮБМШОПК ЧЕТФЙЛБМШОПК УЛПТПУФЙ:
рПМОПЕ ЧТЕНС РПМЕФБ:
дМС ОБИПЦДЕОЙС ДБМШОПУФЙ РПМЕФБ L ОЕПВИПДЙНП ПВТБФЙФШУС Л ЗПТЙЪПОФБМШОПК УПУФБЧМСАЭЕК ДЧЙЦЕОЙС ФЕМБ. лБЛ ХЦЕ ПФНЕЮБМПУШ, РП ЗПТЙЪПОФБМЙ ФЕМП РЕТЕНЕЭБЕФУС ТБЧОПНЕТОП.
1.1.7 тБЧОПРЕТЕНЕООПЕ ДЧЙЦЕОЙЕ ФПЮЛЙ РП ПЛТХЦОПУФЙ
дЧЙЦЕОЙЕ РП ПЛТХЦОПУФЙ СЧМСЕФУС РТПУФЕКЫЙН РТЙНЕТПН ЛТЙЧПМЙОЕКОПЗП ДЧЙЦЕОЙС. уЛПТПУФШ υ ДЧЙЦЕОЙС РП ПЛТХЦОПУФЙ ОБЪЩЧБЕФУС МЙОЕКОПК (ПЛТХЦОПК) УЛПТПУФША. рТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ РП ПЛТХЦОПУФЙ НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ НБФЕТЙБМШОПК ФПЮЛЙ У ФЕЮЕОЙЕН ЧТЕНЕОЙ ОЕ ЙЪНЕОСЕФУС. дЧЙЦХЭБСУС ФПЮЛБ ЪБ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ РТПИПДЙФ ТБЧОЩЕ РП ДМЙОЕ ДХЗЙ ПЛТХЦОПУФЙ. фБОЗЕОГЙБМШОПЕ ХУЛПТЕОЙЕ РТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФПЮЛЙ РП ПЛТХЦОПУФЙ ПФУХФУФЧХЕФ ( aτ ). йЪНЕОЕОЙЕ ЧЕЛФПТБ УЛПТПУФЙ υ РП ОБРТБЧМЕОЙА ИБТБЛФЕТЙЪХЕФУС ОПТНБМШОЩН ХУЛПТЕОЙЕН an, ЛПФПТПЕ ОБЪЩЧБЕФУС ФБЛЦЕ ГЕОФТПУФТЕНЙФЕМШОЩН ХУЛПТЕОЙЕН.
ч ЛБЦДПК ФПЮЛЕ ФТБЕЛФПТЙЙ ЧЕЛФПТ an ОБРТБЧМЕО РП ТБДЙХУХ Л ГЕОФТХ ПЛТХЦОПУФЙ, Б ЕЗП НПДХМШ ТБЧЕО:
рТЙ ПРЙУБОЙЙ НЕИБОЙЮЕУЛПЗП ДЧЙЦЕОЙС, Ч ЮБУФОПУФЙ ДЧЙЦЕОЙС РП ПЛТХЦОПУФЙ, ОБТСДХ У РТСНПХЗПМШОПК ДЕЛБТФПЧПК УЙУФЕНПК ЛППТДЙОБФ ЙУРПМШЪХЕФУС РПМСТОБС УЙУФЕНБ ЛППТДЙОБФ. рПМПЦЕОЙЕ ФПЮЛЙ н ОБ ЛБЛПК-ФП РМПУЛПУФЙ (ОБРТЙНЕТ, ипх) ПРТЕДЕМСЕФУС ДЧХНС РПМСТОЩНЙ ЛППТДЙОБФБНЙ: НПДХМЕН r ТБДЙХУБ ЧЕЛФПТБ ФПЮЛЙ Й ХЗМПН φ — ХЗМПЧПК ЛППТДЙОБФПК, ЙМЙ РПМСТОЩН ХЗМПН (ТЙУХОПЛ 1.10).
хЗПМ φ ПФУЮЙФЩЧБЕФУС ПФ ПУЙ пи ДП ТБДЙХУБ-ЧЕЛФПТБ r РТПФЙЧ ЮБУПЧПК УФТЕМЛЙ. фПЮЛХ п Ч ЬФПН УМХЮБЕ ОБЪЩЧБАФ РПМАУПН УЙУФЕНЩ ЛППТДЙОБФ. уПЧНЕУФЙН РПМАУ ЛППТДЙОБФ УЙУФЕНЩ У ГЕОФТПН ПЛТХЦОПУФЙ, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ; ФПЗДБ r = R (ТЙУХОПЛ 1.11), Б ЙЪНЕОЕОЙЕ РПМПЦЕОЙС ФПЮЛЙ ОБ ПЛТХЦОПУФЙ НПЦЕФ ВЩФШ ПИБТБЛФЕТЙЪПЧБОП ЙЪНЕОЕОЙЕН ∆φ ХЗМПЧПК ЛППТДЙОБФЩ ФПЮЛЙ: ∆φ = φ2 -φ1.
хЗПМ ∆φ ОБЪЩЧБЕФУС ХЗМПН РПЧПТПФБ ТБДЙХУБ — ЧЕЛФПТБ ФПЮЛЙ. ьМЕНЕОФБТОЩЕ (ВЕУЛПОЕЮОП НБМЩЕ) ХЗМЩ РПЧПТПФБ ТБУУНБФТЙЧБАФУС ЛБЛ ЧЕЛФПТЩ.
нПДХМШ ЧЕЛФПТБ dφ ТБЧЕО ХЗМХ РПЧПТПФБ. оБРТБЧМЕОЙЕ ЧЕЛФПТБ dφ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН РПУФХРБФЕМШОПЗП ДЧЙЦЕОЙС ПУФТЙС ЧЙОФБ, ЗПМПЧЛБ ЛПФПТПЗП, ЧТБЭБЕФУС Ч ОБРТБЧМЕОЙЙ ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ, Ф.Е. РПДЮЙОСЕФУС РТБЧЙМХ РТБЧПЗП ЧЙОФБ (ТЙУХОПЛ 1.12).
CТЕДОЕК ХЗМПЧПК УЛПТПУФША ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ ЧПЛТХЗ ПУЙ ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ ωcp, ТБЧОБС ПФОПЫЕОЙА ХЗМБ РПЧПТПФБ ∆φ ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ДМЙФЕМШОПУФЙ ЬФПЗП РТПНЕЦХФЛБ:
хЗМПЧПК УЛПТПУФША (НЗОПЧЕООПК ХЗМПЧПК УЛПТПУФША) ω ОБЪЩЧБЕФУС РТЕДЕМ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОСС ХЗМПЧБС УЛПТПУФШ РТЙ ВЕУЛПОЕЮОПН ХНЕОШЫЕОЙЙ РТПНЕЦХФЛБ ЧТЕНЕОЙ ∆t, ЙМЙ РЕТЧБС РТПЙЪЧПДОБС ПФ ХЗМБ РПЧПТПФБ РП ЧТЕНЕОЙ:
чЕЛФПТ ω ОБРТБЧМЕО ЧДПМШ ПУЙ ЧТБЭЕОЙС РП РТБЧЙМХ РТБЧПЗП ЧЙОФБ, Ф.Е. ФБЛЦЕ ЛБЛ Й dφ (ТЙУХОПЛ 1.13).
рТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФПЮЛЙ РП ПЛТХЦОПУФЙ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ХЗМЩ РПЧПТПФБ ЕЕ ТБДЙХУ-ЧЕЛФПТБ ПДЙОБЛПЧЩ. уМЕДПЧБФЕМШОП, РТЙ ФБЛПН ДЧЙЦЕОЙЙ НЗОПЧЕООБС ХЗМПЧБС УЛПТПУФШ ТБЧОБ УТЕДОЕК ХЗМПЧПК УЛПТПУФЙ: ω = ωcp. хЗПМ РПЧПТПФБ ∆ω ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ, ТБЧОПНЕТОП ДЧЙЦХЭЕКУС РП ПЛТХЦОПУФЙ, ТБЧЕО:
рТПНЕЦХФПЛ ЧТЕНЕОЙ ф, Ч ФЕЮЕОЙЙ ЛПФПТПЗП ФПЮЛБ УПЧЕТЫБЕФ ПДЙО РПМОЩК ПВПТПФ РП ПЛТХЦОПУФЙ, ОБЪЩЧБЕФУС РЕТЙПДПН ПВТБЭЕОЙС (РЕТЙПДПН ЧТБЭЕОЙС), Б ЧЕМЙЮЙОБ υ, ПВТБФОБС РЕТЙПДХ:

ЮБУФПФПК ПВТБЭЕОЙС (ЮБУФПФПК ЧТБЭЕОЙС). ъБ ПДЙО РЕТЙПД ХЗПМ РПЧПТПФБ ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ ТБЧЕО 2π ТБД, РПЬФПНХ 2π = ωT, ПФЛХДБ T = 2π/ω, ЙМЙ ω = 2π/ф = 2πν.
мЙОЕКОБС υ Й ХЗМПЧБС ω УЛПТПУФЙ УЧСЪБОЩ УППФОПЫЕОЙЕН: υ = ω·R. ьФП ЧЙДОП ЙЪ УМЕДХАЭЕЗП ЧЩЧПДБ:
рТЙНЕТ 1. пРТЕДЕМЙФШ НПДХМШ УЛПТПУФЙ Й ГЕОФТПУФТЕНЙФЕМШОПЗП ХУЛПТЕОЙС ФПЮЕЛ ЪЕНОПК РПЧЕТИОПУФЙ ОБ ЬЛЧБФПТЕ. тБДЙХУ ъЕНМЙ РТЙОСФШ ТБЧОЩН 6400 ЛН.
R = 6400 ЛН = 6,4·10 6 Н;
ф = 24 Ю = 8,64·10 4 У;
тЕЫЕОЙЕ: фПЮЛЙ ЪЕНОПК РПЧЕТИОПУФЙ ОБ ЬЛЧБФПТЕ ДЧЙЦХФУС РП ПЛТХЦОПУФЙ ТБДЙХУБ R, РПЬФПНХ НПДХМШ ЙИ УЛПТПУФЙ:
пФЧЕФ: υ = 465 Н/У, БГУ = 0,034 Н /У 2 .
1.1.8 чТБЭБФЕМШОПЕ ДЧЙЦЕОЙЕ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ОЕРПДЧЙЦОПК ПУЙ
дМС ЛЙОЕНБФЙЮЕУЛПЗП ПРЙУБОЙС ЧТБЭБФЕМШОПЗП ДЧЙЦЕОЙС БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ЛБЛПК-ФП ОЕРПДЧЙЦОПК ПУЙ ЙУРПМШЪХАФУС ФЕ ЦЕ ЧЕМЙЮЙОЩ (Й ХТБЧОЕОЙС УЧСЪЙ НЕЦДХ ОЙНЙ), ЮФП Й ДМС ПРЙУБОЙС ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ. рТЙ ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ОЕРПДЧЙЦОПК ПУЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t ХЗМЩ РПЧПТПФБ ТБДЙХУ-ЧЕЛФПТПЧ ТБЪМЙЮОЩИ ФПЮЕЛ ФЕМБ ПДЙОБЛПЧЩ. хЗПМ РПЧПТПФБ ∆φ, УТЕДОСС ωcp Й НЗОПЧЕООБС ω ХЗМПЧЩЕ УЛПТПУФЙ ИБТБЛФЕТЙЪХАФ ЧТБЭБФЕМШОПЕ ДЧЙЦЕОЙЕ ЧУЕЗП БВУПМАФОП ФЧЕТДПЗП ФЕМБ Ч ГЕМПН.
мЙОЕКОБС УЛПТПУФШ υ ЛБЛПК-МЙВП ФПЮЛЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ РТПРПТГЙПОБМШОП ТБУУФПСОЙА R ФПЮЛЙ ПФ ПУЙ ЧТБЭЕОЙС:
рТЙ ТБЧОПНЕТОПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ХЗМЩ РПЧПТПФБ ФЕМБ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ПДЙОБЛПЧЩ ( ∆φ = const ) Й НЗОПЧЕООБС ХЗМПЧБС УЛПТПУФШ ФЕМБ ТБЧОБ УТЕДОЕК ХЗМПЧПК УЛПТПУФЙ ( ω = ωcp ). фБОЗЕОГЙБМШОЩЕ ХУЛПТЕОЙС aτ Х ТБЪМЙЮОЩИ ФПЮЕЛ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ПФУХФУФЧХАФ ( aτ = 0 ), Б ОПТНБМШОПЕ (ГЕОФТПУФТЕНЙФЕМШОПЕ ) ХУЛПТЕОЙЕ an ЛБЛПК-МЙВП ФПЮЛЙ ФЕМБ ЪБЧЙУЙФ ПФ ЕЕ ТБУУФПСОЙС R ДП ПУЙ ЧТБЭЕОЙС:
чЕЛФПТ an ОБРТБЧМЕО Ч ЛБЦДЩК НПНЕОФ ЧТЕНЕОЙ РП ТБДЙХУХ ФТБЕЛФПТЙЙ ФПЮЛЙ Л ПУЙ ЧТБЭЕОЙС.
рТЙ ОЕТБЧОПНЕТОПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ХЗМЩ РПЧПТПФБ ФЕМБ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ОЕПДЙОБЛПЧЩ. хЗМПЧБС УЛПТПУФШ ФЕМБ ω У ФЕЮЕОЙЕН ЧТЕНЕОЙ ЙЪНЕОСЕФУС.
уТЕДОЙН ХЗМПЧЩН ХУЛПТЕОЙЕН εУТ Ч РТПНЕЦХФЛЕ ЧТЕНЕОЙ ∆t = t2 — t1 ОБЪЩЧБЕФУС ЖЙЪЙЮЕУЛБС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА ЙЪНЕОЕОЙС ХЗМПЧПК УЛПТПУФЙ ∆ω = ω2 — ω1 ЧТБЭБАЭЕЗПУС ФЕМБ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ДМЙФЕМШОПУФЙ ЬФПЗП РТПНЕЦХФЛБ:
еУМЙ ХЗМПЧБС УЛПТПУФШ ЪБ РТПЙЪЧПМШОЩЕ ПДЙОБЛПЧЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ЙЪНЕОСЕФУС ПДЙОБЛПЧП ( ∆ω12 = ∆ω34 Й Ф.Д.), ФП εУТ = const (ТБЧОПРЕТЕНЕООПЕ ЧТБЭЕОЙЕ).
хЗМПЧЩН ХУЛПТЕОЙЕН (НЗОПЧЕООЩН ХЗМПЧЩН ХУЛПТЕОЙЕН) ЧТБЭБАЭЕЗПУС ФЕМБ Ч НПНЕОФ ЧТЕНЕОЙ t ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ ε, ТБЧОБС РТЕДЕМХ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОЕЕ ХЗМПЧПЕ ХУЛПТЕОЙЕ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ПФ t ДП t + ∆t РТЙ ВЕУЛПОЕЮОПН ХНЕОШЫЕОЙЙ ∆t, ЙМЙ, ХЗМПЧПЕ ХУЛПТЕОЙЕ — ЬФП РЕТЧБС РТПЙЪЧПДОБС ПФ ХЗМПЧПК УЛПТПУФЙ РП ЧТЕНЕОЙ ЙМЙ ЧФПТБС РТПЙЪЧПДОБС ПФ ХЗМБ РПЧПТПФБ РП ЧТЕНЕОЙ:
йЪНЕОЕОЙЕ ∆ω ХЗМПЧПК УЛПТПУФЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t0 РТЙ ТБЧОПРЕТЕНЕООПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ У ХЗМПЧЩН ХУЛПТЕОЙЕН ε: ∆ω = ε·∆t = ε(t — t0). еУМЙ РТЙ t0 = 0 ОБЮБМШОБС ХЗМПЧБС УЛПТПУФШ ФЕМБ ТБЧОБ ω0, ФП Ч РТПЙЪЧПМШОЩК НПНЕОФ ЧТЕНЕОЙ t ХЗМПЧБС УЛПТПУФШ ФЕМБ ВХДЕФ ω = ω0 + ε·t.
хЗПМ РПЧПТПФБ ∆φ ФЕМБ ЧПЛТХЗ ПУЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t0 РТЙ ТБЧОПРЕТЕНЕООПН ДЧЙЦЕОЙЙ:
фБОЗЕОГЙБМШОБС УПУФБЧМСАЭБС ХУЛПТЕОЙС:

оПТНБМШОБС УПУФБЧМСАЭБС ХУЛПТЕОЙС:
фБЛЙН ПВТБЪПН, УЧСЪШ НЕЦДХ МЙОЕКОЩНЙ Й ХЗМПЧЩНЙ ЧЕМЙЮЙОБНЙ ЧЩТБЦБЕФУС УМЕДХАЭЙНЙ ЖПТНХМБНЙ: S = R·φ, υ = ω·R, aτ = R·ε, an = ω 2 ·R.
Кинематика в физике — основные понятия, формулы и определения с примерами
Содержание:
Основная задача механики — описание движения тел, т. е. выяснение закона (уравнения) их движения. Как отмечал А. Эйнштейн, наиболее фундаментальная проблема, остававшаяся нерешенной на протяжении тысячелетий, — это проблема движения. Собственно, учение о движении стало наукой лишь со времен Галилео Галилея и Исаака Ньютона.
Кинематика, изучает конкретные механические та их взаимодействия с другими телами. Она фактически объединяет простейшие пространственно-временные зависимости, в частности изменение координат тела со временем (как функцию времени).
Поэтому кинематику часто называют геометрией движения.
Кинематика изучает механические движения тел без учета их взаимодействия с другими телами.
Кинематика
Физика изучает разнообразные явления и процессы, происходящие вокруг нас. Как вам известно, в зависимости от их природы различают механические, тепловые, электрические, магнитные, световые и другие физические явления. Раздел физики, который объясняет движение и взаимодействие тел, называется механикой.
Слово «механика» впервые ввел Аристотель. Оно означает «машина».
Механика — одна из древнейших наук. Ее возникновение и развитие связано с практическими потребностями человека. Первые труды по механике, в которых рассматривались свойства простых механизмов и машин, появились еще в Древней Греции. Весомый вклад в ее становление сделали такие корифеи науки, как Аристотель (IV в. до н. э.), Архимед (III в. до н. э.), Леонардо да Винчи (XV в.), Галилео Галилей (XVII в.) и др. В завершенном виде как классическая теория она получила обоснование в работе Исаака Ньютона «Математические начала натуральной философии» (1687 г.). Современная механика, в основе которой лежит теория относительности, создана в начале XX в. Альбертом Эйнштейном.
Основная задача механики состоит в том, чтобы на основании параметров движения тела: координат, пройденного пути, перемещения, угла поворота, скорости, силы и т. д. — найти закон или уравнение, которое описывает это движение.
Основная задача механики состоит в том, чтобы найти уравнение движения тела с помощью параметров, описывающих это движение.
Т. е. если мы при помощи этих физических величин сможем установить положение тела в любой момент времени, то основная задача механики считается решенной. В зависимости от способов ее решения в механике выделяют три раздела: кинематика, динамика и статика.
Кинематика изучает, как движется тело, не вникая в причины, вызывающие именно такое движение. Поэтому кинематические уравнения состоят лишь из пространственных характеристик механического движения: пройденного пути, изменения координат тела, скорости и т. д. В них нет сил, изменяющих это движение.
В переводе с греческого слово кинематика» (kinematos) означает движение.
Механическое движение и траектория движения
Чаще всего в обыденной жизни мы наблюдаем явление, которое называется механическим движением. Например, автомобиль едет по дороге, в небе «плывут» тучи, ребенок катается на качелях, Луна вращается вокруг Земли и т. д. Во всех этих случаях происходит изменение положения одного тела или его частей относительно других. Чтобы убедиться в этом, необходимо выбрать тело отсчета, относительно которого можно фиксировать положение движущегося тела в любой момент времени. Тело отсчета выбирают произвольно. В приведенных примерах это может быть столб или дерево возле дороги, дом, поверхность Земли и т. д.
Для того чтобы описать движение тела, необходимо точно знать его местоположение в пространстве в произвольный момент времени, т. е. уметь определять изменение положения тела в пространстве относительно других тел с течением времени. Как известно, легче всего это можно сделать с помощью системы координат. Например, зафиксировать «адрес» тела как определенное его положение в пространстве, измерив расстояния или углы в некоторой системе координат.
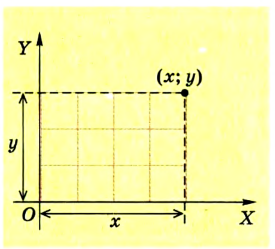
Например, в географии положение тела на земной поверхности задается двумя числами на пересечении меридиана и параллели, которые называются географической долготой и широтой. В математике «адрес» точки чаще всего определяют ее координатами, в частности в прямоугольной (декартовой) системе координат на плоскости — это расстояния х и у (рис. 1.1).
Взаимные изменения положения тела или его частей в пространстве с течением времени называются механическим движением.
Систему координат, как правило, связывают с телом отсчета. В данном случае движущееся тело характеризуется изменением положения в пространстве относительно тела отсчета, т. е. изменением его координат с течением времени.
Математически это можно записать в таком виде: х = x(t); у = y(t).
Для того чтобы определить такое изменение в любой момент времени, с телом отсчета и системой координат необходимо связать средство измерения времени, к примеру секундомер или хронометр. Тогда тело отсчета, связанную с ним систему координат и секундомер как единое целое называют системой отсчета.
Как известно, реальные физические тела имеют форму и объем. Поэтому однозначно задать их положение в пространстве не всегда представляется возможным, поскольку различные их части имеют разные координаты. Однако эту проблему можно упростить, если не брать во внимание размеры тела. Такое возможно лишь при определенных условиях.
Чтобы выяснить их, рассмотрим движение автомобиля. На значительных расстояниях, например на шоссе между Киевом и Харьковом, размерами автомобиля можно пренебречь, поскольку они значительно меньше расстояния между этими городами. Поэтому нет необходимости рассматривать особенности движения каждой части кузова автомобиля — достаточно его представить как движение точки.
Таким образом, для упрощения описания движения тел, когда их размерами при определенных условиях можно пренебречь, применяют понятие материальной точки. Это условное тело, не имеющее размеров, которое определяет положение реального тела в пространстве при помощи координат такой, материальной точки. Ее геометрический образ — невесомая точка, не имеющая размеров. В случае поступательного движения, при котором все точки тела движутся одинаково, любое тело можно считать материальной точкой.
Материальная точка — это физическая модель, при помощи которой представляют реальное тело, пренебрегая его размерами.
Часто кроме движущихся предметов мы наблюдаем тела, пребывающие в состоянии покоя. Однако абсолютно неподвижных тел в природе не существует.
Рассмотрим такой пример. В вагоне на столе стоит бутылка с водой (рис. 1.2). Во время движения поезда разные наблюдатели — пассажир в купе и провожающий на перроне — оценят ее состояние движения по-разному. Для сидящего пассажира она неподвижна, поскольку расстояние от него до бутылки не изменяется. Для провожающего на перроне 16 она движется, потому что изменяет свое положение с течением времени в системе отсчета, связанной с перроном.
Следовательно, состояние покоя является относительным, равно как и состояние движения, поскольку зависит от выбранной системы отсчета. Поэтому в дальнейшем при рассмотрении движения тела мы в первую очередь будем определяться с выбором системы отсчета, потому что от этого нередко зависит сложность уравнений, описывающих данное движение. Правильный выбор системы отсчета ведет к упрощению уравнений движения.
Состояние покоя и состояние движения тела относительны, поскольку зависят от выбора системы отсчета.
Рассмотрим движущееся тело, последовательно фиксируя его положение в определенные моменты времени. Если теперь соединить все точки, в которых побывало тело во время своего движения, то получим мнимую линию, которая называется траекторией движения. Траектория движения может быть видимой (след от самолета на небосклоне, линия от карандаша или ручки при записи в тетради) и невидимой (полет птички, движение теннисного мяча и т. д.).
По форме траектории механическое движение бывает прямолинейным и криволинейным (рис. 1.3).
Положение броуновской частички через определенные промежутки времени.
Рис. 1.3. Различные формы траектории
Траектория прямолинейного движения — прямая линия. Например, падение тела с определенной высоты или движение шарика по наклонному желобу. Во время криволинейного движения тело перемещается по произвольной кривой. Часто реальное движение тел является комбинацией прямолинейного и криволинейного движений. Например, комбинированным есть движение автобуса по маршруту: на разных участках траектория его движения может быть и прямолинейной, и криволинейной.
Поскольку движение тел происходит в определенных системах отсчета, то и траектория рассматривается относительно них. Ведь она отображает во времени последовательные положения тела в некоторой системе отсчета. Поэтому она будет отличаться формой в различных системах отсчета, т. е. траектории движения также относительны. Например, все точки колеса велосипеда относительно его оси описывают окружность, однако в системе отсчета, связанной с землей, эта линия более сложная (рис. 1.4).
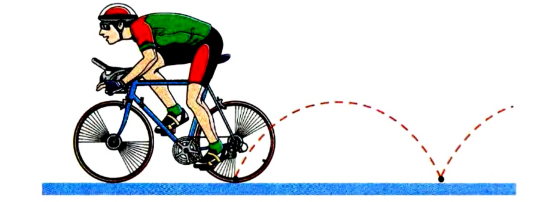
Рис. 1.4. Траектория движения точки обода колеса велосипеда
Путь и перемещение
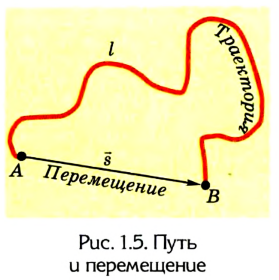
Зная траекторию движения, можно определить путь, пройденный телом: для этого необходимо измерить длину траектории между начальной и конечной точками движения.
Путь — это длина траектории, которую проходит тело или материальная точка за определенный интервал времени. Он обозначается латинской буквой l. Данная физическая величина является скалярной и характеризуется лишь значением длины траектории движения.
В Международной системе единиц (СИ) путь измеряется в метрах (м). На практике используют также другие единицы пути — километр (км), сантиметр (см) и др.
Часто, для того чтобы более полно охарактеризовать движение тела и найти его новое положение, кроме пройденного пути (длины траектории), необходимо указать также направление, в котором двигалось тело. Например, водителю автомобиля приходится ехать по извилистой дороге (рис. 1.5).
Пройденный путь — это длина дороги I, по которой ехал автомобиль. Водитель же совершил перемещение в пространстве из точки А в точку В, которое можно найти, соединив начальное и конечное положение тела прямой линией, указав при этом направление движения.
Следовательно, направленный отрезок прямой, соединяющий начальное положение движущегося тела с конечным, называется перемещением. Перемещение — это векторная величина. Оно обозначается латинской буквой 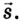
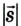
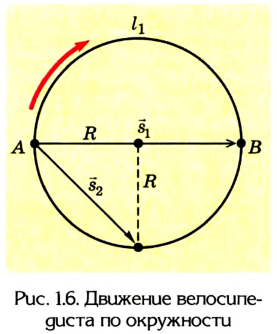
Путь и перемещение могут отличаться своими значениями. Чтобы убедиться в этом, рассмотрим движение велосипедиста по окружности радиуса R= 100 м (рис. 1.6).
Допустим велосипедист стартует в точке А. Проехав половину окружности, он окажется в точке В. Пройденный им путь равен дуге 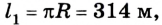
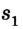
В момент времени, когда велосипедист проедет 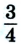
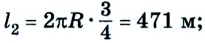
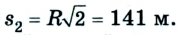
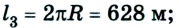
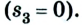
Путь и перемещение имеют также одинаковые значения, когда тело движется прямолинейно лишь в одном направлении.
В рассмотренном нами примере пройденный путь и перемещение разные, отличаются по своему значению. Возникает вопрос: могут ли они совпадать, быть одинаковыми? Можно легко убедиться в том, что такое возможно, если, во-первых, траектория движения будет прямой, во-вторых, движение происходит в одну сторону. Как подтверждение этого, рассмотрим — такой пример.
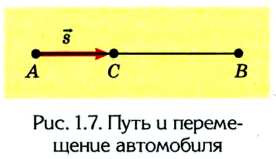
Допустим, что автомобиль движется прямолинейно по шоссе из пункта А в пункт В, а затем возвращается в пункт С. Расстояние между пунктами 2 км и 4 км соответственно, все они размещены на одной прямой (рис. 1.7).
Двигаясь из пункта А в пункт В, автомобиль проходит путь 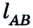
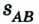
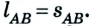
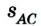
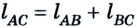
Следовательно, пройденный путь и перемещение по своему значению одинаковы лишь в том случае, если тело движется по прямой и не изменяет направление движения.
Равномерное прямолинейное движение
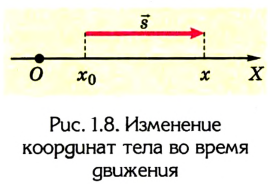
Простейшим видом механического движения является равномерное прямолинейное движение. Это такое движение, при котором тело, двигаясь по прямой, за любые одинаковые интервалы времени совершает одинаковые перемещения. Его траектория — прямая линия. Поэтому его можно описать переменой одной из координат, например х = x(t), если координатная ось совпадает с направлением движения.
Пусть тело в начальный момент движения имеет координату 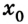
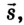
Как известно, в СИ скорость
измеряется в метрах за секунду (м/с). 1 м/с — это скорость такого равномерного прямолинейного движения, при которой тело за 1 с совершает перемещение 1 м. На практике используют также другие единицы скорости, например километр в час:
Поскольку перемещение 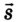
При равномерном движении значение скорости остается постоянным, поскольку за любые равные интервалы времени совершаются равные перемещения.
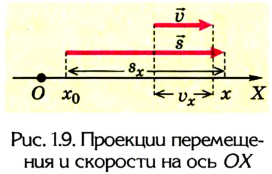
Как известно, основной задачей механики является определение положения тела в пространстве в произвольный момент времени. Следовательно, чтобы ее решить, надо найти координаты тела либо их изменение во времени: х — x(t). В механике такое уравнение называется уравнением движения. При решении задач с использованием уравнения движения векторные величины, характеризующие движение тела, записывают в проекциях на соответствующую ось. Следовательно, из формулы (1) получаем:
Из рисунков 1.8 и 1.9 понятно, что 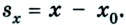
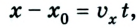

Уравнения равномерного прямолинейного движения:
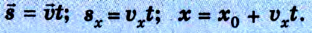
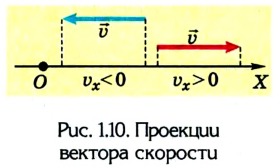
Рассмотрим теперь различные случаи равномерного прямолинейного движения (рис. 1.10).
Из рисунка следует, что если направление движения тела совпадает с направлением координатной оси, то 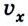
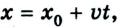
Если же направление движения тела противоположно направлению координатной оси, то 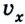
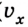
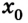
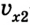
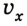
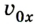
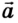
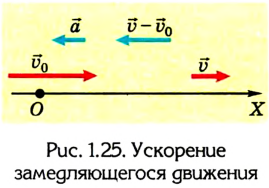
Если скорость тела со временем уменьшается 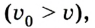
В данном случае в соответствии с выбранным направлением координатной оси ОХ проекция ускорения будет отрицательной
Вместе с тем знак проекции ускорения не определяет характер движения — оно ускоряющееся или замедляющееся, в зависимости от выбора системы отсчета. В этом легко убедиться, если рассмотреть случай, когда оба тела движутся в противоположных направлениях. Тогда одно из тел имеет положительную проекцию ускорения 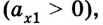
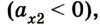
Из формул (1) и (2) можно получить кинематическое уравнение скорости для равноускоренного движения:

или в проекциях на ось ОХ:
Выведем теперь кинематическое уравнение перемещения для равноускоренного движения. Учтем, что скорость во время такого движения постоянно изменяется, например сначала она равна 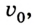
Подставив в данную формулу уравнение (3) и произведя некоторые преобразования, получим: 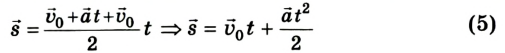
или в проекциях на ось ОХ: 
Если начальная скорость тела равна 0 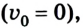

или в проекциях на ось ОХ: 
Для прямолинейного движения, учитывая, что 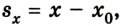
или для случая, когда 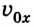

Следует помнить, что в ходе решения задач необходимо учитывать знаки проекций в соответствующих уравнениях.
При определении проекции перемещения не всегда известно время, в течение которого происходило движение. Тогда можно воспользоваться иным уравнением. Чтобы его получить, подставим в кинематическое уравнение 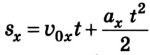
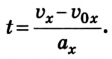

Отсюда 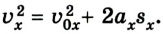
Задача №5
Водитель начинает тормозить в тот момент, когда спидометр автомобиля фиксирует скорость 72 км/ч. Через какое время автомобиль остановится, если он двигался с ускорением 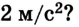
Дано:
По условию задачи спидометр показывает начальную скорость автомобиля 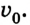
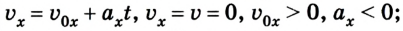
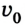
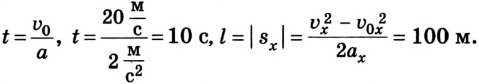
Ответ: автомобиль остановился через 10 с, проехав 100 м.
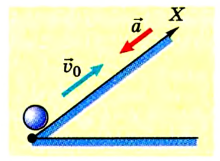
Задача №6
Шарик толкнули по наклонному желобу вверх со скоростью 6 м/с. Шарик движется с ускорением 0,5 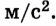
Дано:
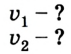
Решение
Направим ось ОХ вдоль желоба (см. рис.).
Учитывая знаки проекций скорости и ускорения, имеем
Отсюда уравнение для 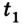
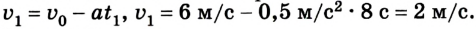
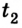
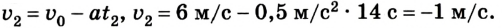
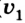
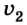
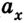
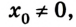
Если 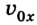
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://cde.osu.ru/demoversion/course120/2_0.html
http://www.evkova.org/kinematika-v-fizike





































































































 (Ф.Л. Б1И= — Б1; И01 = 0);
(Ф.Л. Б1И= — Б1; И01 = 0); (Ф.Л. v2x = — v02 Й a2x = — a2).
(Ф.Л. v2x = — v02 Й a2x = — a2). , ПФЛХДБ v01·t1 + v02·t1 = И02, Ф.Л. Б1 = Б2,
, ПФЛХДБ v01·t1 + v02·t1 = И02, Ф.Л. Б1 = Б2,