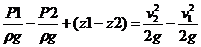Кинематика жидкости расход уравнение расхода

Кинематика жидкости расход уравнение расхода

5-я лекция, 2010 год.

5. КИНЕМАТИКА И ДИНАМИКА ЖИДКОСТИ

5.1. Основные понятия

5.2. Расход. Уравнение расхода

5.3. Уравнение Бернулли для элементарной струйки идеальной жидкости.

Три вида уравнения Бернулли для струйки идеальной жидкости.

5.1. Основные понятия

Кинематика жидкости существенно отличается от кинематики твердого тела. Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют; жидкость состоит из множества частиц движущихся одна относительно другой.

Скорость в данной точке пространства, занятого движущейся жидкостью, является функцией координат этой точки, а иногда и времени.

Задачей кинематики жидкости является определение скорости в любой точке жидкой среды, т. е. нахождение поля скоростей.

Мы сейчас рассмотрим движение идеальной жидкости, то есть жидкости, которая не обладает вязкостью.

В идеальной жидкости, так же как и в неподвижной реальной жидкости, возможен лишь один вид напряжений — нормальные напряжения сжатия, т. е. гидромеханическое давление.

Давление в движущейся идеальной жидкости обладает теми же свойствами, что и в неподвижной жидкости, на внешней поверхности жидкости оно направлено по нормали, а в любой точке внутри жидкости по всем направлениям одинаково.

Течение жидкости может быть установившимся или неустановившимся.

Установившимся называется течение жидкости, при котором давление и скорость являются функциями координат и не зависят от времени.

Давление и скорость могут измениться при перемещении частицы жидкости из одного положения в другое, но в данной неподвижной относительно русла точке давление и скорость при установившемся движении не изменяются во времени.

Последнее положение доказывается подобно тому, как это делалось для неподвижной жидкости (см. п. 1.4): составляются уравнения движения элементарного тетраэдра с учетом сил Д’Аламбера, которые затем вместе с массовыми силами стремятся к нулю при стягивании тетраэдра в точку.

р= f (х, у, z ); v = f ₂(х, у, z ); ,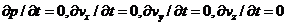

где индексы у скорости означают ее проекции на соответствующие оси, жестко связанные с руслом.

В частном случае установившееся течение может быть равномерным, когда скорость каждой частицы не изменяется с изменением ее координат и поле скоростей остается неизменным вдоль потока .

Примером установившегося течения может служить истечение жидкости из со суда, в котором поддерживается постоянный уровень, или движение жидкости в трубопроводе, создаваемое центробежным насосом с постоянной частотой вращения вала.

Неустановившимся называется течение жидкости, характеристики которого изменяются во времени в точках рассматриваемого пространства.

В общем случае при неустановившемся течении давление и скорость зависят как от координат, так и от времени:

Примерами неустановившегося течения жидкости могут служить быстрое опорожнение сосуда через отверстие в дне или движение во всасывающей или напорной трубе поршневого насоса, поршень которого совершает возвратно-поступательное движение.

Исследование установившихся течений гораздо проще, чем неустановившихся.

При установившемся течении траектории частиц жидкости являются неизменными по времени. При неустановившемся течении траектории различных частиц, проходящих через данную точку пространства, могут иметь разную форму. Поэтому для рассмотрения картины течения, возникающей в каждый данный момент времени, вводится понятие линии тока.

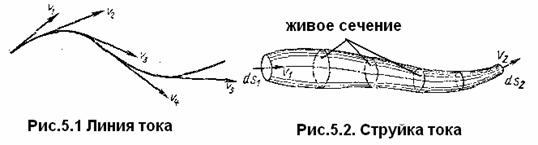
Линией тока называется кривая, в каждой точке которой вектор скорости в данный момент времени направлен по касательной к этой кривой (рис. 5.1).

Очевидно, что в условиях установившегося течения линия тока совпадает с траекторией частицы и не изменяет своей формы с течением времени.

Трубкой тока называется бесконечно малый замкнутый контур, выделенный в данный момент времени в движущейся жидкости, через все точки которого проведены линии тока. Это условная трубчатая поверхность.

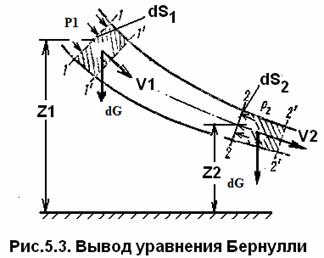
Элементарной струйкой называется часть потока, заключенная внутри трубки тока (рис.5.2).

В любой точке «трубки тока» т.е. на трубчатой поверхности струйки, векторы скорости направлены по касательной, а нормальные к этой поверхности составляющие скорости отсутствуют, следовательно, при установившемся движении ни одна частица жидкости, ни в одной точке трубки тока не может проникнуть внутрь струйки или выйти наружу.

Трубка тока, таким образом, является как бы непроницаемой стенкой, а элементарная струйка представляет собой самостоятельный элементарный поток.

Потоки конечных размеров будем сначала рассматривать, как совокупность элементарных струек, т. е. будем предполагать течение струйным. Из-за различия скоростей соседние струйки будут скользить одна по другой, но не будут перемешиваться одна с другой.

Живым сечением или сечением потока, называется площадь поверхности в пределах потока или струйки, проведенная нормально к линиям тока. Далее будем рассматривать в потоках такие участки, в которых струйки можно считать параллельными и, следовательно, живые сечения плоскими.

Различают напорные и безнапорные течения жидкости. Напорными называют течения в закрытых руслах без свободной поверхности, а безанапорными течения со свободной поверхностью. При напорных течениях давление вдоль потока обычно переменное, при безнапорном на свободной поверхности постоянное и чаще всего атмосферное. Примерами напорного течения могут служить течения в трубопроводах с повышенным (или пониженным) давлением, в гидромашинах или других гидроагрегатах. Безнапорными являются течения в реках, открытых каналах и лотках.

5.2. Расход. Уравнение расхода

Расходом называется количество жидкости, протекающее через живое сечение потока в единицу времени. Это количество можно измерить в единицах объема, в весовых единицах, в единицах массы в связи, с чем различают объемный Q , весовой Q_G и м ассовый расходы Q_m .

Для элементарной струйки, имеющей бесконечно малые площади сечений, можно считать истинную скорость одинаковой во всех точках каждого сечения. Следовательно, для этой струйки расходы равны.

объемный, (м 3 /с) dQ = v * dS , (5.136)

весовой, (Н/с) d Q_G = ρg * dQ , (5.2)

массовый, (кг/с) dQ_m = ρv * dS , (5.3)

где dS – площадь сечения струйки.

Для потока конечных размеров в общем случае скорость имеет различное значение в разных точках сечения, поэтому расход надо определять, как сумму элементарных расходов струек в данном сечении.

Q = 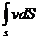. (5.4)

Обычно в рассмотрение вводят среднюю по сечению скорость v _ср = Q / S , откуда средний расход для струйки или потока равен

Условие неразрывности потока основывается на следующих свойствах, законе и предпосылках.

а) трубка тока имеет свойство непроницаемости для внешних, обтекающих ее потоков;

б) закон сохранения вещества;

в) предположение о сплошности (неразрывности) среды для установившегося течения несжимаемой жидкости.

На основании этих предпосылок и свойств можно утверждать, что объемный расход во всех сечениях элементарной струйки (см. рис.5.2) один и тот же

dQ = v ₁ * dS ₁ = v ₂ * dS ₂ → const (вдоль струйки). (5.6)
Это уравнение называется уравнением объемного расхода для элементарной струйки.

Аналогичное уравнение можно составить и для потока конечных размеров, ограниченного непроницаемыми стенками, только вместо истинных скоростей следует ввести средние скорости. В результате

Из последнего уравнения следует, что средние скорости в потоке несжимаемой жидкости обратно пропорциональны площадям сечений:

У равнение расхода (5.6‘) является следствием общего закона сохранения вещества для частных условий, в частности? для условий сплошности (неразрывности) течения.

5.3. Уравнение Бернулли для элементарной струйки

Рассмотрим установившееся течение идеальной жидкости находящейся под действием одной массовой силы — силы тяжести, и выведем для этого случая основное уравнение, связывающее между собой давление в жидкости и скорость ее движения.

Возьмем одну из элементарных струек, составляющих поток, выделим сечениями 1 и 2 участок этой струйки произвольной длины (рис.5.3). Пусть площадь первого сечения равна dS ₁ , скорость в нем V ₁ , давление P ₁ , а высота от произвольной плоскости сравнения Z ₁ . Во втором сечении dS ₂ , V ₂ , P ₂ и Z ₂ .

За бесконечно малый отрезок времени dt выделенный участок струйки переместится в положение 1’ – 2’ .

Применим к массе жидкости в объеме участка струйки теорему о кинетической энергии: работа сил, приложенных к телу, равна приращению кинетической энергии этого тела.

На жидкость действуют силы тяжести и силы давления, нормально к поверхности сечения рассматриваемого участка струйки.

Подсчитаем работу сил давления, сил тяжести и изменение кинетической энергии участка струйки за время dt . Эта теорема выглядит следующим образом.

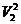
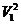
( m )/2 — ( m )/2 = G * h = G * (Z₁-Z₂)

Работа силы давления в первом сечении положительна, так как направление силы совпадает с направлением перемещения, и выражается как произведение силы p ₁* dS на путь V ₁ dt :

Работа силы давления во втором сечении имеет знак минус, так как направление силы прямо противоположно направлению перемещения, и определяется выражением

Силы давления, действующие по боковой поверхности отрезка струйки, работы не производят, так как они нормальны к этой поверхности и к перемещениям.

Работа сил давления равна

Работа силы тяжести равна изменению потенциальной энергии положения участка струйки, поэтому надо из потенциальной энергии жидкости в объеме 1 — 2 вычесть потенциальную энергию жидкости в объеме 1’- 2’ . При этом энергия промежуточного объема 1’- 2 сократится, и останется лишь разность энергии элементов 1- 1’ , 2- 2’ .

ПО уравнению расходов (закон сплошности среды) ( 5.6’ ) объемы и силы тяжести заштрихованных элементов 1 -1’ и 2 — 2’ равны между собой:

Тогда работа силы тяжести выразится как произведение разности высот на силу тяжести dG :

Чтобы подсчитать приращение кинетической энергии рассматриваемого участка струйки за время dt , необходимо из кинетической энергии объема 1’- 2’ вычесть кинетическую энергию объема 1 — 2. При вычитании кинетическая энергия промежуточного объема 1’ — 2 сократится, и останется лишь разность кинетических энергий элементов 2 — 2’ и 1 — 1’ , масса каждого из которых равна dG / g .

Таким образом, приращение кинетической энергии на участке струйки равно

Сложив работу сил давления (см. уравнение 5.7) с работой силы тяжести (5.9) и приравняв эту сумму приращению кинетической энергии (5.10), получим исходное уравнение для трех видов уравнения Бернулли.

Разделим это уравнение на dG (изменение силы тяжести элементарной струйки за время dt ) (см. формулу (5.8) , и произведя сокращения на

Сгруппируем члены, относящиеся к первому сечению, в левой части уравнения, а члены, относящиеся ко второму сечению, в правой:

( 5 . 12 )

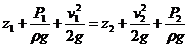
где z — геометрическая высота, или геометрический напор;

Р/ρ g – пьезометрическая высота или пьезометрический напор;

v 2 /2 g — скоростная высота или скоростной напор.

Полученное уравнение называется уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости. Оно было выведено Даниилом Бернулли в 1738 г .

Это уравнение является первой формой уравнения Бернулли, оно

( 5 . 13 )

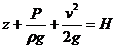
называется полным напором и имеет размерность длины.

Данное уравнение получено путем деления исходного уравнения (5.11), выражающего теорему об изменении кинетической энергии элементарной струйки, на ее изменении ее силы тяжести за время dt .

Уравнение Бернулли (5.13) записано для двух произвольно взятых сечении струйки и выражает равенство полных напоров Н в этих сечениях. Так как сечения взяты произвольно, следовательно, и для любого другого сечения этой же струйки полный напор будет иметь то же значение

(вдоль струйки)

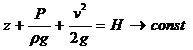
Для идеальной движущейся жидкости вдоль струйки тока сумма трех напоров: геометрического, пьезометрического и скоростного есть величина постоянная.

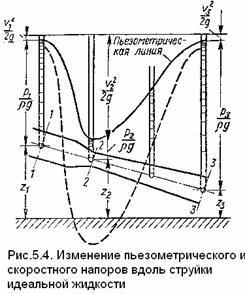
На рис. 5.4 показано изменение всех напоров вдоль струйки.

Линия изменения уровней жидкости в пьезометрах называется пьезометрической линией.

Из уравнения Бернулли и уравнения расхода следует, что если площадь поперечного сечения струйки уменьшается, т. е. струйка сужается, то скорость течения жидкости увеличивается, а давление уменьшается, и наоборот, если струйка расширяется, то скорость уменьшается, а давление возрастает.

На рис. 5.4 площадь поперечного сечения струйки от сечения 1 — 1 к сечению 2 — 2 уменьшается в 4 раза, скоростной напор увеличивается в 16 раз, а сечение 3 — 3 имеет ту же площадь, что и сечение 1-1.

Штриховой линией показано положение пьезометрической линия при тех же сечениях и при увеличении расхода в 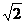раз, вследствие чего скоростные высоты увеличиваются в 2 раза, а в узкой части струйки давление становятся меньше атмосферного.

Уравнение Бернулли можно записать в двух других формах. Разделив уравнение (5.11) на расход dQ = dS ₁* v ₁ dt = dS ₂* v ₂ dt , учитывая, что dG = ρ *g*dQ, а dQ = dG / ρ g, получим

, (5.15)

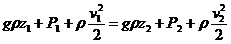
где все величины выражены в виде давлений.

В этой форме члены уравнения Бернулли имеют размерность давления и имеют следующие называния: ρ zg — весовое давление; р — гидромеханическое давление; ρ v 2 /2 — динамическое давление.

Разделив уравнение (5.11) на массу dm элементарного объема, равную ( ρ * v _1* dS ₁) * dt = ( ρ * v _2* dS ₂) * dt и преобразуем это уравнение подобно предыдущему. Тогда вместо выражения (5.15) будем иметь

(5.16)

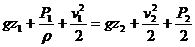
Введем понятие удельной энергии жидкости, в качестве которой рассмотрим отношение энергии к массе или объему.

Нетрудно показать, что члены уравнения (5.16) представляют собой различные формами удельной механической энергии, а именно:

gz — удельная потенциальная энергия (ее еще называют энергией положения), так как частица жидкости массой Δ m , находясь на высоте z , обладает энергией равной Δ mgz , а на единицу массы приходится энергия g Δ mz /Δ m = gz ;

р/ρ — удельная энергия давления (движущейся) жидкости, так как частица массой Δ m при давлении р обладает способностью подняться на высоту h = р/ρ g и приобрести, таким образом, энергию положения Δ mg р/(ρ g ) = р/ρ (после деления на Δ m получаем р/ρ);

сумма gz + р/ρ – удельная потенциальная энергия жидкости;

v 2 /2 — удельная кинетическая энергия жидкости, так как для той же частицы Δ m кинетическая энергия отнесенная к ее массе Δ m v 2 /2 : Δ m = v 2 /2;

Hg = zg + p /ρ+ v 2 /2 – полная удельная механическая энергия движущейся жидкости.

Таким образом, энергетический смысл уравнения Бернулли для элементарной струйки идеальной жидкости заключается в постоянстве вдоль струйки полной удельной энергии жидкости.

Механическая энергия жидкости может иметь три формы: потенциальная энергия, энергия давленияи и кинетическая энергия.

Первая и третья формы механической энергии известны из механики, они свойственны твердым и жидким телам.

Энергия давления является специфической для движущихся жидкостей. В процессе движения идеальной жидкости одна форма энергии может превращаться в другую, однако полная удельная энергия идеальной жидкости при этом как следует из уравнения Бернулли, остается без изменений.

Энергию давления легко преобразовать в механическую работу. Простейшим устройством, с помощью которого осуществляют такое преобразование, является цилиндр с поршнем (рис. 5.5). Покажем, что при этом преобразовании каждая единица массы жидкости совершает работу, численно равную р/ρ.

Пусть площадь поршня равна s , его ход L , избыточное давление жидкости в левой полости цилиндра необходимое для преодоления силы F равно Р = F / S , избыточное давление по другую сторону поршня равно нулю. Преодолевая силу F при перемещении поршня из левого положения, давление совершает работу А = Р SL . Расход жидкости, которую необходимо подвести к цилиндру для совершения этой работы за время t , равен объему цилиндра, т. е. Q t = W = SL .Удельная работа, приходящаяся на 1 кг массы,

Уравнение неразрывности и уравнение Бернулли.

Уравнение неразрывности потока и уравнения Бернулли являются основными уравнениями гидродинамики. При изучении потоков жидкости вводится ряд понятий, характеризующий потоки с гидравлической и геометрической точек зрения.

Такими понятиями являются: площадь живого сечения потока(или живое сечение потока), расход и средняя скорость.

Площадью живого сечения потока, называют площадь сечения потока, приведенную нормально к направлению линии тока, т.е. перпендикулярно движению струйки жидкости. Живое сечение может быть ограничено твердыми стенками полностью или частично. Если стенки ограничивают поток полностью, то движение жидкости называют напорным; Если же ограничение частичное, то движение называется безнапорным.

Напорное движение характеризуется тем, что гидродинамическое давление в любой точке потока отлично от атмосферного и может быть как больше, так и меньше него. Безнапорное движение характеризуется постоянным давлением на свободной поверхности, обычно равным атмосферному.

Содержание статьи

Расходом потока называется количество жидкости, протекающей через поперечное сечение в единицу времени. Если рассматривать поток жидкости, представляющий собой совокупность большого числа элементарных струек, то очевидно, общий расход жидкости для всего потока в целом представляет собой сумму расходов всех отдельных струек.

Для нахождения этой суммы необходимо знать закон распределения скоростей в сечении потока. Так как во многих случаях движения такой закон неизвестен, в общем случае суммирование становится невозможным. Поэтому в гидродинамике вводится предположение, что все частицы жидкости по всему поперечному сечению потока движутся с одинаковой скоростью. Эту воображаемую фиктивную скорость называют средней скоростью потока υ_ср .

Таким образом уравнение расхода для потока будет

υ_ср – средняя скорость потока

F – площадь сечения потока.

Уравнение неразрывности потока жидкости

Теперь вооружившись основными понятиями перейдем к определению уравнения неразрывности потока.

Отделим сечениями 1-1 и 2-2 некоторый отрезок элементарной струйки. В этот отрезок в единицу времени через сечение 1-1 втекает объем жидкости равный

а через сечение 2-2 из него же вытекает объем, равный

Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств – т.е. будем считать, что соблюдается условие сплошности или неразрывности движения.

Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из ней отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечение 1-1 и 2-2, должны быть одинаковы.

Такие соотношения можно составить для любых двух сечений струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки

Это уравнение называется уравнением неразрывности жидкости – оно является первым основным уравнением гидродинамики. Переходя далее к потоку жидкости в целом получаем, что

т.е. средние скорости в поперечных сечениях потока при неразрывности движения обратно пропорциональны площади этих сечений.

Уравнение неразрывности струи жидкости. Уравнение Бернулли.

Вторым основным уравнением гидродинамики является уравнение Бернулли, устанавливающее взаимосвязь между скоростью и давлением в различных сечениях одной и той же струйки.

При рассмотрении уравнения Бернулли также как и в предыдущем случае ограничимся установившемся медленно изменяющимся движением. Выделим в объеме некоторой жидкости одну элементарную струйку и ограничим её в какой-то определенный момент времени Т сечениями 1-1 и 2-2.

Допустим, что через какой-то промежуток времени ΔТ указанный объем переместится в положение 1’ – 1’ и 2’ – 2’. Тогда применяя к движению этого сечению теорему кинетической энергии, определяем, что приращение кинетической энергии движущейся системы материальных частиц равняется сумме работ всех сил, действующих на систему.

Если всё это записать в виде формулы, то

где W – приращение кинетической энергии = m * υ 2 / 2

ΣA – сумма работ действующих сил = P *ΔS

В этих выражениях
m – масса
υ – скорость материальной точки
P – равнодействующая всех сил, приложенных к точке,
ΔS – проекция перемещения точки на направление силы.

Теперь рассмотрим обе части этого выражения по порядку.

Приращение кинетической энергии ΔW

В нашем случае приращение кинетической энергии определяется как разность значений кинетической энергии в двух положениях перемещающегося объема, т.е. как разность кинетической энергии объема образованного сечениями 1-1’ и объема, образованного сечениями 2 – 2’.

Эти объемы являются результатом перемещения за время ΔТ сечений выделенного участка элементарной струйки.

Вспоминая, что по условию неразрывности расход во всех сечениях элементарной струйки одинаков, а следовательно будет равен

масса в этом случае получается равной

Подставляя все это в выражение для кинетической энергии получаем цепочку

ΔW = m * υ 2 ₂ / 2 — m * υ 2 ₁ / 2 = ρ * q * ΔТ * υ 2 ₂ / 2 — ρ * q * ΔТ * υ 2 ₁ / 2

Работа сил действующих на систему ΣA

Теперь перейдем к рассмотрению работы сил, действующих на рассматриваемый объем жидкости. Работа сил тяжести A_Т равна произведению этой силы на путь, пройденный центром массы движущегося объема жидкости по вертикали.

Для рассматриваемой в нашем примере струйки работа сил тяжести будет равна произведению сил тяжести объема занимаемого сечениями 1-1’ и 2 – 2’ на расстояние Z1 –Z2.

Где Z1 и Z2 – расстояния по вертикали от горизонтальной плоскости, называемой плоскостью сравнения до центров масс объемов 1-1’ и 2 – 2’.

Силы давления А_Д , действующие на объем жидкости складываются из сил давления на его боковую поверхность и на концевые поперечные сечения. Работа сил давления на боковую поверхность равна нулю, так как эти силы за все время движения нормальны к перемещению их точек приложения.

Суммарно работа сил давления будет

Подставляя в начальное уравнение

Полученные выражения для ΔW и ΣA получаем

Разделим обе части этого уравнения на m = ρ*q*ΔТ и перегруппируем слагаемые

Учитывая, что сечения 1-1 и 2-2 взяты нами совершенно произвольным образом, это уравнение возможно распространить на всю струйку. Применив его для любых поперечных сечений, взятых по её длине, и представить в общем виде:

Записанные выше два уравнения представляют собой уравнение Бернулли для элементарной струйки жидкости. Сумма трех слагаемых, входящих в это уравнение, называется удельной энергией жидкости в данном сечении струйки. Различают такие энергии как:
Удельная энергия положения = qz
Удельная энергия давления = p/ ρ
Кинетическая удельная энергия = υ 2 / 2

В соответствии с этим уравнение Бернулли для струйки жидкости можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Видео по теме уравнение неразрывности

Полученные в результате многочисленных экспериментов данные из уравнения Бернулли и уравнения неразрывности потока жидкости нашли широкое применение в повседневной жизни.

Уравнение Бернулли широко используется для нахождения скорости истечения жидкости через отверстия.

Уравнение неразрывности обладает широкой универсальностью и справедливо для любой сплошной среды. Принцип уравнения неразрывности используется для формирования сильной и дальнобойной струи воды при тушении пожаров.

Лекция 5

5. КИНЕМАТИКА И ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ-1

5.1. Основные понятия: задачи кинематики, линия тока, трубка тока.

5.2. Расход. Уравнение расхода

5.3 Уравнение неразрывности потока.

5.4. Уравнение Бернулли для элементарной струйки идеальной жидкости.

5.5. Первая форма уравнения Бернулли

5.6. Вторая форма уравнения Бернулли.

5.7. Третья форма уравнения Бернулли.

Рекомендуемые файлы

5.8. Вывод дифференциальных уравнений движения идеальной жидкости

и их интегрирование (уравнений Эйлера)

5.1. Основные понятия

Кинематика жидкости отличается от кинематики твердого тела. Отдельные частицы твердого тела жестко связаны между собой, в жидкой среде такие связи отсутствуют. Жидкость состоит из множества частиц, перемещающихся одна относительно другой и, кроме того, частицы дополнительно движутся совместно.

Идеальная жидкость в гидродинамике — модель жидкости, в которой, в отличие от реальной жидкости, отсутствуют вязкость. При отсутствии вязкости отсутствует внутреннее трение, нет касательных напряжений между двумя соседними слоями.

Моделью идеальной жидкости пользуются при решении задач, в которых вязкость не является определяющим фактором и ею можно пренебречь. Эта модель позволяет найти решение ряда задач о движении жидкостей и газов в каналах различной формы, при истечении струй, при обтекании тел.

В идеальной жидкости, как в неподвижной реальной жидкости, возможны только нормальные напряжения сжатия, т. е. гидромеханическое давление.

Задачей кинематики жидкости является определение скорости в любой точке жидкой среды, т. е. нахождение поля скоростей.

Установившимся называется течение жидкости, при котором давление и скорость являются функциями координат и не зависят от времени.

При установившемся движении давление и скорость могут изменяться при перемещении частицы жидкости из одного положения в другое.

Установившееся течение может быть равномерным, когда скорость каждой частицы не изменяется при изменении ее координат. Поле скоростей остается неизменным вдоль потока.

Примером установившегося течения может служить истечение жидкости из сосуда, в котором поддерживается постоянный уровень, или движение жидкости в трубопроводе, создаваемое центробежным насосом с постоянной частотой вращения вала.

При установившемся течении траектории частиц жидкости от времени не зависят.

Неустановившимся называется течение жидкости, характеристики которого изменяются во времени в точках рассматриваемого пространства.

При неустановившемся течении давление и скорость зависят от координат и от времени:

Примерами неустановившегося течения жидкости могут служить быстрое опорожнение сосуда через отверстие в дне или движение во всасывающей или напорной трубе поршневого насоса, поршень которого совершает возвратно-поступательное движение.

При неустановившемся течении траектории различных частиц, проходящих через данную точку пространства, могут иметь разную форму.

Для изучения течения жидкости вводится понятие линии тока.

Линией тока называется кривая, в каждой точке которой вектор скорости в данный момент времени направлен по касательной к этой кривой (рис.5.1).

Очевидно, что в условиях установившегося течения линия тока совпадает с траекторией частицы и не изменяет своей формы с течением времени.

Трубкой тока называется бесконечно малый замкнутый контур, выделенный в данный момент времени в движущейся жидкости, через все точки которого проведены линии тока. Это условная трубчатая поверхность.

Элементарной струйкой называется часть потока, заключенная внутри трубки тока (рис.5.2).

В любой точке «трубки тока» т.е. на трубчатой поверхности струйки, векторы скорости направлены по касательной, а нормальные к этой поверхности составляющие скорости отсутствуют, следовательно, при установившемся движении ни одна частица жидкости, ни в одной точке трубки тока не может проникнуть внутрь струйки или выйти наружу.

Трубка тока, таким образом, является как бы непроницаемой стенкой, а элементарная струйка представляет собой самостоятельный элементарный поток.

В модели идеальной жидкости потоки конечных размеров рассматривают, как совокупность элементарных струек. Соседние струйки из-за различия скоростей скользят одна по другой, но не перемешиваются.

Живым сечением или сечением струйки δS или потока — S, называется площадь поверхности в пределах струйки или потока, проведенная нормально к линиям тока. Смоченным периметром называется длина части периметра живого сечения, на которой поток соприкасается с твердыми стенками..

Для круглой трубы это длина окружности P = πd, а если труба заполнена наполовину, то P = 0,5πd.

Гидравлическим радиусом называется отношение площади живого сечения к смоченному периметру Rг = S/P. Для потока в трубе круглого сечения:

Rг = S/P = (π/4)*d 2 / (πd)=d/4.

5.2. Расход. Уравнение расхода

Расходом называется количество жидкости, протекающее через живое сечение потока в единицу времени. Это количество можно измерить в единицах объема, веса, массы в связи, с чем различают расходы:

Q – объемный, (м 3 /с);

Для элементарной струйки, имеющей малую площадь сечения, мгновенную скорость принимают одинаковой во всех точках сечения, расход для элементарной струйки:

Объемный — δQ = V*δS, (5.1)

где V — мгновенная скорость в данной точке, δS – площадь сечения струйки.

Для потока конечных размеров в общем случае скорость имеет различное значение в разных точках сечения, поэтому расход равен сумме элементарных расходов струек в данном сечении.

(5.4)

Если использовать среднюю по сечению скорость V_ср = Q/S, то средний расход для струйки или потока равен

5.3 Уравнение неразрывности потока.

Условие неразрывности потока основывается на законе сохранения вещества.

А также на следующих допущениях:

а) трубка тока имеет свойство непроницаемости для внешних, обтекающих ее потоков;

б) предположение о сплошности (неразрывности) среды для установившегося течения несжимаемой жидкости.

На этих основаниях можно утверждать, что объемный расход во всех сечениях элементарной струйки (см. рис.5.2) один и тот же.

Уравнение неразрывности для элементарной струйки (уравнение расхода для элементарной струйки).

Из этого уравнения (5.6′) следует, что средние скорости в потоке несжимаемой жидкости обратно пропорциональны площадям сечений:

Уравнение расхода (5.6‘) является следствием общего закона сохранения вещества при условии сплошности (неразрывности) течения.

5.4. Уравнение Бернулли для элементарной струйки

Установившееся течение идеальной жидкости происходит под действием одной массовой силы — силы тяжести. Для этого случая основное уравнение установившегося течения идеальной жидкости связывает между собой давление в жидкости и скорость ее течения.

Возьмем одну из элементарных струек, составляющих поток, выделим сечениями 1 и 2 участок этой струйки произвольной длины (рис.5.3). Пусть площадь первого сечения равна δS₁, скорость в нем V₁ , давление P₁, а высота от плоскости сравнения Z₁. Во втором сечении δS₂, V₂ , P₂ и Z₂.

За бесконечно малый отрезок времени δt выделенный участок струйки переместится в положение 1’ – 2’.

Применим к массе жидкости в объеме участка струйки теорему о кинетической энергии: работа сил, приложенных к телу, равна приращению кинетической энергии этого тела.

На жидкость действуют силы тяжести и силы давления, нормальные к поверхностям сечений рассматриваемого участка струйки.

Используя формулировку теоремы, подсчитаем работу сил давления, сил тяжести и изменение кинетической энергии участка струйки за время δt:

Работа силы давления в первом сечении положительна, так как направление силы совпадает с направлением перемещения, и выражается как произведение силы p₁*δS на путь V₁δt:

Работа силы давления во втором сечении имеет знак минус, так как направление силы противоположно направлению перемещения, и определяется выражением

Силы давления, действующие по поверхности струйки, работы не производят, так как они нормальны к перемещениям.

Работа сил давления равна

Работа силы тяжести равна изменению потенциальной энергии выделенного объема струйки. Из потенциальной энергии жидкости в объеме 1 — 2 вычтем потенциальную энергию жидкости в объеме 1’- 2’. При этом энергия промежуточного объема 1’- 2 сократится, и останется лишь разность энергии элементов 1- 1’, 2- 2’.

По уравнению расходов (закон неразрывности) (5.6’) объемы и силы тяжести заштрихованных элементов 1 -1’ и 2 — 2’ равны между собой:

Тогда работа силы тяжести выразится как произведение разности высот на силу тяжести δG:

Чтобы подсчитать приращение кинетической энергии рассматриваемого участка струйки за время δt, необходимо из кинетической энергии объема 1’- 2’ вычесть кинетическую энергию объема 1 — 2. При вычитании кинетическая энергия промежуточного объема 1’ — 2 сократится, и останется лишь разность кинетических энергий элементов 2 — 2’ и 1 — 1’, масса каждого из которых равна δG/g.

Таким образом, приращение кинетической энергии на участке струйки равно

Сложив работу сил давления (см. уравнение 5.7) с работой силы тяжести (5.9) и приравняв эту сумму приращению кинетической энергии (5.10), получим исходное уравнение для трех видов уравнения Бернулли.

сохранять на доске!

5.5. Первая форма уравнения Бернулли

Разделим это уравнение на δG — изменение силы тяжести элементарной струйки за время δt, (см. формулу (5.8) , и произведя сокращения на

Сгруппировав члены, относящиеся к первому сечению, в левой части уравнения, а члены, относящиеся ко второму сечению, в правой, получим

Писать!»Уравнение Бернулли для элементарной струйки идеальной несжимаемой жидкости (первая форма уравнения Бернулли)»:

(5.12)

где z — геометрический напор,

Р/ρg — пьезометрический напор,

V 2 /2g — скоростной напор.

Это уравнение полного напора, так как члены, входящие в него имеют размерность длины было выведено Даниилом Бернулли в 1738 г.

Уравнение Бернулли (5.12) записано для двух произвольно взятых сечении струйки и выражает равенство полных напоров Н в этих сечениях. Так как сечения взяты произвольно, следовательно, и для любого другого сечения этой же струйки полный напор будет иметь одно и то же значение.

Для идеальной движущейся жидкости вдоль струйки тока сумма трех напоров: геометрического, пьезометрического и скоростного есть величина постоянная.

На рис. 5.4 показано изменение всех напоров вдоль струйки.

Линия изменения уровней жидкости в пьезометрах называется пьезометрической линией.

Поскольку в уравнении Бернулли суммарный напор постоянен, из уравнения расхода следует: при уменьшении площади поперечного сечения струйки, скорость течения жидкости увеличивается и увеличивается скоростной напор, а пьезометрический напор уменьшается, если площадь струйки увеличивается, скорость уменьшается, а пьезометрический напор возрастает.

Например, если площадь поперечного сечения струйки в сечении 1 — 1 больше, чем в сечении 2 — 2 в 4 раза, скоростной напор увеличивается в 16 раз (рис. 5.4).

В сечении 3 — 3 та же площадь, что и сечение 1-1, и скоростные напоры одинаковы.

5.6. Вторая форма уравнения Бернулли.

Разделив исходное уравнение (5.11) на элементарный объем

. (5.13)

Во второй форме члены уравнения Бернулли имеют размерность давления:

р — гидромеханическое давление;

5.7. Третья форма уравнения Бернулли.

Разделив исходное уравнение (5.11) на массу δm = ρ*g*δW элементарного объема, равную

(5.16)

Удельной энергией жидкости, называется отношение энергии жидкости к ее массе.

В третьей форме члены уравнения Бернулли имеют размерность энергии:

gz — удельная потенциальная энергия.

Частица жидкости массой δm, помещенная высоту z, обладает энергией равной (δmg)z, на единицу массы приходится удельная энергия

Р/ρ — удельная энергия давления жидкости.

Частица массой δm при давлении р обладает способностью подняться на высоту h = P/ρg, и ее потенциальная энергия увеличится на величину равную (δmg)h = δm(P/ρ), на единицу массы увеличение удельной потенциальной энергии

Сумма gz + р/ρ является удельной потенциальной энергией жидкости;

V 2 /2 — удельная кинетическая энергия жидкости.

Сумма Hg = zg+P/ρ+ V 2 /2 называется полной удельной механической энергией движущейся идеальной жидкости.

Энергетический смысл уравнения Бернулли для элементарной струйки идеальной жидкости заключается в постоянстве вдоль струйки полной удельной энергии жидкости.

Механическая энергия жидкости может иметь три формы: потенциальная энергия, энергия давления и кинетическая энергия.

Первая и третья формы механической энергии известны из механики, они свойственны твердым и жидким телам.

Энергия давления является специфической для движущихся жидкостей. В процессе движения идеальной жидкости одна форма энергии может преобразовываться в другую, однако полная удельная энергия идеальной жидкости при этом как следует из уравнения Бернулли, остается без изменений.

Энергию давления легко преобразовать в механическую работу. Простейшим устройством, с помощью которого осуществляют такое преобразование, является гидроцилиндр (рис. 5.5). При этом преобразовании каждая единица массы жидкости совершает работу, численно равную р/ρ.

Пусть площадь поршня равна s, его ход L, избыточное давление жидкости в левой полости цилиндра, необходимое для преодоления силы R, равно р =R/S, избыточное давление по другую сторону поршня равно нулю. Преодолевая силу R при перемещении поршня из левого положения, давление совершает работу А = рSL. Расход жидкости, который необходимо подвести к цилиндру для совершения этой работы за время t , равен объему цилиндра, т. е. Q t = W =SL.Удельная работа, приходящаяся на 1 кг массы,

5.8. Вывод дифференциальных уравнений движения

идеальной жидкости и их интегрирование (уравнений Эйлера).

В потоке идеальной жидкости возьмем произвольную точку М с координатами x, y, z (рис.5.6) и выделим вблизи этой точки малый объем в форме прямоугольного параллелепипеда так, чтобы точка М была одной из его вершин. Пусть ребра этого параллелепипеда будут параллельны координатным осям и соответственно равны δх, δу и δz, тогда его объем равен δW = δх*δу*δz, а масса δМ= ρδхδуδz.

Составим уравнение движения этого объема. Действующая на объем результирующая массовая сила, может быть разложена на составляющие соответственно осям координат, и, будучи отнесена к массе объема, даст единичные массовые силы или проекции ускорений на оси: Х, У и Z.

Проекции массовых сил, действующих на выделенный объем, равны этим составляющим, умноженным на массу выделенного объема.

Если давление в точке М обозначить через Р, давление вдоль оси Х в точке N — будет сумой давления в точке М и приращения по координате Х.

Разность между значениями давлений в этих точках, умноженная на площадь даст нам силу, действующую вдоль оси Х

.

Принцип Д’Аламбера: При движении системы ее положение может рассматриваться, как положение равновесия, если к активным силам, действующим на систему, прибавить фиктивные силы(силы инерции).

По принципу Д’Аламбера силы, которые необходимо ввести в уравнения движения, равны произведению ускорений на массу параллелепипеда.

Уравнения движения выделенного объема жидкости в проекциях на координатные оси будут иметь вид

где X,Y, Z – проекции единичных массовых сил.

Разделим эти уравнения почленно на массу элемента δm = ρ*δхδyδz и перейдем к пределу, устремляя одновременно δх, δy и δz к нулю и, стягивая параллелепипед к точке М, получим уравнения движения жидкости. Это система дифференциальных уравнений движения идеальной жидкости, называемая уравнениями Эйлера.

(5.16)

Члены этих уравнений представляют собой соответствующие ускорения, а смысл каждого из уравнений заключается в следующем: полное ускорение частицы вдоль координатной оси складывается из ускорения от массовых сил и ускорения от сил давления.

Уравнения Эйлера в таком виде справедливы как для несжимаемой, так и для сжимаемой жидкости, а также для случая, когда из массовых сил действует только сила тяжести, и для общего случая относительного движения жидкости. При этом в величины Х, У и Z входят компоненты ускорения переносного движения. Так как при выводе уравнений (5.16) не накладывались условия стационарности движения, то они справедливы и для неустановившегося движения.

Рассматривая установившееся движение жидкости, умножим каждое из уравнений (5.16) на проекции элементарного перемещения по осям и сложим уравнения:

В проекциях на ось X:

В проекциях на ось Y:

В проекциях на ось Z:

Просуммировав эти проекции, получим:

(5.17)

Учитывая, что выражение в скобках является полным дифференциалом давления: .

Произведение проекции скорости на дифференциал скорости можно выразить следующим образом:

Уравнение (5.17) можно переписать в следующем виде

где U – силовая функция.

Интегрирование этого уравнения выполним для основного частного случая установившегося движения идеальной жидкости, когда на жидкость действует лишь одна массовая сила — сила тяжести. При направлении оси вертикально вверх

Подставляя эти значения в уравнение (5.17) получим

Так как для несжимаемой жидкости ρ = const, предыдущее уравнение можно переписать в виде

Это уравнение означает, что приращение суммы трех членов, заключенных в скобки, при перемещении частицы жидкости вдоль линии тока (траектории) равно нулю, следовательно, указанный трехчлен есть величина постоянная вдоль линии тока, а следовательно, и вдоль элементарной струйки, т. е.

z + p/(gρ) + (v 2 /2g) → const.

Таким образом, получили уравнение Бернулли для струйки идеальной жидкости, найденное в предыдущем параграфе другим способом.

Если записать это уравнение для двух сечений струйки 1-1 и 2-2, оно примет вид первой формы уравнения Бернулли:

= Н