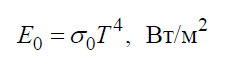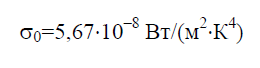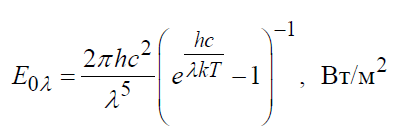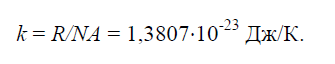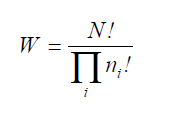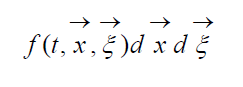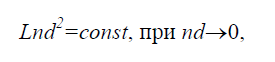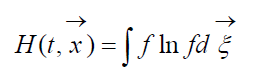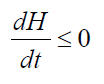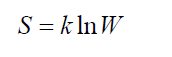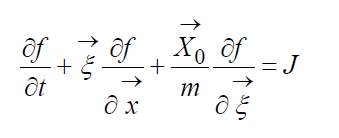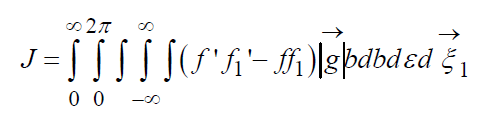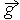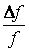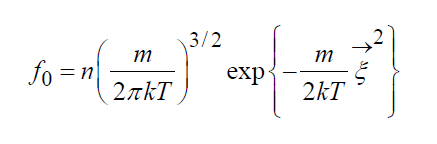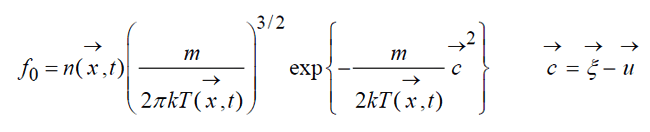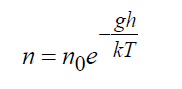Кинетическое уравнение больцмана интеграл столкновений

кинетическое уравнение больцмана

КИНЕТИЧЕСКОЕ УРАВНЕНИЕ БОЛЬЦМАНА — интегродифференц. ур-ние, к-рому удовлетворяют неравновесные одночастичные функции распределения системы из большого числа частиц, напр, ф-ция распределения молекул газа по скоростям и координатам r, ф-ции распределения электронов в металле, фононов в кристалле и т. п. К. у. Б.- осн. ур-ние мик-роскопич. теории неравновесных процессов (кинетики физической), в частности кинетической теории газов. К. у. Б. в узком смысле наз. выведенное Л. Больцма-ном (L. Boltzmann) кинетич. ур-ние для газов малой плотности, молекулы к-рых подчиняются классич. механике. К. у. Б. для квазичастиц в кристаллах, напр. для электронов в металле, наз. также кинетич. ур-ниями или ур-ниями переноса.

К. у. Б. представляет собой ур-ние баланса числа частиц (точнее, точек, изображающих состояние частиц) в элементе фазового объёма ; dr= =dxdydz)и выражает тот факт, что изменение ф-ции распределения частиц со временем t происходит вследствие движения частиц под действием внеш. сил и столкновений между ними. Для газа, состоящего из частиц одного сорта, К. у. Б. имеет вид

где — изменение плотности числа частиц в элементе фазового объёма за единицу времени, F= =F(r,t) — сила, действующая на частицу (может зависеть также и от скорости), — изменение ф-ции распределения вследствие столкновений (интеграл столкновений). Второй и третий члены ур-ния (1) характеризуют соотв. изменения ф-ции распределения в результате перемещения частиц в пространстве и действия внеш. сил. Её изменение, обусловленное столкновениями частиц, связано с уходом частиц из элемента фазового объёма при т. н. прямых столкновениях и пополнением объёма частицами, испытавшими «обратные» столкновения. Если рассчитывать столкновения по законам классич. механики и считать, что нет корреляции между динамич. состояниями сталкивающихся молекул, то

— скорости частиц до столкновения, — скорости тех же частиц после столкновения, — величина относит. скорости сталкивающихся частиц, — дифференц. эфф. сечение рассеяния частиц в телесный угол в лаб. системе координат, — угол между относит. скоростью и линией центров. Напр., для жёстких упругих сфер, имеющих радиус R, = , для частиц, взаимодействующих по закону центр. сил, (b — прицельный параметр, — азимутальный угол линии центров).

К. у. Б. учитывает только парные столкновения между молекулами; оно справедливо при условии, что длина свободного пробега молекул значительно больше линейных размеров области, в к-рой происходит столкновение (для газа из упругих частиц это область порядка диаметра частиц). Поэтому К. у. Б. применимо для не слишком плотных газов. Иначе будет несправедливо осн. предположение об отсутствии корреляции между состояниями сталкивающихся частиц (гипотеза молекулярного хаоса). Если система находится в статистич. равновесии, то интеграл столкновений (2) обращается в нуль и решением К. у. Б. является Максвелла распределение.

При более строгом подходе для построения К. у. Б. исходят из Лиувилля уравнения для плотности распределения всех молекул газа в фазовом пространстве, из к-рого получают систему ур-ний для ф-ций распределения одной, двух и т д. молекул (Боголюбова уравнения). Эту цепочку ур-ний решают с помощью разложения по степеням плотности частиц с использованием граничного условия ослабления корреляций, заменяющего гипотезу молекулярного хаоса.

Решение К. у. Б. при разл. предположениях о силах взаимодействия между частицами — предмет кинетич. теории газов, к-рая позволяет вычислить кинетические коэффициенты и получить макроскопич. ур-ния для процессов переноса (вязкости, диффузии, теплопроводности).

Для квантовых газов значения эфф. сечений рассчитывают на основе квантовой механики с учётом неразличимости одинаковых частиц и того факта, что вероятность столкновения зависит не только от произведения ф-ций распределения сталкивающихся частиц, но и от ф-ций распределения частиц после столкновения. Для фермионов в результате этого вероятность столкновения будет уменьшаться, а для бозонов — увеличиваться. Оператор столкновения в квантовом случае принимает вид

где знак минус соответствует Ферми — Дирака статистике, а знак плюс — Бозе — Эйнштейна статистике, g — статистич. вес состояния (g = l для частиц со спином, равным нулю, и g=2 для частиц со спином),— импульс частицы. Ф-ции нормированы так, что представляют ср. число частиц в точке . Равновесные ф-ции распределения Ферми и Бозе обращают в нуль оператор столкновения (3).

Важным частным случаем К. у. Б. является кинетич. ур-ние для нейтронов, к-рые рассеиваются и замедляются ядрами среды. В этом случае внеш. сил нет и в ур-нии (1) надо положить F=0. Плотность числа нейтронов обычно мала, так что можно пренебречь столкновениями между ними и учитывать лишь их столкновения с ядрами среды (см. Диффузия нейтронов, Замедление нейтронов).

Процессы переноса, связанные с движением электронов в металле, также можно исследовать с помощью К. у. Б. В отсутствие колебаний решётки электроны свободно распространяются в металле н описываются плоскими волнами, модулированными с периодом решётки и зависящими от волнового вектора k; и номера энергетич. зоны l. Тепловое движение атомов решётки нарушает периодичность и приводит к рассеянию электронов (столкновениям между электронами и фононами). Ф-ция распределения электронов n(k, l, t)удовлетворяет К. у. Б. типа (1), в к-ром F= (E и Н — напряжённости электрич. и магн. полей, е — заряд электрона), а интеграл столкновений имеет вид

где n=n(k,l), — волновые векторы и номера зон до и после столкновения, N= =N (f, s) — ф-ция распределения фононов, f и s — волновой вектор и поляризация фононов, — нач. и конечная энергии электрона при возбуждении фонона с энергией — дельта-ф-ция, — матричные элементы перехода электрона из состояния k, l в состояние, к-рые оценивают, исходя из определ. гипотез о механизме взаимодействия электронов с решёткой. Выражение (4) получено в предположении, что время свободного пробега электронов значительно больше неопределённости для времени столкновения. Теория электропроводности, термоэлектрич. и гальвано-магн. явлений в металлах и полупроводниках основана на решении К. у. Б.

В нек-рых случаях конденсиров. систем, когда известен характер теплового движения, можно построить К. у. Б. для элементарных возбуждений (квазичастиц). Напр., теория процессов переноса энергии в кристал-лич. решётке основана на ур-нии такого типа. Если в выражении для потенц. энергии решётки ограничиться квадратичными относительно смещений атомов членами, то тепловое движение атомов в кристалле описывается свободно распространяющимися фононами — квантами нормальных колебаний решётки. Учёт членов 3-й степени приводит к возможности столкновений между фононами. В результате ф-ция распределения фононов N (f, s) будет изменяться во времени согласно кинетич. ур-нию

коэф. при кубич. членах в разложении потенц. энергии кристалла по отклонениям атомов из положения равновесия, — плотность. Ур-ние (5) описывает тройные столкновения фононов с уничтожением двух фононов и рождением одного (и обратные им процессы). Оно является ур-нием баланса фононов, движущихся в волновом пакете с групповой скоростью и сталкивающихся между собой. Теория теплопроводности непроводящих кристаллов основана на решении ур-ния (5) при малых отклонениях от статистич. равновесия.

К. у. Б. применимо также к процессам, в к-рых частицы испытывают взаимные превращения, напр, в теории ливней, образующихся при попадании космич. частиц больших энергий в атмосферу. В этом случае кинетич. ур-ния составляются как система ур-ний баланса для заряж. частиц и фотонов в данном интервале энергии и импульса. Эти ур-ния выражают тот факт, что изменение ф-ции распределения (кроме эффектов рассеяния) происходит вследствие образования пар заряж. частиц фотонами и испускания заряж. частицами фотонов в виде тормозного излучения в поле ядер.

На решении этих ур-ний основана каскадная теория ливней.

Лит. см. при статьях Кинетическая теория газов. Кинетика физическая. Д. Я. Зубарев.

Людвиг Больцман: Именные достижения

Закон излучения Стефана-Больцмана

Согласно закону Стефана – Больцмана плотность интегрального полусферического излучения E₀ зависит только от температуры и изменяется пропорционально четвертой степени абсолютной температуры T:

Постоянная Стефана-Больцмана

Стефана – Больцмана постоянная σ₀ – физическая постоянная, входящая в закон, определяющий объемную плотность равновесного теплового излучения абсолютно черного тела:

Исторически закон Стефана-Больцмана был сформулирован раньше закона излучения Планка, из которого он вытекает как следствие. Закон Планка устанавливает зависимость спектральной плотности потока излучения E₀ от длины волны λ и температуры T:

где λ – длина волны, м; с=2,998 10 8 м/с – скорость света в вакууме; Т – температура тела, К;
h = 6,625 ×10 -34 Дж×с– постоянная Планка.

Постоянная Больцмана

Физическая постоянная k, равная отношению универсальной газовой постоянной R=8314Дж/(кг × K) к числу Авогадро NA=6,022 × 10 26 1/(кг × моль):

Статистика Больцмана

Число различных конфигураций системы из N частиц для данного набора чисел n_i (число частиц, находящихся в i -том состоянии, которому соответствует энергия e _i ) пропорционально величине:

Величина W есть число способов распределения N частиц по энергетическим уровням. Если справедливо соотношение (6) то считается, что исходная система подчиняется статистике Больцмана. Набор чисел n_i , при котором число W максимально, встречается наиболее часто и соответствует наиболее вероятному распределению.

Физическая кинетика – микроскопическая теория процессов в статистически неравновесных системах.

Описание большого числа частиц может успешно осуществляться вероятностными методами. Для одноатомного газа состояние совокупности молекул определяется их координатами и значениями проекций скоростей на соответствующие координатные оси. Математически это описывается функцией распределения, характеризующей вероятность пребывания частицы в данном состоянии:

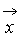
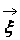
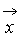
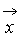
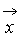
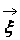
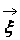
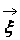
есть ожидаемое число молекул в объеме d d , координаты которых находятся в интервале от до +d, а скорости в интервале от до +d .

Газ Больцмана

Если осредненной по времени потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией, то газ называется идеальным. Идеальный газ называется газом Больцмана, если отношение длины пробега молекул в этом газе к характерному размеру течения L конечно, т.е.

т.к. длина пробега обратно пропорциональна nd 2 (n – числовая плотность 1/м 3 , d – диаметр молекулы, м).

H-функция Больцмана

называют H-функцией Больцмана для единицы объема, которая связана с вероятностью обнаружения системы из молекул газа в данном состоянии. Каждому состоянию соответствуют определенные числа заполнения шестимерных пространственно-скоростных ячеек, на которые может быть разбито фазовое пространство рассматриваемых молекул. Обозначим W вероятность того, что в первой ячейке рассматриваемого пространства окажется N₁ молекул, во второй N₂ и т.д.

С точностью до постоянной, определяющей начало отсчета вероятности, правомерно соотношение:

,

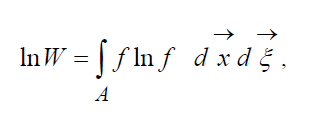
где 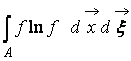– H-функция области пространства А, занятой газом. Из (9) видно, что W и H взаимосвязаны, т.е. изменение вероятности состояния приводит к соответствующей эволюции H функции.

H-теорема Больцмана

Принцип Больцмана

Больцмана принцип устанавливает связь между энтропией S физической системы и термодинамической вероятностью W её состояния:

Кинетическое уравнение Больцмана

(печатается по изданию: Коган М.Н. Динамика разреженного газа. – М.: Наука, 1967.)

где 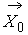– массовая сила, обусловленная наличием различных полей (гравитационного, электрического, магнитного), действующая на молекулу; J – интеграл столкновений. Именно этот член уравнения Больцмана учитывает столкновения молекул друг с другом и соответствующие изменения скоростей взаимодействующих частиц. Интеграл столкновений представляет собой пятимерный интеграл и имеет следующую структуру:

Уравнение (12) с интегралом (13) получено для столкновения молекул, при которых не возникает тангенциальных сил, т.е. сталкивающиеся частицы считаются идеально гладкими.

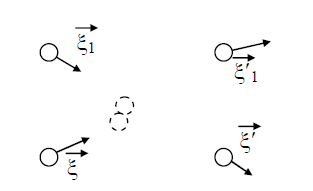
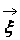
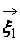
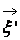
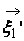
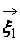
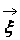
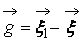
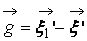
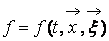
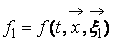
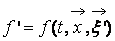
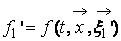
В процессе взаимодействия внутренняя энергия молекул не меняется, т.е. предполагается, что эти молекулы являются идеально упругими. Рассматриваются две группы молекул, имеющих до соударения друг с другом (столкновения) скорости и (рис. 1), а после столкновения соответственно скорости и . Разность скоростей и называется относительной скоростью, т.е. . Ясно, что для гладкого упругого столкновения . Функции распределения f₁‘, f’, f₁ ,f описывают молекулы соответствующих групп после и до столкновений, т.е. ; ; ; .

Рис. 1. Столкновение двух молекул.

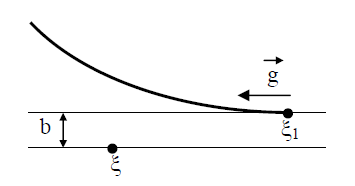
В (13) входят два параметра, характеризующие расположение сталкивающихся молекул друг относительно друга: b и ε; b – прицельное расстояние, т.е. наименьшее расстояние, на которое сблизились бы молекулы при отсутствии взаимодействия (рис. 2); ε называют угловым параметром столкновений (рис. 3). Интегрирование по b от 0 до ¥ и по от 0 до 2 p (два внешних интеграла в (12)) охватывает всю плоскость силового взаимодействия перпендикулярно вектору

Рис. 2. Траектория движения молекул.

Рис. 3. Рассмотрение взаимодействия молекул в цилиндрической системе координат: z, b, ε

Кинетическое уравнение Больцмана выведено при следующих допущениях и предположениях.

1. Считается, что происходит в основном столкновения двух молекул, т.е. роль столкновений одновременно трех и большего числа молекул незначительна. Это допущение позволяет использовать для анализа одночастичную функцию распределения, которая выше названа просто функцией распределения. Учет столкновения трех молекул приводит к необходимости использования в исследовании двухчастичной функции распределения. Соответственно анализ существенно усложняется.

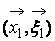
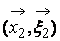
2. Предположение о молекулярном хаосе. Оно выражается в том, что вероятности обнаружения частицы 1 в фазовой точке и частицы 2 в фазовой точке независимы друг от друга.

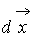
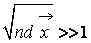
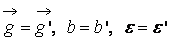
3. Равновероятны столкновения молекул с любым прицельным расстоянием, т.е. функция распределения не меняется на диаметре взаимодействия. Необходимо отметить, что анализируемый элемент должен быть малым, чтобы f в пределах этого элемента не менялась, но в то же время чтобы не была велика относительная флуктуация

. Потенциалы взаимодействия, используемые при вычислении интеграла столкновений, являются сферически симметричными, т.е. .

Распределение Максвелла-Больцмана

Равновесное состояние газа описывается абсолютным Максвелловским распределением, которое является точным решением кинетического уравнения Больцмана:

где m – масса молекулы, кг.

Общее локально-максвелловское распределение иначе называемое распределение Максвелла-Больцмана:

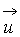
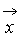
в том случае, когда газ движется как целое со скоростью и переменные n , T зависят от координаты
и времени t .

Формула Больцмана барометрическая

В поле тяготения Земли точное решение уравнения Больцмана показывает:

где n ₀= плотность у поверхности Земли, 1/м 3 ; g – ускорение силы тяжести, м/с 2 ; h – высота, м. Формула (16) является точным решением кинетического уравнения Больцман либо в безграничном пространстве, либо при наличии границ, не нарушающих этого распределения, при этом температура также должна оставаться постоянной.

Эта страница оформлена Пузиной Ю.Ю. при поддержке Российского Фонда Фундаментальных Исследований – проект №08-08-00638.