Пределы применимости линейного закона фильтрации.. Григорян.Н.С. Пределы применимости линейного закона фильтрации
| Название | Пределы применимости линейного закона фильтрации |
| Анкор | Пределы применимости линейного закона фильтрации |
| Дата | 07.12.2021 |
| Размер | 247.98 Kb. |
| Формат файла |  |
| Имя файла | Григорян.Н.С.docx |
| Тип | Закон #294490 |
| страница | 1 из 2 |
 С этим файлом связано 1 файл(ов). Среди них: Подземная Гидромеханика 04,12,2021.docx. С этим файлом связано 1 файл(ов). Среди них: Подземная Гидромеханика 04,12,2021.docx.  Показать все связанные файлы Подборка по базе: Функции. Пределы. Непрерывность..docx, Обр сила закона.doc, МОДЕЛИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОГО ПУТИ, Верховенство правового закона в правовом государстве.doc, 1 Построение множественного линейного уравнения.docx, Закон композиции и пропорциональности. Философия гармонии. Принц, 1493-0614 сп.нн.21.00000000145 сл.499 Агрегат фильтрации топлива, Функции. Пределы. Непрерывность..docx, недостатки закона об образовании в рф.docx, 1-ый и 2-ой замечательные пределы.docx Показать все связанные файлы Подборка по базе: Функции. Пределы. Непрерывность..docx, Обр сила закона.doc, МОДЕЛИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОГО ПУТИ, Верховенство правового закона в правовом государстве.doc, 1 Построение множественного линейного уравнения.docx, Закон композиции и пропорциональности. Философия гармонии. Принц, 1493-0614 сп.нн.21.00000000145 сл.499 Агрегат фильтрации топлива, Функции. Пределы. Непрерывность..docx, недостатки закона об образовании в рф.docx, 1-ый и 2-ой замечательные пределы.docxСодержание
Пределы применимости линейного закона фильтрации. Коэффициент фильтрации, имеет размерность скорости и характеризует скорость потока через единицу площади сечения, перпендикулярного потоку, под действием единичного градиента напора. При исследовании фильтрации газа, нефти и их смесей необходимо разделить влияние свойств пористой среды и флюида. Поэтому для разделения свойств флюида и пористой среды равенство представляют в виде: или где μ – динамический коэффициент вязкости, k – коэффициент проницаемости, который не зависит от свойств жидкости и является динамической характеристикой только пористой среды , м 2 . Проницаемость крупнозернистых песчаников 10 -12 – 10 -13 м 2 (1 – 0,1 мкм 2 ), проницаемость плотных песчаников 10 -14 м 2 (0,01 мкм 2 ). Из-за малости этих величин в нефтепромысловой практике получила размерность 1 Д (Дари) = 1,02·10 -12 м 2 . Коэффициент фильтрации и проницаемости определяются экспериментально (рис. 1.4) и могут быть связаны между собой соотношением: Равенства справедливы, если фильтрационные свойства недеформируемой пористой среды изотропные и однородные, т.е. проницаемость не зависит от направления и постоянна для всех точек. Из формул имеем где перепад напора, приходящийся на единицу длины (модуль градиента давления) можно представить в следующем виде Пермеаметр содержит образец исследуемого грунта, общий расход Q фильтрационного потока поддерживается постоянным, напоры Н 1 и Н 2 измеряют двумя пьезометрами, соединенными с пористой средой в сечениях 1 и 2. где Закон Дари связывает меду собой вектор скорости и градиент фильтрационного давления. Если обе части равенства разделить на площадь сечения, то получим выражение Таким образом, скорость фильтрации равна истинной средней скорости, умноженной на просветность. Заменять просветность на пористость теоретически неправомерно. Равенство можно представить в векторной форме. В случае изотропных фильтрационных свойств векторы скорости фильтрации и градиент фильтрационного давления лежат на одной прямой. Поэтому, если умножить равенство на орт В равенстве множитель Векторное уравнение представляет собой закон Дари для изотропной пористой среды. Знак «минус» в правой части равенства появляется из-за того, что скорость фильтрации направлена в сторону уменьшения приведенного давления. Поэтому векторы скорости фильтрации и градиента фильтрационного давления направлены в разные стороны (градиент давления направлен в сторону роста давления, а скорость фильтрации в обратную сторону – от большего давления к меньшему). Равенство задаёт закон Дари в универсальной безындексной форме записи, справедливой для любой системы координат. В декартовой системе координат равенство записывается в виде где Это равенство можно спроектировать на оси координат Таким образом, закон Дари заключается в том, что скорость фильтрации пропорциональна градиенту давления. Закон Дари имеет силу, если соблюдаются следующие условия:
2) малая скорость фильтрации при небольшом градиенте давления; 3) незначительные изменения скорости фильтрации или градиента давления. Закон Дари справедлив для медленных фильтрационных движений, для которых силы инерции несущественны. Поэтому для таких движений несущественна плотность жидкости, определяющая свойство ее инерции. Закон Дари, в дифференциальной форме он имеет вид: где Знак (-) в левой части формулы означает, что течение газа происходит в направлении, противоположном росту давления. Фундаментальный закон фильтрации устанавливает связь между скоростью фильтрации и градиентом давления. Нелинейные законы фильтрации ввести нумерацию. Проведенные в дальнейшем эксперименты показали, что закон Дари не является универсальным и нарушаются области малых и больших скоростей. Нарушение в области малых скоростей связано с молекулярным эффектом. Причины, вызывающие отклонение от закона Дари при больших скоростях , являются до настоящего времени предметом дискуссии среди исследователей. В 1901 году австрийский ученый Форхгейме, ссылаясь на исследования Мазони, рекомендовал выражать зависимость градиента давления от скорости двучленным законом фильтрации: Двучленный закон фильтрации в дифференциальной форме при прямолинейной фильтрации газа в принятых сейчас обозначениях, без учета силы тяжести имеет два вида записи: где b — дополнительная константа пористой среды, определяемая экспериментально, l – коэффициент макрошероховатости, характеризующий структуру порового пространства, r — плотность газа (жидкости). Первое слагаемое в правой части уравнения учитывает потери давления вследствие вязкости жидкости, второе слагаемое – инерционную составляющую сопротивления движению жидкости, связанную с криволинейностью и извилистостью поровых каналов. При малых скоростях течения природа нелинейности закона фильтрации иная, чем в области больших скоростей фильтрации (больших значений числа Рейнольдса ). Она связана с проявлением неньютоновских свойств фильтрующихся флюидов, а также других физико-химических эффектов и больших поверхностных сил (сил взаимодействия между флюидом и твердым скелетом). При очень малых скоростях фильтрации неньютоновскими свойствами в пористой среде могут обладать даже ньютоновские жидкости. Но с ростом скорости этот эффект в ньютоновских жидкостях исчезает. В нефтегазовом деле к жидкостям, проявляющим неньютоновские свойства, относят аномальные нефти и буровые растворы. Поэтому для качественного изучения вопроса и количественной оценки этих эффектов необходимо отказаться от модели вязкой однородной жидкости и заменить ее какой-либо другой реологической моделью пластового флюида. Ограничимся формулировкой наиболее простого нелинейного закона фильтрации неньтоновских жидкостей, в основе которого лежит модель фильтрации с предельным градиентом. Для случая одномерного линейного потока его можно представить в виде где Закон фильтрации записывают также в виде одночленной степенной формулы: где С и n — постоянные, определяемые опытным путем, причем 1 n При n = 1 из получается закон Дари, при n = 2 – квадратичный закон А.А. Краснопольского. Таким образом, формула имеет два параметра b и k , которые подлежат дальнейшему изучению и установлению связи между ними. Входящий в линейный закон фильтрации Дари коэффициент проницаемости определяется при исследовании кернов или на основе гидродинамических исследований. Исследованиями показано, что для пористых сред коэффициент проницаемости зависти от размера зерен и их дисперсности, коэффициента пористости, формы зерен, степени их сцементированности и. т. д. Л.С. Лейбензон предложил выразить коэффициент проницаемости в виде: где d – линейный размер (диаметр) зерен пористой среды, Sl – безразмерный критерий (число Слихтера), зависящий от коэффициента пористости и структуры порового пространства, т. е. где e — некоторый параметр, характеризующий структуру порового пространства пласта, m – коэффициент пористости. В связи с тем, что линейный закон фильтрации Дари всё-таки является приближенным законом, при увеличении скорости фильтрации жидкости и соответствующем увеличении скоростного напора сделанное ранее при выводе линейного закона фильтрации допущение может оказаться несправедливым, тогда и возникнут погрешности в расчетах. В этих случаях говорят, что линейный закон фильтрации (закон Дари) имеет верхнюю и нижнюю границы применения. Верхняя граница определяется группой причин связанных с проявлением инерционных сил при высоких скоростях фильтрации. Верхнюю границу применимости закона Дари связывают обычно с некоторым критическим (предельным) значением Re кр числа Рейнольдса: где d – линейный размер пористой среды, v – кинематический коэффициент вязкости флюида. В таких случаях принято говорить о так называемых нелинейных законах фильтрации, например выражения. Первая количественная оценка верхней границы применимости закона Дари была выполнена Павловским, который, опираясь на результаты Слихтера, полученные для модели идеального грунта, и полагая характерный размер d равный эффективному диаметру d эф вывел следующую формулу для числа Рейнольдса: Использовав эту формулу и данные экспериментов, Н.Н. Павловский установи, что критическое значение числа Рейнольдса находится в пределах Достаточно узкий диапазон изменения значений Re кр объясняется тем, что в опытах использовались не слишком разнообразные образцы пористых сред. Для удобства обработки результатов многочисленных экспериментов различных авторов В.Н. Щелкачев предложил использовать безразмерный параметр, названный им параметром Дари Отсюда видно, что параметр Дари представляет собой отношение силы вязкого трения к силе давления. Из выражения следует, что если параметр Дари равен единицы то закон Дари справедлив. Таким образом, равенство (28) должно выполняться при Re кр . Данный параметр упрощает исследование границы применимости линейного закона фильтрации. Интервалы критических значений Reдля различных образцов пористых сред
Однако вследствие различной структуры и состава пористых сред получить универсальную зависимость не удается. Нижняя граница определяется проявлением неньютоновских реологических свойств жидкости, ее взаимодействия с твердым скелетом пористой среды при достаточно малых скоростях фильтрации. Задачи из Басниева.1. При фильтрации жидкости с постоянным расходом через несцементированную пористую среду произошло вымывание мелких фракций песка. Изменилась ли при этом скорость фильтрации и средняя скорость движения жидкости? 2. Куб с ребром 1 м наполнили шарами диаметром 10 см каждый, а куб с ребром 1 см точно так же уложили шарами диаметром 1 мм каждый. Пористость какой засыпки больше? 3. Показать, что если образец пористого материала, имеющий объем V и пористость m, разбить на nчастей объемом V i (i = 1, …, n), то 4. Определите пористость фиктивного грунта, сложенного шарами диаметром D, центры которых находятся в вершинах кубической решетки с периодом D. Ответ: 1 – π/6 = 0,476. 5. Определить удельную поверхность фиктивного грунта, пористость которого m = 0,25 и диаметр шаров 0,2 мм. Найти число шаров в 1 м 3 . 6. Определить пористость, удельную поверхность и просветность для рыхлой кубической упаковки шаров. 7. Определить пористость для кубической и гексагональной упаковок шаров. 8. Определить коэффициент проницаемости пористой среды (в м 2 и Дари), если известно, что коэффициент фильтрации k ф = 0,3·10 – 4 см/с, кинематический коэффициент вязкости жидкости ν = 10 – 6 м 2 /с. 9. Определить проницаемость при фильтрации через образец площадью 1 см 2 , при перепаде давления 1 кгс/см 2 с расходом жидкости 1 см 3 /с, если длина образца 1 см, а фильтрующая жидкость имеет динамический коэффициент вязкости 1 сП (один сантипуаз). Решение . Из формулы (1.9) Переведем все размерности в СИ: площадь 1 см 2 = 10 – 4 м 2 , давление 1 кгс/см 2 = 98 кПА, расход 1 см 3 /с = 10 -6 м 3 /с, длина 1 см = 10 -2 м, вязкость 1 сП = 0,01 П (Пуаз) = 0,001 Па · с = 1 мПа·с 10. Определить коэффициент фильтрации для керна, помещенного под углом α к горизонту, если массовый расход жидкости равен Q м , плотность жидкости ρ и вязкость μ, разница напоров в начале и конце керна составляет ΔН, площадь сечения S, длина керна L. 11. Образец пористой среды длиной 10 см и диаметром 5 см после насыщения под вакуумом керосином с плотностью 810 кг/м 3 стал тяжелее на 20 г. Определить коэффициент пористости образца. Оценить влияние размеров поверхностей поровых каналов на величину сил сопротивления, определить суммарную поверхность песчинок, заключенных в 1 м 3 песчаного пласта. Примем форму песчинок шарообразной, диаметр их одинаковым и обозначим: N — число песчинок в 1 м 3 пласта; r — радиус песчинки; поверхность песчинки Тогда Суммарная поверхность Sпесчинок, заключенных в 1 м 3 песчаного пласта, равна: Нарушение Нарушение линейного закона при больших скоростях. Многочисленными экспериментами установлено, что при повышенных скоростях движения закон Дари нарушается. Критерием справедливости закона Дари служит число Рейнольдса – характерная скорость течения; – коэффициент вязкости жидкости; а – характерный размер пористой среды, который разные авторы определяют по-разному. Если число Рейнольдса, определенное по формуле (1.27′), не превосходит некоторого критического значения Re кp , то закон Дари сохраняется, т. е. линейная зависимость между расходом и потерей напора соблюдается. Целью всех экспериментов было установление этого критерия. Первые работы, посвященные этому исследованию, принадлежат акад. Н.Н. Павловскому и американским авторам Фенчеру, Люису и Бёрнсу (Fanchir, Levis and Barnes, 1933). Для обработки опытных данных они использовали формулу Здесь – коэффициент гидравлических сопротивлений. Формула (1.28) может быть формально получена из известной формулы Дарси-Вейсбаха для потерь напора в круглой трубе с некоторой модификацией. Эксперименты проводились с 27 образцами при фильтрации различных жидкостей и газов в сцементированных и несцементированных песчаниках. За линейный параметр приняли В результате обработки опытных данных были получены графические зависимости вида, показанного на рис. 1.6. Рис. 1.6. Результаты опытов по установлению Линейные уравнения и граничные задачи фильтрацииJules Dupuit Существенный вклад в развитие теории напорного и безнапорного движения грунтовых вод внес (Boussinesq) Жозеф Валантен Буссинеск (1842-1929 гг.) и Филипп Форхгеймер (1852-1933 гг.). Ч. Слихтер (1864—1946 гг.), работавший в США, внес значительный вклад в развитие теории фильтрации. Им впервые предложены модели идеального и фиктивного грунта и показано, что пористость и просветность фиктивного грунта зависят не от диаметра частиц, а лишь от плотности их укладки. Основоположниками отечественной школы теории фильтрации являются профессор Н.Е. Жуковский, академики Н.Н. Павловский, JI.C. Лей- бензон. Исследования этих выдающихся ученых, их многочисленных учеников и последователей стали фундаментальной основой развития теории фильтрации в нашей стране. Н.Е. Жуковский (1847-1921 гг.) в 1889 г. опубликовал первую работу по теории фильтрации «Теоретическое исследование о движении подпочвенных вод». Им впервые выведены общие дифференциальные уравнения теории фильтрации, показано, что напор как функция координат удовлетворяет уравнению Лапласа, указано на математическую аналогию теплопроводности и фильтрации. Им исследованы также вопросы капиллярного поднятия воды в пористой среде, решен ряд задач о притоке воды к скважинам. Н.Н. Павловскому (1884-1937 гг.) принадлежит определяющая роль в развитии теории фильтрации в гидротехническом направлении. В опубликованной монографии «Теория движения грунтовых вод под гидротехническими сооружениями и ее основные приложения» изложена разработанная им строгая математическая теория движения фунтовых вод под гидротехническими сооружениями. Им впервые многие задачи фильтрации воды были сформулированы как краевые задачи математической физики. Н.Н. Павловский впервые обосновал и предложил применение метода электрогидродинамической аналогии (ЭГДА) для решения фильтрационных задач, что в последующем нашло широкое применение для решения задач фильтрации воды, нефти и газа в неоднородных коллекторах. Н.Н. Павловский впервые предложил использовать параметр Рей- нольдса в качестве критерия существования закона Дарси, что имеет важное значение для исследования законов сопротивления при фильтрации. Фундаментальные результаты в развитии теории движения грунтовых вод получены академиком П.Я. Полубариновой-Кочиной. Пелаге́я Я́ковлевна Ко́чина (урожд. Полуба́ринова; 1899 — 1999) — советский физик-гидродинамик, академик АН СССР. Леонид Самуилович Лейбензо́н (1879—1951) — русский и советский учёный-механик основатель советской школы ученых и специалистов, специалист в области гидродинамики, теории упругости, теории фильтрации газа и нефти. Теоретические и экспериментальные исследования Л.С. Лейбензона начались в 1921 г. в Баку. Ему принадлежит приоритет в постановке и решении ряда задач нефтегазовой и подземной гидромеханики. Им проведены первые исследования по фильтрации газированных жидкостей, сформулированы задачи нестационарной фильтрации при расчетах стягивания контуров нефтеносности при вытеснении нефти водой, получены фундаментальные результаты в развитии теории фильтрации природного газа. Трудами учеников и последователей академика Л.С. Лейбензона сложилась школа, которая по праву называется школой Л.С. Лейбензона. Выдающийся вклад в развитие теории фильтрации в нефтегазоводоносных пластах внесли академик С.А. Христианович, профессоры Б.Б. Лапук, Исаак Абрамович Чарный, В.Н. Щелкачев и К.С Басниев. Написанные ими монографии и учебники стали классическими и основополагающими. § 2. ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ФИЛЬТРАЦИИ На различных этапах строительства скважины возникает необходимость в решении задач, связанных с оттоком жидкости из скважины и притоком ее в скважину из пласта. Здесь основное значение имеют закономерности движения жидкости в пласте, основанные на решении соответствующих граничных задач теории фильтрации. Фильтрация — это движение жидкостей, газов и их смесей под действием перепада давления в твердом проницаемом теле, пронизанном системой сообщающихся между собой пустот (поры, трещины). Нефть и природные газы заключены в недрах Земли. Их скопления связаны с вмещающими горными породами (пластами) — пористыми и проницаемыми образованиями, имеющими непроницаемые кровлю и подошву. Горные породы, которые могут служить вместилищами нефти и газа и отдавать их при разработке, называются коллекторами. В свою очередь, коллекторы называют пористыми или трещиноватыми в зависимости от геометрии пустот. Природные жидкости (нефть, газ, подземные воды и их смеси) находятся в пустотах (порах и трещинах) коллекторов. Часто находящиеся в пустотном пространстве пласта природные жидкости обозначают общим термином флюид,подразумевая под ним любую из них. Флюид, находящийся в коллекторе, может находиться в состоянии покоя или двигаться. Движение флюидов через твердые (вообще говоря, деформируемые) трещиноватые или пористые среды называется фильтрацией. Фильтрация может быть обусловлена воздействием различных сил: градиентом давления, концентрации, температуры, капиллярными, электромолекулярными и другими силами. Например, движение (фильтрация) расплавленного жира в фитиле свечи или керосина в фитиле керосиновой лампы обусловлено капиллярными силами. Однако в дальнейшем будем рассмотривать течения, вызываемые действием градиента давления или силы тяжести. Поровое пространство осадочных горных пород — сложная система сообщающихся межзернистых пустот, в которой трудно выделить отдельные поровые каналы (рис. 1.1). Размеры пор, например, в песчаных породах составляют обычно единицы или десятки микрометров (мкм). Движение флюидов в пласте происходит с очень малыми скоростями, порядка микрометров в секунду (в гидромеханике движения со столь малыми скоростями часто называются ползущими).
Поэтому процесс фильтрации с высокой степенью точности можно очень часто считать изотермическим. И в то же время при фильтрации в горных породах возникает значительная сила трения. При движении флюидов в пустотном пространстве коллектора соприкосновение между твердым скелетом и жидкостью происходит по огромной поверхности. Например, в 1м 3 пористой среды (песчаника) площадь поверхности пустотного пространства может достигать порядка 10 4 м 2 . Поэтому основным свойством флюида, которое влияет на фильтрацию, является вязкость. В связи с этим обстоятельством вязкость учитывается даже при фильтрации газа, а так как сила трения распределена по всему объему коллектора, то Н.Е. Жуковский предложил при описании фильтрации силу трения считать массовой силой. Строение нефтяных и газовых залежей осложняется значительной неоднородностью и анизотропией свойств пород, их слоистостью, наличием тектонических и стратиграфических нарушений (разрывов сплошности породы). Разведка месторождений, исследование пластов, извлечение нефти и газа осуществляется через отдельные скважины диаметром 10-20 см, отстоящие друг от друга до сотни метров. Объектом изучения в теории фильтрации является движущаяся жидкость (газ, смесь), а скелет тела – средой, в которой это движение происходит. Основная характеристика фильтрационного движения – вектор скорости фильтрации
где
где Подчеркнем, что расходы в формулах (2.28) и (2.29) делятся на полную площадь
где Горные породы, слагающие проницаемые пласты, характеризуются, как правило, сложной структурой флюидосодержащего пространства. Помимо пор они могут обладать развитой системой микро- и макротрещин. В зависимости от степени влияния трещин на фильтрацию жидкости принято различать пористые, трещиноватые и трещиновато-пористые породы. Каждая из этих пород описывается некоторым конечным набором осредненных геометрических характеристик. Важнейшими из них являются пористость Для пористых пород Наряду с пористостью для описания пористого тела используют: просветность Основными геометрическими параметрами трещиноватости являются: раскрытие трещин– расстояние между стенками; объемная плотность трещиноватости – отношение площади поверхности всех трещин в некотором элементарном объеме к величине этого объема; поверхностная плотность трещиноватости – отношение суммы длин следов трещин, выходящих на элементарную площадку, к величине площади последней; густота трещин — отношение количества трещин, секущих нормаль плоскостей, к элементу длины этой нормали; ориентация трещин — в пространстве. Пористые и трещиноватые породы с хаотичным, бессистемным распределением пор или трещин характеризуются изотропией фильтрационных свойств, в то время как породы с упорядоченной системой (большинство трещинных коллекторов) обладают ярко выраженной анизотропией. Особенностью фильтрации в трещиновато-пористых породах является то, что закономерности фильтрации в порах и трещинах могут существенно отличаться. Все это находит отражение в основном соотношении теории фильтрации – законе фильтрации, который устанавливает связь между вектором скорости Существуют по крайней мере три основных фактора, которые влияют на характер (линейный, нелинейный) закона фильтрации: режим фильтрации (ламинарный, турбулентный), реологические свойства (ньютоновская, неньютоновская) и однородность жидкости. Линейные уравнения и граничные задачи фильтрации. 1. Модель ламинарной фильтрации ньютоновских однородных жидкостей в изотропной среде Для этой модели справедлив экспериментально установленный линейный закон фильтрации Дарси
Или в проекциях на оси декартовой системы координат
где Проницаемость имеет размерность площади. Она не зависит от свойств жидкости, является чисто геометрической характеристикой пористой среды. В практике принято проницаемость измерять в мкм 2 . Среда имеет проницаемость 1 мкм 2 если при градиенте давления 10 МПа/м через площадку 10 -4 м2 расход жидкости, вязкость которой 10 -3 Па . с, составляет 10 -6 м 3 /с, т. е. 1мкм 2 = 10 -12 м2 . Проницаемость определяется геометрией порового пространства. Известно множество попыток установить аналитическую зависимость между проницаемостью, пористостью, размером, формой и упаковкой частиц. Для фиктивного грунта Слихтер нашел, что теоретическая проницаемость
а Козени получил
Эти формулы полезны при изучении закономерностей фильтрации только в искусственных пористых телах. Для реальных тел достоверные результаты можно получить лишь по данным измерений расхода и перепада давления в лабораторных условиях на керновом материале или при натуральных испытаниях пластов с последующей интерпретацией полученных результатов. Закон фильтрации (2.30) – это упрощенная форма уравнений движения
неразрывности движения или сохранения массы
и механического состояния
в которых отброшены силы инерции
Имеем симметричный девиатор напряжений Принимается, что при небольших изменениях порового давления пористость и проницаемость среды, а также плотность жидкости линейно зависят от
где К уравнениям (2.30 и (2.31) необходимо присоединить еще уравнение неразрывности движения жидкости (2.22), которое в силу неполного, равного
Уравнения (2.30) – (2.32) образуют, таким образом, замкнутую систему для определения функций классическое уравнение теории фильтрации:
где Если
которое характеризует неупругий (жесткий) режим фильтрации и, следовательно, стационарное поле давления. Это же уравнение имеет место при Для однозначного определения поля давления
и при если на поверхности
если задана нормальная составляющая скорости фильтрации, то
если поверхность
где Ясно, что для уравнения (2.34) начальное условие (2.35) смысла не имеет, а граничные условия вида (2.36) – (2.38) сохраняются. 2. Модель ламинарной фильтрации ньютоновских однородных жидкостей для анизотропной среды. Проницаемость зависит от направления — имеет место обобщенный закон Дарси
где Если воспользоваться системой координат, оси которой совпадают с главными осями тензора
где
Подставляя (2.40) в (2.32) получим уравнение при установившейся фильтрации
Учитывая (2.41), усложняются и граничные условия вида (2.37) и (2.38). Однако граничную задачу, связанную с уравнением (2.42), легко свести к граничной задаче, связанной с уравнением Лапласа (2.34), если вести следующую замену переменных:
где Это означает геометрическое преобразование анизотропной области
При этом граница
преобразуется согласно (2.42) в область, ограниченную эллипсом
или в параметрическом виде
где Для области
решение которого должно удовлетворять заданному граничному условию на окружности (2.45) для соответствующих точек эллипса (2.46). 3.Закономерности фильтрации жидкости в трещиновато-пористых пластах для однородной и изотропной среды. Горная порода рассматривается как сплошная, в любой точке которой имеют место двойная пористость
и уравнениями неразрывности
где индексами 1 и 2 обозначены величины, характеризующие соответственно систему трещин и пор;
– интенсивность перетока жидкости между этими системами; При этом пористости
Однако во многих случаях систему уравнений (2.47) – (2.48) можно упростить, если исходить из следующих условий: а) объем, занимаемый трещинами, много меньше объема пор, т.е. допустимо принять б) изменение пористости
в) проницаемость г) жидкость слабосжимаема так что
где д) вязкость жидкости Физическая сущность перечисленных допущений состоит в том, что в системе трещины – поры рассматривается фильтрация жидкости по трещинам в условиях интенсивного массобмена с жидкостью, находящейся в упругом деформированном поровом пространстве. В результате принятых упрощений уравнения (2.48) примут вид
Подставляя сюда соотношения (2.47), (2.49), (2.51), (2.52) и отбрасывая малые величины высших порядков, получим
где Параметр Легко заметить, что путем исключения одного из давлений система уравнений (2.53) сводится к одному уравнению
где Это уравнение отличается от классического уравнения (2.33) слагаемым, содержащим параметр При жестком режиме фильтрации Следовательно, ставить задачу о фильтрации жидкости в трещиновато-пористой среде имеет смысл при Начальное и граничные условия, которые необходимо присоединить к уравнению (2.54), обладают некоторой особенностью. Прежде всего ясно, что граничную задачу, связанную с уравнением (2.54) следует рассматривать относительно одного из давлений – Если начальные условия В противном случае задачу следует решать относительно давления Если начальное распределение давления
при Но если же согласования нет, то к правым частям соответствующих граничных условий необходимо прибавить слагаемое
Это свидетельствует о том, что заданный скачок граничных условий в порах трещиновато-пористой среды не уничтожается мгновенно, как в обычной пористой среде, а убывает по закону После решения граничной задачи относительно порового давления а скорости фильтрации относительно какой–либо поверхности – по формуле 4. Приизучении фильтрации газа основное значение имеет его высокая сжимаемость, которая на несколько порядков выше сжимаемости пористой среды. Поэтому в уравнении неразрывности (2.32) пренебрегают изменением пористости
К этому уравнению необходимо присоединить уравнение состояния газа
и закон фильтрации, который при небольшой скорости фильтрации имеет вид закона Дарси
где в общем случае В простейшем случае газ можно считать термодинамически идеальным, находящемся при постоянной температуре
где Подстановка (2.58) и (2.59) в (2.57) дает основное нелинейное уравнение теории фильтрации газа
которое впервые было получено Л. С. Лейбензоном в 1930г. Наиболее известный приближенный метод решения этого уравнения основан на линеаризации, по Л. С. Лейбензону, который состоит в том, что левую часть уравнения умножают на Тогда вместо (2.60) необходимо решить линейное уравнение
которое аналогично уравнению (2.33), где Лекция 4. 5. Экспериментально установлено, что иногда линейный закон фильтрации жидкости Рис. 11.Возможные виды нелинейного закона фильтрации Основные причины проявления нелинейных эффектов следующие: а) высокая скорость фильтрации, когда параметр Рейнольдса б) ламинарная фильтрация жидкостей с неньютоновскими свойствами (кривая 2); в) малая скорость фильтрации в слабопроницаемых и неоднородных пластах (кривая 2). Предложены различные аппроксимации нелинейных зависимостей. Например, кривая 1 чаще всего описывается двучленным законом фильтрации
а кривая 2 – законом фильтрыции с предельным градиентом
где, по данным Е. М. Минского, В общем случае к обоим типам кривых применимы степенная и кусочно-линейная аппроксимации
которыми удобно пользоваться при расчетах. Здесь Классическое уравнение теории фильтрации границы применимостиТЕОРИЯ ФИЛЬТРАЦИИ (ЕНТОВ В.М. , 1998), ФИЗИКА Статья содержит элементарное введение в теорию движения жидкостей через пористые тела, примерами которых являются почвы, горные породы и разнообразные природные и искусственные пористые материалы. Главными приложениями теории являются проблемы разработки месторождений нефти и газа, ирригации, управления подземными водами и охраны окружающей среды. Рассматриваются течения однородных жидкостей, кратко обсуждаются течения неоднородных жидкостей. Государственная академия нефти и газа им. И.М. Губкина, Москва Теория фильтрации — раздел гидродинамики, посвященный исследованию движения жидкостей через пористые среды, то есть тела, пронизанные системой сообщающихся между собой пустот (пор). Пористыми являются многие природные тела: грунты, горные породы, древесина, кожа, кость, мягкие ткани животных, а также искусственные материалы: строительные (бетон, кирпич), пищевые (хлеб), искусственная кожа, керамика, металлические детали, полученные методом порошковой металлургии, и т.д. Пористой является почва, верхний слой грунта, служащий основой земледелия. Уже это простое перечисление показывает ту огромную роль, которую играют пористые среды в жизни людей. Характерная особенность всех этих материалов — способность накапливать в себе жидкость и позволять ей двигаться под действием внешних сил. По крайней мере три важнейших аспекта нашей жизни напрямую зависят от движения жидкостей через пористые среды. Прежде всего это движение жидкостей через пористые биоматериалы в живых организмах — обмен жидкостью в клетках и тканях, движение соков в деревьях и злаках и другие незаметные внешне движения управляют процессами транспорта питательных веществ к клеткам и вывода вредных продуктов жизнедеятельности из организмов. Хотя эти процессы идут под контролем и при участии ферментов и других белков, сам транспорт жидкостей играет огромную роль в жизни всех клеток и всех существ. Ту же роль играет движение влаги в почве. В конечном счете именно фильтрующаяся или просачивающаяся в почве вода приносит растениям питательные вещества и служит основой питания всего живого. Движение почвенной влаги, правильная организация орошения и ирригации — одна из важнейших задач теории фильтрации. В последнее время к этой вечной задаче человечества добавилась новая и часто не менее трудная проблема охраны грунтовых вод от загрязнения отходами производства, удобрениями и прочими продуктами жизнедеятельности человечества. Наконец, основные источники энергии XX века — нефть и газ добываются из глубоко залегающих подземных пластов. Накопление нефти и газа в этих пористых пластах-коллекторах и основные технологии извлечения (добычи) управляются законами теории фильтрации и служат одним из главных источников ее задач. Важнейшей количественной характеристикой пористых тел является их пористость m, определяемая как доля объема тела, приходящаяся на поры, или объем пор в единице объема материала. Обычно при этом игнорируются замкнутые изолированные поры и учитываются только соединенные между собой проточные поры. Они образуют поровое пространство — сложную разветвленную и нерегулярную сеть пор. Некоторое представление о структуре порового пространства дает рис. 1, где схематически показан срез пористого материала (зеленым цветом закрашены срезы зерен, белым — внутрипорового пространства). Пористость большинства материалов находится в пределах 0,1-0,4. Взяв для оценки типичное для многих горных пород значение m = 0,25, находим, что в 1 м3 породы объем пор 0,25 м3 = 250 л. Когда речь идет о породах — коллекторах нефти и газа или пластах, насыщенных пресной водой в пустынных районах, пористость является главным параметром, поскольку она определяет запасы месторождения, то есть количество жидкости в данном пласте. Пористость — безразмерная величина, она не зависит от размера частиц, составляющих пористую среду. Более точно, если представить себе два пористых тела, которые геометрически подобны друг другу на микроуровне и отличаются только размером частиц, то их пористость будет одинаковой. (Пористость слоя песчинок, слоя горошин и слоя пушечных ядер одинакова!) Суть в том, что в крупнозернистом материале поры крупнее, однако их число в единице объема среды меньше и эти эффекты как раз компенсируют друг друга. Для большинства приложений важна пропускная способность пористой среды, то есть характеристика того, насколько легко может двигаться в ней жидкость. При одной и той же пористости пропускная способность различных сред может оказаться совершенно разной. Всем известно, как быстро исчезают лужи после дождя в местах с песчаной почвой и как долго стоят они на глинистых грунтах. Способность пористой среды пропускать жидкость характеризуется проницаемостью. Ее определение тесно связано с основным законом движения жидкости в пористой среде, называемом законом Дарси в честь французского инженера Анри Дарси, экспериментально установившего этот закон в 1856 году. Схема опыта Дарси показана на рис. 2. Дарси пропускал воду через набитые песком трубки под действием разности уровней и измерял расход жидкости Q, то есть ее количество, протекающее через трубку в единицу времени. Оказывается, что расход пропорционален разности уровней DH и площади сечения трубки S и обратно пропорционален ее длине L: Если повторить опыт Дарси с жидкостями различной плотности r и вязкости m, то можно убедиться, что расход пропорционален плотности жидкости и обратно пропорционален ее вязкости. Поэтому перепишем формулу (1) в виде Здесь g — ускорение силы тяжести, k — коэффициент пропорциональности, являющийся характеристикой пористой среды и не зависящий от размеров образца и свойств жидкости. Это характеристика и называется проницаемостью пористой среды, а формула (2) представляет собой современную запись закона Дарси в простейшей форме. Сравнивая размерности обеих частей уравнения (2), находим, что проницаемость k имеет размерность площади, то есть измеряется в м2. В таких единицах проницаемость большинства природных пористых сред весьма мала. Так, проницаемость «хорошо» проницаемого песчаника порядка 10-12 м2. Размерность проницаемости показывает, что это чисто геометрическое свойство среды, косвенно определяющее размер ее структуры. Для сред геометрически подобной структуры проницаемость пропорциональна квадрату характерного размера структуры (например, размера зерна). Поэтому в отличие от пористости проницаемость является переменной характеристикой: проницаемости различных сред могут различаться в тысячи и более раз. Именно от проницаемости зависит производительность нефтяных и газовых скважин. Соотношение (2) показывает, что интенсивность течения в пористой среде характеризуется отношением u = Q / S, то есть расходом на единицу площади сечения образца или скоростью фильтрации. Эта величина с размерностью скорости представляет собой плотность потока, рассчитанного на всю площадь сечения образца (а не только на площадь пор). Истинная скорость в среднем в 1/ m раз больше. В опыте, показанном на рис. 2, величина rgDH представляет собой перепад давления Dp на длине образца, поэтому закон Дарси можно переписать в виде Скорость фильтрации направлена в сторону убывания давления, пропорциональна градиенту давления, обратно пропорциональна вязкости жидкости и прямо пропорциональна проницаемости среды. Соотношение (3) используется для определения употребительной внесистемной единицы проницаемости 1 Дарси (1 Д): эта такая проницаемость, при которой градиент давления в 1 физическую атмосферу (760 мм ртутного столба) создает скорость фильтрации 1 см/с при вязкости жидкости 1 мПа » с. Легко подсчитать, что 1 Д = 1,02 » 10-12 м2. В теории движения грунтовых вод имеют дело только с водой, вязкость которой m = 10- 3 Па » с и плотность r = 103 кг/м3. Поэтому вместо давления чаще пользуются пропорциональным ему напором H = p / rg, измеряемым в метрах, а проводимость среды для фильтрационного потока характеризуют коэффициентом фильтрации имеющим размерность скорости. Это скорость, с которой вода вытекает из вертикального насыщенного водой образца под действием силы тяжести. Коэффициент фильтрации меняется от величин порядка 0,001 м/сут для почти непроницаемых глин до 1-10 м/сут для хорошо проницаемых пород (особенно трещиноватых, то есть содержащих систему трещин). Закон Дарси и закон сохранения массы (уравнение неразрывности) в общем случае образуют систему уравнений для отыскания распределения давления и поля скорости фильтрации. Уравнение для давления (или напора) представляет собой уравнение в частных производных, родственное уравнению Лапласа, описывающему распределение потенциала электрического поля. Оно сводится к уравнению Лапласа в случае однородной среды. Это не случайно, так как имеется полная математическая аналогия между распределением электрического тока в проводящем материале и распределением скорости фильтрации в пласте. В этой аналогии ток соответствует скорости фильтрации, электрический потенциал — давлению или напору, проводимость — проницаемости, а закон Ома соответствует закону Дарси. До появления компьютеров электрогидродинамическая аналогия (ЭГДА) широко применялась для решения задач теории фильтрации методом электромоделирования. Фильтрационный поток можно представить разбитым на множество тонких трубок тока, боковые границы которых образованы линиями тока, направленными вдоль вектора скорости фильтрации. Если поток установившийся, то есть не меняется со временем, то через каждое сечение трубки тока протекает в единицу времени одна и та же масса жидкости (массовый расход) Здесь r — плотность жидкости, u — скорость фильтрации, S — площадь сечения трубки тока. Для несжимаемой жидкости (r = const) расход Q = uS вдоль трубки постоянен. В простейших случаях это позволяет найти закон изменения скорости фильтрации вдоль трубки тока. Так, одной из основных для теории фильтрации является задача о притоке к скважине — узкому цилиндрическому отверстию, которое пробурено в пласте для откачки воды, нефти или газа. В окрестности скважины в силу симметрии линии тока направлены радиально к скважине, а площадь сечения трубок тока пропорциональна расстоянию от оси скважины Небольшой отрезок трубки тока между сечениями на расстояниях r и r + Dr представляет собой аналог образца в опыте Дарси, так что для перепада давления на нем имеем Таким образом, для распределения давления p(r) получается простейшее дифференциальное уравнение, решение которого имеет вид Здесь rскв — радиус скважины, pскв — давление в ней. Если известно давление p0 на расстоянии r0 от скважины (такую линию равного давления называют контуром питания), то, используя (5), можно найти формулу для расхода (дебита) Эта формула, называемая формулой Дюпюи, является важнейшей в гидрогеологии и нефтяном деле. В частности, по ней подсчитывается, каков будет дебит скважины — ее производительность при данном перепаде давления p0 — pскв . Одно из примечательных свойств этой формулы — то, что размеры контура питания и скважины входят в нее в виде отношения под знаком логарифма. Это значит, что двукратное увеличение радиуса скважины привело бы к такому же увеличению дебита, как и двукратное уменьшение радиуса контура питания. Однако обычно rскв 100-1000 м. Таким образом, формула Дюпюи указывает, что на производительность скважин основное влияние оказывает малая окрестность скважин. Состояние этой «призабойной зоны» скважин — одна из основных забот инженеров нефтяников и газовиков. К тому же слабая (логарифмическая) зависимость от радиуса контура питания делает ошибку в определении этой достаточно условной величины не столь существенной. Одним из эффективных средств повышения производительности скважин является гидравлический разрыв пласта. В этом методе в пласт под большим давлением нагнетается жидкость. Ее давление выбирается так, чтобы в результате распирающего действия в пласте образовалась трещина, которая затем будет служить каналом для отбора жидкости из пласта. Образовавшуюся трещину закрепляют, закачивая в нее вместе с жидкостью разрыва твердые крупные частицы — закрепитель. Современная технология позволяет создавать трещины гидроразрыва длиной до сотен метров. Используя более сложный математический аппарат, можно получить аналог формулы Дюпюи для скважины с трещиной гидроразрыва и убедиться, что вертикальная трещина длиной 2L эквивалентна по производительности скважине радиуса L /2. Иными словами, скважину радиусом в 10 см легко превратить в эквивалентную скважину радиусом 10 м. Таким образом, с помощью даже умеренного гидроразрыва можно поднять производительность скважины в несколько раз. Формула Дюпюи в виде (6) относится к глубинным пластам, находящимся под большим давлением, когда жидкость стремится подняться выше, но ее не пускают лежащие выше непроницаемые пласты — покрышки. Такой режим, когда жидкость заполняет весь пласт, называется напорным. В верхних слоях грунта часто встречается другая ситуация, когда грунтовые воды заполняют нижнюю часть водоносного слоя, ограниченного снизу непроницаемой границей — водоупором, а в верхней части слоя грунта находится воздух. На свободной поверхности слоя воды давление равно атмосферному, а движущей силой потока является разность уровней воды в различных точках пласта (рис. 3). Такой режим движения называется безнапорным, он особенно важен для грунтовых вод. В частности, для водяной скважины при безнапорном режиме аналог формулы Дюпюи имеет вид Здесь hскв и h0 — уровни в скважине и на контуре питания. До сих пор речь шла лишь о стационарных, не изменяющихся во времени фильтрационных потоках. Однако большинство течений являются в той или иной степени нестационарными. Особенно это относится к техногенным процессам, вызванным хозяйственной деятельностью человека. Нестационарность может проявляться как перемещение границ занятой жидкостью области или как распространение возмущений (волн) давления. Волны давления обусловлены зависимостью запаса жидкости в порах от ее давления. Проще всего понять это на примере газонасыщенной пористой среды. Считая газ идеальным, можно показать, что масса газа в единице объема среды составляет Здесь r — плотность газа, mg — его молекулярная масса, p — давление, T — абсолютная температура, R — универсальная газовая постоянная. Пусть имеется цепочка образцов пористой среды (рис. 4), насыщенных газом при давлении p0 . Если начинать отбор газа из крайнего образца, то давление в нем упадет и возникнет разность давлений между вторым и первым образцами в цепочке. Газ начнет перетекать из второго образца в первый, а давление во втором образце падать. Возмущение по цепочке захватит третий образец, и волна давления постепенно распространится вдоль всей цепочки и тем быстрее, чем меньше сжимаемость газа и сопротивление его движению. Математическая теория, в более строгой постановке описывающая этот мысленный эксперимент, показывает, что характерное расстояние l распространения волны за время t Подставляя характерные для газового месторождения значения k = 10-13 м2, p0 = 10 МПа, m = 0,2, m = = 10- 5 Па » с, получим l = 60 м при t = 1 час, l = 300 м при t = 1 сутки, l = 5 км при t = 1 год. На первый взгляд кажется, что в применении к капельной жидкости (вода, нефть) такое рассуждение приводит из-за несжимаемости жидкости, к бесконечно быстрому распространению волн давления. На самом деле это не так. Любая жидкость хоть немного, но сжимается при повышении давления (вода на 1/2000 при изменении давления на 1 МПа, нефть в несколько раз сильнее). Кроме того, при повышении давления внутри пор в пласте пористость немного увеличивается. Поэтому и в случае жидкости запас ее в пласте увеличивается с повышением давления, а потому и оказывается возможным распространение волны давления. Для нее Здесь Km и Kr — модули всестороннего сжатия сухой пористой среды и жидкости. Формально распространение волн давления в упругодеформируемом пласте, насыщенном упругосжимаемой жидкостью, описывается классическим уравнением теплопроводности, только вместо температуры в нем стоит давление, а вместо коэффициента температуропроводности — коэффициент k. Чтобы подчеркнуть эту аналогию, В.Н. Щелкачев, создатель теории упругого режима фильтрации, назвал уравнение для давления уравнением пьезопроводности, а коэффициент k — коэффициентом пьезопроводности. Его характерные значения (0,1-1) м2/с. Поэтому за 1 с волна давления уйдет на 0,3-1 м, за 1 ч на 18-60 м, за 1 сут — на 100-300 м, за 1 год — на 2-6 км. Иначе говоря, каждый элемент пористой среды, каждый пласт имеет свое характерное время распространения волны давления t L 2 / k. С ростом размера элемента характерное время возрастает пропорционально квадрату линейного размера. Нестационарные процессы, захватывающие большие пластовые системы, имеют характерные времена, измеряемые годами и десятками лет. Точно так же при понижении уровня в водяной скважине от нее начинает распространяться волна понижения уровня. Можно убедиться, что закон ее распространения также определяется корневой зависимостью от времени (7), в которую вместо kp0 / m нужно подставить произведение коэффициента фильтрации на начальный уровень воды Ch0 . Наблюдения за распространением волн давления или волн понижения уровня грунтовых вод позволяют оценить фактическое значение проницаемости пласта или коэффициента фильтрации. Такие обратные методы, основанные на сопоставлении данных наблюдений с теоретическими зависимостями, очень важны, поскольку позволяют заглянуть внутрь подземного резервуара сравнительно доступными средствами. Классическая теория фильтрации, о которой шла речь до сих пор, имеет дело с течением однородной жидкости в пористой среде. В большинстве современных приложений, однако, приходится рассматривать неоднородные системы, многокомпонентные однофазные (растворы) или двух- и трехфазные смеси. Упомянем лишь такие важные области, как загрязнение грунтовых вод, миграция влаги в почвенном слое и вытеснение нефти пластовой или искусственно закачиваемой водой или газом. У каждой из этих систем есть аналог в обычной гидродинамике (скажем, перенос загрязнения потоком воды в реке или течение газонефтяной смеси по трубам). Однако пористая среда в каждом случае вносит свои особенности, так или иначе связанные с малостью размера пор, нерегулярностью и неоднородностью порового пространства и огромной поверхностью контакта жидкости со скелетом. Перечислим наиболее типичные и важные эффекты. Перенос примеси, адсорбция, хроматографическое разделение, диффузия и гидродинамическая дисперсия Примесь, растворенная в потоке, переносится этим потоком и одновременно диффундирует относительно несущей жидкости. Скорость переноса равна скорости жидкости, ширина области диффузионного размывания пропорциональна , где t — время с момента введения примеси, а D — коэффициент диффузии. Если представить себе подобный опыт, выполненный с потоком грунтовых вод (а это часто происходит, когда в грунт проникают сточные воды), то обнаруживаются два важных отличия. Во-первых, скорость переноса оказывается меньше, иногда значительно (в несколько раз), чем средняя скорость потока V = u / m. Во-вторых, диффузионный размыв происходит значительно быстрее, чем это предсказывает теория диффузии, и с разной скоростью вдоль и поперек потока. Отставание примеси от несущего ее потока в пористой среде объясняется явлением адсорбции. Молекулы растворенной в жидкости примеси могут временно закрепляться (адсорбироваться) на поверхности пор. Между раствором и поверхностью устанавливается динамическое равновесие, и среднее количество адсорбированного вещества зависит от его концентрации в растворе: a = a(c). Эта зависимость носит название изотермы адсорбции. Таким образом, в среднем некоторая доля содержащейся в пористой среде примеси не движется вовсе, поэтому средняя скорость примеси меньше скорости жидкости. Более точно: можно показать, что каждое значение концентрации c переносится с постоянной скоростью u(c), причем где штрихом обозначена производная функции. В частности, если изотерма адсорбции линейна, a = Gc, все значения концентрации переносятся с постоянной скоростью и эта скорость тем меньше, чем больше постоянная G, то есть чем сильнее адсорбция. Если примесей несколько и их адсорбция различна, то есть различны постоянные G, то в потоке через пористую колонку они переносятся с разными скоростями. Это явление, обнаруженное экспериментально русским ботаником М.С. Цветом, носит название хроматографии. Оно лежит в основе метода хроматографического анализа химических веществ и хроматографического метода разделения смесей, особо важного при получении чистых веществ. Нетрудно понять, почему хроматографическое разделение отчетливо проявляется в пористой среде и почти незаметно в трубах. Дело здесь в огромной удельной поверхности пористых сред. Чем больше эта поверхность, то есть чем меньше размер зерен, тем больше адсорбция. Поэтому особо тонкопористый активированный уголь используется в качестве адсорбента в противогазах для задержки вредных газов. Хроматографическое разделение существенно влияет на физико-химические процессы повышения нефтеотдачи пластов, основанные на закачке в пласты смесей химических реактивов. Адсорбция в пористых телах обладает особенностями, прямо связанными с удивительной геометрией порового пространства. Согласно молекулярной теории адсорбции, количество адсорбированного вещества увеличивается с ростом его концентрации вблизи поверхности, пока вся поверхность раздела не окажется покрытой мономолекулярным адсорбционным слоем. Зная площадь S *, которая приходится на одну молекулу, и измерив предельную адсорбцию a? , можно вычислить удельную поверхность пористого тела (полную поверхность пор в единице объема среды) где NА — число Авогадро, mg — молекулярная масса адсорбирующегося вещества. (Подобным образом можно было бы измерить поверхность пещеры вымостив ее стены изразцовыми плитками, а потом подсчитав, сколько плиток понадобилось.) Такой метод измерений часто используется в современных лабораториях. Однако результат измерений зависит от размеров используемых в опыте молекул. Чем меньше молекулы, тем больше оказывается измеренная площадь поверхности пор. Это не ошибка, а важнейший научный факт. Объяснение состоит в том, что поверхность реальных пор не гладкая, а сильно и нерегулярно изрезанная, причем изрезанность сохраняется в широком диапазоне масштабов. Выбрав некоторый размер молекулы для измерения, мы исключаем из рассмотрения все неровности малых масштабов и их вклад в поверхность. Подобные поверхности (и геометрические объекты иной размерности) сравнительно недавно стали изучать математики и немедленно обнаружились в некоторых природных объектах; они получили название фрактальных поверхностей или фракталов и являются объектами дробной размерности. Поверхность порового пространства многих реальных тел имеет размерность 2,16-2,99. Далеко не все возможные следствия фрактального строения поверхности пор изучены, здесь еще возможны неожиданные открытия. Вернемся от микроскопического описания к макроскопическому и обратимся к диффузии примеси в фильтрационном потоке. Причиной ускоренной диффузии в пористой среде также оказывается особая геометрия пор, а именно: разброс размеров пор и изменение этих размеров от точки к точке пласта. В результате скорость жидкости испытывает резкие флуктуации от точки к точке пористой среды. Поэтому при одинаковой средней скорости примесь переносится с разной скоростью по различным путям. Возникающий разброс положений частиц примеси внешне выглядит как диффузия, хотя и порожден главным образом гидродинамическими причинами. Он носит название гидродинамической дисперсии. Два основных свойства этой квазидиффузии достаточно очевидны уже из качественной картины: коэффициент диффузии возрастает с ростом скорости фильтрации, а величина его различна в направлении потока и поперек него. Ясно также, что коэффициент диффузии будет тем больше, чем больше характерный масштаб неоднородности потока. В природных пластах, где неоднородность носит случайный характер, вероятность встретить флуктуацию большого масштаба тем больше, чем больший путь проходит жидкая частица. Поэтому наблюдаемое значение эффективного коэффициента гидродинамической дисперсии тем больше, чем больше размер области наблюдения. Все это делает количественный анализ явления гидродинамической дисперсии в пористых средах одним из наиболее сложных разделов теории фильтрации. Наиболее важные и интересные явления происходят при движении в пористой среде нескольких фаз, скажем воды и воздуха в почве или нефти, газа и воды в нефтяных месторождениях. Появление межфазных границ требует учета капиллярных сил. Их роль в природных пластах оказывается определяющей. Это связано с малостью размеров пор. Так, относительная роль капиллярных сил по отношению к силе тяжести и силам вязкого сопротивления определяется отношениями, которые носят название капиллярных чисел: Здесь s — межфазное натяжение, имеющее порядок 10 мН/м. Подставляя сюда характерные значения, легко убедиться в справедливости утверждения о преобладании капиллярных сил. Поэтому в каждом элементе пористой среды фазы стремятся расположиться так, как им диктуют капиллярные силы. При этом мелкие поры оказываются занятыми более смачивающей жидкостью, а крупные — менее смачивающей. Большинство природных пористых сред гидрофильны, и смачивающей жидкостью для них является вода, а несмачивающей — воздух, нефть или газ. Фактически пленка воды почти всегда существует на поверхности скелета грунта. Для несмачивающей фазы остаются расширения пор. Детальная картина сосуществования двух жидкостей в поровом пространстве будет зависеть от их количества. Его обычно характеризуют фазовыми насыщенностями si , i = 1, 2. Насыщенность — это доля порового пространства, занятая данной фазой, так что s1 + s2 = 1. В частности, если насыщенность несмачивающей фазы достаточно мала, меньше некоторого критического значения s* , эта фаза должна распасться на отдельные капли, которые заперты капиллярными силами и неспособны двигаться под действием обычных для пласта перепадов давления. Именно этим объясняется неизбежность защемления некоторого количества остаточной нефти в пласте при вытеснении ее водой. При насыщенности выше критической поровые каналы, занятые данной фазой, образуют связную сеть каналов и, возможно, течение. При критической насыщенности эта сеть каналов разрывается. Такой переход, происходящий при определенном соотношении между числом заполненных и незаполненных поровых каналов, является общим явлением для процессов проводимости во многих неупорядоченных физических системах. Изучение этих критических явлений породило особую область теоретической физики, получившую название теории перколяции (просачивания). Любопытно, что сама эта теория позаимствовала название из теории движения через пористые среды, а теперь возвращается в нее с новыми подходами и результатами. Таким образом, в условиях преобладания поверхностного натяжения две жидкости, смачивающая и несмачивающая, например вода и нефть, занимают при данном соотношении между их насыщенностями строго определенное положение в порах. При этом течение их происходит по «своей» части порового пространства так, как если бы вторая фаза затвердела. Это напоминает течение воды и масла по одной горизонтальной трубе, только в этом случае упорядочивающим фактором является сила тяжести. Поэтому для каждой из фаз справедлив закон Дарси, но проницаемость уменьшается, так как часть порового пространства занята другой фазой. Отношение эффективной проницаемости к абсолютной (однофазной) проницаемости данной среды носит название относительной фазовой проницаемости для данной фазы. В условиях преобладания капиллярных сил относительные фазовые проницаемости — функции насыщенности kri = ki / k (рис. 5). В основном обе фазы движутся под одним перепадом давления (вспомните аналогию с трубой). Суммарный поток через единицу площади сечения U делится на потоки первой и второй фаз u1 и u2 , u1 + u2 = U. Для процессов вытеснения нефти особо важную роль играет функция распределения потоков F (s) = = u1 / U, равная доле воды в совместном потоке воды и нефти. Теория дает для нее выражение Очевидно, 0 # F # 1. График функции F (s) имеет характерную S-образную форму, причем F = 0 при 0 # s # s* и F = 1 при s* # s # 1 (см. рис. 5). Это непосредственно вытекает из общей картины двухфазного течения под контролем капиллярных сил. Функция распределения потоков ясно указывает пути совершенствования извлечения нефти. Все, что способствует уменьшению доли воды в потоке при данной насыщенности, повышает эффективность заводнения. Так, можно пытаться понизить вязкость нефти (см. формулу (11)), для этого в пласт закачивают горячую воду. Можно пытаться увеличить вязкость воды, для этого к воде примешивают специальные добавки — высокомолекулярные полимеры, которые способны сильно увеличивать вязкость воды (в несколько раз при концентрации полимера порядка нескольких сотых процента). Наконец, можно повлиять на капиллярные силы, добавляя к воде поверхностно-активные вещества. Исследование движения многофазных и многокомпонентных систем в пористой среде — физико-химическая подземная гидродинамика представляет собой быстро развивающуюся ветвь теории фильтрации, где методы физики, химии и гидродинамики совместно решают важные практические задачи. Для первичного ознакомления с данной научной областью можно рекомендовать популярную книгу по теории фильтрации [1]. Более строгое, но и более сложное изложение можно найти в учебниках и монографиях 3. 1. Кочина Н.Н., Кочина П.Я., Николаевский В.Н. Мир подземных жидкостей. М.: ИФЗ, 1994. 112 с. 2. Полубаринова-Кочина П.Я. Теория движения грунтовых вод. М.: Наука, 1977. 664 с. 3. Чарный И.А. Основы подземной гидравлики. М.: Гостоптехиздат, 1956. 260 с. 4. Басниев К.С., Власов А.М., Кочина И.Н., Максимов В.М. Подземная гидравлика. М.: Недра, 1986. 303 с. 5. Баренблатт Г.И., Ентов В.М., Рыжик В.М. Движение жидкостей и газов в природных пластах. М.: Недра, 1984. 208 с. Владимир Мордухович Ентов, профессор, доктор технических наук, ведущий научный сотрудник, научный руководитель лаборатории прикладной механики сплошных сред Института проблем механики РАН, профессор Государственной академии нефти и газа им. И.М. Губкина, член-корреспондент РАЕН. Автор 12 книг и более 250 статей по механике сплошных сред и ее приложениям, в частности в нефтяной и газовой промышленности. источники: http://lektsii.org/2-1190.html http://pereplet.ru/obrazovanie/stsoros/498.html |


 — приведенное давление,
— приведенное давление, (10)
(10) или
или  ,
, .
.
 ,
, — коэффициент фильтрации, имеющий размерность скорости;
— коэффициент фильтрации, имеющий размерность скорости; — гидравлический уклон (или градиент давления).
— гидравлический уклон (или градиент давления). , (11)
, (11) имеет размерности скорости, и определяет модуль вектора скорости фильтрации. При определении расхода считается, что вектор скорости фильтрации направлен перпендикулярно плоскости (галерее), через которую фильтруется флюид. Скорость фильтрации – это фиктивная скорость , т.к. она определяется в любой точке сечения пористой среды – и в порах, и в твердом скелете, а на самом деле течение проходит только по поровым каналам с некоторой истинной скоростью υ. Между фиктивной и истинной скоростью существует взаимосвязь:
имеет размерности скорости, и определяет модуль вектора скорости фильтрации. При определении расхода считается, что вектор скорости фильтрации направлен перпендикулярно плоскости (галерее), через которую фильтруется флюид. Скорость фильтрации – это фиктивная скорость , т.к. она определяется в любой точке сечения пористой среды – и в порах, и в твердом скелете, а на самом деле течение проходит только по поровым каналам с некоторой истинной скоростью υ. Между фиктивной и истинной скоростью существует взаимосвязь: или
или 
 , задающий направление фильтрации, получим
, задающий направление фильтрации, получим (13)
(13) представляет собой модуль приведенного давления при линейном законе распределения давления. Тогда можно записать
представляет собой модуль приведенного давления при линейном законе распределения давления. Тогда можно записать
 , (15)
, (15) — орты декартовой системы координат (ось z направлена вертикально вверх).
— орты декартовой системы координат (ось z направлена вертикально вверх). ,
,  ,
,  . (16)
. (16) , (17)
, (17) — градиент давления (сил трения), ω – скорость фильтрации, m — коэффициент динамической вязкости, k – коэффициент проницаемости.
— градиент давления (сил трения), ω – скорость фильтрации, m — коэффициент динамической вязкости, k – коэффициент проницаемости. , (18)
, (18) , (19)
, (19) (20)
(20) , при
, при  , (21)
, (21) , при
, при  ,
, — предельный (начальный) градиент давления, по достижении которого начинается движение жидкости: при меньших значениях градиента давления фильтрационное течение отсутствует, этот параметр измеряется в лабораторных условиях. зависит от начального сдвига жидкости и эффективного диаметра капилляра.
— предельный (начальный) градиент давления, по достижении которого начинается движение жидкости: при меньших значениях градиента давления фильтрационное течение отсутствует, этот параметр измеряется в лабораторных условиях. зависит от начального сдвига жидкости и эффективного диаметра капилляра. (22)
(22) (23)
(23) (24)
(24) ,
,  , (25)
, (25) ,
,
 .
. ,
, , где m i — пористость i-й части. Рассмотреть также случай, когда все V i одинаковы.
, где m i — пористость i-й части. Рассмотреть также случай, когда все V i одинаковы. .
. м 2 = 1Д (Дари) ≈ 1 мкм 2 .
м 2 = 1Д (Дари) ≈ 1 мкм 2 . ; объем песчинки /в формуле ω/
; объем песчинки /в формуле ω/  ; пористость пласта m.
; пористость пласта m. , V 1 – весь объем шаров,V 2 – объем породы.
, V 1 – весь объем шаров,V 2 – объем породы.


 (1.27′)
(1.27′) (1.28)
(1.28) (1.29)
(1.29)



 ,
, – компоненты скорости фильтрации;
– компоненты скорости фильтрации;  – расход жидкости через элементарные площадки
– расход жидкости через элементарные площадки  , проходящие через некоторую точку
, проходящие через некоторую точку  среды перпендикулярно к соответствующим координатным осям. Если через точку
среды перпендикулярно к соответствующим координатным осям. Если через точку  , то проекция вектора
, то проекция вектора 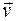 на нормаль к площадке
на нормаль к площадке  равна
равна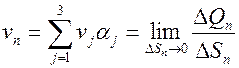 ,
, – направляющие косинусы нормали
– направляющие косинусы нормали 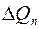 – расход жидкости через площадку
– расход жидкости через площадку  , а не на ее часть, занятую жидкостью. Поэтому величина скорости фильтрации
, а не на ее часть, занятую жидкостью. Поэтому величина скорости фильтрации  не равна истинной скорости движения жидкости
не равна истинной скорости движения жидкости  , они связаны соотношением
, они связаны соотношением ,
,
 – активная, или динамическая, пористость;
– активная, или динамическая, пористость;  и
и  – соответственно элементарный объем среды и ее части, занятых подвижной жидкостью.
– соответственно элементарный объем среды и ее части, занятых подвижной жидкостью.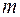 и, аналогично, трещинная пористость
и, аналогично, трещинная пористость  .
. , эффективные диаметры частиц
, эффективные диаметры частиц 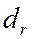 и пор
и пор  . Просветностью называется отношение площади пор ко всей площади сечения, проведенную через данную точку тела. Диапазон изменения теоретической просветности, по Слихтеру, равен 0,093 – 0,214. Параметры
. Просветностью называется отношение площади пор ко всей площади сечения, проведенную через данную точку тела. Диапазон изменения теоретической просветности, по Слихтеру, равен 0,093 – 0,214. Параметры  и
и  определяются по анализу фракционного состава частиц или микроструктуры пор и их кривых распределения.
определяются по анализу фракционного состава частиц или микроструктуры пор и их кривых распределения.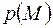 .
. ,
,
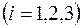 ,
, называется коэффициентом проницаемости, или просто проницаемостью.
называется коэффициентом проницаемости, или просто проницаемостью. ,
,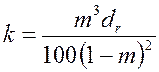 .
. ,
, ,
,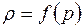 ,
, , а сумма сил
, а сумма сил 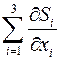 заменена силами трения Ньютона
заменена силами трения Ньютона  . Тогда отпадает надобность в уравнениях состояния (2.24).
. Тогда отпадает надобность в уравнениях состояния (2.24).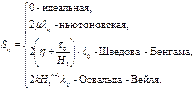
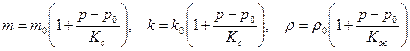
 ,
, 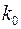 и
и  – соответственно пористость, проницаемость и плотность при начальном давлении
– соответственно пористость, проницаемость и плотность при начальном давлении  ;
;  и
и 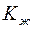 – соответственно модули объемной упругости скелета и жидкости. Кроме того, принимаем, что
– соответственно модули объемной упругости скелета и жидкости. Кроме того, принимаем, что 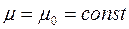 .
. , заполнения элементарного объема
, заполнения элементарного объема  сплошной среды принимает вид
сплошной среды принимает вид .
. ,
,  ,
,  . Но если подставить уравнения (2.30) и (2.31) в (2.32) и учесть, что в реальных ситуациях величины
. Но если подставить уравнения (2.30) и (2.31) в (2.32) и учесть, что в реальных ситуациях величины 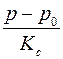 и
и 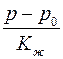 много меньше единицы, то отбросив малые величины высших порядков, получим одно основное
много меньше единицы, то отбросив малые величины высших порядков, получим одно основное ,
, – коэффициент пьезопроводности среды;
– коэффициент пьезопроводности среды;  – приведенный модуль объемной упругости среды;
– приведенный модуль объемной упругости среды; 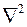 – оператор Лапласа. Пьезопроводность
– оператор Лапласа. Пьезопроводность  имеет размерность м 2 /с.
имеет размерность м 2 /с.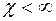
 , то уравнение (2.33) описывает нестационарное поле давления при упругом режиме фильтрации. При
, то уравнение (2.33) описывает нестационарное поле давления при упругом режиме фильтрации. При 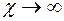
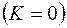 имеем уравнение Лапласа
имеем уравнение Лапласа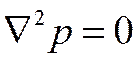 ,
, , т. е. при установившемся режиме фильтрации.
, т. е. при установившемся режиме фильтрации. , ограниченной поверхностью
, ограниченной поверхностью  , необходимо и достаточно, чтобы решение уравнения (2.33) удовлетворяло начальному условию (при
, необходимо и достаточно, чтобы решение уравнения (2.33) удовлетворяло начальному условию (при 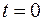 )
)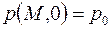 при
при 
 граничным условиям:
граничным условиям: , то
, то при
при  ,
, ,
, ,
, – характерный линейный размер;
– характерный линейный размер;  – коэффициент поверхностного фильтрационного сопротивления, получивший название параметр «скин-эффекта».
– коэффициент поверхностного фильтрационного сопротивления, получивший название параметр «скин-эффекта».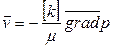 ,
, – тензор проницаемости.
– тензор проницаемости.
 ,
, – проницаемости вдоль главных осей
– проницаемости вдоль главных осей  анизотропии. При этом проекция скорости фильтрации на нормаль к элементарной площадке вычисляется по формуле
анизотропии. При этом проекция скорости фильтрации на нормаль к элементарной площадке вычисляется по формуле .
.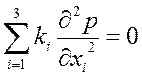 .
.

 – новые координаты.
– новые координаты. , проницаемость которой
, проницаемость которой
 области
области  ,
, .
. .
. ,
,  — полуоси элипса
— полуоси элипса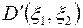 имеем уравнение Лапласа
имеем уравнение Лапласа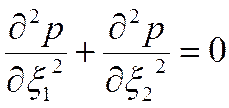 ,
, , проницаемость
, проницаемость  , скорость фильтрации
, скорость фильтрации  и давление
и давление  , связанные законом Дарси
, связанные законом Дарси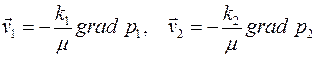

 .
. – новая безразмерная величина, характеризующая данную среду.
– новая безразмерная величина, характеризующая данную среду.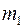 и
и  являются функциями обоих давлений, т.е.
являются функциями обоих давлений, т.е. .
. ;
; и поэтому при небольших изменениях этого давления
и поэтому при небольших изменениях этого давления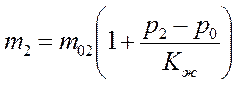 ;
; , т.е. фильтрацией в порах можно пренебречь
, т.е. фильтрацией в порах можно пренебречь  ;
;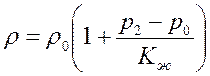 ,
, или
или 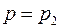 в зависимости от того, рассматривается жидкость в трещинах или в порах;
в зависимости от того, рассматривается жидкость в трещинах или в порах; .
. ,
, – специфическая характеристика трещиновато-пористой среды;
– специфическая характеристика трещиновато-пористой среды;  – своеобразная пьезопроводность среды.
– своеобразная пьезопроводность среды. имеет размерность площади, и для реальных пород его порядок может изменяться в широких пределах – от 10 -1 до 10 6 м 2 .
имеет размерность площади, и для реальных пород его порядок может изменяться в широких пределах – от 10 -1 до 10 6 м 2 . ,
, – параметр, называемый временем запаздывания.
– параметр, называемый временем запаздывания. . В пределе, когда
. В пределе, когда  , среда с двойной пористостью переходит в чисто пористую и уравнения (2.54) и (2.33) совпадают.
, среда с двойной пористостью переходит в чисто пористую и уравнения (2.54) и (2.33) совпадают. или при установившейся фильтрации
или при установившейся фильтрации  .
. или
или  и
и  удовлетворяют первому уравнению (2.53), то задачу целесообразно решать относительно давления
удовлетворяют первому уравнению (2.53), то задачу целесообразно решать относительно давления 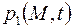 , принимая начальные и граничные условия в виде выражений (2.35) – (2.38). После определения давления
, принимая начальные и граничные условия в виде выражений (2.35) – (2.38). После определения давления 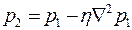 .
.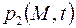 . Но здесь имеет место определенная специфика в задании граничных условий.
. Но здесь имеет место определенная специфика в задании граничных условий.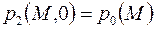 согласовано с граничными условиями
согласовано с граничными условиями  вида
вида ,
, , то в таком виде граничная задача и рассматривается.
, то в таком виде граничная задача и рассматривается. , где
, где 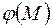 – невязка существующего граничного условия:
– невязка существующего граничного условия:
 . Такое качественное отличие – результат принятого упрощения пренебрежения фильтрацией жидкости в порах, где давление изменяется только благодаря массообмену с жидкостью в трещинах. Аналогично, предположение о жестком характере фильтрации жидкости в трещинах приводит к указанной выше проверке начальных распределений давлений
. Такое качественное отличие – результат принятого упрощения пренебрежения фильтрацией жидкости в порах, где давление изменяется только благодаря массообмену с жидкостью в трещинах. Аналогично, предположение о жестком характере фильтрации жидкости в трещинах приводит к указанной выше проверке начальных распределений давлений 

 .
.

 ;
;  — температура.
— температура. с вязкостью µ=const и плотностью
с вязкостью µ=const и плотностью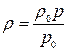 ,
,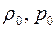 — постоянные величины.
— постоянные величины. ,
,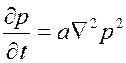 ,
, . Следовательно, все соотношения, полученные до сих пор для жидкости, могут быть в первом приближении использованы и при изучении фильтрации газа, если заменить в них
. Следовательно, все соотношения, полученные до сих пор для жидкости, могут быть в первом приближении использованы и при изучении фильтрации газа, если заменить в них  ,
,  .
.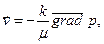 (2.58) нарушается и зависимость между
(2.58) нарушается и зависимость между  принимает вид выпуклой или вогнутой кривой, как показано на рис. 11.
принимает вид выпуклой или вогнутой кривой, как показано на рис. 11.
 превышает критическое значение (зависимость изображена кривой 1 на рис. 11);
превышает критическое значение (зависимость изображена кривой 1 на рис. 11); ,
,
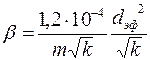 , а, по данным Б. И. Султанова,
, а, по данным Б. И. Султанова,  ;
;  — эффективный диаметр пор;
— эффективный диаметр пор;  ,
,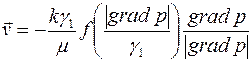 ,
, — параметры модели;
— параметры модели; 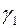 — характерное значение градиента давления;
— характерное значение градиента давления; 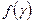 — безразмерная функция, описывающая ломаную линию (см. рис. 11).
— безразмерная функция, описывающая ломаную линию (см. рис. 11).