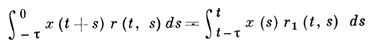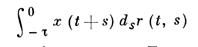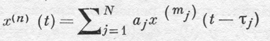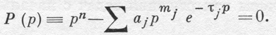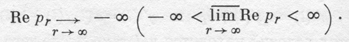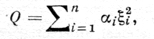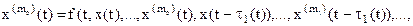Классификация уравнений с отклоняющимся аргументом

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ОТКЛОНЯЮЩИМСЯ АРГУМЕНТОМ

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ОТКЛОНЯЮЩИМСЯ АРГУМЕНТОМ — дифференциальное уравнение, связывающее аргумент, искомую функцию и ее производные, взятые, вообще говоря, при различных значениях этого аргумента. Примеры:

где постоянные а, τ, k заданы; τ в уравнении (1) и t — kt в уравнении (2) — отклонения аргумента. Встречаются и более сложные Д. у. с о. а., включающие большее число отклонений аргумента, могущих представлять собой заданные функции (в частности, если они постоянны, то уравнение часто наз. дифференциально-разностным) или даже зависеть от искомого решения. Эпизодически рассматривались также Д. у. с о. а., в к-рых искомая функция зависит более чем от одного аргумента. Д. у. с о. а. впервые появились в связи с формальным решением уравнений с частными производными и затем неоднократно рассматривались как сами по себе, так и в связи с задачами геометрии, а позднее — в связи с различными приложениями, прежде всего к теории автоматич. управления. Построение систематич. теории Д. у. с о. а. было начато в 1949.

Определение Д. у. с о. а. допускает любые суперпозиции искомого решения [типа x(x(t))] и интегралы от него, поэтому формально класс Д. у. с о. а. включает в себя все уравнения математич. анализа. Все же обычно, говоря о Д. у. с о. а., имеют в виду тот или иной естественный класс дифференциальных уравнений, в к-рых введено отклонение аргумента, допускающее построение содержательной теории. При этом ряд свойств Д. у. с о. а. имеет непосредственную аналогию со свойствами обычных дифференциальных уравнений, тогда как иные свойства являются принципиально новыми.

Уравнение (или система уравнений)

(для системы х и f — векторы), где все τ_j ≥ 0, наз. уравнением (системой) запаздывающего, нейтрального или опережающего типа, если max_jm_j n, соответственно. Для уравнений иных видов такая классификация проводится на основе преобразования к виду (3)

помощью замены t → χ(t), χ — возрастающая функция; напр., уравнение (1) запаздывающего типа при τ ≥ 0 и опережающего (замена t → t + τ) — при τ 0. (4)

Для этого класса Д. у. с о. а. ставится основная начальная задача: заданы начальная точка t₀, начальная функция φ(t), t₀ — τ ≤ t ≤ t₀, и значение x(t₀ + 0); под решением задачи для уравнения (4) понимается функция xt₀, обращающая уравнение (4) в тождество, причем при t > t₀, t — τ ≤ t₀ в правую часть вместо x(t — τ) надо подставлять φ(t — τ). Для решения поставленной задачи можно применить метод шагов: при t₀ t₀, х»(t) непрерывна при t > t₀ + τ и т. д. (свойство сглаживания).

Аналогично ставится начальная задача и строится решение для систем уравнений вида (4) и для уравнений высших порядков. В случае нескольких запаздываний за шаг принимают наименьшее из них. Если τ = τ(t), то φ(t) должна быть задана на всем начальном множестве значений t — τ(t) ≤ t₀, t > t₀. Наличие у τ(t) нулей препятствует применению метода шагов, однако с помощью простых аппроксимационных

или итерационных методов можно доказать теорему о разрешимости начальной задачи, аналогичную приведенной выше. Численные методы ее решения в принципе те же, что для τ ≡ 0. Если заданные функции разрывны или x(t₀ + 0) ≠ φ(t₀), то понятие решения должно быть естественно обобщено.

Решение сформулированной начальной задачи строится только в направлении возрастания t. Другая ее особенность состоит в том, что многообразие решений при произвольной φ(t), вообще говоря, бесконечномерное. (Исключением служат уравнения без предыстории, для к-рых t₀ ≤ t — τ(t) ≤ t при t ≥ t₀;

напр., уравнение (2) при 0 ≤ k ≤ 1, t₀ = 0.) Это существенно отличает теорию Д. у. с о. а. от теории уравнений без отклонения аргумента.

В уравнении (4) запаздывание сосредоточенное. Рассматриваются также уравнения с распределенным запаздыванием, правая часть к-рых включает интегралы

(это — интегро-дифференциальные уравнения типа Вольтерра) или, комбинированный случай,

и т. п. Наиболее общим видом Д. у. с о. а. запаздывающего типа 1-го порядка служит дифференциально-функциональное уравнение типа Вольтерра

х'(t) = F[x(t + s); t], -τ ≤ s ≤ 0,

где правая часть при каждом t > t₀ представляет собой функционал. И для таких уравнений начальная задача разрешима.

Для Д. у. с о. а. нейтрального типа, напр. x'(t) = f(t, x(t), x(t — τ₁), х'(t — τ₂)), τ₁, τ₂ ≥ 0,

постановка и свойства начальной задачи аналогичны указанным выше, однако свойство сглаживания отсутствует; кроме того, возможны осложнения, если переменное запаздывание τ₂(t) имеет нули. Начальная задача для Д. у. с о. а. опережающего типа является некорректной.

Лучше других изучены линейные автономные (т. е. с постоянными коэффициентами и постоянными отклонениями аргумента) Д. у. с о. а. Уравнение (без подобных членов)

(все a_j ≠ 0) имеет частные решения х = е p t , где р удовлетворяет характеристическому уравнению

Здесь Р(р) — квазиполином; k-кратному корню уравнения (6) отвечают решения e p t , . t k-1 e p t уравнения (5). Если хотя бы одно τ_j ≠ 0, то уравнение (6) имеет бесконечное число корней р₁, р₂, . Чтобы уравнение (5) имело запаздывающий (нейтральный) тип, необходимо и достаточно условие

В этих случаях каждое решение уравнения (5) разлагается в ряд по указанным частным решениям, а при решении начальной задачи для уравнения (5) и соответствующего неоднородного уравнения можно пользоваться обычными методами операционного исчисления. Аналогичными свойствами обладают системы уравнений и уравнения с распределенным запаздыванием.

с коэффициентами A_ij, зависящими только от точки x ∈ D. В каждой точке x ∈ D квадратичная форма Q при помощи неособого аффинного преобразования переменных λc = ζ₀(ξ₁, . ξ_n) i = 1, . n, может быть приведена к канонич. виду

где коэффициенты α_i, i = 1, . n, принимают значения 1, -1, 0, причем число отрицательных коэффициентов (индекс инерции) и число нулевых коэффициентов (дефект формы) являются аффинными инвариантами. Когда все α_i = 1 или все α_i = -1, т. е. когда форма Q соответственно положительно или отрицательно определена (дефинитна), уравнение (3) наз. эллиптическим в точке x ∈ D. Если один из коэффициентов α_i отрицателен, а все остальные положительны (или наоборот), то уравнение (3) наз. гиперболическим в точке х. В случае, когда l, 1 n , причем от них существенно зависит область определения искомого решения. К таким задачам относятся, напр., Коши задача с начальными данными, характеристическая задача Коши. Особо ставятся краевые задачи для уравнений смешанного типа. В теории Д. у. с ч. п. значительное внимание уделяется обширному классу смешанных задач. См. Смешанная задача для гиперболического уравнения и системы, Смешанная и краевая задачи для параболического уравнения и системы.

Задача считается в классич. смысле корректно (правильно) поставленной, если она имеет и притом единственное устойчивое решение. Задачи, не удовлетворяющие этим требованиям, до недавнего времени считались лишенными смысла. Начиная с 40-х гг. 20 в. широта диапазона математич. проблем физики, механики и техники заставила расширить не только понятие корректности постановок задач для Д. у. с ч. п., но и понятие самого решения. Были введены так наз. обобщенные решения. Наряду с вопросами существования и единственности точных решений тех или иных задач для Д. у. с ч. п. в приложениях значительную важность приобрели понятия в определенном смысле приближенных решений и фактическое построение таких решений.

Исторически одним из первых методов, позволяющих строить решения ряда задач для важных классов Д. у. с ч. п., является метод разделения переменных, или Фурье метод, к к-рому тесно примыкает метод интегральных преобразований (см. Фурье интеграл). От применения этого метода берет свое начало спектральная теория дифференциальных операторов.

Сравнительно позже был создан параметрикса метод, на основе к-рого построен потенциалов метод. Этот метод позволяет привлекать к исследованию краевых задач для эллиптич. уравнений аппарат интегральных уравнений. Далеко идущим развитием метода параметрикса являются методы теории функций комплексного переменного, успешно применяющиеся при исследовании эллиптич. уравнений с двумя независимыми переменными. См. Дифференциальное уравнение с частными производными; методы комплексного переменного.

Когда изучаемое Д. у. с ч. п. представляет собой уравнение Эйлера для многомерной задачи вариационного исчисления, часто пользуются вариационным методом. Вариационный метод весьма удобен в тех случаях, когда уравнение Эйлера является уравнением эллиптич. типа. См. также Дифференциальное уравнение с частными производными; вариационные методы решения.

Начиная с 30-х гг. 20 в. при исследовании Д. у. с ч. п. широко используются методы функционального анализа, среди к-рых центральное место занимают Шаудера метод и его дальнейшее развитие — метод априорных оценок. Эти методы позволяют сравнительно легко установить существование слабых решений и сильных решений как для линейных, так и для нек-рых классов нелинейных Д. у. с ч. п. См. Дифференциальное уравнение с частными производными; функциональные методы решения.

Среди методов, успешно приводящих к цели при построении приближенных решений Д. у. с ч. п., чаще всего применяются методы конечных разностей исчисления. См. также Гиперболического типа уравнение, численные методы решения; Параболического типа уравнение, численные методы решения; Эллиптического типа уравнение, численные методы решения.

Лит.: [1] Берс Л., Джон Ф., Шехтер М., Уравнения с частными производными, пер. с англ., М., 1966; [2] Бицадзе А. В., Уравнения математической физики, М., 1976; [3] Владимиров В. С., Уравнения математической физики, 2 изд., М., 1971; [4] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964; [5] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 4 изд., М., 1972.

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д — Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.

Дифференциальные уравнения с последействием

Классификация уравнений с отклоняющимся аргументом. Основная начальная задача для дифференциальных уравнений с запаздыванием.

Метод последовательного интегрирования. Принцип сглаживания решений уравнений с запаздыванием.

Принцип сжатых отображений. Теорема существования и единственности решения основной начальной задачи для уравнения с несколькими сосредоточенными запаздываниями. Теорема существования и единственности решения основной начальной задачи для системы уравнений с распределенным запаздыванием.

Непрерывная зависимость решений основной начальной задачи от параметров и начальных функций.

Специфические особенности решений уравнений с запаздыванием. Возможность продолжения решения. Перенос начальной точки. Теоремы о достаточных условиях интервалов слипания. Теорема о достаточных условиях нелокальной продолжимости решений.

Вывод формулы общего решения для линейной системы с линейными запаздываниями.

Исследование уравнений с запаздыванием на устойчивость. Метод Д-разбиений. Метод преобразований Лапласа и его применение к автономным системам.

Применение метода функционалов для исследования устойчивости. Теоремы Н. Н. Красовского о необходимых и достаточных условиях устойчивости. Устойчивость при постоянно действующих возмущениях. Примеры построения функционалов.

Применение метода функций Ляпунова для исследования устойчивости. Теоремы Разумихина об устойчивости, асимптотической устойчивости и неустойчивости решений уравнений с запаздыванием. Примеры построения функций Ляпунова.

Построение программных управлений с запаздыванием в системах с полной и неполной информацией. Теоремы В. И. Зубова. Задача распределения капиталовложений по отраслям. Синтез программных управлений в квазилинейном случае.

Построение оптимальных программных управлений в линейном и нелинейном случаях. Принцип максимума Понтрягина.

Стабилизация системы уравнений управлением с постоянными запаздываниями. Влияние переменного запаздывания на одноосную стабилизацию твердого тела.

Уравнения с распределенным запаздыванием неустойчивого типа. Теоремы о сравнении решений. Исследование решений на участках колебания. Оценки скорости роста решения. Уравнения устойчивого типа. Теорема сравнения.

Уравнения с отклоняющимся аргументом

Определение 1. Дифференциальным уравнением (ДУ) с отклоняющимся аргументом называется дифференциальное уравнение, в которое неизвестная функция и ее производные входят, вообще говоря, при различных значениях аргумента.

Впервые отдельные уравнения такого типа появились в литературе во второй половине 18 столетия (Кондорсе 1771), но систематическое изучение их началось лишь в 20 веке.

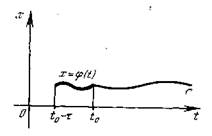
Основная начальная задача для уравнения (1) заключается в определении непрерывного решения x(t) уравнения (1) при t>t₀ при условии, что x(t)=j(t) при t-t£ t £ t₀, где j(t)- заданная непрерывная функция, называемая начальной.

Отрезок t₀-t£ t £ t₀, на котором задана начальная функция, называется начальным множеством и обозначается ; точка t₀ называется начальной точкой. Обычно предполагается, что

Рассмотрим дифференциальное уравнение n-го порядка с L отклонениями аргумента,

,

где отклонения t_I(t)³0. Здесь под x ( k ) (t-t_I(t)) понимается k-я производная от функции x(z), взятая в точке z = t-t_I(t). В дальнейшем предполагается, что все отклонения t_I(t) непрерывны.

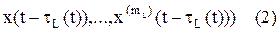
Пусть уравнение (2) разрешимо относительно (t); Обозначим l=m₀-m, где m=max .

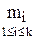
Замечание.Уравнения, для которых l>0, называются уравнениями запаздывающего типа (у них старшая производная, входящая в уравнение, не содержит запаздывания). (ЗФДУ)

Уравнения, для которых l=0, называются уравнениями нейтрального типа (у них старшая производная входит в уравнение, как с запаздыванием, так и без него). (НФДУ)

Уравнения, для которых l / (t)=f (t, x (t), x (t-t)) (1)

с начальным условием x (t)= j(t), t где j(t)- начальная функция, начальное множество, t- запаздывание, t>0(запаздывание t может быть переменным: t=t(t)).

Основная начальная задача (задача Коши) для уравнения (1)заключается в нахождении непрерывного решения x(t), удовлетворяющего уравнению (1) с начальным условием x (t)= j(t), t .

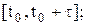
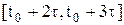
Наиболее естественным методом нахождения решения уравнения (1) является так называемый «метод шагов» (метод последовательного интегрирования ДУ на отрезках , и т. д.), заключающийся в том, что решение x(t) рассматриваемого уравнения определяется из дифференциального уравнения без запаздывания

так как при t₀£t£t₀+t аргумент t-t изменится на начальном множестве

[t₀-t;t₀] и, следовательно, третий аргумент x(t-t) функции f равен начальной функции j₀(t-t).

Предполагая существование решения x =j₁(t) этой начальной задачи на всем отрезке[t₀;t₀+t] , аналогично получаем:

Пример 2.Для уравнения x(t)= 6x(t-1), x=t при 0 £ t £ 1 определить x(t) при 1 / (t)=6(t-1), 1 £ t £ 2, x(1)=1, так как x(1)=1 . Интегрируя, находим:

x(t)= 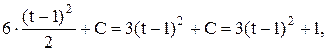(так как 1=3(1-1) 2 +С С=1). При 2 £ t £3: x / (t)=6 [3(t-2) 2 +1], x(2)=4, так как 3(2-1) 2 +1=4, тогда интегрируя:

Заметим, что даже в случае существования непрерывных производных от функций j и f сколь угодно высокого порядка решение основной начальной задачи будет, вообще говоря, иметь разрыв первого рода у производной порядка k в точке t₀+(k-1)t, но производные более низких порядков в этой точке будут уже непрерывны.

Действительно, в точке t₀ x / (t) имеет, вообще говоря, разрыв первого рода, так как интегрируя уравнение

x / (t)=f(t, x(t),j₀(t-t)), t₀ £ t £t₀+t, можно удовлетворить условию

x(t₀)=j₀(t₀),но, вообще говоря, нельзя удовлетворить, кроме того, условию

Таким образом, применение метода шагов становится затруднительным, если запаздывание t мало по сравнению с отрезком, на котором требуется определить решение.