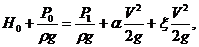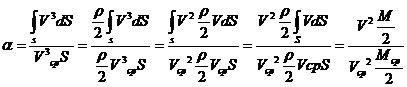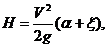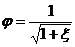Коэффициент скорости в уравнении бернулли

Основы гидравлики

Уравнение Бернулли — фундамент гидродинамики

Бернулли — вне всякого сомнения — имя, знакомое и специалистам, и обывателям, которые хоть немного интересуются науками. Этот человек оставил ослепительный след в истории познавания человечеством окружающего мира, как физик, механик, гидравлик и просто общепризнанный гений, Даниил Бернулли навсегда останется в памяти благодарных потомков за свои идеи и выводы, которые долгое время существования человечества были покрыты мраком неизведанного.
Открытия и законы, которыми Бернулли осветил путь к познанию истины, являются фундаментальными, и придали ощутимый импульс развитию многих естественных наук. К таковым относится и уравнение Бернулли в Гидравлике, которое он вывел почти три века назад. Данное уравнение является основополагающим законом этой сложной науки, объясняющим многие явления, описанные даже древними учеными, например, великим Архимедом.

Попробуем уяснить несложную суть закона Бернулли (чаще его называют уравнением Бернулли), описывающего поведение жидкости в той или иной ситуации.

Выделим в стационарно текущей идеальной жидкости трубку тока, которая ограничена сечениями S₁ и S₂ , (рис. 1) .
(Понятие идеальной жидкости абстрактно, как и понятие всего идеального. Идеальной считается жидкость, в которой нет сил внутреннего трения, т. е. трения между отдельными слоями и частицами подвижной жидкости).
Пусть в месте сечения S₁ скорость течения ν₁ , давление p₁ и высота, на которой это сечение расположено, h₁ . Аналогично, в месте сечения S₂ скорость течения ν₂ , давление p₂ и высота сечения h₂ .

За бесконечно малый отрезок времени Δt жидкость переместится от сечения S₁ к сечению S₁‘ , от S₂ к S₂‘ .

По закону сохранения энергии, изменение полной энергии E₂ — E₁ идеальной несжимаемой жидкости равно работе А внешних сил по перемещению массы m жидкости:

где E₁ и E₂ — полные энергии жидкости массой m в местах сечений S₁ и S₂ соответственно.

С другой стороны, А — это работа, которая совершается при перемещении всей жидкости, расположенной между сечениями S₁ и S₂ , за рассматриваемый малый отрезок времени Δt .
Чтобы перенести массу m от S₁ до S₁‘ жидкость должна переместиться на расстояние L₁ = ν₁Δt и от S₂ до S₂‘ — на расстояние L₂ = ν₂Δt . Отметим, что L₁ и L₂ настолько малы, что всем точкам объемов, закрашенных на рис. 1 , приписывают постоянные значения скорости ν , давления р и высоты h .
Следовательно,

где F₁ = p₁S₁ и F₂ = — p₂S₂ (сила отрицательна, так как направлена в сторону, противоположную течению жидкости; см. рис. 1).

Полные энергии E₁ и E₂ будут складываться из кинетической и потенциальной энергий массы m жидкости:

Подставляя (3) и (4) в (1) и приравнивая (1) и (2) , получим

Согласно уравнению неразрывности для несжимаемой жидкости, объем, занимаемый жидкостью, всегда остается постоянным, т. е.

Разделив выражение (5) на ΔV , получим

где ρ — плотность жидкости.

После некоторых преобразований эту формулу можно представить в другом виде:

Поскольку сечения выбирались произвольно, то в общем случае можно записать:

ρv 2 /2 +ρgh +p = const (6) .

Выражение (6) получено швейцарским физиком Д. Бернулли (опубликовано в 1738 г.) и называется уравнением Бернулли.

Даниил Бернулли (Daniel Bernoulli, 1700 — 1782), швейцарский физик, механик и математик, один из создателей кинетической теории газов, гидродинамики и математической физики. Академик и иностранный почётный член (1733) Петербургской академии наук, член Академий: Болонской (1724), Берлинской (1747), Парижской (1748), Лондонского королевского общества (1750).

Уравнение Бернулли по своей сути является интерпретацией закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Уравнение хорошо выполняется и для реальных жидкостей, для которых внутреннее трение не очень велико.

Величина р в формуле (6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела) , величина ρν 2 /2 — динамическим давлением, величина ρgh — гидростатическим давлением.

Статическое давление обусловлено взаимодействием поверхности жидкости с внешней средой и является составляющей внутренней энергии рассматриваемого элементарного объема жидкости (т. е. характеризуется взаимодействием внутренних частиц жидкости, вызванных внешним возмущением — давлением) , а гидростатическое – положением этого объема жидкости в пространстве (зависит от высоты над поверхностью Земли) .
Динамическое давление характеризует кинематическую составляющую энергии этого объема, поскольку зависит от скорости потока, в котором движется рассматриваемый элементарный объем жидкости.

Для горизонтальной трубки тока изменение потенциальной составляющей ρgh будет равно нулю (поскольку h2 – h1 = 0) , и выражение (6) примет упрощенный вид:

ρv 2 /2 + p = const (7) .

Выражение p + ρν 2 /2 называется полным давлением.

Таким образом, содержание уравнения Бернулли для элементарной струйки при установившемся движении можно сформулировать так: удельная механическая энергия при установившемся движении элементарной струйки идеальной жидкости, представляющая собой сумму удельной потенциальной энергии положения и давления и удельной кинетической энергии, есть величина постоянная.

Все члены уравнения Бернулли измеряются в линейных единицах.

В гидравлике широко применяют термин напор, под которым подразумевают механическую энергию жидкости, отнесенную к единице ее веса (удельную энергию потока или неподвижной жидкости) .
Величину v 2 /2g называют скоростным (кинетическим) напором, показывающим, на какую высоту может подняться движущаяся жидкость за счет ее кинетической энергии.
Величину h_п = p/ρg называют пьезометрическим напором, показывающим на какую высоту поднимается жидкость в пьезометре под действием оказываемого на нее давления.
Величину z называют геометрическим напором, характеризующим положение центра тяжести соответствующего сечения движущейся струйки над условно выбранной плоскостью сравнения.

Сумму геометрического и пьезометрического напоров называют потенциальным напором, а сумму потенциального и скоростного напора — полным напором.

На основании анализа уравнения Бернулли можно сделать вывод, что при прочих неизменных параметрах потока (жидкости или газа) величина давления в его сечениях обратно пропорциональна скорости, т. е. чем выше давление, тем меньше скорость, и наоборот.
Это явление используется во многих технических конструкциях и устройствах, например, в карбюраторе автомобильного двигателя (диффузор), в форме крыла самолета. Увеличение скорости воздушного потока в диффузоре карбюратора приводит к созданию разрежения, всасывающего бензин из поплавковой камеры, а специальная форма сечения самолетного крыла позволяет создавать на его нижней стороне зону повышенного давления, способствующего появлению подъемной силы.

Геометрическая интерпретация уравнения Бернулли

Поскольку напор измеряется в линейных величинах, можно дать графическую (геометрическую) интерпретацию уравнению Бернулли и его составляющим.

На графике (рис. 2) представлена горизонтальная плоскость сравнения 0-0 , относительно которой геометрический напор будет в каждом сечении равен вертикальной координате z центра тяжести сечения (линия геометрического напора проходит по оси струйки) .
Линия К-К , характеризующая потенциальный напор струйки, получена сложением геометрического и пьезометрического напора в соответствующих сечениях (т. е. разница координат точек линии К-К и соответствующих точек оси струйки характеризует пьезометрический напор в данном сечении) .
Полный напор характеризуется линией MN , которая параллельна плоскости сравнения О-О , свидетельствуя о постоянстве полного напора H’_e (удельной механической энергии) идеальной струйки в любом ее сечении.

При движении реальной жидкости, обладающей вязкостью, возникают силы трения между ограничивающими поток поверхностями и между слоями внутри самой жидкости. Для преодоления этих сил трения расходуется энергия, которая превращается в теплоту и рассеивается в дальнейшем движущейся жидкостью. По этой причине графическое изображение уравнения Бернулли для идеальной жидкости будет отличаться от аналогичного графика для реальной жидкости.
Если обозначить h_f потери напора (удельной энергии) струйки на участке длиной L , то уравнение Бернулли для реальной жидкости примет вид:

Для реальной жидкости полный напор вдоль струйки не постоянен, а убывает по направлению течения жидкости, т. е. его графическая интерпретация имеет вид не прямой линии, а некоторой кривой МЕ (рис. 3) . Заштрихованная область характеризует потери напора.

Падение напора на единице длины элементарной струйки, измеренной вдоль оси струйки, называют гидравлическим уклоном:

Гидравлический уклон положителен, если напорная линия снижается по течению жидкости, что всегда бывает при установившемся движении.

Для практического применения уравнения Бернулли необходимо распространить его на поток реальной жидкости:

где α₁ , α₂ — коэффициенты Кориолиса, учитывающие различие скоростей в разных точках сечения потока реальной жидкости.
На практике обычно принимают α₁ = α₂ = α : для ламинарного режима течения жидкости в круглых трубах α = 2, для турбулентного режима α = 1,04. 1,1.

Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности ( S₁v₁Δt = S₂v₂Δt ) видно, что при течении жидкости по горизонтальной трубе, которая имеет различные сечения, скорость жидкости больше в более узких местах (где площадь сечения S меньше) , а статическое давление больше в более широких местах, т. е. там, где скорость меньше. Это можно увидеть, установив вдоль трубы ряд манометров.

Данный опыт показывает, что в манометрической трубке В , которая прикреплена к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С , которые прикреплены к широкой части трубы, что соответствует уравнению Бернулли.

Так как динамическое давление зависит от скорости движения жидкости (газа) , то уравнение Бернулли можно использовать для измерения скорости потока жидкости. Принципиально это свойство жидкости для определения скорости потока реализовано в так называемой трубке Пито – Прандтля (обычно ее называют трубкой Пито ) .

Трубка Пито – Прандтля ( см. рис. 2 ) состоит из двух тонких стеклянных трубок, одна из которых изогнута под прямым углом (Г-образно) , а вторая — прямая.
Одним из свободных концов каждая трубка присоединена к манометру.
Изогнутая трубка имеет открытый свободный конец, направленный против тока и принимающий напор потока жидкости, а вторая погружена в поток перпендикулярно току, и скорость потока на давление внутри трубки не влияет, т. е. внутри этой трубки действует лишь статическая составляющая давления жидкости.
Разница между давлением в первой трубке (полное давление) и второй трубке (статическое давление) , которую показывает манометр, является динамическим давлением, определяемым по формуле:

Определив с помощью трубки Пито — Прандтля динамическое давление в потоке жидкости, можно легко вычислить скорость этого потока:

Уравнение Бернулли также используют для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, с маленьким отверстием в боковой стенке на некоторой глубине ниже уровня жидкости.

Рассмотрим два сечения (на уровне h₁ свободной поверхности жидкости в сосуде и на уровне h₁ выхода ее из отверстия) и применим уравнение Бернулли:

Так как давления р₁ и р₂ в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. р₁ = р₂ , то уравнение будет иметь вид

Из уравнения неразрывности мы знаем, что ν₁/ν₂ = S₂/S₁ , где S₁ и S₂ — площади поперечных сечений сосуда и отверстия.
Если S₁ значительно превышает S₂ , то слагаемым ν₁ 2 /2 можно пренебречь и тогда:

Это выражение получило название формулы Торричелли.
Формулу Торричелли можно использовать для подсчета объемного (или массового) расхода жидкости, истекающего из отверстия в сосуде с поддерживаемым постоянно уровнем под действием атмосферного давления.
При этом используется формула Q = vS (для определения массового расхода – m = ρvS ) , по которой определяется расход жидкости за единицу времени.

Если требуется узнать расход жидкости за определенный промежуток времени t , то его определяют, умножив расход за единицу времени на время t .

Следует отметить, что такая методика расчета расхода реальной жидкости через отверстие в стенке сосуда дает некоторые погрешности, обусловленные физическими свойствами реальных жидкостей, поэтому требует применения поправочных коэффициентов (коэффициентов расхода) .

Пример решения задачи на определение расхода жидкости

Определить примерный объемный расход воды, истекающей из отверстия диаметром 10 мм, проделанном в вертикальной стенке широкого сосуда на высоте h = 1 м от верхнего, постоянно поддерживаемого, уровня воды за 10 секунд.
Ускорение свободного падения принять равным g = 10 м/с 2 .
Коэффициент расхода воды через отверстие — µ_s = 0,62.

По формуле Торричелли определим скорость истечения воды из отверстия:

v = √2gh = √2×10×1 ≈ 4,5 м/с.

Определим расход воды Q за время t = 10 секунд:

Q = µ_svSt = 0,62×4,5×3,14×0,012/4 × 10 ≈ 0,0022 м 3 ≈ 2,2 литра.

На практике расход жидкости в трубопроводах измеряют расходомерами, например, расходомером Вентури. Расходомер Вентури (см рис. 2) представляет собой конструкцию из двух конических патрубков, соединенных цилиндрическим патрубком. В сечениях основной трубы и цилиндрического патрубка устанавливают трубки-пьезометры, которые фиксируют уровень жидкости, обусловленный полным давлением в потоке.

При прохождении жидкости через сужающийся конический патрубок часть потенциальной энергии потока преобразуется в кинетическую, и, наоборот, – при прохождении потока по расширяющемуся коническому патрубку, кинетическая энергия уменьшается, а потенциальная растет. Это сказывается на скорости движения жидкости по рассматриваемым участкам. Перепад высоты уровня жидкости в пьезометрах позволяет рассчитать среднюю скорость потока жидкости на рассматриваемых участках и вычислить объемный расход по внутреннему сечению трубы.
В расходомерах учитываются потери напора в самом приборе при помощи коэффициента расхода прибора φ .

Коэффициент скорости в уравнении бернулли

12-я лекция, 2010

8. ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ

8.1 Истечение через отверстия в тонкой стенке и насадки (короткие трубки) при постоянном напоре.

8.2. Истечение при совершенном сжатии.

8.3 Скорость истечения при совершенном сжатии. Коэффициенты: ε , ξ , φ , μ

8.4 Истечение при несовершенном сжатии

8.5. Истечение под уровень

8.6. Истечение через насадки при постоянном напоре.

8.7 Первый режим течения.

8.8 Второй режим истечения

8.1. Истечение через отверстия и насадки (короткие трубки)

при постоянном напоре.

Рассматривается процесс истечение жидкости из резервуаров через отверстия и насадки в атмосферу и в пространство, заполненное жидкостью.

При истечении запас потенциальной энергии жидкости в резервуаре, переходит в кинетическую энергию свободной струи, при переходе есть потери энергии на трение и завихрение частиц жидкости.

Задачей изучения процесса истечения является определение скорости истечения и расхода жидкости.

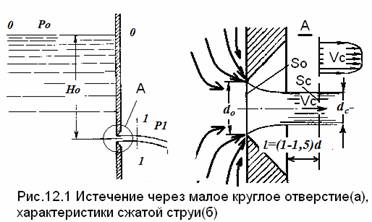
Истечение производится из резервуара с жидкостью под давлением Р₀ на свободной поверхности через круглое отверстие в тонкой стенке на глубине (во много раз большей диаметра отверстия) Н₀ >> d _от (рис. 12.1).

Через отверстие жидкость вытекает в воздушное пространство с давлением Р₁.

Отверстие в стенке имеет острую кромку. Частицы жидкости приближаются к отверстию из всего прилежащего объема, двигаясь ускоренно по различным плавным траекториям (см. рис.12.1б). Струя отрывается от стенки у кромки отверстия и затем сжимается. Формирование сжатого сечения струи происходит на расстоянии примерно одного диаметра отверстия.

Сжатие струи происходит при плавном переходе от различных направлений движения жидкости в резервуаре.

12.2. Истечение при совершенном сжатии.

Совершенным сжатием называется наибольшее сжатие струи, когда диаметр отверстия во много раз меньше напора Н₀.

В этом случае боковые стенки и свободная поверхность жидкости не влияют на поток жидкости к отверстию.

Сжатие струи оценивается коэффициентом сжатия ε, равным отношению площади поперечного сечения струи к площади отверстия

Для определения скорости истечения и расхода из отверстия запишем уравнение Бернулли для движения жидкости от свободной поверхности «0 – 0» в резервуаре и сечением струи «1 – 1» (на рис.12.1а).

В рассматриваемом случае уравнение Бернулли записывается для установившейся скорости, истечение происходит под постоянным напором, над свободной поверхностью «0 – 0» давление равно Р_0, скорость также равна нулю.

В сечении «1 – 1», струя примет цилиндрическую форму, давление Р₁, скорость V ₁ предстоит определить из уравнения Бернулли для потока реальной жидкости.

где ξ— коэффициент, характеризующий сопротивление отверстия, -коэффициент Кориолиса из уравнения Бернулли для потока вязкой жидкости, характеризующий неравномерность распределения скоростей в потоке.

Если умножить числитель и знаменатель выражения для α на ρ/2, можно убедиться, что α является отношением действительной кинетической энергии потока в данном сечении к кинетической энергии этого потока в этом сечения при равномерном распределении скоростей.

Выделив сумму геометрического и пьезометрического напора Н = Н₀ + (Р₀ — Р₁)/(ρ g ), получаем выражение, связывающее скорость истечения и скоростной напор.

12.3 Скорость истечения реальной жидкости при совершенном сжатии.

Коэффициенты: ε , ξ , φ , μ

Из выражения для гидростатического напора, получим формулу для определения скорости истечения из отверстия с острой кромкой для реальной жидкости

, (12.2)

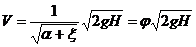
где φ — коэффициент скорости

. (12.3)

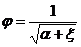
Для идеальной жидкости, так как у нее отсутствует вязкость, трения и потерь на трение нет ξ = 0, α = 1, следовательно, φ = 1.

Скорость истечения идеальной жидкости из отверстия с острой кромкой

(12.4)

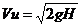
Из формулы (12.2) можно заключить, что коэффициент скорости φ есть отношение скорости истечения реальной жидкости к скорости истечения идеальной жидкости.

, (12.5)

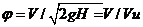
Скорость истечения реальной жидкости меньше идеальной из-за вязкости и трения, поэтому коэффициент скорости φ всегда меньше единицы.

Измерения показывают, что в средней части сечения струи эпюра скоростей является равномерной, поэтому скорость в средней части струи близка к идеальной 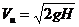, наружный слой жидкости притормаживается при трении о края стенки отверстия. Коэффициент φ рассматривается, как коэффициент по средней скорости.

Умножив скорость истечения на площадь сечения струи, получим выражение для расхода жидкости через отверстие с острой кромкой при совершенном сжатии

. (12.6)

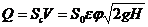
Коэффициентом расхода μ называют произведение значений коэффициентов сжатия ε и скорости φ

Формула для расхода через отверстие с острой кромкой с учетом выражения для μ

(12.7) или

(12.8)

где ΔР — расчетная разность давлений, под действием которой происходит истечение.

По этим формулам определяется расход для всех случаев связанных с истечением из отверстия с острой кромкой и через насадки различных форм.

Из уравнения (12.7) следует, что

(12.9)

Коэффициент расхода есть отношение действительного расхода Q к расходу идеальной жидкости Q _и, определенному по ее скорости 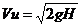. Действительный расход всегда меньше расхода идеальной жидкости, следовательно, коэффициент расхода всегда меньше единицы из-за сжатия струи и трения.

Коэффициенты сжатия струи ε, сопротивления ξ, скорости φ, расхода μ = ε * φ зависят от типа отверстия и насадка и от числа Рейнольдса.

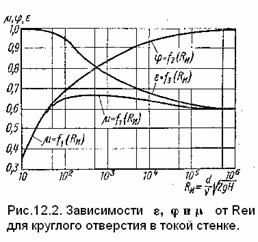
На рис. 12.2 показаны составленные Альтшулем зависимости для коэффициентов ε, φ и μ для круглого отверстия в функции числа R е_и, подсчитанного по скорости истечения идеальной жидкости

R е_и= V _и d /ν = .

Увеличение числа Re означает уменьшение сил вязкости, поэтому коэффициент φ возрастает в связи с уменьшением коэффициента сопротивления ξ (влияние трения становится меньше), коэффициент ε уменьшается из-за уменьшения торможения жидкости у кромки отверстия и увеличения радиусов кривизны струи на входе в цилиндрическую часть. При R е_и →∞ значения коэффициентов приближаются к φ→1 и ε→0,6 и соответствуют истечению идеальной жидкости.

Коэффициент расхода μ, определяемый произведением ε на φ с увеличением Re сначала растет, что связано с сростом φ, а затем уменьшается в связи со значительным падением ε и при больших R е_и равен μ = 0,60÷061.

В области малых Re ( R е_и что сжатие струи отсутствует ε = 1, φ = μ. В этом случае можно пользоваться формулой:

(12.10)

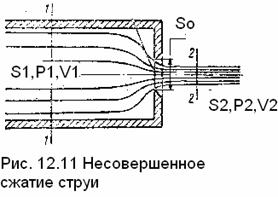
12.3. Истечение при несовершенном сжатии

Несовершенным сжатием струи тогда, когда на формирование струи оказывает влияние близость боковых стенок резервуара.

Боковые стенки успевают направлять жидкость при подходе к отверстию, и струя сжимается в меньшей степени, чем при истечении из резервуара неограниченных размеров при совершенном сжатии. Увеличивается коэффициент сжатия и коэффициент расхода.

При истечении из цилиндрического резервуара через круглое отверстие, расположенное в центре торцевой стенки при больших числах Re , коэффициент сжатия ε₁ можно находить по формуле Жуковского для идеальной жидкости

где n = S ₀/ S ₁ отношение площади отверстия S ₀ к площади S ₁ поперечного сечения резервуара.

Коэффициент скорости φ при несовершенном сжатии мало зависит от отношения n и его находят по графику на рис.12.2, коэффициент сопротивления отверстия ξ можно найти из формулы, связывающей

Коэффициент расхода μ₁ = ε₁ φ , уравнение Бернулли записывается для сечения «1-1» в резервуаре и сечения в наиболее сжатой части струи, где давление равно Р₀ –атмосферному.

. (12.12)

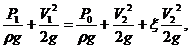
скорость для несовершенного сжатия струи

; (12.13)

расход для несовершенного сжатия струи

(12.14)

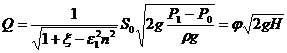
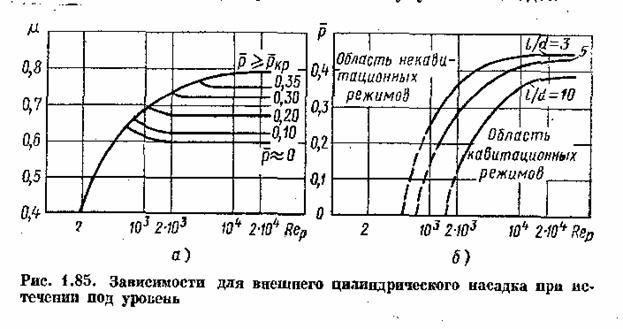
12.5. Истечение под уровень

Истечением под уровень называется истечение жидкости в пространство, заполненное этой же жидкостью (рис. 12.12).

Вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении.

Составляя уравнение Бернулли относительно свободных поверхностей «0 – 0» и «2 – 2» скорости считаем равными нулю, а приравнивая к первой и второй части члены уранения для сжатого сечения получим с учетом коффициента α :

или

1-я сумма, 2-я сумма, 3- сжатое сечение

где Н – обозначен расчетный напор, ξ – коэффициент сопротивления отверстия, имеющий примерно то же значение, что и при истечении в атмосферу, V – скорость истечения в сжатом сечении струи.

Скорость в этом случае

(12.15)

, (12.16)

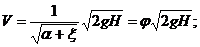
где S_c – площадь сжатого сечения струи, S ₀ – площадь отверстия.

Получились такие же расчетные формулы, что и при истечении в воздух, только расчетный напор Н в данном случае представляет собой разность гидростатических напоров по обе стороны стенки, т.е. скорость и расход не зависят от высоты расположения отверстия.

Коэффициенты сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в воздушную среду.

12.6. Истечение через насадки при постоянном напоре.

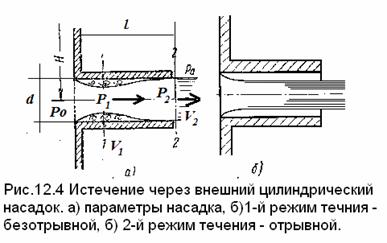
Внешним цилиндрическим насадком называется короткая трубка длиной, равной l = (2÷6) d без закругления входной кромки (рис.12.4а). Истечение через такой насадок в атмосферу может происходить в двух режимах.

12.5.1.Первый режим течения- безотрывный: струя после входа в насадок сжимается примерно как при истечении через отверстие в тонкой стенке.

Затем сжатая часть струи расширяется до размеров отверстия, и из насадка выходит полным сечением. Такой режим истечения называют безотрывным. На выходе диаметр струи равен диаметру отверстия.

Для маловязких жидкостей средние значения коэффициентов для этого режима при больших числах Re равны: μ=φ = 0,8, ξ = 0,5-0,63.

Коэффициент μ расхода такого насадка при этом режиме истечения жидкости зависит от относительной длины насадка l / d и числа Re . Однако и при достаточном значении l / d не всегда возможен этот режим.

Пусть истечение жидкости происходит под действием давления Р₀ в среду газа с давлением Р₂. Расчетный напор в этом случае

В струе на выходе из насадка давление равно Р₂, в суженном месте струи внутри насадка, где скорость увеличена, давление Р₁ меньше, чем Р₂. Чем больше напор, под которым происходит истечение и расход через насадок, тем меньше абсолютное давление Р₁. Разность давлений Р₂ — Р₁ растет пропорционально напору Н.

Покажем это, составив уравнение Бернулли для сечений 1 — 1 и 2 – 2,α = 1 (см. рис.12.4а):

Последний член уравнения представляет собой потерю напора на расширение потока, которое в данном случае происходит примерно так же, как и при внезапном расширении трубы (формула Борда). Сжатие струи внутри насадка можно оценить коэффициентом сжатия ε, как и в случае отверстия, поэтому на основании уравнения расхода

Заменив с помощью этого соотношения скорость V ₁ в уравнении Бернулли на скорость V _2, а ее скорость V ₂ выражением через , найдем падение давления внутри насадка:

(12.18)

Подставляя сюда φ = 0,8 и ε=0.63, получаем

Если истечение происходит в среду, где Р₂ равно постоянному , например, атмосферному давлению, увеличение напора до критической величины Нкр приводит к уменьшению Р₁ — абсолютное давление в сжатом сечение «1 – 1» внутри насадка может уменьшиться до давления насыщенных паров. Поэтому существует величина напора, называемая критическим напором

Следовательно, при Н > H кр давление Р₁ должно стать отрицательным, но отрицательных давлений в жидкости не бывает, поэтому первый режим истечения при

Н > H кр делается невозможным. При Н ≈ H кр происходит внезапное изменение режима истечения, переход от первого режима ко второму (см. рис.12.4в).

12.5.2. Второй режим истечения характеризуется тем, что струя после сжатия уже не расширяется, сохраня цилиндрическую форму, и перемещается внутри насадка, не соприкасаясь с его стенками. Течение становится таким же, как из отверстия в тонкой стенке, с теми же значениями коэффициентов. Следовательно, при переходе от первого режима ко второму скорость возрастает, расход уменьшается, благодаря сжатию струи.

Если через насадок происходит истечение воды в атмосферу, то

Когда давление Р_н.п. насыщенных паров истекающей жидкости соизмеримо с давлением Р₂ среды, в которую происходит истечение, пренебречь величиной Р_н.п. нельзя, в формуле (12.19) следует принять Р₁ = Р_н.п.

Если после перехода от первого режима истечения ко второму уменьшить напор Н, то второй режим будет сохраняться вплоть до самых малых Н. Это значит, что второй режим истечения возможен при любых напорах, следовательно, при Н Н падает до давления насыщенных паров перехода ко второму режиму не происходит, а начинается кавитационный режим, при котором расход перестает зависеть от противодавления Р₂, получается эффект стабилизации расхода. При этом чем меньше относительное противодавление Р₂/ Р₀ = Р_вых/Р_вх = , которое является критерием кавитации, тем шире область кавитации внутри насадка и тем меньше коэффициент расхода μ.

Таким образом, при истечении жидкости через внешний цилиндрический насадок под уровень коэффициент является функцией трех безразмерных критериев, а именно

μ = f ( l / d , Re , ).

Результаты новых экспериментальных исследований этого случаи истечения представлены в безразмерных координатах на рис. 1.85. На рис.1.85а даны зависимости от Re при l / d = 3 для ряда значений , начиная от = 0 и до > , где — критическое значение , соответствующее началу кавитации и, следовательно, критерию ηкр(см. п. 1.23). На рис. 1.85б показаны области кавитационных и безкавитационных режимов истечения через насадки с l / d = 3; 5 и 10. Увеличение при возрастании Re объясняется уменьшением коэффициента ε сжатия струи внутри насадка, т. е. увеличением степени сжатия, а уменьшение при увеличении l / d происходит из-за возрастания давления в сжатом сечении вследствие увеличения потерь на трение по длине насадка.

Таким образом, внешний цилиндрический насадок имеет существенные недостатки: на первом режиме — большое сопротивление и недостаточно высокий коэффициент расхода, а на втором — очень низкий коэффициент расхода. Недостатком является также двойст-венность режима истечения в газовую среду при Н

Чем больше радиус закругления, тем выше коэффициент расхода и ниже коэффициент сопротивления. В пределе при радиусе кривизны, равном толщине стенки, цилиндрический насадок приближается к коноидальному насадку, или соплу.

Коноидальный насадок (рис. 1.86) очерчивается приблизительно по форме естественно сжимающейся струи и, благодаря этому, обеспечивает безотрывность течения внутри насадка в параллельноструйность в выходном сечении. Это весьма распространеный насадок, так как он имеет коэффициент расхода, близкий к единице, и очень малые потери (коэффициент сжатия ε = 1), а также устойчивый режим течения без кавитации.

Значения коэффициента сопротивления те же, что и при плавном сужении (см. п. 1.32), т. е. ξ= 0,03 ÷ 0,1 (большим Re соответствуют малые ξ ‚ и наоборот). В соответствии с этим μ =φ= 0,99÷0,96.

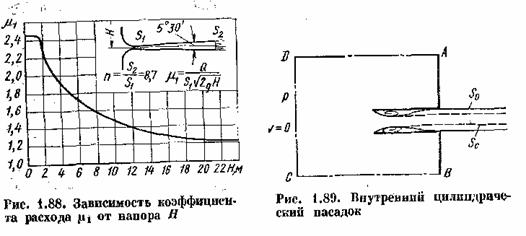
Диффузорный насадок представляет собой комбинацию сопла и диффузора (рис. 1.87).

Приставка диффузора к соплу влечет за собой снижение давления в узком месте насадка, а следовательно, увеличение скорости и расхода жидкости через него. При том жедиаметре узкого сечения, что и у сопла, и том же напоре диффузорный насадок может дать значительно больший расход (увеличение до 2,5 раза), чем сопло.

Такие насадки применяют в том случае, когда заданы диаметр узкого сечения и напор и требуется получить возможно больший расход. Однако, использовать диффузорных насадков можно лишь при небольших напорах Н = 1 ÷4 м, так как иначе в узком месте насадка возникает кавитация. Следствием кавитации являются увеличение сопротивления и уменьшение пропускной способности насадка.

На рис.1.88 показано падение коэффициента расхода диффузорного насадка с увеличением напора вследствие кавитации, возникающей в узком месте насадка при истечении воды в атмосферу.

Коэффициент расхода отнесен к площади узкого сечения, т. е. . Приведенная кривая получена в результате испытания диффузорного насадка, обладающего наивыгоднейшим углом и степенью расширения, которые обеспечивают наибольший коэффициент расхода.

Внутренний цилиндрический насадок или насадок Борда, изображен на рис.1.89. Там же схематически показаны два режима истечения , аналогичные режимам истечения через внешний цилиндрический насадок. Очертания струи при первом режиме показаны сплошными линиями, а при втором – штриховыми. Так как частицы жидкости приближаются к входному отверстию насадка из всего прилежащего объема, а некоторые из них, попадающие на периферию струи, изменяют направление своего движения на 180°, то степень сжатия струи в данном насадке больше, а коэффициент ε меньше, чем во внешнем цилиндрическом насадке. Значение ε в этом случае при истечении идеальной жидкости может быть получено на основании теоремы Эйлера об изменения количества движения (см. п. 1.15). Применим эту теорему к фиксированному объему в виде кругового цилиндра ABCD соосного с насадком, и с основанием CD , достаточно удаленным от насадка, где V =0. Пренебрегая толщиной стенки насадка на основании указанной теоремы при втором режиме истечения получим

где P — давление в центре основания CD , S ₀ и S _с — площади отверстия насадка и сечения струи (силы давления жидкости на кольцевые площади оснований цилиндра ABCD уравновешиваются, а избыточное давление по площади S ₀ в плоскости АВ равно нулю.

С другой стороны, для скорости истечения имеем

1 .

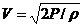
IIосле подстановки второго уравнения в первое и сокращения на Р и ρ получим

Этому значению ε соответствуют значения коэффициентов расхода μ = 0,71 и потерь ξ =1, что подтверждается опытами при первом режиме истечения и больших числах Рейнольдса.

Коэффициент скорости в уравнении бернулли

Уравнение Бернулли для реальной и идеальной жидкости

Уравнение Бернулли позволяет выполнить расчет водоснабжения и отопления: Подобрать диаметры и насосы. В этой статье будет расписан энергетический и геометрический смысл уравнения Бернулли.

График Бернулли и уравнение Бернулли для идеальной жидкости:

График Бернулли и уравнение Бернулли для реальной жидкости:

Смысл уравнения Бернулли

Смысл уравнения Бернули в том, чтобы показать, что внутри системы заполненной жидкостью (участка трубопровода) сохраняется общая энергия между разными точками. То есть на участке трубопровода необходимо выделить две точки, и эти две точки равны друг другу по значению полной энергии. Полная энергия состоит из потенциальной и кинетической энергии.

Назначение уравнения Бернули

Понять, как распределяется давление в системе трубопроводов. А также с помощью уравнения находить неизвестные параметры внутри системы. Например, найти давление в каждой течке пространства системы заполненной жидкостью.

Подробнее на видео: (для запуска видео кликните по окошку) На видео намного больше информации

Решая задачу с уравнением Бернулли, Вы фактически занимаетесь гидравлическим расчетом. О том, как делать гидравлический расчет — написано тут: Конструктор водяного отопления

Задача. Пример решения уравнения Бернулли

По решению задачи необходимо найти давление в точке 2 при известных параметрах: давление и расход.

Как понять уравнение Бернулли?

Для расчета уравнения Бернулли необходимо выбрать две точки в пространстве

Точка 1 – это место где известно давление

Точка 2 – это место где нужно узнать давление

Поймите, что каждый кусок формулы измеряется давлением: м.в.ст. (метр водяного столба)

То есть для того, чтобы быстро считать гидравлику систем водоснабжения и отопления, необходимо меньше всего выражаться в Барах, Паскалях и тому подобное.

Проще выражать давление в единице измерения: м.в.ст. (метр водяного столба)

Вы этим самым упростите себе жизнь… просто другая единица это еще один процесс, который отнимает время.

Сборка формулы уравнения Бернулли

Как избавится от минуса?

Как избавится от множителя (-1)?

Необходимо множитель (-1) помножить на каждый слагаемый член. Знак каждого слагаемого члена меняется на противоположный. То есть (+ на -) (- на +). Далее перестановка слагаемых.

Что такое идеальная жидкость?

Идеальная жидкость — это жидкость, не обладающая внутренним трением. То есть такая жидкость не создает гидравлическое сопротивление.

Реальная жидкость — это жидкость, которая обладает вязкостью. То есть внутренним сопротивлением.

Формула Бернулли для реальной жидкости

Коэффициент Кориолиса – это поправка кинетической энергии на реальную жидкость.

Потому что реальная жидкость движется не равномерно

У реальной жидкости серединная струйка воды движется быстрее остальных. При ламинарном режиме градиент: Чем ближе к стенке, тем медленнее движется поток воды.

Формула коэффициента Кориолиса

Что такое коэффициент Кориолиса?

Коэффициент Кориолиса характеризует отношение действительной кинетической энергии потока жидкости в данном сечении к той кинетической энергии потока, которую он имел бы, если бы все частицы двигались с одинаковой скоростью, равной средней скорости потока.

Чему равен коэффициент Кориолиса?