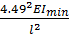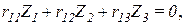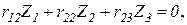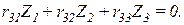Коэффициенты канонических уравнений при расчете на устойчивость это

Методические указания к расчетно-графической работе “Расчет рамно-балочных систем на устойчивость”

Министерство образования и науки

Казанский государственный архитектурно-строительный университет

Кафедра строительной механики

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к расчетно-графической работе

“Расчет рамно-балочных систем

Ш17 Методические указания к расчетно-графической работе “Расчет рамно-балочных систем на устойчивость” / Шакирзянов, . – Казань: КГАСУ, 2011. – 16 с.

Печатается по решению редакционно-издательского совета Казан-ского государственного архитектурно-строительного университета.

Методические указания предназначены для успешного усвоения теоретических знаний, закрепления навыков по расчету сооружений на устойчивость и выполнения расчетно-графической работы (РГР) по устойчивости сооружений.

Определяются общая схема и последовательность выполнения РГР, даются рекомендации для ее самостоятельного выполнения и примеры решения задач расчета рамно-балочных систем на устойчивость методом перемещений.

Кандидат физико-математических наук, профессор кафедры теоретической механики КГАСУ

Ó Казанский государственный

Строительная механика − это наука о принципах и методах расчета сооружений на прочность, жесткость и устойчивость. Поэтому бакалавры и магистры, обучающиеся по направлению “Строительство” и изучающие курс строительной механики, а также аспиранты и специалисты-строители, повышающие квалификацию по этому направлению должны знать теоретические положения, принципы и методы расчета сооружений на устойчивость.

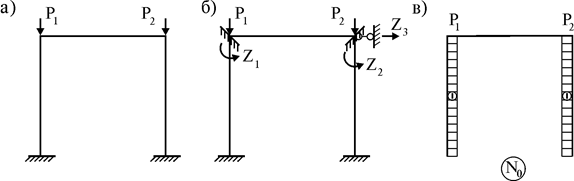
Под воздействием внешней нагрузки в рамно-балочных системах (рис. 1 а) могут возникать большие продольные усилия (рис. 1 б), приводящие к потере устойчивости системы. В таких случаях (рис. 1 в), а также при узловом воздействии нагрузки (рис. 1 г) может ставиться задача проверки этих систем на устойчивость.

Обе эти задачи можно решать методом перемещений по единой методике, если принять упрощающие гипотезы:

– нагрузка прикладывается только в узлах;

– продольные силы вызывают только центральное сжатие;

– при потере устойчивости напряжения остаются в упругой зоне;

– деформации малы и расстояния между узлами сохраняются.

Алгоритм расчета на устойчивость методом перемещений

1. Определение числа неизвестных.

2. Выбор основной системы.

3. Построение эпюры продольных сил N0 в основной системе.

4. Определение параметров устойчивости стержней

.

Все параметры устойчивости необходимо выразить через максимальный из них и обозначить v=max vi , а остальные определить как , где коэффициенты .

5. Запись канонических уравнений.

6. Рассмотрение единичных состояний основной системы.

7. Построение эпюр изгибающих моментов в единичных состояниях.

8. Определение коэффициентов канонических уравнений.

9. Решение уравнения устойчивости .

10. Определение критических сил и приведенных длин сжатых стержней по формулам

, .

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1. На одноэтажную раму действует сосредоточенная сила, направленная вдоль оси одной из стоек (рис. 2 а). Определить величину этой силы, при которой рама достигает критического состояния.

1. Определяем число неизвестных по методу перемещений:

2. Выбираем основную систему (рис. 2 б).

3. Строим эпюру продольных сил в основной системе (рис. 2 в).

4. Параметры устойчивости стержней:

, .

5. Каноническое уравнение будет

(так внешняя нагрузка до момента потери устойчивости не вызывает изгиба элементов, то ).

6. Рассмотрим единичное состояние основной системы (рис. 3 а).

7. В единичном состоянии строим эпюру изгибающих моментов. При этом надо помнить следующее: в стержне 3 в основной системе имеется сжимающие усилие (рис. 2 в), поэтому при построении эпюры изгибающих моментов в этом стержне надо пользоваться специальной таблицей метода перемещений (табл. 2 в приложении), а в стержнях 1 и 2 сжимающие силы отсутствуют, поэтому при построении эпюр моментов в этих стержнях надо использовать обычную таблицу метода перемещений (табл. 3). Тогда эпюра моментов для стержня 3 будет криволинейной, а для стержня 1 будет прямолинейной (рис. 3 б). Следует отметить, что в данной задаче построение этой эпюры не обязательно.

8. По рис. 3 в определяем коэффициент канонического уравнения:

.

9. Каноническое уравнение имеет два решения:

1) , 2) .

Согласно основной системе (рис. 2 б), второе решение соответствует закреплению 3-го стержня в горизонтальном направлении. Поэтому этот стержень, подвергнутый воздействию сжимающей силы P, можно рассматривать отдельно (рис. 3 г).

Такие задачи решаются теоретически, результаты их расчета приведены в приложении в табл. 1. Нашему случаю соответствует 4-ая схема этой таблицы, из которого определяем коэффициент приведенной длины стержня μ=0,7. Тогда

.

Если рассматривать первое решение, то

.

Из него получаем уравнение или .

Тогда, используя табл. 4, определяем корень уравнения .

Итак, получили два решения: 1) , 2) . По критерию Эйлера, критической является наименьшая из них. Поэтому .

10. Определяем величину критической силы и коэффициент приведенной длины стержня. Принимая

,

, .

Как видно из данного примера, уравнение дает завышенное значение приведенной длины стержня (а значит и критической силы). При решении других задач получаются аналогичные результаты. Поэтому в дальнейшем решения типа рассматривать не будем.

Задача 2. Провести расчет рамы, представленной на рис. 4 а, на устойчивость методом перемещений.

1. Определяем число неизвестных по методу перемещений:

2. Выберем основную систему (ОС). Она получается введением двух условных связей − заделки и опоры (рис. 4 б).

3. Строим эпюру продольных сил в основной системе (рис. 4 в). В ней имеются два стержня, в которых есть сжимающие продольные усилия.

4. Параметры устойчивости стержней рамы будут:

, , .

Наибольший из них соответствует 1-му стержню. Поэтому примем его параметр устойчивости за основной и обозначим

.

,

имеем .

5. Запишем систему канонических уравнений:

Эта однородная система уравнений имеет два решения:

1) 2) .

Второе решение, как дающее завышенное значение критического корня, рассматривать не будем. А первое решение с учетом принимает вид

.

Это и есть уравнение устойчивости.

6. Рассмотрим два единичных состояния основной системы, в которых обозначим деформации элементов и реактивные усилия (рис. 5):

7. Используя таблицы метода перемещений, в обоих состояниях строим эпюры изгибающих моментов (рис. 6 а, б).

При этом при построении эпюр в стержнях 1 и 2 (в них учитывается сжатие) основной системы используем специальную таблицу метода перемещений (табл. 2), а при построении эпюр в стержнях 3 и 4 (где сжимающие силы отсутствуют) используем обычную таблицу метода перемещений (табл. 3). Поэтому эпюры моментов для стержней 1 и 2 них будут криволинейными, а для стержней 3 и 4 − прямолинейными.

8. Коэффициенты системы канонических уравнений определяем согласно единичным состояниям (рис. 5) и по рис. 6 а, б:

;

;

9. Решаем уравнение устойчивости. Для этого подставим найденные коэффициенты в уравнение устойчивости и сократим его на EI. Получим трансцендентное уравнение (уравнение с бесконечным числом корней). С целью определения наименьшего положительного корня этого уравнения вначале определим интервал, в котором этот корень находится. Для этого проведем следующие рассуждения:

1) уравнение устойчивости зависит от параметра устойчивости 1-го стержня рамы , поэтому исследуем поведение этого стержня;

2) в состоянии “малой жесткости” рамы, когда изгибные жесткости всех стержней (кроме 1-го) равны нулю (рис. 7 а), стержень 1 можно рассматривать отдельно как показано на рис. 7 б. В этом случае по табл. 1 имеем . Тогда ;

3) в состоянии “большой жесткости”, когда изгибные жесткости всех стержней (кроме 1-го) равны бесконечности (рис. 7 в), стержень 1 можно рассматривать отдельно как показано на рис. 7 г. По табл. 1 принимаем . Тогда, ;

4) в действительности жесткость 1-го стержня находится в интервале от нуля до бесконечности. Следовательно, искомый корень уравнения устойчивости находится между найденными крайними величинами, т. е.

.

Теперь уточним его. Это удобно проводить в следующей табличной форме (значения специальных функций берутся из табл. 4):

Определение коэффициентов канонических уравнений с помощью специальных таблиц

Элементы теории устойчивости

Общие положения

Устойчивость сжатых стержней рассматривалась в курсе сопротивления материалов. Там были получены формулы для критической нагрузки сжатого стержня при различных вариантах закрепления его концов.

При μ =1 Р_кр =

μ =2 Р_кр =

μ =0,7 Р_кр =

μ =0,5 Р_кр =

Общая формула для критической нагрузки сжатого стержня

Как видно, можно записать общую формулу для критической нагрузки:

Р_кр = ,

где v – параметр устойчивости.

Эта формула применяется при расчете рам на устойчивость.

Основные допущения, принимаемые при расчете рам на устойчивость:

1. Действующая на раму нагрузка является узловой.

2. Стержни рамы являются нерастяжимыми и несжимаемыми.

3. Считается, что расстояние между концами стержня при его изгибе не меняется.

Расчет рам на устойчивость удобнее производить методом перемещений.

Основная система и канонические уравнения

Метода перемещений при расчете рам на устойчивость

Основная система метода перемещений при расчете на устойчивость образуется так же, как и при расчете на прочность: сначала определяется степень кинематической неопределимости рамы, а затем ставятся дополнительные связи, число которых равно степени кинематической неопределимости.

Действующая узловая нагрузка не вызывает изгиба стержней рамы. При увеличении нагрузки в некоторый момент произойдет потеря устойчивости: стержни рамы изогнутся, а ее жесткие узлы переместятся.

Линейные и угловые перемещения жестких узлов рамы при потере устойчивости принимаются за неизвестные при расчете на устойчивость методом перемещений.

Канонические уравнения метода перемещений при расчете на устойчивость записываются так же, как и при расчете на прочность, но с одним отличием.

Узловая нагрузка не вызывает реакции в дополнительных связях, поэтому свободные члены канонических уравнений будут равны нулю.

Канонические уравнения метода перемещений при расчете на устойчивость:

Определение коэффициентов канонических уравнений с помощью специальных таблиц

Коэффициенты канонических уравнений определяются в общем так же, как и при расчете на прочность. Предварительно должны быть построены единичные эпюры. Эти эпюры строятся с помощью специальных таблиц. В этих таблицах приведены эпюры изгибающих моментов и опорные реакции для сжато-изогнутых стержней.

Эпюры изгибающих моментов будут криволинейными – следствие влияния сжимающей продольной силы на изгибающий момент.

𝜑₁(v) учитывает влияние сжимающей продольной силы. Значение этой и других функций приведены в таблице метода перемещений при расчете на устойчивость.

Алгоритм расчета на устойчивость

Рассмотрим его на примере рамы (рис. 18.7 а).

1. Определение числа неизвестных: .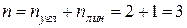

2. Выбор основной системы (рис. 18.7 б).

3. Построение эпюры продольных сил в основной системе (рис. 18.7 в).

4. Определение параметров устойчивости стержней

.

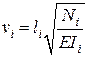
Желательно выразить все параметры устойчивости стержней через максимальный из них и принять v=max v_i.

5. Запись канонических уравнений (в момент потери устойчивости все грузовые коэффициенты равняются нулю):

6. Запись уравнения устойчивости

.

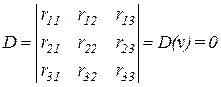
7. Рассмотрение единичных состояний (в этом примере – их три).

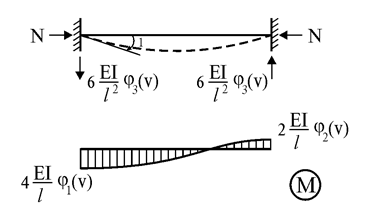
8. Построение единичных эпюр. Для этого используется специальная таблица метода перемещений, учитывающая влияние продольной силы на внутренние усилия стержня. Например, эпюра изгибающих моментов стержня с защемленными концами является криволинейной (рис. 18.8), а величины моментов определяются сложными функциями.

К примеру, одна из этих функций определяется так:

.

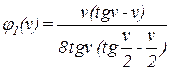
Ввиду сложности этих функций, они определяются по специальной таблице метода перемещений.

9. Определение коэффициентов канонических уравнений.

10. Решение уравнения устойчивости (вычисление ее критического корня ).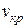

11. Определение критической силы:

.

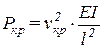
Дата добавления: 2016-01-29 ; просмотров: 1502 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ