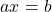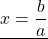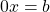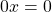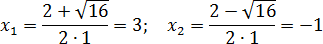Когда квадратное уравнение имеет бесконечное множество решений

Уравнения с бесконечным количеством корней

В каком случае уравнение ax = b имеет единственный корень; имеет бесконечно много корней; не имеет корней? Приведите примеры.

Решение

Линейное уравнение ax = b при a ≠ 0 имеет один корень, при a = 0 и b ≠ 0, не имеет корней, при a = 0 и b = 0 имеет бесконечно много корней (любое число является его корнем).

Примеры:
15 x = 30 − один корень;
0 x = 4 − не имеет корней;
0 x = 0 − имеет бесконечно много корней.

Нашли ошибку?

Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом

1. Линейное уравнение. Приведите Примеры линейных уравнений, имеющих один корень, бесконечно много корней и не имеющих корней.

Попроси больше объяснений
Следить
Отметить нарушение

Что ты хочешь узнать?

Ответ

Проверено экспертом

один корень имеют например

5х=6, или 10х=20, или 5х-4=1 или 9х-7=2 и т.д.

бесконечно много корней имеют например 0х=0; 2(5х+6)=10х+12, или 5х-3х-2х=7-4-3

не имеющие корни например 0х=4 или 2х+5=2х+6 и т.д.

После того, как мы изучили понятие равенств, а именно один из их видов – числовые равенства, можно перейти к еще одному важному виду – уравнениям. В рамках данного материала мы объясним, что такое уравнение и его корень, сформулируем основные определения и приведем различные примеры уравнений и нахождения их корней.

Понятие уравнения

Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:

Уравнением называется равенство с неизвестным числом, которое нужно найти.

Принято обозначать неизвестные маленькими латинскими буквами, например, t , r , m др., но чаще всего используются x , y , z . Иными словами, уравнение определяет форма его записи, то есть равенство будет уравнением только тогда, когда будет приведен к определенному виду – в нем должна быть буква, значение которое надо найти.

Приведем несколько примеров простейших уравнений. Это могут быть равенства вида x = 5 , y = 6 и т.д., а также те, что включают в себя арифметические действия, к примеру, x + 7 = 38 , z − 4 = 2 , 8 · t = 4 , 6 : x = 3 .

После того, как изучено понятие скобок, появляется понятие уравнений со скобками. К ним относятся 7 · ( x − 1 ) = 19 , x + 6 · ( x + 6 · ( x − 8 ) ) = 3 и др. Буква, которую надо найти, может встречаться не один раз, а несколько, как, например, в уравнении x + 2 + 4 · x − 2 − x = 10 . Также неизвестные могут быть расположены не только слева, но и справа или в обеих частях одновременно, например, x · ( 8 + 1 ) − 7 = 8 , 3 − 3 = z + 3 или 8 · x − 9 = 2 · ( x + 17 ) .

Далее, после того, как ученики знакомятся с понятием целых, действительных, рациональных, натуральных чисел, а также логарифмами, корнями и степенями, появляются новые уравнения, включающие в себя все эти объекты. Примерам таких выражений мы посвятили отдельную статью.

В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:

Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.

То есть, к примеру, выражение x + 3 = 6 · x + 7 – это уравнение с переменной x , а 3 · y − 1 + y = 0 – уравнение с переменной y .

В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно уравнениями с двумя, тремя переменными и др. Запишем определение:

Уравнениями с двумя (тремя, четырьмя и более) переменными называют уравнения, которые включают в себя соответствующее количество неизвестных.

К примеру, равенство вида 3 , 7 · x + 0 , 6 = 1 является уравнением с одной переменной x , а x − z = 5 – уравнением с двумя переменными x и z . Примером уравнения с тремя переменными может быть выражение x 2 + ( y − 6 ) 2 + ( z + 0 , 6 ) 2 = 26 .

Корень уравнения

Когда мы говорим об уравнении, сразу возникает необходимость определиться с понятием его корня. Попробуем объяснить, что оно означает.

Нам дано некое уравнение, включающее в себя одну переменную. Если мы подставим вместо неизвестной буквы число, то уравнение станет числовым равенством – верным или неверным. Так, если в уравнении a + 1 = 5 мы заменим букву числом 2 , то равенство станет неверным, а если 4 , то получится верное равенство 4 + 1 = 5 .

Нас больше интересуют именно те значения, с которыми переменная обратится в верное равенство. Они и называются корнями или решениями. Запишем определение.

Корнем уравнения называют такое значение переменной, которое обращает данное уравнение в верное равенство.

Корень также можно назвать решением, или наоборот – оба эти понятия означают одно и то же.

Возьмем пример для пояснения этого определения. Выше мы приводили уравнение a + 1 = 5 . Согласно определению, корнем в данном случае будет 4 , потому что при подстановке вместо буквы оно дает верное числовое равенство, а двойка не будет решением, поскольку ей отвечает неверное равенство 2 + 1 = 5 .

Сколько корней может иметь одно уравнение? Любое ли уравнение имеет корень? Ответим на эти вопросы.

Уравнения, не имеющие ни одного корня, тоже существуют. Примером может быть 0 · x = 5 . Мы можем подставить в него бесконечно много разных чисел, но ни одно из них не превратит его в верное равенство, поскольку умножение на 0 всегда дает 0 .

Также бывают уравнения, имеющие несколько корней. У них может быть как конечное, так и бесконечно большое количество корней.

Так, в уравнении x − 2 = 4 есть только один корень – шесть, в x 2 = 9 два корня – три и минус три, в x · ( x − 1 ) · ( x − 2 ) = 0 три корня – нуль, один и два, в уравнении x=x корней бесконечно много.

Теперь поясним, как правильно записывать корни уравнения. Если их нет, то мы так и пишем: «уравнение корней не имеет». Можно также в этом случае указать знак пустого множества ∅ . Если корни есть, то пишем их через запятую или указываем как элементы множества, заключив в фигурные скобки. Так, если у какого-либо уравнения есть три корня – 2 , 1 и 5 , то пишем – 2 , 1 , 5 или .

Допускается запись корней в виде простейших равенств. Так, если неизвестная в уравнении обозначена буквой y , а корнями являются 2 и 7 , то мы пишем y = 2 и y = 7 . Иногда к буквам добавляются нижние индексы, например, x 1 = 3 , x 2 = 5 . Таким образом мы указываем на номера корней. Если решений у уравнения бесконечно много, то мы записываем ответ как числовой промежуток или используем общепринятые обозначения: множество натуральных чисел обозначается N , целых – Z , действительных – R . Скажем, если нам надо записать, что решением уравнения будет любое целое число, то мы пишем, что x ∈ Z , а если любое действительное от единицы до девяти, то y ∈ 1 , 9 .

Когда у уравнения два, три корня или больше, то, как правило, говорят не о корнях, а о решениях уравнения. Сформулируем определение решения уравнения с несколькими переменными.

Решение уравнения с двумя, тремя и более переменными – это два, три и более значения переменных, которые обращают данное уравнение в верное числовое равенство.

Поясним определение на примерах.

Допустим, у нас есть выражение x + y = 7 , которое представляет из себя уравнение с двумя переменными. Подставим вместо первой единицу, а вместо второй двойку. У нас получится неверное равенство, значит, эта пара значений не будет решением данного уравнения. Если же мы возьмем пару 3 и 4 , то равенство станет верным, значит, мы нашли решение.

Такие уравнения тоже могут не иметь корней или иметь бесконечное их количество. Если нам надо записать два, три, четыре и более значений, то мы пишем их через запятую в круглых скобках. То есть в примере выше ответ будет выглядеть как ( 3 , 4 ) .

На практике чаще всего приходится иметь дело с уравнениями, содержащими одну переменную. Алгоритм их решения мы подробно рассмотрим в статье, посвященной решению уравнений.

Что такое линейное уравнение

Что такое линейное уравнение? Что называется корнем линейного уравнения? Сколько корней имеет линейное уравнение? Что значить решить линейное уравнение?

В курсе алгебры 7 класса линейное уравнение определяется следующим образом.

Определение.

Линейное уравнение с одной переменной — это уравнение вида ax=b, где a и b — числа, x — переменная.

Корнем линейного уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство.

Например, корень уравнения 5x=40 равен 8, так как при x=8 это уравнение превращается в верное числовое равенство:

Количество корней линейного уравнения зависит от значения a (коэффициента перед x).

При a≠0 линейное уравнение имеет единственное решение.

Чтобы найти x, обе части уравнения нужно разделить на число, стоящее перед иксом:

Любое число можно разделить на 2, 5 и числа, которые могут быть представлены в виде произведения только двоек и пятёрок ( например, любое число можно разделить на 10, так как 10=2∙5; на 40, так как 40=2∙2∙2∙5).

В остальных случаях ответ записывают в виде обыкновенной дроби (если дробь неправильная, следует выделить из нее целую часть).

При a=0, b≠0 линейное уравнение

При любом значении x левая часть уравнения равна нулю, а правая — отлична от нуля. То есть нет ни одного значения x, при котором уравнение обратилось бы в верное числовое равенство.

При a=0, b=0 линейное уравнение

имеет бесконечное множество решений.

При любом значении x левая часть уравнения 0x=0 обращается в нуль, в правой части также стоит нуль. Значит, любое число является корнем этого уравнения, то есть, при любом значении x это уравнение обращается в верное числовое равенство.

Возможные решения линейных уравнений можно изобразить в виде схемы.

Решить линейное уравнение — значит, найти корень (корни) уравнения, либо убедиться, что уравнение не имеет корней.

Решение многих уравнений сводится к решению линейных уравнений.

Когда квадратное уравнение имеет бесконечное множество решений

В курсе алгебры 7 класса линейное уравнение определяется следующим образом.

Определение.

Линейное уравнение с одной переменной — это уравнение вида ax=b, где a и b — числа, x — переменная.

Например, корень уравнения 5x=40 равен 8, так как при x=8 это уравнение превращается в верное числовое равенство:

Количество корней линейного уравнения зависит от значения a (коэффициента перед x).

При a≠0 линейное уравнение имеет единственное решение.

Чтобы найти x, обе части уравнения нужно разделить на число, стоящее перед иксом:

При a=0, b≠0 линейное уравнение

При a=0, b=0 линейное уравнение

имеет бесконечное множество решений.

Возможные решения линейных уравнений можно изобразить в виде схемы.

Решение многих уравнений сводится к решению линейных уравнений.

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

— это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

Не имеют корней;
Имеют ровно один корень;
Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.

Дискриминант

Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда — это просто число D = b 2 − 4 ac .

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

Если D D = 0, есть ровно один корень;
Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

x 2 − 8 x + 12 = 0;
5 x 2 + 3 x + 7 = 0;
x 2 − 6 x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

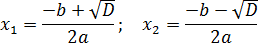
Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D x 2 − 2 x − 3 = 0;

15 − 2 x − x 2 = 0;

x 2 + 12 x + 36 = 0.
Первое уравнение:
x 2 − 2 x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2 x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
Наконец, третье уравнение:
x 2 + 12 x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется , если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид a x 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
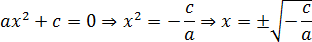
Решение неполного квадратного уравнения
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (− c / a ) ≥ 0. Вывод:
Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (− c / a ) ≥ 0, корней будет два. Формула дана выше;
Если же (− c / a ) c / a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
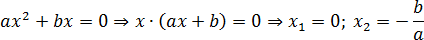
Вынесение общего множителя за скобку
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
x 2 − 7 x = 0 ⇒ x · ( x − 7) = 0 ⇒ x ₁ = 0; x ₂ = −(−7)/1 = 7.
5 x 2 + 30 = 0 ⇒ 5 x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4 x 2 − 9 = 0 ⇒ 4 x 2 = 9 ⇒ x 2 = 9/4 ⇒ x ₁ = 3/2 = 1,5; x ₂ = −1,5.
Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?
Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
За этот урок мы решим 33 квадратных уравнения!
Всех видов, всеми способами.
Ты точно разберешься с этой темой!
И самое главное..
Зачем нужно уметь хорошо и быстро решать квадратные уравнения?
Решение многих других уравнений сводится к решению именно квадратных уравнений!
Будет обидно на экзамене решить какое-нибудь сложное уравнение и запнуться на квадратном.
Потому, давай начнем!
Что такое квадратное уравнение?
В термине «квадратное уравнение» ключевым является слово «квадратное» .
Это значит, что в уравнении обязательно должна присутствовать переменная (тот самый икс) в квадрате.
И при этом не должно быть иксов в третьей (и большей) степени.
Если говорить научным, математическим языком, то.
Квадратное уравнение, это уравнение вида
, , – некоторые числа, причем .
и называют коэффициентами квадратного уравнения,
а – свободным членом .
Сначала научимся определять, что перед нами квадратное уравнение, а не какое-нибудь другое
Пример 1
Избавимся от знаменателя и домножим каждый член уравнения на
Перенесем все в левую часть и расположим члены в порядке убывания степеней икса
Теперь можно с уверенностью сказать, что данное уравнение является квадратным!
Пример 2
Домножим левую и правую часть на :
Это уравнение, хотя в нем изначально был , не является квадратным!
Пример 3
Домножим все на :
Страшно? Четвертая и вторая степени… Однако, если произвести замену , то мы увидим, что перед нами простое квадратное уравнение:
Пример 4
Вроде бы есть , но давай посмотрим внимательнее. Перенесем все в левую часть:
Видишь, сократился – и теперь это простое линейное уравнение!
Теперь попробуй сам определить, какие из следующий уравнений являются квадратными, а какие нет
Проверь ответы
квадратное;
квадратное;
не квадратное;
не квадратное;
не квадратное;
квадратное;
не квадратное;
квадратное.
Математики условно делят все квадратные уравнения на вида:
Два вида квадратных уравний — полные и неполные
Полные квадратные уравнения
Полные квадратные уравнения — это уравнения, в которых коэффициенты и , а также свободный член с не равны нулю (как в примере ).
Кроме того, среди полных квадратных уравнений выделяют приведенные – это уравнения, в которых коэффициент (уравнение из примера один является не только полным, но еще и приведенным!)
Неполные квадратные уравнения
Неполные квадратные уравнения – это уравнения, в которых коэффициент и или свободный член с равны нулю:
Неполные они, потому что в них не хватает какого-то элемента.
Но в уравнении всегда должен присутствовать икс в квадрате. Иначе это будет уже не квадратное, а какое-то другое уравнение.
Зачем придумали такое деление? Казалось бы, есть икс в квадрате, и ладно.
Такое деление обусловлено методами решения.
Рассмотрим каждый из них подробнее.
Для начала остановимся на решении неполных квадратных уравнений – они гораздо проще!
Решение неполных квадратных уравнений
Неполные квадратные уравнения бывают типов:
, в этом уравнении коэффициент равен .
, в этом уравнении свободный член равен .
, в этом уравнении коэффициент и свободный член равны .
Теперь рассмотрим решение каждого из этих подтипов.
Поскольку мы знаем, как извлекать квадратный корень, то давайте выразим из этого уравнения
Выражение может быть как отрицательным, так и положительным.
Число, возведенное в квадрат, не может быть отрицательным, ведь при перемножении двух отрицательных или двух положительных чисел – результатом всегда будет положительное число.
Так что: если , то уравнение не имеет решений.
А если 0″> , то получаем два корня . Эти формулы не нужно запоминать. Главное, ты должен знать и помнить всегда, что не может быть меньше .
Давай попробуем решить несколько примеров.
Пример 5
Теперь осталось извлечь корень из левой и правой части. Ведь ты помнишь как извлекать корни?
Ответ:
Никогда не забывай про корни с отрицательным знаком.
Пример 6
Ответ:
Пример 7
Ой! Квадрат числа не может быть отрицательным, а значит у уравнения
Для таких уравнений, в которых нет корней, математики придумали специальный значок – (пустое множество). И ответ можно записать так:
Ответ:
Вынесем общим множитель за скобки:
Произведение равно нулю, если хотя бы один из множителей равен нулю. А это значит, что уравнение имеет решение, когда:
Таким образом, данное квадратное уравнение имеет два корня. Здесь нет никаких ограничений, так как корень мы не извлекали.
Пример 8
Вынесем общий множитель за скобки:
У этого уравнения два корня.
Ответ:
Самый простой тип неполных квадратных уравнений (хотя они все простые, не так ли?). Очевидно, что данное уравнение всегда имеет только один корень:
Здесь обойдемся без примеров.
Решение полных квадратных уравнений
Напоминаем, что полное квадратное уравнение, это уравнение вида:
Решение полных квадратных уравнений немного сложнее (совсем чуть-чуть), чем приведенных.
Запомни, любое квадратное уравнение можно решить с помощью дискриминанта!
Даже неполное.
Остальные способы помогут сделать это быстрее, но если у тебя возникают проблемы с квадратными уравнениями, для начала освой решение с помощью дискриминанта.
1. Решение квадратных уравнений с помощью дискриминанта.
Решение квадратных уравнений этим способом очень простое, главное запомнить последовательность действий и пару формул.
Если 0″> , то уравнение имеет 2 корня. Нужно особое внимание обратить на шаг 2.
Дискриминант D указывает нам на количество корней уравнения.
Алгоритм Пример:
Шаг 1. Привести уравнение к стандартному виду:
Если уравнение уже дано в таком виде, то этот шаг делать не нужно.
Главное правильно определить коэффициенты и и свободный член .
Шаг 2. Вычислить дискриминант.
Вот его формула:
Шаг 3. Найти корни уравнения по формуле:
Если , то формула на шаге сократится до . Таким образом, уравнение будет иметь всего корень.
Если , то мы не сможем извлечь корень из дискриминанта на шаге . Это указывает на то, что уравнение не имеет корней.
Почему возможно разное количество корней?
Обратимся к геометрическому смыслу квадратного уравнения.
График функции является параболой:
В частном случае, которым является квадратное уравнение, .
А это значит, что корни квадратного уравнения, это точки пересечения с осью абсцисс (ось ).
Парабола может вообще не пересекать ось , либо пересекать ее в одной (когда вершина параболы лежит на оси ) или двух точках.
Кроме того, за направление ветвей параболы отвечает коэффициент . Если 0″> , то ветви параболы направлены вверх, а если – то вниз.
Вернемся к нашим уравнениям и рассмотрим несколько примеров.
Пример 9
Уравнение представлено в стандартном виде, поэтому Шаг 1 пропускаем.
Шаг 2.
0″> , а значит уравнение имеет два корня.
Шаг 3.
Ответ:
Пример 10
Уравнение представлено в стандартном виде, поэтому Шаг 1 пропускаем.
Шаг 2.
, а значит уравнение имеет один корень.
Ответ:
Пример 11
Уравнение представлено в стандартном виде, поэтому Шаг 1 пропускаем.
Шаг 2.
, азначит мы не сможем извлечь корень из дискриминанта. Корней уравнения не существует.
Теперь мы знаем, как правильно записывать такие ответы.
Ответ: Корней нет
2. Решение квадратных уравнений с помощью теоремы Виета
Познакомили поэта с теоремою Виета.
Оба корня он сложил, минус он получил.
А корней произведенье дает из уравнения.
Если ты помнишь, то есть такой тип уравнений, которые называются приведенными (когда коэффициент а равен ):
Такие уравнения очень просто решать, используя теорему Виета:
Сумма корней приведенного квадратного уравнения равна , а произведение корней равно .
Использовать теорему Виета очень легко.
Нужно всего лишь подобрать такую пару чисел, произведение которых равно свободному члену уравнения, а сумма – второму коэффициенту, взятому с обратным знаком.
Рассмотрим несколько примеров:
Пример 12
Это уравнение подходит для решения с использованием теоремы Виета, т.к. .
Сумма корней уравнения равна , т.е. получаем первое уравнение:
А произведение равно :
Составим и решим систему:
Подберем такие пары чисел, произведение которых равно , и проверим, равна ли их сумма :
и . Сумма равна ;
и . Сумма равна ;
и . Сумма равна .
и являются решением системы:
Таким образом, и – корни нашего уравнения.
Ответ: ; .
Пример 13
Уравнение приведенное, а значит:
Свободный член отрицателен, а значит и произведение корней отрицательно. А это возможно только тогда, когда один корень уравнения отрицателен, а другой положителен.
Подберем такие пары чисел, произведение которых равно , а затем определим, какой корней должен иметь отрицательный знак:
Очевидно, что под первое условие подходят только корни и :
Ответ:
Пример 14
Уравнение приведенное, а значит:
Сумма корней отрицательна, а это значит что, по крайней мере, один из корней отрицателен. Но поскольку их произведение положительно, то значит оба корня со знаком минус.
Подберем такие пары чисел, произведение которых равно :
Очевидно, что корнями являются числа и .
Ответ:
КВАДРАТНЫЕ УРАВНЕНИЯ. СРЕДНИЙ УРОВЕНЬ
Что такое квадратное уравнение?
Квадратными называются уравнения, в которых присутствует переменная в квадрате, и при этом нет переменной в степенях, больших .
Другими словами, квадратное уравнение – это уравнение вида , где – неизвестное, , , – некоторые числа, причем .
Число называют старшим или первым коэффициентом квадратного уравнения, – вторым коэффициентом , а – свободным членом .
Потому что если , уравнение сразу станет линейным, т.к. пропадет .
При этом и могут быть равны нулю. В этом стулчае уравнение называют неполным.
Если же все слагаемые на месте, то есть , уравнение – полное.
Методы решения неполных квадратных уравнений
Для начала разберем методы решений неполных квадратных уравнений – они проще.
Можно выделить типа таких уравнений:
I. , в этом уравнении коэффициент и свободный член равны .
II. , в этом уравнении коэффициент равен .
III. , в этом уравнении свободный член равен .
Теперь рассмотрим решение каждого из этих подтипов.
Очевидно, что данное уравнение всегда имеет только один корень:
Число, возведенное в квадрат, не может быть отрицательным, ведь при перемножении двух отрицательных или двух положительных чисел результатом всегда будет положительное число. Поэтому:
если , то уравнение не имеет решений;
если 0″> , имеем учаем два корня
Эти формулы не нужно запоминать. Главное помнить, что не может быть меньше .
Примеры решения квадратных уравнений
Пример 15
Никогда не забывай про корни с отрицательным знаком!
Пример 16
Квадрат числа не может быть отрицательным, а значит у уравнения
Чтобы коротко записать, что у задачи нет решений, используем значок пустого множества .
Пример 17
Итак, это уравнение имеет два корня: и .
Вынесем общим множитель за скобки:
Произведение равно нулю, если хотя бы один из множителей равен нулю. А это значит, что уравнение имеет решение, когда:
Итак, данное квадратное уравнение имеет два корня: и .
Разложим левую часть уравнения на множители и найдем корни:
Методы решения полных квадратных уравнений
1. Дискриминант
Решать квадратные уравнения этим способом легко, главное запомнить последовательность действий и пару формул. Запомни, любое квадратное уравнение можно решить с помощью дискриминанта! Даже неполное.
Алгоритм Пример:
Шаг 1. Привести уравнение к стандартному виду:
Если уравнение уже дано в таком виде, то этот шаг делать не нужно.
Главное правильно определить коэффициенты и и свободный член .
Шаг 2. Вычислить дискриминант. Вот его формула:
Шаг 3. Найти корни уравнения по формуле:
Ты заметил корень из дискриминанта в формуле для корней?
Но ведь дискриминант может быть отрицательным.
Нужно особое внимание обратить на шаг 2. Дискриминант указывает нам на количество корней уравнения.
Если 0″> , то уравнение имеет корня:
Если , то уравнение имеет одинаковых корня, а по сути, один корень:
Такие корни называются двукратными.

Если , то корень из дискриминанта не извлекается. Это указывает на то, что уравнение не имеет корней.

Почему возможно разное количество корней?

Обратимся к геометрическому смыслу квадратного уравнения. График функции является параболой:

В частном случае, которым является квадратное уравнение, .

А это значит, что корни квадратного уравнения, это точки пересечения с осью абсцисс (ось ).

Парабола может вообще не пересекать ось , либо пересекать ее в одной (когда вершина параболы лежит на оси ) или двух точках.

Кроме того, за направление ветвей параболы отвечает коэффициент . Если 0″> , то ветви параболы направлены вверх, а если – то вниз.

4 примера решения квадратных уравнений

источники:

http://www.algebraclass.ru/chto-takoe-linejnoe-uravnenie/

http://ligabeatbox.ru/kogda-kvadratnoe-uravnenie-imeet-beskonechnoe/