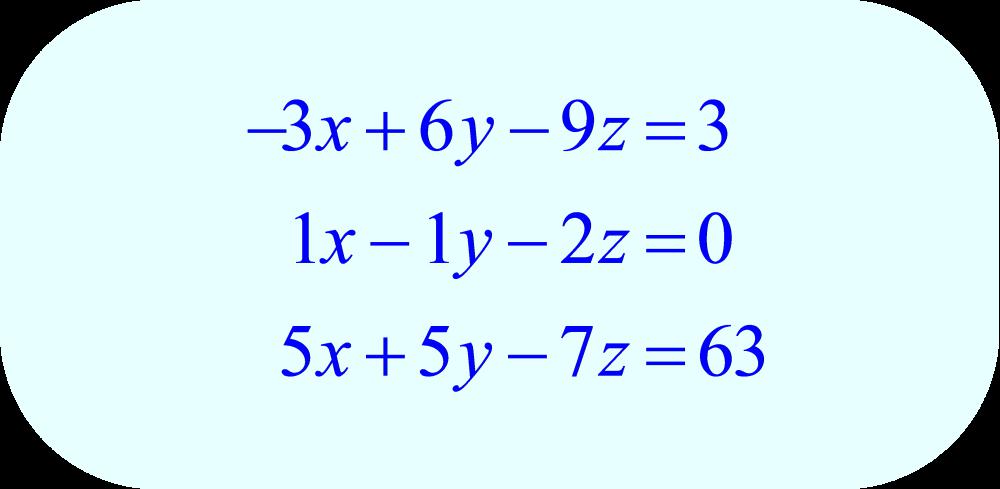Когда нет корней в линейном уравнении

Линейные уравнения

Линейные уравнения – уравнения, которые можно представить в виде \(ax+b=0\), где \(a\) и \(b\) – какие-либо числа.

Проще говоря, это такие уравнения , в которых переменные (обычно иксы) в первой степени . При этом не должно быть переменных в знаменателях дробей .

А тут \(a=0, b=5\) (пояснение: данное уравнение может быть представлено в виде \(0\cdot x+5=0\))

Здесь \(a\) и \(b\) изначально не определены, но преобразовав уравнение, мы сможем их найти.

Тоже самое, \(a\) и \(b\) пока что неизвестны.

Решение линейных уравнений

При решении линейных уравнений, мы стремимся найти корень, то есть такое значение для переменной, которое превратит уравнение в правильное равенство.

В простых уравнениях корень очевиден сразу или легко находиться подбором. Например, понятно, что корнем уравнения \(x+3=5\) будет число \(2\), ведь именно двойка при подстановке ее вместо икса даст \(5=5\) – верное равенство.

Однако в более сложных случаях ответ сразу не виден. И тогда на помощь приходят равносильные преобразования .

Чтобы найти корень уравнения нужно равносильными преобразования привести данное нам уравнение к виду

Это число и будет корнем.

То есть, мы преобразовываем уравнение, делая его с каждым шагом все проще, до тех пор, пока не сведем к совсем примитивному уравнению «икс = число», где корень – очевиден. Наиболее часто применяемыми при решении линейных уравнений являются следующие преобразования:

1. Прибавление или вычитание из обеих частей уравнения одинакового числа или выражения.

Например: прибавим \(5\) к обеим частям уравнения \(6x-5=1\)

Обратите внимание, что тот же результат мы могли бы получить быстрее – просто записав пятерку с другой стороны уравнения и поменяв при этом ее знак. Собственно, именно так и делается школьный «перенос через равно со сменой знака на противоположный».

2. Умножение или деление обеих частей уравнения на одинаковое число или выражение.

Например: разделим уравнение \(-2x=8\) на минус два

Обычно данный шаг выполняется в самом конце, когда уравнение уже приведено к виду \(ax=b\), и мы делим на \(a\), чтобы убрать его слева.

3. Использование свойств и законов математики: раскрытие скобок, приведение подобных слагаемых, сокращение дробей и т.д.

Чаще всего при решении линейного уравнения приходиться делать несколько разных преобразований.

Пример. Решить линейное уравнение \(6(4-x)+x=3-2x\)

Прибавляем \(2x\) слева и справа

Вычитаем \(24\) из обеих частей уравнения

Опять приводим подобные слагаемые

Теперь делим уравнение на \(-3\), тем самым убирая коэффициент перед иксом в левой части.

Ответ найден. Однако давайте его проверим. Если семерка действительно корень, то при подстановке ее вместо икса в первоначальное уравнение должно получиться верное равенство — одинаковые числа слева и справа. Пробуем.

Сошлось. Значит, семерка и в самом деле является корнем исходного линейного уравнения.

Не ленитесь проверять подстановкой найденные вами ответы, особенно если вы решаете уравнение на контрольной или экзамене.

Остается вопрос – а как определить, что делать с уравнением на очередном шаге? Как именно его преобразовывать? Делить на что-то? Или вычитать? И что конкретно вычитать? На что делить?

Ваша цель – привести уравнение к виду \(x=[число]\), то есть, слева икс без коэффициентов и чисел, а справа – только число без переменных. Поэтому смотрите, что вам мешает и делайте действие, обратное тому, что делает мешающий компонент.

Чтобы лучше это понять, разберем по шагам решение линейного уравнения \(x+3=13-4x\).

Давайте подумаем: чем данное уравнение отличается от \(x=[число]\)? Что нам мешает? Что не так?

Ну, во-первых, мешает тройка, так как слева должен быть только одинокий икс, без чисел. А что «делает» тройка? Прибавляется к иксу. Значит, чтобы ее убрать — вычтем такую же тройку. Но если мы вычитаем тройку слева, то должны вычесть ее и справа, чтобы равенство не было нарушено.

Хорошо. Теперь что мешает? \(4x\) справа, ведь там должны быть только числа. \(4x\) вычитается — убираем прибавлением.

Теперь приводим подобные слагаемые слева и справа.

Уже почти готово. Осталось убрать пятерку слева. Что она «делает»? Умножается на икс. Поэтому убираем ее делением.

Решение завершено, корень уравнения – двойка. Можете проверить подстановкой.

Заметим, что чаще всего корень в линейных уравнениях только один. Однако могут встретиться два особых случая.

Какое уравнение не имеет корней? Примеры уравнений

Решение уравнений в математике занимает особое место. Этому процессу предшествует множество часов изучения теории, в ходе которых ученик узнает способы решения уравнений, определения их вида и доводит навык до полного автоматизма. Однако далеко не всегда поиск корней имеет смысл, так как их может попросту не быть. Существуют особые приемы нахождения корней. В данной статье мы разберем основные функции, их области определения, а также случаи, когда их корни отсутствуют.

Какое уравнение не имеет корней?

Уравнение не имеет корней в том случае, если не существует таких действительных аргументов х, при которых уравнение тождественно верно. Для неспециалиста данная формулировка, как и большинство математических теорем и формул, выглядит очень размытой и абстрактной, однако это в теории. На практике все становится предельно просто. Например: уравнение 0 * х = -53 не имеет решения, так как не найдется такого числа х, произведение которого с нулем дало бы что-то, кроме нуля.

Сейчас мы рассмотрим самые базовые типы уравнений.

1. Линейное уравнение

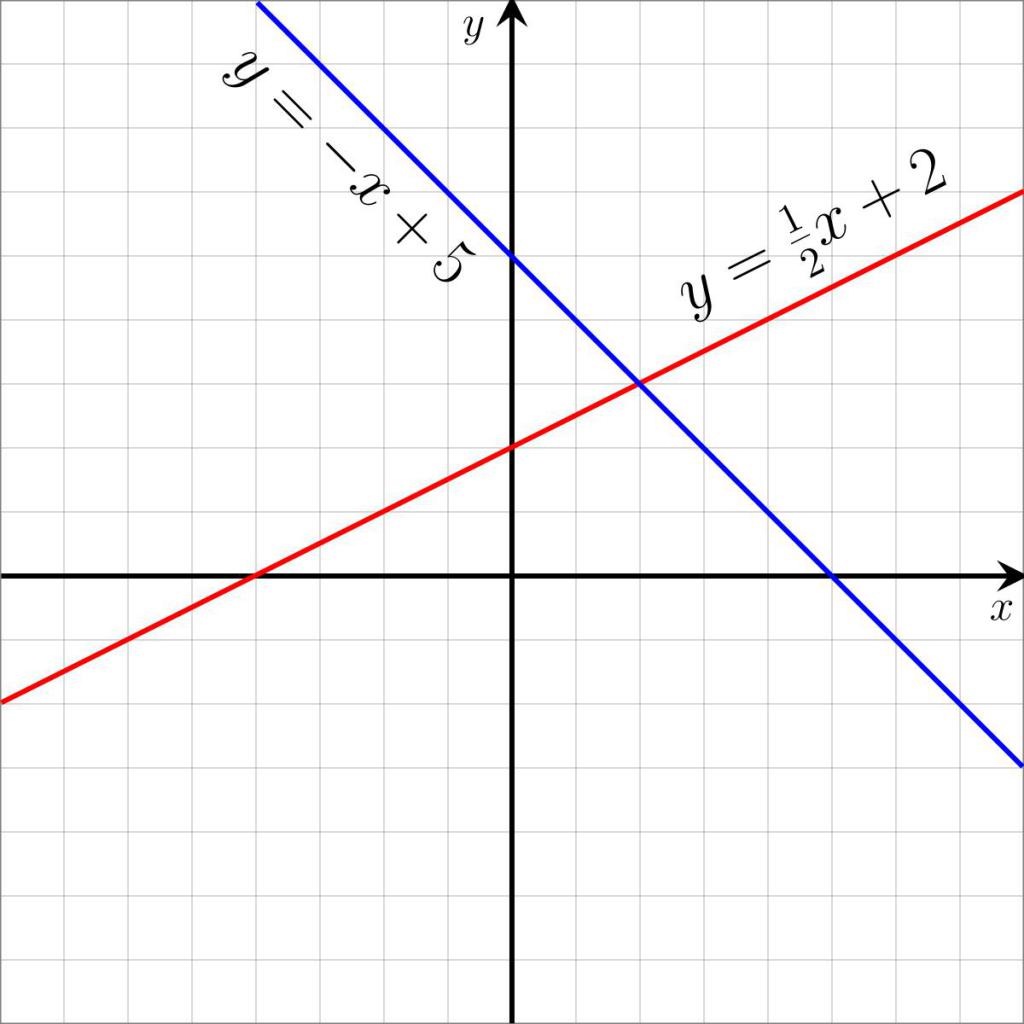
Уравнение называется линейным, если его правая и левая части представлены в виде линейных функций: ax + b = cx + d или в обобщенном виде kx + b = 0. Где а, b, с, d — известные числа, а х — неизвестная величина. Какое уравнение не имеет корней? Примеры линейных уравнений представлены на иллюстрации ниже.

В основном линейные уравнения решаются простым переносом числовой части в одну часть, а содержимого с х — в другую. Получается уравнение вида mx = n, где m и n — числа, а х — неизвестное. Чтобы найти х, достаточно разделить обе части на m. Тогда х = n/m. В основном линейные уравнения имеют только один корень, однако бывают случаи, когда корней либо бесконечно много, либо нет вовсе. При m = 0 и n = 0 уравнение принимает вид 0 * х = 0. Решением такого уравнения будет абсолютно любое число.

Однако какое уравнение не имеет корней?

При m = 0 и n = 0 уравнение не имеет корней из множества действительных чисел. 0 * х = -1; 0 * х = 200 — эти уравнения не имеют корней.

2. Квадратное уравнение

Квадратным уравнением называется уравнение вида ax 2 + bx + c = 0 при а = 0. Самым распространенным способом решения квадратного уравнения является решение через дискриминант. Формула нахождения дискриминанта квадратного уравнения: D = b 2 — 4 * a * c. Далее находится два корня х_1,2= (-b ± √D) / 2 * a.

При D > 0 уравнение имеет два корня, при D = 0 — корень один. Но какое квадратное уравнение не имеет корней? Пронаблюдать количество корней квадратного уравнения проще всего по графику функции, представляющем собой параболу. При а > 0 ветви направлены вверх, при а 2 – 8x + 72 = 0 не имеет корней, так как имеет отрицательный дискриминант D = (–8) 2 – 4 * 1 * 72 = -224. Это значит, что парабола не касается оси абсцисс и функция никогда не принимает значение 0, следовательно, уравнение не имеет действительных корней.

3. Тригонометрические уравнения

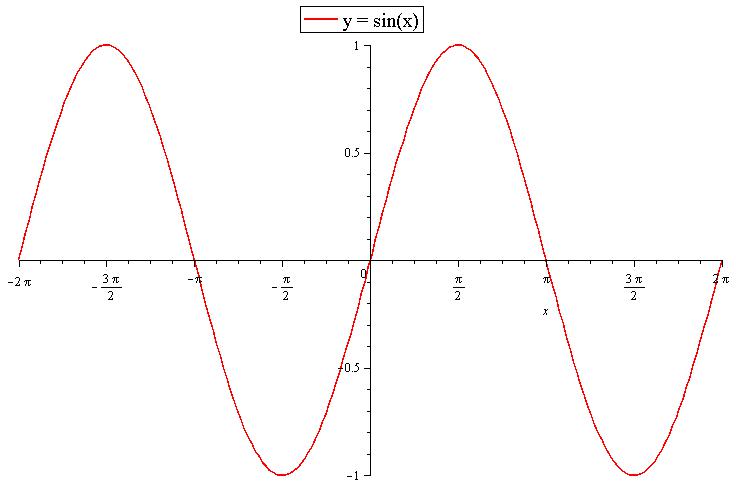
Тригонометрические функции рассматриваются на тригонометрической окружности, однако могут быть представлены и в декартовой системе координат. В данной статье мы рассмотрим две основные тригонометрические функции и их уравнения: sinx и cosx. Так как данные функции образуют тригонометрическую окружность с радиусом 1, |sinx| и |cosx| не могут быть больше 1. Итак, какое уравнение sinx не имеет корней? Рассмотрим график функции sinx, представленный на картинке ниже.

Мы видим, что функция является симметричной и имеет период повторения 2pi. Исходя их этого, можно говорить, что максимальным значением этой функции может быть 1, а минимальным -1. Например, выражение cosx = 5 не будет иметь корней, так как по модулю оно больше единицы.

Это самый простой пример тригонометрических уравнений. На самом деле их решение может занимать множество страниц, в конце которых вы осознаете, что использовали неправильную формулу и все нужно начинать сначала. Порой даже при правильном нахождении корней вы можете забыть учесть ограничения по ОДЗ, из-за чего в ответе появляется лишний корень или интервал, и весь ответ обращается в ошибочный. Поэтому строго следите за всеми ограничениями, ведь не все корни вписываются в рамки задачи.

4. Системы уравнений

Система уравнений представляет собой совокупность уравнений, объединенных фигурной или квадратной скобками. Фигурные скобки обозначают совместное выполнение всех уравнений. То есть если хотя бы одно из уравнений не имеет корней или противоречит другому, вся система не имеет решения. Квадратные скобки обозначают слово «или». Это значит, что если хотя бы одно из уравнений системы имеет решение, то вся система имеет решение.

Ответом системы с квадратными скобками является совокупность всех корней отдельных уравнений. А системы с фигурным скобками имеют только общие корни. Системы уравнений могут включать абсолютно разнообразные функции, поэтому такая сложность не позволяет сказать сразу, какое уравнение не имеет корней.

Обобщение и советы по нахождению корней уравнения

В задачниках и учебниках встречаются разные типы уравнений: такие, которые имею корни, и не имеющие их. В первую очередь, если у вас не получается найти корни, не думайте, что их нет совсем. Возможно, вы совершили где-нибудь ошибку, тогда достаточно лишь внимательно перепроверить ваше решение.

Мы рассмотрели самые базовые уравнения и их виды. Теперь вы можете сказать, какое уравнение не имеет корней. В большинстве случаев сделать это совсем не трудно. Для достижения успеха в решении уравнений требуется лишь внимание и сосредоточенность. Практикуйтесь больше, это поможет вам ориентироваться в материале гораздо лучше и быстрее.

Итак, уравнение не имеет корней, если:

• в линейном уравнении mx = n значение m = 0 и n = 0;
• в квадратном уравнении, если дискриминант меньше нуля;
• в тригонометрическом уравнении вида cosx = m / sinx = n, если |m| > 0, |n| > 0;
• в системе уравнений с фигурными скобками, если хотя бы одно уравнение не имеет корней, и с квадратными скобками, если все уравнения не имеют корней.

Линейное уравнение

теория по математике 📈 уравнения

Уравнение – это равенство, содержащее переменную, значение которой надо найти.

Уравнение с одним неизвестным, содержащим первую степень, называется линейным уравнением с одной переменной. Стандартный вид линейного уравнения ax+b=0, где a и b некоторые числа, а х – переменная. Также стандартным видом уравнения можно считать и вид ax=b.

Так, например, к линейным относятся уравнения:

6х+21=0; 34–2х=0; 34х=17; 89х=0

Уравнения, содержащие несколько слагаемых с переменной или без нее, а также скобки, называются уравнениями, сводящимися к линейным. То есть при его упрощении должно получиться линейное уравнение стандартного вида. К таким уравнениям могут относиться уравнения вида:

х+12=4х–45; 19х–67=98; х=–32+17х; 7(х+13)=89–14х

Решить уравнение – это значит найти все его корни или доказать, что корней нет.

Что такое корень уравнения?

Вспомним, что корнем уравнения называется значение переменной, при котором уравнение обращается в верное равенство.

Корни линейного уравнения

Наличие корней зависит от коэффициентов а и b.

1. Если а=0, то уравнение не имеет корней;
2. Если а=0 и b=0, то корней бесконечное множество (корнем является любое число);
3. Если а≠0 – уравнение имеет единственный корень b:а.

Рассмотрим нахождение количества корней на примерах.

Здесь коэффициент а отличен от нуля. Значит, уравнение имеет один корень.

Здесь коэффициент а равен нулю, поэтому корней нет.

Здесь оба коэффициента равны нулю, поэтому уравнение имеет множество корней, или, еще можно сказать, что корнем уравнения является любое число.

Чтобы найти корни уравнения, надо его решить, используя алгоритм, по которому из одного уравнения мы сможем получить уравнение, равносильное данному. Сначала вспомним, что при переносе слагаемых из одной части в другую, мы получаем уравнение, равносильное данному. Также можно делить или умножать обе части уравнения на одно и то же число.

Алгоритм решения линейного уравнения

1. Раскрыть скобки (при их наличии), используя правило раскрытия скобок;
2. Выполнить перенос слагаемых их одной части в другую (слагаемые с переменной собираем в одной части, слагаемые без переменной – в другой);
3. Привести подобные слагаемые;
4. Найти корень уравнения.

Пример №2. Решить уравнение:

В данном уравнении нет скобок, поэтому выполняем перенос слагаемых, изменяя соответственно знаки у тех слагаемых, которые переносим (обычно слагаемые с переменной собираем слева, а без переменной – справа): 2х–9х=10+11. Теперь приводим подобные слагаемые и получаем: –7х=21. Видим, что корень находится действием деления (неизвестный множитель): х=21:(–7). Ответ х=–3.

При оформлении решения запись оформляем следующим образом:

Пример №3. Решить уравнение:

Здесь мы видим скобки, поэтому сначала раскроем их, помня о том, то число 2 в левой части уравнения надо умножить на каждое слагаемое в скобках, а в правой части уравнения перед скобкой стоит «минус», поэтому изменяем знаки у слагаемых при раскрытии скобок: 5х–2х+16=9х–3х–11. Выполняем перенос слагаемых: 5х–2х–9х+3х=–11–16. Приводим подобные: –3х=–27. Находим корень уравнения: х=–27:(–3). Получаем ответ: х=9

Пример №4. Решить уравнение:

Выполним всё по алгоритму: перенос слагаемых и приведение подобных слагаемых. 2х–2х=3+12; 0х=15. Видим, что коэффициент а=0, поэтому запишем ответ – нет корней, так как надо 15:0, а мы знаем правило, что на нуль делить нельзя.

Имеем линейное уравнение:

Следовательно, начинаем решение с переноса слагаемых (с переменной влево, без переменной – вправо): 3х + 7х= – 5 – 2, не забывая изменять знак у слагаемых, которые переносим. Теперь приводим подобные в каждой части, получаем 10х= –7.

Находим неизвестный множитель делением произведения –7 на известный множитель 10, получаем –0,7.

Запись решения выглядит так:

pазбирался: Даниил Романович | обсудить разбор | оценить