Колесо катится согласно уравнениям определить угловое ускорение

Колесо катится согласно уравнениям определить угловое ускорение

Глава 9. Плоскопараллельное движение твердого тела.

9.3. Угловое ускорение плоской фигуры.

9.3.1. Зависит ли при плоскопараллельном движении угловое ускорение твердого тела от выбора полюса? (Ответ Нет)

9.3.2. Тело совершает плоскопараллельное движение согласно уравне­ниям х_А = 2 sin 4t, у_А = 2 cos 4t, φ = 4 е 2 . Определить угловое ускорение тела. (Ответ 8)

9.3.3. Колесо катится согласно уравнениям х_с = 2t 2 , у_с = 0,5 м. Определить угловое ускоре­ние ε колеса. (Ответ 8)

9.3.4. Центр С барабана, разматывающего нить, движется вертикально вниз по закону у_с = 0,33t 2 . Определить угловое ускорение барабана, если радиус r = 0,066 м. (Ответ 10)

9.3.5. Барабан 1 вращается согласно закону φ = 0,3t 2 . Определить угловое ускорение блока 2, если радиусы R = 0,1 м, r = 0,06 м. (Ответ 0,5)

9.3.6. Кривошип ОА вращается согласно зако­ну φ = 0,5t 2 . Определить угловое ускорение колеса 2. (Ответ 2)

9.3.7. Кривошип ОА вращается согласно закону φ = 0,4t 2 . Определить угловое ускорение под­вижной шестерни, если радиус R = 2t = 0,2 м. (Ответ 0,8)

9.3.8. Барабан 1 вращается согласно закону φ = 0,5t 2 , а ступенчатое колесо 2 катится по наклонной плоскости. Определить угловое ускорение колеса 2, если радиусы r = 0,1 м, R = 0,3 м. (Ответ 0,25)

9.3.9. Стержень АВ длиной 80 см движется в плоскости чертежа. В некоторый момент вре­мени точки А и В стержня имеют ускорения а_А = 5 м/с 2 , а_В = 10 м/с 2 . Определить угло­вое ускорение стержня. (Ответ 6,25)

9.3.10. Точки А и В блоков 2 и 3 с неподвижными осями вращений имеют тангенциальные ускорения а τ _А = 3 м/с 2 и а τ _В = 1 м/с 2 . Определить угловое ускорение подвижного блока 1, если его радиус R = 0,5 м. (Ответ -2)

Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях – решение задачи

Основные законы и формулы, применяемые при решении задач

Вращательное движение вокруг неподвижной оси

Рассмотри твердое тело, вращающееся вокруг неподвижной оси z . Сделаем рисунок. Ось вращения направим перпендикулярно плоскости рисунка, на нас. Пусть φ – угол поворота тела вокруг оси, отсчитываемый от некоторого начального положения. За положительное направление выберем направление против часовой стрелки. Угловая скорость ω равна производной угла поворота по времени t :
.
При , тело вращается против часовой стрелки; при – по часовой. Вектор угловой скорости направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Угловое ускорение ε равно производной угловой скорости по времени:
.
Вектор углового ускорения также направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

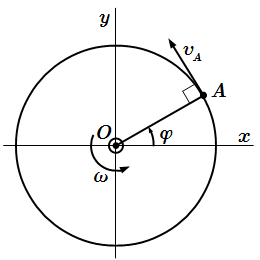
Скорость точки при вращательном движении тела вокруг неподвижной оси

Рассмотрим точку A , принадлежащую твердому телу. Опустим из нее перпендикуляр OA на ось вращения. Пусть – расстояние от точки до оси. Траекторией движения точки A является окружность (или дуга) с центром в точке O радиуса .

Абсолютное значение скорости точки A определяется по формуле:
.
Вектор скорости направлен по касательной к траектории (окружности), перпендикулярно отрезку OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор угловой скорости .

Касательное (или тангенциальное) ускорение точки A определяется аналогично скорости:
.
Оно направлено по касательной к окружности, перпендикулярно OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор углового ускорения .

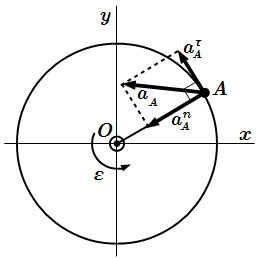
Ускорение точки при вращательном движении тела вокруг неподвижной оси

Нормальное ускорение всегда направлено к центру окружности и имеет абсолютную величину
.

Полное ускорение точки A , или просто ускорение, равно векторной сумме касательного и нормального ускорений:
.
Поскольку векторы и перпендикулярны, то абсолютная величина ускорения точки A определяется по формуле:
.

Поступательное прямолинейное движение

Теперь рассмотрим прямолинейное поступательное движение тела. Направим ось x вдоль его линии движения. Пусть s есть перемещение тела вдоль этой оси относительно некоторого начального положения. Тогда скорость движения всех точек тела равна производной перемещения по времени:
.
При , вектор скорости направлен вдоль оси x . При – противоположно этой оси.

Ускорение точек тела равно производной скорости по времени, или второй производной перемещения по времени:
.
При , вектор ускорения направлен вдоль оси x . При – противоположно.

Соприкосновение тел без проскальзывания

Рассмотрим два тела, находящиеся в зацеплении без проскальзывания. Пусть точка A принадлежит первому телу, а точка B – второму. И пусть, в рассматриваемый момент времени, положения этих точек совпадают. Тогда, если между телами нет проскальзывания, то скорости этих точек равны:
.
Если каждое из тел вращается вокруг неподвижной оси, то равны соответствующие касательные ускорения:
.
Если одно из тел движется поступательно (пусть это второе тело), то ускорение его точек равно касательному ускорению точки соприкосновения первого тела:
.

Пример решения задачи

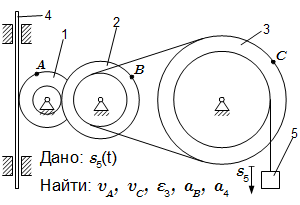
Механизм состоит из ступенчатых колес 1, 2, 3, находящихся в зацеплении и связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 – r₁ = 2 см, R₁ = 4 см, у колеса 2 – r₂ = 6 см, R₂ = 8 см, у колеса 3 – r₃ = 12 см, R₃ = 16 см. На ободьях колес расположены точки A, B и C. Задан закон движения груза: s₅ = t 3 – 6t (см). Положительное направление для s₅ – вниз.

Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.

Указания. Эта задача – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что проскальзывание в ременной передаче и в точках сцепления колес отсутствует. То есть скорости точек колес, находящихся в зацеплении равны, а скорости точек ремня равны скорости точек, лежащих на ободе колес, связанных ременной передачей.

Дано:
t = 2 с; r₁ = 2 см, R₁ = 4 см; r₂ = 6 см, R₂ = 8 см; r₃ = 12 см, R₃ = 16 см; s₅ = t 3 – 6t (см).

Определение скорости и ускорения груза 5

Груз 5 совершает поступательное движение. Поэтому скорости (и ускорения) всех его точек равны. В условии задачи задано смещение s груза относительно некоторого начального положения. Дифференцируя по времени t , находим зависимость скорости точек груза от времени:
.
Дифференцируя скорость груза по времени, находим зависимость ускорения груза от времени:
.

Находим скорость и ускорение груза в заданный момент времени :
см/с;
см/с 2 .

Определение угловых скоростей и ускорений колес

Груз 5 связан нитью с внутренним ободом колеса 3. Поэтому скорости точек внутреннего обода колеса 3 равны скорости груза:
.
Отсюда находим угловую скорость колеса 3 для произвольного момента времени:
.
Здесь подразумевается, что и являются функциями от времени t . Дифференцируя по t , находим угловое ускорение колеса 3:
.
Находим значения угловой скорости и углового ускорения в момент времени с. Для этого подставляем найденные значения и при с:
с –1 ;
с –2 .

Рассмотрим колесо 2. Его внутренний обод связан нитью с внешним ободом колеса 3. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 2 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Рассмотрим колесо 1. Его внутренний обод находится в зацеплении с внешним ободом колеса 2. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 1 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Итак, мы нашли:
ω ₁ = 5.3333 с –1 , ω ₂ = 1.3333 с –1 , ω ₃ = 0.5 с –1 , ε ₁ = 10.6667 с –2 , ε ₂ = 2.6667 с –2 , ε ₃ = 1 с –2 .

Определение скоростей точек A и C

Точка A лежит на окружности радиуса R₁ с центром в точке O₁, расположенной на оси вращения. Поэтому скорость этой точки направлена по касательной к окружности и по абсолютной величине равна
см/с.

Точка C лежит на окружности радиуса R₃ с центром O₃ на оси вращения. Скорость этой точки:
см/с.

Определение ускорения точки B

Точка B лежит на окружности радиуса R₂ с центром O₂, расположенном на оси вращения. Касательное (или тангенциальное) ускорение этой точки направлено по касательной к окружности в сторону, на которую указывает угловое ускорение (по часовой стрелке). По абсолютной величине оно равно
см/с 2 .

Нормальное ускорение всегда направлено к центру окружности. По абсолютной величине оно равно
см/с 2 .

Полное ускорение равно векторной сумме касательного и нормального ускорений:
.
Поскольку касательное ускорение перпендикулярно нормальному, то для абсолютной величины полного ускорения имеем:
см/с 2 .

Определение ускорения рейки 4

Рейка 4 движется поступательно по направляющим. Она находится в зацеплении с внешним ободом колеса 1. Поэтому ее скорость равна скорости точек внешнего обода колеса 1:
.
Дифференцирую по времени, получаем ускорение рейки в произвольный момент времени:
.
Подставляем численные значения для момента времени t = 2 с :
см/с 2 .

см/с; см/с; с –2 ; см/с 2 ; см/с 2 .

Автор: Олег Одинцов . Опубликовано: 25-10-2019

Угловое ускорение Как рассчитать и примеры

угловое ускорение это изменение, которое влияет на угловую скорость, принимая во внимание единицу времени. Он представлен греческой буквой альфа, α. Угловое ускорение является векторной величиной; следовательно, он состоит из модуля, направления и смысла.

Единицей измерения углового ускорения в Международной системе является радиан в секунду в квадрате. Таким образом, угловое ускорение позволяет определить, как угловая скорость изменяется во времени. Угловое ускорение, связанное с равномерно ускоренными круговыми движениями, часто изучается.

Таким образом, при равномерно ускоренном круговом движении значение углового ускорения является постоянным. Наоборот, при равномерном круговом движении значение углового ускорения равно нулю. Угловое ускорение эквивалентно в круговом движении тангенциальному или линейному ускорению при прямолинейном движении.

На самом деле его значение прямо пропорционально значению тангенциального ускорения. Таким образом, чем больше угловое ускорение колес велосипеда, тем больше испытываемое ускорение.

Следовательно, угловое ускорение присутствует как в колесах велосипеда, так и в колесах любого другого транспортного средства, при условии изменения скорости вращения колеса..

Аналогично, угловое ускорение также присутствует в колесе, поскольку оно испытывает равномерно ускоренное круговое движение, когда оно начинает свое движение. Конечно, угловое ускорение также можно найти в карусели.

• 1 Как рассчитать угловое ускорение?
  • 1.1 Равномерно ускоренное круговое движение
  • 1.2 Крутящий момент и угловое ускорение
• 2 примера
  • 2.1 Первый пример
  • 2.2 Второй пример
  • 2.3 Третий пример
• 3 Ссылки

Как рассчитать угловое ускорение?

В общем, мгновенное угловое ускорение определяется из следующего выражения:

В этой формуле ω — угловая скорость вектора, а t — время.

Среднее угловое ускорение также можно рассчитать из следующего выражения:

В частном случае плоского движения бывает, что как угловая скорость, так и угловое ускорение являются векторами с направлением, перпендикулярным плоскости движения..

С другой стороны, модуль углового ускорения можно рассчитать по линейному ускорению с помощью следующего выражения:

В этой формуле а — тангенциальное или линейное ускорение; и R — радиус вращения кругового движения.

Круговое движение равномерно ускорено

Как уже упоминалось выше, угловое ускорение присутствует в равномерно ускоренном круговом движении. По этой причине интересно знать уравнения, которые управляют этим движением:

θ = θ₀ + ω₀ ∙ t + 0,5 ∙ α ∙ t 2

В этих выражениях θ — угол, пройденный в круговом движении, θ₀ начальный угол, ω₀ начальная угловая скорость, а ω угловая скорость.

Крутящий момент и угловое ускорение

В случае линейного движения, согласно второму закону Ньютона, для того, чтобы тело приобрело определенное ускорение, требуется сила. Эта сила является результатом умножения массы тела и ускорения, которое испытало то же самое.

Однако в случае кругового движения сила, необходимая для придания углового ускорения, называется крутящим моментом. Короче говоря, крутящий момент можно понимать как угловую силу. Обозначается греческой буквой τ (произносится «тау»).

Аналогичным образом, необходимо учитывать, что во вращательном движении момент инерции I тела выполняет роль массы в линейном движении. Таким образом, крутящий момент кругового движения рассчитывается по следующему выражению:

В этом выражении I — момент инерции тела относительно оси вращения.

примеров

Первый пример

Определить мгновенное угловое ускорение движущегося тела, совершающего вращательное движение, с учетом выражения его положения во вращении Θ (t) = 4 т. 3 я. (Где i — единичный вектор в направлении оси x).

Также определите значение мгновенного углового ускорения, когда прошло 10 секунд с начала движения..

решение

Выражение угловой скорости можно получить из выражения положения:

ω (t) = d Θ / dt = 12 т 2 я (рад / с)

Как только мгновенная угловая скорость была вычислена, мгновенное угловое ускорение может быть вычислено как функция времени.

α (t) = dω / dt = 24 t i (рад / с) 2 )

Чтобы вычислить значение мгновенного углового ускорения по истечении 10 секунд, необходимо только заменить значение времени в предыдущем результате..

α (10) = = 240 i (рад / с) 2 )

Второй пример

Определите среднее угловое ускорение тела, которое испытывает круговое движение, зная, что его начальная угловая скорость была 40 рад / с и что через 20 секунд она достигла угловой скорости 120 рад / с..

решение

Из следующего выражения вы можете рассчитать среднее угловое ускорение:

Третий пример

Каково будет угловое ускорение колеса, которое начинает двигаться с равномерно ускоренным круговым движением, пока через 10 секунд оно не достигнет угловой скорости в 3 оборота в минуту? Каким будет тангенциальное ускорение кругового движения в этот период времени? Радиус колеса составляет 20 метров.

решение

Во-первых, необходимо преобразовать угловую скорость из оборотов в минуту в радианы в секунду. Для этого выполняется следующее преобразование:

ω_F = 3 об / мин = 3 ∙ (2 ∙ Π) / 60 = Π / 10 рад / с

Как только это преобразование выполнено, можно рассчитать угловое ускорение, учитывая, что:

Π / 10 = 0 + α ∙ 10

α = Π / 100 рад / с 2

А тангенциальное ускорение возникает в результате действия следующего выражения: