Кольцо вычетов системы линейных уравнений

Алгоритм решения систем линейных уравнений в кольцах вычетов

Алевтина Шахова 6 лет назад Просмотров:

1 Авдошин С.М., Савельева А.А. Алгоритм решения систем линейных уравнений в кольцах вычетов Разработан эффективный алгоритм решения систем линейных уравнений в кольцах вычетов [], эквивалентный по сложности известному алгоритму решения систем в полях Галуа ([2], [4]). Приведены результаты сравнительного анализа предложенного алгоритма и существующих аналогов ([3], [0], [8]) на основе асимптотической оценки их временной сложности. Показано, что разработанный метод является корректным и существенно снижает трудоемкость алгоритмов дискретного логарифмирования. Введение Объектом исследования данной работы являются методы решения систем линейных уравнений в кольцах вычетов. Такие системы возникают в алгоритмах факторизации и дискретного логарифмирования (см., например, метод Диксона, алгоритм Копперсмита-Одлыжко-Шреппеля «COS» и алгоритм решета числового поля в [3]). Частным случаем колец вычетов являются поля Галуа, т.е. кольца вычетов по модулю простых чисел. Методы решения систем в таких полях известны (см., например, метод Гаусса (последовательного исключения) в [2, с.89], [4, с.42]). Модификацией метода Гаусса является метод Жордана. Однако для решения систем линейных уравнений в кольцах вычетов эти методы, вообще говоря, неприменимы. Проиллюстрируем сказанное. Рассмотрим систему линейных уравнений: 26x+ 3y = 4 () 9x+ 34y = в поле Галуа Z 37 и в кольце вычетов Z 36. В соответствии с методом Жордана требуется с помощью элементарных преобразований над строками привести матрицу к единичной. Для получения единичного элемента на диагонали в поле действительных чисел используется деление на число a, равное ведущему элементу; аналогом этой операции в кольце вычетов является умножение на элемент, обратный к a. Обратный элемент по модулю можно найти как решение уравнения: ax (mod ) (2) Для его вычисления используется расширенный алгоритм Евклида (см. [7, с. 744], [0, с.227]). На рис. приведено описание этого алгоритма. Если a и — взаимно простые числа, т.е. НОД( a, ) = = ax + y, то 2 ; в противном случае коэффициент Безу x является решением уравнения ( ) уравнение ( ) 2 не имеет решения и элемент a необратим в кольце Z. Как показано в [7, с.743], время работы алгоритма Евклида при вычислении НОД ( ab, ), где a > b 0, составляет O(log b ). Тогда

2 сложность операции вычисления обратного элемента в кольце Z можно оценить как O(log ). Метод Жордана с учетом алгоритма Евклида имеет временную сложность O( n ( n m+ log ) ) для системы n уравнений с m неизвестными в Z. Евклид( ab, ). d x y a 0 n r s b 0 2. c d / n 3. d x y 0 d x y n r s c n r s 4. ЕСЛИ n > 0 5. ТО перейти к шагу 2; 6. ИНАЧЕ вернуть( d, x, y, r, s ) Рис. В результате вычислений, приведенных ниже, получаем решение системы в поле Галуа Z 37 : x = 6, y = 23. [] [] ( 26 = 0 ) 30 3 [2] [] [2] [] 30 3 [2] ( 23 = 29 ) 30 3 [] [2] [2] Однако в кольце вычетов по модулю = 36 система () не может быть решена ни с помощью метода Жордана, ни с помощью метода Гаусса, поскольку все коэффициенты при неизвестных являются делителями нуля ([9, с.75]) и, следовательно, не является обратимыми. Таким образом, получить единичный элемент на диагонали умножением на какой-либо элемент кольца невозможно. Тем не менее, конечность области определения позволяет убедиться в том, что решение данной системы в Z 36 существует ( x = 7, y = 22), и притом единственно. Для решения систем линейных уравнений в кольцах вычетов необходимы специальные методы. Обзор существующих методов Анализ методов решения систем линейных уравнений в кольцах вычетов, описанных в современной литературе, выявил ряд недостатков, которые затрудняют использование этих алгоритмов на практике. В монографии [3] задача сводится к решению систем линейных уравнений над полями Галуа. Пусть

3 где систем t q α = m = ( ) ax b(mod ), i=, n 3 i i =, тогда решение системы ( ) m = 3 сводится к решению семейства ( ) ax b(mod q α ), i=, n, =, t 4 i i где неизвестные значения x (mod q α ) для фиксированного представляются в виде α α x x + x q x q (mod q ), 5 0, α Здесь 0 xl q, l = 0, α. Редуцируя систему ( 4 ) к модулю q, получаем систему уравнений: над полем Галуа виде ( ) q m = 5 с известными i0 поделив на i 0 ax b(mod q), i=, n ( ) Z. Если мы найдем все x,, 0 = m, то, подставляя x в x в систему ( ) 4, редуцируя ее к модулю q, мы получим систему линейных уравнений над полем 2 q и затем относительно неизвестных x,, = m, и т.д. В конечном счете, найдя значение x (mod q α ) для всех, мы восстановим x (mod ) по китайской теореме об остатках (см. [0, с.420]). 2 2 В нашем примере = 36 = 2 3, т.е. для решения одной системы в кольце вычетов придется решить 4 системы над полями Галуа. Но основным недостатком метода является необходимость разложения на множители числа : вопрос о существовании алгоритма факторизации с полиномиальной сложностью является одной из открытых проблем современной теории чисел. Другой метод предполагает сведение системы линейных уравнений в кольце вычетов к системе линейных диофантовых уравнений. При помощи одного из известных алгоритмов (см. [3] или [0]) расширенная матрица системы ( A b ) приводится к ступенчатому виду ( A b ) и вычисляется правая матрица перехода R размером ( m+ ) ( m+ ), такая, что: ( A b) R = ( A b ). На основании матрицы R можно получить общее решение системы. Проиллюстрируем применение данного способа на примере. Система линейных диофантовых уравнений, соответствующая системе ( ) в Z 36, имеет вид: 26x+ 3y+ 36v = 4. 9x+ 34y + 36v2 = Ее общее решение в кольце целых чисел: Z q

4 x = t t (-2492) y = t0 (-324) + t 5688, t0, t Z v = t0 (-857) + t 5048 v2 = 0 + t0 0 + t Редуцируя результат к модулю 36, получаем: x = 7, y = 22. Однако при решении систем линейных уравнений в кольцах вычетов наблюдается экспоненциальный рост длины коэффициентов. Так, в нашем примере коэффициенты исходной матрицы ограничены числом 36, тогда как в 6 целых числах мы получили общее решение с коэффициентами

0. Заметим, что этот результат соответствует системе в кольце вычетов, состоящей всего лишь из двух уравнений с двумя неизвестными. Для того, чтобы избежать экспоненциального роста длины коэффициентов, разработаны специальные методы решения систем линейных алгебраических уравнений над кольцом целых чисел, такие как модификация метода Гаусса и построение нормальной диагональной формы Смита (см. [8, с. 8]). Несмотря на то, что эти алгоритмы являются полиномиальными, их сложность существенно превышает сложность алгоритма Гаусса при решении систем в полях Галуа. Так, для системы из n уравнений с n неизвестными, коэффициенты которой по абсолютной величине не превосходят α, временная сложность модифицированного алгоритма Гаусса при использовании самого быстрого алгоритма умножения составляет O( n 4 (log α + log n ) ). Трудоемкость построения нормальной диагональной формы Смита матрицы 2 O n m 2 logα. A, где a α, i, n,, m n m i = =, ограничена величиной ( ) Метод решения систем линейных уравнений в кольцах вычетов, предлагаемый в данной работе, лишен недостатков вышеописанных алгоритмов и показал свою эффективность при программной реализации. Описание метода В основе разработанного метода лежит преобразование строк матрицы с использованием коэффициентов Безу, которые позволяет вычислить расширенный алгоритм Евклида (см. рис.). В результате работы алгоритма получаем: НОД ( ab, ) = d= a x+ b y, 0 = n = a r+ b s. a = 26 = a, b= 9 = a : НОД (26, 9) = = 26 ( ) + 9 (3), 0= 26 (9) + 9 ( 26). При 2 Применяя к -й и 2-й строке расширенной матрицы системы () преобразования, соответствующие преобразованиям алгоритма Евклида над поступающими на его вход коэффициентами a = 26 и a 2 = 9, в результате мы получаем матрицу, строчно эквивалентную исходной (см. [5, с.27]):

5 [] [] [2] [] [2] 9 34 [2] [] 9 34 [] [2] [] [2] [2] [] [] [2] [] [2] [2] В полученной матрице: A(, ) x y A(, ) = A(2, ) r s A(2, ), где x, y, r, s удовлетворяют условию: НОД ( a, a2) = a x + a2 y, 0 = a r + a2 s (запись A(, ) используется для обозначения -й строки расширенной матрицы A). Коэффициенты Безу x =, y = 3, r = 9, s = 26 можно получить, оперируя лишь коэффициентами a и a 2. Тогда цепь преобразований ( 6 ) сводится к одному преобразованию следующего вида: [] [] =[] 35 + [2] [2] =[] 9 + [2] 0 [2] С учетом того, что коэффициент a 22 = 7 обратим в Z 36 : 7 3(mod36), преобразуем матрицу к единичной и получаем решение: [] [] =[] + [2] [2] =[2] 3 [2] В общем виде алгоритм решения систем линейных уравнений в кольцах вычетов, представляющий собой модификацию метода Жордана, описан на рис.2. Доказательство корректности Предложенный алгоритм является корректным, т.е. полученная в результате преобразований система равносильна исходной (иначе говоря, решения системы не теряются и новые решения не появляются). 3 в матричном виде: Запишем систему уравнений ( ) Ax = b ( 7) Тогда по теореме о равносильности систем линейных уравнений: Если U — обратимая ( n n) коммутативное кольцо с единицей), тогда система уравнений ( ) системе ( UA) x = Ub. (Доказательство см. в [5, с.58]). Следствие из этой теоремы: ( 6) -матрица над R (R — произвольное 7 равносильна Если матрицы ( A, b ) и ( C, δ ) строчно эквивалентны, то система уравнений ( 7 ) равносильна системе Cx = δ.

6 Поскольку преобразования матрицы в описанном модифицированном методе Жордана базируются на элементарных преобразованиях строк (элементарными преобразованиями строк матрицы с элементами из коммутативного кольца с единицей называют (см. [6, с.85]) умножение любой ее строки на обратимый элемент кольца; прибавление к любой ее строке другой строки, умноженной на произвольный элемент кольца; транспозицию строк), то полученная на выходе алгоритма матрица строчно эквивалентна исходной (см. Модиф _ Жордан( A ). n Число _ Строк( A) 2. i 3. ДЛЯ = i+, n ЦИКЛ 4. НОД ( aii, ai ) = aii x + ai y ВЫЧИСЛИТЬ x, y, r, s : 0 = aii r + ai s 5. Ai (, ) x y Ai (, ) A(, ) r s A(, ) 6. ЕСЛИ коэффициент a ii необратим в Z 7. ТО выйти из алгоритма <матрица вырождена>8. ИНАЧЕ <обнуляем все элементы i го столбца выше ведущего>9. A(, i ) A(, i ) a ii 0. A(, ) A(, ) A( i, ) ai, =, i. i i+ 2. ЕСЛИ i n 3. ТО перейти к шагу 2; 4. ИНАЧЕ вернуть( A) [5, с.27]). Тогда приведенному выше следствию соответствующие системы уравнений являются равносильными. Что и требовалось доказать. Оценка сложности Предложенный алгоритм обладает временной сложностью ( ( log )) Рис.2 O n nm+ для системы в кольце вычетов по модулю, в которой n — число уравнений системы, m — число неизвестных. Для получения этой формулы воспользуемся оценкой временной b сложности алгоритма Евклида T( a, b) = O + logϕ НОД ( a, b), где a > b 0, ϕ = ( + 5) 2 (доказательство этой оценки предлагается в [7, с.745], в качестве упражнения). На каждом -м шаге процедура, реализующая алгоритм Евклида, вызывается раз: первым параметром является текущее значение ведущего

7 элемента, в качестве второго на вход последовательно подаются ai ( i = +, n) и. Пусть di — значение ведущего элемента на i -й итерации цикла: d0 = a, d = НОД ( a, a+, ) = НОД ( d0, a+, ). d = НОД ( d, a ). d = НОД ( d, a ). +, n n n, Тогда число операций оценивается неравенством: n < di ai, >min, + log ( n ) + log НОД ( d, a ). i= i i, Помимо этого, на каждом -м шаге над элементами матрицы производится порядка 2( n )( m+ ) 2nm операций. Число шагов алгоритма для системы равно n. Получаем временную сложность алгоритма: n ( ) ( ). Tn (, ) = 2 nm+ ( n ) + log On ( nm+ log ) = Заключение В заключение приведем сравнительный анализ временной сложности предложенного алгоритма и алгоритмов, описанных в современной литературе, для системы n уравнений с m неизвестными в кольце вычетов Z ( t q α = = ). Алгоритм Модифицированный метод Жордана Метод сведения к полям Галуа* Метод сведения к диофантовым уравнениям (с построением матрицы Смита) Временная сложность ( ( + log )) O n nm t O n ( n m α + log ) + ln lnln e = 2 O n m 2 log р ( ) ln ln ln *Оценка временной сложности этого метода дана при условии использования для разложения на множители числа наиболее эффективного на сегодняшний день (см. [7, c.779]) алгоритма «квадратичного решета» () Померанца, имеющего временную сложность L ( ) + o ln ln ln, где L ( ) e =.

8 Список литературы. Авдошин С.М., Савельева А.А. Свидетельство об официальной регистрации программы для ЭВМ : «Программа решения систем линейных уравнений в кольцах вычетов». Зарегистрировано в Реестре программ для ЭВМ Ван дер Варден Б.Л. Алгебра. — М.: Наука, с. 3. Василенко О.Н. Теоретико-числовые алгоритмы в криптографии. М.: МЦНМО, с. 4. Гантмахер Ф.Р. Теория матриц. Гостехиздат, с. 5. Глухов М.М., Елизаров В.П., Нечаев А.А. Алгебра: Учебник. В 2-х т. Т. I — М.: Гелиос АРВ, с. 6. Джекобсон Н. Теория колец (Перевод с английского Н. Я. Виленкина). М.: Государственное издательство иностранной литературы, с. 7. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. М.: МЦНМО, с. 8. Кузнецов М.И., Бурланков Д.Е., Чирков А.Ю., Яковлев В.А. Компьютерная алгебра: Учебник. Нижегородский Государственный Университет им. Н.И. Лобачевского. htt:// с. 9. Курош А.Г. Теория групп (Издание третье, дополненное). М.: «НАУКА», Главная редакция физико-математической литературы, с. 0. Ноден П., Китте К. Алгебраическая алгоритмика. Пер. с франц. — М.: Мир, с.

Области целостности в теории колец

Областью целостности называют коммутативное кольцо без делителей нуля. Так, кольцо целых чисел есть область целостности.

Теорема 2.9. Конечная область целостности является полем.

Поле — это кольцо, умножение которого коммутативно, а каждый ненулевой элемент а имеет обратный элемент относительно умножения. Так как область целостности, по определению, является коммутативным кольцом, то достаточно доказать, что для конечной области целостности любой ненулевой элемент обратим, т.е. для всякого существует единственный , такой, что .

Фиксируем произвольный элемент и определяем отображение множества всех ненулевых элементов в себя по формуле ( в области целостности при и ). Отображение является инъекцией, поскольку из равенства вытекает равенство , откуда ввиду отсутствия делителей нуля и . Так как носитель по условию теоремы конечен, то, согласно теореме 1.8, также и биекция. Поэтому для любого существует единственный элемент , такой, что . В частности, при равенство выполнено для некоторого однозначно определенного , то есть .

Доказательство теоремы 2.9 опирается на условие конечности кольца. Это условие действительно важно. Пример кольца целых чисел показывает, что бесконечная область целостности может и не быть полем.

Теорема 2.9 имеет интересные следствия. Рассмотрим кольцо вычетов по модулю .

Следствие 2.2. Кольцо вычетов по модулю является полем тогда и только тогда, когда — простое число.

Пусть является полем. Покажем, что в этом случае число р простое. Предположим, что оно составное. Тогда найдутся такие числа и , что . Поскольку в этом случае , по крайней мере числа и являются в кольце делителями нуля и — не поле. Следовательно, число не может быть составным.

Пусть — простое число. Предположим, что элементы и кольца будут делителями нуля, т.е. . При простом равенство произведения нулю по модулю означает, что либо делится на , либо делится на , т.е. либо , либо . Учитывая неравенства и , заключаем, что либо , либо . Таким образом, при простом делителей нуля нет и кольцо , как конечная область целостности, является полем.

Мультипликативная группа вычетов по модулю

Мультипликативную группу поля вычетов по модулю обозначают и называют мультипликативной группой вычетов по модулю .

Для произвольного легко видеть, что ненулевые элементы и кольца будут делителями нуля тогда и только тогда, когда произведение делится на (т.е. ). Например, в кольце делителями нуля будут элементы 2 и 6, 3 и 4, 3 и 8, 4 и 6, 4 и 9, 6 и 6, 6 и 8, 6 и 10, 8 и 9.

Замечание 2.3. Следствие 2.2 допускает интерпретацию с точки зрения теории чисел: каково бы ни было простое число , для всякого ненулевого найдется единственное ненулевое , такое, что . Этот результат имеет место именно в силу того, что для каждого элемента поля есть обратный элемент относительно умножения. Это — один из примеров применения общей алгебры к теории чисел.

Пример 2.14. В заключение приведем «таблицу сложения» (табл. 2.1) и «таблицу умножения» (табл. 2.2) для поля .

Таблицы, подобные приведенным выше, которые определяют операции в конечных алгебрах, носят название таблиц Кэли. Из таблиц Кэли для поля вычетов по модулю 5 следует, что в этом поле выполняются слегка шокирующие при первом взгляде равенства: и т.п. Но ни о каких «отрицательных» числах и ни о каких «дробях» тут речи нет, поскольку рассматриваются другие объекты — остатки при делении на 5. Просто равенство означает, что элемент 1 есть элемент, противоположный 4 в аддитивной группе вычетов по модулю 5: . Аналогично по умножению — в мультипликативной группе вычетов по модулю 5 элемент 3 есть обратный к 2 , так как , а элемент 4 обратен к себе самому.

Пример 2.15. Рассмотрим пример решения системы линейных алгебраических уравнений в поле . При записи уравнений будем опускать знак ©5 умножения там, где это не приводит к недоразумениям. Будем решать систему

используя метод Гаусса. Домножив первую строку на 3 и прибавив ее ко второй строке, получим

Воспользовавшись таблицами Кэли, вычислим коэффициенты при переменных. В итоге имеем

Из последнего уравнения находим . Подставив во второе уравнение, будем иметь

Из первого уравнения после подстановки найденных значений переменных получим

Таким образом, и — решение системы линейных уравнений.

Заметим в заключение, что известная техника решения систем линейных алгебраических уравнений в полях действительных или комплексных чисел может быть без изменения перенесена на любое поле.

Модель натурального числа II

Структура конечного кольца вычетов по составному модулю

Замысел работы. Создать такую математическую модель большого числа, которая позволила бы находить его делители, исключая схему перебора возможных их вариантов. При построении модели полагаем известными все ее элементы: значение N = dмdб, позицию его в контуре натурального ряда чисел (НРЧ), оба делителя, их свойства.

Определяемыми неизвестными характеристиками такой универсальной модели являются функциональные зависимости одних переменных модели от других. Эти зависимости должны иметь характер законов и выполняться всегда (для всех чисел) независимо от масштаба чисел. Формирование работоспособной модели числа оказалось достаточно сложным и объемным процессом, поэтому принято решение разбить его на 2 статьи (Часть I здесь).

В настоящее время ситуация с моделированием чисел и факторизацией как пишут Манин и Панчишкин близка к тупику или уже в тупике.

В этой статье на основе закона распределения делителей (ЗРД см.здесь ) числа рассматривается вопрос о структуре конечного числового кольца вычетов (КЧКВ) и о том, как неизвестные нам делители N управляют возникновением полных квадратов — квадратичных вычетов (КВВ) в списке квадратичных вычетов, которые доступны нашему наблюдению. Часть понятий и определений вводилась в части I и здесь повторяются не все из них.

Тривиальные области списочной многострочной модели (СММ) нечетного числа

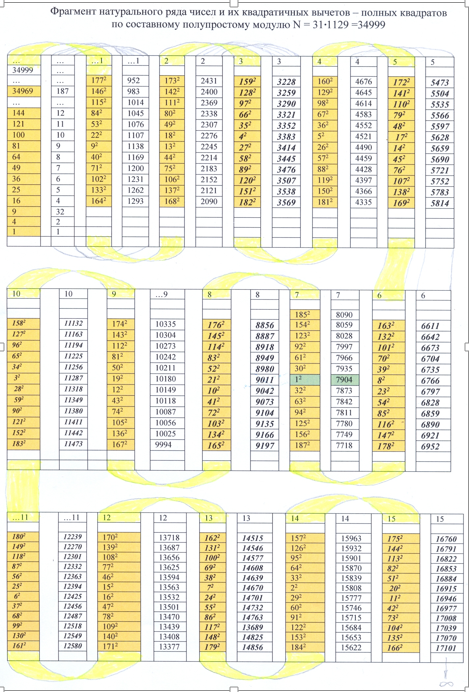
Будем рассматривать натуральный ряд чисел с добавленным слева нулевым элементом и считать, что его элементы размещены в ячейках регистра бесконечной длины. Для каждого элемента хо вычисляется квадрат, помещаемый в ячейку с таким же номером ленты другого бесконечного регистра с заливкой желтого цвета (рис.1). Если же задать составное нечетное натуральное число (СННЧ) N в качестве модуля конечного числового кольца вычетов, то лента с квадратами преобразуется.

В ее ячейки будут включены не просто квадраты (хо), а квадратичные вычеты чисел r_л ≡ хо 2 (mod N) по модулю этого составного числа N=dмdб. Для ячеек двух этих регистровых полос будет выполняться условие комплементарности. При этом мы ограничиваемся рассмотрением лишь фрагмента НРЧ от 0 до N — 1.

Добавление к фрагменту слева нулевого элемента и введение операций (+) и (·) превращает его в конечное числовое кольцо вычетов по модулю N. Если квадратичный вычет получает значение полного квадрата, то КВВ обозначается — квадратичный вычет квадрат (КВК).

Введем несколько определений.

Определение. Списочной многострочной моделью (СММ, СМ-моделью) числа называется таблица строк заданного вида (формата из 8 именованных полей: r_л, х1, хо, t, p, r_c , tп, r_п). Ниже привожу расчетные формулы для переменных.

r_л≡хо 2 (modN)≡x1 2 (modN)-квадратичный вычет левый;
х1 = N — xо — дополнение хо до модуля;
хо — текущий номер строки СММ;
t=х1 — хо =t1 + tо — разность слагаемых строки; раскладывается в сумму смежных;
p =t1tо — произведение смежных слагаемых;
r_с ≡ ¼(t 2 –1)(mod N) =t1tо(modN); средний вычет в строке;
t_пi = 2xоi — 1; нечетное число; сумма номеров смежных строк;
r_п ≡х1хо(modN=N — r_л — произведение слагаемых; правый вычет в строке.

Определение. (ТКВК) Тривиальной областью строк СМ-модели называется начальное множество строк списка, следующих подряд, содержащих в качестве r_л (левого КВВ) монотонно возрастающие полные квадраты.

Определение. Границей ТКВК (левый 1-й верхний порог) называется наибольший КВК – полный квадрат, не превышающий составного модуля N, например, для N =34999, граница ТКВК
r_лmax ≡ √N (mod N) = √34999 = 187.
Извлекаемые квадратные корни округляются до целых значений.

Определение. (ТССС) Тривиальной областью строк СМ-модели (внизу списка) называется множество строк конца списка, следующих снизу вверх подряд, содержащих монотонно возрастающие разности нечетных чисел
t = x1-xо от 1 до границы (порога), а в качестве вычетов r_с (полные квадраты за вычетом первой степени) и обладающие свойством сохранять смежность сомножителей (ССС).

Определение. Границей ТССС (средний 1-й нижний порог) называется наибольший КВК без первой степени квадрата, например, для N =34999, граница ТССС
r_сmax ≡ (хо 2 -хо) (mod N) =187 2 -187 = 34782.
Здесь рассматриваем составное нечетное число N=dмdб и его делители с целью формирования модели N. Для этого в НРЧ определяем положение чисел кратных делителям, промежутки между ними, КВВ элементов, выделяя среди них равные полным квадратам. Конечной целью процесса моделирования является факторизация числа N, обеспечивающая атаку на шифр RSA, исключая перебор вариантов.

Рисунок 1 — фрагмент НРЧ, реализующий конечное числовое кольцо вычетов по модулю N

Тип модели

Под типом модели будем понимать степень различия (разность) делителей модуля N. Если в области строк ТКВК имеет место пересечение (строки, содержащие левые и правые вычеты из тривиальных областей) одной или более строк с тривиальной областью ТССС, то это первый тип моделей (рабочий), если пересечение пусто, то это модели второго типа.

К первому типу относятся все RSA-числа и многие другие, в которых значения делителей с одной стороны не являются близкими, а с другой — не очень удаленными друг от друга на числовой оси НРЧ. Поясним сформулированные условия.

Числа N в СММ могут существенно различаться не только своими значениями, но и делителями. Сами делители также могут иметь различия (малые и большие значения) при близких значениях их произведений, т.е. N1 и N2 близки, а их делители N1 = 11·1129 = 12419 существенно различаются на 1129 – 11 = 1118 или N2 = 101·123 = 12423 всего на 123 – 101 = 22 единицы.

Числа, включающие в качестве делителей квадраты, имеют свои особенности. Указанные различия проявляются специфически в СМ-моделях и всегда желательно учитывать такую специфику N.

Например, в канонической СМ-модели (N = a(a+2) близнецы) дублируемые КВК следуют смежными парами, сумма первых степеней которых постоянна и равна среднему числу (a + 1).

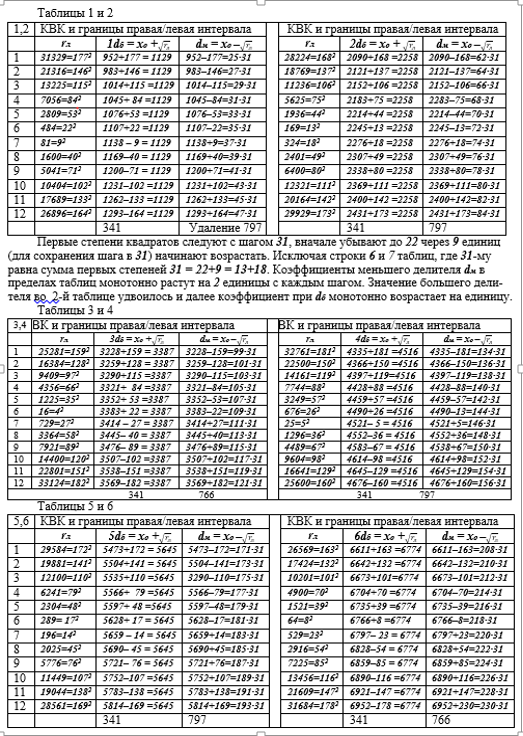
Пример 1. (Делители числа значительно удалены друг от друга). Пусть N = 31·1129 = 34999; это число удовлетворяет основной теореме факторизации N = 34999 = 19 +30·1166.
rс(1) = 26250 = 3·rл(0) = 3·8750, контур НРЧ 34999 +35001 = 70000 с номером kп =70000:8 = 8750, инвариант N равен kп/2 = 4375, отсюда интервал для N содержит слагаемых 31 и среднее слагаемое равно dб = 1129, меньшее число tпм= 1 + dб – dм = 1+1129 –31 =1099 и большее число интервала tпб= dб + dм – 1= 1129 + 31–1 = 1159; действительно,
15(tпм+ tпб) + dб =15·2258 +1129 = 34999.

Инвариант числа представляется суммой номеров 15 контуров и половиной номера большего контура
275+276+277+278+279+280+281+282+283+284+285+286+287+288+289+290/2= 4375.
Контур с номером k = 282 (центр) имеет длину L(282) = 8·282 = 1127 + 1129 = 2256.
Границы интервала и контуров левая Гл(k = 275) = (2·275 –1) 2 = 301401, для интервала правая Гп(k = 290) = (2·290) 2 = 336400. Разность границ Гп – Гл = 336400 – 301401 = 34999 = N.
Граница ТКВК хо_max = √N= 187 = 6·31 + 1; хо (rc = 0) = 3952;
первая ближняя к началу НРЧ точка хо = 952 дубля с КВК(177) = 31329 = 177 2 .

В этой точке с использованием закона распределения делителей (ЗРД) определяются делители:
dм·25 = 952 – 177 = 775 = 31·25;
dб = 952 + 177 = 1129.

Рассмотрим поведение КВВ (всего имеется 187 КВК), дублирующих (181 КВК) тривиальной области списка. Квадрат числа 31 и квадраты его кратных не дублируются, так как число 31 является делителем N.
Определение. Аттрактором (притягивающим к себе квадраты элементом НРЧ) будем называть точку (клетку) НРЧ, соответствующую значению кратному dб.

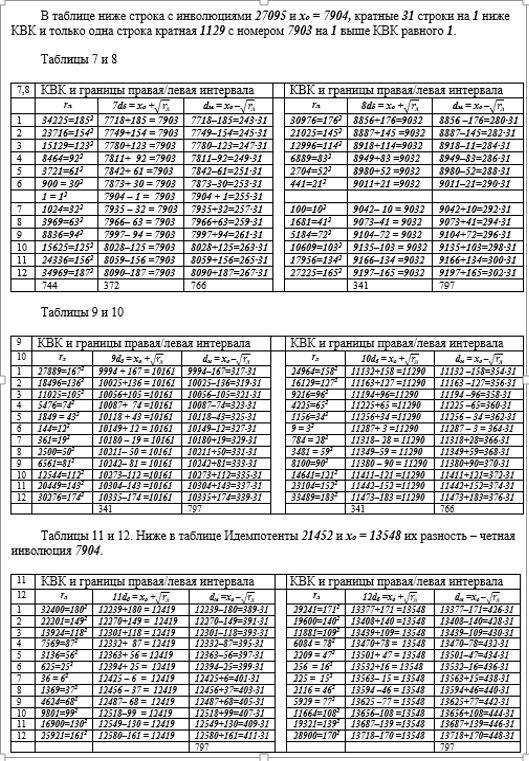
Распределение КВК до середины списка обладает определенной регулярностью, КВК группируются по 12 строк с интервалом между ними 31 позиция, и интервал между группами строк равен 797 либо 766 строк. Это следует из анализа таблиц. Существует 15 групп с 1 по 15. В пределах групп возникают аттракторы, строки как бы притягивающие к себе полные квадраты КВК-дубли. Аналогичная ситуация имеет место и для 2-й половины списка.

Определение. Областью аттрактора назовем множество точек в окрестности аттрактора, значения квадратичных вычетов которых содержат КВК, не превышающие границы тривиальной области ТКВК.

Для более ясного представления и понимания как все устроено с делителями N в НРЧ вначале будем рассматривать картину хорошо разделяемых областей аттракторов. Текст будем сопровождать числовым примером, в котором роль модуля играет полупростое число
N =31·1129 = 34999. Следовательно, аттракторами будут точки кратные dб (числа: 1·1129, 2·1129 = 2258, 3·1129 =3387, …, 15·1129) и их дополнения до модуля для 2-й половины списка.

Клетка, выделенная заливкой зеленого цвета — инволюция КЧКВ. Желтым цветом в полосе выделены КВК для каждого аттрактора. Соединения полосы переменной хо (без заливки) не везде показаны (не загромождают рисунок), но фактически имеют место, являются сплошной лентой.

Пока хо малы (левая желтая колонка верхней части таблицы) их квадраты 187 штук (хо 2 2 –1)(mod N), где
t = х1 – хо = N – 2хо разность значений, также порождает ещё одну другую тривиальную область значений переменной (r_с), обозначаемую (ТССС).

ТССС – область строк модели, содержащая вычеты (r_с), которые следуют в возрастающем порядке и представляют собой вычеты, со свойством после приведения по модулю (после редукции) сохранять смежность сомножителей. По аналогии с первой тривиальной областью для (r_л) значения из области ТССС также повторяются (дублируются) в других точках хо при продолжении преобразований списка нечетных чисел.

Эта область также характеризуется порогом, при превышении которого произведение смежных слагаемых редуцируется и результат (уменьшенное значение) уже чаще не сохраняет смежность меньших сомножителей, чем сохраняет. При сохранении свойства говорят средний вычет имеет свойство ССС- сохранение смежности сомножителей.

Устройство моделей натурального ряда чисел (НРЧ) и отдельного составного нечетного натурального числа (СННЧ) можно представить разными математическими зависимостями. Каждая из моделей ее автором ориентируется, приспосабливается к конкретной задаче или группе задач, представляющих интерес для исследования. Здесь будем рассматривать списочную многострочную модель (СММ) составного натурального числа
N = dm·dб.

На числовой оси с шагом, равным большему делителю dб, размечаются точки (позиции): dб, 2dб, 3dб, …, dм·dб – аттракторы. После этого аналогичную разметку выполняем для меньшего делителя dm. Последняя точка в обоих случаях совпадает с N.

Между размеченными с разным шагом точками возникает множество интервалов разной длины четной и нечетной, среди которых имеются такие интервалы, которые называются решающими, задачу разложения числа N на множители, так как именно они обеспечивают нахождение делителей составного модуля КЧКВ
N = dм·dб.

В соответствии с законом распределения делителей (ЗРД) решающий задачу факторизации больших чисел (ЗФБЧ) интервал своими границами [Гл, Гп] должен иметь точки кратные разным делителям N.

Поскольку относительно произвольной точки кратной dб группируются точки кратные dm с КВК и их 2 или более слева и справа от dб, то точки кратные dб называют (Аi) аттракторами («притягивающими»). Для решающих интервалов между построенными точками их границы выбираются кратными одна меньшему делителю, другая – большему.

Для установления решающих интервалов и их границ выполняем детальный анализ окрестностей точек аттракторов (dб) (см.табл.1-15). При разметке числовой оси каждый аттрактор (Аi) как бы накрывается коротким интервалом (величиной из dm позиций, точек), совпадая с одной из промежуточных. Расстояние (в числе точек) аттрактора до ближайшей одной из границ накрывающего малого интервала всегда четное, до другой – нечетное.

Пример 2. Пусть задан составной модуль приведения N = dm·dб = 31·1129 = 34999 конечного числового кольца вычетов. Числовая ось (фрагмент ряда) разбита точками с шагами dm = 31 и dб = 1129. Требуется представить картину подобного разбиения фрагмента на отрезки и определить положение решающих ЗФБЧ интервалов с их характеристиками.

Решение. Начнем с первой (i = 1) точки (аттрактора А1) с координатой равной dб. Эта точка принадлежит замкнутому малому интервалу [31·36=1116, 1147 = 1116+31], накрывающему ее, 36dm 2 (mod 34999) = 81 = 9 2 и этот результат указывает на то, что этот интервал решающий, т. е. обеспечивает вычисление делителей модуля N. Вычисления делителей пока отложим.

Перейдем к рассмотрению интервала [1116, 1129] слева от А1 аттрактора, длина которого 13. Он не имеет целочисленной средней точки и не является решающим, но положение легко исправимо, переносом левой границы (Гл) в другую более близкую к началу координат (дальше от аттрактора) и кратную dм точку.

Исправленный новый интервал [Гл, Гп] = [1116 – 31, 1129] — решающий и он приобретает вид [1085, 1129] с изменившейся длиной 1129 – 1085 = 44, т. е. уже имеет среднюю точку, координата которой равна хц = ½ (Гл+ Гп) = ½ (1085 + 1129) = 1107.

В этой точке, следуя ЗРД, квадратичный вычет по заданному составному модулю также должен быть равен полному квадрату. В этом легко убедиться выполнив вычисления 1107 2 (mod 34999) = 484 = 22 2 , что также обеспечивает в соответствии с ЗРД вычисление делителей модуля.

Таким образом, найдены два (справа и слева) решающих ЗФБЧ интервала для аттрактора А1, т. е. точки 1·dб, ближайшей (i = 1) среди кратных к началу координат. Зададимся вопросом ограничено ли количество решающих интервалов для этого аттрактора? Если да, то чем определяется это ограничение?

Замечание. Квадратичные вычеты-дубли (за пределами области строк ТКВК), являющиеся полными квадратами – это всегда КВК центров решающих интервалов. Они являются дублями КВК из ТКВК. Их количество в ТКВК конечно и допустимое значение наибольшего из них ограничено.

В рассматриваемом примере порог maxКВК = r_лmax =√N=√34999=187,080, т. е. превышает 6-кратную длину малого интервала 6·31 = 186 187.

Следовательно, все значения КВК (дубли из ТКВК) могут принимать значения, не превышающие 187. Что касается количества решающих интервалов, группируемых аттракторами, то анализ ситуации показывает следующее.

Мощность множества ТКВК – это 187 элементов кольца, из которых не дублируются КВК кратных значений kmdm, km = 1(1)(187/ dm). В примере имеется шесть таких значений 31, 62, 93, 124, 157, 186. Строки СМ-модели в своем составе содержат строки, кратные разным делителям.

Строк кратных dб всего 15 = ½ (dm – 1), так в каждой из них сумма номера строки хо = dб и его дополнения х1 =N-dб остается постоянной равной N, т. е. дополнение х1 также кратно числу dб.

Из анализа нашего примера следует, что существует всего 15 аттракторов Аi, i = 1(1)15 и с каждым из них связаны по (186 – 6)/15 = 12 решающих интервалов, с центрами которых связаны дубли из ТКВК. Другими словами, сдвигаясь к началу координат с шагом 31, увеличиваем решающий интервал, КВВ в центре которого – получаем новый полный квадрат.

Пример 3. Используя данные примера А, вычислим решающие интервалы, наиболее удаленные влево и вправо от аттрактора А1. Левые интервалы:
[Гл, Гп] = [1116 – 62, 1129] = [1054, 1129] этот интервал не имеет целочисленной центральной точки хц = ½(Гл +Гп) = ½ (1054 + 1129) = 1091,5.
Обе границы интервалов должны быть нечетными числам кратными разным делителям.

Сдвигаемся еще на один dm интервал [1116 – 93, 1129] = [1023, 1129] и находим центр
хц = ½ (Гл + Гп) = ½ (1023 + 1129) = 1076, в котором
КВВ = КВК = 1076 2 (mod 34999) = 2809 = 53 2 .

Заметим, что положение центров (53 – 22 = 31) интервалов, как и их протяженности √(r_л) изменяются на величину кратную dм, а левой границы на 2dм. Таким образом, левые (правые) границы решающих интервалов и их центры принимают конкретные значения (здесь граница 1129 постоянная):

Зачеркнутые числа выходят за пределы допустимых элементов КЧКВ.

Для аттрактора А2 = 2dб и всех последующих вычисления аналогичные. Их результаты приведены далее в таблицах 1-15.

В работе здесь рассмотрена контурная модель НРЧ, связанная с изучением возможностей решения задачи факторизации больших чисел (ЗФБЧ). Особенность модели состоит в том, что в ней НРЧ представлен непрерывной последовательностью нумерованных (номер k = 1(1) ∞) контуров (блоков), размер которых (L(k)) с увеличением номера возрастает, но остается всегда кратным числу 8, L(k) = 8k.

Каждый контур представляет множество позиций НРЧ, где крайние позиции содержат квадраты нечетных последовательных чисел. Эти крайние позиции называются границами контура:
левая
(Гл(k) = (2k – 1) 2 ) и
правая
(Гп(k) = (2k + 1) 2 , Гп(k) > Гл(k)).

Все контуры образованы двумя полуконтурами с размерами левый полуконтур m(k) = 4k –1 и правый контур – M(k) = 4k+1. Полуконтуры в k-м контуре имеют общую границу
Гц(k) = (2k) 2 – квадрат четного числа.

Длина (размер) каждого полуконтура – нечетное число и M(k)– m(k)= 2, а их сумма равна
M(k) + m(k) = L(k) длине k-го контура, левая и правая границы которого совпадают с левой границей меньшего и с правой – большего полуконтура.

С введением понятий контура и полуконтура модель НРЧ можно представить как непрерывную последовательность нечетных чисел 1, 3, 5, … ∞, в которой каждое число является полуконтуром некоторого k -го контура, где при известном значении N полуконтура, номер контура определяется соотношением k =¼(N ± 1).

Знак (+) соответствует левому полуконтуру и (–) – правому. Любое составное нечетное натуральное число (СННЧ) N >9, будем рассматривать как полуконтур или интервал в НРЧ с длиной N. Длина интервала – нечетное число равное сумме нечетного количества последовательных слагаемых (полуконтуров), в которой количество слагаемых равно меньшему делителю N, а среднее слагаемое – большему делителю N.

В действительности нам известны лишь N и, что оно составное, равно произведению двух простых чисел.

Рассматриваются составные нечетные натуральные числа (СННЧ) среди которых нет чисел N =k 2 полных нечетных квадратов.

Дело в том, что такие квадраты дают другую картину распределения квадратичных вычетов (КВВ) элементов кольца, отличающуюся от картины для полупростых чисел N = pq, p 2 из тривиальной области не дублируются в списочной многострочной модели (СММ) числа и закон распределения делителей (ЗРД) в такой ситуации не работает.

Напомним, что в СММ при дублировании одного из вычетов строки дублируются и другие два. При этом, если делители p и q не очень близки (далеки) друг от друга, то в области тривиальных строк ТКВК имеются две строки, содержащие средние вычеты со свойством, сохранять смежность сомножителей (ССС).

Утверждение. Для двух нечетных произвольных простых чисел p и q их сумма ∑ и разность Δ четные и либо их сумма ∑ = (р + q), либо их разность Δ = (р – q) делится на 4.

Расстояние (в числе строк) между этими строками равно меньшему делителю р. Номер верхней строки с дублируемым средним вычетом определяется соотношением хов = (р – q):4. Отсюда номер нижней строки равен хон = хов + р. Положение этих (верхняя и нижняя) строк определяются элементами колонки Тп, которые кратны меньшему делителю.

В случае, когда разность делителей Δ = (р – q) не делится на 4, а сумма делится, то номер верхней строки равен хов = хон – ½ Δ, где хон = (р + q):4.

В области строк СММ тривиальных средних вычетов, также появляются две строки, содержащие средние вычеты и дублируемые левые КВВ, с теми же значениями вычетов, что и в верхней части модели.

Области аттракции модуля сравнения N = 34999 конечного числового кольца

Размах области аттракции постоянный для всех аттракторов (равен 341 строке), кроме той, что содержит инволюцию (увеличен на dm =31 строку).

Между областями аттракции интервалы либо 766, либо 797 строк. Области хорошо разделены, хотя их влияние друг на друга не исключается.

Сближение значений делителей изменяет (уменьшает) удаленность областей вплоть до того, что области «наезжают» одна на другую и разобраться с решающими интервалами становится проблематично. Но закон распределения делителей (ЗРД) числа работает и в этих условиях. Здесь возникает множество вопросов, ответы на которые пока не получены.