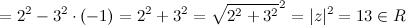Комплексно сопряженные числа
Если $z=a+b i$, то число $\overline
То есть у комплексно сопряженных чисел действительные части равны, а мнимые отличаются знаком.
Например. Комплексно сопряженным к числу $z=2-i$ есть число $\overline
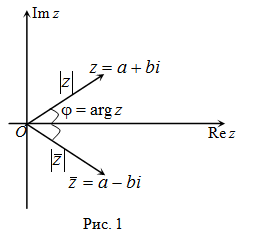
На комплексной плоскости комплексно сопряжённые числа получаются зеркальным отражением друг друга относительно действительной оси.
Свойства комплексно сопряженных чисел
1) Если $z=\overline
Например. $z=2 \in R \Rightarrow \overline
2) Для любого комплексного числа $z$ сумма $z+\overline
Например. Пусть $z=2-3 i$, тогда $\overline
$z+\overline
3) Для произвольного комплексного числа $z=a+b i$ произведение $z \cdot \overline
Например. Пусть $z=2-3 i$, комплексно сопряженное к нему число $\overline
4) Модули комплексно сопряженных чисел равны: $|z|=|\overline
5) $\overline
6) $\overline
9) Если $z=a+b i$ и $\overline
Что такое комплексно сопряженные числа
В данной публикации мы рассмотрим, что такое комплексно сопряженные числа, а также перечислим их основные свойства. Представленная теоретическая информация сопровождается практическими примерами для лучшего понимания.
Определение комплексно сопряженных чисел
Дано комплексное число . Комплексно сопряженным к нему является число (для обозначения используется черточка сверху).
Таким образом, у комплексно сопряженных чисел действительные части одинаковые, а мнимые отличаются по знаку.
Пример:
Для числа комплексно сопряженным является .
Геометрическая интерпретация
Если перенести комплексно сопряженные числа на комплексную плоскость, то они будут зеркальным отражением друг друга относительно действительной оси (RE).
Свойства комплексно сопряженных чисел
1. Если z = z , значит число z является действительным.
Пример:
z = 2, значит , следовательно , т.е. .
2. Модули комплексно сопряженных чисел равны, т.е. . А так как такие числа на комплексной плоскости зеркальны, то их аргументы отличаются по знаку.
3. Сумма комплексно сопряженных чисел – это действительное число: .
4. Произведение комплексно сопряженных чисел равняется квадрату их модуля и является действительным числом: .
Модуль считается так:
5. Для и справедливо:
6. Для произвольных комплексных чисел z1 и z2 :
Комплексные числа
 Алгебраическая форма записи комплексных чисел Алгебраическая форма записи комплексных чисел |
 Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме |
 Комплексно сопряженные числа Комплексно сопряженные числа |
 Модуль комплексного числа Модуль комплексного числа |
 Деление комплексных чисел, записанных в алгебраической форме Деление комплексных чисел, записанных в алгебраической форме |
 Изображение комплексных чисел радиус-векторами на координатной плоскости Изображение комплексных чисел радиус-векторами на координатной плоскости |
 Аргумент комплексного числа Аргумент комплексного числа |
 Тригонометрическая форма записи комплексного числа Тригонометрическая форма записи комплексного числа |
 Формула Эйлера. Экспоненциальная форма записи комплексного числа Формула Эйлера. Экспоненциальная форма записи комплексного числа |
 Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме |
 Извлечение корня натуральной степени из комплексного числа Извлечение корня натуральной степени из комплексного числа |
Алгебраическая форма записи комплексных чисел
Пусть x и y — произвольные вещественные числа.
Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.
Множество комплексных чисел является расширением множества вещественных чисел, поскольку множество вещественных чисел содержится в нём в виде пар (x, 0) .
Комплексные числа, заданные парами (0, y) , называют чисто мнимыми числами .
Для комплексных чисел существует несколько форм записи: алгебраическая форма записи, тригонометрическая форма записи и экспоненциальная (показательная) форма записи .
Алгебраическая форма — это такая форма записи комплексных чисел, при которой комплексное число z, заданное парой вещественных чисел (x, y) , записывается в виде
| z = x + i y . | (1) |
где использован символ i , называемый мнимой единицей .
Число x называют вещественной (реальной) частью комплексного числа z = x + i y и обозначают Re z .
Число y называют мнимой частью комплексного числа z = x + i y и обозначают Im z .
Комплексные числа, у которых Im z = 0 , являются вещественными числами .
Комплексные числа, у которых Re z = 0 , являются чисто мнимыми числами .
Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.
Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме
Умножение комплексных чисел z1 = x1 + i y1 и z2 = x2 + i y2 , так же, как и операции сложения и вычитания, осуществляется по правилам умножения двучленов (многочленов), однако при этом учитывается важнейшее равенство, имеющее вид:
| i 2 = – 1 . | (2) |
По этой причине
Комплексно сопряженные числа
Два комплексных числа z = x + iy и 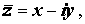
Операция перехода от комплексного числа к комплексно сопряженному с ним числу называется операцией комплексного сопряжения , обозначается горизонтальной чертой над комплексным числом и удовлетворяет следующим свойствам:
 |  |
 |  |
 |  |
 |  |
 |  |
Модуль комплексного числа
Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое | z | и определенное по формуле
Для произвольного комплексного числа z справедливо равенство:
а для произвольных комплексных чисел z1 и z2 справедливы неравенства:
 |  |
 |  |
 |  |
 |  |
Замечание . Если z — вещественное число, то его модуль | z | равен его абсолютной величине.
Деление комплексных чисел, записанных в алгебраической форме
Деление комплексного числа z1 = x1 + i y1 на отличное от нуля комплексное число z2 = x2 + i y2 осуществляется по формуле
Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:
Деление на нуль запрещено.
Изображение комплексных чисел радиус-векторами координатной плоскости
Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.
Назовем рассматриваемую плоскость комплексной плоскостью , и будем представлять комплексное число z = x + i y радиус–вектором с координатами (x , y).
Назовем ось абсцисс Ox вещественной осью , а ось ординат Oy – мнимой осью .
При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.
Аргумент комплексного числа
Рассмотрим радиус–вектор произвольного, но отличного от нуля, комплексного числа z .
Аргументом комплексного числа z называют угол φ между положительным направлением вещественной оси и радиус-вектором z .
Аргумент комплексного числа z считают положительным, если поворот от положительного направления вещественной оси к радиус-вектору z происходит против часовой стрелки, и отрицательным — в случае поворота по часовой стрелке (см. рис.).
Считается, что комплексное число нуль аргумента не имеет.
Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где k — произвольное целое число, то вводится, главное значение аргумента , обозначаемое arg z и удовлетворяющее неравенствам:
Тогда оказывается справедливым равенство:
Если для комплексного числа z = x + i y нам известны его модуль r = | z | и его аргумент φ , то мы можем найти вещественную и мнимую части по формулам
 | (3) |
Если же комплексное число z = x + i y задано в алгебраической форме, т.е. нам известны числа x и y , то модуль этого числа, конечно же, определяется по формуле
 | (4) |
а аргумент определяется в соответствии со следующей Таблицей 1.
Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.
Таблица 1. – Формулы для определения аргумента числа z = x + i y
| Расположение числа z | Знаки x и y | Главное значение аргумента | Аргумент | Примеры |
| Положительная вещественная полуось | 0 | φ = 2kπ |  | |
| Первый квадрант |  |  |  | |
| Положительная мнимая полуось |  |  |  | |
| Второй квадрант |  |  |  | |
| Отрицательная вещественная полуось | Положительная вещественная полуось | |||
| Знаки x и y | ||||
| Главное значение аргумента | 0 | |||
| Аргумент | φ = 2kπ | |||
| Примеры |  |
| Расположение числа z | Первый квадрант |
| Знаки x и y | |
| Главное значение аргумента |  |
| Аргумент |  |
| Примеры |  |
| Расположение числа z | Положительная мнимая полуось |
| Знаки x и y | |
| Главное значение аргумента |  |
| Аргумент |  |
| Примеры |  |
| Расположение числа z | Второй квадрант |
| Знаки x и y | |
| Главное значение аргумента |  |
| Аргумент |  |
| Примеры |  |
| Расположение числа z | Отрицательная вещественная полуось | ||||||||||
| Знаки x и y | Третий квадрант | ||||||||||
| Знаки x и y | Отрицательная мнимая полуось | ||||||||||
| Знаки x и y | Четвёртый квадрант | ||||||||||
| Знаки x и y | |||||||||||
| z = r (cos φ + i sin φ) , | (5) |
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .
Запись комплексного числа в форме (5) называют тригонометрической формой записи комплексного числа .
Формула Эйлера. Экспоненциальная форма записи комплексного числа
В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера :
| cos φ + i sin φ = e iφ . | (6) |
Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде
| z = r e iφ , | (7) |
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .
Запись комплексного числа в форме (7) называют экспоненциальной (показательной) формой записи комплексного числа .
Из формулы (7) вытекают, в частности, следующие равенства:
а из формул (4) и (6) следует, что модуль комплексного числа
или, что то же самое, числа e iφ , при любом значении φ равен 1.
Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме
Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.
Действительно, умножение и деление двух произвольных комплексных чисел 

Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.
При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.
Возведение комплексного числа z = r e iφ в натуральную степень осуществляется по формуле
Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Извлечение корня натуральной степени из комплексного числа
Пусть 
Корнем n — ой степени из числа z0 , где 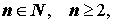
| z n = z0 . | (8) |
Для того, чтобы решить уравнение (8), перепишем его в виде
и заметим, что два комплексных числа, записанных в экспоненциальной форме, равны тогда и только тогда, когда их модули равны, а разность аргументов равна 2kπ , где k — произвольное целое число. По этой причине справедливы равенства
следствием которых являются равенства
 | (9) |
Из формул (9) вытекает, что уравнение (8) имеет n различных корней
 | (10) |
причем на комплексной плоскости концы радиус-векторов zk при k = 0 , . , n – 1 располагаются в вершинах правильного n — угольника, вписанного в окружность радиуса 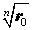
Замечание . В случае n = 2 уравнение (8) имеет два различных корня z1 и z2 , отличающихся знаком:
Пример 1 . Найти все корни уравнения
то по формуле (10) получаем:
Пример 2 . Решить уравнение
Решение . Поскольку дискриминант этого квадратного уравнения отрицателен, то вещественных корней оно не имеет. Для того, чтобы найти комплексные корни, выделим, как и в вещественном случае, полный квадрат:
http://microexcel.ru/kompleksno-sopryajennye-chisla/
http://www.resolventa.ru/spr/algebra/complex.htm