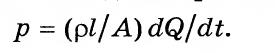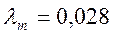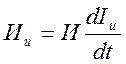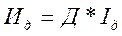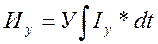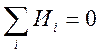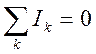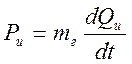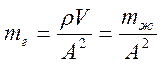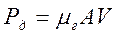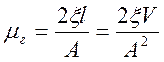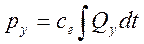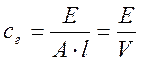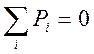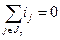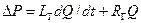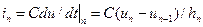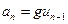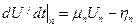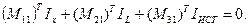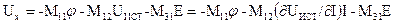Компонентные и топологические уравнения гидравлической системы

Компонентные и топологические уравнения гидравлической системы

В гидравлической системе фазовыми переменными типа потока являются расходы ( , м 3 /с, а типа потенциала — давле­ния р, Н/м 2 (Па).

При выводе компонентных уравнений используем уравне­ния Эйлера, Навье—Стокса и Гука, полученные для одномерной системы с распределенными параметрами.

Для перехода к модели с сосредоточенными параметрами осуществим аппроксимацию моделей микроуровня путем замены частных производных фазовых переменных по пространственным координатам отношениями конечных разностей.

Уравнение Эйлера для трубопровода постоянного сечения

(3.16)

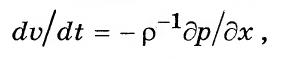
где V — скорость потока жидкости в трубопроводе; р — плотность жидкости; х — геометрическая координата.

Разделим трубопровод на ряд участков длиной I и заменим частную производную др/дх отношением конечной разности

(3.17) (3.17)

где Р1, Р2 — давления в узлах дискретизации 1 и 2, т.е. на грани­цах выделенных участков трубопровода.

Здесь учтено, что градиент давления вдоль трубопровода 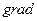р = др/дх отрицателен (давление падает по мере удаления от

Расход жидкости в трубопроводе выразим через скорость потока :

(3.18) (3.18)

где А — площадь поперечного сечения трубопровода.

Подставим значения др/дх из (3.17) и из (3.18) в уравне­ние (3.16) и найдем выражение для определения р:

(3.19) (3.19)

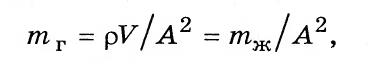
где т _г — коэффициент массы, кг/м 4 ; V — объем жидкости в вы­деленном участке трубопровода длиной I: У=А ; т_ж — масса жид­кости в этом участке.

С учетом (3.19) уравнение Эйлера (3.16) после дискретиза­ции приводится к виду

(3.20)

Сопоставляя (3.20) с выражением (3.1), приходим к выводу, что уравнение Эйлера отображает только инерционные свойст­ва жидкости.

Рассмотрим линеаризованное уравнение Навье – Стокса

(3.21)

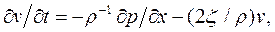
где — коэффициент линеаризованного вязкого трения жидкости.

Учитывая выражения (3.17) и (3.18), получаем

(3.22)

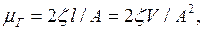
где — коэффициент гидравлического сопротивления,

С учетом выражений (3.19) и (3.22) уравнение Навье – Стокса после дискретизации приводиться к виду

(3.23)

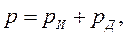
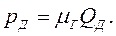
Из выражения (3.23) следует, что уравнение Навье – Стокса отображает инерционные и диссипативные свойства жидкости. В этом случае где — величина потерь давления на преодоление трения при движении потока жидкости в трубопроводе, а — затраты давления на разгон жидкости. Полагая и аддитивными величинами, выделим инерционный и диссипативный элементы участка трубопровода. Компонентное уравнение инерционного элемента соответствует выражению (3.20), а диссипативного элемента имеет вид

(3.24)

(3.25)

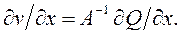
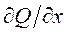
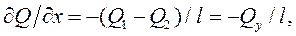
позволяет учесть упругие свойства жидкости. Выразим скорость потока v через расход Q по формуле (3.18). Тогда Заменим отношением конечной разности

(3.26)

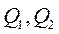
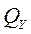
где — расходы в узлах дискретизации трубопровода 1 и 2; — изменение расхода, обусловленное сжимаемостью жидкости.

В выражении (3.26) учтено, что при возрастании давления происходит увеличение объемной деформации жидкости и величина расхода жидкости при удалении от источника уменьшается.

На основе уравнения (3.25) с учетом выражения (3.26) найдем выражение для определения давления упругого элемента, полагая Е не зависящим от р:

(3.27)

(3.28)

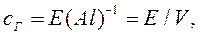
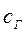
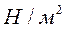
где — коэффициент гидравлической жесткости, ; Е – модуль объемной упругости жидкости, .

В результате получаем компонентное уравнение упругого элемента гидравлической системы

(3.29)

Фазовые переменные , , представляют собой внутренние потенциалы исследуемой гидравлической системы, характеризующие взаимодействие выделенных дискретных элементов и определяющие потери давления источника на преодоление сил инерции жидкости и сообщение ей кинетической энергии, на деформацию жидкости и изменение ее потенциальной энергии, а также на преодоление сил внутреннего трения жидкости.

Коэффициенты , и являются параметрами соответственно инерционных, упругих и диссипативных элементов гидравлической системы.

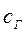
Топологические уравнения имеют вид

; (3. 30)

(3.31)

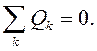
Первое уравнение выражает условие равновесия потенциалов, действующих на сосредоточенные массы, а второе – условие непрерывности потоков жидкости.

Разработка динамической модели гидравлической системы. Моделирование и анализ статического состояния гидросистемы

Страницы работы

Содержание работы

СОДЕРЖАНИЕ

1 Исходные данные 2

2 Разработка динамической модели гидравлической системы 3

2.1 Компонентные и топологические уравнения гидросистемы 4

2.2 Описание гидросистемы и разработка схемы динамической модели 4

2.3 Построение орграфа гидросистемы 7

2.4 Составление матрицы инциденций 9

2.5 Использование узлового метода 10

2.6 Определение параметров элементов модели 13

2.7 Использование структурно–матричного метода, формирование математической модели 13

3 Моделирование и анализ статического состояния гидросистемы 16

3.1 Разработка статической модели гидросистемы 16

3.2 Формирование матрицы Якоби в статической модели гидросистемы

3.3 Решение систем уравнений статической модели методом Ньютона 18

4 Моделирование и анализ переходных процессов 20

4.1 Формирование матрицы Якоби в динамической модели 21

4.2 Выбор параметров интегрирования 22

4.3 Решение системы дифференциального уравнения методом Эйлера 24

4.3 Решение системы дифференциального уравнения методом Эйлера 27

Приложение А 29

Приложение Б 43

Приложение В 44

1 ИСХОДНЫЕ ДАННЫЕ

Рисунок 1 – Принципиальная схема гидросистемы

Таблица 1 — Параметры гидросистемы

Толщина стенки трубопровода, м

Коэф-нт местных сопротивлений

Давление потребителя, Па

Масло веретенное АУ: ;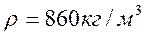

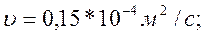
Е_с=1,7*10 8 Па.

Сталь: Е_тр=2,1*10 11 Па

Коэффициент потерь на трение при турбулентном потоке

2 РАЗРАБОТКА динамической модели гидравлической системы

2.1 Компонентные и топологические уравнения гидросистемы

В методе сосредоточенных масс, каждый элемент рассматривается простым, т. е. наделенный одним физическим свойством. Состояние простого элемента характеризуется одной фазовой переменной типа потока и одной типа потенциала, математическая модель, выражающая зависимость между этими переменными называется компонентным уравнением. Компонентное уравнение получается, на основе физических законов имеет, следующий вид:

— для инерционного элемента:

— для диссипативного элемента:

— для упругого элемента:

Для получения полной математической модели необходимо объединить все компоненты уравнения в общую систему уравнения. Объединение осуществляется на основе физических законов, выражающих условие равновесия и непрерывности, уравнение этих законов называют топологическим уравнением, и они описывают характер взаимодействия между простыми элементами.

— Условие равновесия записываются для фазовых переменных типа потенциала:

— Условие непрерывности для фазовой переменной типа потока:

Если фазовая переменная векторной величины, учитывает только топологию, а компонентных уравнениях используются только абсолютные значения.

В гидравлической системе фазовая переменная типа потока расхода – Q, м 3 /с, а типа потенциала давление — р, Па или Н*м 2 .

— Компонентное уравнение инерционного элемента:

получается на основе уравнения Эйлера.

где, р — плотность;

V – объем жидкости в выделенном участке трубопровода длинной l.

где, А – площадь поперечного сечения трубопровода;

m_ж – масса жидкости в участке трубопровода.

Инерционные свойства обусловлены затратами давления на разгон жидкости.

— Компонентное уравнение диссипативного элемента:

получается с учетом уравнения Навье – Стокса.

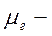
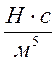
где, коэффициент гидравлического сопротивления .

где, 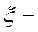коэффициент для линеаризованного вязкого трения жидкости (по справочнику).

— Компонентное уравнение упругого элемента:

где, с_г – коэффициент гидравлической жесткости Н/м 5 .

где, Е – модуль объемной упругости жидкости Н/м 2 .

1 Условие равновесия потенциалов:

2 Условие непрерывности потоков:

.

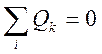
2.2 Описание гидросистемы и разработка схемы динамической модели

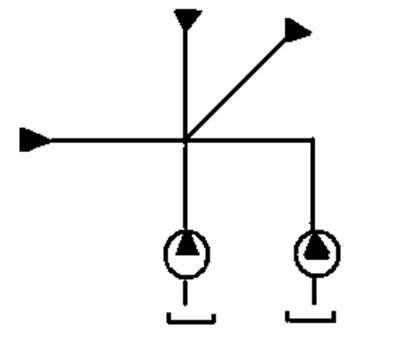
На рисунке 1 приведена принципиальная схема, гидравлической системы, состоящей: из трех гидромагистралей потребителя – 1,4,5; двух насосов – 2,3 и соединительной магистрали – 2,3.

При построении динамической модели учтем основные свойства гидравлической системы, будем считать магистрали сравнительно короткими и рассматривать их, как дискретные элементы (магистрали), рассматриваем как сосредоточенную, так как длина соединительной магистрали значительно меньше магистрали потребителей, то в первом приближении массой жидкости в ней можно пренебречь.

Внешнее воздействие на гидросистему создаются потребителями и насосами, при чем воздействие потребителей, представляет собой источники потенциалов, воздействие насосов, источники потока. Источники потенциалов описываются функциями давлений P_i=F(t), характеризующий потери напора в гидроаппарате и потребителя, а источник потока, функция расхода (подача насоса), Q_н=const.

Упругий элемент, учитывающий сжимаемость в газожидкостной смеси и деформированность стенок трубопровода, подключают в точку ветвления гидравлической магистрали. Он осуществляет дифференциальное соединение всех инерционных элементов и источников потока. На рисунке 2 представлена схема динамической модели гидросистемы.

Математические модели в процедурах анализа на макроуровне

Исходные уравнения моделей.Исходное математическое описание процессов в объектах на макроуровне представлено системами обыкновенных дифференциальных и алгебраических уравнений. Аналитические решения таких систем при типичных значениях их порядков в практических задачах получить не удается, поэтому в САПР преимущественно используются алгоритмические моде­ли. В этом параграфе изложен обобщенный подход к формированию алгоритмических моделей на макроуровне, справедливый для большинства приложений.

Исходными для формирования математических моделей объектов на макроуровне являются компонентные и топологические уравнения.

Компонентными уравнениями называют уравнения, описывающие свойства элементов (компонентов), другими словами, это уравнения математических моделей элементов (ММЭ).

Топологические уравнения описывают взаимосвязи в составе моделируемой системы.

В совокупности компонентные и топологические уравнения конкретной физической системы представляют собой исходную математическую модель системы (ММС).

Очевидно, что компонентные и топологические уравнения в системах различной физической природы отражают разные физические свойства, но могут иметь одинаковый формальный вид. Одинаковая форма записи математических соотношений позволяет говорить о формальных аналогиях компонентных и топологических уравнений. Такие аналогии существуют для механических поступательных, механических вращательных, электрических, гидравлических (пневматических), тепловых объектов. Наличие аналогий приводит к практически важному выводу: значительная часть алгоритмов формирования и исследования моделей в САПР оказывается инвариантной и может быть применена к анализу проектируемых объектов в разных предметных областях. Единство математического аппарата формирования ММС особенно удобно при анализе систем, состоящих из физически разнородных подсистем.

В перечисленных выше приложениях компонентные уравнения имеют вид:

и топологические уравнения

Различают фазовые переменные двух типов, их обобщенные наименования – фазовые переменные типа потенциала (например, электрическое напряжение) и типа потока (например, электрический ток). Каждое компонентное уравнение характеризует связи между разнотипными фазовыми переменными, относящимися к одному компоненту (например, закон Ома описывает связь между напряжением и током в резисторе), а топологическое уравнение – связи между однотипными фазовыми переменными в разных компонентах.

Модели можно представлять в виде систем уравнений или в графической форме, если между этими формами установлено взаимно однозначное соответствие. В качестве графической формы часто используют эквивалентные схемы.

Примеры компонентных и топологических уравнений.Рассмотрим несколько типов систем.

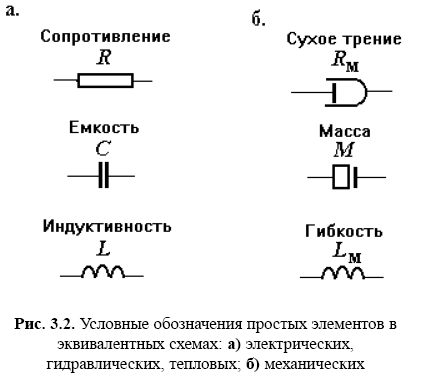
Электрические системы. В электрических системах фазовыми переменными являются электрические напряжения и токи. Компонентами систем могут быть простые двухполюсные элементы и более сложные двух- и многополюсные компоненты. К простым двухполюсникам относятся следующие элементы: сопротивление, емкость и индуктивность, характеризуемые одноименными параметрами R, С, L. В эквивалентных схемах эти элементы обозначают в соответствии с рис. 3.2,а.

Компонентные уравнения простых двухполюсников:

для R: u = i R (закон Ома), (3.3)

для C: i = C du/dt, (3.4)

для L: u = L di/dt, (3.5)

где и – напряжение (точнее, падение напряжения на двухполюснике), i – ток.

Эти модели лежат в основе моделей других возможных более сложных компонентов. Большая сложность может определяться нелинейностью уравнений (3.3) – (3.5) (т.е. зависимостью R, С, L от фазовых переменных), или учетом зависимостей параметров R, С, L от температуры, или наличием более двух полюсов. Однако многополюсные компоненты могут быть сведены к совокупности взаимосвязанных простых элементов.

Топологические уравнения выражают законы Кирхгофа для напряжений (ЗНК) и токов (ЗТК). Согласно ЗНК, сумма напряжений на компонентах вдоль любого замкнутого контура в эквивалентной схеме равна нулю, а в соответствии с ЗТК сумма токов в любом замкнутом сечении эквивалентной схемы равна нулю:

где Кр – множество номеров элементов р-гоконтура, J_q – множество номеров элементов, входящих в q-есечение.

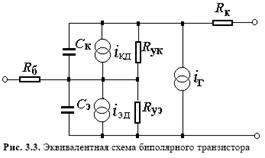
Примером ММ сложного компонента может служить модель транзистора. На рис. 3.3 представлена эквивалентная схема биполярного транзистора, на которой зависимые от напряжений источники тока i_эд = i_тэехр(u_э/(mφ_T)) и i_кд = i_ткехр(u_к/(mφ_T)) отображают статические вольтамперные характеристики p-n переходов, i_тэ и i_тк – тепловые токи переходов, mφ_T – температурный потенциал, и_э и и_к_ напряжения на эмиттерном и коллекторном переходах, С_э и С_к – емкости переходов, R_уэ и R_ук – сопротивления утечки переходов, R₆ и R_K – объемные сопротивления тел базы и коллектора, i_г = Bi_эд– B_иi_кд _источник тока, моделирующий усилительные свойства транзистора, В и В_и – прямой и инверсный коэффициенты усиления тока базы. Здесь и_э, и_к, i_эд, i_кд, i_г– фазовые переменные, а остальные величины – параметры модели транзистора.

Механические системы. Фазовыми переменными в механических поступательных системах являются силы и скорости. Используют одну из двух возможных электромеханических аналогий. В дальнейшем будем использовать ту из них, в которой скорость относят к фазовым переменным типа потенциала, а силу считают фазовой переменной типа потока. Учитывая формальный характер подобных аналогий, в равной мере можно применять и противоположную терминологию.

Компонентное уравнение, характеризующее инерционные свойства тел, в силу второго закона Ньютона имеет вид

F= M du/dt (3.8)

где F – сила; M – масса; u – поступательная скорость.

Упругие свойства тел описываются компонентным уравнением, которое можно получить из уравнения закона Гука. В одномерном случае (если рассматриваются продольные деформации упругого стержня)

где G – механическое напряжение; Е – модуль упругости; ε = Δl/l – относительная деформация; Δl – изменение длины l упругого тела под воздействием G. Учитывая, что G = F/S, где F – сила, S – площадь поперечного сечения тела, и дифференцируя (3.9), имеем

где g =(SE/l)- жесткость (величину, обратную жесткости, называют гибкостью L_M); и = d(Δl)/dt – скорость.

Диссипативные свойства в механических системах твердых тел выражаются соотношениями, характеризующими связь между силой трения и скоростью взаимного перемещения трущихся тел, причем в этих соотношениях производные сил или скоростей не фигурируют, как и в случае описания с помощью закона Ома диссипативных свойств в электрических системах.

Топологические уравнения характеризуют, во-первых, закон равновесия сил: сумма сил, приложенных к телу, включая силу инерции, равна нулю (принцип Даламбера), во-вторых, закон скоростей, согласно которому сумма относительной, переносной и абсолютной скоростей равна нулю.

В механических вращательных системах справедливы компонентные и топологические уравнения поступательных систем с заменой поступательных скоростей на угловые, сил – на вращательные моменты, масс – на моменты инерции, жесткостей – на вращательные жесткости.

Условные обозначения простых элементов механической системы показаны на рис. 3.2,б.

Нетрудно заметить наличие аналогий между электрической и механической системами. Так, токам и напряжениям в первой из них соответствуют силы (либо моменты) и скорости механической системы, компонентным уравнениям (3.4) и (3.5) и фигурирующим в них параметрам С и L, – уравнения (3.8) и (3.10) и параметры М и L_M, очевидна аналогия и между топологическими уравнениями. Далее параметры С и М будем называть емкостными (емкостного типа), параметры L и L_M – индуктивными (индуктивного типа), а параметры R и R_тр = 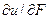– резистивными (резистивного типа).

Имеется и существенное отличие в моделировании электрических и механических систем: первые из них одномерны, а процессы во вторых часто приходится рассматривать в двух- (2D) или трехмерном (3D) пространстве. Следовательно, при моделировании механических систем в общем случае в пространстве 3D нужно использовать векторное представление фазовых переменных, каждая из которых имеет шесть составляющих, соответствующих шести степеням свободы.

Однако отмеченные выше аналогии остаются справедливыми, если их относить к проекциям сил и скоростей на каждую пространственную ось, а при графическом представлении моделей использовать шесть эквивалентных схем – три для поступательных составляющих и три для вращательных.

Гидравлические системы. Фазовыми переменными в гидравлических системах являются расходы и давления. Как и в предыдущем случае, компонентные уравнения описывают свойства жидкости рассеивать или накапливать энергию.

Рассмотрим компонентные уравнения для жидкости на линейном участке трубопровода длиной Δl и воспользуемся уравнением Навье-Стокса в следующей его форме (для ламинарного течения жидкости)

где р – плотность жидкости; U– скорость; Р – давление; а – коэффициент линеаризованного вязкого трения. Так как U = Q/S, где Q – объемный расход; S – площадь поперечного сечения трубопровода, то, заменяя пространственную производную отношением конечных разностей, имеем

,

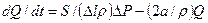
где ΔР – падение давления на рассматриваемом участке трубопровода. L_г= Δlρ/S – гидравлическая индуктивность, отражающая инерционные свойства жидкости, R_г= 2a/ρ – гидравлическое сопротивление, отражающее вязкое трение.

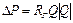
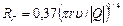
Примечание.В трубопроводе круглого сечения радиусом r удобно использовать выражение для гидравлического сопротивления при ламинарном течении: R_г = δυΔl/πr 4 ), где υ – кинематическая вязкость; в случае турбулентного характера течения жидкости компонентное уравнение для вязкого трения имеет вид при .

Интерпретация уравнения (3.11) приводит к эквивалентной схеме рис. 3.4.

Явление сжимаемости жидкости описывается компонентным уравнением, вытекающим из закона Гука

Дифференцируя (3.12) и учитывая, что объемный расход Q связан со скоростью U= d(Δl)/dt соотношением Q = U S, получаем

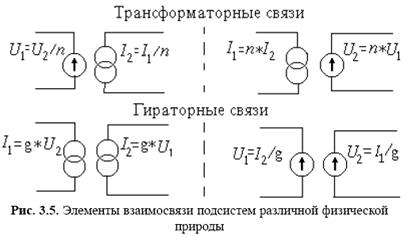
Связь подсистем различной физической природы. Используют следующие способы моделирования взаимосвязей подсистем: с помощью трансформаторной, гираторной связей и с помощью зависимости параметров компонентов одной подсистемы от фазовых переменных другой. В эквивалентных схемах трансформаторные и гираторные связи представлены зависимыми источниками фазовых переменных, показанными на рис. 3.5. На этом рисунке k и п – коэффициенты трансформации; g – передаточная проводимость; U_j и I_j ,- фазовые переменные в j-й цепи; j=1 соответствует первичной, а j=2 – вторичной цепи.

Представление топологических уравнений.Известен ряд методов формирования ММС на макроуровне. Получаемые с их помощью модели различаются ориентацией на те или иные численные методы решения и набором базисных, переменных, т.е. фазовых переменных, остающихся в уравнениях итоговой ММС. Общим для всех методов является исходная совокупность топологических и компонентных уравнений (3.1)-(3.2).

При записи топологических уравнений удобно использовать промежуточную графическую форму – представление модели в виде эквивалентной схемы, состоящей из двухполюсных элементов. Общность подхода при этом сохраняется, так как любой многополюсный компонент можно заменить подсхемой из двухполюсников. В свою очередь эквивалентную схему можно рассматривать как направленный граф, дуги которого соответствуют ветвям схемы. Направления потоков в ветвях выбираются произвольно (если реальное направление при моделировании окажется противоположным, то это приведет лишь к отрицательным численным значениям потока).

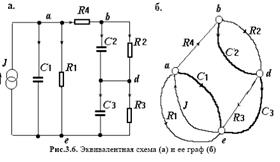
Примернекоторой простой эквивалентной схемы и соответствующего ей графа приведен на рис. 3.6. Для конкретности и простоты изложения на рис. 3.6 использованы условные обозначения, характерные для электрических эквивалентных схем, по той же причине далее в этом параграфе часто применяется электрическая терминология. Очевидно, что поясненные выше аналогии позволяют при необходимости легко перейти к обозначениям и терминам, привычным для механиков.

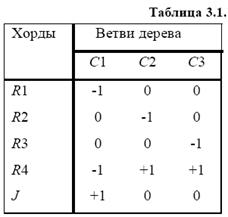
Для получения топологических уравнений все ветви эквивалентной схемы разделяют на подмножества хорд и ветвей дерева. Имеется в виду покрывающее (фундаментальное) дерево, т.е. подмножество из (β-1 дуг, не образующее ни одного замкнутого контура, где β – число вершин графа (узлов эквивалентной схемы). На рис. 3.6,б показан граф эквивалентной схемы рис. 3.6,а, толстыми линиями выделено одно из возможных покрывающих деревьев.

Выбор дерева однозначно определяет вектора напряжений U_x и токов I_x хорд, напряжений U_вд и токов I_вд ветвей дерева и приводит к записи топологических уравнений в виде

где М– матрица контуров и сечений, М Т – транспонированная М-матрица.

В М-матрице число строк соответствует числу хорд, число столбцов равно числу ветвей дерева. М-матрица формируется следующим образом. Поочередно к дереву подключаются хорды. Если при подключении к дереву р-й хорды q-я ветвь входит в образовавшийся контур, то элемент M_pq матрицы равен +1 при совпадении направлений ветви и подключенной хорды, M_pq= -1 при несовпадении направлений. В противном случае M_pq = 0.

Для схемы на рис. 3.6 М-матрица представлена в виде табл. 3.1

Особенности эквивалентных схем механических объектов.Для каждой степени свободы строят свою эквивалентную схему. Каждому телу с учитываемой массой соответствует узел схемы (вершина графа). Один узел, называемый базовым, отводится телу, отождествляемому с инерциальной системой отсчета.

Каждый элемент массы изображают ветвью, соединяющей узел соответствующего массе тела с базовым узлом; каждый элемент упругости – ветвью, соединяющей узлы тел, связанных упругой связью; каждый элемент трения – ветвью, соединяющей узлы трущихся тел. Внешние воздействия моделируются источниками сил i

В качестве примера на рис. 3.7,а изображена некоторая механическая система – тележка, движущаяся по дороге и состоящая из платформы А, колес В1, В2 и рессор С1, C2. На рис. 3.7,б приведена эквивалентная схема для вертикальных составляющих сил и скоростей, на которой телам системы соответствуют одноименные узлы, учитываются массы платформы и колес, упругость рессор, трение между колесами и дорогой; неровности дороги вызывают воздействие на систему, изображенное на рис. 3.7,б источниками силы.

Характеристика методов формирования ММС.Исходную систему компонентных и топологических уравнений (3.1) и (3.2) можно рассматривать как окончательную ММС, которая и подлежит численному решению. Численное решение этой системы уравнений предполагает алгебраизацию дифференциальных уравнений, например, с помощью преобразования Лапласа или формул численного интегрирования. В программах анализа нелинейных объектов на макроуровне, как правило, применяются формулы численного интегрирования, примером которых может служить неявная формула Эйлера

где V_i— – значение переменной V на i-м шаге интегрирования; h_n= t_n– t_n-1 – шаг интегрирования. Алгебраизация подразумевает предварительную дискретизацию независимой переменной t (вместо непрерывной переменной t получаем конечное множество значений t_n), она заключается в представлении ММС в виде системы уравнений

с неизвестными V_n и Z_n, где использовано обозначение Z = dV/dt. Эту систему алгебраических уравнений, в общем случае нелинейных, необходимо решать на каждом шаге численного интегрирования исходных дифференциальных уравнений.

Однако порядок этой системы довольно высок и примерно равен 2α+γ, где α – число ветвей эквивалентной схемы (каждая ветвь дает две неизвестные величины – фазовые переменные типа потока и типа потенциала, за исключением ветвей внешних источников, у каждой из которых неизвестна лишь одна фазовая переменная), γ – число элементов в векторе производных. Чтобы снизить порядок системы уравнений и тем самым повысить вычислительную эффективность ММС, желательно выполнить предварительное преобразование модели (в символическом виде) перед ее многошаговым численным решением. Предварительное преобразование сводится к исключению из системы части неизвестных и соответствующего числа уравнений. Оставшиеся неизвестные называют базисными. В зависимости от набора базисных неизвестных различают несколько методов формирования ММС.

Согласно методу переменных состояния (более полное название метода – метод переменных, характеризующих состояние), вектор базисных переменных W состоит из переменных состояния. Этот вектор включает неизбыточное множество переменных, характеризующих накопленную в системе энергию. Например, такими переменными могут быть скорости тел (кинетическая энергия определяется скоростью, так как равна Ми 2 /2), емкостные напряжения, индуктивные токи и т.п. Очевидно, что число уравнений не превышает γ. Кроме того, итоговая форма ММС оказывается приближенной к явной форме представления системы дифференциальных уравнений, т.е. к форме, в которой вектор dW/dt явно выражен через вектор W, что упрощает дальнейшее применение явных методов численного интегрирования. Метод реализуется путем особого выбора системы хорд и ветвей дерева при формировании топологических уравнений. Поскольку явные методы численного интегрирования дифференциальных уравнений не нашли широкого применения в программах анализа, то метод переменных состояния также теряет актуальность и его применение оказывается довольно редким.

В классическом варианте узлового метода в качестве базисных переменных используются узловые потенциалы (т.е. скорости тел относительно инерциальной системы отсчета, абсолютные температуры, перепады давления между моделируемой и внешней средой, электрические потенциалы относительно базового узла). Число узловых потенциалов и соответственно уравнений в ММС оказывается равным β-1, где β – число узлов в эквивалентной схеме. Обычно β заметно меньше α и, следовательно, порядок системы уравнений в ММС снижен более чем в два раза по сравнению с поряд­ком исходной системы.

Однако классический вариант узлового метода имеет ограничения на применение и потому в современных программах анализа наибольшее распространение получил модифицированный узловой метод.

Узловой метод. Матрицу контуров и сечений М в узловом методе формируют следующим образом. Выбирают базовый узел эквивалентной схемы и каждый из остальных узлов соединяют с базовым фиктивной ветвью. Именно фиктивные ветви принимают в качестве ветвей дерева, а все реальные ветви оказываются в числе хорд. Поскольку токи фиктивных ветвей равны нулю, а вектор напряжений фиктивных ветвей есть вектор узловых потенциалов φ, то уравнения (3.13) и (3.14) принимают вид

U + Mφ = 0 (3.16)

M T I = 0 (3.17)

где U и I- векторы напряжений и токов реальных ветвей.

Компонентные уравнения алгебраизуются с помощью одной из формул численного интегрирования, линеаризуются с помощью разложения в ряд Тейлора с сохранением только линейных членов, и их представляют в виде

где G_n – диагональная матрица проводимостей, рассчитанная в точке t_n; A_n – вектор, зависящий от значений фазовых переменных на предшествующих шагах интегрирования и потому уже известный к моменту времени t_n. Каждая ветвь (за исключением идеальных источников напряжения) имеет проводимость, которая занимает одну из диагональных клеток матрицы проводимостей. Окончательно ММС получаем, подставляя (3.18) и затем (3.16) в (3.17):

M T I_n=M T (G_nU_n + A_n) =-M T G_nMφ_n +M T A_n = 0

где Я_n=М Т G_nM – матрица Якоби, В_n = М Т А_n – вектор правых частей. Отметим, что матрица М имеет размер равен α×(β-1), матрица G_n –α×α, а матрица Якоби имеет размер – (β-1)×(β-1).

Система (3.19) является системой линейных алгебраических уравнений, полученной в результате дискретизации независимой переменной, алгебраизации дифференциальных уравнений и линеаризации алгебраических уравнений. Алгебраизация приводит к необходимости пошагового вычислительного процесса интегрирования, линеаризация – к выполнению итерационного вычислительного процесса на каждом шаге интегрирования.

Рассмотрим, каким образом определяются проводимости ветвей.

Для резистивных ветвей проводимость – величина, обратная сопротивлению R.

При использовании неявного метода Эйлера проводимость емкостной ветви получается из ее компонентного уравнения следующим образом.

На п-мшаге интегрирования

проводимость 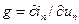и при С = const получаем

при этом в вектор правых частей входит элемент

Проводимость индуктивной ветви можно найти аналогично:

Аналогично определяют проводимости и при использовании других разностных формул численного интегрирования, общий вид которых

где μ_n зависит от шага интегрирования, η_n от значений вектора U на предыдущих шагах.

Классический вариант узлового метода имеет ограничения на применение. Так, недопустимы идеальные (с бесконечной проводимостью) источники напряжения, зависимые источники, аргументами которых являются токи, а также индуктивности, поскольку в классическом варианте токи не входят в число базисных переменных. Устранить эти ограничения довольно просто – нужно расширить совокупность базисных координат, включив в нее токи-аргументы зависимых источников, а также токи ветвей индуктивных и источников напряжения. Полученный вариант метода называют модифицированным узловым методом.

Согласно модифицированному узловому методу, в дерево при построении матрицы М включают ветви источников напряжения и затем фиктивные ветви. В результате матрица М принимает вид (табл. 3.2), где введены обозначения: U_ИCT(I) – источники напряжения, зависящие от тока; Е(t) – независимые источники напряжения; I_ИСТ(I) – источники тока, зависящие от тока; L – индуктивные ветви; M_ij— – подматрица контуров хорд группы i и сечений фиктивных ветвей группы j.

Те же обозначения U_ИCT, I, E, I_ИСТ будем использовать и для соответствующих векторов напряжений и токов. Назовем ветви, токи которых являются аргументами в выражениях для зависимых источников, т.е. входят в вектор I, особыми ветвями. Остальные ветви (за исключением индуктивных) – неособые. Введем также обозначения: I_L – вектор индуктивных токов; I_x и U_x. – векторы токов и напряжений неособых ветвей; G_x, G_L, G_I– диагональные матрицы проводимостей ветвей неособых, индуктивных, особых.

Уравнение закона токов Кирхгофа (3.17) для фиктивных ветвей имеет вид

Исключим вектор I_Х с помощью компонентного уравнения (3.18), а вектор I_ИСТ с помощью очевидного уравнения

I_ИСТ=KI

где 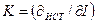– матрица передаточных коэффициентов источников тока. Используем также выражение (3.16), принимающее вид

Получаем систему из трёх матричных уравнений с неизвестными векторами φ,I, I_L:

; (3.20)

; (3.21)

, (3.22)

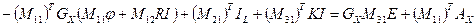
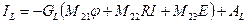
где обозначено 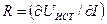. Эта система и является итоговой ММ в узловом модифицированном методе.

Замечания:

1. Вектор индуктивных токов нельзя исключить из итоговой системы уравнений, так как его значения входят в вектор A_L на последующих шагах численного интегрирования.

2. Источники тока, зависящие от напряжений, относятся к неособым ветвям, их проводимости входят в матрицу G_x, которая при этом может иметь недиагональный вид.

3. Источники напряжения, зависящие от напряжений, в приведенных выше выражениях не учитываются, при их наличии нужно в матрице М выделить столбец для этих ветвей, что приводит к появлению дополнительных слагаемых в правых частях уравнений (3.19) – (3.21).

Дата добавления: 2017-03-29 ; просмотров: 907 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ