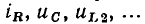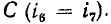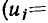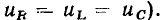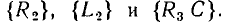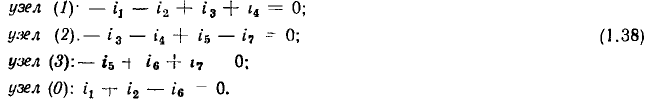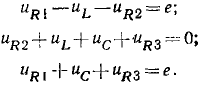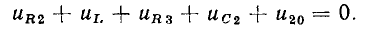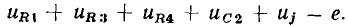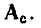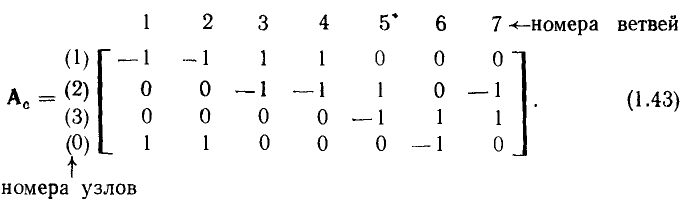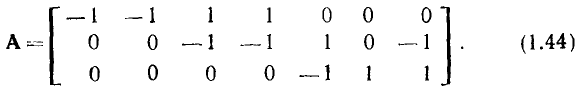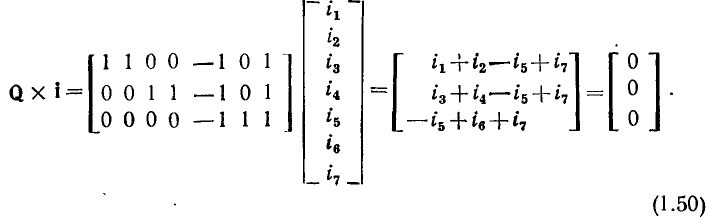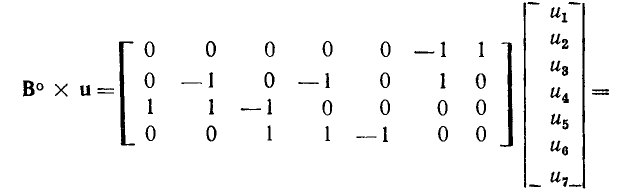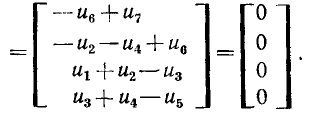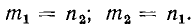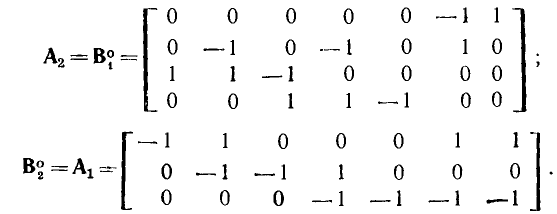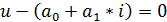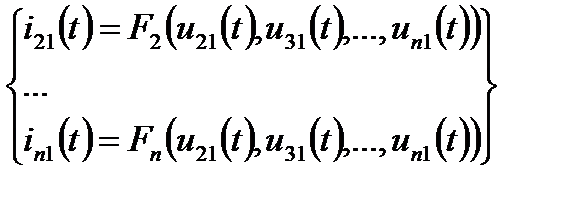Компонентные уравнения электрических цепей это

Топологии электрических цепей

Содержание:

Топология цепей:

Электрическая схема — это условное графическое изображение электрической цепи. В связи с тем что в теории цепей рассматривают исключительно эквивалентные схемы, в дальнейшем под термином «электрическая схема» или просто «схема» будем понимать именно эквивалентную схему электрической цепи. Схема электрической цепи определяет, таким образом, состав идеализированных активных и пассивных элементов моделирующей цепи, замещающей исследуемую цепь в рамках рассматриваемой задачи, параметры этих элементов и способ их соединения между собой.

Помимо идеализированных активных и пассивных элементов на схемах электрических цепей изображаются также идеализированные вспомогательные элементы: выводы цепи или ее частей, соединительные проводники и элементы коммутации. К элементам коммутации относят элементы, позволяющие изменять количество идеализированных пассивных и активных элементов, их параметры или способ соединения (переключатели, ключи и т. д.). При построении моделирующих цепей и изображении их схем предполагается, что идеализированные вспомогательные элементы не способны запасать электрическую энергию или преобразовывать ее в другие виды энергии, т. е. они не обладают сопротивлением, емкостью или индуктивностью. Поэтому, если реальные вспомогательные элементы электрической цепи характеризуются паразитными параметрами (сопротивлением, емкостью или индуктивностью), значения которых существенны в рамках решаемой задачи, то эти элементы

следует представить их моделирующими цепями, составленными из идеализированных вспомогательных элементов и соответствующих идеализированных пассивных элементов.

Способ изображения .идеализированных активных, пассивных и вспомогательных элементов и их взаимное расположение на схеме не оказывают влияния на характер электрических процессов в исследуемой цепи.

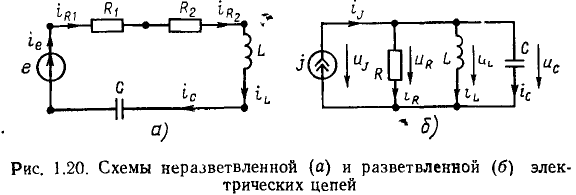
При необходимости на схеме указывают положительные направления токов и напряжений: для токов через внешние выводы цепи или через ее элементы — стрелками непосредственно на соединительных проводниках или выводах (рис. 1.20); для напряжений на отдельных элементах или участках цепи — стрелками между выводами соответствующих элементов или участков цепи (рис. 1.20, б). Положительные направления напряжений на пассивных элементах, а также на идеализированных активных элементах на схемах, как правило, не указывают.

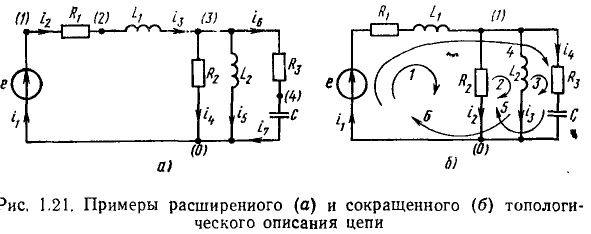
Рядом со стрелками, указывающими положительные направления токов или напряжений, проставляют их условные буквенные обозначения, например

Внешние выводы отдельных участков моделирующей цепи, по аналогии с внешними выводами реальных элементов электрической цепи, называют полюсами. В зависимости от числа полюсов участки Цепей делят на двухполюсники и многополюсники (трехполюсники, четырехполюсники, N-полюсники). Двухполюсник может состоять из одного или .нескольких идеализированных двух полюсных элементов (см., например, рис. 1.9—1.11) или может вообще не содержать идеализированных активных и пассивных элементов (например, короткозамыкающий двухполюсник или перемычка). Важное значение в теории цепей имеют многополюсники с четырьмя выводами — четырехполюсники (см. далее гл. 8). Отметим, что цепи, моделирующие реальные двухполюсные элементы, всегда являются двухполюсниками, в то время как цепи, моделирующие N-полюсные элементы, могут содержать менее чем N внешних выводов. Например, пятиэлектродным электронным лампам — пентодам, имеющим в зависимости от конструкции 5—7 внешних выводов, соответствуют схемы замещения по переменному току с 3—4 выводами.

В зависимости от характера соединения идеализированных двухполюсных элементов различают неразветвленные и разветвленные цепи. В неразветвленной цепи (рис. 1.20, а) через все элементы протекает один и тот же ток. В разветвленных цепях (рис. 1.20, б и рис. 1.21, а) токи через различные элементы могут быть неодинаковы.

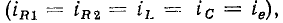
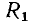
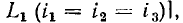
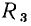
Соединение группы идеализированных двухполюсных элементов, при котором через них протекает один и тот же ток, называется последовательным. Например, в неразветвленной цепи, схема которой представлена на рис. 1.20, а, все элементы включены последовательно а в разветвленной цепи (рис. 1.21, а) имеется две группы последовательно включенных элементов [источник напряжения е, сопротивление и индуктивность а также сопротивление и емкость

Соединение группы двухполюсных элементов, при котором все элементы находятся под одним и тем же напряжением, называется параллельным. Так, в разветвленной цепи, схема которой приведена на рис. 1.20, б, все элементы включены параллельно

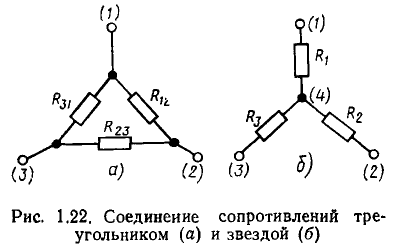
Комбинация последовательного и параллельного соединений элементов называется смешанным соединением (рис. 1.21, а). В ряде случаев соединение между входящими в цепь элементами не может быть отнесено ни к последовательному, ни к параллельному, ни к смешанному. К числу таких соединений относятся соединения треугольником (рис. 1.22, а) и звездой (рис. 1.22, б), которые являются частными случаями соединения N-угольником (рис. 1.23, а) и N-лучевой звездой (рис. 1.23, б). Характер соединения между идеализированными элементами цепи определяет ее топологические (структурные) свойства, для описания которых используют понятия ветви, узла и контура.

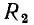
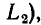
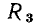
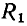
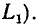
Ветвь представляет собой участок электрической цепи, вдоль которого протекает один и тот же ток. Она может состоять из одного или нескольких последовательно полюсных элементов. Например, в электрической цепи, схема которой приведена на рис. 1.21, б, можно выделить ветви, составленные из одного (ветви, содержащие сопротивление или индуктивность двух (ветвь, содержащая сопротивление и емкость С) и трех элементов (ветвь с источником напряжения е, сопротивлением и индуктивностью Так как каждую ветвь можно рассматривать как двухполюсник, то соединения ветвей можно характеризовать теми же терминами, что и соединения идеализированных двухполюсных элементов (параллельное, последовательное и т. д.). Например, электрическую цепь, схема которой изображена на рис. 1.21, б, можно рассматривать как параллельное соединение четырех ветвей:

Место соединения ветвей называется у злом, причем место соединения двух ветвей называют устранимым узлом (при соединении двух ветвей текущие через них токи имеют одинаковые значения, поэтому две такие ветви могут быть заменены одной).

Иногда, в частности при автоматизированном составлении уравнений, описывающих процессы в электрических цепях, бывает удобно рассматривать каждый из идеализированных двухполюсных элементов, входящих в моделирующую цепь, в качестве отдельной ветви, при этом необходимо принимать во внимание все узлы, в том числе и устранимые. Будем называть такое топологическое описание цепи расширенным (см. рис. 1.21, а). При сокращенном топологическом описании цепи (см. рис. 1.21,5) группы последовательно включенных элементов рассматриваются в качестве отдельных ветвей и устранимые узлы во внимание не принимаются; таким образом, количество ветвей и, следовательно, количество рассматриваемых токов уменьшается (в нашем случае с 7 до 4).

Ветви электрической цепи нумеруют арабскими цифрами, начиная с единицы. Номера ветвей удобно выбирать совпадающими с номерами соответствующих токов, в этом случае номера ветвей на схеме можно не указывать. Узлы электрической цепи нумеруют, начиная с нуля. Порядок нумерации узлов значения не имеет, однако номер «0» удобно присваивать заземленному узлу или узлу, к которому сходится наибольшее число ветвей. Номера узлов условимся обозначать арабскими цифрами в круглых скобках, проставленными около соответствующего узла.

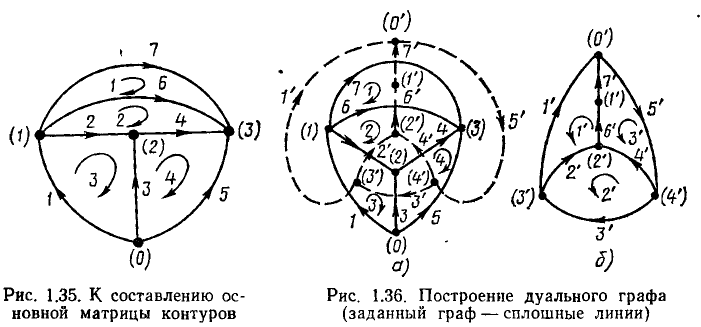
Любой замкнутый путь, проходящий по нескольким ветвям цепи, называется контуром. Например, в электрической цепи, схема которой приведена на рис. 1.21, б можно выделить шесть контуров, образованных ветвями <1,2>, <2,3>, <3,4>, <1,4>, <2,4>и <1,3>. Неразветвленная цепь (см. рис. 1.20, а) содержит только один контур.

Контур характеризуют направлением обхода (порядком перечисленных ветвей), причем каждая ветвь и каждый узел, входящие в контур, проходятся только один раз. Направление обхода контура выбирают произвольно и указывают изогнутой стрелкой (см. рис. 1.21, б).

В отличие от электрических элементов моделирующих цепей ветви, узлы и контуры называются топологическими элементами. Степень сложности исследования процессов в электрических цепях во многом определяется числом топологических элементов. В зависимости от их числа различают простейшие и сложные цепи. К простейшим цепям относятся одноконтурная (например, см. рис. 1.20, а) и двухузловая (например, см. рис. 1.20, б) цепи, к сложным— цепи с числом узлов более двух и числом контуров более одного.

Понятие о компонентных и топологических уравнениях. Законы Кирхгофа

Математическое описание процессов в электрических цепях базируется на уравнениях двух типов: компонентных и топологических.

Компонентные уравнения (уравнения ветвей) устанавливают связь между током и напряжением каждой ветви. Количество таких уравнений равно числу ветвей, а вид каждого из них зависит только от состава ветви, т. е. от входящих в ее состав идеализированных двухполюсных элементов. При расширенном топологическом описании число ветвей и, следовательно, количество компонентных уравнений равны числу идеализированных двухполюсных элементов, а компонентные уравнения имеют наиболее простой вид — они вырождаются в рассмотренные ранее уравнения, связывающие между собой ток и напряжение на зажимах идеализированных активных и пассивных элементов. Таким образом, уравнения, составленные на основании закона Ома (1.9), (1.10), представляют собой компонентные уравнения для ветви, содержащей один идеализированный пассивный элемент — сопротивление. При сокращенном топологическом описании количество компонентных уравнений уменьшается в соответствии с уменьшением числа ветвей, но сами уравнения имеют более сложный вид.

Топологические уравнения отражают свойства цепи, которые определяются только ее топологией и не зависят от того, какие электрические элементы входят в состав ветвей. К топологическим уравнениям относятся, в частности, уравнения, составленные на основании первого и второго законов Кирхгофа.

Первый закон Кирхгофа устанавливает связь между токами ветвей в каждом из узлов цепи: алгебраическая сумма мгновенных значений токов всех ветвей, подключенных к каждому из узлов моделирующей цепи, в любой момент времени равна нулю.

В соответствии с первым законом Кирхгофа для каждого из узлов идеализированной цепи (как при расширенном, так и при сокращенном топологическом описании) может быть составлено уравнение баланса токов в узле

где k — номер ветви, подключенной к рассматриваемому узлу. Суммирование токов производится с учетом выбранных положительных направлений: всем токам, одинаково ориентированным относительно узла, приписывается одинаковый знак. Условимся токи, направленные от узла, брать со знаком плюс, а токи, направленные к узлу, — со знаком минус. Такой выбор не носит принципиального характера, а сделан только для удобства последующего изложения, поскольку изменение знаков, приписанных токам, соответствовало бы умножению правой и левой частей (1.37) на —1. Токи ветвей, в которых содержатся управляемые или неуправляемые источники тока и напряжения, учитываются в уравнении (1.37) наравне с токами других ветвей.

Пример 1.1.

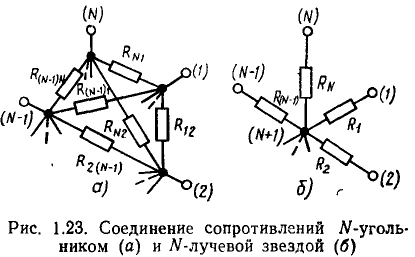
Составим уравнения баланса токов для всх узлов цепи, схема которой изображена на рис. 1.24,а:

Если сгруппировать токи, направленные к узлу и перенести их в правую часть уравнения (1.37), а в левой части оставить токи, направленные от узла, то первый закон Кирхгофа можно сформулировать таким образом: сумма мгновенных значений токов, направленных к любому узлу цепи, в любой момент времени равна сумме токов, вытекающих из этого узла. Первый закон Кирхгофа является следствием закона сохранения заряда (уравнения непрерывности) и отражает тот факт, что в узлах идеализированной электрической цепи заряды не накапливаются и не расходуются.

На основании первого закона Кирхгофа можно составить уравнение баланса токов и для так называемого обобщенного узла, который представляет собой часть моделирующей цепи, охваченную произвольной замкнутой поверхностью. В этом случае в уравнении <1.37) алгебраически суммируются токи всех ветвей, входящих в

обобщенный узел, т. е. токи всех ветвей, пересекаемых указанной замкнутой поверхностью. Так, для обобщенного узла, выделенного пунктирной линией на рис. 1.24, а, уравнение баланса токов

Нетрудно убедиться, что уравнение (1.39) вытекает из уравнения (1.38).

Второй закон Кирхгофа устанавливает связь между напряжениями ветвей, входящих в произвольный контур: алгебраическая сумма мгновенных значений напряжений всех ветвей, входящих в любой контур-моделирующей цепи, в каждый момент времени равна нулю.

В соответствии со вторым законом Кирхгофа для каждого контура можно составить уравнения баланса напряжений ветвей

где k—номера ветвей, входящих в рассматриваемый контур. Суммирование напряжений производится с учетом их положительных направлений и выбранного направления обхода контура. Если положительное направление напряжения ветви совпадает с направлением обхода контура, то оно входит в (1.40) со знаком плюс, в противном случае— со знаком минус. Изменение направления обхода контура, очевидно, соответствует умножению левой и правой частей (1.40) на —1.

Пример 1.2.

Составим уравнения баланса напряжений ветвей для всех контуров цепи, схема которой приведена на рис. 1.24, б (номера напряжений ветвей совпадают с номерами соответствующих токов):

Уравнения по второму закону Кирхгофа можно составить не только для напряжений ветвей, но и для напряжений элементов, входящих в ветви каждого контура. Представляя напряжение каждой ветви в виде суммы напряжений элементов этой ветви и принимая во внимание, что положительное направление напряжения источника э. д. с. противоположно направлению э. д. с., систему уравнений (1.40) можно преобразовать к следующему виду:

Здесь — напряжения каждого из элементов рассматриваемого контура, за исключением напряжений источников э. д. с.; 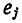— э. д. с. источников напряжения, действующих в контуре.

Используя (1.42), можно несколько видоизменить формулировку второго закона Кирхгофа: алгебраическая сумма мгновенных значений напряжений на элементах любого контура моделирующей цепи в каждый момент времени равна алгебраической сумме мгновенных значений э. д. с. источников напряжения, действующих в этом контуре. Напряжения на элементах контура и э. д. с. источников напряжения входят в (1.42) со знаком плюс, если положительные направления напряжений на элементах и направления э. д. с. источников напряжения совпадают с направлением обхода контура. В противном случае соответствующие слагаемые в (1.42) берутся со знаком минус.

Пример 1.3.

Запишем уравнения баланса напряжений на элементах всех контуров цепи (рис. 1.24. б):

Второй закон Кирхгофа является следствием закона сохранения энергии и отражает тот факт, что энергия, затраченная сторонними силами на перенос произвольного заряда внутри источников, входящих в контур, равна энергии, затрачиваемой источниками на перенос этого заряда через пассивные элементы контура.

Следует подчеркнуть, что закон сохранения энергии выполняется при переносе заряда по любому замкнутому пути (не обязательно полностью проходящему через ветви цепи). 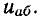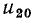Поэтому уравнения по второму закону Кирхгофа можно составить для любой совокупности элементов, образующих путь для электрического тока от произвольно выбранного узла (а) электрической цепи к узлу (б) с учетом напряжения между конечными точками этого пути Например, для ветвей 3 и 2 (рис. 1.24, а), образующих путь для электрического тока между узлами (2) и (0) электрической цепи, уравнение по второму закону Кирхгофа с учетом напряжения между этими узлами запишется в виде

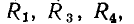
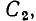
Для контуров, в которых есть источники тока, уравнения баланса напряжений составляют по общему правилу, причем напряжение на источнике тока учитывается в левой части уравнения (1.42). Так, для контура, образованного ветвями с сопротивлениями емкостью источником напряжения е и источником тока j (рис. 1.24, а), уравнение баланса напряжений

Так как вид и число уравнений, составленных на основании законов Кирхгофа, не зависят от того, какие элементы входят в состав цепи, а определяются только ее топологическими особенностями, то уравнения баланса токов и напряжений можно применять для математического описания процессов в моделирующих цепях, составленных из двухполюсных элементов любого типа (как линейных, так и нелинейных) при любой форме токов и напряжений независимых источников.

Очевидно, что количество уравнений баланса токов и напряжений равно сумме числа узлов и числа контуров исследуемой цепи. Можно убедиться, что не все из составленных уравнений будут линейно независимыми. Например, любое из четырех уравнений (1.38) может быть получено как линейная комбинация из трех других уравнений: так, уравнение для узла (0) можно получить суммируя уравнения, составленные для узлов (1), (2), (3), и умножая правую и левую части полученного уравнения на —1. Аналогично уравнения (1.41) не являются линейно независимыми.

В то же время на основании законов Кирхгофа для каждой цепи можно составить несколько различных систем линейно независимых топологических уравнений. Например, любые три уравнения из (1.38) и любые два уравнения из (1.41) образуют систему линейно независимых у равнений.

Будем называть системой независимых узлов и системой независимых контуров любые совокупности узлов и контуров цепи, для которых можно составить системы линейно независимых уравнений по законам Кирхгофа. Определение числа независимых узлов и контуров, а также выделение систем соответствующих узлов и контуров являются основными задачами топологии цепей.

Топологические графы электрических цепей

В общем случае граф есть совокупность отрезков произвольной длины и формы, называемых ветвями (ребрами), и точек их соединения, называемых узлами (вершинами). В теории электрических цепей в основном находят применение направленные, или ориентированные, графы, у которых каждому ребру приписывается определенное направление, указываемое стрелкой. Различают направленные топологические графы и направленные графы прохождения сигналов. Направленный топологический граф является упрощенной моделью электрической цепи, отражающей только ее топологические (структурные) свойства. Направленный граф прохождения сигналов представляет собой наглядное графическое изображение системы уравнений, описывающей процессы в электрической цепи. В дальнейшем будем называть направленный граф прохождения сигналов сигнальным графом, а направленный топологический граф просто графом цепи.

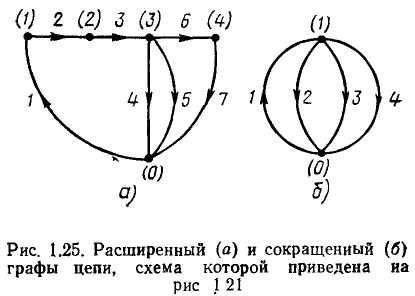
Граф электрической цепи строят по ее эквивалентной схеме. Каждую ветвь цепи заменяют при этом отрезком произвольной длины и формы — ветвью графа, а каждый узел цепи преобразуют в узел графа. На ветвях графа стрелками указывают их направления, которые совпадают с положительным направлением токов, протекающих по соответствующим ветвям цепи. Нумерация ветвей и узлов графа таже, что и нумерация ветвей и узлов схемы. Расширенному топологическому описанию цепи (см. рис. 1.21, а) соответствует расширенный граф цепи (рис. 1.25, а), сокращенному топологическому описанию (см. рис. 1.21,6) — сокращенный (рис. 1.25,6).

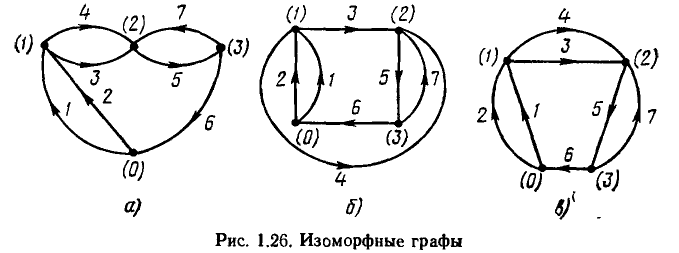
Свойства графа не зависят от формы и длины ветвей, а также от взаимного расположения узлов графа на плоскости и определяются только числом ветвей р, числом узлов q и способом соединения ветвей между собой. Графы, имеющие одинаковые количества узлов и ветвей, соединенных между собой одинаковым образом, называются изоморфными (рис. 1.26). Изменяя длину и форму ветвей, а также взаимное расположение узлов графа на плоскости, можно получить бесчисленное множество графов, изоморфных исходному. Такие преобразования графа называются изоморфными преобразованиями. Каждый из вариантов изображения графа, полученный путем таких преобразований, называется его геометрической реализацией.

Если узел i является концом ветви j, то говорят, что они инцидентны (от англ, incidence — сфера действия, охват). Каждая ветвь графа инцидентна двум узлам. Часть графа, которая наряду с некоторым подмножеством ветвей графа содержит и все инцидентные им узлы, называется подграфом.

Степенью узла называется число ветвей графа, инцидентных данному узлу. На рис. 1.25, а узлы (1) и (4) имеют вторую степень, узлы (0) и (3) — четвертую.

Графы, изоморфные с точностью до узлов второй степени, называются гомеоморфными. После удаления из гомеоморфных графов узлов второй степени и объединения инцидентных этим вершинам ветвей гомеоморфные графы становятся изоморфными. Таким образом,

графы соответствующий расширенному и сокращенному топологическому описанию цепи, являются гомеоморфными. Примером гомеоморфных графов являются графы, изображенные на рис. 1.25.

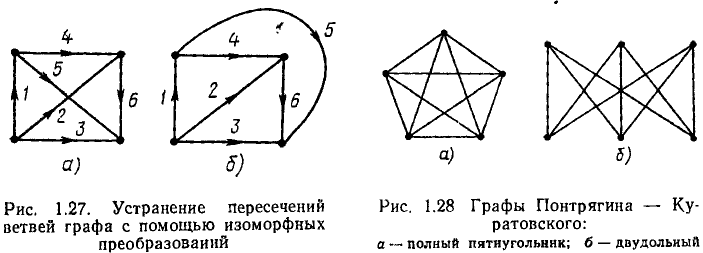
Планарным (плоским) называется такой граф, который в результате изоморфных преобразований может быть изображен на плоскости без пересечения ветвей. Так, граф, изображенный на рис. 1.27, а, содержит две пересекающиеся ветви, однако он является планарным, так как существует изоморфный ему граф, не имеющий пересечения ветвей (рис. 1.27, б). Можно убедиться, что все графы, содержащие не более четырех узлов, являются планарными.

Непланарный (объемный) граф не может быть изображен на плоскости без пересечения ветвей (рис. 1.28). При удалении из представленных на рисунке графов любой ветви они становятся планарными. Полный пятиугольник и двудольный граф (рис. 1.28) называют также графами Понтрягина—Куратовского. Доказано, что произвольный граф является планарным тогда и только тогда, когда он не содержит подграфов, гомеоморфных одному из графов Понтрягина—Куратовского. Электрическая схема, которой соответствует планарный граф, также называется планарной. Непланарной схеме соответствует непланарный граф. Таким же образом вводятся понятия планарной и непланарной идеализированных электрических цепей.

Планарный граф делит плоскость, на которой он изображен, на внешнюю и внутренние области. Внутренние области, ограниченные ветвями графа, называются ячейками или окнами графа. Внешняя по отношению к графу часть плоскости называется базисной ячейкой.

Путь — это подграф, являющийся последовательностью соединенных между собой ветвей, выбранных таким образом, что каждому узлу (за исключением двух узлов, называемых граничными) инцидентны две ветви, а граничным узлам инцидентно по одной ветви (рис. 1.29). Каждая ветвь и каждый узел встречаются в пути только один раз.

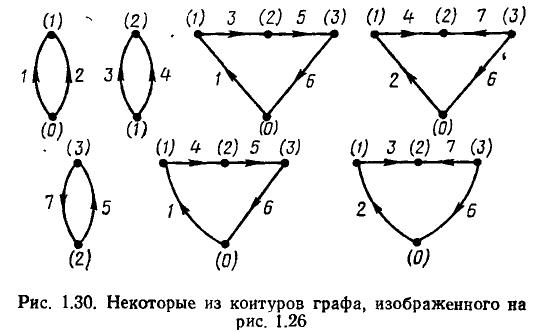
Замкнутый путь, т. е. путь, у которого начальные и конечные узлы совпадают, называется контуром (рис. 1.30). Каждому из узлов контура инцидентны две ветви. Очевидно, что между контурами графа и контурами исходной цепи существует взаимно однозначное соответствие.

Связный граф — это граф, между любыми двумя узлами которого существует, по крайней мере, один путь (см. рис. 1.25—1.28).

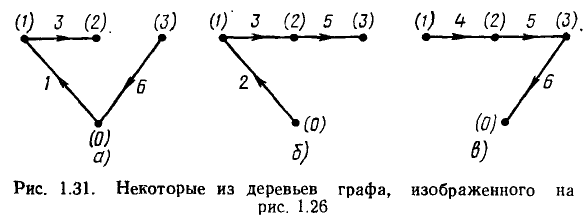
Деревом связного графа называется связный подграф, включающий все узлы графа, но не содержащий ни одного контура. Ветви графа, вошедшие в дерево, называются ветвями дерева; ветви, не вошедшие в дерево, называются связями (главными ветвями, хордами). Каждому графу может быть поставлено в соответствие несколько деревьев, отличающихся друг от друга составом ветвей дерева (рис. 1.31). Каждое из деревьев графа, содержащего р ветвей и q узлов, имеет 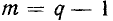ветвей дерева и

главных ветвей. При построении деревьев графов электрических це

пей в число ветвей дерева обязательно вносят ветви, соответствующие идеализированным источникам напряжения. Ветви графа, соответствующие ветвям цепи, содержащим идеализированные источники тока, в число ветвей дерева не включают.

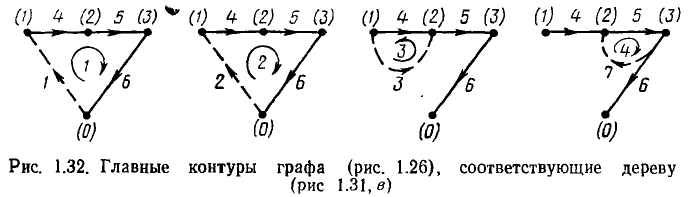
Добавление к дереву графа любой главной ветви образует контур. Контуры, образованные поочередным добавлением к дереву графа его главных ветвей, называются главными контурами (рис. 1.32). Таким образом, главный контур состоит из ветвей дерева и одной главной ветви.

Каждому дереву соответствует своя система из главных контуров, причем главные контуры, соответствующие определенному дереву, отличаются один от другого, по крайней мере, одной ветвью, а именно главной ветвью, входящей в каждый из главных контуров.

Каждому главному контуру обычно присваивают номер и приписывают ориентацию (направление обхода), совпадающие с номером и ориентацией соответствующей главной ветви.

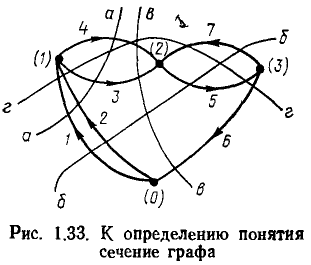
Сечением графа называется совокупность ветвей связного графа, пересекаемых замкнутой линией (линией сечения) или замкнутой поверхностью (поверхностью сечения), разделяющей граф на две части, причем ни одна из ветвей графа не пересекается дважды. Если удалить из связного графа ветви, образующие сечения, он распадается на две части, одна из которых может быть изолированным узлом.

Каждую из частей графа, лежащую по одну из сторон линии (поверхности) сечения можно рассматривать как обобщенный узел. Так, совокупности ветвей <1, 2, 3, 4>, <1, 2, 5, 7>, <3, 4, 6>, пересекаемых линиями а, б, в соответственно (рис. 1.33), образуют сечения, потому что при удалении каждой из этих совокупностей ветвей граф распадается на две части. Ветви, пересекаемые линией г, не образуют сечения, так как при удалении этих граф распадается более чем на две части.

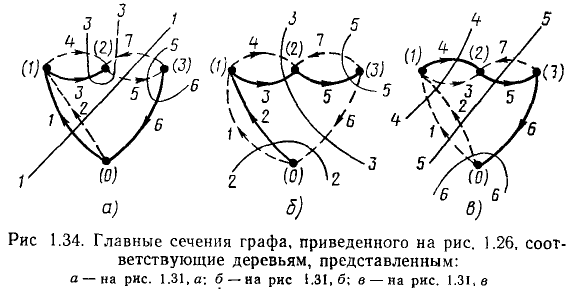
Главным сечение графа называется такое сечение, в которое входит только одна ветвь выбранного дерева. Остальные ветви, входящие в главное сечение, являются связями (рис. 1.34). Количество главных сечений равно количеству ветвей дерева, т. е. m = q— 1. Каждому дереву может быть поставлена в соответствие своя система главных сечений, причем главные сечения, соответствующие выбранному дереву, отличаются друг от друга, по крайней мере, одной ветвью — ветвью дерева, входящей в каждое из сечений. Главным сечениям графа присваивают номера и приписывают ориентацию, совпадающие с номером ориентацией относительно соответствующей ветви дерева и ее сечения.

Если одна из частей, на которые граф делится линией сечения, представляет собой изолированный узел, то соответствующее сечение называется каноническим (сечения 3 и 6 на первом из графов, изображенных на рис. 1.34).

Топологические матрицы

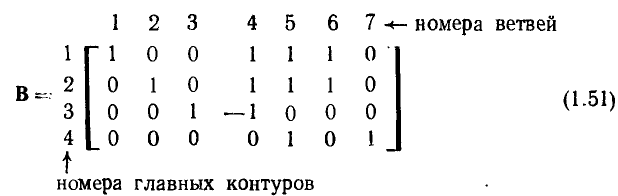
Топологические матрицы служат для аналитического описания графов. Такое описание можно представить в виде списка (перечня) ветвей графа с указанием, каким узлам они инцидентны и с какой ориентацией, или с помощью полной матрицы узлов

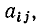
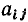
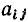
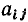
Полная матрица узлов (полная матрица инциденций, матрица соединений, структурная матрица) — это таблица, в которой число столбцов равно числу ветвей графа р, а число строк равно числу узлов q. Номера строк совпадают с номерами узлов (строка с нулевым номером обычно располагается последней), номера столбцов совпадают с номерами ветвей. Элемент матрицы расположенный на пересечении i-й строки и j-го столбца, может принимать значения +1, —1 и 0: = +1, если ветвь j инцидентна узлу i и направлена от этого узла; = —1, если ветвь j инцидентна узлу i и направлена к этому узлу; = 0, если ветвь j не инцидентна узлу i. Так, графу, изображенному на рис. 1.26, а соответствует полная матрица инциденций

Нетрудно убедиться, что эта же полная матрица узлов (1.43) соответствует и всем графам, изоморфным графу, изображенному на рис. 1.26, а, в частности графам, приведенным на рис. 1.26, б, в. Таким образом, все изоморфные графы описываются одной и той же полной матрицей узлов. Имея полную матрицу узлов, всегда можно восстановить исходный граф с точностью до изоморфизма.

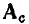
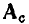
Число ненулевых элементов в каждой строке матрицы равно числу ветвей, инцидентных соответствующему узлу, т. е. степени узла. В каждом столбце имеется только два ненулевых элемента: +1 и —1, так как каждая ветвь инцидентна двум узлам и направлена от одного из них к другому. Сумма всех элементов каждого столбца, а следовательно, и сумма всех строк полной матрицы узлов равна нулю, т. е. строки полной матрицы узлов являются линейно зависимыми.

На практике обычно используют сокращенную (редуцированную) матрицу узлов А, которая получается из полней матрицы узлов путем отбрасывания любой из ее строк. Обычно отбрасывают строку, соответствующую узлу с номером 0, который будем называть базисным узлом. Так, отбрасывая строку с номером 0 у полной матрицы узлов (1.43), получаем сокращенную матрицу узлов А цепи, граф которой изображен на рис. 1.26:

В теории графов доказывается, что все строки сокращенной матрицы узлов линейно независимы. Зная сокращенную матрицу узлов, соответствующую некоторому графу, всегда можно найти его полную матрицу узлов, для чего необходимо дополнить А одной строкой так, чтобы сумма всех строк матрицы 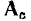равнялась нулю,

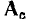
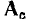
В связи с тем что каждая строка матриц и А несет информацию о том, какие ветви и с какой ориентацией подключены к определенному узду цепи, эти матрицы можно использовать для записи уравнений по первому закону Кирхгофа. Действительно, умножая полную матрицу узлов на матрицу-столбец токов ветвей i, получаем

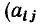
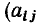
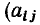
Каждая строка этого выражения есть алгебраическая сумма токов ветвей, подключенных к соответствующему узлу цепи, причем если ветвь направлена от узла, то соответствующий ток имеет знак плюс =+1), если ветвь направлена к узлу, то знак минус= —1), Если же ветвь не инцидентна рассматриваемому узлу, то соответствующее слагаемое равно нулю = 0).

Тогда в соответствии с первым законом Кирхгофа окончательно имеем

В связи с тем что строки полной матрицы узлов являются линейно зависимыми, система уравнений (1.45) также будет линейно зависимой.

Для получения системы линейно независимых уравнений, составленных по первому закону Кирхгофа, можно воспользоваться сокращенной матрицей инциденций, строки которой являются линейно независимыми:

Таким образом, для любой цепи можно составить 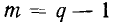линейно независимых уравнений баланса токов, и, следовательно, любые m узлов графа представляют собой систему независимых узлов.

Пример 1.4.

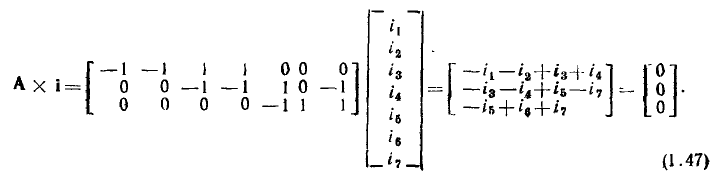
Составим систему линейно независимых уравнений баланса токов для цепи, граф которой изображен на рис. 1.26. Подставляя в (1.46) сокращенную матрицу узлов этой цепи (1.44), находим

Как и следовало ожидать, система уравнений (1.47) совпадаете системой | уравнений (1.38), составленной на основании первого закона Кирхгофа для 1,2 и 3-го узлов рассматриваемой цепи.

Для матричной записи уравнений баланса токов в обобщенных узлах цепи и уравнений баланса напряжений используют матрицу главных сечений и матрицу главных контуров.

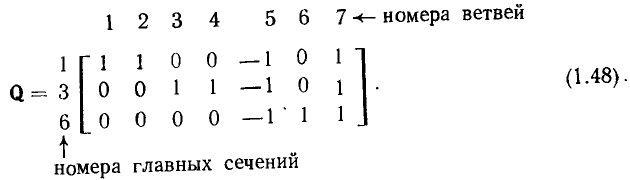
Матрица главных сечений Q (матрица сечении) представляет собой таблицу, число столбцов которой равно числу ветвей графа р, а число строк — числу главных сечений

(номера столбцов совпадают с номерами ветвей, а номера строк с нотами главных сечений, т. е. с номерами соответствующих ветвей дерева).

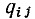
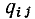
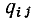
Каждая строка матрицы главных сечений характеризует состав ветвей графа, входящих в данное сечение. Элементы i-й строки принимают значение +1, если j-я ветвь графа входит в состав i-гo сечения причем ее ориентация совпадает с ориентацией сечения, т.е. с ориентацией соответствующей ветви дерева относительно линии сечения; =-1, если j-я ветвь входит в i-е сечение а ее ориентация противоположна ориентации сечения; = 0, если j-я ветвь не входит в i-e сечение.

Матрица главных сечений, соответствующая графу, приведенному на рис. 1.34, а, имеет следующий вид:

Используя матрицу главных сечений, можно в компактной форме записать систему из m=q-1 уравнений, составленных на основании первого закона Кирхгофа для главных сечений графа, соответствующих выбранному дереву:

где i — вектор токов ветвей.

Уравнения (1 49) являются линейно независимыми, так как каждое из них отличается от остальных, по крайней мере, одним током — током ветви дерева, входящей в данное главное сечение.

Подставляя (1.48) в (1.49), получим систему линейно независимых уравнений баланса токов для главных сечений графа (рис. 1.34, а).

Если какое-либо из главных сечений графа является каноническим, то уравнение баланса токов для этого сечения с точностью до знака совпадает с уравнением баланса токов для соответствующего изолированного узла. Так, в системе уравнений (1.50) второе и третье уравнения, составленные для канонических сечений 3 и 6, совпадают со вторым и третьим уравнениями в системе уравнений (147), составленными соответственно для узлов 2 и 3 той же цепи. Если все главные сечения графа являются каноническими, то матрицы узлов А и сечений Q совпадают с точностью до знака элемента строки.

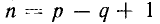
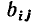
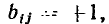
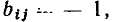
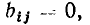
Матрица главных контуров В представляет собой таблицу, в которой число столбцов равно числу ветвей графа р, а число строк — числу главных контуров, т. е. числу главных ветвей графа (номера столбцов совпадают с номерами ветвей, а номера строк—с номерами главных контуров). Элементы i-й строки могут принимать значения +1, —1 и 0; если j-я ветвь входит в состав i-гo контура, причем ее ориентация совпадает с ориентацией контура; если ориентация j-й ветви, входящей в i-й контур, не совпадает с ориентацией контура; если j-я ветвь не входит в i-й контур. Например, матрица главных контуров В графа (см. рис. 1.26), соответствующая дереву графа, приведенному на рис. 1.31, в, имеет следующий вид;

Матрицу главных контуров можно использовать для записи уравнений, составленных на основании второго закона Кирхгофа. Пусть исследуемая цепь содержит р ветвей, q узлов и 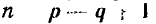главных контуров. Умножая матрицу главных контуров В на матрицу столбец напряжений ветвей u, получаем

Каждая строка этого выражения представляет собой алгебраическую сумму напряжений ветвей, входящих в i-й главный контур, причем правило суммирования напряжений ветвей совпадает с соответствующим правилом, установленным для записи уравнений баланса напряжений в контуре (1.40). Так как в соответствии со вторым законом Кирхгофа сумма напряжений ветвей, входящих в каждый контур, в любой момент времени равна нулю, то окончательно имеем

Выражение (1.52) является матричной формой записи уравнений баланса напряжений для главных контуров цепи. Уравнения, входящие в (1.52), являются линейно независимыми, так как каждое из них отличается от остальных, по крайней мере, одним напряжением — напряжением главной ветви, замыкающей данный контур.

Таким образом, система из главных контуров, соответствующих выбранному дереву, является системой независимых контуров. Следовательно, для каждой цепи можно составить п независимых уравнений по второму закону Кирхгофа.

Пример 1.5.

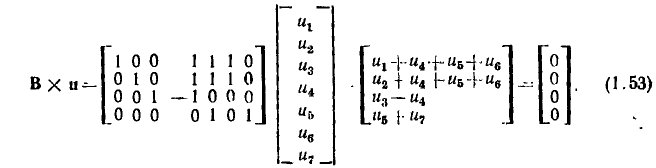
Рассмотрим применение матрицы контуров для формирования системы линейно независимых уравнений баланса напряжений для цепи, граф которой приведен на рис. 1.26. Умножая матрицу главных контуров этой цепи (1.51) на матрицу-столбец напряжений ветвей u, получаем

Следует отметить, что при выборе системы независимых контуров было использовано достаточное условие независимости уравнений, заключающееся в том, что для линейной независимости системы уравнений достаточно, чтобы каждое из уравнений содержало, по крайней мере, одну независимую переменную величину, отсутствующую в других уравнениях. Так как это условие не является необходимым, то для каждой цепи можно найти и другие системы независимых контуров, которые в ряде случаев могут не совпадать ни с одной из систем: главных контуров. В частности, ячейки плоского графа, число которых оказывается равным представляют собой систему независимых контуров. Их состав может быть описан матрицей основных контуров которая строится аналогично матрице главных контуров (контуры, соответствующие каждой из ячеек, нумеруют от 1 до n, каждому из них приписывают произвольную ориентацию). Например, для графа электрической цепи, изображенного на рис. 1.35:

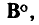
В этом случае матрица основных контуров не совпадает ни с одной из возможных для данного графа матриц главных контуров.

Матрицу 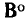можно, как и матрицу В, использовать для записи системы линейно независимых уравнений баланса напряжений:

Так, используя (1.54), можно составить систему уравнений баланса напряжений для ячеек графа, изображенного на рис. 1.35:

Следует подчеркнуть, что понятие ячейки (окна) было введено ранее только для плоских графов и что только для них возможен выбор ячеек в качестве независимых контуров.

Дуальные графы и дуальные цепи

Два плоских графа называются дуальными, если матрица узлов одного из них А равна матрице основных контуров В° другого и наоборот:

Очевидно, что дуальные графы должны иметь одинаковое число ветвей 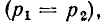причем число ветвей дерева одного из них m должно быть равно числу главных ветвей n другого:

Для построения графа, дуального заданному (рис. 1.36, а), необходимо внутри каждой ячейки исходного графа разместить узел дуального графа [(1′), (2′) и т. д.], кроме того, один узел дуального графа располагается во внешней по отношению к исходному графу части плоскости, т. е. в базисной ячейке. Узлы дуального графа соединяются между собой ветвями так, чтобы каждая ветвь исходного графа пересекала одну ветвь дуального графа (пунктир на рис. 1.36, а). Номера узлов дуального графа совпадают с номерами контуров исходного графа, внутри которых они размещены. Узлу дуального графа, расположенному в базисной ячейке, присваивается номер 0′. Пересекающимся между собой ветвями исходного и дуального графов присваиваются одинаковые номера. Ориентация ветвей и контуров дуального графа (рис. 1.36, б) выбирается таким образом, чтобы обеспечить выполнение равенств (1.56).

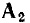
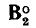
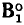
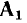
Нетрудно убедиться, что матрицы узлов и основных контуров дуального графа (рис. 1.36,6) равны соответственно матрицам основных контуров и узлов исходного графа:

Как видно из рис. 1.36, ячейки дуального графа соответствуют узлам исходного графа, а узлы дуального графа — ячейкам исходного. Последовательному соединению ветвей исходного графа соответствует параллельное соединение ветвей дуального графа и наоборот. Если сформулированное правило нахождения дуального графа применить для построения графа, дуального изображенному на рис. 1.36, б, то получится граф, изоморфный исходному графу (рис. 1.36, а сплошные линии).

Используя понятие дуального графа, легко обобщить введенное ранее понятие дуальных цепей. Две цепи называются дуальными, если они имеют дуальные графы и каждому элементу одной цепи соответствует дуальный элемент другой.

Для построения дуальной цепи сначала находят граф, дуальный расширенному топологическому графу исходной цепи, а затем каждую ветвь дуального графа заменяют элементом, дуальным элементу, расположенному в соответствующей ветви исходной цепи.

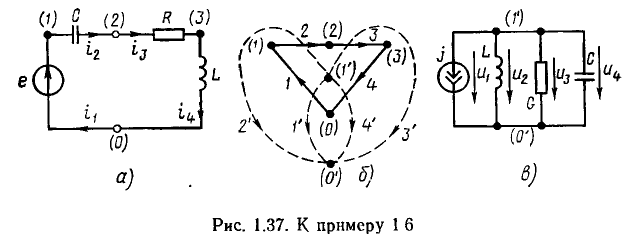
Пример 1.6.

Построим цепь, дуальную приведенной на рис. 1.37, а. На рис. 1.37, б сплошными линиями показан граф исходной цепи, а пунктирными — дуальный ему граф (направление ветвей исходного графа соответствует направлению токов ветвей исходной цепи, а направление ветвей дуального графа—направлению напряжения ветвей дуальной цепи). Цепь, дуальная исходной, изображена на рис. 1.37, в.

Из определения дуальной цепи и равенств (1.56) следует, что уравнения баланса токов для одной из дуальных цепей будут совпадать с Уравнениями баланса напряжений для другой при условии, что в соответствующих уравнениях токи ветвей одной цепи будут заменены на напряжения ветвей другой цепи и наоборот. Это свойство дуальных Цепей иногда используют в качестве определения дуальных цепей.

В заключение заметим, что непланарные графы не имеют дуальных графов, в связи с чем идеализированной электрической цепи, схема которой не является планарной, не может быть поставлена в соответствие дуальная цепь.

• Уравнения электрического равновесия цепей
• Линейные цепи при гармоническом воздействии
• Нелинейные резистивные цепи
• Преобразование схем электрических цепей
• Законы и правила Кирхгофа для электрических цепей
• Линии с распределенными параметрами
• Идеализированные пассивные элементы
• Идеализированные активные элементы

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Компонентные и топологические уравнения электрической цепи

Математическое описание процессов в сложных цепях, состоящих из большого числа элементов, основывается на компонентных и топологических уравнениях.

Компонентныминазываются уравнения, которые устанавливают зависимость между разнотипными переменными, относящиеся к одному из элементов цепи, например, уравнения (2.1), (2.5) и (2.10), связывающие ток и напряжение в пассивных элементах цепи , , .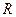

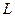
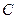
Используя компонентные уравнения, можно составить уравнение, связывающие напряжение и ток любой ветви электрической цепи. Например, для ветви, показанной на рис. 3.5, такое уравнение будет иметь вид

.

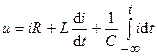
Топологическиминазываются уравнения, которые устанавливают зависимость между однотипными переменными цепи, обусловленную структурой цепи, например, уравнения, которые устанавливают зависимость между токами либо между напряжениями ветвей цепи. Примером таких уравнений являются уравнения, которые составляются на основании законов Кирхгофа, сформулированные Густавом Кирхгофом в 1845 году.

Согласно первому закону Кирхгофаалгебраическая сумма токов ветвей, подключенных к одному и тому же узлу цепи, равна нулю

, (3.1)

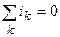
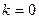
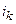
где — номер ветви, подключенной к рассматриваемому узлу; — ток k-ой ветви.

При составлении уравнения (3.1) токи, направленные к узлу, записываются в уравнение со знаком «плюс», а токи, направленные от узла, — со знаком «минус». С физической точки зрения первый закон Кирхгофа выражает тот факт, что в узле электрической цепи невозможно ни накопления, ни исчезновение электрического заряда, то есть сколько электрических зарядов подходит к узлу, столько же и уходит от него за один и тот же промежуток времени.

Число независимых уравнений, которые можно составить по первому закону Кирхгофа, определяется числом независимых узлов цепи

,

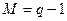
где 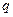— общее число узлов цепи.

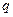
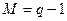
Последний -й узел является зависимым, поскольку уравнение, составленное для него по первому закону Кирхгофа, может быть получено путём линейного преобразования уравнений, составленных для остальных узлов цепи.

Например, для узла цепи, показанной на рис. 3.6, уравнение, составленное по первому закону Кирхгофа, будет иметь вид

.

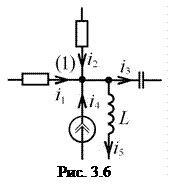
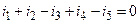
Если в последнем уравнении токи, втекающие в узел, оставить в левой части уравнения, а токи, вытекающие из узла, перенести в правую части уравнения, то получим уравнение

,

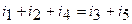
в соответствии с которым первый закон Кирхгофа можно сформулировать следующим образом: в любой момент времени сумма токов, втекающих в узел, равна сумме токов, вытекающих из этого узел.

Второй закон Кирхгофагласит, что алгебраическая сумма напряжений на пассивных элементах и источниках тока, входящих в состав замкнутого контура электрической цепи, равна алгебраической сумме э.д.с. идеальных источников напряжения, действующих в этом контуре,

, (3.2)

где — номер ветви; — алгебраическая сумма напряжений на пассивных элементах и источнике тока, водящего в состав -ой ветви; — э.д.с. -го идеального источника напряжения, действующего в контуре.

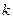
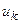
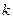
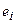
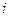
Если направление напряжения на элементе ветви контура совпадает с направлением обхода контура, то оно записываются в левую часть уравнения (3.2) со знаком «плюс», в противном случае оно записывается со знаком «минус». Аналогичным образом записываются в правую часть уравнения (3.2) э.д.с. идеальных источников напряжения, действующих в контуре.

С физической точки зрения второй закон Кирхгофа выражает тот факт, что работа по перемещению единичного электрического заряда по замкнутому контуру цепи равна нулю.

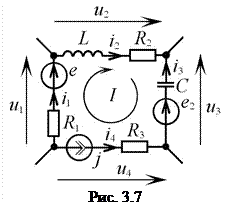
Число независимых уравнений, которые можно составить по второму закону Кирхгофа равно число независимых контуров цепи, которое, в свою очередь, определяется числом главных ветвей графа цепи,

,

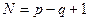
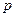
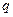
где и — общее число ветвей и узлов электрической цепи соответственно.

Например, для контура электрической цепи (рис. 3.7) уравнение, составленное по второму закону Кирхгофа, будет иметь вид

,

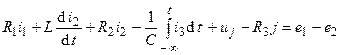
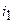
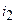
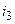
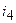
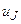
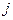
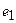
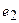
где , , , — токи ветвей; — напряжение на источнике тока , действующем в 4-ой ветви; и — э.д.с. источников напряжения, действующих в контуре.

Перегруппировав слагаемые в (3.2), можно записать второй закон Кирхгофа в виде

, (3.3)

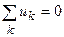
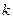
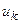
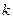
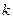
где — номер ветви контура; — напряжение -ой ветви, которое. определяется как алгебраическая сумма напряжений на пассивных элементах, а также на источниках тока и э.д.с., входящих в состав -ой ветви

В соответствии с уравнением (3.3) второй закон Кирхгофа можно сформулировать следующим образом. Алгебраическая сумма напряжений ветвей, образующих замкнутый контур электрической цепи, равна нулю.

Напряжения ветвей, направления которых совпадают с направлением обхода контура, подставляют в уравнение (3.3) со знаком «плюс», а не совпадающие — со знаком «минус». Уравнения (3.2) и (3.3) идентичны. Для расчётов уравнение (3.2) является более удобным, поскольку в нём неизвестные напряжения на пассивных элементах и источниках тока записаны в левой части уравнения, а известные э.д.с. источников напряжения — в правой части уравнения, что уменьшает вероятность ошибок при составлении уравнений.

Дата добавления: 2017-09-01 ; просмотров: 5412 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Компонентные и системные уравнения, описывающие цепь

Закономерности, описывающие поведение элементов цепи (элементные или компонентные законы)

Это математические выражения, связывающие между собой переменные, описывающие состояние элемента – токи через выводы элемента и напряжения между выводами этого элемента. Такие математические уравнения называют элементными или компонентными законами. Такие законы могут иметь вид алгебраических или дифференциальных уравнений. Количество таких уравнений для элемента с n выводами равно (n‑1).

Простейший вид элемента – с двумя выводами (двухполюсник). Его поведение описывается зависимостью между двумя величинами: iиu. Ее называют вольт-амперной характеристикой ВАХ.

Какая из переменных является независимой (аргументом) – любая.
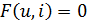
С математической точки зрения – любая.

Как можно определить ВАХ экспериментально? Изменяя одну из величин и измеряя обе.

Элемент называют линейным, если ВАХ – полином первого порядка

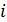
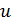
Может ли быть так, что при заданном значении аргумента функция не определяется однозначно?
Может ли быть так, что при постоянном значении аргумента 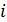функция не сохраняет постоянства?

Пример с конденсатором.
Пример с термозависимым резистором (саморазогрев).
Пример с диодом – нелинейный элемент

Эксперимент по снятию ВАХ резистора и полупроводникового диода а) вручную, б) с помощью характериографа

Простой вариант формирования системы компонентных уравнений для n-полюсника:

· Выбрать один из выводов в качестве базового.

· Задать величины напряжений между каждым из оставшихся и базовым выводом (возможность этого является следствием второго закона Кирхгофа).

· Измерять токи через каждый из выводов за исключением базового.

Система из (n-1) уравнений, описывающая поведение n-полюсника будет иметь вид

здесь F символизирует зависимость, которая может быть алгебраической, либо содержать производные и (или) интегралы переменных u(t) и i(t).

Энергетические свойства элементов электрических цепей.

Диссипативность: (необратимое) превращение электрической энергии в тепло

Переход части электрической энергии в тепло при протекании тока по диссипативным элементам. Компонентное уравнение диссипативного элемента цепи. Потери энергии в электронных информационных устройствах. Почему энергия не может быть сколь-угодно малой.

Большая группа элементов цепей обладает свойством, состоящим в том, что вся энергия, доставляемая токами, протекающими через выводы, превращается внутри таких элементов в тепло. Такие элементы называют диссипативными[2]. Примером такого элемента является резистор, используемый в электронных цепях для …. () Компонентное уравнение диссипативного двухполюсника имеет вид

(2.4)

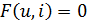
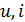
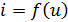
Запись уравнения в таком виде подчёркивает тот факт, что ни одна из двух переменных не является причиной изменения другой величины, т.е. аргументом, независимой переменной, может быть любая из них. Во многих книгах утверждается (считается), что независимой переменной, причиной является изменение напряжения, в то время как изменение тока это следствие, и компонентное уравнение переписывают в виде

(2.5)

Однако утверждение о «первичности» напряжения ошибочно.

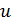
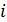
Характеристики диссипативных элементов часто называют «вольт-амперными», поскольку в выражении присутствуют две переменные: напряжение и ток . И вновь отметим, что в приведённом уравнении обе переменные могут изменяться во времени.

Вольт-амперная характеристика 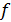может быть функцией любого вида. Так, например, у полупроводниковых диодов характеристики существенно нелинейны и весьма различны для разных типов диодов.

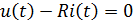
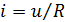
Для металлических проводников компонентная зависимость весьма близка к прямой пропорциональной ‑ это всем известный «закон Ома» , записываемый обычно в виде . Однако при значительной величине тока вследствие саморазогрева зависимость может оказаться весьма «причудливой» (например, для нити лампы накаливания).

В электротехнических устройствах используются многочисленные элементы с числом выводов, превышающим два. Прежде всего, это транзисторы, у которых три вывода (у некоторых полевых транзисторов может быть четыре вывода). Вольт-амперные характеристики многополюсных диссипативных элементов представляют собой семейство функций нескольких аргументов. Количество функций, а также количество аргументов в каждой функции на единицу меньше количества выводов многополюсника.

Емкость: (обратимое) накопление энергии в электрическом поле (заряженного конденсатора).

Запасание части электрической энергии в реактивных элементах цепи ‑ в виде энергии электрического поля в конденсаторе или в виде энергии магнитного поля в индукторе. Компонентные уравнения реактивных элементов (накопителей энергии).

Некоторые виды элементов цепей способны обратимо накапливать электрическую энергию в электрическом или в магнитном поле.

Компонентное уравнение элемента цепи, способного накапливать энергию в электрическом поле (электростатического накопителя), в общем случае имеет вид

(2.6)

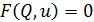
Это соотношение иногда называют «вольт-кулонной» характеристикой. Однако при описании электрической цепи, содержащей электростатический накопитель, состояние цепи описывают, используя только напряжения и токи (и, может быть, их производные и интегралы). Этого можно достигнуть, использовав соотношение между зарядом и током (используемого в определении единицы заряда ):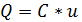

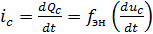
(2.7)

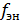
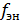
Любой фрагмент электрической цепи, в котором имеются две точки, между которыми существует ненулевое напряжение, обладает свойствами электростатического накопителя. Вид функции зависит от свойств среды, окружающей фрагмент цепи. (Правильные, но непонятные слова). Известно более 300 веществ (сегнетоэлектрики), для которых функция существенно нелинейна.

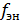
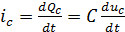
Для большинства веществ функция имеет вид прямой пропорциональной зависимости:

(2.8)

В последней формуле 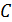– электрическая ёмкость электростатического накопителя, постоянный параметр, измеряемый в фарадах.

Изготавливаются и используются в электрических цепях конденсаторы – двухполюсники, обладающие свойством электростатического накопителя. При проектировании и изготовлении конденсаторов принимают специальные меры для обеспечения постоянства величины их емкости.

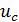
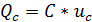
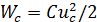
Конденсатор, заряженный до напряжения (и хранящий заряд ) в своём электрическом поле, в соответствии с (2.1) содержит энергию . Из формулы вольт-кулонной характеристики (2.6) и (2.7) могут быть сделаны весьма важные для дальнейшего выводы:
а) скорость изменения напряжения на электростатическом накопителе тем больше, чем больше величина перезаряжающего тока,
б) напряжение на электростатическом накопителе не может измениться скачком, поскольку для этого необходим ток бесконечно большой величины, что физически не реализуемо.

Индуктивность: (обратимое) накопление энергии в магнитном поле тока.

Компонентное уравнение элемента цепи, способного накапливать энергию в магнитном поле (электромагнитного накопителя), имеет вид:

(2.9)

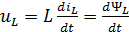
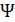
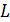
Соотношение (2.9) иногда называют «вебер-амперной характеристикой», поскольку оно устанавливает связь между величиной суммарного магнитного потока (потокосцепления) и величиной тока, создающего этот поток. Величина потокосцепления измеряется в веберах, (как и магнитный поток). Коэффициент пропорциональности называется индуктивностью и измеряется в единицах генри.

Любой фрагмент реальной электрической цепи в некоторой степени обладает свойствами магнитного накопителя, поскольку вокруг проводника с током всегда возникает магнитное поле.

Из формулы вебер-амперной характеристики (2.9) следуют важные для дальнейшего изложения выводы
а) скорость изменения тока в электромагнитном накопителе тем больше, чем больше величина напряжения между его выводами,
б) ток в магнитном накопителе не может измениться скачком, поскольку для этого напряжение между выводами магнитного накопителя должно стать бесконечно большим, что физически не реализуемо.

Для линейных двухполюсников математическое выражение этих свойств:

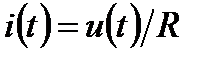
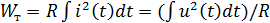
Резистивность (диссипативность): и
это соотношение известно как Закон Ома – ВАХ идеального резистора

Емкость электрическая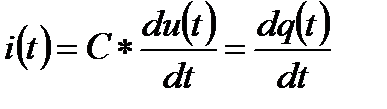
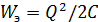
вольт-кулонная характеристика электростатического накопителя энергии

Индуктивность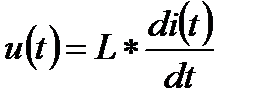
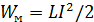
вебер-амперная характеристика электромагнитного накопителя энергии

Два последних соотношения никак не называются, хотя все три формулы представляют собой простейшие математические модели для трех видов двухполюсников: резистора, конденсатора и катушки индуктивности (индуктора).

Любой реальный двухполюсник обладает всеми тремя свойствами, только в разной степени.

В каких случаях можно пренебречь отдельными свойствами. На этот вопрос можно ответить, проведя анализ энергетического баланса.