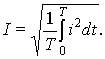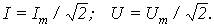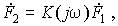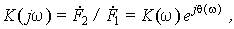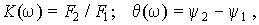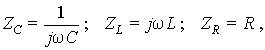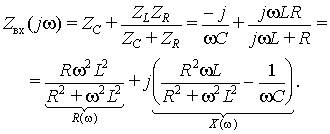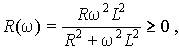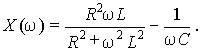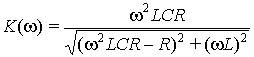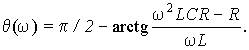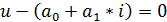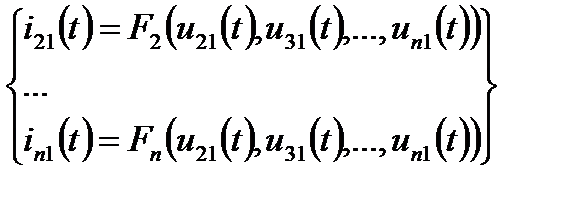Компонентные уравнения в комплексной форме

Основные характеристики синусоидальных сигналов

Синусоидальные токи и напряжения наиболее распространены из всех переменных во времени сигналов. Они легко генерируются в широком диапазоне частот, а их основные характеристики — амплитуду и частоту — удобно измерять и регистрировать. Расчет динамических режимов электрических цепей, находящихся под действием переменных источников e(t) и J(t), включающих емкости и индуктивности — динамические элементы, сложнее, чем анализ резистивных цепей. Общий подход к расчету, основанный на применении компонентных уравнений и уравнений Кирхгофа сохраняется. Однако уравнения цепи теперь будут дифференциальными, так как в них входят связи между токами и напряжениями на динамических элементах: uL = L di/dt; iC = C du/dt. Тем не менее, анализ синусоидальных режимов можно проводить на более простой математической основе, без составления и интегрирования дифференциальных уравнений. Результаты такого анализа могут служить базой для исследования цепей при воздействии сигналов более сложной формы, как периодических, так и непериодических.

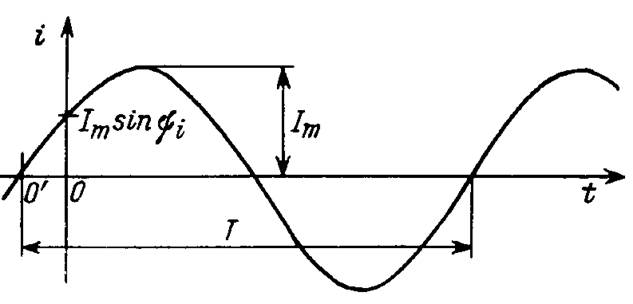
Синусоидальный ток характеризуется амплитудой Im и периодом T (рис.1).

При произвольном выборе начала отсчета времени его математическое выражение имеет вид i(t) = Im sin (wt + yi), где w — круговая (угловая) частота, w = 2pf (f — циклическая частота, определяющая число периодов колебаний за единицу времени), начальная фаза yi — аргумент синуса, отсчитываемый от ближайшей точки перехода через нуль 0′ в положительном направлении. Аналогичны выражения для синусоидального напряжения u, ЭДС e, тока источника J:

u = Um sin (wt + yu); e = Em sin (wt + ye); J = Jm sin (wt + yj)

Энергетические характеристики синусоидальных сигналов обычно описываются действующими значениями тока I, равными среднеквадратичному за период значению:

Аналогично вводятся действующие значения напряжения U и напряжения ЭДС E. Действующие значения наиболее часто используют для характеристики интенсивности синусоидальных сигналов: электроизмерительные приборы проградуированы так, что они показывают действующие значения синусоидальных токов и напряжений. Для синусоидальных величин вычисление интеграла в последнем выражении приводит к соотношениям:

Приведенное общее выражения действующего значения справедливо также и для периодических сигналов, отличных по форме от синусоидальных.

В линейной цепи, находящейся достаточно долго под действием синусоидальных источников одной частоты f с неизменными амплитудами, токи и напряжения на всех участках будут иметь также синусоидальную форму с той же частотой, так как при протекании по катушке синусоидального тока iL(t) напряжение на ней uL = L di/dt также синусоидально, поскольку синусоидальные функции сохраняют свою форму при дифференцировании. Аналогично связаны напряжение и ток конденсатора. При суммировании синусоидальных токов и напряжений на отдельных участках цепи в уравнениях Кирхгофа их форма также не изменяется.

Поэтому анализ синусоидального режима в цепи сводится к определению амплитуд и начальных фаз отдельных токов и напряжений, которым отвечают частные решения дифференциальных уравнений, описывающих процесс. Их можно найти, даже не составляя эти дифференциальные уравнения.

Токи и напряжения на различных участках цепи имеют различные начальные фазы — компонентные соотношения для индуктивности и емкости выражают то, что токи и напряжения на них не совпадают по фазе. Поэтому при анализе цепи возникает необходимость суммирования сигналов с различными начальными фазами.

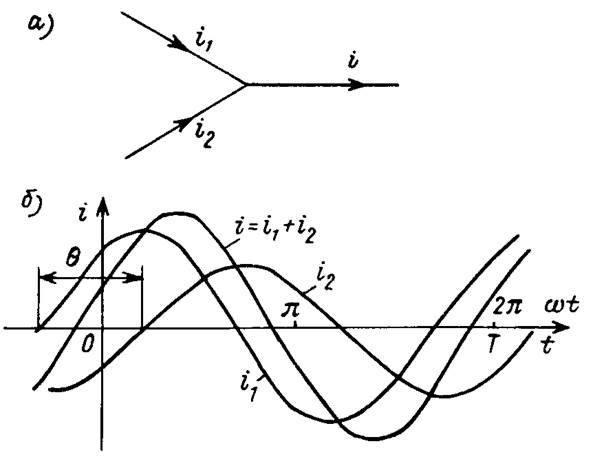
Разность фаз двух синусоидальных сигналов одной частоты y1 – y2 = 0 называется их фазовым сдвигом. При y1 > y2 (q > 0) говорят, что ток i1 опережает по фазе ток i2 (рис. 2, б), и наоборот, i2 отстает по фазе от тока i1. При q = 0 сигналы совпадают по фазе, одновременно достигая максимума и переходя через нуль. Два сигнала с q = p находятся в противофазе, сигналы с q = ± p/2 находятся в квадратуре

Если сходящиеся в узле (рис. 2, а) синусоидальные токи имеют фазовый сдвиг i1(t) = Im1 sin (wt + y1), i2(t) = Im2 sin (wt + y2), то для их суммы i(t) = Im sin (wt + y) = i1(t) + i2(t) нахождение амплитуды Im и начальной фазы y по временным зависимостям громоздко (рис. 2, б).

В цепях синусоидального тока уравнения Кирхгофа нельзя применять к амплитудам (или действующим значениям) токов и напряжений, не совпадающих по фазе. Алгебраическое суммирование токов и напряжений в соответствии с законами Кирхгофа возможно лишь для мгновенных значений i или u.

1. Связи между синусоидальными напряжениями и токами в активном сопротивлении, в индуктивности, в емкости.

Используя компонентные уравнения, установим связь между основными характеристиками тока и напряжения на элементах. Подставив мгновенные значения тока i = Im sin wt в компонентные уравнения для uR и uL и напряжения u = Um sin wt — в iC, получим выражения для uR, uL и iC, приведенные в Таблице 7.1, из которых следуют соотношения между амплитудами и действующими величинами напряжений и токов U и I. Отношение U/I = Um/Im представляет сопротивление элемента — активное R и реактивные — XL (индуктивное) и XC (емкостное). Размерность всех сопротивлений — Ом. Обратные величины I/U представляют проводимости элементов — активную G и реактивные: BL (индуктивную) и BC (емкостную). Значения реактивных сопротивлений (и проводимостей) зависят от частоты. Выражения для мгновенных токов и напряжений i и u показывают, что ток и напряжение на резисторе совпадают по фазе, на индуктивности ток отстает от напряжения на угол p/2, а на емкости ток опережает напряжение на p/2.

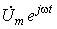
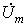
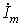
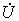
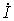
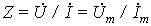
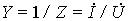
Переход к комплексным характеристикам элементов осуществляется с помощью комплексных изображений мгновенного тока для сопротивления и индуктивности и напряжения для емкости. Подстановка их в компонентные уравнения приводит к комплексным изображениям uR, uL и iC, приведенным в Табл. 1, из которых получаем соотношения комплексных амплитуд напряжений и токов элементов и действующих значений и . Они выражают закон Ома в комплексной форме, в которой выступают комплексные сопротивления элементов . Обратные им величины — это комплексные проводимости . Комплексный характер сопротивлений и проводимостей Z и Y отражает информацию о фазовых сдвигах токов и напряжений на элементах.

Связи между синусоидальными напряжениями и токами на элементах R, L, C

Характеристика	Связи между напряжениями и токами на элементах
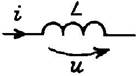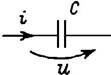Во временной области
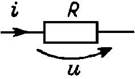
Компонентное уравнение	u = Ri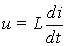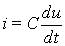
Мгновенные значения тока и напряжения	i = Im sin wt; uR = RIm sin wt	i = Im sin wt; uL = wLIm cos wt = = wLIm sin (wt + p/2)	u = Um sin wt; iC = wCUm cos wt = = wCUm sin (wt + p/2)
Амплитуда	Um = RIm	Um = wLIm	Um = (1/wC)Im
Действующие ток и напряжение	U = RI	U = wLI	U = (1/wC)I
Сопротивление Проводимость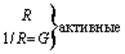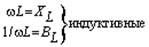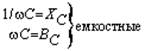
Начальная фаза тока и напряжения	yu = yi	yu = yi + p/2	yu = yi – p/2
Угол сдвига фаз между током и напряжением j = yu – yi	p/2	– p/2
Графики тока и напряжения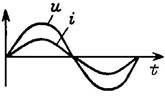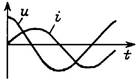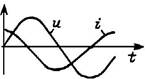
Векторная диаграмма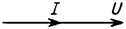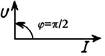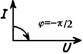

2. Входные и передаточные функции цепей синусоидального тока

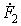
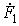
Применение комплексного метода сводит соотношения между мгновенными токами i(t) и напряжениями u(t), выражаемые дифференциальными уравнениями, к алгебраическим соотношениям между их комплексными изображениями I(jw), U(jw). Поэтому составленные для цепи уравнения в комплексной форме позволяют алгебраически выразить любой комплексный ток или напряжение – выходную величину через входную величину — напряжение или ток, подаваемые к входным зажимам:

где K(jw) — передаточная функция цепи, являющаяся рациональной дробью аргумента jw, коэффициенты полиномов числителя и знаменателя которой выражаются через параметры цепи. Передаточная функция является комплексным числом

модуль которого K(w) выражает отношение действующих значений (или амплитуд) выходного и входного сигналов, а ее аргумент q(w) определяет фазовый сдвиг между ними:

где y2 и y1 — начальные фазы обоих сигналов.

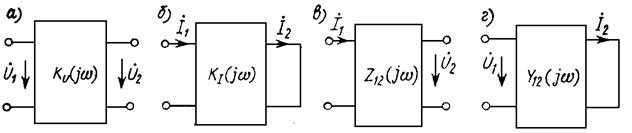
Размерность передаточной функции определяется размерностями связываемых ею величин. Если входная и выходная величины — напряжения (рис. 3, а), то передаточная функция K(jw) безразмерна; то же относится и к случаю, если обе величины являются токами (рис. 3, б). Если выходная величина — напряжение, а входная — ток (рис. 3, в), то говорят о передаточном сопротивлении Z12(jw) и наконец, соотношение между входным напряжением и выходным током определяет передаточная проводимость Y12(jw) (рис. 3, г).

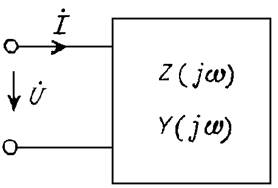
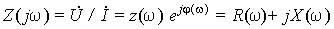
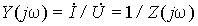
Входные величины — комплексное сопротивление двухполюсника (рис. 4) и входная проводимость также выражаются рациональными дробями аргумента jw.

Модулем комплексного входного сопротивления является полное сопротивление цепи Z(w), его аргументом j(w) — фазовый сдвиг между напряжением и током, вещественная часть R(w) — активное, а мнимая часть X(w) — реактивное сопротивление.

Для комплексной входной проводимости аналогично имеем

Y(jw) = y(w) e-jj(w) = G(w) — jB(w),

где y(w), G(w) и B(w) — полная, активная и реактивная проводимости цепи.

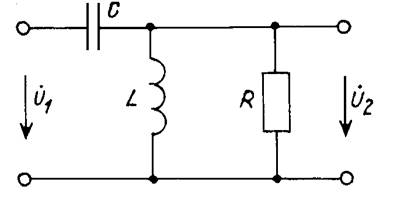
Определим входные и передаточные функции для цепи (рис. 5).

Выражая комплексные сопротивления ветвей

запишем входное сопротивление цепи:

Вещественная часть входного сопротивления пассивной цепи неотрицательна:

а его мнимая часть может быть как положительной, так и отрицательной

Получим выражение для передаточной функции рассматриваемой цепи по напряжению:

где ZLR = jwLR/(jwL + R) (при переходе к последнему выражению числитель и знаменатель дроби были умножены на wC).

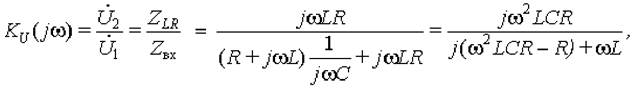
Передаточная комплексная функция имеет модуль

Амплитудные и фазные частотные характеристики. При анализе процессов преобразования сигналов электрическими цепями представляет интерес исследование зависимостей передаточных и входных функций рассматриваемой цепи от частоты. График частотной зависимости модуля передаточной функции называется амплитудно-частотной характеристикой, а график зависимости аргумента передаточной функции — фазочастотной характеристикой. Обе зависимости, построенные в широком частотном диапазоне, дают наглядное преобразование о характере преобразования сигналов данной цепью.

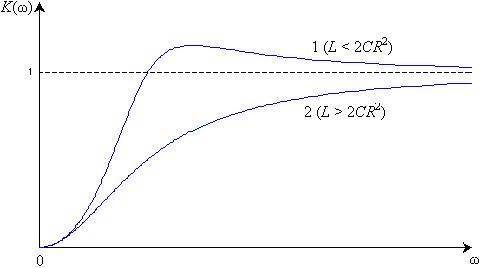
На рис. 6 по приведенным выше зависимостям построены частотные характеристики цепи рис.5.

Из них следует, что эта цепь пропускает преимущественно сигналы высоких частот. В зависимости от соотношения ее амплитудно-частотная характеристика имеет максимум (кривая 1), либо монотонно увеличивается от нулевого значения при w = 0 до K(w) = 1 при w ® ¥. Оба эти предельных режима легко проанализировать. При w = 0 (режим постоянного тока) конфигурация цепи упрощается, так как постоянный ток не протекает через конденсаторы, а индуктивности представляют для него нулевое сопротивление. Поэтому для определения передаточной функции на постоянном токе конденсаторы в схеме следует разомкнуть, а катушки — закоротить. Получим чисто резистивную цепь, анализ которой существенно проще. Аналогично при w ® ¥ сопротивления конденсаторов цепи стремятся к нулю, а сопротивления катушек неограниченно возрастают. Поэтому для анализа цепи при высоких частотах следует, наоборот, закоротить конденсаторы и разомкнуть катушки, что опять сводит задачу к расчету чисто резистивной цепи.

Применим сформулированные правила к анализу асимптотических режимов при w ® 0 и w ® ¥ в рассматриваемой цепи.

Существуют и другие способы представления частотных свойств передаточных функций: путем изображения частотных характеристик вещественной и мнимой частей K(jw) = Kв(w) + jKм(w) либо с помощью построения на комплексной плоскости кривой, которая отвечает совокупности значений K(jw), соответствующих различным частотам — амплитудно-фазовая частотная характеристика.

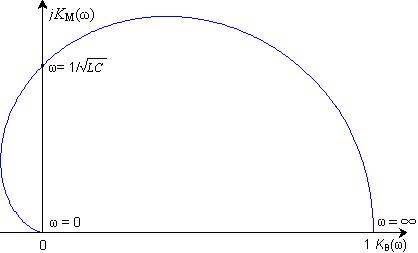
На рис. 7. изображена амплитудно-фазовая частотная характеристика передаточной функции цепи (рис. 8.3).

Для ее построения при отдельных значениях частоты находят вещественную и мнимую части передаточной функции: Kв(w) = K(w) cos q; Kм(w) = K(w) sin q. Эти значения соединяют на комплексной плоскости непрерывной кривой, которая наглядно позволяет проследить характер изменения K(jw) при изменении w от нуля до бесконечности.

Аналогично изображают и частотные характеристики входных функций: сопротивления Z(jw) = R(w) + jX(w) = z(w)e jj(w) — его вещественной и мнимой частей R(w) и X(w), модуля z(w) и фазового сдвига j(w) или проводимости Y(jw).

Дата добавления: 2016-04-02 ; просмотров: 4229 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Компонентные уравнения в комплексной форме

7.3. СВЯЗИ МЕЖДУ СИНУСОИДАЛЬНЫМИ НАПРЯЖЕНИЯМИ И ТОКАМИ
НА ЭЛЕМЕНТАХ R , L , C

Используя компонентные уравнения, установим связь между основными характеристиками тока и напряжения на элементах. Подставив мгновенные значения тока i = I m sin w t в компонентные уравнения для u R и u L и напряжения u = U m sin w t — в i C , получим выражения для u R , u L и i C , приведенные в Таблице 7.1, из которых следуют соотношения между амплитудами и действующими величинами напряжений и токов U и I . Отношение U / I = U m / I m представляет сопротивление элемента — активное R и реактивные — X L (индуктивное) и X C (емкостное). Размерность всех сопротивлений — Ом. Обратные величины I / U представляют проводимости элементов — активную G и реактивные: B L (индуктивную) и B C (емкостную). Значения реактивных сопротивлений (и проводимостей) зависят от частоты. Выражения для мгновенных токов и напряжений i и u показывают, что ток и напряжение на резисторе совпадают по фазе, на индуктивности ток отстает от напряжения на угол p /2, а на емкости ток опережает напряжение на p /2.

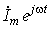
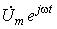
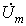
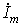
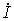
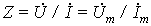
Переход к комплексным характеристикам элементов осуществляется с помощью комплексных изображений мгновенного тока для сопротивления и индуктивности и напряжения для емкости. Подстановка их в компонентные уравнения приводит к комплексным изображениям u R , u L и i C , приведенным в Табл. 7.1, из которых получаем соотношения комплексных амплитуд напряжений и токов элементов и действующих значений и . Они выражают закон Ома в комплексной форме , в которой выступают комплексные сопротивления элементов . Обратные им величины — это комплексные проводимости . Комплексный характер сопротивлений и проводимостей Z и Y отражает информацию о фазовых сдвигах токов и напряжений на элементах.

Связи между синусоидальными напряжениями и токами на элементах R , L , C

Компонентные и системные уравнения, описывающие цепь

Закономерности, описывающие поведение элементов цепи (элементные или компонентные законы)

Это математические выражения, связывающие между собой переменные, описывающие состояние элемента – токи через выводы элемента и напряжения между выводами этого элемента. Такие математические уравнения называют элементными или компонентными законами. Такие законы могут иметь вид алгебраических или дифференциальных уравнений. Количество таких уравнений для элемента с n выводами равно (n‑1).

Простейший вид элемента – с двумя выводами (двухполюсник). Его поведение описывается зависимостью между двумя величинами: iиu. Ее называют вольт-амперной характеристикой ВАХ.

Какая из переменных является независимой (аргументом) – любая.
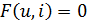
С математической точки зрения – любая.

Как можно определить ВАХ экспериментально? Изменяя одну из величин и измеряя обе.

Элемент называют линейным, если ВАХ – полином первого порядка

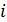
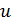
Может ли быть так, что при заданном значении аргумента функция не определяется однозначно?
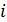
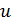
Может ли быть так, что при постоянном значении аргумента функция не сохраняет постоянства?

Пример с конденсатором.
Пример с термозависимым резистором (саморазогрев).
Пример с диодом – нелинейный элемент

Эксперимент по снятию ВАХ резистора и полупроводникового диода а) вручную, б) с помощью характериографа

Простой вариант формирования системы компонентных уравнений для n-полюсника:

· Выбрать один из выводов в качестве базового.

· Задать величины напряжений между каждым из оставшихся и базовым выводом (возможность этого является следствием второго закона Кирхгофа).

· Измерять токи через каждый из выводов за исключением базового.

Система из (n-1) уравнений, описывающая поведение n-полюсника будет иметь вид

здесь F символизирует зависимость, которая может быть алгебраической, либо содержать производные и (или) интегралы переменных u(t) и i(t).

Энергетические свойства элементов электрических цепей.

Диссипативность: (необратимое) превращение электрической энергии в тепло

Переход части электрической энергии в тепло при протекании тока по диссипативным элементам. Компонентное уравнение диссипативного элемента цепи. Потери энергии в электронных информационных устройствах. Почему энергия не может быть сколь-угодно малой.

Большая группа элементов цепей обладает свойством, состоящим в том, что вся энергия, доставляемая токами, протекающими через выводы, превращается внутри таких элементов в тепло. Такие элементы называют диссипативными[2]. Примером такого элемента является резистор, используемый в электронных цепях для …. () Компонентное уравнение диссипативного двухполюсника имеет вид

(2.4)

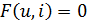
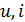
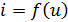
Запись уравнения в таком виде подчёркивает тот факт, что ни одна из двух переменных не является причиной изменения другой величины, т.е. аргументом, независимой переменной, может быть любая из них. Во многих книгах утверждается (считается), что независимой переменной, причиной является изменение напряжения, в то время как изменение тока это следствие, и компонентное уравнение переписывают в виде

(2.5)

Однако утверждение о «первичности» напряжения ошибочно.

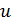
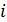
Характеристики диссипативных элементов часто называют «вольт-амперными», поскольку в выражении присутствуют две переменные: напряжение и ток . И вновь отметим, что в приведённом уравнении обе переменные могут изменяться во времени.

Вольт-амперная характеристика 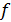может быть функцией любого вида. Так, например, у полупроводниковых диодов характеристики существенно нелинейны и весьма различны для разных типов диодов.

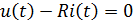
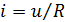
Для металлических проводников компонентная зависимость весьма близка к прямой пропорциональной ‑ это всем известный «закон Ома» , записываемый обычно в виде . Однако при значительной величине тока вследствие саморазогрева зависимость может оказаться весьма «причудливой» (например, для нити лампы накаливания).

В электротехнических устройствах используются многочисленные элементы с числом выводов, превышающим два. Прежде всего, это транзисторы, у которых три вывода (у некоторых полевых транзисторов может быть четыре вывода). Вольт-амперные характеристики многополюсных диссипативных элементов представляют собой семейство функций нескольких аргументов. Количество функций, а также количество аргументов в каждой функции на единицу меньше количества выводов многополюсника.

Емкость: (обратимое) накопление энергии в электрическом поле (заряженного конденсатора).

Запасание части электрической энергии в реактивных элементах цепи ‑ в виде энергии электрического поля в конденсаторе или в виде энергии магнитного поля в индукторе. Компонентные уравнения реактивных элементов (накопителей энергии).

Некоторые виды элементов цепей способны обратимо накапливать электрическую энергию в электрическом или в магнитном поле.

Компонентное уравнение элемента цепи, способного накапливать энергию в электрическом поле (электростатического накопителя), в общем случае имеет вид

(2.6)

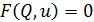
Это соотношение иногда называют «вольт-кулонной» характеристикой. Однако при описании электрической цепи, содержащей электростатический накопитель, состояние цепи описывают, используя только напряжения и токи (и, может быть, их производные и интегралы). Этого можно достигнуть, использовав соотношение между зарядом и током (используемого в определении единицы заряда ):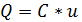

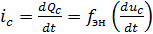
(2.7)

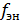
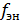
Любой фрагмент электрической цепи, в котором имеются две точки, между которыми существует ненулевое напряжение, обладает свойствами электростатического накопителя. Вид функции зависит от свойств среды, окружающей фрагмент цепи. (Правильные, но непонятные слова). Известно более 300 веществ (сегнетоэлектрики), для которых функция существенно нелинейна.

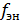
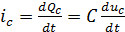
Для большинства веществ функция имеет вид прямой пропорциональной зависимости:

(2.8)

В последней формуле 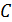– электрическая ёмкость электростатического накопителя, постоянный параметр, измеряемый в фарадах.

Изготавливаются и используются в электрических цепях конденсаторы – двухполюсники, обладающие свойством электростатического накопителя. При проектировании и изготовлении конденсаторов принимают специальные меры для обеспечения постоянства величины их емкости.

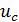
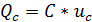
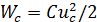
Конденсатор, заряженный до напряжения (и хранящий заряд ) в своём электрическом поле, в соответствии с (2.1) содержит энергию . Из формулы вольт-кулонной характеристики (2.6) и (2.7) могут быть сделаны весьма важные для дальнейшего выводы:
а) скорость изменения напряжения на электростатическом накопителе тем больше, чем больше величина перезаряжающего тока,
б) напряжение на электростатическом накопителе не может измениться скачком, поскольку для этого необходим ток бесконечно большой величины, что физически не реализуемо.

Индуктивность: (обратимое) накопление энергии в магнитном поле тока.

Компонентное уравнение элемента цепи, способного накапливать энергию в магнитном поле (электромагнитного накопителя), имеет вид:

(2.9)

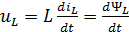
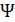
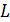
Соотношение (2.9) иногда называют «вебер-амперной характеристикой», поскольку оно устанавливает связь между величиной суммарного магнитного потока (потокосцепления) и величиной тока, создающего этот поток. Величина потокосцепления измеряется в веберах, (как и магнитный поток). Коэффициент пропорциональности называется индуктивностью и измеряется в единицах генри.

Любой фрагмент реальной электрической цепи в некоторой степени обладает свойствами магнитного накопителя, поскольку вокруг проводника с током всегда возникает магнитное поле.

Из формулы вебер-амперной характеристики (2.9) следуют важные для дальнейшего изложения выводы
а) скорость изменения тока в электромагнитном накопителе тем больше, чем больше величина напряжения между его выводами,
б) ток в магнитном накопителе не может измениться скачком, поскольку для этого напряжение между выводами магнитного накопителя должно стать бесконечно большим, что физически не реализуемо.

Для линейных двухполюсников математическое выражение этих свойств:

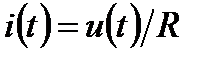
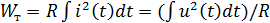
Резистивность (диссипативность): и
это соотношение известно как Закон Ома – ВАХ идеального резистора

Емкость электрическая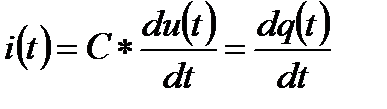
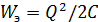
вольт-кулонная характеристика электростатического накопителя энергии

Индуктивность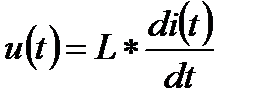
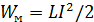
вебер-амперная характеристика электромагнитного накопителя энергии

Два последних соотношения никак не называются, хотя все три формулы представляют собой простейшие математические модели для трех видов двухполюсников: резистора, конденсатора и катушки индуктивности (индуктора).

Любой реальный двухполюсник обладает всеми тремя свойствами, только в разной степени.

В каких случаях можно пренебречь отдельными свойствами. На этот вопрос можно ответить, проведя анализ энергетического баланса.