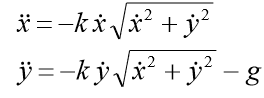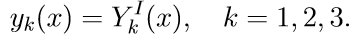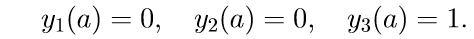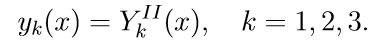МОДЕЛИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Дата добавления: 2015-06-12 ; просмотров: 8136 ; Нарушение авторских прав
Цель работы: освоение методики моделирования линейных дифференциальных уравнений в системе MATLAB и SIMULINK.
I. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1.1. Линейное дифференциальное уравнение.
Многие физические процессы, такие как колебания маятника, движение стрелки гальванометра, изменение высоты при посадке самолета, процессы в электрическом колебательном контуре могут быть описаны линейным однородным дифференциальным уравнением второго порядка
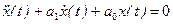
Здесь а0, а1 – постоянные коэффициенты, определяющие характер процесса, точкой обозначается производная по времени. Амплитуда переменной x(t) зависит от начальных условий, например, от начального отклонения x0 маятника и его начальной скорости 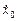
Вид теоретического решения дифференциального уравнения (1) определяется корнями его характеристического полинома
Если корни вещественные и различные р1 = a1`, р2 = a2`, то решение имеет вид
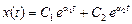
Если корни комплексные р1,2 =a ± ib , то решение имеет вид
Постоянные С1 и С2 находят, подставляя начальные условия в выражения для x(t) и 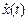
Пример 1. Дано дифференциальное уравнение
Его характеристическое уравнение p 2 + 2p + 2 = 0 имеет корни 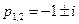
Дифференцируя, находим выражение для 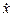
При t = 0 с учетом начальных условий получаем C1 = 2, С2 = 1. Следовательно,
Эффективным средством решения дифференциальных уравнений является численное моделирование в одном из математических пакетов (MATHCAD, MATLAB, SIMULINK и др.). График решения x(t) наблюдается на экране дисплея. В пакете MATLAB для этой цели имеются команды initial, lsim, ode23, ode45, dsolve. Дополнительныe возможности для пользователя предоставляет моделирование в SIMULINK.
1.2. Структурное моделирование линейных дифференциальных уравнений.
При структурном моделировании дифференциальных уравнений в пакете SIMULINK необходимо составить схему моделирования. На ней изображаются вычислительные блоки (усилители, сумматоры, интеграторы) и связи между ними. При проведении моделирования эта схема набирается на экране дисплея с помощью мыши или клавиатуры. По своему смыслу этот процесс аналогичен вводу программы, однако он более прост и нагляден. Подробная информация о реализации таких схем в SIMULINK имеется в разделе 3 учебного пособия Мироновского Л.А., Петровой К.Ю. «Введение в MATLAB» (ГУАП, 2006).
Рассмотрим методику составления схемы моделирования на примере однородного линейного дифференциального уравнения второго порядка
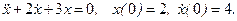
Для построения схемы моделирования воспользуемся методом понижения производной (методом Кельвина). В нем можно выделить четыре шага.
Шаг 1. Разрешаем исходное уравнение относительно старшей производной. В частности для уравнения (2) получаем 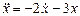
Шаг 2. Полагаем старшую производную известной и выполняем ее последовательное интегрирование, получая все низшие производные и саму переменную х. В случае уравнения (2) для этого потребуется два последовательно включенных интегратора, на выходах которых получим сигналы 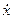
Шаг 3. Формируем старшую производную, используя уравнение, полученное на первом шаге. В нашем примере для этого потребуется сумматор, складывающий сигналы 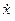
Шаг 4. Объединяем схемы, полученные на втором и третьем шагах, в общую схему моделирования, указываем начальные условия интеграторов.
Применение этой методики для уравнения (2) приводит к схеме, показанной на рис. 1. Она содержит два интегратора, два масштабных усилителя и сумматор (обозначен кружочком).
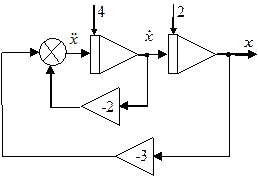 Рис. 1. Схема моделирования уравнения (2) Рис. 1. Схема моделирования уравнения (2) |
Выходной сигнал схемы подается на имитатор осциллографа (блок Scope) или передается в рабочее пространство MATLAB (блоки OUT или ToWorkspase).
1.3. Системы линейных дифференциальных уравнений первого порядка.
Многие технические объекты можно описать системой n линейных дифференциальных уравнений первого порядка:
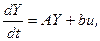
где и – входной сигнал; Y – вектор-столбец выходных переменных yi; b – вектор-столбец коэффициентов bi; A – квадратная матрица коэффициентов aij, 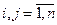
Например, при моделировании летательного аппарата составляющими вектора Y могут быть текущие координаты самолета и скорости их изменения, тогда матрица A будет характеризовать динамику самолета, а слагаемое bи описывать управляющие воздействия, формируемые летчиком или автопилотом.
Один из методов решения системы дифференциальных уравнений основан на предварительном переходе от системы (3) к одному уравнению n-го порядка. Для этого из уравнений системы и из уравнений, полученных их дифференцированием, исключают все переменные кроме одной. Для нее получают одно дифференциальное уравнение. Решая его, определяют эту переменную, а остальные находят, по возможности, без интегрирования.
Пример 2. Дана система из двух дифференциальных уравнений
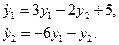
После дифференцирования первого уравнения получаем:
Чтобы исключить у2, вычтем отсюда удвоенное первое уравнение системы (4):
Мы получили линейное неоднородное дифференциальное уравнение второго порядка. Общее решение этого уравнения представляет собой сумму общего решения соответствующего однородного уравнения и частного решения 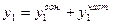
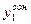
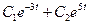
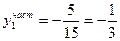
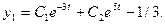
Для определения постоянных коэффициентов С1 и С2 используют начальные условия системы. Аналогичным образом этот метод применяется и для систем уравнений более высоких порядков
1.4. Моделирование системы линейных дифференциальных уравнений.
Если задача описывается системой дифференциальных уравнений первого порядка, то для ее моделирования по методу понижения производной достаточно составить схемы для каждого уравнения отдельно. Например, схема моделирования системы уравнений (4) будет иметь вид, показанный на рис. 2.
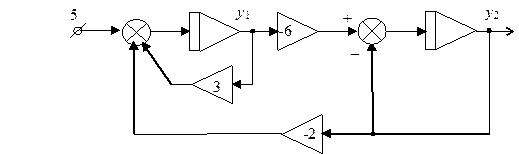 Рис. 2. Схема моделирования системы уравнений (4) Рис. 2. Схема моделирования системы уравнений (4) |
Для наблюдения графиков сигналов у1(t), у2(t) в SIMULINK используется блок осциллографа SCOPE, а для наблюдения фазовой траектории у2 = f (у1) – блок осциллографа XY Graph.
2. ЗАДАНИЕ ПО РАБОТЕ И СОДЕРЖАНИЕ ОТЧЕТА
1. Теоретическое решение уравнения (1) при заданных значениях а0, а1 и начальных условиях x(0) = 5, 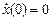
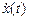
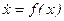
2. Схема моделирования заданного уравнения применительно к SIMULINK.
Теоретическое решение системы дифференциальных уравнений (3) для случая
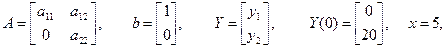
Схема моделирования исходной системы уравнений применительно к SIMULINK.
3. ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
- Набрать в SIMULINK схему моделирования уравнения (1), установить коэффициенты и начальные условия.
- Получить осциллограммы x(t),
и
, сравнить их с теоретическими графиками. Варьировать шаг и метод интегрирования.
- Набрать схему моделирования системы уравнений (3), установить коэффициенты и начальные условия (5).
- Получить осциллограммы у1(t), у2(t) и у2 = f(y1), сравнить их с теоретическими графиками. Варьировать шаг и метод интегрирования.
- Выполнить моделирование системы уравнений (3) в MATLAB, используя команду lsim. Cравнить графики, полученные в MATLAB и SIMULINK.
4. КОНТРОЛЬНЫЕ ВОПРОСЫ
- Решить следующие линейные дифференциальные уравнения:
а)
б)
- При каком значении а и при каких начальных условиях решение уравнения
имеет вид:
- В чем заключается метод понижения производной? Пользуясь этим методом, составить схемы моделирования для всех вариантов п.1.
- Используя метод понижения производной, составить схемы моделирования следующих дифференциальных уравнений:
а) 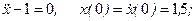
в)
г)
- Схема моделирования представляет собой кольцо из трех интеграторов с единичными коэффициентами и одинаковыми начальными условиями. Найти моделируемое дифференциальное уравнение и его аналитическое решение.
- Как изменятся графики решения линейного однородного дифференциального уравнения при замене знаков всех начальных условий на противоположные?
- Описать процедуру перехода от системы дифференциальных уравнений к одному уравнению и обратную процедуру, рассмотрев случай n=3. Привести пример.
- Составить схему моделирования и найти решение системы линейных дифференциальных уравнений
если матрица A имеет вид
ВАРИАНТЫ ЗАДАНИЙ ПО РАБОТЕ № 2
| № | ||||||||||||
| a1 | 0,1 | 0,1 | 0,5 | 0,1 | 0,1 | 0,5 | 0,1 | 0,1 | 0,5 | 0,1 | 0,1 | 0,6 |
| a0 | 0,4 | 1,6 | 4,8 | 0,5 | 1,8 | 5,0 | 0,6 | 2,0 | 5,4 | 0,7 | 2,2 | 5,8 |
| a11 | -1,0 | -1,0 | -1,0 | -1,0 | -1,0 | -1,0 | -1,0 | -0,9 | -0,9 | -0,9 | -0,9 | -0,9 |
| a12 | 1,0 | 0,8 | 0,7 | 0,6 | 0,57 | 0,4 | 0.35 | 1,0 | 0,8 | 0,7 | 0,6 | 0,5 |
| a22 | -2,0 | -1,8 | -1,7 | -1,6 | -1,5 | -1,4 | -1,3 | -1,9 | -1,7 | -1,6 | -1,5 | -1,4 |
| № | ||||||||||||
| a1 a0 | 0,1 0,8 | 0,3 2,4 | 6,0 | 0,9 8,8 | 0,1 0,9 | 0,3 2,6 | 0,7 6,4 | 1.1 9,0 | 0,2 1,0 | 0,3 2,8 | 0,8 6,8 | 0,6 5,8 |
| a11 | -0,9 | -0,9 | -0,8 | -0,8 | -0,8 | -0,8 | -0,8 | -0,8 | -0,8 | -0,5 | -0,5 | -0,5 |
| a12 | 0,4 | 0,3 | 1,0 | 0,8 | 0,7 | 0,6 | 0.5 | 0,4 | 0,3 | 1,0 | 0,8 | 0,7 |
| a22 | -1,3 | -1,6 | -1,6 | -1,6 | -1,5 | -1,4 | -1,3 | -1,2 | -1,1 | -1,5 | -1,3 | -1,2 |
Ответы на контрольный вопрос 1а,б,в,г:
а. 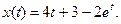
в.
г.
Численное решение математических моделей объектов заданных системами дифференциальных уравнений
Введение:
При математическом моделировании ряда технических устройств используются системы дифференциальных нелинейных уравнений. Такие модели используются не только в технике, они находят применение в экономике, химии, биологии, медицине, управлении.
Исследование функционирования таких устройств требуют решения указанных систем уравнений. Поскольку основная часть таких уравнений являются нелинейными и нестационарными, часто невозможно получить их аналитическое решение.
Возникает необходимость использовать численные методы, наиболее известным из которых является метод Рунге — Кутты [1]. Что касается Python, то в публикациях по численным методам, например [2,3], данных по применение Рунге — Кутты крайне мало, а по его модификации — методу Рунге-Кутта-Фельберга вообще нет.
В настоящее время, благодаря простому интерфейсу, наибольшее распространение в Python имеет функцию odeint из модуля scipy.integrate. Вторая функция ode из этого модуля реализует несколько методов, в том числе и упомянутый пятиранговый метод Рунге-Кутта-Фельберга, но, вследствие универсальности, имеет ограниченное быстродействие.
Целью настоящей публикации является сравнительный анализ перечисленных средств численного решения систем дифференциальных уравнений с модифицированным автором под Python методом Рунге-Кутта-Фельберга. В публикации так же приведены решения по краевым задачам для систем дифференциальных уравнений (СДУ).
Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
Для одного дифференциального уравнения n – го порядка, задача Коши состоит в нахождении функции, удовлетворяющей равенству:
и начальным условиям
Перед решением эта задача должна быть переписана в виде следующей СДУ
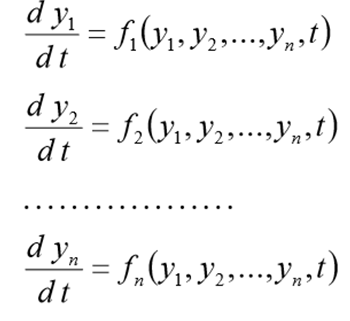
с начальными условиями
Модуль имеет две функции ode() и odeint(), предназначенные для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (задача Коши). Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.
Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат odeint(func, y0, t[,args=(), . ]) Аргумент func – это имя Python функции двух переменных, первой из которых является список y=[y1,y2. yn], а второй – имя независимой переменной.
Функция func должна возвращать список из n значений функций 
Второй аргумент y0 функции odeint() является массивом (или списком) начальных значений 
Третий аргумент является массивом моментов времени, в которые вы хотите получить решение задачи. При этом первый элемент этого массива рассматривается как t0.
Функция odeint() возвращает массив размера len(t) x len(y0). Функция odeint() имеет много опций, управляющих ее работой. Опции rtol (относительная погрешность) и atol (абсолютная погрешность) определяют погрешность вычислений ei для каждого значения yi по формуле
Они могут быть векторами или скалярами. По умолчанию
Вторая функция модуля scipy.integrate, которая предназначена для решения дифференциальных уравнений и систем, называется ode(). Она создает объект ОДУ (тип scipy.integrate._ode.ode). Имея ссылку на такой объект, для решения дифференциальных уравнений следует использовать его методы. Аналогично функции odeint(), функция ode(func) предполагает приведение задачи к системе дифференциальных уравнений вида (1) и использовании ее функции правых частей.
Отличие только в том, что функция правых частей func(t,y) первым аргументом принимает независимую переменную, а вторым – список значений искомых функций. Например, следующая последовательность инструкций создает объект ODE, представляющий задачу Коши.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
При численном решении задачи Коши
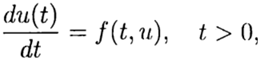

по известному решению в точке t =0 необходимо найти из уравнения (3) решение при других t. При численном решении задачи (2),(3) будем использовать равномерную, для простоты, сетку по переменной t с шагом т > 0.
Приближенное решение задачи (2), (3) в точке 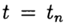

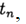


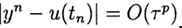

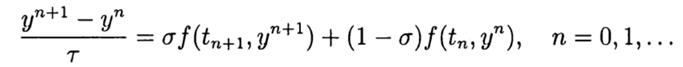
При 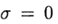
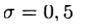
Явные схемы второго и более высокого порядка аппроксимации удобно строить, ориентируясь на метод предиктор-корректор. На этапе предиктора (предсказания) используется явная схема
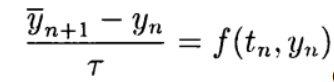
а на этапе корректора (уточнения) — схема
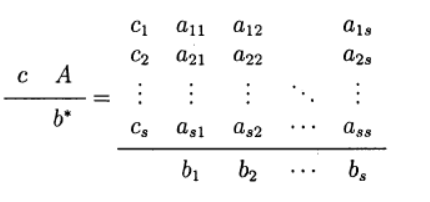
В одношаговых методах Рунге—Кутта идеи предиктора-корректора реализуются наиболее полно. Этот метод записывается в общем виде:

Формула (6) основана на s вычислениях функции f и называется s-стадийной. Если 
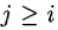

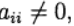

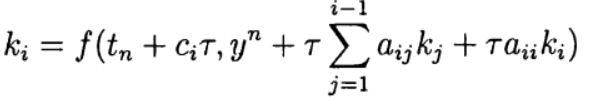
О таком методе Рунге—Кутта говорят как о диагонально-неявном. Параметры 
Одним из наиболее распространенных является явный метод Рунге—Кутта четвертого порядка

Метод Рунге—Кутта— Фельберга
Привожу значение расчётных коэффициентов 
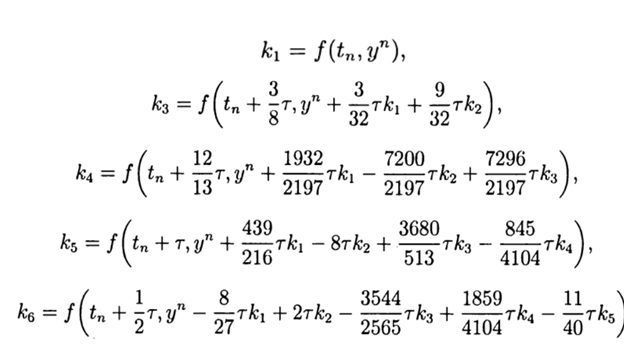
С учётом(9) общее решение имеет вид:
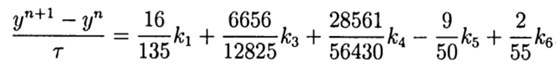
Это решение обеспечивает пятый порядок точности, остаётся его адаптировать к Python.
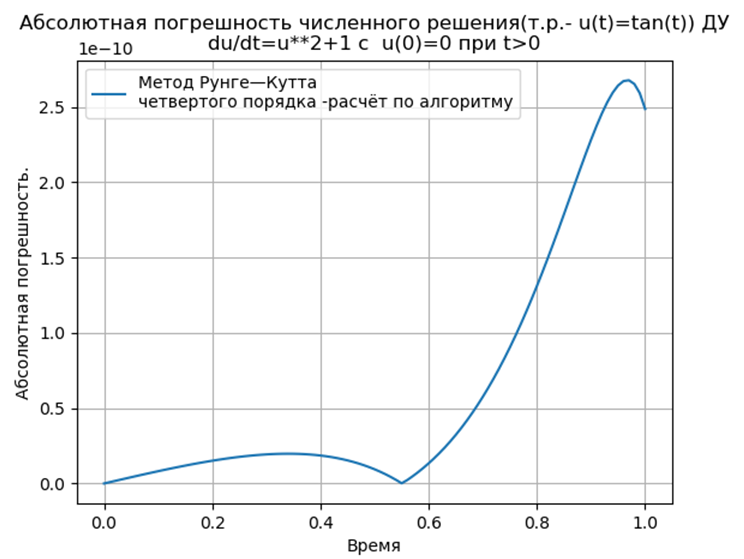
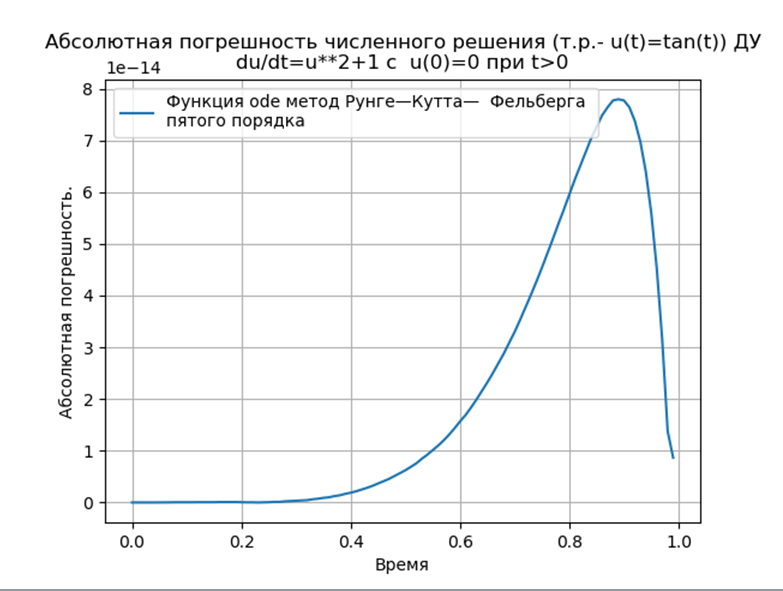
Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения  с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
Адаптированные к Python методы Рунге—Кутта и Рунге—Кутта— Фельберга имеют меньшую абсолютную, чем решение с применением функции odeint, но большую, чем с использованием функции edu. Необходимо провести исследование быстродействия.
Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
Сравнительный анализ проведём на примере модельной задачи, приведенной в [2]. Чтобы не повторять источник, приведу постановку и решение модельной задачи из [2].
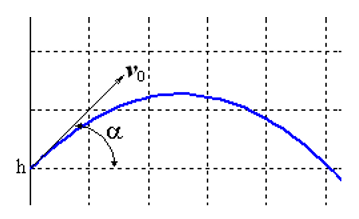
Решим задачу Коши, описывающую движение тела, брошенного с начальной скоростью v0 под углом α к горизонту в предположении, что сопротивление воздуха пропорционально квадрату скорости. В векторной форме уравнение движения имеет вид
где 



Особенность этой задачи состоит в том, что движение заканчивается в заранее неизвестный момент времени, когда тело падает на землю. Если обозначить 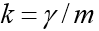
К системе следует добавить начальные условия: 

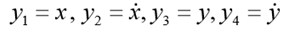
Для модельной задачи положим 
Flight time = 1.2316 Distance = 5.9829 Height =1.8542
Flight time = 1.1016 Distance = 4.3830 Height =1.5088
Flight time = 1.0197 Distance = 3.5265 Height =1.2912
Flight time = 0.9068 Distance = 2.5842 Height =1.0240
Время на модельную задачу: 0.454787
Для реализации средствами Python численного решения СДУ без использования специальных модулей, мною была предложена и исследована следующая функция:
def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6
Функция increment(f, t, y, tau) обеспечивает пятый порядок численного метода решения. Остальные особенности программы можно посмотреть в следующем листинге:
Время на модельную задачу: 0.259927
Предложенная программная реализация модельной задачи без использования специальных модулей имеет почти в двое большее быстродействие, чем с функцией ode, однако нельзя забывать, что ode имеет более высокую точность численного решения и возможности выбора метода решения.
Решение краевой задачи с поточно разделёнными краевыми условиями
Приведем пример некоторой конкретной краевой задачи с поточно разделенными краевыми условиями:
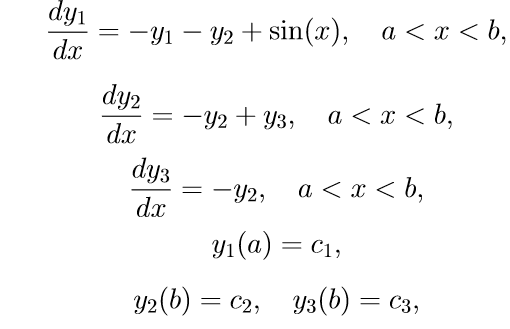
Для решения задачи (11) используем следующий алгоритм:
1. Решаем первые три неоднородные уравнения системы (11) с начальными условиями 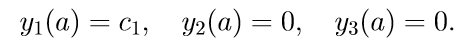
Введем обозначение для решения задачи Коши:
2. Решаем первые три однородные уравнения системы (11) с начальными условиями 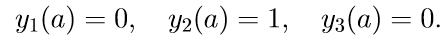
Введем обозначение для решения задачи Коши:
3. Решаем первые три однородные уравнения системы (11) с начальными условиями
Введем обозначение для решения задачи Коши:
4. Общее решение краевой задачи (11) при помощи решений задач Коши записывается в виде линейной комбинации решений: 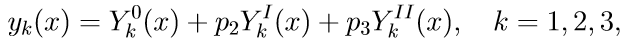
где p2, p3 — некоторые неизвестные параметры.
5. Для определения параметров p2, p3, используем краевые условия последних двух уравнений (11), то есть условия при x = b. Подставляя, получим систему линейных уравнений относительно неизвестных p2, p3:

Решая (12), получим соотношения для p2, p3.
По приведенному алгоритму с применением метода Рунге—Кутта—Фельберга получим следующую программу:
y0[0]= 0.0
y1[0]= 1.0
y2[0]= 0.7156448588231397
y3[0]= 1.324566562303714
y0[N-1]= 0.9900000000000007
y1[N-1]= 0.1747719838716767
y2[N-1]= 0.8
y3[N-1]= 0.5000000000000001
Время на модельную задачу: 0.070878
Вывод
Разработанная мною программа отличается от приведенной в [3] меньшей погрешностью, что подтверждает приведенный в начале статьи сравнительный анализ функции odeint с реализованным на Python метода Рунге—Кутта—Фельберга.
3. Н.М. Полякова, Е.В. Ширяева Python 3. Создание графического интерфейса пользователя (на примере решения методом пристрелки краевой задачи для линейных обыкновенных дифференциальных уравнений). Ростов-на-Дону 2017.
Компьютерное моделирование «Дифференциальные уравнения»
по компьютерному моделированию
Введение
Цель данной работы – составление математической модели процесса, описанного в сюжетной задаче и разрешение соответствующего дифференциального уравнения. В качестве математической модели процесса предполагается использование дифференциального уравнения. Задачи моделирования:
классификация полученной модели;
аналитическое, численное и символьное решение полученного дифференциального уравнения;
построение графиков решений, найденных разными методами;
оценка погрешности численного решения;
анализ полученных результатов.
В качестве инструментального средства для компьютерного моделирования выбраны пакеты Mathcad и Maple . Выбор пакета Mathcad обусловлен тем, что:
математические выражения в среде Mathcad записываются в общепринятой нотации;
в пакет встроен мощный математический аппарат, позволяющий решать сложные задачи и находить решение задачи Коши;
пакет имеет мощные средства графического представления информации.
Выбор пакета Maple обусловлен тем, что данный пакет имеет интегрированный символьный процессор, позволяющий производить аналитические преобразования, и, в частности, получать решение задачи Коши в аналитическом виде.
§1. Понятие о дифференциальных уравнениях.
Определение 1. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.
Определение 2 . Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
Порядком дифференциального уравнения называется наивысший порядок производной, входящей в это уравнение.
Определение 3. Дифференциальным уравнением первого порядка называется соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:
Определение 4. Дифференциальное уравнение 
Такое уравнение можно представить также в виде:
Перейдем к новым обозначениям
После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.
Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение.
1 .1 Задача Коши.
Во многих задачах, которые приводятся к дифференциальным уравнениям, требуется найти решение, принимающее заданное значение при заданном значении независимой переменной. Такая задача называется начальной задачей Коши.
Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям.
Задачу Коши для ОДУ первого порядка

формулируют так: найти решение x(t) уравнения (1.1), такое,
где x 0 , t 0 — заданные числа. Условие (1.2) называют на-
начальным условием, или условием Коши, а функцию х( t ),
удовлетворяющую ОДУ (1.1) и начальному условию (1.2), —
решением задачи Коши.
Пусть х = x(t) — решение ОДУ (1.1), определенное в ин-
интервале ( t 0 — δ , t 0 + δ ), δ > 0. Интегральной кривой ОДУ (1 .1)
будет график функции х = x(t). Можно, следовательно, задачу
Коши сформулировать так: найти интегральную кривую ОДУ
(1.1), проходящую через заданную точку (t 0 , x 0 ).
1. 2 Метод Эйлера.
Дано 
Пусть требуется найти решение задачи Коши (1), (2) на замкнутом интервале [ x 0 , X ]. Разделим этот интервал на n равных частей точками 
применим метод Эйлера.
Выберем произвольный отрезок 
Погрешность будет определяться следующей формулой:

где 


1.3 Метод Рунге-Кутта (метод 4-ого порядка).
Метод Рунге–Кутта часто применяется для решения дифференциальных уравнений и систем уравнений из-за его высокой точности. Отличительная особенность метода – уточнение наклона интегральной кривой за счет вычисления производной не только в начале текущего отрезка интегрирования, но и, например, в середине отрезка (для двучленных схем Рунге–Кутта) или четырехкратное вычисление производных в методе четвертого порядка.
Рассмотрим задачу Коши

Тогда приближенное значение в последующих точках вычисляется по итерационной формуле:

где
Погрешность будет оцениваться следующим равенством:
§2. Технология решения дифференциальных уравнений в пакете Maple .
Аналитическое (символьное) решение ОДУ.
Maple позволяет решать дифференциальные уравнения как аналитически, так и численно. Для решения ОДУ предназначена функция dsolve ( deqn , var , opt ) , где deqn – одно дифференциальное уравнение n -го порядка или система дифференциальных уравнений первого порядка (заданная в виде множества), var – переменная или переменные, относительно которых ищется решение, opt – необязательный аргумент, в котором можно указать вид представления решения.
Общее решение дифференциального уравнения зависит от произвольных постоянных, которые обозначаются как _ С1 , _ С2 ,… _ С N.
Решение задачи Коши в Maple .
Производные в начальных условиях задачи Коши записываются с помощью дифференциального оператора D , например, вторая производная y в точке ноль задается как D ( D ( y ))(0) или ( D @@2)( y )(0).
При решении задачи Коши (краевой задачи) выражение deqn должно иметь структуру множества, т.е неупорядоченный набор данных, перечисленных через запятую и заключенных в фигурные скобки, и содержать помимо уравнения начальные условия (краевые условия).
Графическое представление решения ОДУ.
Для графического представления результатов решения дифференциальных уравнений используем функцию:
Plot(f(x), x=x_min..x_max, y=y_min..y_max, opt) . Где f ( x ) – функция, для которой строиться график, x = x _ min .. x _ max – диапазон изменения независимой переменной х , y = y _ min .. y _ max – диапазон отображения графика по оси ординат, opt – набор опций, задающих стиль построения графика (толщину и цвет кривых, тип кривых, метки на них и т.д.). Последние два аргумента необязательны и могут отсутствовать.
§3. Технология решения дифференциальных уравнений в пакете MathCad .
Дифференциальные уравнения (ДУ), являясь основой математического естествознания, широко используются в качестве математических моделей реальных процессов. Многие физические и научно-технические задачи, особенно относящиеся к анализу динамических систем и к их математическому моделированию, базируются на решении ДУ и систем таких уравнений.
Одним из преимуществ компьютерного решения ДУ в системе Mathcad является возможность предоставления получаемых результатов в графическом виде, что позволяет получать наиболее полную информацию о поведении решения и исследовать его.
Рассмотрим встроенные функции Mathcad, предназначенные для решения ДУ которые использовались в данной курсовой работе. Несмотря на различные методы поиска решения, каждая из этих функций требует, чтобы были заданы, по крайней мере, следующие величины, необходимые для поиска решения:
набор точек, в которых нужно найти решение;
само ДУ, записанное в некотором специальном виде.
Замечание: с помощью встроенных функций получаем частное решение ДУ, соответствующее заданным начальным или граничным условиям, т.е. решаем задачу Коши или краевую задачу соответственно.
Встроенные функции системы Mathcad
Предназначена для решения систем ОДУ в форме Коши методом Рунге-Кутта четвёртого порядка с фиксированным шагом.
y – вектор начальных условий размерности n, где n – порядок ОДУ или число уравнений в системе(если решается система уравнений). Для ОДУ первого порядка вектор начальных условий вырождается в одну точку y 0 .
x1,x2 – граничные точки интервала, на котором ищется решение ДУ. Начальные условия, заданные в векторе y, — это значение решения в точке x1.
N – число точек(не считая начальной точки), в которых ищется приближённое решение. Число строк в матрице, возвращаемой функцией rkfixed, равно N+1.
D(x,y) — вектор функция, состоящая из n элементов и содержащая первые производные искомых функций, т.е. правые части системы ОДУ, представленных в нормальной форме форме Коши). Для ОДУ первого порядка вырождается в скалярную функцию.
В результате решения получается матрица, состоящая из n – столбцов(n – порядок ОДУ или число элементов в вектор-функции D (x, y ), где первый столбец содержит точки, в которых ищется приближённое решение, оставшиеся столбцы содержат
для ОДУ 1-го порядка: значения найденного приближённого решения y ( x ) в соответствующих точках 1-го столбца;
§4. Этапы проведения вычислительного эксперимента
Анализ объекта исследования, построение описательной модели.
Замена реального объекта его знаковой информационной моделью.
Построение компьютерной модели:
Mathcad ( метод Рунге-Кутта)
— задаем вектор начальных условий;
— представляем данное дифференциальное уравнение в векторной форме;
2) Mathcad (метод Эйлера):
— задаем начальную точку интервала, находим шаг вычислений;
— задаем вектор начальных условий;
— задаем функцию для вычисления последующих значений;
— записываем реккурентные формулы для вычисления значений функции;
3) Maple (символьное решение)
— задаем дифференциальное уравнение.
4. Проведение расчетов на компьютере, компьютерный эксперимент.
1) Mathcad (метод Рунге-Кутта):
— применение встроенной функции rkfixed для решения дифференциального уравнения;
2) Mathcad (метод Эйлера):
— применение рекуррентных формул для нахождения решения дифференциального уравнения;
3) Maple (символьное решение)
— применение встроенной функции dsolve ;
5. Анализ результатов моделирования;
6. Формулировка прогнозов и выводов.
§5. Постановка задачи.
Кривая проходит через точку (1,2) и обладая тем свойством, что отношение ординаты любой ее точки к абсциссе пропорционально угловому коэффициенту касательной к этой кривой, проведенной в той же точке с коэффициентом пропорциональности К=3. Найти уравнение кривой.
Для решения задачи необходимо знать следующее:
Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке. Угловой коэффициент которой выражается производной.
y = y ( x ) – искомая кривая
k – коэффициент пропорциональности
График искомой кривой должен выглядеть:
Погрешность метода Эйлера не должна превосходить (-2) степени. Погрешность метода Рунге-Кутта не должна превосходить (-5) степени.
§6. Составление модели процесса. Аналитическое решение.
Пусть y = y ( x ) – искомая кривая. Так как кривая проходит через точку А(1,2), то y (1)=2. Учитывая тот факт, что тангенс угла касательной равен коэффициенту при x в уравнении касательной получим:
Получаем задачу Коши:
Решим это дифференциальное уравнение:

Подставим получившееся значение в наше уравнение. Получим:

Ответ: Искомая кривая
Анализ результатов и выводы
При аналитическом решении дифференциального уравнения была получена кривая 
Список используемой литературы
Алексеева Т.А. Компьютерное моделирование в пакете Mathcad (дифференциальные уравнения). Методические указания к курсовой работе. – С-Пб: Ленинградский государственный университет им. А.С. Пушкина, 2005.
Алексеева Т.А. Информационные технологии в математике. Часть I . (Система Mathcad ). Учебное пособие. – С-Пб: Ленинградский государственный университет им. А.С. Пушкина, 200 5 .
Алексеева Т.А., Жихарева А.А. Информационные технологии в математике. Часть II . (пакет Maple ). Учебное пособие. – С-Пб: Ленинградский государственный университет им. А.С. Пушкина, 2007.
Алексеева Т.А. Компьютерное моделирование в пакете Maple (дифференциальные уравнения). Методические указания к курсовой работе. – С-Пб: Ленинградский государственный университет им. А.С. Пушкина, 200 3 .
Матвеев Н.М. Дифференциальные уравнения. – M: Просвещение, 1989г.
Приложение
Maple
Найдем общее решение дифференциального уравнения
Решим задачу Коши с заданными начальными условиями
Warning, the name changecoords has been redefined
Mathcad
Решим уравнение с разделяющимися переменными
Численное решение
Решение с шагом h = 0.1
погрешность решения с шагом h = 0,1 —
сравнение с точным решением

http://habr.com/ru/post/418139/
http://infourok.ru/kompyuternoe-modelirovanie-differencialnie-uravneniya-2023155.html
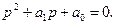
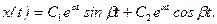
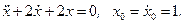
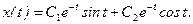
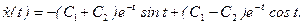
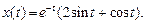
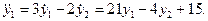
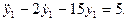
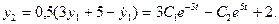
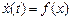 , сравнить их с теоретическими графиками. Варьировать шаг и метод интегрирования.
, сравнить их с теоретическими графиками. Варьировать шаг и метод интегрирования.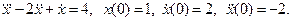
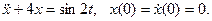
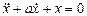 имеет вид:
имеет вид: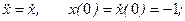
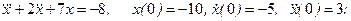
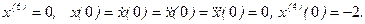
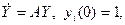 если матрица A имеет вид
если матрица A имеет вид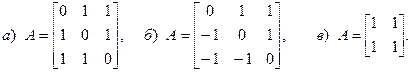
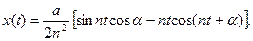

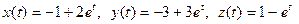
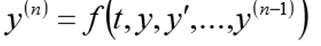
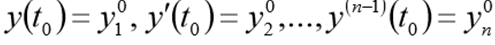


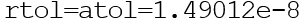
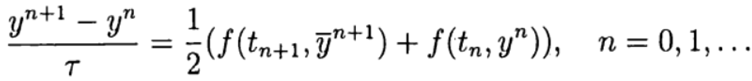
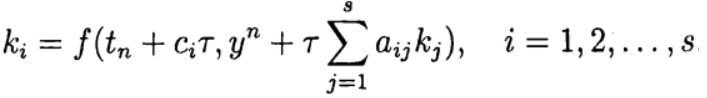
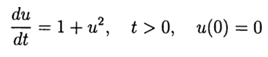 с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга