Математическое описание.
Этапы составления математического описания. Наиболее общим приемом разработки математического описания является блочный принцип составления математического описания. Согласно этому принципу составление математического описания базируется на результатах системного анализа объекта моделирования, выделение отдельных подсистем, или блоков модели и их описанию. Общее описание объекта выполняется путем объединения описания отдельных блоков на основе структурного анализа с учетом взаимосвязей между отдельными блоками.
Состав математического описания. В составе математического описания, разработанного на основе физико-химической природы протекающих в системе процессов, можно выделить следующие группы уравнений:
1. Уравнения баланса масс и энергии, записанные с учетом выбранной структуры потоков веществ и количества взаимодействующих фаз.
2. Уравнения «элементарных» процессов для локальных элементов потоков. К ним относятся описания процессов массо- и теплообмена, скоростей химических реакций, фазовых переходов и т.д.
3. Теоретические, полуэмпирические или эмпирические соотношения между параметрами процесса. Например, зависимость коэффициента теплопередачи от скоростей потоков и их состава, зависимость теплоемкости от состава и т.д.
Ограничения на параметры процесса. При моделировании некоторых процессов необходимо учитывать ограничения на диапазон изменения некоторых параметров. Например, температура процесса не должна превышать допустимую температуру, при которой материал сохраняет прочность, давление в аппарате не должно превышать допустимого, скорости потоков не должны превышать возможности насосного оборудования и т.д.
Общим требованием для всех моделей является то, что число уравнений и различных соотношений, включенных в математическое описание, должно быть равно числу внутренних, т.е. зависящих от режима моделируемого объекта параметров, находимых в результате моделирования.
Типы уравнений. Для математического описания различных свойств моделируемых объектов обычно применяют следующие типы уравнений:
· Конечные алгебраические или трансцендентные уравнения – для описания стационарных режимов работы объектов с сосредоточенными параметрами.
· Обыкновенные дифференциальные уравнения – для описания стационарных режимов работы объектов с распределенными параметрами или для описания нестационарных режимов работы объектов с сосредоточенными параметрами.
· . Дифференциальные уравнения в частных производных – для описания динамики объектов с распределенными параметрами или для описания стационарных режимов работы объектов, с несколькими пространственными координатами.
Иногда, для описания динамики объектов с распределенными параметрами рассматривают времена релаксации отдельных параметров. Тогда выделив параметры, для которых времена релаксации очень малы, можно для них приравнять частные производные по времени нулю. В этом случае можно получить так называемые квазинестационарные модели. Для описания динамики таких объектов можно использовать более простые уравнения.
Дата добавления: 2015-08-14 ; просмотров: 4301 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Математическое описание, расчеты и исследование технологических процессов на вычислительных машинах
8.1 Математическое описание, расчеты и исследование технологических процессов на вычислительных машинах
При исследовании промышленных объектов и систем управления возможность экспериментирования обычно весьма ограничена, и эксперимент дает лишь частичную информацию о характеристиках объекта. Такую информацию можно использовать для решения конкретной инженерной задачи или проверки теоретического расчета для данной конструкции и режима работы объекта, однако она недостаточна для теоретических обобщений. Значительно более полную информацию об объекте или системе управления можно получить при помощи математического описания и исследования его на вычислительных машинах.
В результате конкретизированного описания получают математические модели реальных систем. В математически подобных явлениях процессы имеют различную физическую природу, но описываются одинаковыми уравнениями. Математическое моделирование – метод исследования физических явлений (в том числе и технологических процессов) с помощью специальных моделей, основанный на идентичности формы уравнений и однозначности соотношений между переменными в уравнениях оригинала и модели.
Математическую модель процесса можно построить двумя путями:
- создать теоретическую модель путем глубокого изучения физико-химических закономерностей, присущих процессу; построить формальную аппроксимацию исследуемого процесса, рассмотрев его как черный ящик и использовав зависимости между выходными и входными величинами, установленные экспериментальным путем.
Теоретическую модель можно разработать в период исследования объекта управления или на стадии его проектирования. Такие модели универсальны и описывают целую группу аналогичных объектов. Их недостатками являются сложность и неполная адекватность реальным процессам. Для получения не только качественной картины, но и достоверных количественных зависимостей обычно нужно корректировать теоретическую модель по данным исследования реального процесса.
Модели, созданные на основании экспериментальных статистических данных, достаточно просты и приспособлены для реализации в управляющих машинах. Однако их невозможно разработать на стадии проектирования нового процесса, и они пригодны только для того конкретного объекта, на котором производилось исследование. Для распространения таких моделей на другие однотипные процессы необходима их корректировка.
Возможен и комбинированный подход – в теоретической модели неизвестные и сложные зависимости, некоторые коэффициенты уравнений и т. п. определяются экспериментальным путем. Математические модели исследуются на вычислительных машинах и устройствах прямой аналогии.
Основные этапы работ по математическому моделированию технологических процессов следующие.
Составление формализованного математического описания элементарных процессов для каждого звена исследуемой системы. Составление математической модели процесса – системы уравнений, описывающей элементарные процессы для всех звеньев; уравнений связи между элементарными процессами; уравнений, описывающих ограничения процесса. При решении задач оптимизации система уравнений дополняется целевой функцией.
Для получения модели САУ модель процесса дополняется уравнениями управляющих устройств.
Составление алгоритма решения задачи на вычислительной машине, программирование для цифровых вычислительных машин (ЦВМ) или составление схемы набора для аналоговых (АВМ). Исследование модели на вычислительной машине для выявления особенностей процесса или САУ и решения задач оптимизации.
Рассмотрим решение этих задач на конкретных примерах.
8.2 Составление дифференциальных уравнений, описывающих переходные процессы
Для составления уравнений переходного процесса автоматическая система разделяется на звенья с минимальным числом степеней свободы. При исследовании сложных систем задача облегчается составлением структурных схем. Для каждого звена записывается дифференциальное уравнение переходного процесса на основании физического или химического закона, которому он подчиняется. Например, для математического описания переходных процессов перемещения жидкостей, газов или паров используется закон сохранения материи; при описании процессов теплообмена применяется закон сохранения энергии и т. д.
Математическое выражение закона, которому подчиняется описываемый переходный процесс в элементарном звене, является дифференциальным уравнением звена. Составив дифференциальное уравнение для всех элементарных звеньев системы, получим систему уравнений, описывающую исследуемый переходный процесс в целом.
(«1») Большинство управляемых объектов является, строго говоря, нелинейными системами с распределенными параметрами, поэтому точное математическое описание их обычно приводит к сложным нелинейным дифференциальным уравнениям в частных производных. Для решения дифференциальных уравнений обычными математическими методами, нужно проанализировать физическую сущность процесса и упростить задачу, сделав ряд обоснованных предположений и исключив из уравнения члены высшего порядка малости, не оказывающие существенного влияния на переходный процесс.
Следует иметь в виду, что использование для расчетов ЦВМ позволяет решать весьма сложные задачи. Поэтому при оценке допустимой и целесообразной степени упрощения математического описания нужно исходить из необходимой точности решения поставленной задачи в зависимости от того, является ли целью исследования определение только качественной картины процесса, получение конкретного инженерного решения или тонкий анализ с возможно более полным учетом всех факторов.
Рассмотрим примеры составления дифференциальных уравнений различных систем, начиная с простейших.
8.2.1 Одноемкостные системы с сосредоточенными параметрами
Автоматическая система или отдельное звено обладают сосредоточенными параметрами, если их поведение определяется конечным числом независимых переменных. Число степеней свободы такой системы равно числу независимых переменных величин этой системы.
Переходные процессы в системах с сосредоточенными параметрами описываются обыкновенными дифференциальными уравнениями. Примерами подобных систем с одной степенью свободы могут служить физический маятник, двигатель внутреннего сгорания с маховиком (при управлении числом оборотов), одноемкостный технологический аппарат (при регулировании уровня жидкости в нем).
Состояние перечисленных систем определяется одним параметром: отклонением центра тяжести маятника от равновесия, угловой скоростью вращения маховика двигателя, высотой уровня жидкости в аппарате, В качестве простейшего примера рассмотрим процесс теплообмена баллона стеклянного ртутного термометра с окружающей средой.
При изменении температуры среды ртуть, заключенная в баллоне термометра, поглощает или отдает тепло. Переходный процесс подчиняется закону сохранения энергии.
Для упрощения математического описания этого процесса сделаем следующие предположения.
Система состоит из одной тепловой емкости, сосредоточенной в ртути. Тепловой емкостью тонкой стеклянной стенки термометра пренебрегаем, так как она незначительна по сравнению с тепловой емкостью ртути. Система обладает сосредоточенным параметром, т. е. температура одинакова во всем объеме ртути. Основанием для этого служит высокий коэффициент теплопроводности ртути. Потерями тепла пренебрегаем. Это справедливо в случае хорошей тепловой изоляции места установки термометра и небольшой части термометра, выступающей из аппарата. Коэффициент теплопередачи и теплоемкость ртути в пределах изменения измеряемой температуры постоянны.
С учетом сделанных допущений тепловой баланс термометра в переходном процессе опишется линейным дифференциальным уравнением первого порядка
где к – коэффициент теплопередачи; А – поверхность теплообмена; с – теплоемкость ртути, заключенной в баллоне; – температура среды, окружающей баллон термометра; – температура ртути в баллоне термометра.
Уравнение (8.1) перепишем в виде:
В правой части уравнения принято писать члены, определяющие внешнее воздействие на систему, а в левой – описывающие переходный процесс в системе под действием возмущения.
Описанную одноемкостную систему можно рассматривать как элементарное апериодическое звено. Аналогичную форму дифференциальных уравнений имеют переходные процессы в одноемкостных тепловых, гидравлических, электрических и других системах с сосредоточенными параметрами, обладающих самовыравниванием.
(«2») Переходные процессы в одноемкостных системах с сосредоточенными параметрами, не обладающих самовыравниванием, описываются уравнениями аналогичными, т. е. их можно рассматривать как элементарные интегрирующие звенья.
8.2.2 Многоемкостные системы с сосредоточенными параметрами
При математическом описании многоемкостных систем необходимо различать независимые и взаимодействующие емкости.
Если система состоит из независимых емкостей с сосредоточенным параметром, то переходный процесс в каждой из емкостей (звеньев) зависит от значения ее постоянной времени – предполагается, что запаздывание отсутствует – и от возмущающего воздействия. Такие системы легко представить структурно в виде цепочки из детектирующих элементарных звеньев, соединенных последовательно или параллельно.
При взаимодействующих емкостях с сосредоточенными параметрами переходный процесс в каждой емкости зависит не только от ее постоянной времени, но и от параметров соседних емкостей, что осложняет исследование. Ниже будет показано, что систему с взаимодействующими емкостями можно представить в виде эквивалентной системы с таким же количеством независимых емкостей, постоянные времени этой системы отличаются от таковых исходной системы.
Рассмотрим пример, иллюстрирующий это положение для двухъемкостных систем, хотя оно применимо и для систем с любым количеством емкостей.
В системе, состоящей из двух теплообменников, вода проходит последовательно через оба теплообменника, нагреваясь острым паром. Благодаря интенсивному барботажу пара жидкость хорошо перемешивается, поэтому теплообменники можно приближенно рассматривать как одноемкостные аппараты с сосредоточенным параметром. Температура во втором по ходу жидкости теплообменнике не влияет на температуру в первом, т. е. система состоит из двух независимых емкостей.
Тепловой баланс для первого теплообменника:
где – температура холодной воды на входе в теплообменник; – температура в первом теплообменнике; – тепловая емкость (или объем) воды в первом теплообменнике; с – тепловая емкость (или объем) воды, протекающей через теплообменники в единицу времени.
Тепловой баланс для второго теплообменника:
где – температура во втором теплообменнике; – тепловая емкость (или объем) воды во втором теплообменнике.
Продифференцируем уравнение (8.4), подставим полученное значение в уравнение (8.3) и исключим неизвестную температуру и ее производную.
Получим уравнение теплового баланса системы:
Отношения и имеют размерность времени и являются постоянными времени теплообменников. Перепишем уравнение (8.5) в виде:
Такой вид уравнения типичен для любой системы с двумя детектирующими емкостями с сосредоточенными параметрами. Структурно ее можно изобразить двумя последовательно соединенными элементарными апериодическими звеньями (при наличии самовыравнивания в емкостях).
Переходный процесс в системе, состоящей из двух независимых звеньев, определяется решением уравнения (8.6):
(«3») В качестве примера системы с двумя взаимодействующими емкостями рассмотрим переходный процесс в стеклянном ртутном термометре с защитной металлической гильзой (рисунок 8.1). Примем те же упрощающие предположения, что и в рассмотренном выше примере.
Рисунок 8.1 – Поперечное сечение ртутного термометра в защитной металлической гильзе (взаимодействующие емкости)
Тепловой баланс в неустановившемся состоянии для тепловой емкости защитной гильзы выразится уравнением:
где – коэффициент теплопередачи от окружающей среды к наружной стенке защитной гильзы; – коэффициент теплопередачи от гильзы к термометру; – наружная поверхность защитной гильзы; – поверхность баллона термометра; – температура среды, окружающей защитную гильзу, – температура стенки защитной гильзы; – температура ртути в баллоне.
Аналогично для тепловой емкости ртути тепловой баланс определится по уравнению:
Исключим из этих уравнений неизвестную температуру стенки гильзы. Преобразовав и продифференцировав уравнение (8.9), получим:
Подставим правую часть уравнения (8.9) в уравнение (8.8):
Решение уравнения (8.12) дает переходный процесс в системе, состоящей из двух взаимодействующих звеньев:
(«4») Уравнение (8.13) аналогично уравнению (8.7), следовательно, систему с двумя взаимодействующими звеньями с постоянными времени и можно рассматривать как систему с двумя независимыми звеньями с новыми постоянными времени и. Этот вывод важен для структурного анализа и моделирования автоматических систем.
Если в уравнении (8.14) член мал по сравнению с и, то разница между постоянными времени исходной системы с взаимодействующими звеньями и эквивалентной системы с независимыми звеньями будет мала и ею можно пренебречь.
Эффект взаимодействия звеньев возрастает, когда их постоянные времени близки по величине, однако нужно иметь в виду, что он зависит от индивидуальных значений величин, определяющих и.
Важно определить, при каких условиях взаимодействие между звеньями настолько существенно, что его необходимо учитывать два варианта установки ртутного термометра в защитной гильзе. По первому варианту, термометр установлен в толстостенной стальной гильзе без антикоррозионного покрытия, масло в гильзу не залито.
Значения постоянных времени эквивалентной системы определяют следующие величины:
Таким образом, величина мала по сравнению с и, и взаимодействие емкостей настолько мало, что им можно пренебречь.
По второму варианту, толщина стенки стальной гильзы уменьшена почти вдвое, гильза покрыта снаружи антикоррозионной пленкой с малой теплопроводностью, промежуток между термометром и гильзой залит маслом для улучшения условий теплообмена. Параметры системы изменились следующим образом:
Взаимодействие звеньев системы значительно, и его необходимо учитывать в расчетах и при моделировании. Покажем, что вид дифференциального уравнения переходного процесса (а, следовательно, и его динамические свойства) зависит от структуры системы, а не от ее физической природы и конструктивного оформления.
В качестве примера рассмотрим электрическую систему, состоящую из двух сопротивлений и двух емкостей (рисунок 8.2), и сравним ее с приведенной выше тепловой системой, состоящей из двух взаимодействующих емкостей.
Рисунок 8.2 – Электрическая система второго порядка
Переходные процессы в электрической цепи подчиняются законам Кирхгофа. Баланс токов для каждой из емкостей и описывается уравнениями:
Исключим из уравнений (8.16) и (8.17) неизвестное промежуточное напряжение и произведем преобразования, аналогичные сделанным в случае (8.12):
Дифференциальное уравнение (8.18) аналогично уравнению (8.12).
Между переходными процессами в тепловых, гидравлических, электрических, механических и других динамических системах существует аналогия. Во многих случаях они описываются однотипными дифференциальными уравнениями. Следовательно, результаты исследования динамических процессов в одних системах можно перенести на системы, подчиняющиеся другим физическим законам, но описываемые аналогичными уравнениями. На этом основан метод математических аналогий. Этот метод позволяет использовать хорошо изученные переходные процессы в электрических системах для моделирования других, менее изученных систем, физическое моделирование которых слишком дорого и трудоемко.
8.2.3 Многоемкостные системы с распределенными параметрами
Системы с распределенными параметрами имеют бесконечное число степеней свободы. Примерами подобных систем могут служить различные теплообменные аппараты. При нарушении теплового равновесия на входе возмущающее воздействие постепенно распространяется через стенку теплообменника и через вещество, заполняющее выходную емкость. Чтобы описать переходный процесс, нужно знать величину теплового потока в каждой точке стенки и нагреваемого (или охлаждаемого) вещества. Переходные процессы в системах с распределенными параметрами описываются дифференциальными уравнениями в частных производных.
(«5») Промышленные управляемые объекты, как правило, обладают распределенными параметрами. Однако часто их можно с достаточной для практики точностью рассматривать, как системы с сосредоточенными параметрами. Например, в одноемкостном теплообменнике смешения пар, подаваемый через барботер непосредственно в нагреваемую жидкость, барботируя через нее, интенсивно ее перемешивает, и поэтому температура жидкости в разных точках приблизительно одинакова. На этом же основании массо — и теплообмен между жидкостью и барботирующими через нее парами на тарелке ректификационной колонны обычно рассматривается как процесс, происходящий в системе с сосредоточенными параметрами. Такое упрощение позволяет производить инженерные расчеты, принимая, что температура или состав жидкости на тарелке во всех точках одинаковы, Изменение давления в трубопроводах и аппаратах, полностью заполненных несжимаемой жидкостью, распространяется в них со скоростью звука. Переходные процессы в коротких трубопроводах и одноемкостных аппаратах при изменении давления жидкости или скорости ее потока продолжаются лишь доли секунды и в большинстве задач управления этими величинами можно пренебрегать. Однако, если изменяется не давление, а температура или состав жидкости в трубопроводе, то такое упрощение недопустимо вследствие небольшой скорости потока.
В более сложных случаях можно заменить систему с распределенными параметрами несколькими системами с сосредоточенными параметрами и чистым запаздыванием. Это справедливо, в частности, когда сопротивление звеньев потоку вещества или энергии мало по сравнению с их емкостью или наоборот. Например, рассмотренная выше тепловая система, состоящая из термометра в защитной гильзе, обладает распределенными параметрами, но мы, сделав ряд упрощающих допущений, рассматривали ее как состоящую из двух звеньев с сосредоточенными параметрами.
Если систему (или звено) с распределенными параметрами разделить на достаточно большое количество элементарных звеньев с емкостями и сопротивлениями, то каждое из этих элементарных звеньев с постоянными времени можно рассматривать как звено с сосредоточенными параметрами.
На этом основывается метод упрощенного аналитического определения динамических характеристик тепло-массообменных аппаратов, по которому многоемкостные аппараты непрерывного действия рассматриваются как ряд связанных между собой отдельных емкостей с сосредоточенными параметрами и элементами запаздывания.
При таком подходе динамические характеристики можно определить из обыкновенного дифференциального уравнения. Порядок уравнения определяется принятым числом емкостей и с его увеличением возрастает, что затрудняет исследование. Этот метод наиболее распространен, но не универсален. В ряде случаев он может привести к ошибочным выводам. Кроме того, исследование дифференциального уравнения в частных производных значительно более низкого порядка, чем обыкновенное дифференциальное уравнение, описывающее свойства одного и того же объекта, может быть проще.
8.3 Экспериментальное определение динамических и статических характеристик промышленных объектов управления
Ввиду недостаточной изученности объектов управления и необходимости принимать при их математическом описании ряд упрощающих допущений в настоящее время динамические и статические характеристики объектов, определенные экспериментально, являются наиболее достоверными и принимаются в качестве эталонов для проверки результатов математического исследования. Кроме того, для решения конкретных инженерных задач на производстве, например для выбора регулятора и расчета его оптимальной настройки, чаще применяются экспериментальные методы определения характеристик объектов управления, так как математическое исследование требует высокой квалификации исследователей и обычно применения вычислительных машин.
При разнообразии статических и динамических характеристик, представляющих интерес для оптимального проектирования объекта или для разработки системы управления, экспериментальное определение всех их весьма трудоемко, а главное – результаты нельзя использовать для аналогичных производств, отличающихся по мощности. Поэтому целесообразнее исследовать все возможные варианты характеристик объектов или систем управления путем математического моделирования с экспериментальной проверкой отдельных наиболее важных результатов. Таким образом, исследование процесса (объекта, системы) должно состоять из следующих основных этапов:
предварительного математического описания статики и динамики процесса; выбора способа математического моделирования : при помощи цифровой или аналоговой вычислительных машин; программирования задач для расчетов на ЦВМ или составления схем набора задач на АВМ; решения основных задач выбранным способом; экспериментального получения данных для проверки и уточнения математической модели; уточнения математической модели и исследования всех свойств статических и динамических характеристик объекта (системы).
Типовые объекты управления химической, нефтехимической и нефтеперерабатывающей промышленности в большинстве случаев можно рассматривать как слабонелинейные системы, для экспериментального исследования которых применимы методы, разработанные для линейных систем.
8.3.1 Экспериментальное определение динамических характеристик
Зависимости между входными и выходными величинами процесса можно получить в переходных режимах в виде кривых разгона и импульсных характеристик или в установившихся колебательных режимах в виде частотных характеристик.
Снятие кривых разгона проще, чем определение других динамических характеристик. Кривые разгона снимаются нанесением единичного скачкообразного возмущающего воздействия на входе в объект, приведенный предварительно в состояние равновесия.
Если в эксплуатационных условиях нельзя снять кривую разгона при достаточно большом и продолжительном возмущающем воздействии, то можно получить импульсные характеристики. При нанесении импульсного возмущающего воздействия объект находится в переходном режиме недолго. Поэтому амплитуда возмущения в данном случае может быть значительно больше, чем при снятии кривой разгона.
При снятии частотных характеристик значение регулируемой величины непрерывно колеблется вокруг заданного, поэтому амплитуда возмущающего воздействия может быть больше, чем при снятии кривых разгона. Частотные характеристики получаются нанесением периодических возмущающих воздействий (синусоидальной, трапецеидальной или прямоугольной формы) на входе в систему и регистрацией установившихся периодических колебаний на выходе объекта.
Опыты можно поставить как со специальной аппаратурой, так и при помощи стандартных контрольно-измерительных приборов, имеющихся в любом заводском цехе КИП. Во всех случаях нужно иметь аппаратуру для нанесения вынужденных возмущающих воздействий определенной формы, амплитуды и частоты и для регистрации всех входных и выходных величин.
Приборы для проведения экспериментов должны иметь требуемый класс точности и необходимые пределы измерения. По записи на диаграмме регистрируемого прибора определяется характеристика не объекта, а системы: объект – измерительный прибор. Поэтому статические и динамические характеристики измерительных приборов должны быть известны, чтобы определить характеристику самого объекта, Если характеристики объекта определяются для расчета настройки регулятора, то желательно снимать их при помощи этого же регулятора. Тогда для расчета настройки регулятора не нужно располагать характеристикой его измерительной системы. Она условно относится к объекту. До снятия характеристики первичных приборов необходимо их подготовить и проверить.
Подготовка приборов состоит из следующих этапов: внешнего осмотра; проверки на герметичность (опрессовка); проверки наличия гистерезиса, устранения чрезмерного гистерезиса; проверки соответствия классу точности прибора; установки плунжера индукционного датчика в среднее положение при заданном значении измеряемой величины; определения статической характеристики прибора. Подробнее этот вопрос изложен в инструкциях, прилагаемых к приборам, а также в работах.
(«6») Статическая характеристика регулирующего органа, которым наносится возмущающее воздействие, не имеет большого значения при снятии кривых разгона, импульсных и частотных (метод прямоугольной волны) характеристик. Но получение гармонических возмущающих воздействий возможно только при работе в пределах линейной части рабочей расходной характеристики регулирующего органа. Если она значительно отличается от линейной, то ее нужно спрямить профилированием регулирующего органа или применением специального профилированного кулачкового устройства для передачи движения от сервомотора к регулирующему органу. Следует иметь в виду, что расходная характеристика регулирующего органа зависит от рабочих условий, поэтому ее нужно определять в условиях, близких к эксплуатационным.
Снятие характеристики производится следующим образом. Определяется начальный пропуск при закрытом положении регулирующего органа. Затем перемещают регулирующий орган и через каждые 10–15% хода (отсчитываемого по шкале указателя положения штока) измеряют расход среды через него. Таким же образом снимается статическая характеристика при обратном ходе регулирующего органа.
Объект регулирования или отдельный участок его, включенный в цепь регулирования, во время проведения опытов должен находиться в нормальном эксплуатационном состоянии. При чрезмерном загрязнении поверхности теплообмена ее нужно очистить. Гильзы для установки термометров очищаются и заполняются маслом. При измерении температуры жидкости, стекающей по насадке, принимаются меры, обеспечивающие постоянное полное омывание защитной гильзы или чувствительного элемента термометра. Штуцеры для отбора давления и соединительные трубки продувают, проверяют, нет ли в них дросселирования вследствие засорения или частичной заварки отверстия. Регулирующий орган очищают от возможных засорений (песка, ракушечника, сорванного манжета запорного вентиля и т. д.) и снимают его рабочую расходную характеристику.
Снятию динамических характеристик должна предшествовать обязательная стабилизация нагрузки объекта регулирования на выбранном значении. При слабо нелинейных свойствах объекта нужно определять его характеристики при минимальной, нормальной и максимальной нагрузках. Продолжительность предварительной стабилизации нагрузки зависит от инерционности объекта и может составлять от десятков минут до нескольких часов (например, для тарельчатых ректификационных колонн).
Величина и продолжительность возмущающих воздействий должны быть достаточными для получения четких записей переходного процесса или установившихся колебаний, не искаженных случайными флуктуациями. Обычно величина возмущающего воздействия выбирается в пределах 15–40% от максимальной, но всегда должна находиться в пределах, допустимых по технологическому режиму.
Для определения настройки регулятора возмущающее воздействие должно наноситься тем регулирующим органом, на который будет воздействовать регулятор. При более полном исследовании свойств объекта нужно определить его характеристики по всем возможным каналам передачи возмущающих и управляющих воздействий.
При проведении эксперимента в производственных условиях часто значительные трудности и ограничения возникают, когда нужно нанести возмущающие воздействия и изменить режим работы объекта, а также в случае продолжительной стабилизации процесса и устранения незапланированных возмущающих воздействий во время эксперимента. Поэтому количество опытов должно быть минимально необходимым, они должны быть тщательно спланированы и подготовлены.
Снятие кривой разгона
Кривая разгона объекта с одной регулируемой величиной снимается следующим образом. Диаграммы контрольно-измерительных приборов и регулятора с ускоренным приводом настраивается синхронно. Процесс приводится в состояние равновесия при заданной нагрузке. Принимаются меры для устранения всех случайных возмущающих воздействий. Исполнительный механизм присоединяется к панели дистанционного управления. После достижения равновесия производится единичное скачкообразное возмущение регулируемой величины быстрым перемещением регулирующего органа. На диаграмме регулятора отмечается положение пера в момент нанесения возмущения для отсчета времени чистого запаздывания.
Возмущающее воздействие измеряют непосредственно или косвено – по начальному и конечному положениям исполнительного механизма или регулирующего органа, если известна рабочая расходная характеристика последнего. Одновременное измерение и запись нескольких быстро изменяющихся величин можно произвести многошлейфовым осциллографом. Если допустима запись через небольшие промежутки времени (при медленно протекающих переходных процессах), то для этой цели удобно использовать электронный потенциометр ЭПП-09, имеющий до 12 каналов. Время переключения каналов от 1 до 5 сек.
Сравнение кривых разгона объекта по всем регулируемым величинам для всех возможных возмущающих воздействий позволяет определить главные и перекрестные каналы распространения этих воздействий (как возмущающих, так и регулирующих), отделить основные, первичные реакции объекта от вторичных. Расчет передаточных функций главных и перекрестных каналов объекта на основании экспериментальных частотных или временных характеристик показывает относительную величину внутренних связей регулируемых величин и дает возможность решить, будет, ли работоспособна схема несвязанного регулирования (с учетом только главных каналов) или нужна схема взаимосвязанного, автономного или инвариантного регулирования.
Снятие частотных характеристик
Подготовка и проверка контрольно-измерительных приборов, регулятора и объекта производятся описанными выше способами. Величина возмущения принимается такой, при которой колебания регулируемого параметра будут иметь амплитуду в допустимых пределах и достаточную для расчета.
Важный фактор – выбор формы возмущающих воздействий на входе в объект регулирования. Желательным видом входных возмущений являются синусоидальные колебания. В линейной системе колебания на выходе могут отличаться от колебаний на входе только по величине амплитуды и по фазе. Чтобы получить АФХ объекта при синусоидальных колебаниях, достаточно сравнить выходные и входные колебания для ряда различных частот. Однако создание гармонических колебаний на входе в объект регулирования в заводских условиях может оказаться сложным.
Для упрощения опытов удобно возбуждать на входе в объект периодические колебания в виде «прямоугольной волны». При этом не нарушается режим работы объекта и не снижается точность результатов. Метод «прямоугольной волны» не требует применения генератора колебаний и линеаризации расходной характеристики регулирующего органа, часто необходимой для создания гармонических колебаний. Периодические колебания в виде волны прямоугольной формы могут создаваться вручную любым регулирующим органом, имеющимся на входе в исследуемый объект.
Возмущающие воздействия производятся регулирующим клапаном. На время опыта на штоке клапана укрепляется ограничитель хода, позволяющий перемещать клапан только в определенных пределах, нужных для создания желательной амплитуды колебания регулируемой величины. При проведении опытов на промышленном объекте со взрывоопасным продуктом ограничитель хода не устанавливается, так как возможно внезапное изменение нагрузки объекта. Применение ограничителя хода клапана требует постоянной нагрузки объекта регулирования. В случае необходимости можно быстро перейти на ручное управление вентилем, устанавливаемым на обводной линии регулирующего клапана.
Возбуждение периодических возмущений параметра с постоянной амплитудой колебаний без ограничителя хода клапана затруднительно. В этом случае нужны жесткая возвратная пружина клапана, слабая затяжка сальниковой набивки с хорошей смазкой и пневматическое позиционное реле, облегчающее установку клапана в заданное положение и увеличивающее его чувствительность.
Для получения четкой частотной характеристики важно, каким способом наносятся возмущения. Наиболее просто возбуждать периодические колебания с постоянной амплитудой возмущения. После записи двух-трех установившихся колебаний период возмущений изменяют, и вновь записывают установившиеся колебания при неизменной величине возмущения. Существенными недостатками этого способа являются незначительные амплитуды и дрейф оси «колебаний регулируемой величины. Обработка таких диаграмм затруднительна, а последующие расчеты по ним неточны.
Усиление возмущения на входе в объект приводит к отклонению регулируемой величины от заданного значения, что в ряде случаев недопустимо по технологическому режиму. Желательно увеличивать возмущения до 25–30%, но не допускать изменения параметра сверх заданных пределов. Для этого, в отличие от описанного способа, устанавливают зону изменения регулируемой величины, по выходе из которой изменяют количество входящих в аппарат вещества или энергии, возвращающее параметр в заданную Зону (рисунок 8.3).
Рисунок 8.3 – Определение частотной характеристики объекта методом «прямоугольной волны» при заданной зоне изменения регулируемой величины
(«7») При повышении регулируемой величины (в данном примере – температуры) до (точки 1 и 3) скачкообразно увеличивается подача охлаждающей воды. При понижении температуры до (точки 2 и 4) подача охлаждающей воды скачкообразно уменьшается. Возмущения подачи воды продолжаются до получения записи трех периодов установившихся колебаний регулируемой температуры.
Следует учесть, что вследствие тепловой инерции объекта регулирования после изменения знака возмущающего воздействия температура продолжает некоторое время изменяться в прежнем направлении и выходит из заданной зоны. Поэтому заданная зона должна быть уже допустимых по технологическому режиму пределов изменения температуры. Выход регулируемого параметра из заданной зоны тем значительнее, чем больше возмущающее воздействие и инерционность процесса.
Изменяя величину возмущающего воздействия и ширину заданной зоны, можно получить колебания регулируемой величины требуемой частоты. Если предварительно сделан расчет АФХ по кривой разгона регулируемой величины, то частотная характеристика снимается только для периода колебаний, вызвавшего сомнение при расчете. Если кривая разгона не определялась, то следует снять частотную характеристику при трех-четырех периодах колебаний в диапазоне рабочих частот процесса регулирования, например при частоте двухпозиционного регулирования, затем при частотах, равных 0.8; 0.6 и 0.4 от этой величины. Двухпозиционное регулирование является верхним пределом диапазона рабочих частот для регулируемой системы с ПИ-регулятором (так как оно соответствует сдвигу фаз колебаний на 180°).
Рисунок 8.4 – Структурная схема прибора для определения динамических характеристик инфранизко-частотных объектов
Входные и выходные параметры объекта измеряются, преобразуются в пропорциональные электрические величины и вводятся в прибор через входные устройства 1. В приборе имеется шесть входных устройств соответственно числу одновременно регистрируемых параметров. Сигнал постоянного напряжения с каждого входного устройства подводится к коммутатору 2, который поочередно подключает цепи к измерительному устройству 3. Измерение сигналов в нем осуществляется компенсационным методом. Автоматическая компенсация обеспечивается электронным усилителем 4 и балансирным двигателем 5, механически воздействующим на измерительное устройство 3 посредством печатающей каретки 6. Для перемещения диаграммной бумаги, работы коммутатора и равномерного вращения генераторов 9 и 10 электрических и пневматических колебаний используется синхронный электродвигатель 7. Редуктор 8 предназначен для получения требуемой частоты генерируемых колебаний (см. рисунок 8.4).
При получении вялых, нечетких колебаний следует увеличить возмущение, изменив соответственно ширину заданной зоны. Частотные характеристики снимаются, как и кривые разгона, при максимальной, нормальной и минимальной нагрузках объекта регулирования.
Необходимость экспериментального исследования автоматических систем с продолжительностью переходного процесса от долей секунды до десятков минут вызвала потребность в низкочастотных генераторах гармонических колебаний и целом комплексе низкочастотной аппаратуры для проведения частотного анализа систем.
Прибор для определения динамических характеристик инфранизкочастотных объектов разработан и изготовлен Центральным научно-исследовательским институтом комплексной автоматизации (ЦНИИКА). Прибор состоит из двух основных частей – генератора электрических и пневматических синусоидальных колебаний и регистратора (рисунок 8.5).
Рисунок 8.5 – Схема для определения частотных характеристик в замкнутой САР: 1 – объект управления; 2 – регулятор; 3 – генератор колебаний; 4 – регистратора-датчик
Во Всесоюзном теплотехническом институте разработана схема для определения частотных характеристик в замкнутой системе автоматического регулирования. Метод основан на генерировании синусоидальных колебаний в системе, состоящей из исследуемого объекта и регулятора. Такой способ проведения эксперимента обеспечивает сохранение заданного среднего значения регулируемой величины независимо от характеристики регулирующего органа и возможность генерирования колебаний со значительной амплитудой без нарушения нормального технологического режима при неограниченной длительности эксперимента.
На вход регулятора, подключенного к исследуемому объекту, поступают синусоидальные колебания от генератора. Регулятор настраивают так, чтобы затухание переходных процессов в системе регулирования происходило достаточно интенсивно. Эта настройка осуществляется опытным путем, так как к началу эксперимента нет данных о динамических характеристиках объекта. На вход регулятора подается два сигнала – отклонение регулируемой величины у и синусоидальный сигнал от генератора. При отсутствии сигнала от генератора регулятор стремится поддерживать регулируемую величину около заданного постоянного значения. Функция генератора синусоидальных колебаний, подключенного к регулятору, сводится к периодическому изменению задания регулятору по закону синусоидальных колебаний. Таким образом, регулируемая величина у «следит» за гармоническим сигналом гарм.
Положение оси колебаний регулируемой величины не зависит от характеристики регулирующего органа. Если период вынужденных колебаний велик по сравнению с временем протекания переходных процессов в системе, то регулируемая величина, «копирует» гармонический сигнал. При малых периодах колебания регулируемой величины обычно также близки к синусоидальным, так как большинство объектов хорошо фильтрует высокие частоты.
8.4 Расчет амплитудно-фазовой характеристики и составление дифференциального уравнения системы на основании динамических характеристик, определенных опытным путем
Определение амплитудно-фазовой характеристики по кривой разгона
Для определения АФХ кривая разгона регулируемой системы разделяется ординатами, проведенными через равные промежутки времени (рисунок 8.6). Замена исследуемой кривой ступенчатой линией тем точнее, чем больше число ординат, разделяющих кривую. Однако стремиться к весьма точной замене кривой путем разделения ее большим числом ординат нецелесообразно, так как точность самих значений ординат не очень велика. При плавных кривых достаточная для практических целей точность достигается обычно при числе ординат от 5 до 15.
Рисунок 8.6 – Кривая разгона автоматической системы
(«8») Для кривых разгона 1 и 2 (рисунок 8.7) амплитудно-фазовую характеристику рекомендуется вычислять по формуле:
где ; – относительная частота; w – частота процесса; – частота среза; – интервал разделения; В – первая разность ординат; к – порядковый номер; – первая ордината.
Если кривая разгона имеет вид 3 (рисунок 8.7), то для улучшения сходимости ряда нужно пользоваться формулой:
где ; – первая разность ординат; – вторая разность; к=1, 2, 3 и т. д.
В приведенных формулах значения АФХ даны для случая воздействия на систему максимального возмущения, принятого за единицу, которое может быть вызвано, например, перемещением регулирующего органа из одного крайнего положения в другое. На практике обычно возмущение меньше максимального, поэтому №(1а) нужно разделить на коэффициент возмущения, равный отношению произведенного возмущения к максимальному:
где – возмущающий параметр до нанесения возмущения; – возмущающий параметр, после нанесения возмущения; – максимальное значение возмущающего параметра.
Рисунок 8.7 – Типичные кривые разгона
При начальном запаздывании (рисунок 8.6) формула для вычисления АФХ имеет вид:
В общем случае АФХ выражается формулой:
В приведенных формулах АФХ является функцией относительной частоты X, изменяющейся в пределах, что позволяет использовать для расчетов таблицу 1.
Таблица 1 – Данные для расчета амплитудно-фазовых характеристик
Конечные уравнения математического описания могут быть
Рассмотренные на предыдущей лекции примеры свидетельствуют о том, что абстрактная характеристика данной системы может быть получена с помощью полезных типов математического описания. Однако при этом естественно возникает вопрос: а для чего вообще нужно какое-либо математическое описание? Ответ на этот вопрос в значительной степени связан с нетривиальностью современных научных результатов и необходимостью уметь выделять существенные свойства описательных моделей. Кроме того, использование именно математического описания обусловлено следующими важными соображениями:
- Компактность. Словесное (или вербальное) описание системы (или процесса), как правило представляет собой нагромождение нечетких высказываний, которые лишь затуманивают существо дела. Избавиться от таких нечетких и не до конца продуманных соображений помогает компактная математическая символика. Математическое описание дает нам аналог знакомой картины и оказывается информативнее любого словесного описания.
- Ясность. Использование математического описания позволяет каждому аспекту изучаемого процесса поставить в соответствие определенный математический символ, в результате чего становится нагляднее взаимосвязь, существующая между различными параметрами процесса. Более того, подобное сопоставление позволяет гораздо проще, чем словесное описание, установить, не были ли упущены какие-либо существенные переменные, или, напротив, не были ли внесены какие-либо дополнительные несущественные сложности при построении описания.
Возможность численного анализа. Как только сделан выбор какого-либо математического описания, последнее «начинает жить» собственной жизнью, более или менее независимой от самого исследуемого процесса.
Другими словами, математическим описанием можно манипулировать в соответствии с обычными законами логики в надежде получить нетривиальное представление о самой системе. Кроме того, математическая модель дает основу для численного анализа, с помощью которого могут быть получены данные не только описательного, но и прогностического характера. Рассмотрим кратко некоторые типы математического описания, которые чаще других используются в математических конструкциях больших систем.
Внутреннее описание
Со времен Ньютона динамические процессы описывали на языке дифференциальных (или разностных) уравнений, т.е. в терминах некоторых естественно выбранных переменных, таких как положение, температура, скорость и т.д. В общем виде такое описание может быть представлено как:
dz/dt = f[z(t), x(t), t], z(0) = z0, y(t) = h[z(t), x(t), t],
где z(t) — n-мерный вектор, компоненты которого описывают состояние системы в момент времени t; y(t) — p-мерный вектор наблюдаемых выходов системы; x(t) — m-мерный вектор входов системы, z0 — начальное состояние системы.
В дискретном времени динамика системы может быть описана с помощью разностных соотношений z(k+1) = F[z(k), x(k), k], z(0) = z0, y(k) = H[z(k), x(k), k].
Наиболее важным свойством такого описания является то, что оно дает нам представление о поведении системы в некоторой локальной окрестности текущего состояния. При этом неявно предполагается, что локальная информация может быть каким-то образом «собрана воедино», что позволит понять глобальное (во времени или пространстве) поведение системы. Такой подход оказался достаточно обоснованным для анализа многих физических и технических задач. Простые примеры локального описания можно найти в элементарной физике. Известно, например, что колебательное движение груза (маятника) единичной массы, подвешенного на нерастяжимой и невесомой нити единичной длины, описывается уравнением (4.1):
d 2 z/dt 2 + a⋅dz/dt + sin(z) = x(t)
где а — коэффициент трения, x(t) — внешня сила, действующая на груз, z(t) — отклонение груза от положения равновесия.
Таким образом, уравнение (4.1) описывает мгновенное изменение положения и скорости маятника как функцию его текущего состояния (положения) и скорости, т.е. мы имеем локальное описание в координатах «положение-скорость», что характерно для всех описаний динамических процессов на языке дифференциальных или разностных уравнений.
Интересно отметить, что математические описания такого типа начали использовать только со времен Ньютона. До этого при описания физических процессов придерживались точки зрения, высказанной Аристотелем, согласно которой важность целого превыше важности его составляющих. Другими словами, значимость элементов, составляющих некоторое множество, трактовалась через значимость самого множества как целого. Однако возможность использования такого подхода в случае менее изученных объектов, в особенности систем социально-экономической природы, вовсе не очевидна.
Взгляды Аристотеля господствовали в физике на протяжении многих столетий, пока Галилей не высказал иную точку зрения, которая впоследствии была обоснована Ньютоном: целое объясняется свойствами его элементарных (локальных) составляющих, так называемый холистский подход. Сложность современной жизни, проявляющаяся в политике, экономике, социологии стимулирует возрождение интереса к холистским теориям.
Внешнее описание
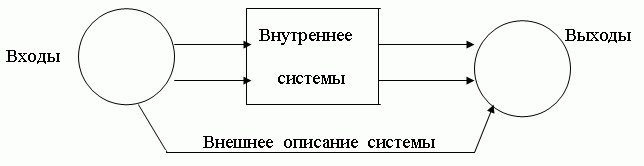
Тип математического описания, с которым чаще всего приходится иметь дело ученому-экспериментатору, — это связь «вход-выход». Во многих отношениях такое описание диаметрально противоположно частному, локальному описанию, поскольку оно не содержит деталей и единственным доступным источником информации является закономерность (отображение), связывающая выходы системы с ее входами. При этом ничего не известно о внутреннем механизме преобразования входов в выходы. По этой причине связь вход-выход часто называют «внешним описанием» системы в отличие от «внутреннего» (или локального) описания (см. рис.4.1).
Внутреннее и внешнее описания позволяют рассматривать систему как устройство, образующее входы и выходы в соответствии с правилами, определенными внутренним описанием. Иными словами, система является информационным процессом в некотором обобщенном смысле.
Рис.4.1 — Внешнее и внутреннее описание системы
Очевидно, что внутреннее описание говорит нам гораздо больше о способе действия системы, поскольку каждое такое описание порождает внешнее описание. Тем не менее построение модели системы часто связано с решением диаметрально противоположного вопроса: может ли внутренняя модель «объяснить» каждое внешнее описание? Ответом на этот вопрос по существу является решение так называемой «задачи реализации», которая представляет собой один из важнейших аспектов теории систем.
Наиболее «сырая» возможная ситуация, при которой возникает необходимость в описании типа «вход-выход», имеет место, когда мы располагаем всего лишь таблицей элементов (часто чисел), характеризующих реакцию (выходы) системы на различные внешние воздействия (входы). В этом случае внешнее описание системы эквивалентно отображению:
где через X обозначено множество возможных входов, а через Y множество возможных выходов системы. Как отмечалось во многих задачах (в частности, психологии, экономики и общественных наук) множества X и Y представляют собой конечный набор элементов, связь между которыми описывается с помощью функции f.
Пример
Предположим, что эксперт, изучающий «черный» ящик не имеет ни малейшего представления ни о его природе, ни о его содержимом. Вместе с тем эксперт может производить над ним некоторые действия (входы) и наблюдать их результаты (выходы). Предположим для определенности, что
элементами множества X и множества Y являются показания различных измерительных приборов. Тогда описание эксперимента типа «вход-выход» могло бы быть таким:
| Время | Вход | Выход |
|---|---|---|
| 10:05 | Эксперт не производит никаких действий | Прибор издает звуковой сигнал частотой 240 Гц |
| 10:06 | Эксперт нажал на кнопку «A» | Частота сигнала возросла до 480 Гц |
| 10:07 | Эксперт случайно нажал на кнопку «B» | Ящик нагрелся на 20°C и начал вибрировать |
Этот довольно тривиальный пример показывает, что входы и выходы системы являются функциями времени, т.е. нельзя один и тот же эксперимент провести дважды! Единственное, что можно сделать, — это провести следующий эксперимент, который хотя и незначительно, но будет отличаться от предыдущего.
Менее тривиальный пример внешнего описания системы дает «бихевиористская» школа психологов, для которой характерным является проведение эксперимента и запись его результатов в формате «воздействие-реакция». По мнению представителей этой школы, такое внешнее описание системы дает максимум информации, которую вообще можно получить о ее структуре и функционировании. В то же время «познавательная» школа придерживается другой точки зрения, утверждая, что единственным удовлетворительным описанием системы может быть только внутренняя модель.
Основываясь на довольно общих результатах теории систем, можно показать, что это спор ни о чем. Обе школы, в сущности, утверждают одно и то же, и с точки зрения теории систем эти дебаты столь же содержательны, как и дискуссии относительно того, какая сторона монеты наиболее полно отражает ее стоимость.
Описание систем с конечным числом состояний
В тех случаях, когда предположение конечномерности пространства состояний заменяется предположением о конечности числа его элементов, мы имеем дело с классом систем, анализ которых возможен с помощью чисто алгебраических методов. Важность такой замены трудно переоценить, поскольку совокупность систем с конечным числом состояний включает все последовательные цифровые вычислительные машины.
Математическое описание системы с конечным числом состояний включает:
- множество допустимых входов — X,
- множество допустимых выходов — Y,
- множество состояний — Z,
- функцию перехода — : Z X Z,
- функцию выхода — : Z X Y,
При этом предполагается, что множества X, Y и Z конечны. Это позволяет представить описание системы в виде:
В литературе такое представление часто называют схематическим.
Как отмечалось, ограничения вычислительного характера с неизбежностью вынуждают нас явно или неявно сводить каждую системную задачу к виду, указанному выше. Поэтому необходимы тщательное изучение и понимание алгебраической структуры подобных «конечных» описаний, которая основывается на теории конечных полугрупп. Рассмотрение этой теории выходит за рамки настоящего курса лекций.
Пример
Пусть система состоит из симметрий вращения правильного треугольника. Тогда некоторые возможные конечные пространства состояний могут иметь вид:
Рис.4.2 — Конечные пространства
Для описания системы достаточно любого из этих пространств состояний, однако только некоторые из них удобнее использовать для вычислений результата воздействия на состояние системы. Следовательно, пространство состояний вовсе не обязательно должно быть непосредственно привязано к реальному физическому процессу. Это чисто математическая условность, введенная для упрощения проблемы определения реакции системы на заданные внешние воздействия.
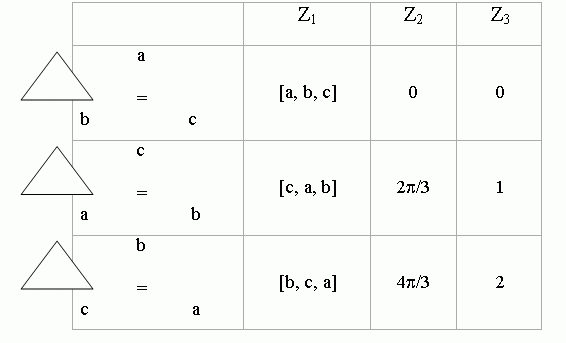
Пусть имеются два возможных отображения σ1 и σ2, переводящие одно состояние системы в другое и соответствующие повороту треугольника вокруг центра тяжести на 120 и 240 градусов соответственно. Результаты применения этих отображений к различным пространствам состояний можно представить в виде таблицы:
| zi | σ1(zi) | σ2(zi) | |
|---|---|---|---|
| z1 → | [a, b, c] [c, a, b] [b, c, a] | [c, a, b] [b, c, a] [a, b, c] | [b, c, a] [a, b, c] [c, a, b] |
| z2 → | 0 2π/3 4π/3 | 2π/3 4π/3 0 | 4π/3 0 2π/3 |
| z3 → | 0 1 2 | 1 2 0 | 2 0 1 |
Пространство z1 на первый взгляд излишне сложное, оказывается вполне пригодным для более сложных систем, например в случае симметрий более общего вида, где могут присутствовать отображения типа σ. В то же время пространства z2 и z3 не допускают очевидных обобщений на более сложные случаи с сохранением простоты вычислений.
Способ выбора конкретного пространства состояний системы называется ее координатизацией. При этом важно установить, всегда ли существует координатизация, которую можно считать «хорошей» с точки зрения описания поведения системы. Ключевым моментом проблемы координатизации является алгебраическая структура модели системы в пространстве состояний.
http://pandia.ru/text/79/085/56413.php
http://victor-safronov.ru/systems-analysis/lectures/zhivickaya/06.html