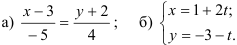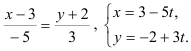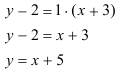Контрольная работа на тему: прямая на плоскости, кривые второго порядка
Прямая на плоскости. Кривые второго порядка
Задание: Составление уравнений прямых.
Цель: формирование умения составлять уравнения прямых на плоскости.
Задание для самостоятельной внеаудиторной работы:
7.1. Опираясь на обобщающие таблицы, изучите, какими способами можно задать прямую, и какие виды уравнения прямой существуют.
7.2. В треугольнике 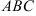
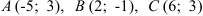
а) прямой 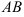
б) медианы 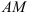
в) прямой, проходящей через точку 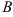
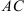
г) прямой, проходящей через точку 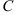
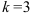
7.3. 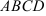
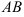
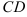
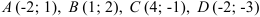
а) диагонали 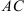
б) прямой, параллельной основаниям, проходящей через точку 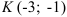
в) прямой, проходящей через точку 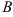
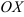
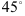
г) средней линии трапеции в каноническом виде;
д) прямой, проходящей через точку 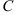
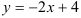
7.4. Запишите уравнение прямой во всех видах (общем, каноническом, параметрическом, с угловым коэффициентом) и постройте эту прямую:
Методические указания по выполнению работы:
Уравнением линии на плоскости называется уравнение с двумя переменными 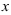
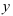
Прямые — самые простые линии на плоскости. Им соответствуют уравнения первой степени.
При решении задач удобно использовать следующие обобщающие таблицы:
Способы задания прямой

Виды уравнений прямой
Рассмотрим примеры решения типовых задач.
Пример 1.
Составьте уравнение прямой, проходящей через точку 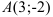
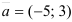
Решение:
Определим способ задания прямой: с помощью точки 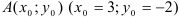
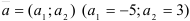
Подставим координаты точки и направляющего вектора в уравнение 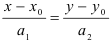
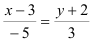
Подставим координаты точки и направляющего вектора в уравнение
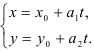
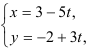
Ответ:
Пример 2.
Составьте уравнение прямой, проходящей через точки 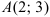
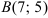
Решение:
Подставив в формулу 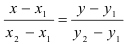
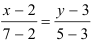
Ответ: 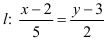
Пример 3.
Составьте уравнение прямой, проходящей через точку 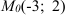
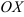
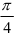
Решение:
Найдём угловой коэффициент прямой: 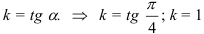
Подставим 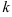
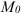
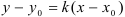
Ответ: 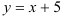
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
4.1.8. Примеры решения задач по теме «Уравнение прямой на плоскости»
Даны уравнения двух сторон параллелограмма: 2Х + У + 3 = 0 и 2Х – 5У + 9 = 0 и уравнение одной из его диагоналей: 2Х – у — 3 = 0. Найти координаты вершин этого параллелограмма.
Выясните, уравнения каких сторон даны в условии задачи: параллельных или
Смежных, и как расположена данная диагональ по отношению к данным сторонам.
Выясним, уравнения каких сторон даны в условии задачи: параллельных или
Следовательно, прямые пересекаются, то есть даны уравнения смежных сторон параллелограмма.
Условие параллельности прямых

Пусть даны уравнения сторон АВ и AD. Тогда координаты точки А будут решением системы уравнений:
Теперь определим, уравнение какой диагонали: АС или BD – нам известно. Если это диагональ АС, то на ней лежит точка А, следовательно, координаты этой точки должны удовлетворять уравнению диагонали. Проверим:
Значит, точка А не лежит на данной прямой, то есть дано уравнение диагонали BD.
Тогда вершина В лежит на прямых АВ и BD, значит, ее координаты найдем из системы:
Система уравнений для определения координат точки D составлена из уравнений прямых AD И BD:
Остается найти координаты точки С. Составим уравнения прямых ВС и DC.
Поскольку ВС параллельна AD, их угловые коэффициенты равны. Найдем угловой коэффициент прямой AD:
Тогда ВС можно задать уравнением
Найдем координаты точки С, решив систему из двух полученных уравнений:
Найти точку, симметричную точке А(2; 1) относительно прямой, проходящей через точки В(-1; 7) и С(1; 8).
Представьте себе, что вам нужно Построить искомую точку на плоскости. Последовательность действий при этом можно задать так:
1) провести прямую ВС;
2) провести через точку А прямую, перпендикулярную ВС;
3) найти точку О пересечения этих прямых и отложить на прямой АО по другую сторону прямой ВС отрезок ОА1 = АО.
Представим себе, что нам нужно Построить искомую точку на плоскости. Последовательность действий при этом можно задать так:
4) провести прямую ВС;
5) провести через точку А прямую, перпендикулярную ВС;
6) найти точку О пересечения этих прямых и отложить на прямой АО по другую сторону прямой ВС отрезок ОА1 = АО.
Тогда точка А1 будет симметричной точке А относительно прямой ВС.
Теперь заменим каждое из действий составлением уравнений и вычислением координат точек.
1) Найдем уравнение прямой ВС в виде:
2) Найдем угловой коэффициент прямой ВС:
Прямая АО Перпендикулярна прямой ВС, поэтому
Составим уравнение прямой АО:
3) Найдем координаты точки О как решение системы:
4) Точка О – середина отрезка АА1, поэтому
Найти угол между прямыми L1: 3Х – у + 5 = 0 и L2: 2Х + У – 7 = 0.
Если J – угол между прямыми L1 и L2, то J = A2 — A1, где A2 и A1 – углы, образованные прямыми L1 и L2 с положительной полуосью Ох. Тогда
Где K1 и K2 – угловые коэффициенты прямых L1 и L2.
Если J – угол между прямыми L1 и L2, то J = A2 — A1, где A2 и A1 – углы, образованные прямыми L1 и L2 с положительной полуосью Ох. Тогда
Где K1 и K2 – угловые коэффициенты прямых L1 и L2. Найдем K1 и K2: для L1
Y = 3X + 5, K1 = 3; для второй: Y = -2X + 7, K2 = -2. Следовательно,
Для прямых А1х + В1У + С1 = 0 И А2Х + В2У + С2 = 0

Определить, лежит ли точка М(2; 3) внутри или вне треугольника, стороны которого заданы уравнениями 4Х – у – 7 = 0, Х + 3У – 31 = 0, Х + 5У – 7 = 0.
Если точка М расположена внутри треугольника АВС, то ее отклонение δ от каждой стороны треугольника имеет тот же знак, что и для вершины, не лежащей на этой стороне, а если точка М лежит вне треугольника, то по крайней мере с одной из вершин она окажется в разных полуплоскостях относительно стороны треугольника.
Пусть первое уравнение задает сторону АВ, второе – ВС, третье – АС. Найдем координаты точек А, В и С:
Для ответа на вопрос задачи отметим, что:
1) если точка М расположена внутри треугольника АВС, то ее отклонение δ от каждой стороны треугольника имеет тот же знак, что и для вершины, не лежащей на этой стороне (т. е. точка М расположена относительно каждой стороны треугольника в одной полуплоскости с третьей вершиной);
2) если точка М лежит вне треугольника, то по крайней мере с одной из вершин она окажется в разных полуплоскостях относительно стороны треугольника (на рисунке: точки М1 и В расположены по разные стороны от прямой АС).
Составим нормальные уравнения сторон треугольника АВС:
Вычислим соответствующие отклонения:
1) для точек М и А относительно прямой ВС:
2) для точек М и В относительно прямой АС:
3) для точек М и С относительно прямой АВ:
Итак, точки М И С лежат по разные стороны от прямой АВ. Следовательно, точка М расположена вне треугольника АВС.
Ответ: Точка М расположена вне треугольника АВС.
Для треугольника АВС с вершинами А(-3; -1), В(1; 5), С(7; 3) составить уравнения медианы и высоты, выходящих из вершины В.
Составьте уравнение медианы как прямой, проходящей через точки В и М – середину стороны АС, а высоты – как прямой, проходящей через точку В и перпендикулярной стороне АС.
1) Медиана ВМ проходит через точку В и точку М – середину отрезка АС. Найдем координаты точки М:
Тогда уравнение медианы можно записать в виде:
2) Высота ВН перпендикулярна стороне АС. Составим уравнение АС:
Ответ: медиана ВМ: 4Х + У – 9 = 0; высота ВН: 5Х + 2У – 15 = 0.
Определить, при каком значении А прямая
Параллельна оси ординат. Написать уравнение прямой.
Если прямая параллельна оси ординат, то в уравнении Ах + Ву + С = 0
Если прямая параллельна оси ординат, то в уравнении Ах + Ву + С = 0
В = 0, С ≠ 0. Из условия В = 0 получаем: А2 – 1 = 0, А = ± 1.
При А = 1 С = 2 + 7 – 9 = 0 – второе условие не выполняется (получившаяся при этом прямая -4Х = 0 не параллельна оси Оу, а совпадает с ней).
При А = -1 получим: -6Х – 14 = 0, 3Х + 7 = 0.
Составить уравнения всех прямых, проходящих через точку М(2; 3) и отсекающих от координатного угла треугольник площадью 12.
Составьте уравнение искомой прямой «в отрезках»:
Где |A| и |B| — длины отрезков, отсекаемых прямой на координатных осях. Тогда
Откуда |Ab| = 24. Кроме того, координаты точки М(2; 3) должны удовлетворять уравнению «в отрезках».
Составим уравнение искомой прямой «в отрезках»:
Где |A| и |B| — длины отрезков, отсекаемых прямой на координатных осях. Тогда
Откуда |Ab| = 24. Кроме того, координаты точки М(2; 3) должны удовлетворять уравнению «в отрезках». Таким образом, для А и B можно составить систему уравнений:
Следовательно, условию задачи удовлетворяют три прямые:
Домашняя контрольная работа по теме уравнение прямой на плоскости
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Домашняя контрольная работа №4 « Уравнение прямой и окружности на плоскости »
1) В координатной плоскости постройте треугольник по точкам.
2) Составьте уравнения сторон, как уравнение прямой, проходящей через две точки:

3) Чтобы составить уравнение медианы АМ, нужно сначала найти координаты точки М, как середины отрезка ВС, по формулам: 

4) Уравнение высоты ВН, найдем как уравнение прямой, проходящей через точку В, перпендикулярно стороне АС. ( 



5) Составим уравнение прямой l , как уравнение прямой проходящей через точку С, параллельно вектору 




6) Пусть 






7) Уравнение окружности имеет вид: 

8) Сначала необходимо найти координаты центра, т.е середину отрезка АВ ( по формулам из пункта (в)), а затем найти радиус, как половину диаметра, т.е половину длины отрезка АВ.
Задача: Треугольник АВС, задан координатами своих вершин (по 3 балла за задание)
Постройте указанный треугольник,
Составьте уравнение стороны АВ,
Составьте уравнение медианы АМ,
Составьте уравнение высоты ВН,
Составьте уравнение прямой l , проходящей через точку С параллельно стороне АВ,
Найдите точку пересечения медианы АМ и высоты ВН
Составьте уравнение окружности с центром в точке А и проходящей через точку М,
Составьте уравнение окружности с диаметром АС,
Все точки и лини, указанные в пунктах 1 – 8 нужно указать на рисунке.
12 баллов – «3», 18 баллов – «4», 22 балла – «5».
Задачи для самостоятельного решения
http://matica.org.ua/metodichki-i-knigi-po-matematike/lineinaia-algebra-i-analiticheskaia-geometriia/4-1-8-primery-resheniia-zadach-po-teme-uravnenie-priamoi-na-ploskosti
http://infourok.ru/domashnyaya-kontrolnaya-rabota-po-teme-uravnenie-pryamoy-na-ploskosti-2015435.html