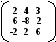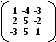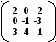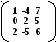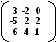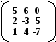Контрольная работа «Методы решения систем линейных уравнений»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Контрольная работа №1
Системы линейных уравнений ТЕМА 1. Системы линейных уравнений.
Матрицы и действия с ними.
Определители и их основные свойства.
Методы решения систем линейных уравнений.
СПИСОК ЛИТЕРАТУРЫ
Ильин В. А., Позняк Э. Г. Линейная алгебра: Учеб. для вузов.-5-е изд., стер. — М.: Физматлит, 2002. – 317 с.
Беклемишев Д. В. Курс линейной алгебры и аналитической геометрии: — М.: Физматлит, 2003. – 303 с.
Клетеник Д. В. Сборник задач по аналитической геометрии: Учеб. пособие для втузов / ред. Ефимов Н. В. – 17-е изд., стер. – СПб: Профессия, 2001. – 199 с.
Бугров Я.С., Никольский С.М. Высшая математика: Учеб.для вузов: в 3т.-5-е изд., стер.-М.:Дрофа.- (Высшее образование. Современный учебник). т.1. Элементы линейной алгебры и аналитической геометрии.-2003.-284 с.
Данко П.Е. и др. Высшая математика в упражнениях и задачах (с решениями): в 2 ч./ Данко П.Е., Попов А.Г., Кожевникова Т.Я -6-е изд..-М.: ОНИКС 21 век, ч.1. -2002.-304 с.
Решение типового варианта контрольной работы.
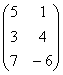
Задача 1. Вычислить определитель 
Решение. Для вычисления определителя третьего порядка будем использовать известную формулу Саррюса (правило треугольников), которое может быть записано следующей формулой:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Решим систему матричным способом, для этого вычислим обратную матрицу 


Решим систему методом Крамера. Главный определитель системы:


Запишем и вычислим вспомогательные определители

Ответ:
Решим систему методом Гаусса, для этого составим расширенную матрицу системы и упростим ее приведением к треугольному виду.



Таким образом, система равносильна системе
Находим
Ответ: 

При решении всеми методами одной и той же системы, мы получим один ответ.
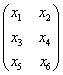
Задача 3. Выполнить действия:
Решение. Выполним решение по действиям.



Ответ: 
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Если 





Пример:
Произведение 
Произведение 
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:

Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера
Задача 3. Выполнить действия:
Контрольная работа №1.
Задача 1. Вычислить определитель:
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера
Контрольная работа по теме » Матрицы. Действия с матрицами. Решение систем уравнений методом Гаусса, Крамера, матричным методом.»
В результате освоения учебной дисциплины «Элементы высшей математики» обучающийся должен уметь:
- выполнять операции над матрицами и решать системы линейных уравнений;
Просмотр содержимого документа
«Контрольная работа по теме » Матрицы. Действия с матрицами. Решение систем уравнений методом Гаусса, Крамера, матричным методом.»»
По теме: «Матрица. Определители. Решение систем уравнений»
(4B – 2A) * K 17) C * (2B – 3D)
(2C – 3D) * E 18) C * (2K – 3E)
(2D – 3C) * K 19) C * (-4D – 2B)
A * (2C + 3D) 20) D * (-3C + 3B)
B * (3A – 2E) 21) D * (-2E – 2A)
(4D – 2C) * E 22) D * (5B – 4C)
(-2E + 3D) * C 23) E * (-4B + 2A)
(-2K + B) * D 24) E * (-4K – 2C)
10) (-2A — K) * B 25) E * (2K – 4C)
11)A * (3B + 2C) 26) E * (5A + 3B)
12) A * (2C – 4K) 27) K * (5B – 3A)
14) B * (2E – 3D) 29) K * (2E + 2D)
15) B * (2D + 3E) 30) K * (-3A + 2D)
2. Решить систему уравнений:
1) Матричным способом
2) Методом Гаусса
3) Методом Крамера
1
2x + y +z =7 5x – 3y – z = -6 -x – y + z = -4
x + 2y + 7z = 8 3x + y + 2z = 7 -2x + y – 3z = 3
x + y + 2z = 9 y + z = 4 4x – y – 3z = 5
2) x + 2y + 3z = 3 12) 3x + 4y – 3z = 11 22) 5x + y – z = -2
3x + y + 2z = 7 2x + y – 3z = 3 3x – y + 2z = 5
2x + 3y + z = 3 -3x – y + 5z = -3 2x + 2y – z = -1
3) 6x + 2y – z = 2 13) x – y – z = 0 23) 7x – 3y – 2z = 6
4x – y + 3 = -3 -x + 3y + 2z = 3 x + 3y + z = 9
3x + 2y -2z = 3 4x – y + 3z = -1 2x – y – 2z = 0
4
2x + y + 3z = 13 -x – y + 2z = -2 x + y = 3
x + y + z = 6 -3x + у +5z = 1 -x – y – 4z = 1
3x + y + z = 8 2x + y + z = 7 5x – 2y + z = 0
5) 2x + y – z = 6 15) 4x – y + 3z = 8 25) 4x + 4y + z = 7
3x – y + 2z = 5 -x + 3y + 2z = 9 3x – y + z = 2
4x + 2y – 5z = 9 x – y – z = -4 -2x – y + 2z = 5
6) x – 2y + 3z = 6 16) 5x – 4y + z = -4 26) 2x + 2y + z = 9
2x + 3y – 4z = 7 2x – y – z = 1 2x + y – 3z = 3
3x – 2y – 5z = 6 3x – y + 2z = -1 -x – 2y + 2z = -4
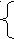
7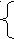
4x + 3y + 2z = 16 2x – y + z = 2 x + 3y + 4z = 4
2x – 3y + z = 17 5x – 4y + 2z = 2 2x – 3y – 2z = -2
8 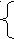
3x – 2y + z = 10 x – y + 2z = 2 11x + 2y – z = -1
x + 5y – 2z = -15 2x – 3y + z = —1 10x + z = 3
2x – 2y – z = 3 -3x + y – z = -5 x – y + z = 2
9) 5x – 3y + 4z = 11 19) 2x + y – 2z = 4 29) 4x + y – 5z = 5
2x – y – 2z = -6 -2x + y + z = -1 x – 5y + 5z = -3
3x – 2y + z = 2 -3x – y + 3z = -5 -x + y – z = -1
1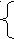
2x + y + z = 0 3x – 2y – z = 1 2x – y = -1
x – 2y + z = 0 5x + y – z = 10 2x + 3y +5z = 18
11. Решение матричных уравнений
Рассмотрим простейшие матричные уравнения вида А×Х = В (14) и Х×А = В (15).
Возможны два случая: 1) матрица А Квадратная невырожденная; 2) матрица А — либо вырожденная, либо прямоугольная.
1) Если А – квадратная и |А| ¹ 0, то уравнения (14) и (15) имеют единственное решение каждое: Х = А-1×В и Х = В×А-1 соответственно, если эти произведения определены. И не имеют решения, если они не определены.
2) А – квадратная матрица, но |А| = 0, либо А — прямоугольная матрица. Если матрица А Имеет размерность M´n, а матрица В – Размерность Р´к, то, при M ¹ Р уравнение (14) не имеет решения, а при N ¹ к не имеет решения уравнение (15). Если же M = Р , то в уравнении (14) матрица Х Должна иметь К столбцов, а в уравнении (15) она должна иметь Р Строк. Решение этих матричных уравнений сводится к решению систем линейных уравнений.
Пример 5. Найдите матрицу Х, Если А×Х = В, Где А = 
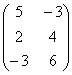
Из примера 5 следует, что матрица А Имеет обратную, поэтому Х = А-1×В. Используя найденную в примере 5 матрицу А-1, Получим Х = 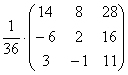

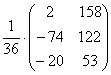
Пример 6. Найдите матрицу Х, Если Х×А = В, где А = 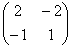
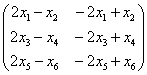
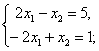
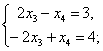
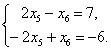
http://multiurok.ru/files/kontrol-naia-rabota-po-tiemie-matritsy-dieistviia.html
http://matica.org.ua/metodichki-i-knigi-po-matematike/lineinaia-algebra-uchebnoe-posobie-z-i-andreeva/11-reshenie-matrichnykh-uravnenii