Корень частного уравнения определяется по графикам

Урок алгебры по теме: «Графический способ решения уравнений». 8-й класс

Разделы: Математика

Класс: 8

— систематизация знаний учащихся по теме,

— формирование прочных навыков и умений при решении уравнений графическим способом,

— выработка умений применять известные знания в незнакомой ситуации,

— выработка способности учащихся к обобщению частных случаев.

— сознательное усвоение учащимися алгебраических понятий и связей между ними,

— формирование приемов поиска решений задач с параметрами.

— формирование графической культуры,

— возбуждение и развитие интереса учащихся к самостоятельному творчеству.

— дидактический раздаточный материал.

Перед уроком на экране слайд № 1

1. Организационный момент (1 минута)

(Учитель сообщает классу дату проведения урока, тему урока. На экране слайд № 3)

• Если вы хотите научиться плавать,

то смело входите в воду,

научиться решать задачи –

Д. Пойа “Математическое открытие”

— Мы знаем, что графический способ решения уравнений применяется довольно редко. Но существует достаточно много задач, в которых важен поиск не самих корней уравнений — их значений, а только количество корней.

Представим себе, что в середине января вас посылают в лес собирать грибы. Хотя вы отлично знаете технологию сбора грибов, вы в лес не пойдете. Опыт поколений показывает, что зимой грибы не растут. Вернемся к нашей задаче. Графическим способом можно найти количество корней, что облегчает их поиск, или доказать, что их нет, а тогда зачем решать уравнение?

Работать мы сегодня будем по следующей схеме (слайд №4):

Мы покажем связь тем изученных на предыдущих уроках, “преобразование графиков функций”, “графики функций”, “свойства функции”, будем решать уравнения графическим способом, находить количество корней уравнения с помощью графического метода, а также познакомимся с решением уравнения с параметром графическим способом.

2. Проверка знаний учащихся по теме “Функции. Графики функций. Преобразования графиков функций” (5-7 минут)

На экране (слайд № 5) вы видите функции. Вам необходимо назвать виды функции и линии, которые являются графиками функций.

y =

А сейчас три ученика (учитель называет фамилии) строят графики функций (слайд № 6), а класс пишет математический диктант (слайд № 7).

Пусть графически задана функция у=f(х). Я называю преобразование графика, а вам необходимо это преобразование записать с помощью формулы.

1. Сдвиг графика функции y=f(x) по оси ОХ

2. Сдвиг графика функции y=f(x) по оси ОУ

3. Сдвиг графика функции y=f(x) по оси ОХ на а ед. вправо и сдвиг по оси ОУ на b ед. вниз

4. Растяжение по оси ОУ, если b>1; сжатие по оси ОУ , если 0 0 и отражение этой части графика относительно оси ОУ для х 0 и отражение графика функции y=f(x) относительно оси ОХ для у 0 и b 0

(Во время проверки диктанта учитель проверяет правильность построения графиков функций, работает с учениками у доски).

3. Пропедевтика темы 9 класса “Свойства функций” (слайд № 8)

А теперь вспомним свойства функций, которые необходимы при решении уравнений графическим способом (на экране свойства функции, схема)

Опишите по данной схеме свойства квадратичной функции (график функции построен одним из учащихся, работающим около доски).

4. Графический способ решения уравнений. (7-10 минут)

А теперь перейдем непосредственно к графическому методу решения уравнений (слайд № 9).

Прочитайте алгоритм решения уравнения графическим способом (на слайде появляются пункты алгоритма).

Задание №1. (слайд № 10)

Решите графически уравнение х?+6х+8=0. (На доске уже построен график функции у=х?+6х+8, а учащиеся строят его у себя в тетрадях).

Вопросы во время работы учащихся с графиком:

1. Какая функция соответствует левой части уравнения?
2. Какая функция соответствует правой части уравнения?
3. Назовите вид функции у=0.
4. Что является графиком этой функции? (Показать на доске цветным мелом)
5. Сколько корней имеет уравнение? (Показать точки на графике)
6. Какие корни? (Записать корни уравнения)

Данное уравнение имеет и другие графические решения (слайды № 11-12). Посмотрим на экран (комментарии слайдов).

Запишем уравнение равносильное данному x?+6x=-8. Рассмотрим функции соответствующие левой и правой частям уравнения.

Вопросы:

1. Какая линия является графиком функции y=x?+6x ?
2. Какая линия является графиком функции у=-8 ?
3. Сколько корней имеет данное уравнение?
4. Какие корни?

Какое еще решение квадратного уравнения можно рассмотреть? (Комментарии учителя к решению уравнения x?=-6x-8, слайдам № 13-14)

Задание № 2 Решите графически уравнения:

(Учитель работает со слайдами № 15-18 , а ученики выполняют работу в одной системе координат).

Задание дополнительное (слайд № 19).

Задание № 3 Указать число корней уравнения x?+6x+8 = (х+1)/ (х-2)

Чтобы указать количество корней последнего уравнения (слайды № 20-24 ) необходимо построить графики функций соответствующих частям уравнения в одной системе координат.

Вопрос: Сколько корней имеет данное уравнение?

5. Проверка домашнего задания. (2 минуты)

Вашим домашним заданием было построение графика кусочно заданной функции (слайд № 25)

y =

(Комментарии учащихся построения графика, одновременно показ слайдов).

Меня интересуют две точки графика функции с абсциссами х=0 и х=1.

(Комментарии учащихся, одновременно показ слайда № 26).

Если возникли затруднения, то необходимы наводящие вопросы:

1. Почему я выделила эти аргументы функции? (Они не входят в область определения функции)
2. Как на графике показывают точки? (Выкалывают)

Задание (слайд № 27)

• Пусть задана функция y=f(x), где:

f(x) =

Указать количество корней уравнения

f(x) = а, где а – параметр.

График функции соответствующей левой части уравнения вы построили дома. Все дополнительные построения наносите на чертеж. (Слайды № 28-29)

Вопросы классу.

1. Является ли данная функция ограниченной?
2. Назовите наименьшее значение функции?

Рассмотрим функцию соответствующую правой части уравнения.

Вопросы.

1. Назовите вид функции и линии, которые являются графиками функций у=а.
2. Как могут располагаться по отношению к графику функции y=f(x) эти прямые?
3. При каком значении параметра а графики функций не пересекаются? (могут назвать конкретные числа, необходимо обобщить и сослаться на свойство ограниченности функции)?

При различных значениях параметра а мы будем получать различное количество точек пересечения графиков функций y=f(x) и у=а. (Рассмотреть по слайду все случаи. Одновременно учащиеся наносят на свои рисунки все графики).

Как определить количество корней уравнения? (По алгоритму решения уравнения графическим способом количество корней уравнения определяется по количеству точек пересечения графиков функций соответствующих левой и правой частям уравнения).

Теперь проведем анализ полученного рисунка и по количеству точек пересечения и ответим на вопрос задачи: сколько корней имеет данное уравнение при различных значениях параметра а?

Ответ: нет корней при a 3;

два корня при -4

три корня при 2

Если на уроке останется время, можно провести работу по закреплению графического решения уравнений с параметрами по чертежу, сделанному в начале урока одним из учащихся. Эту работу можно провести в виде самостоятельной работы, в ответ учащиеся записывают только значения параметра а и количество корней.

Задача . На доске график функции

Указать количество корней уравнения

f(x) =а, где а – параметр.

7. Итог урока.

Подведем итог нашего урока, а для этого ответим на вопросы (слайд № 30):

Домашнее задание (слайд № 31)

Заканчиваем урок высказыванием Р.Баха “Иллюзии” (слайд №32)

• Надо же как все просто.
• Как научиться ходить.

3.1. Отделение корней нелинейного уравнения

Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a, b], которому он принадлежит.

На первом этапе определяется число корней, их тип. Определяется интервал, в котором находятся эти корни, или определяются приближенные значения корней.

В инженерных расчетах, как правило, необходимо определять только вещественные корни. Задача отделения вещественных корней решается Аналитическими и Графическими методами.

Аналитические методы основаны на функциональном анализе.

Для алгебраического многочлена n-ой степени (полинома) с действительными коэффициентами вида

Pn(x) = an x n + an-1xn-1 +. +a1x+ a0 = 0, (an >0) (3.2)

Верхняя граница положительных действительных корней определяется по формуле Лагранжа (Маклорена):

, (3.3)

Где: k ³ 1 – номер первого из отрицательных коэффициентов полинома;

B – максимальный по модулю отрицательный коэффициент.

Нижнюю границу положительных действительных корней можно определить из вспомогательного уравнения

(3.4)

Если для этого уравнения по формуле Лагранжа верхняя граница равна R1, то

= (3.5)

Тогда все положительные корни многочлена лежат в интервале

≤x+≤.

Интервал отрицательных действительных корней многочлена определяется с использованием следующих вспомогательных функций.

и .

≤x–≤ = =.

Рассмотрим пример отделения корней с использованием этого аналитического метода.

Методом Лагранжа определим границы положительных и отрицательных корней многочлена.

3×8 – 5×7 – 6×3 – x – 9 = 0

K = 1 B = |– 9| an = 3

= 4

9×8 + x7 + 6×5 + 5x – 3 = 0

k = 8 B = 3 an = 9

Отсюда границы положительных корней 0,5 ≤ x+ ≤ 4

3×8 + 5×7 + 6×3 + x – 9 = 0

=

9×8 – x7 – 6×5 – 5x – 3 = 0

K = 1 B = 6 an = 9

Следовательно, границы отрицательных корней –2 ≤ x– ≤ –0,6

Формула Лагранжа позволяет оценить интервал, в котором находятся все действительные корни, положительные или отрицательные. Поэтому, для определения расположения каждого корня необходимо проводить дополнительные исследования.

Для трансцендентных уравнений не существует общего метода оценки интервала, в котором находятся корни. Для этих уравнений оцениваются значения функции в особых точках: разрыва, экстремума, перегиба и других.

На практике получил большее распространение Графический метод приближённой оценки вещественных корней. Для этих целей строится график функции по вычисленным её значениям.

Графически корни можно отделить 2-мя способами:

1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это приближенные значения корней уравнения.На графике 3 корня.

Рис. 3.1 Отделение корней на графике f(x).

2. Преобразовать f(x)=0 к виду j(x) = y(x), где j(x) и y(x) – элементарные функции, и определить абсциссу пересечений графиков этих функций.

На графике 2 корня.

Рис. 3.2 Отделение корней по графикам функций j(x) и y(x).

Графический метод решения нелинейных уравнений широко применяется в технических расчётах, где не требуется высокая точность.

Для отделения вещественных корней можно использовать ЭВМ. Алгоритм отделения корней основан на факте Изменения знака функции в окрестности корня. Действительно, если корень вещественный, то график функции пересекает ось абсцисс, а знак функции изменяется на противоположный.

Рассмотрим Схему алгоритма отделения корней нелинейного уравнения на заданном отрезке в области определения функции.

Алгоритм позволяет определить приближённые значения всех действительных корней на отрезке [a, b]. Введя незначительные изменения в алгоритм, его можно использовать для определения приближённого значения максимального или минимального корня.

Приращение неизвестного Δx не следует выбирать слишком большим, чтобы не «проскочить» два корня.

Недостаток метода – использование большого количества машинного времени.

Графический метод. Описание, примеры решения уравнений

Эта статья посвящена одному из направлений функционально-графического метода решения уравнений, а именно, графическому методу. Сначала дано описание графического метода: раскрыта его суть, сказано, на чем базируется метод, приведено его обоснование, обговорены особенности метода, связанные с точностью. Дальше идет практическая часть: записан алгоритм решения уравнений графическим методом и показаны решения характерных примеров.

В чем состоит метод и на чем он базируется

Графический метод решения уравнений состоит в использовании графиков функций, отвечающих частям уравнения, для нахождения с их помощью решения уравнения. Базируется он на следующем утверждении:

Решение уравнения f(x)=g(x) есть множество абсцисс точек пересечения графиков функций y=f(x) и y=g(x) .

Обоснованием этого утверждения займемся в следующем пункте. А сейчас выудим из него полезные сведения.

Основное из них таково: по количеству точек пересечения графиков функций y=f(x) и y=g(x) можно судить о количестве корней уравнения f(x)=g(x) , а по абсциссам точек пересечения можно судить о корнях этого уравнения. Проиллюстрируем сказанное.

Взглянем на чертеж, на котором изображены графики функций и .

Очевидно, в видимой области графики изображенных функций не имеют точек пересечения. За пределами видимой области графики тоже не имеют точек пересечения. Это мы можем утверждать в силу известного нам поведения графиков степенных функций и линейных функций. Отсутствие точек пересечения позволяет нам сделать вывод, что уравнение не имеет решений.

Другой пример. На следующем рисунке изображены графики функций и .

Сколько точек пересечения мы видим? Две. Известное поведение графиков показательных функций и линейных функций позволяет утверждать, что за пределами видимой области точек пересечения нет. Значит, графики функций и пересекаются в двух точках, следовательно, уравнение имеет два корня. А каковы значения этих корней? Для ответа на этот вопрос определяем абсциссы точек пересечения графиков. По рисунку находим, что абсциссы точек пересечения есть −2 и 1 . Через проверку подстановкой убеждаемся, что это действительно корни уравнения :

Здесь стоит заметить, что к проверке подстановкой мы обратились не случайно. Дело в том, что найденные по графикам значения корней можно считать лишь приближенными до проведения проверки. Подробнее об этом мы поговорим в одном из следующих пунктов этой статьи, раскрывающем особенности графического метода.

Обоснование метода

Докажем, что множество решений уравнения f(x)=g(x) есть множество абсцисс точек пересечения графиков функций y=f(x) и y=g(x) . Для этого достаточно показать, во-первых, что если x₀ – корень уравнения f(x)=g(x) , то x₀ – это абсцисса одной из точек пересечения графиков функций y=f(x) и y=g(x) , и, во-вторых, если x₀ – абсцисса одной из точек пересечения графиков функций y=f(x) и y=g(x) , то x₀ – корень уравнения f(x)=g(x) . Приступаем к доказательству.

Пусть x₀ – корень уравнения f(x)=g(x) . Тогда f(x₀)=g(x₀) – верное числовое равенство. Это равенство можно трактовать так: значения функции y=f(x) и y=g(x) в точке x₀ совпадают. А из этого следует, что x₀ – абсцисса одной из точек пересечения графиков функций y=f(x) и y=g(x) .

Первая часть доказана. Переходим к доказательству второй части.

Пусть x₀ – абсцисса одной из точек пересечения графиков функций y=f(x) и y=g(x) . Это означает, что значения функций y=f(x) и y=g(x) в точке x₀ равны, значит, f(x₀)=g(x₀) . А из этого равенства следует, что x₀ – корень уравнения f(x)=g(x) .

Так доказана вторая часть.

Особенности метода

Графический метод предполагает использование графиков функций. В общем случае построение графиков функций – дело непростое. Поэтому, графический метод решения уравнения обычно применяется лишь тогда, когда функции, отвечающие частям уравнения, довольно простые в плане построения графиков, и при этом не видно другого аналитического метода решения. Это одна из особенностей графического метода решения уравнений.

Другая особенность касается получаемых по графикам результатов. Полученные по графикам результаты можно считать лишь приближенными. Дело здесь в том, что сами по себе графики функций — вещь не совсем точная (но при этом очень наглядная и во многих отношениях удобная), особенно если говорить о графиках, построенных от руки. Это следует из принципов, которыми мы руководствуемся при построении графиков функций. Что мы делаем для построения графика функции в общем случае? Проводим исследование функции, чтобы получить ряд «опорных» точек, таких как граничные точки области определения, максимумы-минимумы, точки перегиба, и понять поведение функции на всех интервалах ее области определения. После этого определяем несколько контрольных точек. Дальше переносим все определенные в ходе исследования точки на координатную плоскость и, сейчас внимание, соединяем их плавной линией в соответствии с выясненным в ходе исследования поведением функции. Эта «плавная линия» и есть график функции. О какой точности можно здесь говорить? Понятно, что она определяется точностью нашего построения.

С приближенными, найденными по графикам, значениями корней уравнения можно так или иначе работать. В некоторых случаях определенные по графикам значения корней оказываются точными значениями, в чем позволяет убедиться проверка подстановкой. В других случаях есть возможность уточнить значения корней до требуемой степени точности, для этого существуют специальные методы уточнения значений корней. А вот если по графикам нет возможности определить количество корней, не говоря уже об их значении, то, почти наверняка, стоит отказываться от графического метода решения уравнения. Добавим наглядности сказанному.

Давайте посмотрим на изображенные в одной прямоугольной системе координат графики функций и y=−x 2 +6·x−5 .

По этому чертежу сложно судить даже о количестве корней уравнения , не говоря уже про их значения с приемлемой степенью точности. Здесь можно лишь грубо сказать, что если корни есть, то их значения находятся на промежутке от нуля до трех. Такую прикидку мы даем по той причине, что графики функций в обозначенном промежутке очень близки, почти совпадают. Если есть возможность построить графики более точно в обозначенном промежутке, то это немного проясняет картину:

Сейчас мы видим три точки пересечения, даже можем приближенно указать их абсциссы: 1 , 2 и 2,7 . Но опять же, это не более чем приближенные результаты, нуждающиеся в проверке и строгом обосновании.

Учитывая оговоренные особенности графического метода решения уравнения, для себя можно принять следующее: к графическому методу стоит обращаться лишь тогда, когда функции, отвечающие частям уравнения, довольно простые в плане построения графиков, когда по построенным графикам можно с уверенностью указать точное количество точек их пересечения, и когда не просматривается альтернативный метод решения.

Алгоритм решения уравнений графическим методом

Анализ приведенной выше информации позволяет записать алгоритм решения уравнений графическим методом. Чтобы решить уравнение графически, надо:

• Построить в одной прямоугольной системе координат графики функций, отвечающие левой и правой частям уравнения.
• По чертежу определить все точки пересечения графиков:
  • если точек пересечения нет, то решаемое уравнение не имеет корней,
  • если точки пересечения имеются, то переходим к следующему шагу алгоритма.
• По чертежу определить абсциссы всех точек пересечения графиков – это приближенные значения всех корней исходного уравнения.
• Если есть основания полагать, что некоторые или все определенные на предыдущем шаге значения являются точными значениями корней решаемого уравнения, то осуществить их проверку, например, подстановкой.

Дадим краткий комментарий к последнему шага алгоритма. Иногда определенные по чертежу приближенные значения корней оказываются точными. Обычно это касается целых значений. Но, опять же, прежде чем утверждать, что найденные значения является точными корнями уравнения, сначала нужно осуществить проверку этих значений, например, проверку подстановкой.

Решение примеров

Графический метод решения уравнений начинает входить в арсенал изучающих математику в 7 классе сразу же после знакомства с координатной плоскостью и самой первой функцией – линейной функцией y=k·x+b . Именно тогда мы сталкиваемся с заданиями, наподобие следующего: с помощью графика линейной функции y=2·x−6 определить, при каком значении x будет y=0 [1, с. 50-51]. Для ответа на поставленный вопрос мы строим график указанной линейной функции y=2·x−6 .

По чертежу находим точку пересечения графика с осью Ox (ось Ox отвечает графику функции y=0 ), и определяем абсциссу точки пересечения: x=3 . По сути, мы решаем уравнение 2·x−6=0 графическим методом.

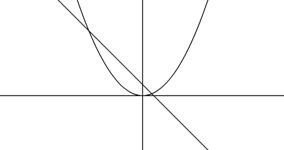
Чуть позже в 7 классе изучается функция y=x 2 . После этого опять заходит разговор о графическом методе решения уравнений, но уже более детальный, где метод уже называется своим именем и дается его алгоритм [1, с. 149-151; 2, с. 109]. Там с его помощью решаются уравнения, одной части которых отвечает функция y=x 2 , а другой – линейная функция y=k·x+b . Например, уравнение x 2 =x+1 . Для его решения строятся в одной системе координат соответствующие графики функций y=x 2 и y=x+1 :

Графики, очевидно, пересекаются в двух точках. Можно определить приближенные значения их абсцисс: .

В 8 классе изучаются новые виды функций: y=k/x , квадратичная функция y=a·x 2 +b·x+c , . И, естественно, рассматривается графический метод решения соответствующих уравнений. Особенно тщательно разбирается графическое решение квадратных уравнений. В учебнике Мордковича А. Г. приведены аж пять способов графического решения уравнения x 2 −2·x−3=0 [2, с. 127-131].

И так далее: изучаются функции , степенные функции, тригонометрические, показательные, логарифмические, …, — рассматривается решение соответствующих уравнений графическим методом. Так к концу школьного курса математики мы начинаем воспринимать графический метод решения уравнений как общий метод, позволяющий решать уравнения не только определенных видов, но и уравнения, в которых уживаются самые разнообразные функции: показательные с корнями, тригонометрические с логарифмическими и т.д. Покажем решение такого уравнения.

Решите уравнение

В заключение вспомним, что в этой статье при разговоре об особенностях графического метода решения уравнений мы обращались к иррациональному уравнению . В качестве «благодарности» этому уравнению за помощь в обретении знаний приведем ссылку на его решение графическим методом.