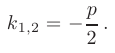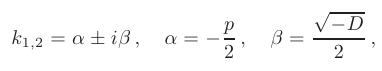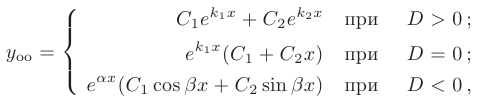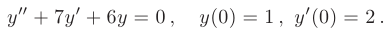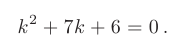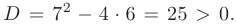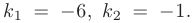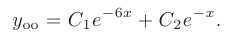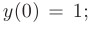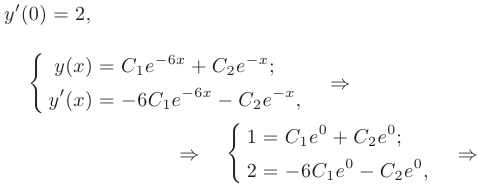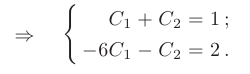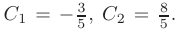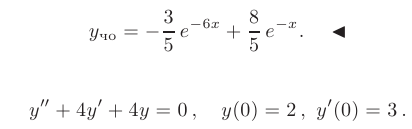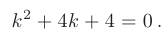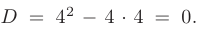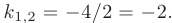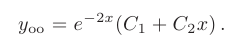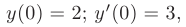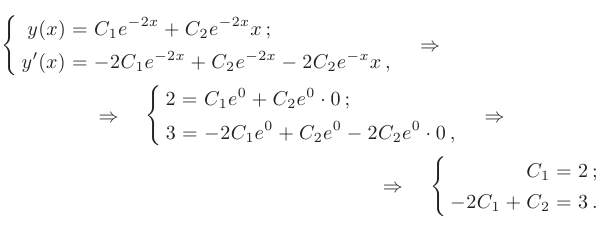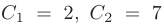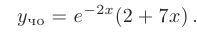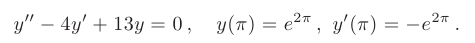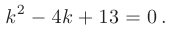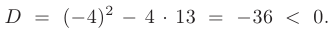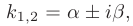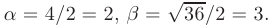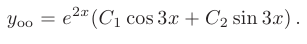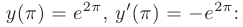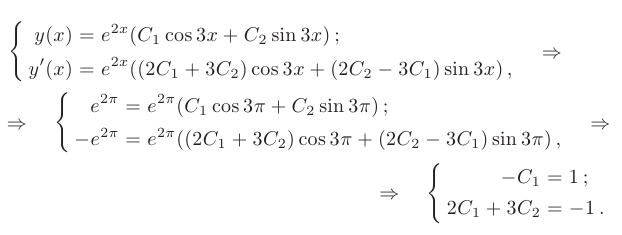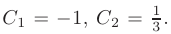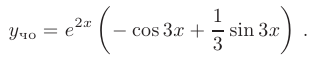Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)
Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами имеют вид
где p и q — действительные числа. Рассмотрим на примерах, как решаются однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Решение линейного однородного однородного дифференциального уравнения второго порядка зависит от корней характеристического уравнения. Характеристическое уравнение — это уравнение k²+pk+q=0.
1) Если корни характеристического уравнения — различные действительные числа:
то общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид
2) Если корни характеристического уравнения — равные действительные числа
(например, при дискриминанте, равном нулю), то общее решение однородного дифференциального уравнения второго порядка есть
3) Если корни характеристического уравнения — комплексные числа
(например, при дискриминанте, равном отрицательному числу), то общее решение однородного дифференциального уравнения второго порядка записывается в виде
Примеры решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
Найти общие решения однородных дифференциальных уравнений второго порядка:
Составляем характеристическое уравнение: k²-7k+12=0. Его дискриминант D=b²-4ac=1>0, поэтому корни — различные действительные числа.
Отсюда, общее решение этого однородного ДУ 2-го порядка есть
Составим и решим характеристическое уравнение:
Корни действительные и различные. Отсюда имеем общее решение данного однородного дифференциального уравнения:
В этом случае характеристическое уравнение
Корни различны и действительны. Поэтому общее решение однородного дифференциального уравнения 2-го порядка здесь
Поскольку корни действительны и равны, для этого дифференциального уравнения общее решение записываем как
Характеристическое уравнение здесь
Так как дискриминант — отрицательное число, корни характеристического уравнения — комплексные числа.
Общее решение этого однородного дифференциального уравнения второго порядка имеет вид
Отсюда находим общее решение данного диф. уравнения:
Примеры для самопроверки.
Найти общее решение однородных дифференциальных уравнений второго порядка с постоянными коэффициентами:
Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами в математике
Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами
Рассмотрим метод решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами:
Линейной комбинацией функций 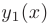
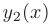
где 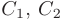
Функции 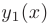
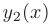
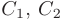
Теорема 7.2. Если 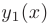
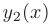
Следовательно, чтобы найти общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, надо знать два его частных линейно независимых решения: 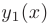
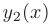
Будем искать частное решение дифференциального уравнения в виде 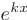
Очевидно, функция 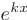
которое называется характеристическиль уравнением исходного дифференциального уравнения.
Как известно, для корней данного квадратного трехчлена возможны три случая.
- Если дискриминант больше нуля
, то корни характеристического уравнения действительные, простые:
- Если дискриминант равен нулю (
= 0), то корни характеристического уравнения действительные, кратные:
- Если дискриминант меньше нуля (
где 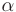
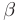
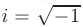
Теорема 7.3. Общее решение 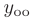
где 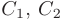
Пример:
Найти частные решения заданных линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами, удовлетворяющие начальным условиям:
► Составим характеристическое уравнение, заменяя в дифференциальном уравнении производные неизвестной функции у соответствующими степенями неизвестного 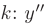
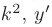
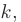
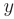
Дискриминант уравнения больше нуля:
В таком случае, корни характеристического уравнения действительные, простые:
Следовательно, общее решение дифференциального уравнения имеет вид
Частное решение получим из общего, используя для определения произвольных постоянных заданные начальные условия:
Решая полученную систему, находим значения произвольных постоянных:
После подстановки найденных значений в общее решение, искомое частное решение принимает вид
► Составим характеристическое уравнение:
Дискриминант уравнения равен нулю:
В таком случае, корни характеристического уравнения действительные, кратные:
Следовательно, общее решение дифференциального уравнения имеет вид
Найдем производную общего решения и определим произвольные постоянные из начальных условий:
Находим значения произвольных постоянных:
и подставим их в общее решение. Искомое частное решение принимает вид
Составим характеристическое уравнение:
Дискриминант меньше нуля:
В таком случае, корни характеристического уравнения комплексно-сопряженные:
Следовательно, общее решение дифференциального уравнения имеет вид
Используем для определения произвольных постоянных заданные начальные условия:
После подстановки найденных значений в общее решение, получим:
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://www.matematika.uznateshe.ru/odnorodnye-differencialnye-uravneniya-vtorogo-poryadka-s-postoyannymi-koefficientami/
http://lfirmal.com/linejnoe-odnorodnoe-differentsialnoe-uravnenie-vtorogo-poryadka-s-postoyannyimi-koeffitsientami-v-matematike/
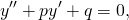
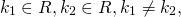
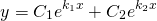
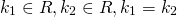
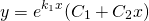
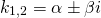
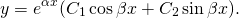
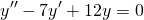
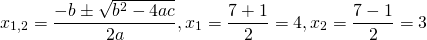
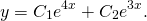
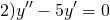
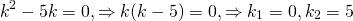
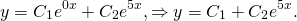
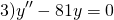
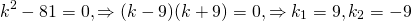
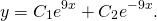
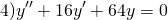
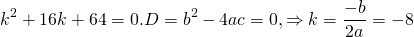
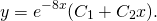
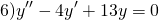
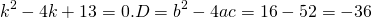
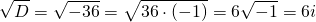
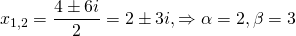
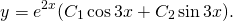
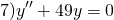
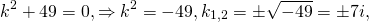
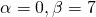

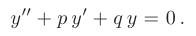
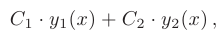
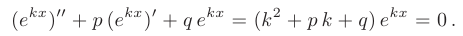
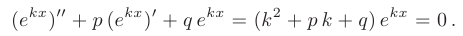
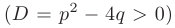 , то корни характеристического уравнения действительные, простые:
, то корни характеристического уравнения действительные, простые: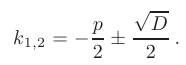
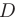 = 0), то корни характеристического уравнения действительные, кратные:
= 0), то корни характеристического уравнения действительные, кратные: