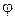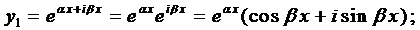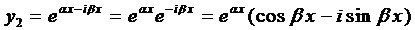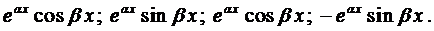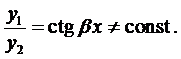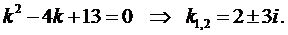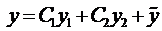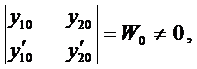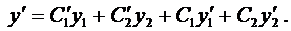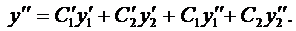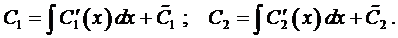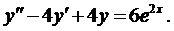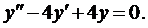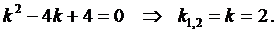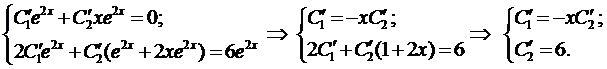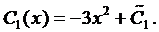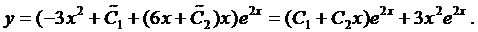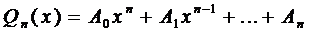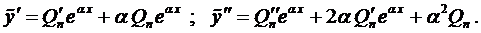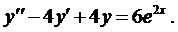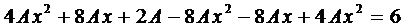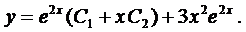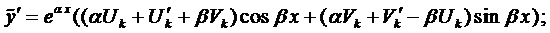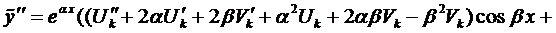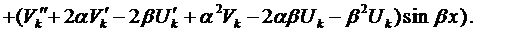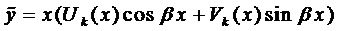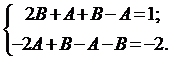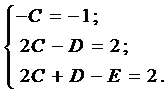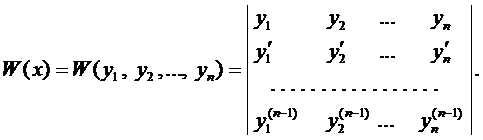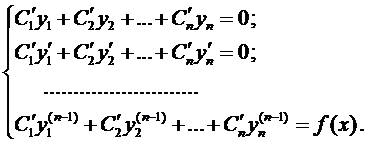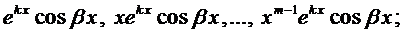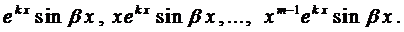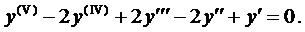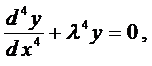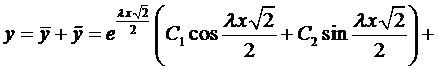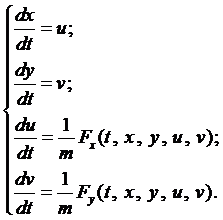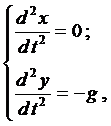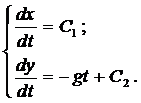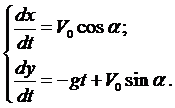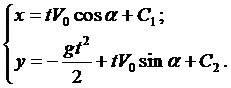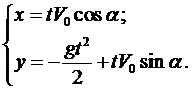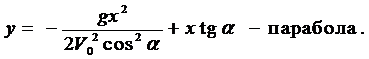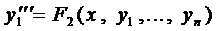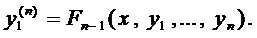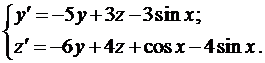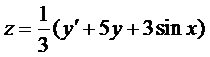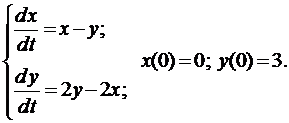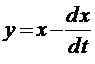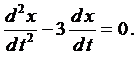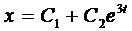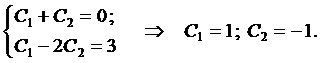корней характеристического уравнения
Одним из косвенных показателей качества систем управления является степень удаленности корней характеристического уравнения замкнутой САУ от мнимой оси комплексной плоскости. Пусть ближайшие к мнимой оси комплексно-сопряженные корни устойчивой системы имеют значение
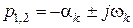
Расстояние 
Угол φ, образуемый лучами, проведенными из начала координат через эти корни, характеризует колебательность системы. Степенью колебательности системы (коэффициентом затухания колебаний) называют количественную характеристику, определяемую выражением

Чтобы система обладала заданной колебательностью, все корни характеристического уравнения должны вписываться в угол 2φ (см. рис. 7.2). Для большинства систем управления допустимое перерегулирование 
Рис. 7.2. Область расположения корней
с заданными показателями 
При корневых методах оценки качества системы, т. е. по расположению корней характеристического полинома, исходят из следующих соображений.
Решение однородного уравнения, характеризующего свободное движение системы, представляет собой сумму затухающих экспонент вида (6.2). Полагая, что качество САУ в основном определяется ближайшим к мнимой оси вещественным корнем или ближайшей к мнимой оси парой комплексно-сопряженных корней (доминирующих корней), можно записать
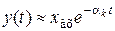
Полагая, что зона δ установления переходного процесса составляет (2…5)% от установившегося значения 


Следовательно, задаваясь временем регулирования, можно рассчитать минимальное (по модулю) значение вещественных частей корней характеристического уравнения.
Аналогично можно связать степень колебательности m системы со степенью затухания колебаний. Пусть по условиям технологии требуется, чтобы каждая последующая амплитуда колебаний затухала в k раз по сравнению с предыдущей. Тогда
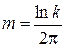
Пусть k=10, тогда в соответствие с (7.4) получим m=0,336 и
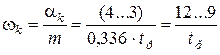
Таким образом, задаваясь временем регулирования 

Для построения в плоскости параметров областей, обеспечивающих требуемые показатели качества регулирования целесообразно использовать метод D-разбиения [6]. В качестве примера используем уравнение Вышнеградского, описывающего в параметрической форме характеристический полином 3-го порядка,

где A и B – обобщенные параметры характеристического уравнения.
Подставим выражение для комплексного корня 

Приравнивая нулю вещественную и мнимую части, получим


Полагая 


Рис. 7.3. Границы областей устойчивости,
колебательности и апериодичности на
Полагая 

Поскольку на кривой 1 ω ≠ 0, а на кривых 2 и 3 ω = 0, то области I и III являются областями комплексных, а область II – вещественных корней (см. рис. 7.3). Следовательно, если параметры A, B принадлежат области II, то переходные процессы имеют апериодический характер, причем, чем эти параметры больше, тем процессы более затянуты. Если параметры принадлежат области I, то переходные процессы имеют колебательный характер, причем, чем больше A и меньше B, тем выше колебательность. Область III является областью монотонности решения однородного дифференциального уравнения, соответствующего (7.5), а, следовательно, переходные процессы, имея колебательный характер, тем не менее, затухают монотонно (без перерегулирования).
Диаграмма Вышнеградского [19] помимо приведенных кривых содержит кривые равных вещественных частей комплексных корней (равной степени устойчивости), причем для двух случаев расположения корней, когда ближайшими к мнимой оси являются комплексные корни и, когда ближайшим к мнимой оси расположен вещественный корень (на рис. 7.3 эти кривые не показаны). В частности, на границе областей I и III (кривая 4) все три корня равно удалены от мнимой оси.
Требования повысить быстродействие и одновременно снизить перерегулирование в системе являются противоречивыми друг другу, что заставляет искать компромисс. В общем случае, с точки зрения переходного процесса наилучшей считается САУ, у которой все корни характеристического уравнения n-го порядка равны друг другу (на практике редко реализуется), т. е.
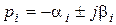
В этом случае перерегулирование не превышает 10%, а время нарастания регулирования является минимальным.
Если все корни являются вещественными, то система характеризуется отсутствием перерегулирования, т. е. апериодическими переходными процессами. Время регулирования будет тем меньше, чем меньше среднегеометрический корень 
При анализе качества системы корневыми методами необходимо учитывать влияние нулей передаточной функции на переходный процесс.
Прежде всего, нужно проверить, насколько близки нули к полюсам.
Если нуль и полюс совпадают, то их нужно сократить, и они не будут влиять на качество системы. Порядок системы при этом, естественно, будет понижен.
Если полюсы и нули передаточной функции не совпадают, то полюсы определяют отдельные составляющие переходного процесса (апериодические и гармонические), а нули определяют удельный вес каждой из этих составляющих. Чем ближе нуль передаточной функции расположен к какому-либо полюсу, тем меньше его вклад в переходную характеристику составляющей, соответствующей данному полюсу.
7.2.2. Интегральные оценки качества
В основе интегральных оценок качества лежит предположение, что качество регулирования тем выше, чем меньше площадь между кривой переходного процесса и заданным значением регулируемой переменной. Интегральные оценки качества являются строгой математической формулировкой понятия качества системы, и их минимизация позволяет определить оптимальные параметры системы управления, т. е. решить задачу параметрического синтеза системы. Для этой цели применяются процедуры безусловной и условной оптимизации [2, 6, 10-12, 19-21].
Наибольшее применение для косвенной оценки качества САУ находят интегральные оценки вида [6, 11, 12, 19]:





где 
С – некоторый весовой коэффициент, характеризующий допустимую скорость изменения ошибки регулирования, а, следовательно, выходной координаты в переходном процессе.
В критерии (7.8) подынтегральное выражение линейно относительно ошибки регулирования и такая оценка применяется только для апериодического переходного процесса, когда ошибка имеет положительный знак.
Интегральная квадратичная оценка (ИКО) вида (7.9) применяется при колебательном характере переходных процессов, характеризующихся сменой знака ошибки регулирования. Интегральная квадратичная оценка (7.10) применяется в тех случаях, когда требуется учитывать ограничения энергии управления.
Широко используемым видом оценки качества является интеграл от модуля ошибки (ИМО) – (7.11), позволяющем учесть смену знака подынтегральной функции.
Чтобы уменьшить вклад начальной ошибки в интеграл (7.11) и учесть связанную с этим ошибку была предложена [6] оценка в виде интеграла от взвешенного модуля ошибки (ИВМО) в виде (7.12).
Рассмотрим пример. Пусть передаточная функция замкнутой системы 2-го порядка имеет вид:

где 
Нормированное значение собственной частоты принято 

Рис. 7.4. Интегральные оценки
качества системы второго порядка
Как видим, оценка ИВМО по сравнению с ИКО имеет ярко выраженный минимум (хорошую избирательность), соответствующий 
Рассмотрим еще один пример. Пусть передаточная функция замкнутой системы имеет достаточно общий вид нерекурсивного фильтра n-го порядка:

Безусловная оптимизация систем первого-четвертого порядка (n=1…4), описываемых передаточными функциями (7.14), по критерию ИВМО дает оптимальные значения коэффициентов полиномов знаменателей этих передаточных функций, приведенные в табл. 7.1. Значения коэффициентов нормированы относительно собственной частоты колебаний 
На рис. 7.5 приведены кривые переходных процессов, соответствующих оптимальным по критерию ИВМО фильтрам первого-четвертого порядка.
| Порядок системы | Полином знаменателя передаточной функции |
| n=1 |  |
| n=2 |  |
| n=3 |  |
| n=4 |  |
Значения коэффициентов нормированы относительно собственной частоты колебаний 
Рис. 7.5. Переходные характеристики, соответствующие
оптимизации систем по ИВМО
Графики построены в зависимости от нормированного времени 
Кроме приведенных оценок для оптимизации систем управления применяются и другие интегральные критерии качества, в частности, лежащие в основе синтеза фильтров Баттерворта, широко применяемых при настройке контуров электромеханических систем управления.
8. Метод пространства состояний
Широкое распространение компьютеров и мощных систем программирования побуждает к исследованию САУ во временной области, а, следовательно, к непосредственному использованию описания динамических систем управления в форме обыкновенных дифференциальных уравнений без перехода к операторной форме. Кроме того, как уже отмечалось, векторно-матричные формы описания и исследования применимы не только к одномерным, линейным, стационарным САУ, но и к широкому классу многомерных, нелинейных и нестационарных САУ.
Чтобы получить пригодную для компьютерного синтеза и анализа модель САУ, необходимо представить ее в переменных состояния системы, используя далеко не единственный набор переменных. Следует отметить, что описание систем во временной области в векторно-матричной форме лежит в основе современной теории управления и оптимизации. В настоящей главе рассмотрены вопросы применения метода пространства состояния к непрерывным системам управления.
8.1. Векторно-матричное описание САУ
Состояние системы – это совокупность значений переменных системы (координат состояния), существенных с точки зрения решаемой задачи. В общем случае, в это число включают не только выходные и внутренние переменные САУ, но и задающие воздействия, и доминирующие возмущающие воздействия внешней среды. Чем полнее достоверной информации о состоянии системы в текущий момент времени, тем проще определить будущие значения всех ее переменных. Инженерно-технический персонал, разрабатывающий и эксплуатирующий технические системы управления, оперирует, как правило, с такими физическими переменными, которые могут быть измерены с помощью соответствующих датчиков. К таким физическим переменным САУ относят ускорение, скорость, перемещение, давление, расход, температуру, уровень и т. п. Координатами датчиков технологических координат САУ являются другие переменные — напряжение, ток, частота следования импульсов, двоичный код и т. п., что дает исследователю возможность выбора для синтеза и анализа необходимого набора координат состояния САУ.
Векторно-матричная модель многомерной, нелинейной, нестационарной САУ записывается в виде [6, 10, 11, 19]


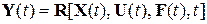
где X(t), U(t),F(t), Y(t) – соответственно векторы состояния, управления, возмущения и выходных (управляемых) координат системы,


В уравнении (8.1) вектор управления U(t) является, в общем случае, некоторой нелинейной нестационарной функцией задающих координат, координат состояния и возмущения САУ и призван обеспечить оптимальное управление системой. Описание многомерных, нелинейных, нестационарных САУ в форме (8.1) не позволяет, как правило, получить инженерное решение задачи структурно-параметрического синтеза оптимального управления U(t) или такое решение приводит к неоправданным затратам на реализацию (в техническом или экономическом аспектах). В большинстве случаев такие модели сводят к одномерным или многомерным линейным (линеаризованным) квазистационарным моделям, для которых имеются развитые методы и инженерные методики синтеза оптимального управления.
Линейную (линеаризованную) модель многомерной стационарной (квазистационарной) САУ представляют в виде системы обыкновенных дифференциальных уравнений первого порядка в форме Коши:



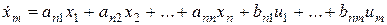
Эту же систему дифференциальных уравнений можно представить в векторно-матричной форме [6, 11, 19]:

где 



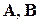


В общем случае, на объект управления помимо управляющих воздействий действуют возмущающие воздействия. В этом случае векторно-матричную модель системы представляют в виде

где 


Выходные (управляемые) переменные не всегда непосредственно принадлежат вектору состояния. В линейных САУ они линейно связаны с переменными состояния, управляющими и возмущающими переменными. В этом случае к уравнениям (8.3), (8.4) присоединяют алгебраические линейные уравнения

или 
где 
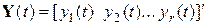
K, L, M – стационарные матрицы соответственно размерностей (r 


Следует отметить, что приведенные уравнения (8.1)…(8.6) дают описание лишь объекта управления или разомкнутой системы, если вектор управления U(t) не является функцией координат состояния САУ. В замкнутых линейных САУ управление обычно формируют как линейную форму координат состояния и, в общем случае, возмущения САУ.
В качестве примера приведем векторно-матричное описание ранее рассматриваемого электродвигателя постоянного тока как объекта регулирования по цепи якоря. Пусть выходной (регулируемой) координатой является скорость вращения двигателя. Полагая, что напряжение возбуждения 



Воспользуемся векторно-матричной моделью линейных САУ в виде (8.4), (8.5). Зададимся векторами состояния, управления и возмущения в виде:

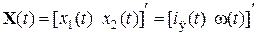


По уравнениям (8.7) найдем матрицы состояния, управления и возмущения:
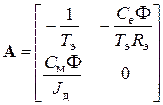


Поскольку выходная переменная всего одна и ей является координата состояния 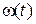
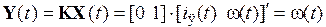
По описанию системы в форме векторно-матричных уравнений (ВМУ) можно непосредственно получить эквивалентную передаточную функцию (ПФ) и, наоборот, зная ВМУ системы, можно получить ее ПФ. Для этого в системе MATLAB имеется две функции: функция tf и функция ss.
Пусть ВМУ системы имеет вид (8.3), (8.5). Применительно к системе MATLAB ВМУ записывают в виде

Для получения ВМУ в системе MATLAB необходимо определить функцию ss(A,B,C,D). Для преобразования ВМУ к ПФ системы необходимо записать:
sys_ss=ss(A,B,C,D); % Формирование ВМУ системы;
sys_tf=tf(sys_ss), % Преобразование ВМУ к ПФ системы.
Для обратного преобразования ПФ к ВМУ необходимо записать:
sys_tf=tf(num,den); % Формирование ПФ системы;
sys_ss=ss(sys_tf); Преобразование ПФ к ВМУ системы.
Рассмотрим пример. Пусть ПФ системы имеет вид
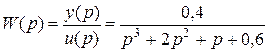
Тогда запишем скрипт преобразования ПФ к ВМУ и обратного преобразования ВМУ к ПФ:
sys_tf=tf(num,den); % Формирование ПФ системы;
sys_ss=ss(sys_tf); %Преобразование ПФ к ВМУ системы;
Пример комплексной подстановки при решении линейного неоднородного дифференциального уравнения
Метод понижения порядка линейного неоднородного дифференциального уравнения с комплексными корнями характеристического уравнения
Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами n-го порядка:
(1) .
Мы полагаем, что коэффициенты этого уравнения являются действительными числами. Здесь мы рассматриваем случай, когда характеристическое уравнение
(2)
имеет комплексные корни.
Для решения уравнения (1), применим метод понижения порядка. Поскольку коэффициенты характеристического уравнения (2) являются действительными числами, то его комплексные корни являются попарно комплексно сопряженными. Пусть – два комплексно сопряженные корня: . Запишем исходное уравнение (1) в следующем виде:
(3) ,
где – оператор дифференцирования.
Обозначим:
.
Тогда уравнение (3) принимает следующий вид:
.
Сделаем подстановку:
(4) .
Получаем уравнение первого порядка с комплексным коэффициентом :
.
Или
(5) .
Решение этого уравнения имеет следующий вид (см. страницу метод понижения порядка ):
,
где – комплексная постоянная.
Далее замечаем, что поскольку исходное уравнение (1) имеет действительные коэффициенты, то переменная u и ее производная u′ должны быть действительными. Выразим комплексный корень через действительную и мнимую части:
.
Подставим в (4):
.
Извлекая мнимую часть, получаем:
.
Отсюда
.
Таким образом, в случае с комплексными корнями, один этап решения приводит к понижению порядка на две единицы.
Пример решения дифференциального уравнения
Решить уравнение
(П1) .
Перепишем уравнение в следующем виде:
.
Вводим обозначение :
.
Характеристическое уравнение
имеет комплексные корни: . Тогда
.
Переписываем исходное уравнение:
;
.
Делаем подстановку:
;
(П2) .
Тогда уравнение принимает вид:
;
(П3) .
Это линейное неоднородное дифференциальное уравнение первого порядка. Ищем решение с помощью интегрирующего множителя. Умножим на и выполняем преобразования:
;
;
(П4) ,
где – комплексная постоянная; – действительные постоянные.
Вычисляем интеграл в (П4) с помощью подстановки .
.
Выразим арктангенс через логарифм, используя уравнение: .
;
.
Отсюда
(П5) .
Теперь в правой части (П6) нам нужно отделить вещественную и мнимую части. Мнимая часть уравнения (П6) и даст искомое решение y .
Для преобразования логарифма, используем формулу: . Далее замечаем, что . Тогда при имеем:
.
При :
.
Оба случая можно записать одной формулой:
,
где при нужно взять верхний знак ′+′; при – нижний знак ′–′.
Подставим в (П6) и выполним преобразования:
;
.
Переобозначим постоянную :
(П7) .
Теперь преобразуем экспоненту с помощью формулы Эйлера: , и выразим комплексную постоянную через действительную и мнимую части: . Подставляем в (П7):
.
Выполняем преобразования:
.
Тогда
.
Отделяем мнимую часть:
.
Автор: Олег Одинцов . Опубликовано: 20-07-2013 Изменено: 26-08-2020
Корни комплексно-сопряженные, т.е. .
Вначале покажем, что если 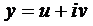
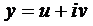
Подчеркнутый член и выражение в скобках равны нулю.
Итак, в этом случае частные решения имеют вид
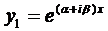
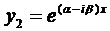
Если воспользоваться формулой Эйлера, которая будет доказана позже,

и, как показано выше, решениями уравнения (1) будут являться функции:
Очевидно, линейно-независимыми среди них будут
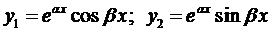
Так как
Окончательно, общее решение будет иметь вид

Пример 3. Найти общее решение уравнения 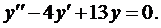
Составим характеристическое уравнение:
Воспользуемся формулой (5):
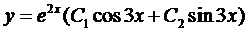
4.4. Линейные неоднородные дифференциальные уравнения второго порядка
Общий вид линейного неоднородного дифференциального уравнения второго порядка (ЛНДУ-2)
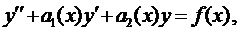
где функции 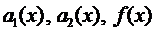
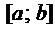
Ему соответствует однородное уравнение
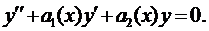
Пусть известно общее решение уравнения (7)
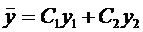
Теорема (о структуре общего решения ЛНДУ-2). Общее решение ЛНДУ-2 является суммой частного решения 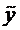
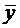
Вначале покажем, что 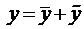
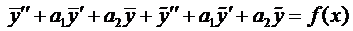
Сумма первых трёх членов левой части равенства равна нулю, так как 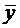
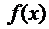
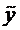
Таким образом, 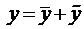
Теперь покажем, что для любых начальных условий вида 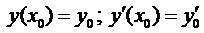
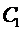
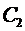
в эти условия, тогда получим систему
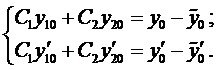
Система (9) является линейной системой для определения 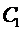
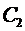
так как 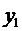
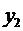
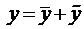
Замечание. Если 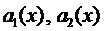
4.5. Метод вариации произвольных постоянных (метод Лагранжа)
Пусть нам известно общее решение уравнения (7), т.е. 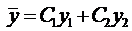
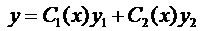
Продифференцируем это равенство:
В силу произвольности выбора функций 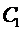
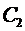
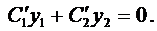
Подставляя 
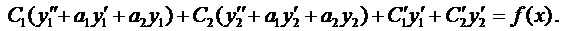
Выражения в скобках в формуле (11) равны нулю, объединяя полученные результаты, приходим к системе
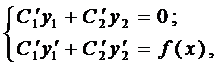
из которой единственным образом находятся 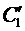
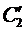
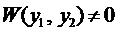
Пример 4. Методом вариации произвольных постоянных найти общее решение уравнения
Найдём общее решение соответствующего однородного уравнения
Составим характеристическое уравнение
Воспользуемся формулой (4) 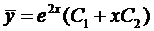
Здесь 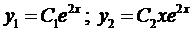
Составим систему (12)
Интегрируя последнее уравнение системы, находим 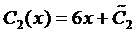
Окончательно получим общее решение
4.6. ЛНДУ-2 с постоянными коэффициентами со специальной правой частью
Общий вид линейного неоднородного дифференциального уравнения
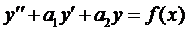
где 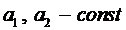
Как известно, общее решение уравнения (1) имеет вид 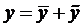

1. 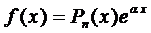
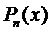
Зададим вид частного решения в форме 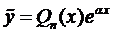
многочлен п-ой степени с неопределёнными коэффициентами. Найдём его производные:
Подставим эти выражения в уравнение (1) и сократим на
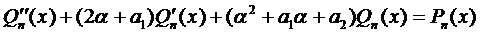
Здесь возможны случаи:
1.1. Число 
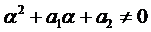
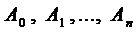
1.2. Число 
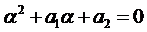
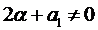
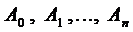
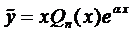
1.3. Число 
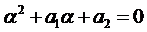
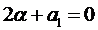
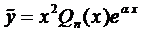
Рассмотренные три случая можно объединить общим правилом
Правило 1 . Если правая часть уравнения (1) имеет вид 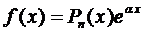
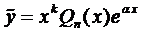
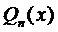
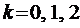

Пример 1. Найти общее решение уравнения
На предыдущей лекции было найдено общее решение соответствующего однородного уравнения

Частное решение будем искать в виде 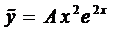
Подставим это выражение в наше уравнение и сократим на 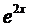
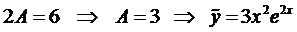
Тогда общее решение будет иметь вид
2. 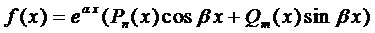
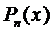
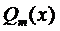
Частное решение будем искать в виде
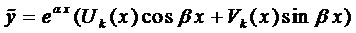
где 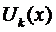
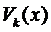
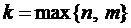
Если подставить эти выражения в уравнение (1), сократить на 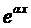
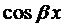
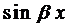
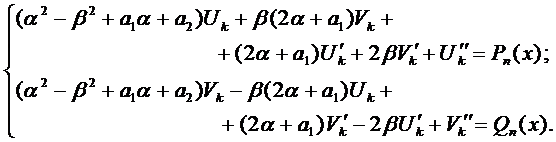
Если подставить числа 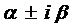
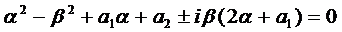
2.1. Числа 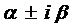
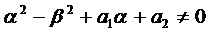
Тогда слева в уравнениях (3) стоят многочлены степени 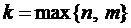
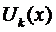
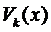
2.2. Числа 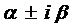
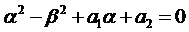
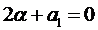
Тогда слева в уравнениях (3) стоят многочлены степени на единицу меньшую, чем k и, рассуждая аналогично, как и ранее, частное решение ищем в виде
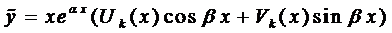
Правило 2. Если правая часть уравнения (1) имеет вид
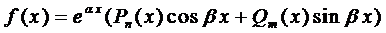
то частное решение следует искать в виде
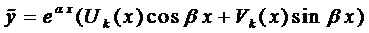
если 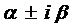
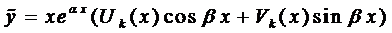
если 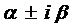
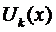
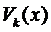
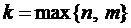
Замечание 1. Правило 2 справедливо и для случая 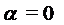
и, если 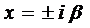
Замечание 2. Если правая часть уравнения (1) представляет собой сумму двух функций, относящихся к правилам 1-2, то частное решение в силу линейности уравнения ищется в виде суммы двух функций, которые определяются соответственно правилами 1-2.
Пример 2. Найти частное решение уравнения
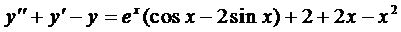
Здесь правая часть уравнения представляется в виде суммы двух функций:
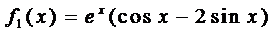
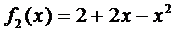
Поэтому решение ищем в виде 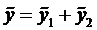
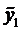
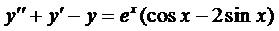
а 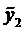
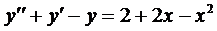
Для этого случая решение имеет вид (случай 2.1)
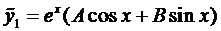
Подставим это выражение в уравнение (4):
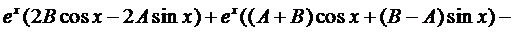
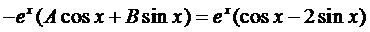
Сократим на 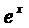
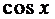
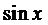
Из решения системы получаем
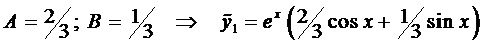
Решение уравнения (5) ищем в виде (случай 1.1)
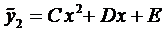
Подставим это выражение в уравнение (5)
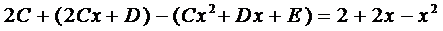
Приравнивая коэффициенты при 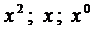
Из решения системы последовательно находим
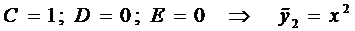
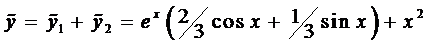
Лекция № 43. Тема 5 : Линейные ДУ высших порядков
5.1. Линейные дифференциальные уравнения п-го порядка
Общий вид линейного дифференциального уравнения п-го порядка (ЛДУ — п)
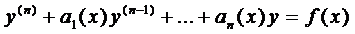
Ему соответствует однородное уравнение п-го порядка
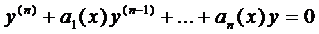
Определение 1. Функции 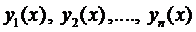
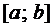
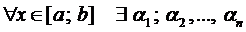
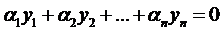
Для выяснения ЛЗ или ЛНЗ решений уравнения (2) также используется определитель Вронского, который для данного случая имеет вид
При этом, если 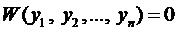
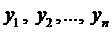
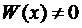
Справедливы также теоремы о структуре решений уравнений (1-2):
Теорема 1. Если 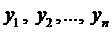
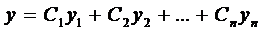
где 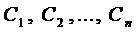
Теорема 2. Общее решение ЛНДУ — п есть сумма частного решения 
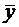
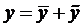
Доказательства этих теорем аналогичны, как и для случая ЛДУ – 2.
Если известно общее решение соответствующего однородного уравнения (2), то общее решение уравнения (1) можно находить методом вариации произвольных постоянных. Тогда система для нахождения функций 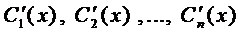
Остановимся на случае, когда все коэффициенты 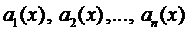
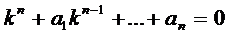
По характеру корней уравнения (3) определяются частные ЛНЗ решения:
Правило. Каждому действительному корню k характеристического уравнения (3) т-ой кратности соответствует т ЛНЗ решений вида
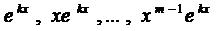
Каждой паре комплексных корней 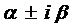
Для случая уравнения со специальной правой частью 

Пример 1. Найти общее решение ДУ
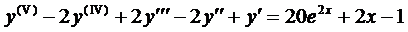
Ему соответствует однородное уравнение
Составим характеристическое уравнение
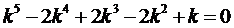
Найдём его корни
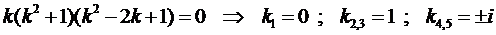
Тогда, согласно правилу, получаем общее решение однородного уравнения
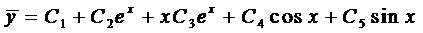
Частное решение неоднородного уравнения будем искать в виде 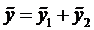
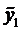
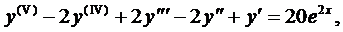
а 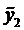
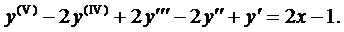
Так как число 2 не является корнем характеристического уравнения, то 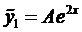
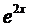
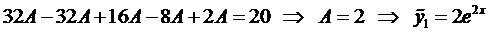
Частное решение уравнения (5) ищем в виде
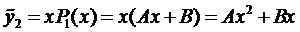
так как нуль является корнем характеристического уравнения.
Подставим это выражение в уравнение (5):
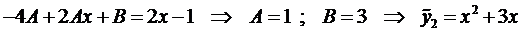
Таким образом, получаем общее решение данного уравнения
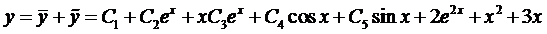
5.2*. Понятие о краевой задаче
При решении некоторых задач требуется проинтегрировать ДУ не при начальных условиях (задача Коши), а с учётом значений искомой функции или её производных в некоторых точках. Условия, налагаемые на значения функции, её производных на концах отрезка, называются краевыми условиями, а соответствующая задача – краевой задачей.
При этом для корректности решаемой задачи число таких условий должно быть равно числу констант в общем решении. Такие задачи рассматриваются в курсе сопротивления материалов, а ещё более общие задачи встречаются в курсе уравнений математической физики.
Рассмотрим в качестве примера задачу изгиба балки на упругом основании.
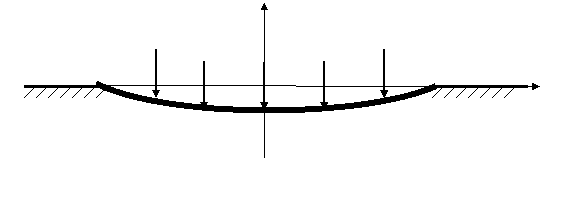
Дифференциальное уравнение прогиба балки имеет вид
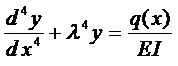
где l упругая постоянная, характеризующая свойства основания, Е — модуль упругости балки, I — момент инерции площади поперечного сечения балки, q(x) — интенсивность внешней нагрузки.
Этому уравнению соответствует однородное уравнение
для которого характеристическое уравнение имеет вид
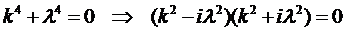
Непосредственно легко проверить, что его корнями являются
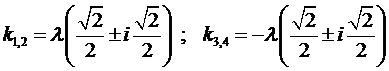
Этим корням соответствует общее решение
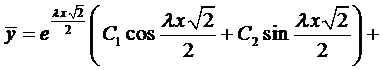
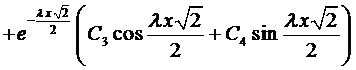
Рассмотрим случай, когда 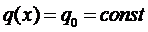
Тогда частное решение будем искать в виде 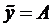
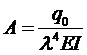
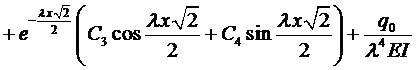
Константы 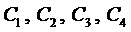
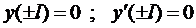
Подставляя в эти граничные условия полученное выражение для прогиба (6), получим систему четырёх уравнений для определения 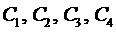
Лекция № 44. Тема 6 : Системы дифференциальных уравнений
6.1. Нормальные системы дифференциальных уравнений
К решению систем дифференциальных уравнений приводят, в частности, задачи по исследованию колебательных процессов в технике, физике, меха-нике. Вибрации сооружений, электромагнитные колебания, колебания упру-гих тел — все эти процессы описываются системами дифференциальных уравнений.
В качестве примера рассмотрим движение материальной точки массой т в плоскости Оху. Согласно второму закону Ньютона имеем
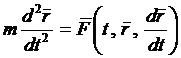
Спроектируем векторное равенство на координатные оси
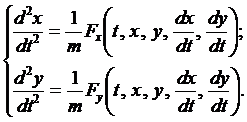
Получена система дифференциальных уравнений относительно двух неизвестных функций 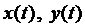
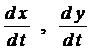
Будем рассматривать системы дифференциальных уравнений, каждое уравнение которой разрешено относительно старшей производной – канонические системы. Такую систему, путём введения дополнительных функций, всегда можно привести к эквивалентной ей системе дифференциальных уравнений первой порядка (ДУ-1), разрешенных относительно производной.
Например, приведём систему (1) к системе ДУ-1.
Введём функции 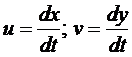
Поэтому в дальнейшем будем рассматривать только такие системы.
Определение 1. Нормальной системой дифференциальных уравнений называется система дифференциальных уравнений вида
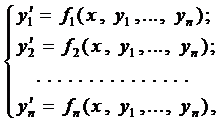
где 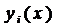
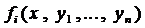
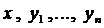
Определение 2. Решением системы (2) называется совокупность п дифференцируемых функций: 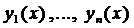
Определение 3. Совокупность функций 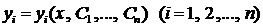
1. Эти функции являются решением системы при любых значениях 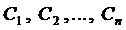
2. Для любых начальных условий вида
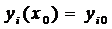
из области G можно найти такие значения 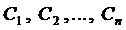
Задача Коши для системы (2) формулируется следующим образом: Найти такое решение 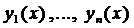
Теорема (о существовании и единственности решения задачи Коши).
Если правые части системы ДУ (2) и их частные производные по переменным 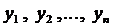
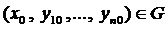
Пример 1*. Определить траекторию полёта снаряда, выпущенного из орудия под углом a к горизонту со скоростью V0. Сопротивлением воздуха пренебречь.
Вначале лекции были рассмотрены общие уравнения (1), которые можно применить для данной задачи
где g — ускорение свободного падения. Проинтегрируем каждое уравне-ние системы
Константы интегрирования 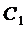
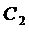
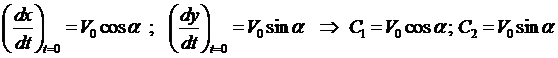
Тогда система примет вид
Ещё раз проинтегрируем
Константы интегрирования 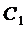
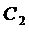
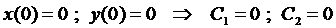
Таким образом, решением системы являются функции
Исключая параметр t, приходим к уравнению траектории
6.2. Решение нормальных систем ДУ методом исключений
Решение системы (2) сводится к решению ДУ-п методом исключений.
Продифференцируем по х первое уравнение системы (2)
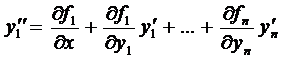
С учетом остальных уравнений системы это выражение примет вид
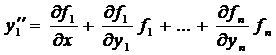
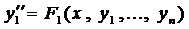
Аналогично, ещё раз продифференцировав, получаем
и т. д., пока не найдём п-ую производную
Таким образом, получаем систему п уравнений
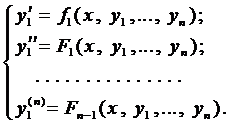
Из первых п — 1 уравнений системы (4) выразим 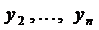
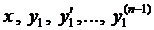
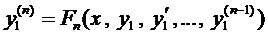
Решая уравнение (5), находим 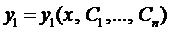
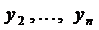
Замечание 1. Из приведённых выше рассуждений видна структура общего решения системы дифференциальных уравнений (2).
Замечание 2. Часто систему уравнений можно сразу сводить к уравнению (5), минуя систему (4). В частности, это относится к линейным системам дифференциальных уравнений.
Пример 2. Найти общее решение системы
Из первого уравнения найдем
и подставим во второе уравнение
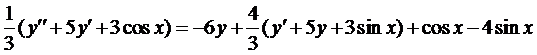
Умножим на 3 и приведём подобные члены

Составим характеристическое уравнение
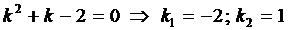
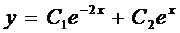
Тогда, с учетом выражения для z, получаем
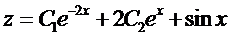
Пример 3. Решить задачу Коши
Из первого уравнения находим
и подставляем во второе уравнение
Составим характеристическое уравнение
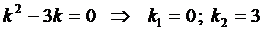
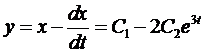
Из начальных условий получаем систему для нахождения 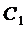
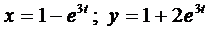
http://1cov-edu.ru/differentsialnye-uravneniya/lineinie_postoyannie_koeffitsienti/neodnorodnie_ponizhenie_poryadka/primer_kompleksnie/
http://lektsii.org/18-72797.html