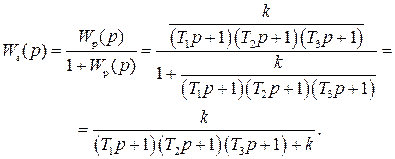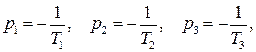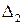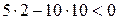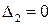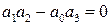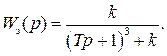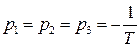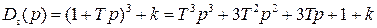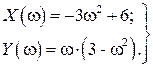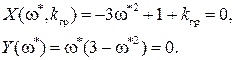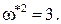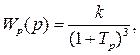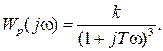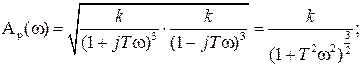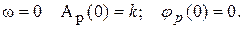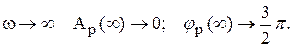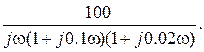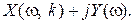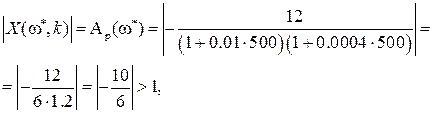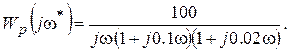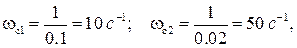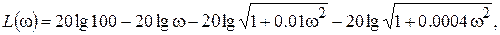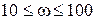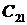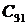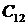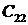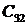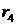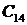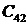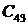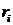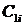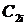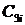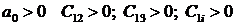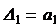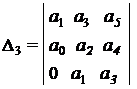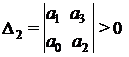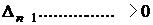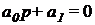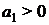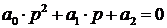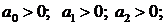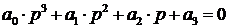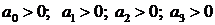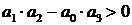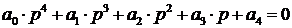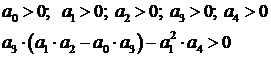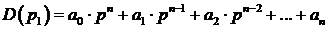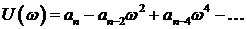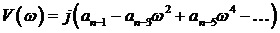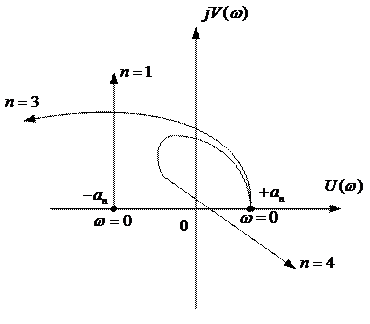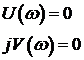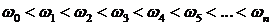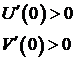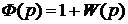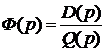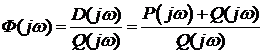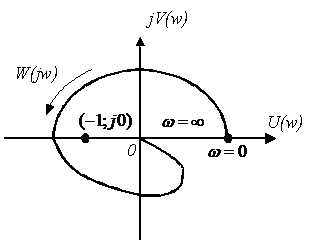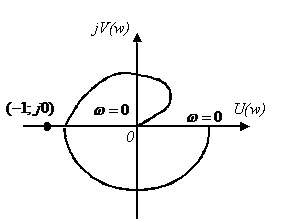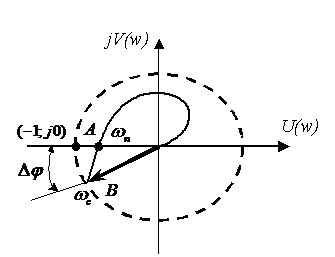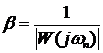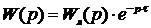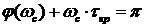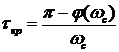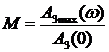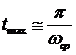Критерии устойчивости (Лекция)
2. Корневой критерий
3. Критерий Стодолы
4. Критерий Гурвица
5. Критерий Михайлова
6. Критерий Найквиста
7. Показатели качества
8. Прямые показатели качества
9. Корневые показатели качества
10. Частотные показатели качества
Важным показателем АСР является устойчивость, поскольку основное ее назначение заключается в поддержании заданного постоянного значения регулируемого параметра или изменение его по определенному закону. При отклонении регулируемого параметра от заданной величины (например, под действием возмущения или изменения задания) регулятор воздействует на систему таким образом, чтобы ликвидировать это отклонение. Если система в результате этого воздействия возвращается в исходное состояние или переходит в другое равновесное состояние, то такая система называется устойчивой. Если же возникают колебания со все возрастающей амплитудой или происходит монотонное увеличение ошибки е, то система называется неустойчивой.
Для того, чтобы определить, устойчива система или нет, используются критерии устойчивости:
1) корневой критерий,
2) критерий Стодолы,
3) критерий Гурвица,
4) критерий Найквиста,
5) критерий Михайлова и др.
Первые два критерия являются необходимыми критериями устойчивости отдельных звеньев и разомкнутых систем. Критерий Гурвица является алгебраическим и разработан для определения устойчивости замкнутых систем без запаздывания. Последние два критерия относятся к группе частотных критериев, поскольку определяют устойчивость замкнутых систем по их частотным характеристикам. Их особенностью является возможность применения к замкнутым системам с запаздыванием, которыми является подавляющее большинство систем управления.
2. Корневой критерий
Корневой критерий определяет устойчивость системы по виду передаточной функции. Динамической характеристикой системы, описывающей основные поведенческие свойства, является характеристический полином, находящийся в знаменателе передаточной функции. Путем приравнивания знаменателя к нулю можно получить характеристическое уравнение, по корням которого определить устойчивость.
Корни характеристического уравнения (они обозначены звездочкой) могут быть как действительные, так и комплексные и для определения устойчивости откладываются на комплексной плоскости.
Виды корней характеристического уравнения:
положительные (корень № 1);
комплексные сопряженные (4);
По кратности корни бывают:
одиночные (1, 2, 3);
сопряженные (4, 5): si = a ± j w ;
Корневой критерий формулируется следующим образом:
Линейная АСР устойчива, если все корни характеристического уравнения лежат в левой полуплоскости. Если хотя бы один корень находится на мнимой оси, которая является границей устойчивости, то говорят, что система находится на границе устойчивости. Если хотя бы один корень находится в правой полуплоскости (не зависимо от числа корней в левой), то система является неустойчивой.
Иными словами, все действительные корни и действительные части комплексных корней должны быть отрицательны. В противном случае система неустойчива.
Пример 4.1. Передаточная функция системы имеет вид:

Характеристическое уравнение: s 3 + 2 s 2 + 2.25 s + 1.25 = 0.
Следовательно, система устойчива.
3. Критерий Стодолы
Этот критерий является следствием из предыдущего и формулируется следующим образом: Линейная система устойчива, если все коэффициенты характеристического полинома положительны.
То есть, для передаточная из примера 4.1 по критерию Стодола соответствует устойчивой системе.
4. Критерий Гурвица
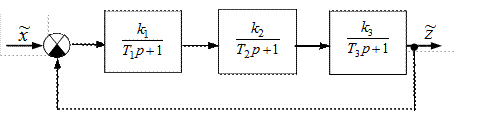
Критерий Гурвица работает с характеристическим полиномом замкнутой системы. Как известно, структурная схема АСР по ошибке имеет вид, как показано на рисунке ниже.
Wp — передаточная функция регулятора,
Wy — передаточная функция объекта управления.
Определим передаточную функцию для прямой связи (передаточную функцию разомкнутой системы): W ¥ = Wp Wy .
Далее с учетом наличия отрицательной обратной связи получаем передаточную функцию замкнутой системы:

Как правило, передаточная функция разомкнутой системы имеет дробно-рациональный вид:

Тогда после подстановки и преобразования получаем:

Отсюда следует, что характеристический полином замкнутой системы (ХПЗС) можно определить как сумму числителя и знаменателя W ¥ :
D з( s ) = A ( s ) + B ( s ).
Для определения устойчивости по Гурвицу строится матрица таким образом, чтобы по главной диагонали были расположены коэффициенты ХПЗС с an +1 по a 0. Справа и слева от нее записываются коэффициенты с индексами через 2 ( a 0, a 2, a 4… или a 1, a 3, a 5 …). Тогда для устойчивой системы необходимо и достаточно, чтобы определитель и все главные диагональные миноры матрицы были больше нуля.
Если хотя бы один определитель будет равен нулю, то система будет находится на границе устойчивости.
Если хотя бы один определитель будет отрицателен, то система неустойчива не зависимо от числа положительных или нулевых определителей.
Пример. Дана передаточная функция разомкнутой системы

Требуется определить устойчивость замкнутой системы по критерию Гурвица .
Для этого определяется ХПЗС :
D(s) = A(s) + B(s) = 2s 4 + 3s 3 + s 2 + 2s 3 + 9s 2 + 6s + 1 = 2s 4 + 5s 3 + 10s 2 + 6s + 1.
Поскольку степень ХПЗС равна n = 4, то матрица будет иметь размер 4х4. Коэффициенты ХПЗС равны а4 = 2, а3 = 5, а2 = 10, а1 = 6, а0 = 1.
Матрица имеет вид:
(обратите внимание на сходство строк матрицы: 1 с 3 и 2 с 4). Определители:

Поскольку все определители положительны, то АСР устойчива.
5. Критерий Михайлова
Описанные выше критерии устойчивости не работают, если передаточная функция системы имеет запаздывание, то есть может быть записана в виде

где t — запаздывание.
В этом случае характеристическое выражение замкнутой системы полиномом не является и его корни определить невозможно. Для определения устойчивости в данном случае используются частотные критерии Михайлова и Найквиста.
Порядок применения критерия Михайлова:
1) Записывается характеристическое выражение замкнутой системы:
D з (s) = A(s) + B(s) . e — t s .
2) Подставляется s = j w : D з (j w ) =Re( w ) + Im( w ).
3) Записывается уравнение годографа Михайлова D з( j w ) и строится кривая на комплексной плоскости.
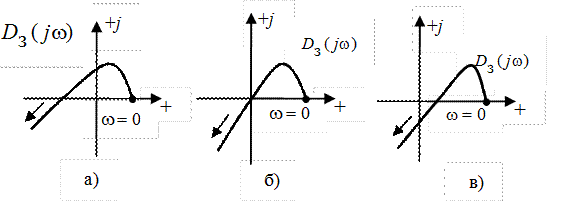
Для устойчивой АСР необходимо и достаточно, чтобы годограф Михайлова (см. рис.), начинаясь при w = 0 на положительной вещественной полуоси, обходил последовательно в положительном направлении (против часовой стрелки) при возрастании w от 0 до ¥ n квадрантов, где n — степень характеристического полинома.
Если годограф Михайлова проходит через начало координат, то говорят, что система находится на границе устойчивости.
6. Критерий Найквиста
Данный критерий аналогичен критерию Михайлова, но работает с АФХ системы, поэтому более сложен для расчетов.
1) Определяется передаточная функция разомкнутой системы 
2) Определяется число правых корней m .
3) Подставляется s = j w : W ¥ ( j w ).
4) Строится АФХ разомкнутой системы.
Для устойчивости АСР необходимо и достаточно, чтобы при увеличении w от 0 до ¥ АФХ W ¥ ( j w ) m раз охватывала точку (-1; 0), где m — число правых корней разомкнутой системы.
Если АФХ проходит через точку (-1; 0), то замкнутая система находится на границе устойчивости.
В случае, если характеристическое уравнение разомкнутой системы A ( s ) = 0 корней не имеет (т.е. m = 0), то критерий, согласно критерию, замкнутая система является устойчивой, если АФХ разомкнутой системы W ¥ ( j w ) не охватывала точку (-1; 0), в противном случае система будет неустойчива (или на границе устойчивости).
7. Показатели качества
Если исследуемая АСР устойчива, то может возникнуть вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям. На практике качество регулирования может быть определено визуально по графику переходной кривой, однако, имеются точные методы, дающие конкретные числовые значения.
Показатели качества разбиты на 4 группы:
1) прямые — определяемые непосредственно по кривой переходного процесса,
2) корневые — определяемые по корням характеристического полинома,
3) частотные — по частотным характеристикам,
4) интегральные — получаемые путем интегрирования функций.
8. Прямые показатели качества
К ним относятся: степень затухания y , перерегулирование s , статическая ошибка ест, время регулирования tp и др.

Предположим, переходная кривая, снятая на объекте, имеет колебательный вид (см. рис. 1.38).
Сразу по ней определяется установившееся значение выходной величины ууст.
Степень затухания y определяется по формуле

где А1 и А3 — соответственно 1-я и 3-я амплитуды переходной кривой.
Перерегулирование s = 
Статическая ошибка ест = х — ууст, где х — входная величина.
Время достижения первого максимума t м определяется по графику.
Время регулирования tp определяется следующим образом: Находится допустимое отклонение D = 5% ууст и строится «трубка» толщиной 2 D . Время tp соответствует последней точке пересечения y ( t ) с данной границей. То есть время, когда колебания регулируемой величины перестают превышать 5 % от установившегося значения.
9. Корневые показатели качества
К ним относятся: степень колебательности m , степень устойчивости h и др.
Не требуют построения переходных кривых, поскольку определяются по корням характеристического полинома. Для этого корни полинома откладываются на комплексной плоскости и по ним определяются:
Степень устойчивости h определяется как граница, правее которой корней нет, т.е.
h = min 
где Re ( si ) — действительная часть корня si .
Степень колебательности m рассчитывается через угол g : m = tg g . Для определения g проводятся два луча, которые ограничивают все корни на комплексной плоскости. g — угол между этими лучами и мнимой осью. Степень колебательности может быть определена также по формуле:
m = min 
10. Частотные показатели качества
Для определения частотных показателей качества требуется построение АФХ разомкнутой системы и АЧХ замкнутой системы.
По АФХ определяются запасы: D A — по амплитуде, D j — по фазе.
Запас D A определяется по точке пересечения АФХ с отрицательной действительной полуосью.
Для определения D j строится окружность единичного радиуса с центром в начале координат. Запас D j определяется по точке пересечения с этой окружностью.
По АЧХ замкнутой системы определяются показатели колебательности по заданию М и ошибке МЕ как максимумы соответственно АЧХ по заданию и АЧХ по ошибке.
Связи между показателями качества.Описанные выше показатели качества связаны между собой определенными соотношениями:




Определение устойчивости САР
В замкнутой САР (рис. IV. 27) заданы (в числовом выражении)
Рис. IV. 27. Функциональная схема замкнутой САР
Определить устойчивость разомкнутой и замкнутой САР и найти kгр.
Для решения поставленной задачи воспользуемся критерием Гурвица. Найдем передаточные функции, а затем и характеристические уравнения разомкнутой и замкнутой систем.
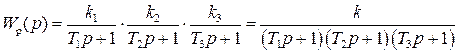
где 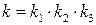
Для разомкнутой системы характеристическое уравнение имеет вид
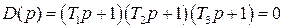
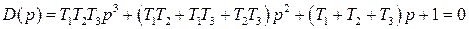
а для замкнутой САР получается
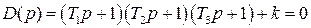
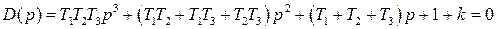
Нетрудно понять, что для исследования устойчивости разомкнутой САР применять критерий устойчивости Гурвица излишне, ибо непосредственно из вида характеристического уравнения разомкнутой системы (IV. 3. 11) легко найти, что все корни левые
т. е. разомкнутая САР при всегда положительных Т1, Т2, Т3 устойчива.
Вот по виду характеристического уравнения замкнутой САР (IV. 3. 12) так просто, как в предыдущем случае, определить соответствующие корни не удается, поэтому приходится применить критерий устойчивости Гурвица . При введении обозначений
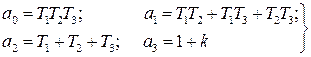
характеристическое уравнение замкнутой САР (IV. 3. 13) примет вид
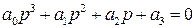
В разделе IV. 2. 2 было выяснено, что для САР с характеристическим уравнением третьего порядка для устойчивости необходимо и достаточно при положительных коэффициентах ai( i =0, 1, 2,3) выполнение условия ( IV. 2. 3)
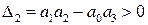
Из (IV. 3. 14) видно, условия ai>0 при положительных Т1, Т2, Т3 и k всегда выполняются, а для проверки условия (IV. 2.3) надо в него подставить заданные значения параметров Т1, Т2, Т3 и k и определить знак минора
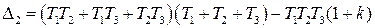
Если этот минор больше нуля, то заданная замкнутая САР устойчива.
Граничный коэффициент усиления kгр найдется из предпоследнего минора, приравненного к нулю
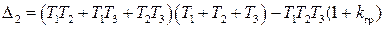
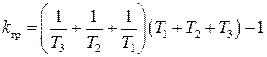
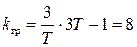
Характеристическое уравнение САР имеет вид
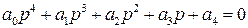
Определить устойчивость САР.
Так как заданное характеристическое уравнение 4-го порядка имеет один неположительный коэффициент (а4=0), то, согласно условию Стодолы (что в данном случае совпадает с критерием Гурвица) САР не сожжет быть устойчивой, а только либо нейтральной либо неустойчивой.
Запишем заданное характеристическое уравнение в другом виде
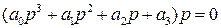
Видно, что один из корней – нулевой. САР будет находиться на границе устойчивости, если все остальные корни характеристического уравнения левые (при наличии хотя бы одного правого корня САР будет неустойчивой). Эти остальные корни будут левыми, если выполняются условия устойчивости для уравнения
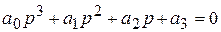
а именно (согласно разделу IV. 2. 2)
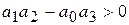
После подстановки значений коэффициентов последнее неравенство
не выполняется, следовательно САР неустойчива.
Передаточная функция разомкнутой САР имеет вид
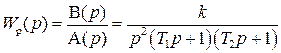
Определить устойчивость замкнутой САР.
Характеристическое уравнение замкнутой САР определяется выражением
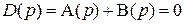
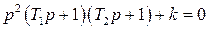
После простого преобразования получим
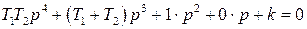
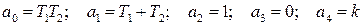
Согласно критерию Гурвица для устойчивости системы необходимо, чтобы все ai( i=0, 1, 2, 3, 4) > 0. В нашем же случае 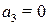
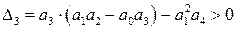
Учитывая что 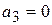
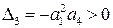
Поскольку 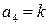
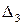
Переходная функция разомкнутой САР имеет вид
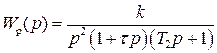
где 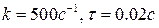
Определить постоянную времени Тгр, при которой замкнутая САР находиться на границе устойчивости.
Получим характеристическое уравнение замкнутой САР
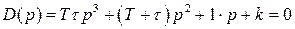
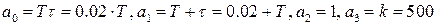
Граница устойчивости определяется из равенства нулю второго минора
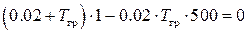
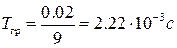
Характеристический полином САР 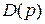
Каково изменение аргумента 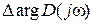
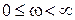
Характеристическое уравнение 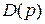
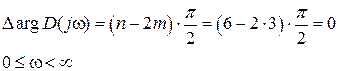
Какой из указанных годографов Михайлова замкнутой системы
Рис. IV. 28. Годографы Михайлова для устойчивой, нейтральной и неустойчивой замкнутой систем.
соответствует САР с передаточной функцией
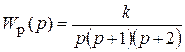
Характеристический полином замкнутой системы имеет вид
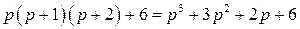
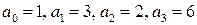
Для этого полинома второй минор оказывается равный нулю
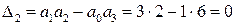
т.е. замкнутая САР находится на границе устойчивости, что соответствует годографу Михайлова, имеющему вид рис. IV. 28, б.
Определить устойчивость разомкнутой и замкнутой САР и найти kгр.
Запишем передаточные функции разомкнутой
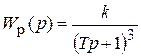
а замкнутой САР
Поскольку из характеристического уравнения разомкнутой САР
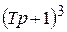
следует, что все три его корня
при положительном Т есть левые, то, значит, разомкнутая САР устойчива.
Для определения устойчивости замкнутой САР применим критерий Михайлова.
Характеристический полином замкнутой системы, имеющий третий порядок,
после замены 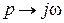
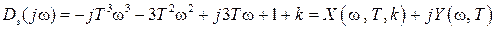
В этом выражении мы выделили действительную часть 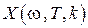
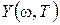
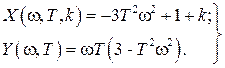
Ответ на вопрос – устойчива ли замкнутая САР можно получить по виду годографа Михайлова, зависящего от конкретных значений параметров k и T. Пусть для определенности k =5, T =1 с. Тогда соотношения (IV. 3. 15) примут
Задаваясь численными значениями 
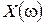
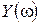

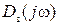
 | 1.42 | 1.5 | 1.73 | ∞ |
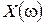 | -0.75 | -3 | -6 | ∞ |
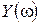 | 1.42 | 1.125 | -2 | ∞ |
Рис. IV. 29. Годограф Михайлова.
Поскольку годограф Михайлова, начинается на положительном отрезке действительной оси, с ростом частоты от 0 до 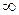
Определим теперь kгр. В разделе IV. 3. 2 было показано, что на границе устойчивости годограф Михайлова проходит через начало координат, т.е. выполняются условия (IV. 3. 4) .
В нашем случае при k = kгр, 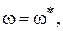
Из второго из этих уравнений, отбрасывая неверное решение 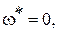
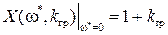
Подставляя это значение граничной частоты в выражение для 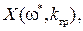
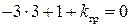
т.е. kгр = 8, как и в примере П. IV. 1.
П. IV. 8. Предыдущую задачу П. IV. 7. решить с помощью критерия Найквиста.
Передаточную функцию разомкнутой системы мы получили в виде
откуда ясно, что все корни характеристического уравнения левые и, значит, разомкнутая система устойчива.
Если провести замену 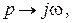
Построим эту характеристику. Найдем сначала 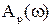
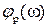
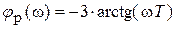
При
При
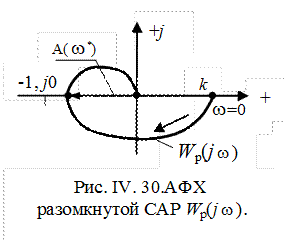
Следовательно, качественно АФХ разомкнутой системы Wp(j 
Устойчивость системы в замкнутом состоянии зависит от того, охватывает ли 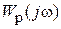




Из заданной операторной формы управления системы получим
Wp(j 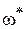
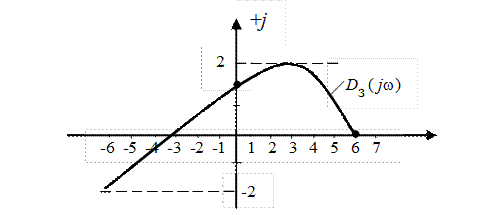
В отличии от предыдущего примера для разнообразия АФХ разомкнутой САР Ap( 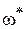
Wp(j 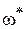
Для этого нужно освободиться от мнимости в знаменателе выражения для
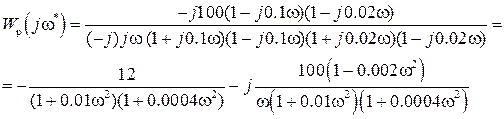
Определим величину 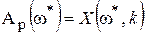
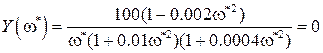
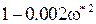
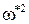
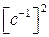
При подстановке этого значения частоты в X( 
отсюда следует, что замкнутая САР неустойчива.
kгр 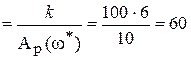
П. IV. 10. Предыдущий пример решить с помощью логарифмического критерия устойчивости.
В предыдущем примере мы нашли, что АФХ разомкнутой системы имеет вид
Получим отсюда выражение для АЧХ Ap( 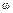
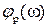
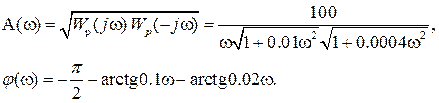
Имея в виду, что
а сопрягающие частоты
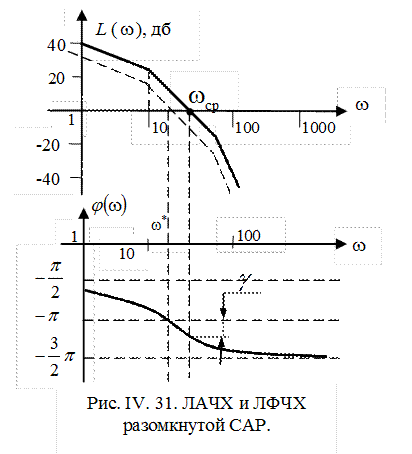
Построим асимптотическую ЛАЧХ и качественный вид ФЧХ разомкнутой системы.
Найдем частоту среза 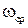
запишем выражение для ЛАЧХ на втором участке
На частоте среза 
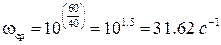
Значение фазочастотной характеристики 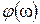
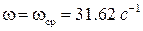
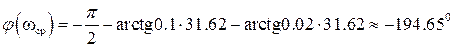
Следовательно, запас устойчивости по фазе для данной системы будет отрицательным
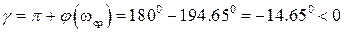
а сама система в замкнутом состоянии неустойчива.
Граничный коэффициент усиления 
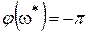

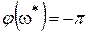
Из (IV. 3. 19) получим
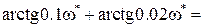
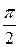
Из тригонометрии известно, что
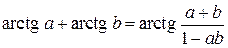
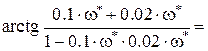
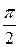
Величине 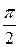
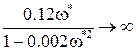
а это для 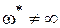
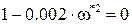
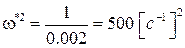
а сама частота 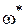
Величину 
Подставим сюда 
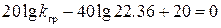
Отсюда 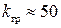
В предыдущем примере для той же задачи мы получили 

Вопросы для самопроверки.
1. Что понимается под устойчивостью системы?
2. Каковы признаки устойчивости САР?
3. Сформулируйте условие Стодолы.
4. Как найти граничное значение параметра по критерию устойчивости Гурвица.
5. Расскажите о принципе аргумента.
6. Что такое годограф Михайлова? Как он проходит в случае границы устойчивости системы?
7. Сформулируйте критерий устойчивости Найквиста для всех трех видов устойчивости разомкнутой САР.
8. Прокомментируйте связь логарифмического критерия устойчивости с критерием Найквиста.
9. Какие запасы устойчивости Вы знаете?
Дата добавления: 2016-04-14 ; просмотров: 4900 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Корни характеристического уравнения разомкнутой системы
Характер свободного движения всей системы при наличии различных корней определяется суммой свободных составляющих формулы (3.3.), причем система бывает устойчивой, если все вещественные корни отрицательные и комплексные корни имеют отрицательную вещественную часть. Если корни нанести на плоскость комплексного переменного, то можно выделить устойчивые, неустойчивые и нейтральные зоны.




Линейная САУ устойчива, если корни характеристического уравнения расположены слева от мнимой оси. Система считается нейтральной, если корни принадлежат мнимой оси.
Неустойчивой система считается для случая, когда корни лежат справа от мнимой оси.
Вышеперечисленные условия устойчивости используются для формулирования необходимого условия устойчивости линейных САУ.
Кроме выше записанного необходимое условие устойчивости можно записать, используя известное в математике выражение:
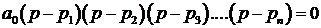
Подставив в выражение (3.6.) только устойчивые корни характеристического уравнения можно заметить, что после раскрытия скобок в уравнении (3.6.) устойчивой системы все коэффициенты характеристического уравнения будут положительными.
Необходимое условие устойчивости – положительность всех коэффициентов характеристического уравнения. В том случае, если один из коэффициентов отрицателен – линейную систему нельзя считать устойчивой.
Для уравнений первого и второго порядка условие положительности коэффициентов характеристического уравнения является кроме необходимого еще и достаточное условие. Это можно охарактеризовать тем, что уравнения первого и второго порядка просты для нахождения корней. Начиная с третьего и выше порядков характеристические уравнения трудно разрешить в нахождении корней простыми способами вычисления. Поэтому в теории автоматического управления разработаны упрощенные правила – критерии нахождения устойчивости линейных систем.
Существует два вида критериев: алгебраические и частотные. С математической точки зрения все рассматриваемые критерии равнозначны.
§ 3.2.3 Алгебраический критерий устойчивости. Критерий Рауса
Данный критерий устойчивости был разработан в 1878 г . английским математиком Раусом и который был сформулирован в виде некого правила или алгоритма, который можно представить в виде таблицы (матрицы).
Таблица Рауса составляется на основании характеристического уравнения линейной системы вида:
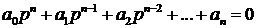
Покажем эту таблицу:
Порядок заполнения таблицы Рауса:
1) в первой строке таблицы Рауса в порядке увеличения индексов записываются коэффициенты характеристического уравнения (3.7), имеющие четный индекс: 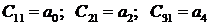
2) во второй строке записывают в порядке возрастания индексов коэффициенты характеристического уравнения (3.7.) с нечетными индексами: 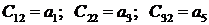
Любой из остальных коэффициентов таблицы Рауса записывается в соответствии со следующими выражениями:
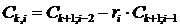
к – столбец, i – строка
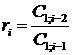
Число строк таблицы Рауса равно степени характеристического уравнения + 1 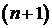
Условие устойчивости Рауса: для того, чтобы линейная САУ была устойчивой необходимо и достаточно чтобы коэффициенты первого столбца таблицы Рауса имели один и тот же знак, т.е. при 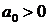
§ 3.2.4 Алгебраический критерий устойчивости. Критерий Гурвица
В 1895 г . немецкий математик Гурвиц разработал алгебраический критерий устойчивости в форме определителей, состоящих из коэффициентов характеристического уравнения (3.7).
В основе рассматриваемого критерия лежит построение главного определителя Гурвица из коэффициентов характеристического уравнения (3.7).
Порядок составления главного определителя Гурвица:
1. Записываем главную диагональ определителя Гурвица, составленную из коэффициентов характеристического уравнения от 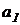
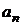
2. Вверх от главной диагонали записывают столбцы, составленные из коэффициентов характеристического уравнения с последовательно возрастающими индексами;
3. Вниз от главной диагонали записываем столбцы составленные из коэффициентов характеристического уравнения с последовательно убывающими индексами;
4. Оставшиеся пустые места определителя заполняются нулями, т.е. нули проставляются на места, где должны быть коэффициенты с индексами больше 0 и меньше 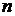
Главный определитель Гурвица имеет вид:
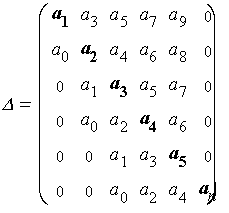 |
После построения главного определителя Гурвица, в нем очеркиваются диагональные миноры и тем самым получаются определители более низших порядков.

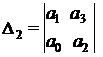
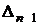
Критерий устойчивости Гурвица: для того, чтобы система автоматического управления (САУ) была устойчивой необходимо и достаточно, чтобы все определители Гурвица (3.11) имели знаки одинаковые со знаком первого коэффициента характеристического уравнения 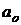
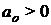
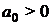
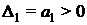
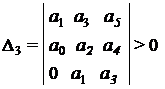
В случае, если хоть одно из условий не выполняется, то систему считают неустойчивой.
Раскрывая все определители Гурвица можно для уравнений 1-го, 2-го, 3-го и 4-го порядков записать более простую форму критерия устойчивости. Такая форма записи получила название следствия из критерия Гурвица или ее называют критерием Леера-Шепорда.
1) Для характеристического уравнения 1-го порядка:
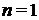
необходимым и достаточным является, чтобы:
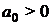
2) Для характеристического уравнения 2-го порядка:
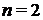
необходимым и достаточным является, чтобы:
3) Для характеристического уравнения 3-го порядка:
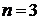
необходимым и достаточным является, чтобы:
4) Для характеристического уравнения 4-го порядка:
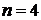
необходимым и достаточным является, чтобы:
§ 3.2.5 Частотный критерий устойчивости. Критерий Михайлова
Все частотные критерии, в том числе и критерий Михайлова, основаны на хорошо известном из курса высшей математики «Принципа аргумента», который позволяет отобразить необходимое условие устойчивости на частотной плоскости.
Все элементарные вектора 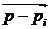

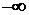
Этот частотный критерий устойчивости был сформулирован в 1938 г . советским ученым Михайловым и является интерпретацией принципа аргумента, позволяя судить об устойчивости системы наблюдая за поведением кривой называемой кривой Михайлова.
За основание построения кривой берется характеристический полином вида:
Произведя замену 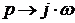
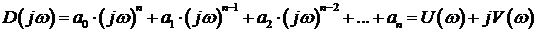
При изменении частоты 
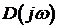
Для устойчивых систем кривая Михайлова начинаясь при 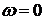

Критерий Михайлова: для того, чтобы САУ была устойчивой, необходимо и достаточно, чтобы кривая или годограф Михайлова при изменении 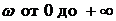
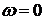
Нейтральные САУ (граница устойчивости):
Анализируя кривую Михайлова можно вывести следствие из него: при прохождении кривой Михайлова числа квадрантов комплексной плоскости, происходит последовательное поочередное пересечение действительной и мнимой соей, т.е.:
Значение частот при которых происходит пересечение кривой с вещественной или мнимой осью, должны является корнями уравнений (3.20) и (3.21), причем 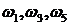
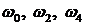
В связи с выше записанным следствие кривой Михайлова можно сформулировать следующим образом: САУ будет устойчивой тогда и только тогда, когда вещественная 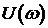
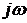
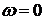
Для реализации этого следствия определяются только корни уравнения 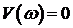
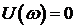
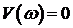
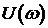
§ 3.2.6 Частотный критерий. Критерий Найквиста
Этот критерий разработан в 1923 г . американским ученым Найквистом. Он позволяет судить об устойчивости замкнутой системы по поведению АФЧХ разомкнутой системы.
Вектор 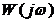

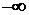
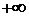
Кривая, описываемая окончанием этого вектора есть АФЧХ разомкнутой системы, причем следует отметить, что вид этой характеристики симметричен относительно начала координат, т.е.
Для доказательства критерия Найквиста используют дополнительную функцию вида:
Причем в знаменателе такой функции будет записан характеристический полином разомкнутой системы, а в числителе характеристический полином замкнутой системы:
В случае замены оператора Лапласа р на 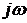
Пусть характеристическое уравнение замкнутой системы 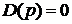
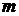
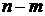
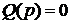
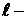
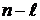
При рассмотрении этого критерия так же работает принцип аргумента, который определяет, что устойчивой система является, когда вектор 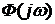
Разомкнутая система являющееся неустойчивой и имеющая 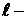
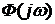

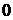
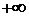
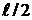
Найквистом было отмечено, что движение вектора 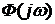
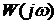
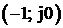
Критерий устойчивости Найквиста: если разомкнутая система автоматического управления неустойчива, то для того чтобы замкнутая система была устойчивой необходимо и достаточно, чтобы АФЧХ разомкнутой системы 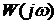

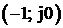
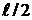
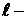
При сложной форме характеристик 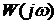
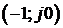
Для анализа поведения таких характеристик применяют «правило переходов» Ципкина. Назовем переход АФЧХ через действительную ось слева от точки 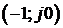

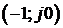
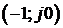
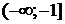
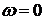
Критерий Найквиста для рассматриваемого варианта: если разомкнутая САУ неустойчива, то для того чтобы замкнутая система стала устойчива необходимо и достаточно, чтобы разность между положительным и отрицательным переходами АФЧХ разомкнутой системы через отрезок вещественной оси 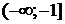

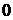
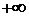
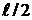
Критерий Найквиста для случая, когда разомкнутая система устойчива имеет следующую формулировку: если САУ разомкнутая устойчива, то замкнутая система будет устойчивой, если АФЧХ разомкнутой системы 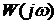
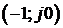
Достоинство критерия Найквиста заключается в том, что его можно использовать даже если неизвестны структуры отдельных звеньев системы, достаточно получить АФЧХ. Кроме того, рассматриваемый критерий позволяет анализировать устойчивость систем обладающих запаздыванием.
§ 3.2.7. Частотный критерий устойчивости – логарифмический частотный критерий
Критерий Найквиста позволяет судить от устойчивости системы по логарифмическим частотным характеристикам, т.е. можно заметить, что критерий Найквиста можно анализировать используя простые с точки зрения построения логарифмические частотные характеристики. Поэтому рассматриваемый критерий часто называют критерием Найквиста в логарифмической форме.
Передаточная функция разомкнутой системы обычно представляет собой произведение элементарных динамических звеньев, асимптотические характеристики которых представляют собой ломаные прямые линии.
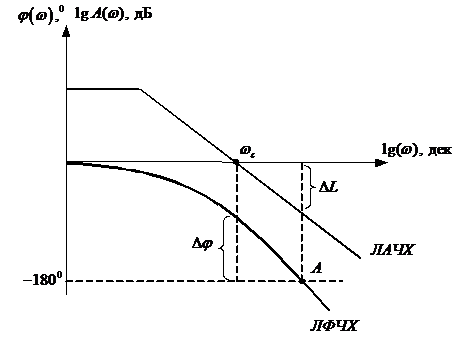
Устойчивость с использованием логарифмического критерия позволяет построив совмещено ЛАЧХ и ЛФЧХ разомкнутой системы судить об устойчивости замкнутой системы.
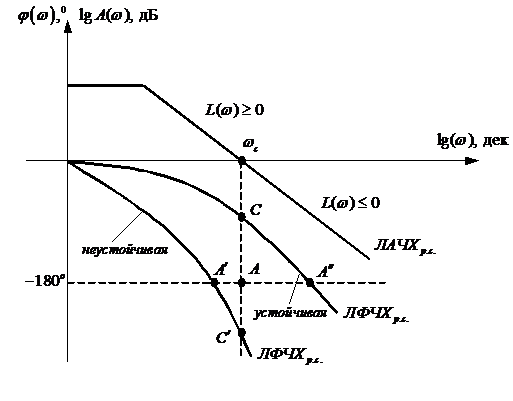
Замкнутая система автоматического управления устойчива, если при 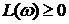
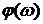
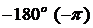
1) система устойчивая в разомкнутом состоянии будет устойчивой и в замкнутом, если точка А ЛФЧХ определяемая фазой 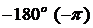
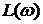
2) САУ неустойчивая в разомкнутом состоянии будет устойчива в замкнутой, если при изменении 
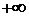
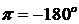
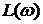
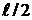
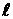
Следствие к первому случаю: САУ будет устойчивая в замкнутом состоянии, если ЛФЧХ неустойчивой разомкнутой системы при 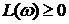
§ 3.2.8. Запасы устойчивости
При проектировании систем автоматики стремятся обеспечить их устойчивость с некоторой гарантией, чтобы изменение параметров системы в процессе ее работы не могли привести к неустойчивости системы. Для реализации такого тезиса необходимо, чтобы система обладала определенным запасом устойчивости. Запас устойчивости определяет удаленность параметров системы от границы устойчивости.
Положение системы на границе устойчивости можно определить, используя критерий устойчивости. Качественную характеристику удаления системы от границы устойчивости дают критерии Гурвица и Михайлова. Четкую количественную характеристику запаса устойчивости как по амплитуде, так и по фазе дает критерий Найквиста и логарифмический критерий.
В соответствии с критерием Найквиста система находится на границе устойчивости, если годограф Найквиста проходит через точку с координатами 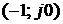
Покажем использование критерия Найквиста для нахождения запаса устойчивости по фазе и амплитуде:
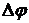
Запас устойчивости по модулю может быть в данном случае рассчитан как:
Значение модуля АФЧХ разомкнутой системы 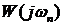
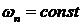
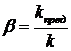
где 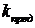
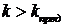
Запас устойчивости по фазе 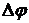
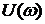
Определение устойчивости по логарифмическим частотным характеристикам может быть осуществлено достаточно простым способом. Необходимо на совмещенных логарифмических частотных характеристиках построить вертикальные проекции между осью абсцисс и значением -180º которые проведены через точки 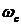
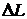
Запасы устойчивости влияют не только на работоспособность (устойчивость) системы, но также характеризуют качество работы системы. В реальных системах обычно 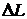
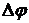
§ 3.2.9. Устойчивость систем обладающих запаздыванием
Значительное число объектов сельскохозяйственного назначения описываются математической моделью, в состав которой входит звено транспортного запаздывания, при этом общая передаточная функция такой системы состоит из произведения передаточной функции линейной части системы и передаточной функции звена транспортного запаздывания
Частотная передаточная функция в данном случае может быть записана в виде:
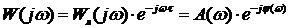
где 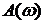
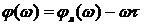
Звено чистого запаздывания не изменяет амплитуду АФЧХ, но создает дополнительный отрицательный сдвиг по фазе, зависящий от частоты 
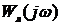
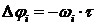
Оценку устойчивости систем с запаздыванием можно также выполнить используя логарифмический частотный критерий.
Очень часто анализируя устойчивость рассмотренных систем необходимо бывает установить значение запаздывания при котором система находится на границе устойчивости. Такое время носит название критического времени запаздывания и оно определяется из следующего выражения:
§ 3.3. Качества работы САУ
§ 3.3.1. Общие положения о качестве работы
Факт устойчивости или неустойчивости САУ говорит лишь о том, что переходная или свободная составляющая процесса регулирования с течением времени расходится или затухает, но такой анализ не дает ответа на такие важные вопросы как: быстрота затухания переходного процесса, форма кривой процесса регулирования и т.д. Поэтому следует отметить, что теория устойчивости является необходимым, но не достаточным условием практической пригодности САУ. Любая такая система кроме устойчивости должна еще обладать и требуемым качеством работы. Качество работы систем автоматики характеризует точность ее работы как в установившемся так и переходном режимах. Иными словами можно отметить, что качество работы системы автоматики характеризует точность воспроизведения системой задающего воздействия.
Проблема качества систем автоматики может быть поставлена как задача анализа, т.е. оценка уже спроектированной САУ или как задача синтеза, т.е. проектирование САУ заранее оговоренными показателями качества. При рассмотрении таких задач будем полагать, что САУ описывается системой дифференциальных уравнений с постоянными коэффициентами. При изменении воздействия 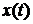
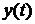
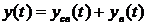
где 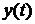
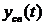
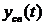
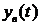
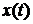
Качество работы системы автоматики можно оценить по виду переходного процесса и по его составляющим 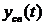
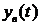
1) показатели качества переходного процесса 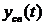
2) показатели качества, характеризующие вынужденную составляющую 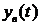
Показатели качества, определяемые непосредственно по кривой переходного процесса называют прямыми оценками качества, косвенные оценки качества не требуют нахождение кривой переходного процесса. Косвенные методы разделяют на: корневые, интегральные и частотные.
§ 3.3.2. Оценка качества регулирования при гармонических воздействиях
При гармонических воздействиях качество системы принято оценивать по амплитудо-фазовой, амплитудо-частотной и логарифмическим частотным характеристикам.
Для оценки качества переходных процессов системы можно использовать следующие величины: показатель колебательности М, резонансная (собственная частота) 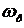
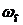
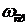
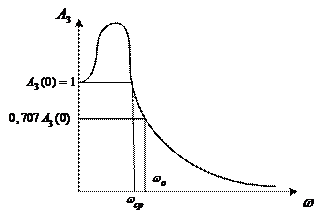
Показатель колебательности М – это отношение максимального значения АЧХ 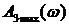
при 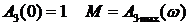
Показатель колебательности характеризует склонность системы к колебаниям. Чем выше М, тем менее качественная система при прочих равных условиях.
Частоту 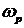
Полоса пропускания системы – это интервал частот от 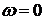
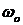
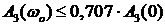
или при 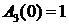
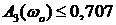
Частота среза 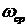
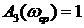
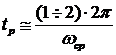
если переходный процесс имеет одно-два колебания, то время достижения переходной характеристикой первого максимума
Склонность системы к колебаниям характеризуется величинами ее запасов устойчивости по модулю и по фазе. Запасы устойчивости рассчитывают по АФЧХ и ЛЧХ. В хорошо демпфированных системах запас устойчивости по амплитуде колеблется в пределах от 6 до 20 дБ, а запас по фазе – от 30 до 60º.
Т.к. рассмотренные выше показатели косвенно определяют быстродействие, перерегулирование и т.п., то они могут быть использованы и для расчета систем, находящихся под воздействием непериодических возмущений.
http://helpiks.org/7-85660.html
http://feklistovstudio.narod.ru/12.htm