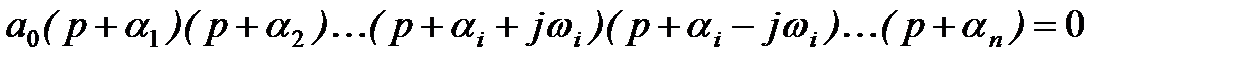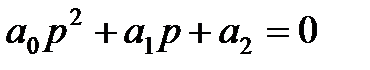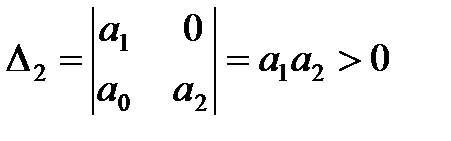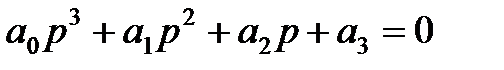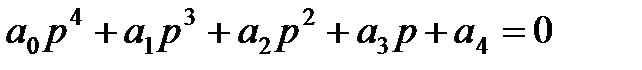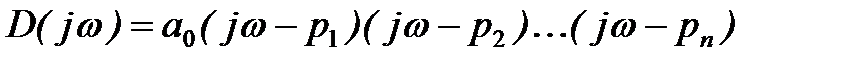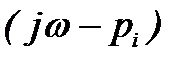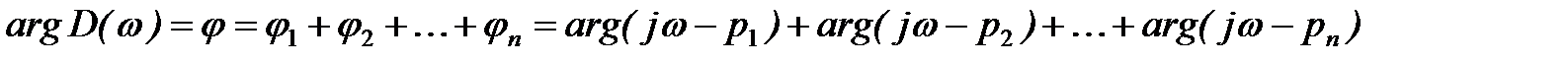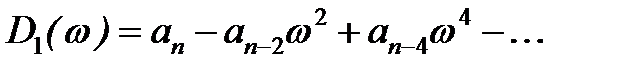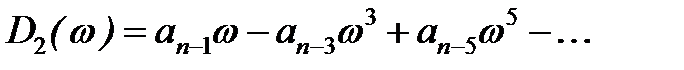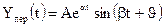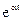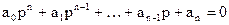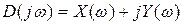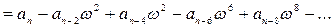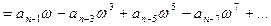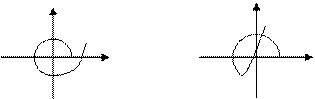Глава 3. Устойчивость линейных систем
§ 1. Определение и условие устойчивости
Одной из основных динамических характеристик САР является её устойчивость. Под устойчивостью понимается свойство системы возвращаться к состоянию установившегося равновесия после устранения возмущения, нарушившего равновесие.
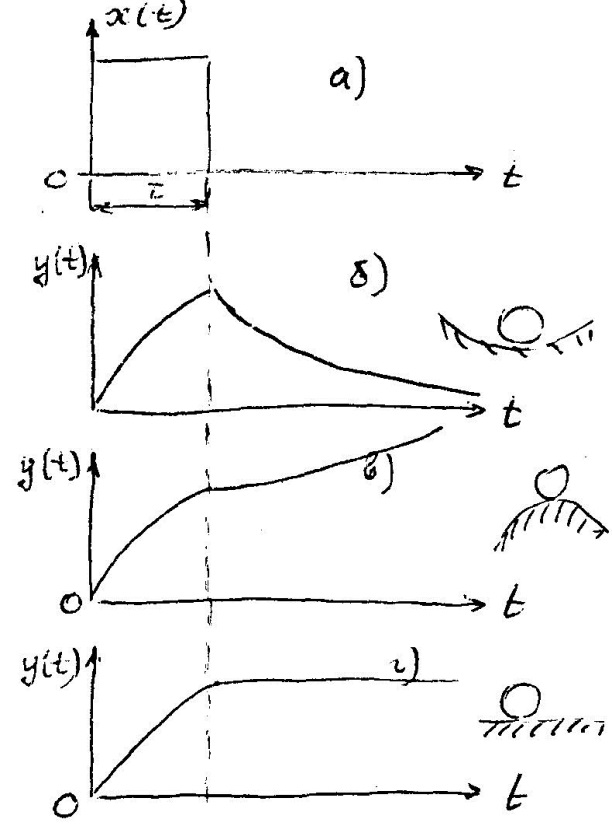
Устойчивость системы определяется характером протекания переходного процесса, возникающего при нарушении равновесия каким-либо возмущающим воздействием. Переходный процесс, представляющий собой закон изменения регулируемой величины y(t) во времени, зависит как от свойств системы, так и от вида возмущения.
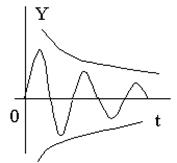
Условие устойчивости определяет три основных вида движения системы: движение устойчивой системы (рис. 1б), движение неустойчивой системы (рис. 1в) и движение нейтральной системы (системы, находящейся на границе устойчивости) (рис. 1г). Рисунок 1 показывает, что устойчивость системы определяется характером её движения после прекращения действия входного воздействия (при t > τ).
В случае устойчивой системы переходный процесс со временем затухает, и система вновь возвращается в устойчивое состояние. Таким образом, устойчивую систему можно определить также как систему, переходные процессы в которой являются затухающими. Для неустойчивых систем характерен процесс ухода от установившегося состояния.
Приведённые понятия устойчивости определяют устойчивость установившегося режима системы. Однако, система может работать в условиях непрерывно изменяющихся воздействий, когда установившийся режим вообще отсутствует. С учётом этих условий работы можно дать следующее, более общее определение устойчивости: система устойчива, если её выходная величина остаётся ограниченной в условиях действия на систему ограниченных по величине возмущений.
Определим, от чего зависит устойчивость САР. Для этого рассмотрим уравнение динамики системы, которое в общем случае имеет вид:
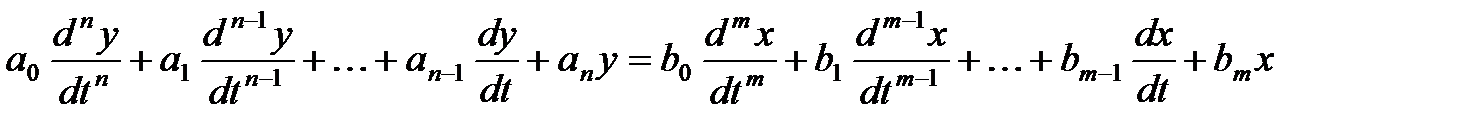
Характер переходных процессов в системе определяется видом левой части дифференциального уравнения (1).
Уравнение (1) является неоднородным дифференциальным уравнением, так как его правая часть не равна нулю.
Процесс регулирования определяется решением дифференциального уравнения как сумма двух решений:
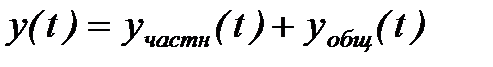
где 
В случае 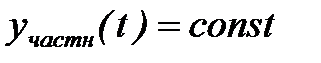
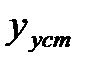
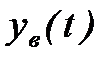
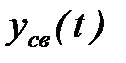
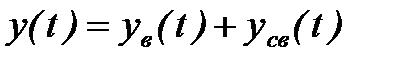
САР будет устойчивой, если с течением времени при 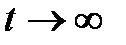
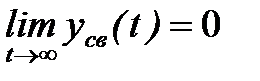
Выражение (3) определяет основное условие устойчивости системы. Найдём свободную составляющую из уравнения (1). Для этого необходимо решить однородное дифференциальное уравнение
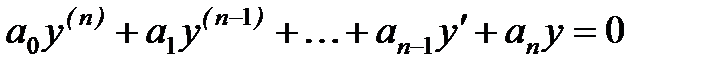
Тогда характеристическое уравнение, соответствующее (4), имеет вид
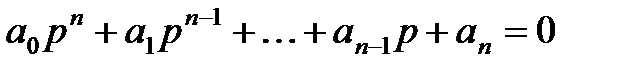
где p – комплексное число, которое является решением (корнем) характеристического уравнения.
Общее решение однородного дифференциального уравнения имеет вид
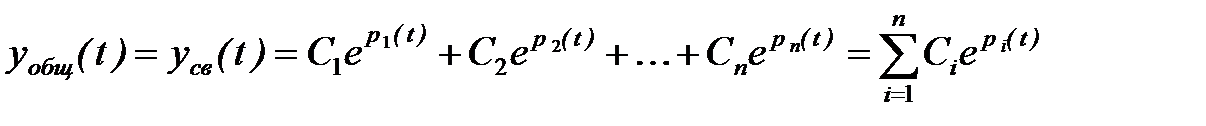
где 
Так как в понятие устойчивости системы входит только факт наличия или отсутствия затухания переходного процесса, то устойчивость линейной САР не зависит от вида правой части дифференциального уравнения (1) и определяется только характеристическим уравнением (5).
Определим, какие свойства корней характеристического уравнения необходимы и достаточны для того, чтобы САР была устойчивой.
Корни могут быть вещественными, комплексными и чисто мнимыми.
Рассмотрим эти случаи.
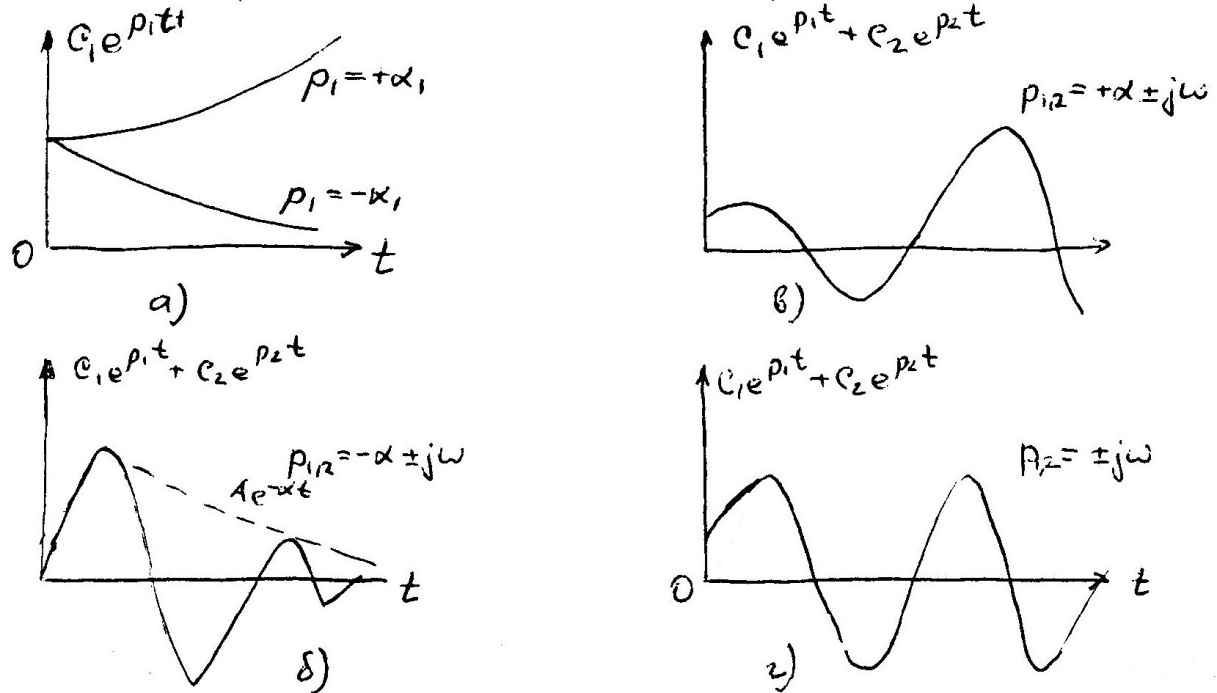
1. Вещественный корень.
Пусть один из корней, например 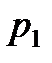
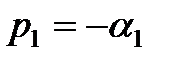
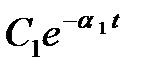
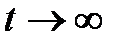
При 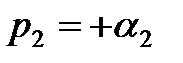

2. Комплексные корни.
Комплексные корни всегда получаются попарно сопряжёнными. При отрицательной вещественной части два корня, например p1 и p2 будут иметь вид 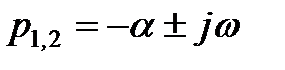
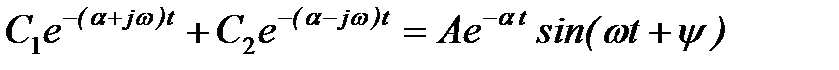
где А и 
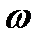
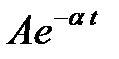
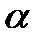
Очевидно, что в этом случае получаются затухающие колебания (рис. 2б).
В случае 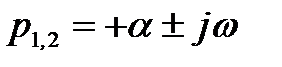
3. Чисто мнимые корни.
В этом случае 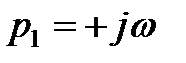

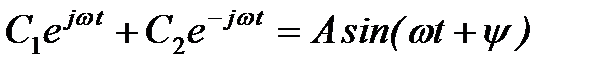
Такой процесс изображён на рис. 2г.
Следовательно, для затухания переходного процесса необходимо, чтобы вещественные корни и вещественные части комплексных корней характеристического уравнения были бы отрицательными, так как

Если хотя бы один корень будет иметь положительную вещественную часть, то он даёт расходящуюся составляющую переходного процесса и САР будет неустойчивой. Таким образом, необходимым и достаточным условием устойчивости САР являются отрицательность вещественных частей всех корней её характеристического уравнения.
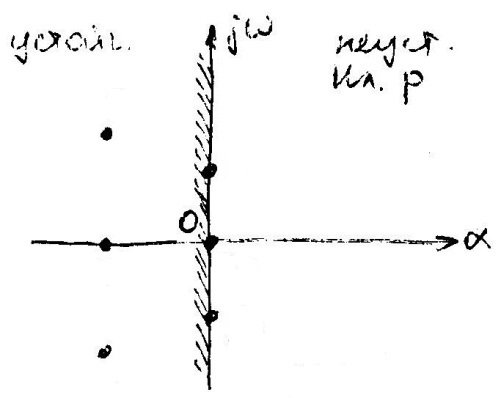
Корни характеристического уравнения можно представить в виде точек на комплексной плоскости корней (рис. 3).
| p5 |
| p6 |
| p4 |
| p3 |
| p2 |
| p1 |
| Рисунок 3 |
В связи с этим условие устойчивости системы можно сформулировать следующим образом: система будет устойчивой, если все корни характеристического уравнения этой системы будут располагаться в левой полуплоскости (левые корни) и неустойчивой, если хотя бы один корень находится в правой полуплоскости (правый корень).
Таким образом, мнимая ось комплексной плоскости представляет собой границу устойчивости системы. Система будет находиться на границе устойчивости при наличии:
В обоих случаях предполагается, что все остальные корни лежат в левой полуплоскости.
В первом случае корень попадает в начало координат. Это значит, что в характеристическом уравнении (5) свободный член 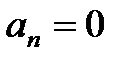
и САР будет устойчивой не относительно регулируемой величины 
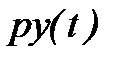
На границе устойчивости второго типа, которая называется колебательной границей устойчивости, два корня попадают на ось мнимых. В этом случае САР будет иметь незатухающие колебания с постоянной амплитудой (рис. 2г).
Покажем, что необходимым (но не достаточным) условием устойчивости системы является положительность всех коэффициентов характеристического уравнения. Действительно, если известны все корни характеристического уравнения p1, p2,…, pn, то оно может быть представлено в виде
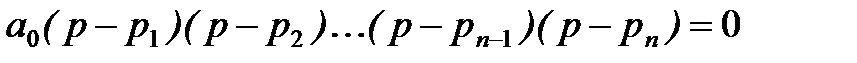
В устойчивой системе все вещественные корни 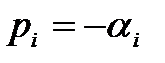
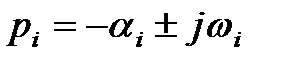
Тогда уравнение (7) при подстановке значений корней можно записать так
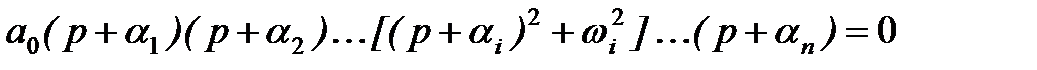
Очевидно, что при раскрытии скобок в этом уравнении все коэффициенты характеристического уравнения должны быть положительны, так как перемножая и складывая положительные величины 
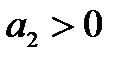
Необходимое условие устойчивости является достаточным для уравнений первого и второго порядков, в чём легко убедиться непосредственно.
§ 2. Критерии устойчивости
Практически для определения устойчивости необязательно знать численные значения корней характеристического уравнения. Достаточно убедиться только в отрицательности вещественных частей корней. Поэтому целесообразно воспользоваться более простым методом определения устойчивости, основанном на выявлении отрицательности вещественных частей корней (без нахождения их значений). Такие методы основываются на использовании критериев устойчивости и выделении областей устойчивости. Рассмотрим эти критерии.
1. Критерий Рауса-Гурвица
Этот критерий относится к алгебраическим критериям, накладывающим ограничения на коэффициенты характеристического уравнения.
Этот критерий был предложен английским математиком Раусом в 1845 г., а затем вновь выведен и дополнен Гурвицем в 1893 г.
Рассмотрим этот критерий в форме Гурвица.
Пусть характеристическое уравнение системы имеет вид
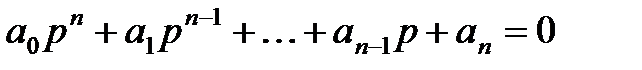
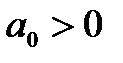
Тогда для устойчивости линейной САР необходимо и достаточно, чтобы были положительными главный определитель Гурвица и все его дислокальные миноры, т.е. при
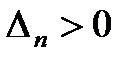
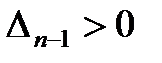
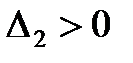
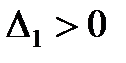
Диагональные миноры (определители Гурвица) представляют собой диагональные определители квадратной матрицы Гурвица n-го порядка
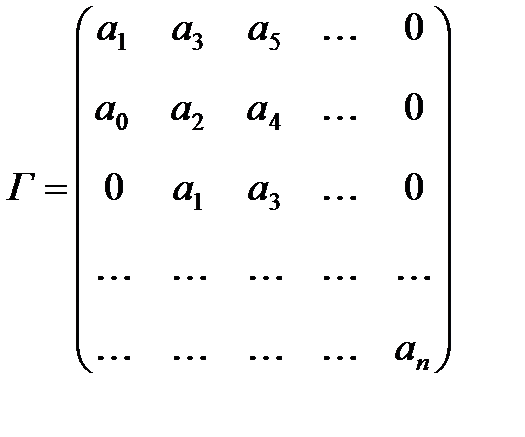
составленной из коэффициентов уравнения (1). При этом
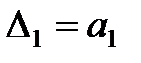
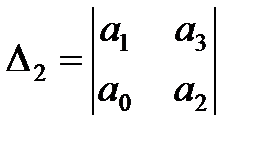
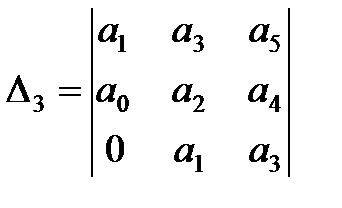

Матрица Гурвица составляется следующим образом. По главной диагонали выписываются все коэффициенты по порядку от 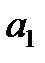
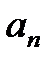
Из матрицы (2) следует, что главный определитель Гурвица можно записать
Если 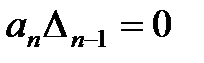
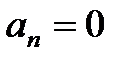
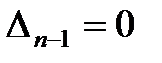
Следует отметить, что из условия 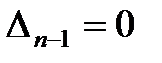
Критерий Рауса-Гурвица целесообразно использовать для уравнений не выше четвёртой-пятой степени. В этих случаях условия устойчивости имеют следующий вид:
1. Для уравнения первого порядка (n=1)
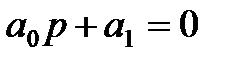


2. Для уравнения второго порядка (n=2)
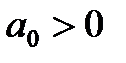
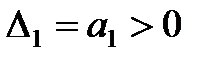
или 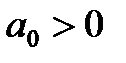

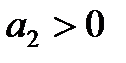
Таким образом, для уравнений первого и второго порядков необходимым и достаточным условием является только положительность всех коэффициентов характеристического уравнения.
3. Для уравнения третьего порядка (n=3)
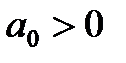

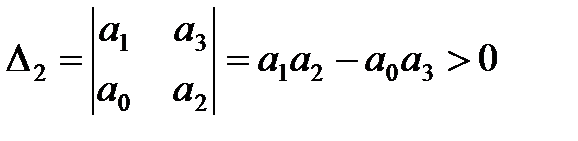
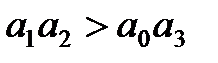
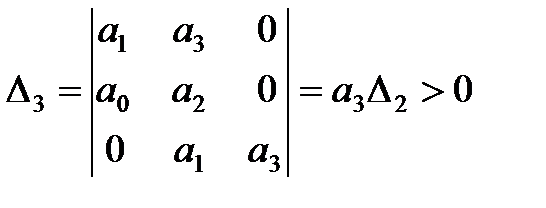

Следовательно, в этом случае САР будет устойчивой, если
1) 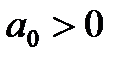
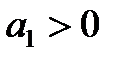
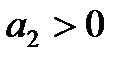
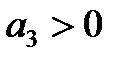
2) 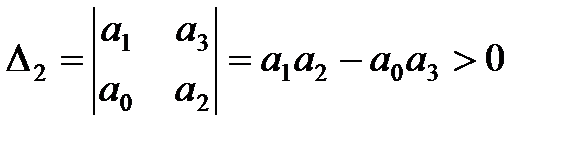
4. Для уравнения четвёртой степени (n=4)
1) 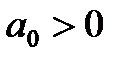
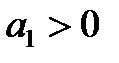
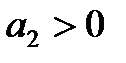
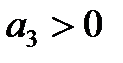
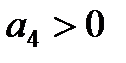
2) 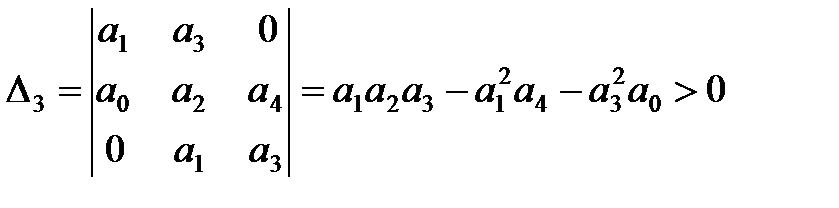
Таким образом, для уравнений третьего и четвёртого порядков должны быть положительными кроме всех коэффициентов предпоследние определители Гурвица.
2. Критерий устойчивости Михайлова
Этот критерий принадлежит к числу частотных критериев и позволяет судить об устойчивости замкнутой системы по виду годографа, построенного с помощью характеристического уравнения.
Передаточная функция замкнутой системы
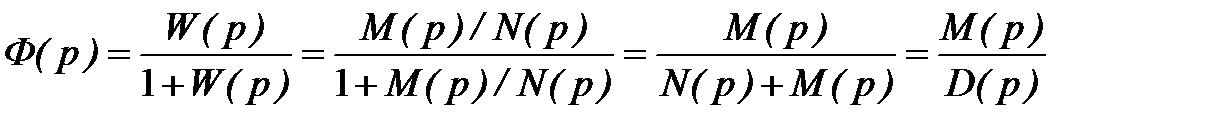
где 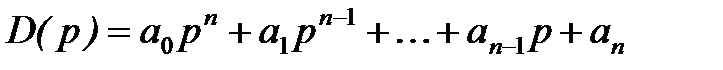
характеристический полином замкнутой системы.
В уравнении (3) произведём замену 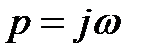
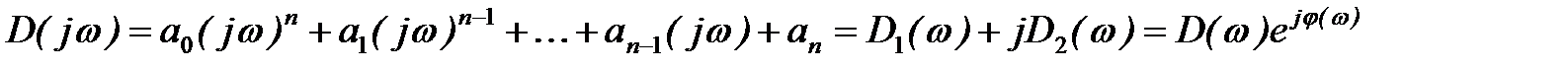
где 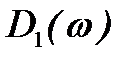
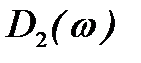
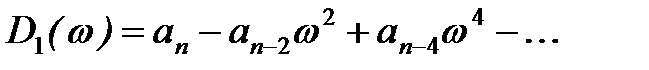

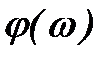
Если изменять значение частоты 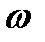
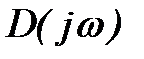
Выясним связь между видом кривой Михайлова и корнями характеристического уравнения. Для этого определим, чему должен равняться угол поворота φ вектора 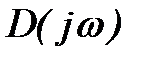
Запишем характеристический полином в виде произведения сомножителей
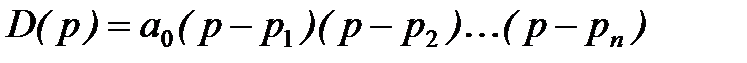
где 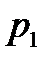
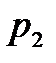

Аналогично характеристический вектор можно представить в виде
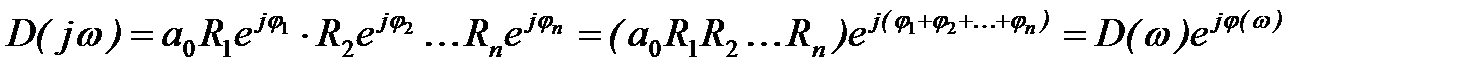
где 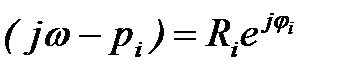
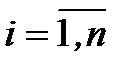
На плоскости комплексного переменного величина 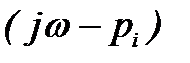
| А |
| В |
| О |
| С |
| α |
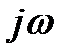 |
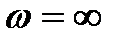 |
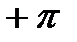 |
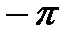 |
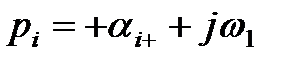 |
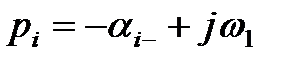 |
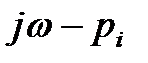 |
При изменении ω от -∞ до ∞ и постоянном значении 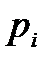
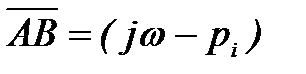
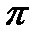
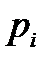
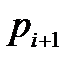
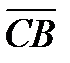

Из (4) следует, что аргумент вектора 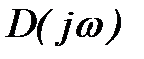
Если предположить, что в правой полуплоскости расположено k корней характеристического уравнения, то в левой полуплоскости их будет (n-k). Тогда изменение аргумента вектора 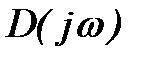
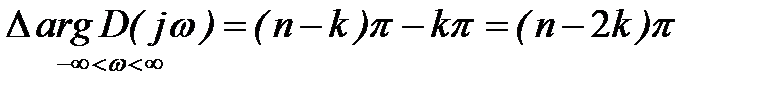
Формула (5) определяет изменение аргумента вектора 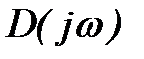
Диапазон отрицательных частот 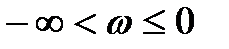
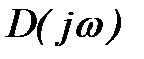
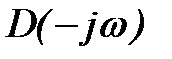
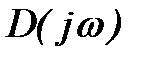
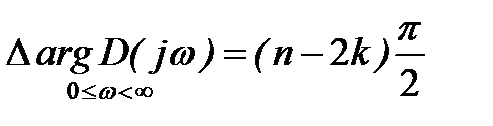
Если все корни характеристического уравнения лежат в левой полуплоскости (система устойчива), то k=0 и следовательно
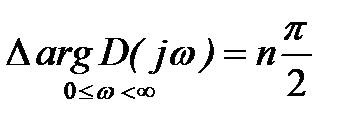
Формула (7) определяет необходимые и достаточные условия устойчивости системы в замкнутом состоянии и одновременно являются математической формулировкой критерия устойчивости Михайлова: для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы вектор 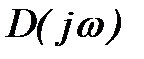
На рис. 5а приведены типичные кривые (годографы) Михайлова для устойчивых систем, описываемых уравнениями от первого (n=1) до пятого (n=5) порядков. Для удобства сравнения коэффициенты 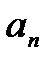
Если условия устойчивости по Михайлову не выполняются, то система будет неустойчивой (рис. 5б).
Система будет находиться на границе: апериодической устойчивости (рис. 5в), когда имеется нулевой корень, и годограф Михайлова начинает своё движение из начала координат; колебательной устойчивости (рис. 5г), если имеются сопряжённые мнимые корни, и годограф Михайлова проходит при частотах, отличных от нуля, через начало координат.
Если система при расчёте окажется неустойчивой, то, используя уравнение (6), можно определить количество корней характеристического уравнения 
| | | следующая лекция ==> | |
| Художественные системы в проектировании одежды | | | Конструктивные решения полов малоэтажных зданий |
Дата добавления: 2015-08-11 ; просмотров: 5920 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
корней характеристического уравнения
Одним из косвенных показателей качества систем управления является степень удаленности корней характеристического уравнения замкнутой САУ от мнимой оси комплексной плоскости. Пусть ближайшие к мнимой оси комплексно-сопряженные корни устойчивой системы имеют значение
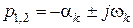
Расстояние 
Угол φ, образуемый лучами, проведенными из начала координат через эти корни, характеризует колебательность системы. Степенью колебательности системы (коэффициентом затухания колебаний) называют количественную характеристику, определяемую выражением

Чтобы система обладала заданной колебательностью, все корни характеристического уравнения должны вписываться в угол 2φ (см. рис. 7.2). Для большинства систем управления допустимое перерегулирование 
Рис. 7.2. Область расположения корней
с заданными показателями 
При корневых методах оценки качества системы, т. е. по расположению корней характеристического полинома, исходят из следующих соображений.
Решение однородного уравнения, характеризующего свободное движение системы, представляет собой сумму затухающих экспонент вида (6.2). Полагая, что качество САУ в основном определяется ближайшим к мнимой оси вещественным корнем или ближайшей к мнимой оси парой комплексно-сопряженных корней (доминирующих корней), можно записать
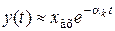
Полагая, что зона δ установления переходного процесса составляет (2…5)% от установившегося значения 


Следовательно, задаваясь временем регулирования, можно рассчитать минимальное (по модулю) значение вещественных частей корней характеристического уравнения.
Аналогично можно связать степень колебательности m системы со степенью затухания колебаний. Пусть по условиям технологии требуется, чтобы каждая последующая амплитуда колебаний затухала в k раз по сравнению с предыдущей. Тогда
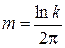
Пусть k=10, тогда в соответствие с (7.4) получим m=0,336 и
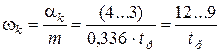
Таким образом, задаваясь временем регулирования 

Для построения в плоскости параметров областей, обеспечивающих требуемые показатели качества регулирования целесообразно использовать метод D-разбиения [6]. В качестве примера используем уравнение Вышнеградского, описывающего в параметрической форме характеристический полином 3-го порядка,

где A и B – обобщенные параметры характеристического уравнения.
Подставим выражение для комплексного корня 

Приравнивая нулю вещественную и мнимую части, получим


Полагая 


Рис. 7.3. Границы областей устойчивости,
колебательности и апериодичности на
Полагая 

Поскольку на кривой 1 ω ≠ 0, а на кривых 2 и 3 ω = 0, то области I и III являются областями комплексных, а область II – вещественных корней (см. рис. 7.3). Следовательно, если параметры A, B принадлежат области II, то переходные процессы имеют апериодический характер, причем, чем эти параметры больше, тем процессы более затянуты. Если параметры принадлежат области I, то переходные процессы имеют колебательный характер, причем, чем больше A и меньше B, тем выше колебательность. Область III является областью монотонности решения однородного дифференциального уравнения, соответствующего (7.5), а, следовательно, переходные процессы, имея колебательный характер, тем не менее, затухают монотонно (без перерегулирования).
Диаграмма Вышнеградского [19] помимо приведенных кривых содержит кривые равных вещественных частей комплексных корней (равной степени устойчивости), причем для двух случаев расположения корней, когда ближайшими к мнимой оси являются комплексные корни и, когда ближайшим к мнимой оси расположен вещественный корень (на рис. 7.3 эти кривые не показаны). В частности, на границе областей I и III (кривая 4) все три корня равно удалены от мнимой оси.
Требования повысить быстродействие и одновременно снизить перерегулирование в системе являются противоречивыми друг другу, что заставляет искать компромисс. В общем случае, с точки зрения переходного процесса наилучшей считается САУ, у которой все корни характеристического уравнения n-го порядка равны друг другу (на практике редко реализуется), т. е.
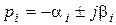
В этом случае перерегулирование не превышает 10%, а время нарастания регулирования является минимальным.
Если все корни являются вещественными, то система характеризуется отсутствием перерегулирования, т. е. апериодическими переходными процессами. Время регулирования будет тем меньше, чем меньше среднегеометрический корень 
При анализе качества системы корневыми методами необходимо учитывать влияние нулей передаточной функции на переходный процесс.
Прежде всего, нужно проверить, насколько близки нули к полюсам.
Если нуль и полюс совпадают, то их нужно сократить, и они не будут влиять на качество системы. Порядок системы при этом, естественно, будет понижен.
Если полюсы и нули передаточной функции не совпадают, то полюсы определяют отдельные составляющие переходного процесса (апериодические и гармонические), а нули определяют удельный вес каждой из этих составляющих. Чем ближе нуль передаточной функции расположен к какому-либо полюсу, тем меньше его вклад в переходную характеристику составляющей, соответствующей данному полюсу.
7.2.2. Интегральные оценки качества
В основе интегральных оценок качества лежит предположение, что качество регулирования тем выше, чем меньше площадь между кривой переходного процесса и заданным значением регулируемой переменной. Интегральные оценки качества являются строгой математической формулировкой понятия качества системы, и их минимизация позволяет определить оптимальные параметры системы управления, т. е. решить задачу параметрического синтеза системы. Для этой цели применяются процедуры безусловной и условной оптимизации [2, 6, 10-12, 19-21].
Наибольшее применение для косвенной оценки качества САУ находят интегральные оценки вида [6, 11, 12, 19]:





где 
С – некоторый весовой коэффициент, характеризующий допустимую скорость изменения ошибки регулирования, а, следовательно, выходной координаты в переходном процессе.
В критерии (7.8) подынтегральное выражение линейно относительно ошибки регулирования и такая оценка применяется только для апериодического переходного процесса, когда ошибка имеет положительный знак.
Интегральная квадратичная оценка (ИКО) вида (7.9) применяется при колебательном характере переходных процессов, характеризующихся сменой знака ошибки регулирования. Интегральная квадратичная оценка (7.10) применяется в тех случаях, когда требуется учитывать ограничения энергии управления.
Широко используемым видом оценки качества является интеграл от модуля ошибки (ИМО) – (7.11), позволяющем учесть смену знака подынтегральной функции.
Чтобы уменьшить вклад начальной ошибки в интеграл (7.11) и учесть связанную с этим ошибку была предложена [6] оценка в виде интеграла от взвешенного модуля ошибки (ИВМО) в виде (7.12).
Рассмотрим пример. Пусть передаточная функция замкнутой системы 2-го порядка имеет вид:

где 
Нормированное значение собственной частоты принято 

Рис. 7.4. Интегральные оценки
качества системы второго порядка
Как видим, оценка ИВМО по сравнению с ИКО имеет ярко выраженный минимум (хорошую избирательность), соответствующий 
Рассмотрим еще один пример. Пусть передаточная функция замкнутой системы имеет достаточно общий вид нерекурсивного фильтра n-го порядка:

Безусловная оптимизация систем первого-четвертого порядка (n=1…4), описываемых передаточными функциями (7.14), по критерию ИВМО дает оптимальные значения коэффициентов полиномов знаменателей этих передаточных функций, приведенные в табл. 7.1. Значения коэффициентов нормированы относительно собственной частоты колебаний 
На рис. 7.5 приведены кривые переходных процессов, соответствующих оптимальным по критерию ИВМО фильтрам первого-четвертого порядка.
| Порядок системы | Полином знаменателя передаточной функции |
| n=1 |  |
| n=2 |  |
| n=3 |  |
| n=4 |  |
Значения коэффициентов нормированы относительно собственной частоты колебаний 
Рис. 7.5. Переходные характеристики, соответствующие
оптимизации систем по ИВМО
Графики построены в зависимости от нормированного времени 
Кроме приведенных оценок для оптимизации систем управления применяются и другие интегральные критерии качества, в частности, лежащие в основе синтеза фильтров Баттерворта, широко применяемых при настройке контуров электромеханических систем управления.
8. Метод пространства состояний
Широкое распространение компьютеров и мощных систем программирования побуждает к исследованию САУ во временной области, а, следовательно, к непосредственному использованию описания динамических систем управления в форме обыкновенных дифференциальных уравнений без перехода к операторной форме. Кроме того, как уже отмечалось, векторно-матричные формы описания и исследования применимы не только к одномерным, линейным, стационарным САУ, но и к широкому классу многомерных, нелинейных и нестационарных САУ.
Чтобы получить пригодную для компьютерного синтеза и анализа модель САУ, необходимо представить ее в переменных состояния системы, используя далеко не единственный набор переменных. Следует отметить, что описание систем во временной области в векторно-матричной форме лежит в основе современной теории управления и оптимизации. В настоящей главе рассмотрены вопросы применения метода пространства состояния к непрерывным системам управления.
8.1. Векторно-матричное описание САУ
Состояние системы – это совокупность значений переменных системы (координат состояния), существенных с точки зрения решаемой задачи. В общем случае, в это число включают не только выходные и внутренние переменные САУ, но и задающие воздействия, и доминирующие возмущающие воздействия внешней среды. Чем полнее достоверной информации о состоянии системы в текущий момент времени, тем проще определить будущие значения всех ее переменных. Инженерно-технический персонал, разрабатывающий и эксплуатирующий технические системы управления, оперирует, как правило, с такими физическими переменными, которые могут быть измерены с помощью соответствующих датчиков. К таким физическим переменным САУ относят ускорение, скорость, перемещение, давление, расход, температуру, уровень и т. п. Координатами датчиков технологических координат САУ являются другие переменные — напряжение, ток, частота следования импульсов, двоичный код и т. п., что дает исследователю возможность выбора для синтеза и анализа необходимого набора координат состояния САУ.
Векторно-матричная модель многомерной, нелинейной, нестационарной САУ записывается в виде [6, 10, 11, 19]


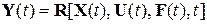
где X(t), U(t),F(t), Y(t) – соответственно векторы состояния, управления, возмущения и выходных (управляемых) координат системы,


В уравнении (8.1) вектор управления U(t) является, в общем случае, некоторой нелинейной нестационарной функцией задающих координат, координат состояния и возмущения САУ и призван обеспечить оптимальное управление системой. Описание многомерных, нелинейных, нестационарных САУ в форме (8.1) не позволяет, как правило, получить инженерное решение задачи структурно-параметрического синтеза оптимального управления U(t) или такое решение приводит к неоправданным затратам на реализацию (в техническом или экономическом аспектах). В большинстве случаев такие модели сводят к одномерным или многомерным линейным (линеаризованным) квазистационарным моделям, для которых имеются развитые методы и инженерные методики синтеза оптимального управления.
Линейную (линеаризованную) модель многомерной стационарной (квазистационарной) САУ представляют в виде системы обыкновенных дифференциальных уравнений первого порядка в форме Коши:



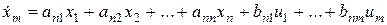
Эту же систему дифференциальных уравнений можно представить в векторно-матричной форме [6, 11, 19]:

где 



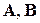


В общем случае, на объект управления помимо управляющих воздействий действуют возмущающие воздействия. В этом случае векторно-матричную модель системы представляют в виде

где 


Выходные (управляемые) переменные не всегда непосредственно принадлежат вектору состояния. В линейных САУ они линейно связаны с переменными состояния, управляющими и возмущающими переменными. В этом случае к уравнениям (8.3), (8.4) присоединяют алгебраические линейные уравнения

или 
где 
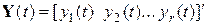
K, L, M – стационарные матрицы соответственно размерностей (r 


Следует отметить, что приведенные уравнения (8.1)…(8.6) дают описание лишь объекта управления или разомкнутой системы, если вектор управления U(t) не является функцией координат состояния САУ. В замкнутых линейных САУ управление обычно формируют как линейную форму координат состояния и, в общем случае, возмущения САУ.
В качестве примера приведем векторно-матричное описание ранее рассматриваемого электродвигателя постоянного тока как объекта регулирования по цепи якоря. Пусть выходной (регулируемой) координатой является скорость вращения двигателя. Полагая, что напряжение возбуждения 
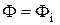



Воспользуемся векторно-матричной моделью линейных САУ в виде (8.4), (8.5). Зададимся векторами состояния, управления и возмущения в виде:

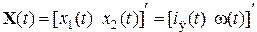


По уравнениям (8.7) найдем матрицы состояния, управления и возмущения:
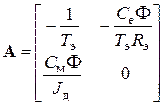


Поскольку выходная переменная всего одна и ей является координата состояния 
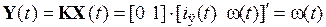
По описанию системы в форме векторно-матричных уравнений (ВМУ) можно непосредственно получить эквивалентную передаточную функцию (ПФ) и, наоборот, зная ВМУ системы, можно получить ее ПФ. Для этого в системе MATLAB имеется две функции: функция tf и функция ss.
Пусть ВМУ системы имеет вид (8.3), (8.5). Применительно к системе MATLAB ВМУ записывают в виде

Для получения ВМУ в системе MATLAB необходимо определить функцию ss(A,B,C,D). Для преобразования ВМУ к ПФ системы необходимо записать:
sys_ss=ss(A,B,C,D); % Формирование ВМУ системы;
sys_tf=tf(sys_ss), % Преобразование ВМУ к ПФ системы.
Для обратного преобразования ПФ к ВМУ необходимо записать:
sys_tf=tf(num,den); % Формирование ПФ системы;
sys_ss=ss(sys_tf); Преобразование ПФ к ВМУ системы.
Рассмотрим пример. Пусть ПФ системы имеет вид
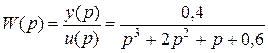
Тогда запишем скрипт преобразования ПФ к ВМУ и обратного преобразования ВМУ к ПФ:
sys_tf=tf(num,den); % Формирование ПФ системы;
sys_ss=ss(sys_tf); %Преобразование ПФ к ВМУ системы;
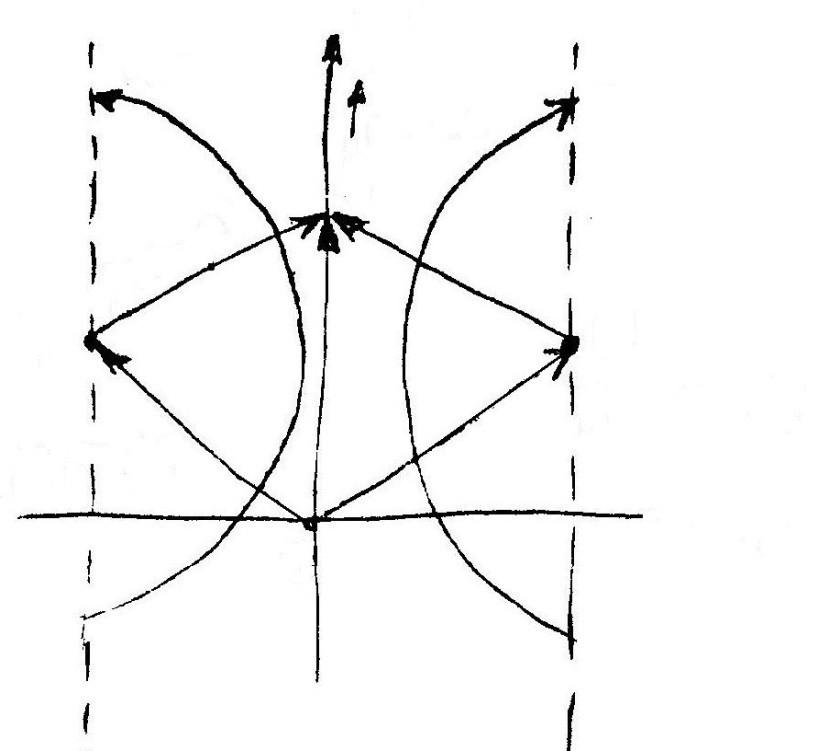
Корневые критерии устойчивости
1) 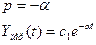
Устойчивая система.
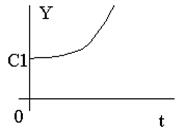
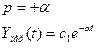
Неустойчивая система
3) 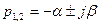
отрицательной вещественной частью
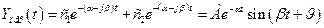
затухающие гармонические колебания

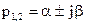
Неустойчивая система
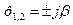

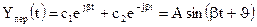 |
монотонный колебательный процесс
с постоянной частотой и амплитудой.
Система на границе устойчивости.
Вывод:Чтобы САУ была устойчивой необходимо, чтобы вещественные части корней были отрицательными. Если хотя бы один корень имеет положительную вещественную часть, то процесс будет расходящийся а система – неустойчива.
Если корень равен 0, то малейшее появление отрицательной составляющей сделает процесс устойчиво колебательным, а положительной – неустойчиво колебательным.
Часто корни характеристического уравнения при анализе устойчивости систем изображают на комплексной плоскости – плоскости корней характеристического уравнения
Комплексная плоскость мнимой осью разбивается на 2 части. Левую сторону называют областью устойчивости,а правую – областью неустойчивого движения.
Если корни лежат на мнимой оси или в 0, то система находится на границе устойчивости.
Вывод:Для устойчивости САУ необходимо и достаточно, чтобы все корни характеристического уравнения лежали слева от мнимой оси плоскости корней. Если хоть один корень справа, то система неустойчива. Таким образом, мнимая ось есть граница, за которую корни не должны переходить.
Если система имеет хотя бы один нулевой корень или хотя бы одну пару чисто мнимых корней, а все остальные корни имеют отрицательную вещественную часть, то система находится на границе устойчивости. При этом выделяют 3 типа границ устойчивости линейных систем:
1. Апериодическая граница устойчивости, которая соответствует р=0. Когда корень – нуль, то в характеристическом уравнении и система будет устойчива относительно скорости изменения управляемой величины, а сама управляющая величина может принимать произвольное значение. Система является нейтрально устойчивой.
2. Колебательная граница устойчивости, которой соответствуют чисто мнимые корни
В связи с тем, что корни характеристического уравнения определять трудно для систем высокого порядка, были разработан целый ряд критериев, с помощью которых судят об устойчивости систем.
Алгебраические критерии.
Критерий устойчивости Гурвица.
При рассмотрении алгебраических критериев используются лишь коэффициенты характеристического уравнения и необходимые и достаточные условия устойчивости систем.
Необходимое условие является справедливым для всех систем:
Все коэффициенты характеристического уравнения должны быть положительными
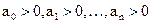
Для устойчивости линейной САУ по критерию Гурвица необходимо и достаточно, чтобы были положительными n главных определителей матрицы коэффициентов характеристического уравнения заданной системы (знаменатель передаточной функции):
Матрица коэффициентов
По диагонали от левого верхнего угла до правого нижнего выписывают все коэффициенты по порядку от а1 до аn. Каждая строка дополняется коэффициентами с возрастающими индексами слева направо так, чтобы чередовались строки с чётными и нечётными индексами. В случае отсутствия даннного коэффициента или если его индекс n, то на его место пишется 0.






0 




Если аn=0 , то имеет место апериодическая граница устойчивости.

Критерий Раусса.
Так же базируется на коэффициентах характеристического уравнения, из которого строится таблица.

| а0 | а2 | а4 | а6 | а8 |
| а1 | а3 | а5 | а7 | а9 |
| b1 | b2 | b3 | b4 | |
| c1 | c2 | c3 | … | … |
| … | … | … | … | … |
Для устойчивости системы все коэффициенты 1-го столбца должны быть больше 0
Частотные критерии
Критерий Михайлова.
Критерий базируется на поведении кривой, которую описывает конец вектора (X(ω),Y(ω)) замкнутой системы при изменении частоты от 0 до + 
Возьмём характеристический полином следующего вида:
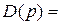
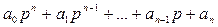
Подставим в него 
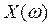
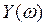
Изобразим годограф Михайловавыражения 
Берём значения 

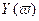
Формулировка критерия Михайлова.
Чтобы САР была устойчивой, необходимо и достаточно, чтобы вектор D(jω) при изменении частоты от 0 до +∞ начал движение с точки, лежащей на положительной вещественной оси, и, вращаясь только против часовой стрелки и нигде не обращаясь в нуль, прошел последовательно n квадрантов комплексной плоскости, повернувшись на угол n∙π/2, где n – степень характеристического уравнения D(jω)=0
Другими словами, требуется, чтобы кривая Михайлова проходила последовательно 

Устойчивая Неустойчивая Апериодическая Колебательная
граница устойчивости граница устойчивости
Другая формулировка критерия Михайлова:
Она состоит в использовании свойства перемежаемости корней многочленов 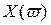

Идя по кривой Михайлова от т. 

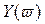

Это значит, что корни уравнений 

Кривые 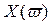

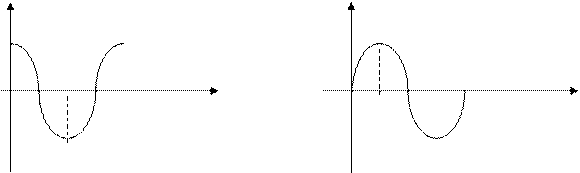
Перемежаться должны корни 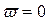

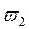
Условием устойчивости системы является перемежаемость корней полиномов вещественной и мнимой частей комплексной передаточной функции. Нарушение этого условия говорит о неустойчивости системы.
ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры.
ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала.
Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот.
Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.).
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
http://poisk-ru.ru/s49289t1.html
http://zdamsam.ru/a41379.html