Корни характеристического уравнения в матлаб

9 -е занятие по MATLAB

ЛАБОРАТОРНАЯ РАБОТА № 9

Синтез наблюдающего устройства

для стационарной линейной системы управления.

Цель работы: освоение методов синтеза асимптотического наблюдающего устройства (наблюдателя) для стационарной линейной системы управления со скалярным управлением при отсутствии случайных помех. Анализ динамических свойств системы с наблюдателем.

I. Синтез наблюдателя на основе модального управления.

Наблюдающим устройством называется динамическая система, которая восстанавливает вектор состояния заданной системы на основе измерения входного и выходного воздействий при известной структуре (матрицы А, В, С) заданной системы.

Если система, для которой восстанавливается полный вектор состояния, описывается векторным уравнением

(1)

то наблюдатель имеет следующее уравнение:

(2)

где u — скалярное входное управляющее воздействие, — оценка вектора состояния , — матрица усиления наблюдателя.

Наблюдатель будет называться асимптотическим, если

(3)

где — вектор ошибки восстановления.

Вычитая из первого уравнения (1) второе (2), получим уравнение относительно ошибки восстановления

(4)

Для выполнения соотношения (3) необходимо так подобрать (синтезировать) матрицу наблюдателя , чтобы собственные числа матрицы в (4) были с отрицательными действительными частями.

Для системы (1) со скалярным управлением (с одним входным воздействием) рассчитаем матрицу на основе синтеза модального управления.

Характеристическое уравнение для определения собственных чисел матрицы имеет вид

. (5)

Известно, что собственные числа матрицы не изменятся, если эту матрицу транспонировать. Поэтому корни характеристического уравнения (5) также не изменятся, если оно будет записано для транспонированной матрицы , т.е.:

. (6)

Уравнение (6) может отвечать следующей системе:

(7)

с модальным управлением

(8)

т.е. замкнутая система (7) на управление (8) имеет вид

(10)

для которой характеристическое уравнение будет аналогично (6):

. (11)

Система (7) является дуальной к системе (1) в смысле Калмана.

Таким образом, если будет рассчитано модальное управление для системы (7), то матрица коэффициента усиления наблюдателя будет определяться как

, (12)

где T — символ транспонирования.

Расчет модального управления начинается с приведения системы (7) к каноническом виду с помощью матрицы преобразования подобия N :

, (13)

где — матрица-строка, которая вычисляется по соотношению

(14)

Расчет матрицы по выражению (6) возможен, если система (7) полностью управляема по Калману и, соответственно, система (1) полностью наблюдаема.

Модальное управление где Z — вектор переменных состояния канонической системы, определяется по следующим соотношениям (расчет элементов):

(15)

где — коэффициенты характеристического уравнения системы (1), — коэффициенты характеристического уравнения

(16)

с желаемыми корнями которые выбираются из условия асимптотической устойчивости, т.е. в левой полуплоскости комплексной плоскости корней.

Переход к требуемой матрице усиления наблюдателя осуществляется следующим образом:

(17)

. (18)

Расчет матрицы усиления наблюдателя сводится к следующим этапам:

1) Проверка системы на полную наблюдаемость по Калману;

2) Определение коэффициентов характеристического уравнения системы (1);

3) Задание желаемых корней в левой полуплоскости и определение коэффициентов характеристического уравнения (16);

4) Расчет матрицы модального управления по соотношениям (15);

5) Расчет матрицы преобразования подобия по соотношениям (13), (14);

6) Собственно расчет матрицы усиления наблюдателя по выражению (18).

Пример 1. Синтез наблюдателя для линейной системы 3-го порядка, заданной передаточной функцией вида

. (19)

Знаменатель передаточной функции определяет собой и характеристическое уравнение заданной системы с коэффициентами

(20)

В системе MATLAB коэффициенты характеристического уравнения можно определить с помощью встроенной функции poly , которая определяет и коэффициент при старшей степени комплексной переменной. Для (19):

1.0000 1.7500 0.8750 0.1250

С помощью функции poly можно определить и коэффициенты системы управления, заданной в пространстве состояний.

С учетом (19) запишем модель объекта управления в пространстве состояний, полагая :

(21)

Матрицы объекта управления в соответствии с (21) имеют вид

(22)

Уравнение выхода примем в виде . Тогда

(23)

Проверка объекта управления на полную наблюдаемость:

т.е. объект полностью наблюдаем.

Определение коэффициентов характеристического уравнения по заданным корням:

где i — мнимая единица,

или

т.е. (24)

Для вычисления коэффициентов уравнения можно применить poly от вектора заданных корней, т.е. poly([ l ₁ ; l ₂ ; l ₃ ]) .

Расчет матрицы :

(25)

Расчет матрицы преобразования подобия :

(26)

(27)

Расчет матрицы усиления наблюдателя:

= (28)

— проверить корни характеристического уравнения ошибки восстановления.

— решить дифференциальное уравнение ошибки восстановления со следующими начальными условиями: .

— синтезировать наблюдатель с другими задаваемыми корнями характеристического уравнения ошибки: <-3, -5, -7>; <-2, -6, -18>.

II. Синтез модального управления при не полностью известном векторе состояния системы .

Синтезируем модальное управление для системы (21) вида

(29)

где — матрица усиления модального управления, синтезированная по матрицам объекта А и В, — восстановленный вектор состояния или вектор состояния наблюдателя, для которого матрица усиления получена в виде (28).

В соответствии с теоремой разделимости матрицу можно синтезировать не зависимо от наблюдателя.

1) Проверка объекта управления на полную управляемость по Калману:

Объект полностью управляем.

2) Расчет матрицы преобразования подобия N :

(30)

3) Задание собственных чисел матрицы замкнутой системы:

4) Определение коэффициентов характеристического уравнения замкнутой системы:

или

5) Расчет матрицы модального управления для канонической системы

. (31)

6) Расчет матрицы модального управления :

(32)

7) Анализ системы с модальным управлением и наблюдающим устройством.

Система дифференциальных уравнений в матричном виде:

(33)

где А, В, С — матрицы объекта и выхода определяются по (22), (23); — определяется по (32); — определяется по (28). Начальные условия по . Начальные условия по восстановленному вектору состояния .

В системе MATLAB решение (33) может быть принято в виде:

% Сначала создается М-файл как М-функция под именем, например, difn1

A =[0 1 0;0 0 1;-0.125 -0.875 -1.75];

K =[64.5401 43.1549 8.1540];

% Сценарий решения дифуравнения (3) под именем didn11

plot(t,z),grid,legend( ‘x_1’ , ‘x_2’ , ‘x_3’ , ‘xv_1’ , ‘xv_2’ , ‘xv_3’ ),

где ‘x_1′,’x_2′,’x_3’ — переменные состояния системы управления,

‘xv_1′,’xv_2′,’xv_3’ — переменные состояния наблюдателя.

— построить графики переходных процессов для соответствующих пар переменных состояния объекта управления и наблюдателя.

— построить переходные процессы системы (33) для различных значений начальных условий: <0, 0, 0, 1, 2 ,3>, <10, 0, -10, 0, 0, 0>, <0, 0, 0, 10, 0, -10>.

— написать программу, совмещающую в себе синтез модального управления, синтез наблюдателя и анализ переходных процессов системы управления с асимптотическим наблюдающим устройством.

III. Синтез модального управления и наблюдающего устройства для неустойчивого объекта в системе MATLAB.

Дано: передаточная функция неустойчивого объекта управления

(34)

Требуется синтезировать асимптотически устойчивую систему с обратной связью по состоянию при не полностью известном векторе состояния объекта.

Задача заключается в синтезе модального управления и асимптотического наблюдающего устройства.

% Анализ переходного процесса по заданной передаточной функции (34)

» step(W2),grid,ylabel (‘Амплитуда выходной координаты объекта’)

% Описание объекта управления в пространстве состояний

% Выделение матриц A, B, C, D объекта управления по заданной системе пространства состояний s1

% Проверка объекта на полную управляемость и полную наблюдаемость

» с t 1=ctrb(s1) % Формирование матрицы управляемости

» rank( ct 1) % Вычисление ранга матрицы управляемости

»o b 1=obsv(s1) % Формирование матрицы наблюдаемости

» rank( ob 1) % Вычисление ранга матрицы наблюдаемости

% Так как ранг матрицы управляемости и ранг матрицы наблюдаемости равен трем, то объект полностью управляем и полностью наблюдаем, поскольку размерность объекта также равна третьему порядку.

3 . 1. Синтез модального управления вида с помощью acker

% Матрицы объекта принимаем из системы s1: s1=ss(W2)

» P 1=[-3;-5+4*i;-5-4*i]; % Желаемый вектор собственных значений

» [Kр]=acker(A,B,P1) % Для объектов с одним входным воздействием

11.7500 70.8750 123.1250

% Исследование синтезированной системы

» s2=ss(A-B*K,B,C,D); % Формирование системы с регулятором

% Анализ переходного процесса синтезированной системы

% Переходный процесс является установившимся, т.е. система устойчивая

— исследовать переходные процессы синтезированной системы на основе решения системы дифференциальных уравнений с помощью ode45 .

— исследовать переходные процессы синтезированной системы с помщью команды lsim .

3.2. Синтез асимптотического наблюдателя.

% Определение коэффициентов характеристического уравнения объекта, заданного передаточной функцией или представленного в пространств состояний

» a= poly(W2) % Можно применить и poly( s1 )

1.0000 1.2500 0.1250 -0.1250

% Коэффициенты характеристического уравнения объекта равны:

% Сформируем вектор-строку коэффициентов a012:

-0.1250 0.1250 1.2500

% Определение коэффициентов характеристического уравнения ошибки восстановления по желаемым корням

» P 2=[-1;-1.5;-2]; % Вектор желаемых корней

1.0000 4.5000 6.5000 3.0000

% Коэффициенты характеристического уравнения ошибки равны:

% Сформируем вектор-строку коэффициентов d012:

3.0000 6.5000 4.5000

% Формирование модальной матрицы для дуальной канонической системы

3.1250 6.3750 3.2500

Расчет матрицы преобразования подобия :

[A,B,C,D]=ssdata(s1); %Выделение матриц из заданной системы

»N1=[0 0 1]*inv([C’ A’*C’ A’^2*C’]) % Формирование вспомогательной матрицы

0.5547 0.2427 -0.4160

% Расчет матрицы усиления наблюдателя:

Задание. Для системы с модальным управлением и наблюдателем выполнить следующее:

— исследовать переходные процессы в системе (35) с помощью step

(35)

— исследовать переходные процессы в системе (35) с помощью lsim

IV. Синтез модального управления и наблюдающего устройства для неустойчивого объекта с векторным входом и векторным выходом в системе MATLAB.

Дано: система дифференциальных уравнений с тремя управляющими воздействиями

(36)

Матрицы А, В, С, D :

(37)

Матрицу С задали так, чтобы иметь векторный выход

Система (36) неустойчивая:

» eig(A) % Вычисление собственных чисел матрицы А

0.5000 % Положительное собственное число обуславливает неустойчивость

% Анализ переходного процесса в неустойчивой системе по функции lsim

» u1=ones(size(T(:))); % Формирование единичной функции времени

» u2=ones(size(T(:))); % Формирование единичной функции времени

» u3=ones(size(T(:))); % Формирование единичной функции времени

» U=[u1,u2,u3]; % Вектор управляющих воздействий

» lsim(A,B,C,D,U,T),grid,title(‘Исходная неустойчивая система’)

% Переходные процессы по выходным координатам стремяться к бесконечности

Синтез модального управления по функции place

% Задаем вектор Р желаемых собственных значений

% Определяем матрицу K_r модального управления

% Исследуем переходные процессы системы с модальным управлением

» u1=ones(size(T(:))); % Формирование единичной функции времени

» u2=ones(size(T(:))); % Формирование единичной функции времени

» u3=ones(size(T(:))); % Формирование единичной функции времени

» U=[u1,u2,u3]; % Вектор управляющих воздействий

» lsim(A- B*Kr ,B,C,D,U,T),grid,title(‘Система с модальным управлением’)

— с помощью расчетного режима функции lsim построить графики переходных процессов исходной системы по переменным вектора выхода в одной системе координат.

— то же самое выполнить для системы с модальным управлением.

Если полный вектор состояния не может быть использован в цепи обратной связи модального управления, то необходимо синтезировать наблюдатель, который формирует оценку вектора состояния.

Синтез асимптотического наблюдателя.

% Задаем вектор Pn собственных значений матрицы системы ошибки восстановления

% Вычисляем матрицу модального управления для дуальной системы

» Kn=Knt’ % Операция транспонирования

Kn = [0, 0;1.2, 0;3, 0.5] % Матрица усиления наблюдателя

% Анализ переходных процессов относительно ошибки восстановления, т.е.

, (38)

где .

% Зададим начальные условия по

% Для построения переходных процессов используем initial

% Зададим матрицу Се выхода системы ошибки

» Ce=[1 0 0;0 1 0;0 0 1];

% При задании формата initial принимем матрицу В=0 и матрицу D=0 соответствующих размерностей

— синтезировать матрицу усиления наблюдателя для различных задаваемых собственных значений системы (38): <-0.1; -0.2; -0.25>, <-10; -20; -25>, <-100; -200; -250>, <-3; -4+7*i; -4-7*i>.

— применить числовой режим функции initial и построить в одной системе координат переходные процессы по всем переменным состояния ошибки.

Анализ синтезированной системы с асимптотическим наблюдателем.

В задачу входит построение переходных процессов синтезированной системы с наблюдателем и сравнение получаемых процессов для системы с модальным управлением без наблюдающего устройства.

Система с модальным управлением без наблюдающего устройства:

(39)

Считается, что вектор состояния Х (t) доступен для измерений в целях реализации закона управления

Для анализа переходных процессов по отработке начальных условий зададим следующий вектор начальных состояний:

Задание. Составить программу для анализа (39) по программе для (38).

Система с модальным управлением и с наблюдающим устройством:

(40)

Анализ переходных процессов в (40):

% Задание вектора начальных условий

» Z0=[1;2;3;0;0;0]; % Первые три элемента по , последующие — по

% Формирование коагулированной матрицы A0 системы (40) по известным матрицам и вычисленным

» Kr = [ 4 , 7.6 , 0 ; -2.8 , 2.75 , 0 ; 0 , 1 , 3.6 ];

» A0=[A,-B*Kr;Kn*C, (A-B*Kr-Kn*C)]; % Размер А0 равен 6 ´ 6

% Формирование вспомогательной матрицы С0 для определения характера изменения каждой переменной состояния системы (40)

» С0=eye(size(A0)) ; % Единичная матрица от размера А0 (здесь 6 ´ 6)

% Формирование вспомогательной матрицы В0 системы (40), которая равна нулю

» B0=zeros(length(A0(:,1)),length(A0(:,length(B(1,:))))) ; % размер n ´ r ( здесь 6 ´ 6)

% Формирование вспомогательной матрицы D 0 системы (40), которая равна нулю

% Применение функции initial для анализа переходных процессов (40)

» initial( A0 , B0,C0,D0 , Z 0) % Процессы по всем переменным

Анализ попарных переходных процессов в числовом режиме initial с формированием отдельных графических окон — figure

% Y0 — вектор выхода системы (40), Z — вектор состояния системы (40)

» figure(1),plot(t,Y0),grid,,title(‘Вектор выхода’), figure(2),plot(t,Z),grid,title(‘Вектор состояния’)

% Можно каждый из графических окон можно описывать отдельно

% Пример попарного представления в различных окнах

— изменить вспомогательную матрицу С0 и проанализировать переходные процессы по Y0 и Z в соответствии с (41).

— попарно сравнить переходные процессы по Х(t) в системе (40) и в системе (39).

Анализ устойчивости с помощью MATLAB

Этот раздел мы начнем с критерия Рауса-Гурвица и покажем, какое простое и удобное средство предоставляет MATLAB для вычисления корней характеристического уравнения. Если характеристическое уравнение содержит один варьируемый параметр, то можно отразить в виде диаграммы изменение положения корней в зависимости от этого параметра.

В данном разделе будет введена функция for, с помощью которой последовательность инструкций повторяется заданное число раз.

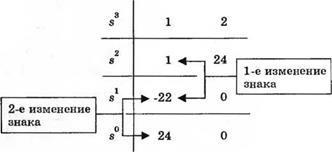
Критерий Рауса-Гурвица. Как было отмечено выше, критерий Рауса-Гурвица определяет необходимое и достаточное условие устойчивости. Если задано характеристическое уравнение с постоянными коэффициентами, то с помощью критерия Рауса-Гурвица можно определить число корней, расположенных в правой полуплоскости. Например, рассмотрим характеристическое уравнение замкнутой системы, изображенной на рис. 6.10:

q(s) = s3 + s2 + 2s + 24 = 0 .

Замкнутая система управления с передаточной функцией As) = y[s)/ff(s) =

= l/Cs3 + s2 + 2s + 24)

Соответствующая таблица Рауса приведена на рис. 6.11. Два изменения знака в первом столбце указывают на наличие двух корней уравнения в правой полуплоскости; следовательно, замкнутая система неустойчива. С помощью MATLAB мы можем проверить этот результат, непосредственно вычислив корни характеристического уравнения, как это показано на рис. 6.12. Для этого необходимо использовать функцию pole, которая вычисляет корни алгебраического полинома.

Таблица Рауса для замкнутой системы с передаточной функцией 7s) = 1AS3 + s2 + 2s + 24)

Использование функции pole для вычисления полюсов замкнутой системы, изображенной на рис. 6.10

»numg=[1]; deng=[1 1 2 23]; sysg=tf(numg, deng);

1 0000 + 2 8 попадают в правую полуплоскость.

Программа на рис. 6.14 содержит функцию for. Эта функция обеспечивает выполнение одной и той же серии инструкций заданное число раз. Она в сочетании с инструкцией end образует цикл повторяющихся вычислений. На рис. 6.15 приведен формат функции for, а также пример ее использования. В примере цикл повторяется 10 раз. На /-м шаге, где 1 0. Это значит, что мы можем ограничить область поиска значениями 0 0. Сначала с помощью MATLAB мы найдем границу устойчивости в плоскости параметров К и а. Затем мы сможем найти пары значений (К, а), принадлежащих области устойчивости, таких, которые удовлетворяли бы ограничению на установившуюся ошибку. Эта процедура, показанная на рис. 6.16, включает в себя задание диапазона значений К и а и вычисление корней характеристического уравнения для конкретных значений этих параметров. Для каждого К мы найдем первое значение а, при котором по крайней мере один корень характеристического уравнения попадает в правую полуплоскость. Этот процесс повторяется до тех пор, пока не будет пройден весь диапазон значений К и а. Найденные пары чисел (К’, а) определяют границу между областями устойчивости и неустойчивости.

На рис. 6.16 область слева от графика зависимости а =/(К) является областью устойчивости. Если считать, что r(t) = At, I > 0, то установившаяся ошибка

СИНТЕЗ МОДАЛЬНОГО РЕГУЛЯТОРА С НАБЛЮДАЮЩИМ УСТРОЙСТВОМ. Курсовая работа защищена с оценкой руководитель старший преподаватель

Название	Курсовая работа защищена с оценкой руководитель старший преподаватель
Анкор	СИНТЕЗ МОДАЛЬНОГО РЕГУЛЯТОРА С НАБЛЮДАЮЩИМ УСТРОЙСТВОМ
Дата	27.09.2021
Размер	0.54 Mb.
Формат файла
Имя файла	KursovRab.Koval.1832..docx
Тип	Курсовая #237732

С этим файлом связано 1 файл(ов). Среди них: Класс точности практичраб.pdf.

Показать все связанные файлы Подборка по базе: Контрольная работа (1).docx, Курсовая работа — Разработка бизнес-плана.doc, курсовая работа Предупреждение преступлений, связанных с незакон, практическая работа 1.docx, Практическая работа 1.docx, Курсовая работа ИСУ.doc, Бакаева И.А. Практическая работа.docx, Лабораторная работа №2.doc, Расчетно-графическая работа Ахметов.docx, Самостоятельная работа по теме 3.3. Немецкий язык.docx

Федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

КУРСОВАЯ РАБОТА
ЗАЩИЩЕНА С ОЦЕНКОЙ

РУКОВОДИТЕЛЬ

старший преподаватель	М.С. Брунов
должность, уч. степень, звание	подпись, дата	инициалы, фамилия

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К КУРСОВОЙ РАБОТЕ

«СИНТЕЗ МОДАЛЬНОГО РЕГУЛЯТОРА С НАБЛЮДАЮЩИМ УСТРОЙСТВОМ»

по дисциплине: ОСНОВЫ ТЕОРИИ УПРАВЛЕНИЯ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	1832	К.Р. Коваль
подпись, дата	инициалы, фамилия

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 1

ЗАДАНИЕ НА РАБОТУ 13

1. Преобразование модели системы в виде передаточное функции в модель в пространстве состояний. 15

2.Исследование системных свойств управляемости и наблюдаемости системы. 16

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Описание системы в пространстве состояний

Состояние системы – это совокупность таких переменных, знание которых позволяет, при известном входе и известных уравнениях динамики, описать будущее состояние системы и значение ее выхода.

Уравнения состояний линейной стационарной системы имеют следующий общий вид:

где X – вектор-столбец состояния [n × 1]; А – матрица коэффициентов объекта [n × n]; В – матрица входа [n × m]; U – вектор входа (управления) [m × 1]; Y – вектор выхода [k × 1]; С – матрица выхода [k × n]; D – матрица влияния входа непосредственно на выход системы [k × m].

Размер вектора состояния n равен порядку системы.

Рисунок 1. Структура системы в пространстве состояний.
У
равнениям состояния соответствует структурная схема, показанная на рис. 1.

На практике часто рассматриваются скалярные системы (с одним входом и одним выходом). Матрица D обычно нулевая.

Переход от передаточной функции к уравнениям состояния

Передаточная функция (ПФ) объекта имеет вид:

Корни полинома знаменателя называются полюсами ПФ, а корни числителя ПФ соответственно, нулями передаточной функции. Статические свойства системы определяются коэффициентом усиления, который при ненулевых a₀ и b₀ может быть вычислен по формуле:

Динамические свойства определяются расположением полюсов ПФ на комплексной плоскости.

В
ыбор переменных состояния неоднозначен, одной и той же ПФ могут соответствовать разные модели в пространстве состояний, однако если использовать каноническую форму управляемости, то переход от ПФ к уравнениям состояния будет однозначным, например, для системы 3-го порядка:

Если входной и выходной сигнал являются скалярными величинами, то передаточная функция разомкнутой системы выражается через матрицы A, B, C.

Анализ системных свойств объекта управления

При анализе систем в пространстве состояний важное значение имеют свойства управляемости и наблюдаемости.

Система, описываемая матрицами А и В, называется полностью управляемой, если её можно перевести из любого начального состояния X(0) в любое конечное X(t) с помощью управления U(t) за конечное время. Управляемость системы описывается условием:

Для системы с одним входом и одним выходом матрицы управляемости имеет размер n×n:

Если детерминант этой матрицы отличен от нуля, то система управляема.

Система, описываемая матрицами А и С, является наблюдаемой тогда и только тогда, когда существует конечное время Т такое, что начальное состояние X(0) может быть определено в результате наблюдения выходной переменной y(t), t ∈ T при заданном управлении u(t)

Наблюдаемость системы описывается условием:

Для системы с одним входом и одним выходом матрица наблюдаемости (размером n × n) имеет вид:

Если детерминант этой матрицы отличен от нуля, то система наблюдаема

Модальное управление

Рассмотрим САУ, описываемую линейным дифференциальным уравнением в операторной форме:

Общее решение этого линейного неоднородного дифференциального уравнения ищется в виде двух слагаемых:

где y_B – вынужденное и y_CB – свободное движение системы.

Вынужденная составляющая решения находится из исходного дифференциального уравнения приравниванием к нулю всех производных в левой и правой частях уравнения, так что при установившемся значении входного сигнала u_уст получаем:

Свободная (переходная) составляющая ищется как общее решение однородного дифференциального уравнения:

где A(s) – характеристический полином (знаменатель ПФ).

Решение имеет вид:

где – i–й корень характеристического полинома, – i-я постоянная интегрирования, определяемая из начальных условий.

Мода – это часть свободной составляющей решения дифференциального уравнения. Сумма отдельных мод определяет динамику системы.

Корни характеристического полинома могут быть четырех типов:

Вещественного типа λ = α. Такой корень дает составляющую решения вида:

При α 0 – возрастать.

Комплексно – сопряженного типа: λ 1,2 = α ± jβ. Составляющая решения имеет вид:

Здесь возникают колебания выходной переменной, которые будут затухать по амплитуде при α 0.

Чисто мнимые корни. В этом случае α = 0, и

колебания будут иметь постоянную амплитуду.

Нулевой корень. В этом случае в характеристическом полиноме

отсутствует свободный член: a0 = 0.

Здесь система находится на границе устойчивости, и при любых начальных условиях движения асимптотически затухают к положению равновесия (система устойчива в целом) или расходятся (система не устойчива).

Если изобразить корни характеристического уравнения системы точками на комплексной плоскости, то общее условие устойчивости линейной системы можно сформулировать еще так: условием устойчивости системы является расположение всех полюсов ПФ в левой комплексной полуплоскости.

Модальный синтез предполагает формирование таких обратных связей по состоянию, при которых обеспечивается заданное расположение полюсов замкнутой системы.

Сигнал управления описывается формулой:

где K – неизвестный вектор коэффициентов, который требуется найти при выполнении модального синтеза.

Формула (2) предполагает, что цель управления заключается в достижении начала координат в пространстве состояний. Иначе для заданного состояния Xg(t) надо использовать выражение:

Рассмотрим уравнения состояния замкнутой системы:

где g(t) – заданный входной сигнал (установка).

Рисунок 2. Структура замкнутой системы в пространстве состояний.
Э
тим уравнениям соответствует структура, приведенная на рис.2.

Свободное движение системы (при g(t) = 0) описывается выражением:

где K – вектор коэффициентов обратной связи.

Решение этого уравнения определяется формулой:

Следовательно, устойчивость и характеристики переходного процесса в системе определяются собственными числами матрицы A – BK.

Основная теорема модального управления гласит, что если линейная динамическая система является управляемой, то линейная обратная связь может быть выбрана таким образом, что матрица (А – ВK) будет иметь желаемый спектр (желаемое расположение полюсов замкнутой системы).

Выбор положения полюсов замкнутой системы

Рисунок 3. Понятие степени устойчивости.
Первый шаг модального синтеза заключается в выборе желаемого расположения полюсов замкнутой системы (т. е. формирование эталонной модели). Этот выбор можно сделать двумя способами: 1. Рассматривая корневые критерии качества системы. 2. Используя стандартные полиномиальные формы, задающие расположение полюсов замкнутой системы. g(t) Y(t) B C A u(t) X(t) K ∫ dX(t)/dt 15 Рассмотрим корневые критерии качества. Для оценки быстродействия системы используется понятие степени устойчивости η, под которой понимается абсолютное значение вещественной части ближайшего к мнимой оси корня (рис. 3, где показан вариант, когда ближайшим к мнимой оси является вещественный корень (слева), и вариант, к
огда к мнимой оси ближе пара комплексно-сопряженных корней (справа).

Корни, имеющие наименьшую по модулю вещественную часть, дают в переходном процессе наиболее медленно затухающую составляющую. Такие корни называют доминирующими.

Зная степень устойчивости, можно приближенно оценить время переходного процесса по формуле:

Эта оценка справедлива при значительном удалении ближайшего от мнимой оси полюса от других полюсов. При кратных полюсах формулу использовать нельзя.

Запас устойчивости системы оценивается колебательностью. Система имеет склонность к колебаниям, если характеристическое уравнение содержит комплексные корни η1,2= –α ± jβ.

Колебательность оценивается по формуле:

Если система имеет несколько комплексно-сопряженных корней, то ее колебательные свойства определяет пара комплексных корней, для которой µ принимает наибольшее отношение.

По значению колебательности можно приближенно оценить перерегулирование

Следует учитывать, что динамические характеристики системы (переходный процесс) зависят не только от расположения полюсов ПФ, но и от расположения ее нулей. Выбирая расположение полюсов, можно всегда гарантировать устойчивость замкнутой системы, но прямые показатели качества регулирования могут не совсем совпадать с заданными.

Рассмотрим использование стандартных полиномов.

О
дин из возможных подходов заключается в обеспечении одинаковости всех корней характеристического уравнения. Каждый корень λ должен быть отрицательным, а величина его модуля λ₀ определяется требованиями к быстродействию. Левая часть характеристического уравнения обращается в бином Ньютона (s + λ₀) n , разворачивая который, можно получить стандартные значения коэффициентов характеристического уравнения. Биномиальные стандартные формы для систем до четвертого порядка имеют вид:

При таком подходе обеспечивается апериодичность переходного процесса. Чем больше λ₀, тем меньше время переходного процесса, поскольку

Рисунок 4. Распределение Баттерворта для систем 3,4 и 5-го порядка.
С
уществуют и другие стандартные формы, например, форма Баттервота, в соответствии с которой корни должны располагаться в левой полуплоскости на окружности радиуса λ₀ на одинаковых угловых расстояниях друг от друга (рис. 4)

С
тандартные формы Баттерворта для систем до четвертого порядка имеют вид:

Полином Баттерворта обеспечивает заданное время переходного процесса и перерегулирование в пределах 15%. Для многих реальных систем переходный процесс с небольшим перерегулированием предпочтительнее апериодического процесса. Значения полюсов легко рассчитать из геометрических соображений.

Расчет коэффициентов обратных связей

Если задан желаемый характеристический полином замкнутой системы

т
о рассчитать вектор коэффициентов обратных связей K можно с помощью формулы Аккермана, которая имеет вид:

Наблюдающее устройство полного порядка

Метод модального управления предполагает, что все компоненты вектора состояния X могут быть измерены, но на практике некоторые компоненты могут быть неизвестны по одной из двух причин:

− измерительных приборов может быть недостаточно;

− некоторые компоненты вектора X могут не иметь физического смысла.

Однако если система является наблюдаемой, то все компоненты вектора X могут быть восстановлены по наблюдениям вектора Y.

Н
аблюдающее устройство полного порядка представляет собой динамическую систему, которая является моделью объекта:

где X (t) − оценка состояния объекта, Y(t) — оценка выхода.

Если начальное состояние объекта и модели совпадают, и модель адекватна объекту, то можно полагать в любой момент времени, что

Однако практически добиться полной адекватности объекта и модели невозможно, трудно добиться и полного равенства начальных условий. Поэтому на практике можно рассчитывать лишь на выполнение условия

Подобным свойством обладают так называемые асимптотические наблюдающие устройства.

А
симптотическое наблюдающее устройство использует обратную связь по ошибке восстановления вектора состояния, так что работа системы с наблюдающим устройством описывается уравнениями:

где N – матрица параметров наблюдающего устройства.

Рисунок 5. Система с наблюдателем и регулятором.
Н
а рис. 21 показана блок-схема системы с регулятором и наблюдателем.

Решение этого уравнения определяется формулой

Таким образом, если собственные числа матрицы A – NC имеют отрицательную вещественную часть, то с течением времени ошибка состояния уменьшится до нуля. Соответственно, при синтезе наблюдателя нужно выбрать положение корней характеристического уравнения:

Понятно, что процессы в наблюдателе должны протекать более быстро, чем переходный процесс в системе. Эмпирически установлено, что наблюдатель должен обладать быстродействием, в 2 − 4 раза превышающим быстродействие системы.

Моделирование при наличии выходных шумов

Шумы (помехи) на выходе системы обычно связаны с ошибками датчиков, хотя возможны другие причины для их возникновения. При моделировании мы будем использовать псевдослучайные процессы с нормальным распределением и математическим ожиданием равным нулю. Мерой разброса значений случайного процесса является дисперсия. Ее размерность равна квадрату измеряемой величины, что на практике не всегда удобно. Поэтому применяется такая характеристика, как СКО, которая рассчитывается, как корень квадратный из дисперсии.

ЗАДАНИЕ НА РАБОТУ

1) Представить исходную систему в пространстве состояний. Исследовать устойчивость, управляемость и наблюдаемость системы.

2) Спроектировать модальный регулятор и наблюдатель полного порядка. Собрать в Matlab Simulink схему замкнутой системы с регулятором и наблюдателем. Обеспечить выполнение заданных критериев качества в замкнутой системе.

3) Исследовать переходные процессы в замкнутой системе при наличии шумов измерений.

ХОД РАБОТЫ

1. Преобразование модели системы в виде передаточное функции в модель в пространстве состояний.

Передаточная функция (вариант №2):

w=tf([0 17],[1 0.7 0.1 1])% заданная ПФ

w1=ss(w)% переход от ПФ в пространстве состояний

t
itle(‘No controller’);

Рисунок 6. Полученная модель после преобразований

Рисунок 7. Реакция ПФ на единичное ступенчатое воздействие.
П
осле преобразования получили идентичную передаточную функцию, соответственно реакция на единичные ступенчатые воздействия будет одинаковая (рис.7).

Найдем спектр матрицы A:

Некоторые из собственных значений спектра находятся в правой полуплоскости, значит исходная система неустойчива. Убедимся в этом построив переходную характеристику системы.

Cистема неограниченно возрастает, что означает – система неустойчива.

2. Исследование системных свойств управляемости и наблюдаемости системы.

W=ctrb(w1) % матрица управляемости

det(W) % определитель матрицы управляемости

p=[-1 -1 -1]; % Желаемые собственные значения (полюсы)

Проверка системы на управляемость показала, что система полностью управляема . Можно спроектировать модальный регулятор с любым желаемым спектром для замкнутой системы.

Q=obsv(w1) % матрица наблюдаемости

det(Q) % определитель матрицы наблюдаемости

p1=[-1 -1 -1]; % Желаемые собственные значения (полюсы)

Для наблюдающего устройства задали полюса, обеспечивающие большее быстродействие (то есть в два раза большие по модулю). Система наблюдаема, т.к. .

Два варианта модального регулятора, заданные расположением полюсов замкнутой системы с помощью полиномов Ньютона и Баттерворта.

p=[-3 -3 -3]*2 % Желаемые полюсы

w5=ss(w1.a-w1.b*K,w1.b,w1.c,w1.d) %Система с регулятором

km2=1/dcgain(w5) % Маcштабирующий коэффициент

Рисунок 8. Модальный регулятор, с полюсами, заданными с помощью полинома Ньютона.
title(‘Modal controller and km’);

Каждый корень λ должен быть отрицательным, а величина его модуля λ₀ определяется требованиями к быстродействию. Левая часть характеристического уравнения обращается в бином Ньютона (s+λ₀) n, разворачивая который, можно получить стандартные значения коэффициентов характеристического уравнения. При таком подходе обеспечивается апериодичность переходного процесса. Чем больше λ₀, тем меньше время переходного процесса

p=[-7 -2+3i -2-3i] % Желаемые полюсы

w6=ss(w1.a-w1.b*K,w1.b,w1.c,w1.d) %Система с регулятором

km3=1/dcgain(w6) % Маcштабирующий коэффициент

step(km3*w6); grid;

Рисунок 9. Модальный регулятор, расположение полюсов которого задан полиномом Баттервота.

Рисунок 10. Модель системы с модальным регулятором.
М
одель системы с модальным регулятором в MatLabSimulink:

Рисунок 11. Система с модальным регулятором.
Видно, что рисунки 9 и 11 идентичны, что свидетельствует о правильной сборке модели. Результаты получились одинаковыми (процесс перерегулирования в пределах 15%).

Модель системы в MatLab Simulink. Изменение начальных условий объекта управления и скорости наблюдателя.

Начальные условия модели, следующие:

p=[-1 -1 -1] % Желаемые полюсы

p1=[-2 -2 -2] % Желаемые собственные значения (полюсы)

w6=ss(w2.a-w2.b*K,w2.b,w2.c,w2.d) %Система с регулятором

Рисунок 12. Модель системы с регулятором и наблюдателем.
k
m3=1/dcgain(w6) % Маcштабирующий коэффициент

Рисунок 13. Скорость регулятора равна скорости наблюдателя.
С корость наблюдателя в 1 раз больше скорости регулятора:

Рисунок 14. Скорость наблюдателя в 2 раза больше скорости регулятора.
Скорость наблюдателя в 2 раза больше скорости регулятора:

Рисунок 16. Скорость наблюдателя в 4 раза больше скорости регулятора
С
корость наблюдателя в 4 раза больше скорости регулятора:

Сравнивая рисунки 13 и 14, видим, что увеличение скорости наблюдателя привело к уменьшению времени сходимости наблюдателя. Также к уменьшению размаха колебаний выходной координаты и наблюдателя, уменьшилось время регулирования. Для системы рекомендуется устанавливать скорость наблюдателя в 4 и более раз превосходящую скорость регулятора.

Исследование системы при изменении дисперсии шума.

Начальные условия оставим из предыдущего пункта, начнем увеличивать дисперсию фиксируя реакцию системы:

Рисунок 15. Модель системы с регулятором, наблюдателем и блоком помех.

Дисперсия 0.0001:

Шумы создают статические ошибки в установившемся режиме (когда переходный процесс уже закончился). Время моделирования было установлено — 10 секунд, чтобы исследовать поведение системы в установившемся режиме. С увеличением дисперсии выходного шума увеличивается время регулирования.

Дисперсия, при которой график, при регулировании, остаётся в 5%(0.975-1.025) коридоре с небольшим запасом – var=0.0001

ЗАКЛЮЧЕНИЕ

По итогу работы получили следующие сведения:

После преобразование модели системы в виде передаточной функции в модель в пространстве состояний, получили абсолютно идентичные функции с одинаковой реакцией на единичное воздействие.
Исследовав системные свойства управляемости и наблюдаемости системы определили, что система управляема и наблюдаема .
Построили два варианта модального регулятора, заданные расположением полюсов замкнутой системы с помощью полиномов Ньютона и Баттерворта.

При построении с помощью полинома Ньютона мы получили статическую ошибку равную нулю, то есть масштабирующий коэффициент был рассчитан правильно.

источники:

http://msd.com.ua/sovremennye-sistemy-upravleniya/analiz-ustojchivosti-s-pomoshhyu-matlab/

http://topuch.ru/kursovaya-rabota-zashishena-s-ocenkoj-rukovoditele-starshij-pr/index.html